Fundamental Role of Axial Stress in Compensatory Adaptations by Arteries

Abstract

Arteries exhibit a remarkable ability to adapt to diverse genetic defects and sustained alterations in mechanical loading. For example, changes in blood flow induced wall shear stress tend to control arterial caliber and changes in blood pressure induced circumferential wall stress tend to control wall thickness. We submit, however, that the axial component of wall stress plays a similarly fundamental role in controlling arterial geometry, structure, and function, that is, compensatory adaptations. This observation comes from a review of findings reported in the literature and a comparison of four recent studies from our laboratory that quantified changes in the biaxial mechanical properties of mouse carotid arteries in cases of altered cell-matrix interactions, extracellular matrix composition, blood pressure, or axial extension. There is, therefore, a pressing need to include the fundamental role of axial wall stress in conceptual and theoretical models of arterial growth and remodeling and, consequently, there is a need for increased attention to evolving biaxial mechanical properties in cases of altered genetics and mechanical stimuli.

INTRODUCTION

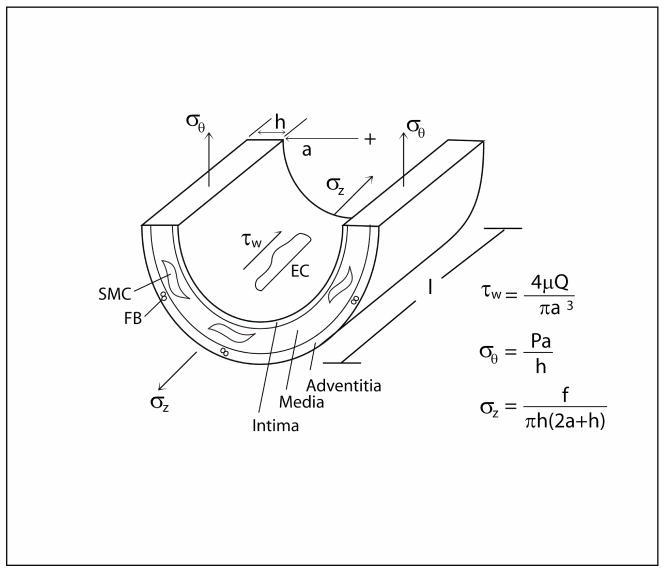
Mechanics has long been recognized as a fundamental contributor to the physiology and pathophysiology of arteries (e.g., Young, 1808; Roy, 1880). Notwithstanding the complexity of the geometry, properties, and applied loads in vivo (Humphrey, 2002), salient features of arterial wall mechanics can be appreciated by considering a generic straight, cylindrical segment (Figure 1). Arteries consist of three layers (intima, media, and adventitia) dominated by three types of cells (endothelial, smooth muscle, and fibroblast, respectively). Each of these types of cells responds to changes in its local mechanical environment (e.g., Chien et al., 1998; Li and Xu, 2007; Grinnell, 2003), thus emphasizing important interactions between the wall mechanics and mechanobiology. Three stresses – flow induced wall shear and intramural circumferential and axial – dominate the mechanical behavior and thereby regulate the three primary geometric variables of importance: luminal radius, wall thickness, and axial length. Nevertheless, most attention in the literature has focused on roles of wall shear stress and circumferential wall stress.

Figure 1.

Schema of the three primary geometric variables (radius a, thickness h, and length l) defining a straight segment of an artery and the associated three primary stresses (wall shear and intramural circumferential and axial) that act on the wall, which consists of three layers (from the inner to outer wall – intima, media, and adventitia, respectively) occupied by three cell types respectively (endothelial – EC, smooth muscle – SMC, and fibroblast – FB).

In this review, we first bring together diverse observations from the literature to emphasize important aspects of axial wall stress. Next, we discuss four illustrative cases of arterial growth and remodeling wherein axial stress plays a fundamental role. Specifically, we consider effects of altered cell-matrix interactions, altered extracellular matrix composition, altered blood pressure, and altered axial extension. The first two cases highlight genetic mutations that elicit developmental changes whereas the second two cases represent adaptive responses to altered loads by otherwise healthy mature arteries. Despite these different types of perturbation from normal, the arterial wall compensates in each case via a reduction in axial stretch, that is, an increase in unloaded length. Understanding the means by which such changes occur requires consideration of the underlying structure of the wall. For example, we highlight the importance of the collagen-to-elastin ratio and the different natural configurations, material properties, and rates of turnover of the key structural constituents. We conclude that axial wall stress is a fundamental contributor to arterial homeostasis and it must be given increased attention both experimentally and theoretically.

BACKGROUND

Hemodynamics plays a fundamental role in controlling arterial geometry, structure, and function, thus it is not surprising that most attention in arterial mechanics has focused on effects of sustained alterations in blood flow or pressure. Among others, Kamiya and Togawa (1980), Langille et al. (1989), Rudic et al. (1998), and Sho et al. (2004) demonstrated that sustained increases in blood flow lead to an increased arterial caliber whereas sustained decreases in flow lead to a decreased caliber. These tissue-level responses are consistent with mechanobiological observations from cell culture (Malek and Izumo, 1992; Uematsu et al., 1995) that increased wall shear stress upregulates endothelial production of nitric oxide (NO; a potent vasodilator) and decreased wall shear stress upregulates endothelial production of endothelin-1 (ET-1; a potent vasoconstrictor). Among others, Wolinsky (1970), Matsumoto and Hayashi (1996), Courtman et al. (1998), and Hu et al. (2007) demonstrated that sustained increases in blood pressure cause significant thickening of the arterial wall whereas sustained decreases in transmural pressure cause thinning of the wall. Again, these tissue-level findings (with thickening resulting from increased matrix deposition and cellularity) are consistent with mechanobiological observations that increased cyclic stretch causes smooth muscle cells to synthesize more collagen (Leung et al., 1976; Li et al., 1998) and to proliferate (Wilson et al., 1993). In summary, the arterial wall appears to grow and remodel in cases of sustained alterations in blood flow and pressure so as to restore wall shear stress and circumferential wall stress toward homeostatic targets (Davies, 1995; Langille, 1996; Humphrey, 2008). It is straightforward clinically to measure blood flow (e.g., via ultrasound or PC-MRI) and blood pressure (e.g., via tonometry or catheter-based transducers), hence there is considerable promise that arterial mechanobiology and biomechanics can and will impact clinical care.

It has been known for more than a century (cf. Fuchs, 1900) that arteries also experience significant axial stretches (and stresses) in vivo, yet it is perhaps because of the lack of a direct method of clinical measurement that there has been less attention to this aspect of the biomechanics. Nevertheless, Patel and Fry (1966) emphasized the importance of “longitudinal tethering of arteries” and Cox (1975) and Dobrin (1986) recognized that unique arterial wall behaviors at the in vivo axial stretch could confer some “hemodynamic benefit.” van Loon et al. (1977) reported a particularly important finding in this regard. Briefly, they showed that plots of axial force-length data collected in vitro at different fixed pressures reveal a unique cross-over point that estimates well the in vivo value of axial stretch (Table 1). In other words, the axial force needed to maintain an artery at its in vivo axial stretch does not change with acute pressurization over normal ranges, which is confirmed via plots of axial force versus pressure in standard in vitro pressure-diameter tests performed at the in vivo stretch. In contrast, the force increases or decreases with acute increases in pressure if the artery is held at an axial stretch above or below its in vivo value, respectively. This discovery was confirmed by Weizsacker et al. (1983) and Brossellet and Vito (1995); it is significant for three reasons. First, it provides a simple in vitro method to estimate in vivo axial stretch, particularly when direct measurements are difficult (e.g., small animals wherein changes in body position affect the measurement). Second, this constancy of axial force (or stress) during cyclic pressurization appears favorable teleologically, supporting the idea that “arteries are adapted [multiaxially] to their function” (van Loon et al., 1977). Third, this finding shows that the inherent microstructure of the artery, not perivascular tethering, confers this beneficial property. Most recently, Stalhand et al. (2005) used, with good success, the constancy of in vivo axial force during the cardiac cycle as a constraint in nonlinear parameter estimations of in vivo wall properties.

Table 1.

Paired values of axial prestretch in canine common carotid arteries measured directly or estimated from the cross-over point in cyclic axial force-length tests at different pressures (from van Loon et al., 1977). Note the much greater specimen-to-specimen variability than differences between methodology.

In-Vivo Stretch (measured)	In-Vivo Stretch (estimated)
1.53	1.51
1.64	1.67
1.63	1.60
1.61	1.67
1.52	1.54
1.65	1.68
1.64	1.61
1.42	1.42
1.51	1.55
1.34	1.32
1.41	1.43
1.54±0.10	1.55±0.11

Lehman et al. (1991) reported a significant lengthening of rabbit cerebral arteries in response to sustained increases in blood flow, which was confirmed in carotid arteries by Sho et al. (2004) and which can result in gross tortuosity. Vaishnav et al. (1990) reported a significant decrease in the in vivo axial stretch (from 1.66 to 1.27) of canine aorta after 6 to 8 weeks of hypertension. More recently, Jackson et al. (2002) showed in vivo that an imposed 22% increase in axial extension of the carotid artery in a rabbit resulted in a rapid normalization of the axial stretch. That is, via an “unprecedented” rate of synthesis of extracellular matrix, the “stretched artery grew into its new length.” This ability of an artery to grow longer when held at a fixed increased axial extension has been confirmed in organ culture (Clerin et al., 2003; Han et al., 2003) and supports the concept that the arterial wall adapts in response to altered multiaxial stimuli to restore all stresses (cf. Figure 1) toward homeostatic values. Although responses are much more complex when axial extension is decreased from normal (Jackson et al., 2005), we see overall that there is considerable evidence that changes in axial length/stretch are important to diverse adaptations.

Recall, therefore, that circumferential and axial wall stresses (σ_θ, σ_z) depend on both the circumferential and the axial stretch (λ_θ, λ_z) as revealed by usual constitutive relations, namely¹

$${\sigma }_{\theta }={\widehat{\sigma }}_{\theta }({\lambda }_{\theta },{\lambda }_z),{\sigma }_z={\widehat{\sigma }}_z({\lambda }_{\theta },{\lambda }_z).$$ (1)

Hence, a decrease in axial stretch could either decrease the axial and the circumferential stresses given an unchanging constitutive behavior or maintain the values of stress despite changing constitutive behaviors if so needed to restore values to homeostatic. Gleason and Humphrey (2005) showed that salient features of arterial adaptations to an imposed axial extension can be modeled mathematically using the same theoretical framework that describes adaptations to sustained increases in flow (Gleason et al., 2004) and pressure (Gleason and Humphrey, 2004). In other words, adaptations by arteries in response to diverse mechanical stimuli appear to occur via similar cell-mediated mechanisms and we should think of such adaptations within a common conceptual and theoretical framework based on all stresses acting on the wall.

FOUR ILLUSTRATIVE CASES

Altered Cell-Matrix Interaction

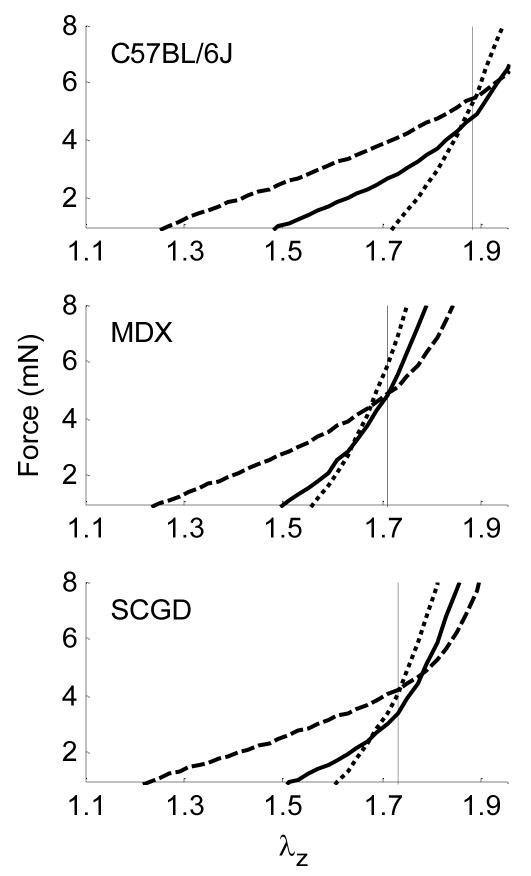
Muscular dystrophy results in skeletal muscle weakness and wasting. It is caused by genetic defects in components of the dystrophin-glycoprotein complex (Cohn and Campbell, 2007). This complex consists of transmembrane proteins that link the actin cytoskeleton to the extracellular matrix in muscle cells, including vascular smooth muscle, and thereby plays a role similar to integrins. In fact, defects in the dystrophin-glycoprotein complex may lead initially to an increased load carrying by integrins, and thus stress concentrations, that may contribute to a local fibrosis that often characterizes muscular dystrophy (Petrof et al., 1993). We studied effects of deficiencies in the dystrophin-glycoprotein complex on the biaxial mechanical properties of common carotid arteries in two mouse models of muscular dystrophy (Dye et al., 2007). One model (mdx) lacked the cytoskeletal protein dystrophin whereas the other model (scgd−/−) lacked the transmembrane protein sarcoglycan-delta. Cyclic pressure-diameter tests were performed at three different axial stretches and cyclic axial force-length tests were performed at three different transmural pressures. Recalling the discovery by van Loon et al. (1977), the axial force-length tests (Figure 2) revealed a significantly lower in vivo basal axial stretch in the two muscular dystrophy models (1.74 and 1.78) than in the wild-type control (1.88). Whereas circumferential stress-stretch responses differed for the three genotypes when studied at a common axial stretch, responses were not statistically different when tested at their individual in vivo axial stretches (Figure 6 in Dye et al., 2007). This finding suggests that, by decreasing their in vivo axial stretch, the carotids in the muscular dystrophy mouse models were able to decrease the overall in-plane biaxial stresses and restore the biaxial mechanical behavior toward normal. Such a compensatory adaptation during development could be beneficial by lowering stresses that act at integrins.

Figure 2.

Averaged axial force-stretch data at fixed pressures of 60 (----), 100 (——), and 160 () mmHg for passive carotid arteries of wild-type control (C57BL/6J), dystrophin-deficient (MDX), and sarcoglycan-delta null (SGCD) mice. Note that cross-over points/intersections estimate the in vivo axial stretch (vertical lines), which were slightly higher for arteries at basal tone. Data replotted from Dye et al. (2007).

Altered Extracellular Matrix Composition

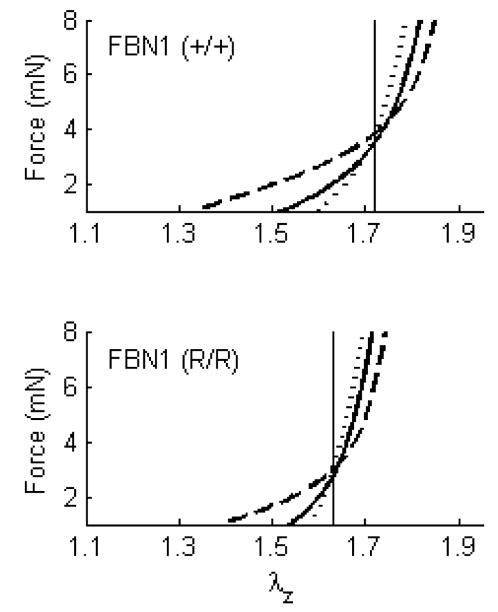
Marfan syndrome is characterized by abnormal bone growth, lens dislocation, and, of particular importance herein, aortic dilation and dissection. This disease results from mutations in the gene encoding the elastin-associated extracellular matrix glycoprotein fibrillin-1 (Pyeritz, 2000). In contrast to early hypotheses, it now appears that fibrillin-1 serves primarily in tissue homeostasis, not elastogenesis (Ramirez and Pereira, 1999; Marque et al., 2001). When fibrillin-1 is absent or diminished, elastin may be more susceptible to both mechanically induced fragmentation, which can accelerate fatigue damage in large arteries, and protease activity. We studied effects of fibrillin-1 deficiency on the biaxial mechanical properties of carotid arteries in a mouse model of Marfan syndrome (Eberth et al., 2008a). Briefly, mice homozygous for the mgR mutation produce normal fibrillin-1, but at levels one-fourth of normal. We subjected carotid arteries from homozygous (mgR/mgR), heterozygous (mgR/+), and wild-type (+/+) control mice to the aforementioned series of cyclic biaxial mechanical tests. The axial force-length tests (Figure 3) revealed a significantly lower in vivo axial stretch in the mgR/mgR mice (1.63) relative to their wild-type controls (1.71) – indeed, this ~5% reduction in axial stretch is similar to the ~7% reduction in carotids from an elastin haploinsufficiency model (Wagenseil et al., 2005). Yet, circumferential stress-stretch responses were similar between the two genotypes when tested at their individual in vivo axial stretches (Figure 5 in Eberth et al., 2008a). It appears, therefore, that the carotids having increased susceptibility to stress-induced intramural damage compensated during development to reduce overall wall stress biaxially, which would seem to be protective and thereby delay fragmentation or degradation of the elastic fibers.

Figure 3.

Averaged axial force-stretch data at fixed pressures of 60 (----), 100 (——), and 140 () mmHg for carotid arteries of wild-type control FBN1 (+/+) and fibrillin-1 deficient FBN1 (mgR/mgR) = (R/R). Note that cross-over points/intersections estimate the in vivo axial stretch (vertical lines). Data replotted from Eberth et al. (2008a).

Altered Hemodynamic Loading

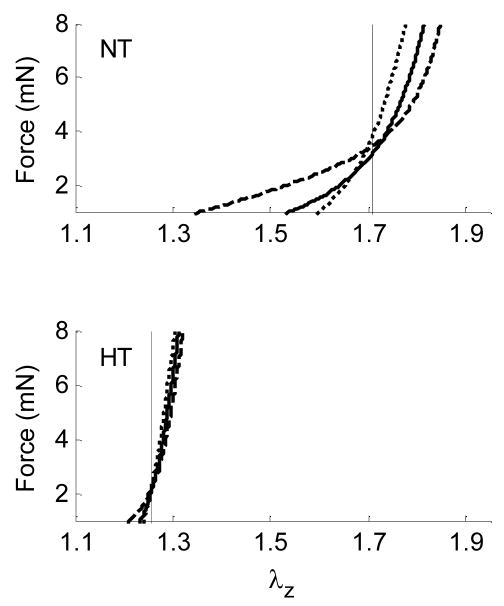
Hypertension is a significant risk factor for many cardiovascular, neurovascular, and renovascular diseases, including heart attacks, stroke, and end-stage kidney failure. Hypertension causes, and is caused by, significant remodeling of both large (conduit) and small (resistance) arteries (Dzau et al., 1994). We used a transverse aortic arch banding model to study the effects of hypertension in the carotid artery of wild-type mice from the fibrillin-1 study (Eberth et al., 2008b); the pulse pressure increased significantly in the right (RCCA-B HT), but not the left (LCCA-B NT), common carotid artery following banding, thus enabling paired tests in each animal. Carotid arteries were excised 5 to 8 weeks after banding and tested biaxially. The axial force-length tests (Figure 4) revealed a significantly lower in vivo axial stretch in the hypertensive right carotid artery (RCCA-B HT=1.27) relative to both the left carotid (LCCA-B NT=1.67) and true controls (CCA WT=1.72). Again, circumferential stress-stretch behavior was similar among the three groups when tested at their individual in vivo axial stretches, thus suggesting an effective compensatory adaptation in maturity. This ~27% reduction in the in vivo axial stretch is similar to the ~24% reduction reported by Vaishnav et al. (1990) in a canine model of hypertension.

Figure 4.

Averaged axial force-stretch data at fixed pressures of 60 (----), 100 (——), and 140 () mmHg for carotid arteries of wild type mice (FBN1+/+) that were nearly normotensive NT or hypertensive HT (i.e., experienced an ~30% increase in pulse pressure for 5 to 8 weeks). Note that cross-over points/intersections estimate the in vivo axial stretch (vertical lines). Data replotted from Eberth et al. (2008b).

Altered Axial Extension

Bypass procedures are used to treat diverse vascular diseases, including coronary artery disease and abdominal aortic aneurysms. Although not usually emphasized, replacing a segment of an artery with a native, synthetic, or tissue engineered graft can easily change the axial stretch of the remaining native vessels. To study acute effects of increased axial extension, we excised carotid arteries from FVB/N mice and maintained them in organ culture for 2 days above, near to, or below their in vivo axial stretch (Gleason et al., 2007). In particular, the axial force needed to maintain the length constant increased with acute pressurization on day 0 when tested at a fixed axial stretch (1.95) that was above the in vivo value (1.87); yet, when maintained in culture for 2 days at the higher than in vivo extension (i.e., 1.95 not 1.87), the vessel remodeled such that the axial force required to maintain that length decreased with culture time and did not vary much with acute pressurization on day 2 (Figure 5). In other words, in just 2 days, these mature arteries appeared to grow into their new length so as to restore biomechanical properties toward normal (cf. Jackson et al., 2002). See the original paper for further results on cultures at and below the in vivo stretch.

Figure 5.

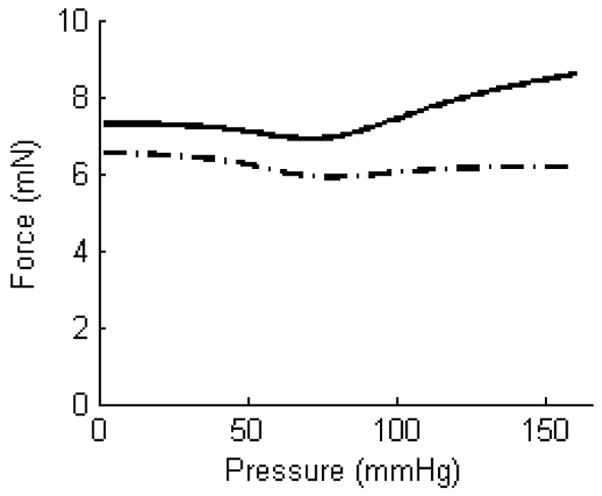
Axial force-pressure data collected during cyclic pressurization tests performed on the same artery at the same axial extension before (——) and after two days of culture (). In particular, the solid curve shows data before culture at an axial extension of 1.95, which was well above the in vivo value of 1.87 (FVB/N mice); the dot-dashed curve shows data at the same extension following two days of culture at that extension. As it can be seen, the vessel tended to exhibit a near constant force after two days suggesting it had adapted to its elevated stretch.

DISCUSSION

Classical thinking in arterial mechanics suggests that blood flow primarily controls luminal radius and blood pressure primarily controls wall thickness. This scenario can be appreciated via expressions for mean stresses (Humphrey, 2002):

$${\tau }_w=\frac{4\mu Q}{\pi a^3},{\sigma }_{\theta }=\frac{Pa}{h},$$ (2)

where μ is the blood viscosity, Q the volumetric flowrate, a the luminal radius, P the pressure, and h the wall thickness. Although there is typically little attention paid to the axial direction, consider a simple thought experiment. If pressure increases (e.g., hypertension), one would expect the deformable wall to distend. This acute increase in radius would not only increase the circumferential stress further, it would also decrease the wall shear stress. The latter would be expected to cause the endothelium to downregulate NO and upregulate ET-1 to induce a mild constriction to return the luminal radius toward normal. Because of the increased pressure, however, the circumferential stress would remain high and the wall would thicken to restore this stress toward normal. Within this context, consider the mean axial stress

$${\sigma }_z=\frac{f}{\pi h(a2+h)},$$ (3)

where f is the applied axial load². Hence, a nearly unchanged luminal radius but increased thickness could reduce the axial stress below its normal value unless the axial force increased appropriately. Recall, however, that experiments reveal a decreased in vivo axial stretch in hypertension (Wolinsky, 1970; Vaishnav et al., 1990; Eberth et al., 2008b). To understand how the net axial force could increase while the associated axial stretch decreases requires consideration of the structure of the wall.

Arteries consist of multiple types of collagen, microfibrils, elastin, diverse proteoglycans, and three primary cell types. Although we seek to understand wall biomechanics in terms of all constituents, Karnik et al. (2003) said it well: “The myriad associations and interactions between the many structural proteins, proteoglycans and growth factors of the vascular matrix makes it difficult to distinguish the effects of each element from another.” It continues to be advantageous, therefore, to focus on the three primary structural constituents – elastin, collagen, and smooth muscle – in both conceptual and mathematical models of the arterial wall.

Vascular elastin is produced and organized primarily during the perinatal period, it is highly elastic, and it is biologically very stable, with a half-life on the order of the lifespan of the organism (Mathieux and Weiss, 2005). Consistent with these characteristics, Davis (1995) suggested that elastin is mature before the aorta reaches 25% of its final diameter, which implies that “elastic laminae stretch as the vessel grows in diameter” (i.e., they are under considerable circumferential tension in maturity). Bendeck et al. (1994) measured changes in carotid artery length during the perinatal period in lambs. They reported a 48% increase in length from 120 days gestation (with full term at ~147 days) to 21 days postpartum, which suggests that the intramural elastin could be under significant axial tension due to development. Indeed, Dobrin et al. (1990) reported that nearly all of the axial prestretch in healthy arteries is due to the presence of intramural elastin, not collagen. Zeller and Skalak (1998) exposed unloaded segments of rat saphenous arteries to elastase or collagenase and similarly suggested “collagen may be under a residual compression” and “elastin under a residual tension.” It appears, therefore, that both the residual stress in and the axial retraction of an artery result in large part from releasing some of the tension in the highly elastic and prestretched elastin upon excision (Cardamone et al., 2009).

Given that collagen and smooth muscle are necessarily compressed by recoiling elastin in “unloaded” excised states, recall that collagen and smooth muscle turnover continually and are likely deposited at preferred stretches (stresses) in vivo (Valentin et al., 2008). Hence, returning to our thought experiment above (cf. equation 3), an increased deposition of stressed collagen in hypertension could increase wall thickness, reduce the axial retraction following transection, and increase the force needed to maintain the axial length – all of which are consistent with salient features of hypertension. Dajnowiec et al. (2007) showed further that the mitotic axis of dividing vascular smooth muscle cells aligns with the direction of applied force. They suggested that “this capacity of force transduction to orient mitosis has the potential to contribute greatly to the preferential wall thickening that accompanies hypertension, the growth of arterial diameter that follows elevation of blood flow rate, and the lengthwise growth of arteries that occurs when adjacent tissues grow or hypertrophy.” We conclude, therefore, that the distinct natural (i.e., stress-free) configurations, material properties, and rates of turnover of individual structurally significant constituents within the wall are fundamental to arterial adaptation, hence one should use materially nonuniform biomechanical models (cf. Humphrey and Rajagopal, 2003; Gleason et al., 2004; Valentin et al., 2008) rather than the more common, materially uniform, phenomenological ones (cf. Fung, 1990; Humphrey, 2002).

The particular importance of elastin and collagen to wall mechanics suggests that it would be interesting to collect together results for arteries from multiple species, each of which have a different collagen-to-elastin ratio (C:E). Table 2 shows that normal increases in C:E correlate well with decreased axial prestretch in diverse carotid arteries, as would be expected based on the aforementioned observations. Indeed, this finding is consistent with data in Eberth et al. (2008b), who reported a C:E of 1.49 in hypertensive carotids (with in vivo stretches of 1.27) but a C:E of 0.57 in contralateral controls (with in vivo stretches of 1.67). Noting that the C:E increases in Marfan syndrome, elastin haploinsufficiency, and aging (due to decreased elastin and possibly increased collagen) as well as in hypertension (due to an increased deposition of collagen), it is not surprising that the associated in vivo axial lengths increase or the in vivo axial stretch decreases (cf. Wolinsky, 1970; Berry and Greenwald, 1976b; Vaishnav et al., 1990; Wagenseil et al., 2005; Eberth 2008). When results are collected for different arteries from the same species (canine), we again find that the largest normal collagen-to-elastin ratio (coronary arteries) associates with the smallest axial prestretch (Table 3). Interestingly, however, values for some of the other canine arteries do not reveal a clear trend, probably because the collagen-to-elastin ratios are similar and the reported prestretches are not statistically different (recall from Table 1 the ±0.1 variations even within a single study on a single type of artery). It would be of interest, therefore, to quantify the C:E in carotids from different strains of mice to determine if this could explain, in part, the observed differences in normal values of in vivo axial stretch (Figure 6); strain-dependent differences in morphological, biomechanical, and functional properties have been reported previously in both mice and rats (Harmon et al., 2000; Behmoaras et al., 2005). The C:E is but simple metric, however, and many other factors certainly play a role, as, for example, altered collagen orientation, cross-linking, and interactions with proteoglycans.

Table 2.

Correlation between the ratio of intramural collagen to elastin (C:E) and the in vivo axial prestretch of common carotid arteries from multiple species. Note, too, that smaller values of C:E correlate with higher values of the mean heart rate (beats per minute), emphasizing the important role of elastin in cyclically distended arteries. Indeed, elastin is absent in arteries within invertebrates or primitive vertebrates having low pulse pressures, presumably because elastic fibers enable large arteries to “damp out the pulsatile flow and blood pressure” (Faury, 2001) and they confer arteries with the “properties of elastic recoil and resilience” (Mathieux and Weiss, 2005). Data from Cox (1975), van Loon et al. (1977), Weizsacker et al. (1983), Lacolley et al. (2001), Jackson et al. (2002), and Gleason et al. (2007). Collagen and elastin contents are not listed for the human data because age was not specified for the in vivo stretch data.

Carotid Artery (Species)	Heart Rate	Collagen (%)	Elastin (%)	C:E (ratio)	In Vivo Stretch
Mouse	600	23.8	28.5	0.84	1.84
Rat	270	39.7	35.5	1.12	1.70
Rabbit	230	43.1	21.6	2.00	1.62
Dog	90	52.3	24.8	2.11	1.53
Human	60	-	-	-	1.20

Table 3.

Additional relations between the ratio of intramural collagen to elastin (C:E) and in vivo axial prestretch for different types of arteries from one species (canine). Data are from Patel and Fry (1966), Cox (1975), van Loon et al., (1977), and Dobrin (1997). Note, however, that considerable variation exists in reports on percent collagen and elastin, as, for example, values for the coronary artery range from 47.9 to 55.8% collagen and from 15.6 to 20.4% elastin. Moreover, as revealed by Table 1, there exist significant variations in axial prestretch (±0.1) even for one type of artery studied within a single lab.

Canine Artery (type)	Collagen (%)	Elastin (%)	C:E (ratio)	In Vivo Stretch
Abdominal Aorta	45.5	30.1	1.51	1.46
Iliac	43.2	28.7	1.51	1.45
Femoral	44.5	24.5	1.82	1.48
Renal	45.0	23.9	1.88	1.54
Carotid	50.1	24.6	2.04	1.55
Coronary	54.0	19.2	2.81	1.39

Figure 6.

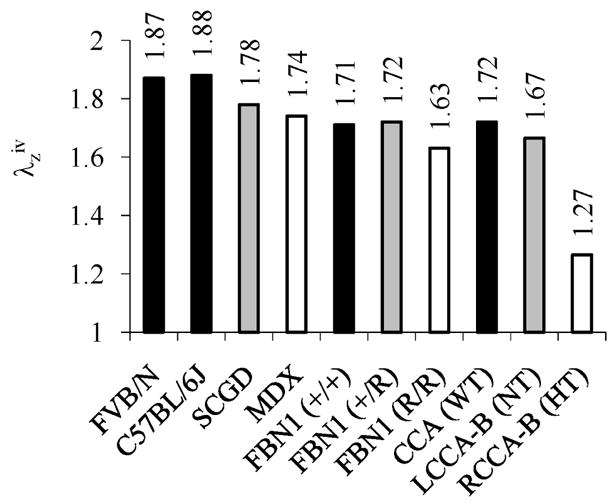
Summary of in vivo axial stretches ( ${\lambda }_z^{iv}$) for mouse carotid arteries tested in our laboratory. Controls for each experiment are in black. Findings are consistent with reports by Harmon et al. (2000) that marked variations exist in structure and function among carotid arteries from different strains of mice.

In conclusion, alterations in axial stretch during maturity appear to be controlled primarily by a local deposition or removal of extracellular matrix and cells (Dajnowiec et al., 2007). If an artery has more control over local axial force than it does over local blood flow and pressure (which are controlled by cardiac output and distal resistances), it may exploit this capability in compensatory responses. Indeed, in the four very different illustrative cases examined herein – altered cell-matrix interactions in muscular dystrophy, altered matrix composition in fibrillin-1 deficiency, altered pulse pressure in transverse aortic arch banding, and altered axial extension in organ culture – it appears that the mouse common carotid arteries used marked changes in axial stretch to return the overall state of stress toward a homeostatic target. We submit, therefore, that axial stretch and stress play important roles in arterial biomechanics and mechanobiology; the tension built into intramural elastin during development, which can be relieved in part by an increased deposition of collagen, a proliferation or hypertrophy of smooth muscle, or an increased fragmentation or degradation of elastin, appears to be fundamental in this regard. Given the explosion of interest in mathematically modeling arterial growth and remodeling (e.g., Rachev, 2000; Taber and Humphrey, 2001; Humphrey and Rajagopal, 2003; Gleason et al., 2004; Hariton et al., 2007; Kuhl et al., 2007; Driessen et al., 2008; Alford et al., 2008; Valentin et al., 2008), there is a pressing need to include the fundamental role of axial wall stress in addition to the well accepted roles of wall shear stress and circumferential wall stress. Because of the difficulty of inferring axial quantities from in vivo data, mathematical modeling will continue to be particularly important (cf. Stalhand et al., 2005). Such modeling depends, however, on robust experimental data on the mechanobiology and the biomechanics, including detailed information on evolving biaxial mechanical properties of the arterial wall and contributions of individual constituents, which demands the use of materially nonuniform constitutive relations and consideration of the different layers constituting the wall. Although understanding better the fundamental role of axial stress promises increased insight into both physiology and pathophysiology, it is important to emphasize that stress-mediated growth and remodeling can be ineffective in extreme situations. For example, compensatory adaptations to some genetic defects may be largely effective during development under normal hemodynamics, yet the adaptive capacity will probably be compromised in extreme exercise or hypertension. Maladaptations could put the person at increased risk to vascular disease, which will be important to appreciate as we seek to design improved clinical interventions and medical devices.