Abstract
We have developed a computer-aided detection (CAD) system to detect clustered microcalcification automatically on full-field digital mammograms (FFDMs) and a CAD system for screen-film mammograms (SFMs). The two systems used the same computer vision algorithms but their false positive (FP) classifiers were trained separately with sample images of each modality. In this study, we compared the performance of the CAD systems for detection of clustered microcalcifications on pairs of FFDM and SFM obtained from the same patient. For case-based performance evaluation, the FFDM CAD system achieved detection sensitivities of 70%, 80%, and 90% at an average FP cluster rate of 0.07, 0.16, and 0.63 per image, compared with an average FP cluster rate of 0.15, 0.38, and 2.02 per image for the SFM CAD system. The difference was statistically significant with the alternative free-response receiver operating characteristic (AFROC) analysis. When evaluated on data sets negative for microcalcification clusters, the average FP cluster rates of the FFDM CAD system were 0.04, 0.11, and 0.33 per image at detection sensitivity level of 70%, 80%, and 90%, compared with an average FP cluster rate of 0.08, 0.14, and 0.50 per image for the SFM CAD system. When evaluated for malignant cases only, the difference of the performance of the two CAD systems was not statistically significant with AFROC analysis.
1. Introduction
Mammography is the most effective and low-cost method to date for the early detection of breast cancers. The use of screen-film mammography (SFM) has resulted in an increase survival rate of women with breast cancer. However, it has been reported that a substantial fraction of breast cancers which are visible upon retrospective analyses of the SFMs are not detected initially (Beam et al., 1996; Harvey et al., 1993). New research efforts in digital detector technology and computer-aided detection (CAD) techniques are improving the performance of mammography to higher levels. In the last few years, several full-field digital mammography (FFDM) manufacturers have obtained approval from the Food and Drug Administration (FDA) of the United States (U. S.) for clinical use. It is important to know the relative accuracy of FFDM and SFM in the screening setting. Several clinical trials have been conducted to compare the performance of FFDM with that of SFM in populations of women presenting for screening or diagnostic mammography. In the prospective clinical trial (Lewin et al., 2001; Lewin et al., 2002) in an asymptomatic population, GE Senographe 2000D systems were used and 6736 paired SFM and FFDM examinations were performed on 4489 patients. It was found that FFDM resulted in significantly fewer recalls than did SFM, however, the difference in detection rate of the 42 cancers and the area under the receiver operating characteristic (ROC) curve ( Az ) for the two modalities were not statistically significant. In the Norwegian studies (also called Oslo I and Oslo II) (Skaane et al., 2003; Skaane and Skjennald, 2004; Skaane et al., 2005a) with GE Senographe 2000D systems, it was also found that there was no statistically significant difference in cancer detection rate between FFDM and SFM for screening populations. The Digital Mammographic Screening Trial (DMIST) was conducted by the American College of Radiology Imaging Network to compare primarily the accuracy of FFDM and SFM in asymptomatic women screening for breast cancer. This large study enrolled 49,528 women from 35 U.S. and Canadian sites, in which all available (five) types of digital mammography machines were used (Pisano et al., 2005). They reported a similar overall diagnostic accuracy of FFDM and SFM. However, the performance of FFDM was significantly better than that of SFM for women under the age of 50 years, women with radiographically dense breasts, and premenopausal or perimenopausal women.
The use of a CAD system as an objective ‘second reader’ is considered to be one of the promising approaches that may help radiologists improve the sensitivity of mammography. The majority of studies to date have shown that CAD can improve radiologists’ detection accuracy without substantially increasing the recall rates (Chan et al., 1990; Warren Burhenne et al., 2000; Freer and Ulissey, 2001; Brem et al., 2003; Destounis et al., 2004; Helvie et al., 2004). This improvement is not simply a shifting of the operating point because being “more conservative” does not address the radiologists’ observational oversights (Birdwell and Ikeda, 2006). Since breast imaging specialists detect more cancers and more early-stage cancers, and have lower recall rates than general radiologists (Burnside et al., 2002), the value of CAD may vary among readers (Gur et al., 2004; Feig et al., 2004). A number of CAD algorithms have been developed for SFMs and FFDMs. For CAD, FFDMs may provide the advantages of having higher signal-to-noise ratio (SNR) and detective quantum efficiency (DQE), wider dynamic range, and higher contrast sensitivity than SFMs. Commercial CAD systems have been adapted to be used with FFDMs (O’Shaughnessy et al., 2001; Skaane et al., 2005b).
The difference in performance of human readers for cancer detection on FFDMs and that on SFMs has been investigated in previous studies (Lewin et al., 2001; Lewin et al., 2002; Skaane et al., 2003; Skaane and Skjennald, 2004; Skaane et al., 2005a; Skaane et al., 2005b; Cole et al., 2004; Pisano et al., 2005). Since the detection of cancers with a computerized program can also be affected by the image properties of the mammograms from different modalities, it is important to compare the performance between the CAD systems for FFDMs and for SFMs. The presence of clustered microcalcifications (MCs) is an important indication of breast cancer (Kopans, 1997). The purpose of the current study was to compare the performance of CAD systems for detection of microcalcification clusters (MCCs) on pairs of FFDM and SFM obtained from the same patient. We have previously developed a CAD system for the detection of MCCs on digitized SFMs (Gurcan et al., 2002; Chan et al., 1987; Chan et al., 1995). To adapt the CAD system to FFDMs, we incorporated a preprocessing step to convert the FFDM raw images to an image of which the pixel values are inversely proportional to the logarithm of x-ray intensity, and the system parameters were retrained at stages that are sensitive to image noise (Ge et al., 2006).
2. Materials and method
2.1. Data Sets
Institutional Review Board (IRB) approval and informed consent were obtained to collect the paired FFDM and SFM data sets in the Department of Radiology at the University of Michigan. Each data set contained 96 cases with 192 images. All cases had two mammographic views: the craniocaudal (CC) view and the mediolateral oblique (MLO) view or the lateral (LM or ML) view. For the majority of the cases (90 cases), the time interval between the examination with SFM and that with FFDM for the same patient was less than 3 months. The FFDM data set in this study was acquired with a GE Senographe 2000D FFDM system. The GE system has a CsI phosphor/a:Si active matrix flat panel digital detector with a pixel size of 100μm × 100μm and the raw images were digitized to 14 bits per pixel. The SFM data set was acquired with GE DMR mammography systems. The SFMs were digitized using a LUMISCAN 85 laser scanner with an OD range of 0-4.0. The digitizer was calibrated so that the gray values were linearly and inversely proportional to the OD, with a slope of -0.001 OD unit/pixel value. The SFM data set was digitized at a pixel size of 50μm × 50μm with 12-bit gray levels. The image matrix size was reduced by averaging every 2 × 2 adjacent pixels and down-sampling by a factor of 2, resulting in images with the same pixel size as that of FFDM images.
Each mammogram was assessed by a Mammography Quality Standards Act (MQSA) radiologist and a polygon was drawn to enclose each MCC. The radiologist marked the clusters on an image as c0, c1, c2, based on the degree of concern. In this study, we concentrated on the detection rather than the classification of the malignant/benign nature of the MCCs so that both malignant and benign MCCs were considered to be positive cases. There were 96 different c0 clusters in the data set, one for each case, of which 28 were proven by biopsy to be malignant and 68 were proven to be benign. The 192 c0 marks in the FFDM data set matched those in the SFM data set. There were a total of eight c1 and one c2 marks that were not biopsied or followed up and they were not counted as true positive (TP) or false positive (FP) clusters in the evaluation. The same radiologist gave a rating for the subtlety of the MCCs on a scale of 1 (most obvious) to 10 (most subtle) relative to the visibility range of MCCs encountered in clinical practice. The distributions of the subtlety ratings for SFM and FFDM data sets are shown in figure 1(a). The likelihood of malignancy (LM) ratings were also provided on a scale of 0 (least likely to be malignant) to 10 (most likely to be malignant). Figure 1(b) shows the distributions of the likelihood of malignancy ratings for SFM and FFDM data sets. The distributions of the sizes for the c0 clusters, estimated by the radiologist as its longest dimension of the bounding polygon, in both data sets are shown in figure 1(c). The differences in the subtlety ratings, LM ratings, and cluster sizes between the MCCs in the SFM and FFDM data sets were not statistically significant (two-tailed paired t-test p>0.05). The coordinates of individual MCs in the FFDM images were manually identified by marking the locations of individual MCs with a cursor when the GE-processed FFDM image was displayed on a workstation at full resolution. The individual MCs were used for training of a convolution neural network (CNN) classifier for FP reduction, as described below. For the SFMs, we had already prepared an independent data set with manually identified MCs for training the CNN in a previous study. Since the MCs from the previous data set were also random samples from the patient population and they should be statistically similar to those of the current data set, we did not need to identify the individual MCs in this data set for CNN training.
Figure 1.
(a) The distribution of the subtlety rating of the MCCs (1: most obvious, 10: most subtle). (b) The distribution of the likelihood of malignancy rating of the MCCs (0: least likely to be malignant, 10: most likely to be malignant). (c) The distribution of the longest dimension of the MCCs.
The data set of 192 images (SFM or FFDM) was separated into two independent, equal-sized subsets with the malignant cases equally distributed to the two subsets. Each subset contained 48 cases with 96 images, of which 14 cases were malignant (figure 2). The subset groupings for the SFMs and FFDMs contain the same cases to facilitate the comparison of test results of the subsets of the two modalities. Two-fold cross-validation was chosen for the training and testing of our CAD systems. In one cross-validation cycle, one subset was used for training the CAD system parameters and classifiers. The training subset was further partitioned into a training set and a validation set for training the CNN (for FFDMs) and the linear discriminant analysis (LDA) classifiers (for both FFDMs and SFMs), as described below. After the CAD system was trained, its parameters and classifiers would be fixed and its performance evaluated on the independent subset. The training and test subsets were then switched and the process was repeated. The overall detection performance was evaluated by combining the performances for the two test subsets.
Figure 2.
The data subsets for the design of our FFDM and SFM CAD systems. The data set was separated into two independent subsets in a cross-validation training and testing scheme. When a given subset is used for training of the CAD system, the samples were further separated into a training set and a validation set for training the CNN classifier or the LDA classifier. The trained CAD system was then applied to the other subset for evaluation of its test performance.
Another FFDM data set of 108 cases with 216 images and another SFM data set of 71 cases with 142 images were collected. These two data sets are independent of each other. These mammograms were verified to be negative for MCCs although they may contain other soft tissue abnormalities based on review by experienced breast radiologists. These data sets were used to evaluate the FP cluster detection rate on “normal” mammograms by our CAD systems.
2.2. Methods
The FFDM CAD system and the SFM CAD system used similar computer vision techniques for detecting MCCs. The CAD system includes six stages: (1) preprocessing, (2) image enhancement, (3) segmentation of individual MC candidates, (4) FP reduction for individual MCs using rule-based classifiers and a CNN classifier, (5) regional clustering of MCs, and (6) FP reduction for MCCs using stepwise LDA feature selection and classification. The block diagram of our CAD system is shown in figure 3. The system parameters for steps (1) to (5) were designed for the SFM CAD system in our previous study (Chan et al., 1987; Chan et al., 1995; Gurcan et al., 2002). In this study, we used the same system parameters at the image enhancement stage (step 2), individual MC segmentation stage (step 3) and regional clustering stage (step 5) for both the SFM and FFDM CAD systems.
Figure 3.
The block diagram of our CAD systems for detection of microcalcification clusters on FFDMs and SFMs.
For the SFM CAD system, the preprocessing stage (step 1) and FP reduction stage (step 4) were the same as before. An LDA classifier was added as step (6) because we found that this additional step was useful for FP reduction in the course of designing the FFDM CAD system. For the FFDM CAD system, we implemented a preprocessing step for the input raw images (step 1), and retrained the global thresholding and the CNN classifier (step 4) in addition to the new LDA classifier (step 6) because of the different SNR properties of the FFDM.
We will describe the major steps of the CAD systems for the SFM and FFDM collectively and pointed out the differences whenever applicable. Details of the design process for each stage can be found in the literature (Chan et al., 1987; Chan et al., 1995; Ge et al., 2006; Gurcan et al., 2002).
2.2.1. Preprocessing and Image Enhancement
For the SFM CAD system, the digitized images were used as the input. For the FFDM CAD system, the raw images were used as the input and an inverted logarithmic transformation (Burgess, 2004) was applied to the raw pixel values. The digitized SFM image or the transformed FFDM image is first subjected to an automated breast boundary segmentation algorithm. Further steps are only applied to the segmented breast area to reduce computation time. A difference-image technique using an 8×8 box-rim filter was used to enhance the SNR of the MCs for both the FFDM and SFM CAD systems.
2.2.2. Segmentation and FP Reduction of Individual MCs
A global thresholding procedure was then used to segment the individual MC candidates (signals) from the difference image. The procedure automatically searched for the gray level threshold applied to the entire breast area such that the number of signal candidates in the entire breast area is within a predefined range of 400 to 500. The signal candidates are refined using an adaptive gray level thresholding method in which the pixels within a signal are segmented based on their connectivity and the local SNR (Chan et al., 1987).
In the FP reduction stage, the signals are classified as either positive or negative using a combination of rule-based feature classification and a trained CNN classifier. Two features, namely, the area and the contrast of the signal, are first used to exclude small-area (less than 3 pixels) signals that are likely to be noise and high-contrast (10 times higher than the background root-mean-square noise) signals that are likely to be artifacts or large benign calcifications. A CNN classifier is trained independently for the FFDM and the SFM CAD systems to further differentiate true MCs and FP signals. The optimal architecture of CNN was selected in our previous study (Gurcan et al., 2002). The CNN for the SFM CAD system was trained (Gurcan et al., 2002) using a different data set (with 547 true MCs and 540 FPs for training, and 533 true MCs and 553 FPs for validation) from the SFM data set used in the current study so that the trained CNN could be applied to either image subsets (figure 2) for independent testing. For the FFDM CAD system, we used the manually identified MCs and the FP signals, which were signals that did not coincide with the manually identified MC locations, detected by the CAD system on the training subset to train the CNN classifier. There were 535 and 669 true MCs in subset 1 and subset 2, respectively. Equal number of FPs was randomly sampled from the detected candidates when the subset was used as a training set. When a given subset of the available data set was used for training the CAD system, the cases in the subset were further separated into a training set and a validation set (figure 2). Each of the training or validation set within a training subset thus contained over 250 true MCs and 250 FPs. The validation set was used to monitor the performance of the trained CNN and stop the training process. The other subset was reserved for independent testing. The training of the CNN was discussed in detail elsewhere (Ge et al., 2006). For both the SFM and FFDM CAD systems, the CNN classifier threshold was empirically chosen by training as 0.4 to remove signals with low CNN scores. As described in next subsection, the CNN scores were also used to generate features which were combined with morphological features for FP reduction.
2.2.3. Regional Clustering and FP Reduction for MCCs
Potential clusters are identified by a regional clustering procedure (Chan et al., 1995; Chan et al., 1994) based on the fact that true MCs of clinical interest always appear in clusters on mammograms. A cluster was dynamically grown until no more potential signals in the neighborhood were within 0.5 cm of its centroid. A cluster is considered to be positive if the number of its members is greater than 3. The clustering process continues until no more clusters can be grown in the breast region. The remaining signals which are not found to be members of any potential clusters are considered as isolated noise objects and excluded.
In order to differentiate true MCCs from clusters of normal noisy structures, we extracted features (Chan et al., 1998; Ge et al., 2006) from each of the clusters found at the stage of regional clustering and built an LDA classifier. A total of 25 features (21 morphological features, 4 CNN features) were extracted for each of the clusters. These include the number of MCs in a cluster, the maximum, the average, the standard deviation, and the coefficient of variation for each of the five morphological features (size, mean density, eccentricity, moment ratio, and axis ratio (Chan et al., 1998)) of the individual MCs in the cluster, the minimum, the maximum, and the mean of the CNN output values in the cluster, and the average of the first three highest CNN output values of the MCs. Detailed description of these features can be found in the literature (Chan et al., 1998; Ge et al., 2006).
Feature selection with stepwise LDA was applied to obtain the best feature subset and reduce the dimensionality of the feature space to design an effective classifier. At each step one feature was entered or removed from the feature pool by analyzing its effect on the selection criterion, which was chosen to be the Wilks’ lambda in this study. Stepwise feature selection involves the selection of three thresholds, namely, Fin, Fout, and tolerance. We used a two-fold cross-validation method (figure 2) such that the test subset was not involved in feature selection. The training set and the Az value for the validation set were used to determine the best values of these thresholds that could provide high classification accuracy with a relatively small number of features. The chosen set of thresholds was then used to select a final set of features and LDA coefficients using the entire training subset. The training of the LDA classifiers for FFDM and SFM CAD systems was performed independently but the same subset groupings of the cases as shown in figure 2 were used for both processes.
2.2.4. Evaluation Methods
The scoring method of computerized detection of MCCs used in this study has been described in detail in our previous study for SFMs (Gurcan et al., 2002). Briefly, there are two sets of inputs to the automatic scoring program. The first consists of the overlay files, in which the extent of each MCC is drawn by an expert radiologist as a polygon. The second consists of outputs of the automated MCC detection program, which are the smallest rectangular bounding boxes enclosing the detected MCCs. The scoring program automatically calculates the intersection of the areas enclosed by these rectangles and the polygons. If the ratio of the intersection area to either the rectangle or the polygon area is more than 40%, as determined in the previous study (Gurcan et al., 2002), then the cluster enclosed by the polygon is considered to be detected. If a polygon area intersects with more than one rectangular region, only one TP finding is recorded.
FROC analysis was used to evaluate the overall detection performance of the CAD system. FROC curves were presented on a per-cluster and a per-case basis. For cluster-based FROC analysis, the MCC on each mammogram was considered an independent true object; the sensitivity was thus calculated relative to 96 clusters in each of the two test subsets. For case-based FROC analysis, the same MCC imaged on the two-view mammograms was considered to be one true object and detection of either or both clusters on the two views was considered to be one TP detection; the sensitivity was thus calculated relative to 48 clusters in each of the two test subsets. We also used the data set negative for MCCs to estimate the FP cluster detection rate on normal mammograms. For each modality, we applied the two trained CAD systems obtained in the two-fold cross-validation scheme separately to the negative data set. For a given trained CAD system, the average FP rate was determined by counting the detected clusters on the negative mammograms while the detection sensitivity was determined by counting the TPs on the test subset. A test FROC curve was then derived by combining the sensitivity from the test subset and the average FP rate from the negative data set at the corresponding detection thresholds. After the test FROC curve was estimated separately for each of the two trained CAD systems, an overall FROC curve was derived by averaging the FP rates at the corresponding sensitivities along the two test FROC curves. The overall FROC curve represented the average test performance of our CAD system for MCC detection for the given modality.
For estimation of the statistical significance in the differences between the FROC curves of the two modalities, we used the alternative free-response ROC (AFROC) analysis42 proposed by Chakraborty et al. In the AFROC method, FROC data are first transformed to AFROC data which tracks the tradeoff between sensitivity and the number of FP images, defined as an image with one or more FP responses (Chakraborty, 1989), instead of the number of FP responses per image. The ROCKIT software and statistical significance tests for ROC analysis developed by Metz et al (Metz et al., 1998) can then be used to analyze the AFROC data. The area under the fitted AFROC curve, A1, is used to evaluate the detection performance.
3. Results
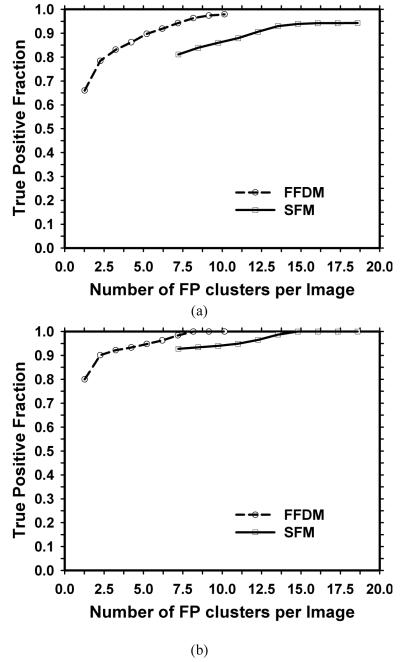
We first evaluated the performance of the system by comparing the test FROC curves without the FP cluster reduction stages. The FROC curves were generated by varying the local SNR threshold k in the range of 1.9 to 3.7. Figure 4 compares the average test FROC curves for FFDM and SFM. Figure 4(a) shows that a cluster-based sensitivity of 94% can be achieved at about 8 FP clusters/image for the FFDM CAD system, and about 15 FP clusters/image for the SFM CAD system. At these FP cluster rates, both CAD systems detected the cluster on at least one view for all the cases (100% case-based sensitivity) as shown in figure 4(b). Some high-contrast image structures other than MCs are also segmented as MC candidates at the global and local thresholding stages. The two rule-based features used in the CAD systems, the area and the contrast of the MC candidate, can exclude small or bright areas due to noise and high-contrast artifacts but are not very discriminatory against FP signals that are more similar to MCs. The digitized images are noisy and have more artifacts than FFDMs because of screen-film artifacts and the additional digitization process. This may be the reason that the average FP cluster rate for the SFM CAD system is higher than that for the FFDM CAD system. Figure 5 shows typical examples of ROIs containing a MC candidate with CNN score less than 0.4 for the SFM CAD system.
Figure 4.
The average test FROC curves from the FFDM CAD system and the SFM CAD system without the FP cluster reduction stages. The FROC curves were obtained by varying the local SNR thresholds and the FP cluster rates were estimated from the test subsets with MCCs. (a) Cluster-based FROC curves, and (b) case-based FROC curves.
Figure 5.

Typical examples of ROIs containing a MC candidate with CNN score less than 0.4 from one of the test subsets for the SFM CAD system. First row: CNN scores in the range of 0.0 and 0.1; Second row: CNN scores in the range of 0.1 and 0.2; Third row: CNN scores in the range of 0.2 and 0.3; Fourth row: CNN scores in the range of 0.3 and 0.4. The size of each ROI is 16× 16 pixels (1.6 × 1.6mm2).
The fitted ROC curves for classification of the detected signals as MCs and FP signals using the trained CNN classifiers for the FFDM and SFM CAD systems are shown in figure 6. The Az value for the CNN classifier trained for FFDM was 0.96 for both validation sets in the training subsets (see figure 2), compared with Az values of 0.91 for the SFM validation set. The lower discriminatory power of the CNN for SFMs may also be attributed to the higher noise on SFMs. For the FFDM CAD system, the rule-based classifiers and the CNN classifier reduced the FP cluster rates substantially with a small loss of sensitivities, as shown in table 1. At the same FP cluster rates, the sensitivity of the SFM CAD system is lower than that of the FFDM CAD system. The average test FROC curves for the FFDM and SFM CAD systems with FP reduction including the rule-based classification and the CNN and LDA classifiers are shown in figure 7. The FP cluster rates were estimated from the test subsets with MCCs. At an FP cluster rate of 1.0 per image, the detection rates are shown in table 2. Fifteen more clusters were detected by the FFDM CAD system. The difference in the detection rates on FFDMs and SFMs was statistically significant with McNemar chi-square test (p<0.05). The FP cluster rates at detection sensitivities of 70%, 80%, and 90% are also summarized in table 3(a). The cluster-based and case-based test FROC curves for the FFDM CAD system are about 5% to 10% higher in sensitivity than the corresponding curves for the SFM CAD system at the same FP cluster rates. We applied the AFROC analysis for testing the significance of the difference between the cluster-based test FROC curves for the two modalities. The results are summarized in table 4(a). The A1 value was 0.81±0.02 and 0.83±0.02, respectively, for test subset 1 and 2 for the FFDM CAD system, and 0.73±0.02 and 0.74±0.02, respectively, for the SFM CAD system. The difference between the fitted AFROC curves for the two CAD systems was statistically significant (p<0.05) for both test subsets.
Figure 6.
Fitted ROC curves for classification of detected signals as microcalcifications and FPs using a CNN classifier for FFDM CAD system ( Az = 0.96 for both validation subsets), and SFM CAD system ( Az = 0.91 for the validation set). Note that the CNN for the SFM CAD system was trained with a different data set.
Table 1.
Comparison of the test performance of CAD systems with and without the rule-based classifier and the CNN classifier at the stage of FP reduction for individual MCs. The local SNR threshold level was set to be 2.4 and the CNN threshold level was 0.4 for both CAD systems
| Sensitivity | FPs/image | ||||
|---|---|---|---|---|---|
| Set 1 | Set 2 | Set 1 | Set 2 | ||
| FFDM | without FP MC reduction | 97.9% | 96.9% | 8.45 | 9.01 |
| with FP MC reduction | 93.8% | 93.8% | 3.38 | 3.45 | |
| SFM | without FP MC reduction | 96.9% | 93.8% | 18.23 | 15.12 |
| with FP MC reduction | 87.5% | 85.6% | 3.73 | 3.98 | |
Figure 7.
The average test FROC curves from the FFDM CAD system and the SFM CAD system with the FP cluster reduction stages. The FROC curves were obtained by varying the LDA thresholds and the FP cluster rates were estimated from the test subsets with MCCs. (a) Cluster-based FROC curves, and (b) case-based FROC curves.
Table 2.
Analysis with 2 × 2 table of the number of detected MCCs in the test subsets for the FFDM and the SFM CAD systems with the FP reduction stages. The detection rates were evaluated at an FP cluster rate of 1.0 per image. Fifteen more clusters were detected by FFDM CAD system. The difference of detection rates was statistically significant (p<0.05) by the McNemar test
| SFM |
Total | |||
|---|---|---|---|---|
| TPs | FNs | |||
| FFDM | TPs | 146 | 20 | 166 |
| FNs | 5 | 21 | 26 | |
| Total | 151 | 41 | 192 | |
Table 3.
Comparison of the test performance of the FFDM and SFM CAD systems with the CNN and LDA classifiers at different detection sensitivities. (a) The FP cluster rates were estimated from the test subsets with MCCs. (b) The FP cluster rates were estimated from the test sets without MCCs
| (a) | (b) | ||||||
|---|---|---|---|---|---|---|---|
| Sensitivity | 70% | 80% | 90% | 70% | 80% | 90% | |
| Cluster-based | FFDM | 0.21 | 0.61 | 1.50 | 0.15 | 0.31 | 0.81 |
| SFM | 0.38 | 1.21 | -- | 0.16 | 0.38 | -- | |
| Case-based | FFDM | 0.07 | 0.16 | 0.63 | 0.04 | 0.11 | 0.33 |
| SFM | 0.15 | 0.38 | 2.02 | 0.08 | 0.14 | 0.50 | |
Table 4.
Estimation of the statistical significance in the difference between the FROC performance of the FFDM CAD system and that of the SFM CAD system (a) for both benign and malignant cases, and (b) for malignant cases only, in the test subsets. The cluster-based test FROC curves with the FP cluster rates obtained from the test set with MCCs were compared
| A1 (AFROC) | ||||
|---|---|---|---|---|
| (a) All cases | (b) Malignant cases | |||
| Test subset 1 | Test subset 2 | Test subset 1 | Test subset 2 | |
| FFDM CAD system | 0.81±0.02 | 0.83±0.02 | 0.91±0.04 | 0.87±0.05 |
| SFM CAD system | 0.73±0.02 | 0.74±0.02 | 0.81±0.06 | 0.88±0.05 |
| p-value | 0.003 | 0.004 | 0.070 | 0.431 |
We also used the data set without MCCs to evaluate the FP cluster detection rate on normal cases. The average cluster-based and case-based test FROC curves are compared in figure 8. These FP cluster rates evaluated on normal data sets are also summarized in table 3(b). Although the performance of FFDM CAD system was still better than that of SFM CAD system, the difference was smaller when the FP cluster rates were evaluated on the normal data sets. We compared the performance of the classifiers in FP reduction. Table 5 summarizes the FP rates and FP reduction percentages of FFDM and SFM CAD systems when the FP cluster rates were evaluated on the normal data sets and the MCC data sets at two different sensitivity levels. The FP reduction percentages of the classifiers of the FFDM CAD system were slightly better in the normal data set than in the MCC data set, despite the fact that the normal data set was an independent test set for the FFDM classifiers. The FP reduction percentage for the FFDM CAD system was, on average, slightly higher than that for the SFM CAD system when the FP cluster rates were evaluated on the normal data sets or the MCC data sets, consistent with the better performance of the CNN classifier of the FFDM system shown in figure 6.
Figure 8.
The average test FROC curves from the FFDM CAD system and the SFM CAD system with the FP cluster reduction stages. The FROC curves were obtained by varying the LDA thresholds and the FP cluster rates were estimated from the test sets without MCCs. (a) Cluster-based FROC curves, (b) Case-based FROC curves.
Table 5.
Comparison of FP cluster rates and FP reduction percentages of FFDM and SFM CAD systems estimated on the normal data sets and the test set with MCCs
| Sensitivity | 80% | 85% | 80% | 85% | |
|---|---|---|---|---|---|
| FP cluster rates before classifiers | FP cluster rates (% FP reduction) after classifiers | ||||
| Normal Set | FFDM | 2.18 | 2.97 | 0.31 (86%) | 0.43 (86%) |
| SFM | 2.51 | 4.11 | 0.38 (85%) | 0.83 (80%) | |
| MCC Set | FFDM | 2.59 | 3.85 | 0.61 (76%) | 0.83 (78%) |
| SFM | 6.72 | 9.00 | 1.21 (82%) | 2.96 (67%) | |
The detection performance of a CAD system for malignant clusters is more important than its performance for detecting all clusters. The average cluster-based and case-based test FROC curves for detection of malignant MCCs for the FFDM and SFM CAD systems are compared in figure 9. The performance of either the FFDM or the SFM CAD system on the malignant test subset is better than that on the entire test subset shown in figure 7. The cluster-based FROC curve for the FFDM CAD system is about 5% to 10% higher in sensitivity than the corresponding curve for the SFM CAD system at the same FP cluster rates. However, the case-based FROC curves for the two CAD systems have similar performance. The AFROC analysis results for the difference between the cluster-based test FROC curves for the two modalities are summarized in table 4(b). The difference between the fitted AFROC curves for the two CAD systems for malignant MCCs did not achieve statistical significance (p>0.05) for either test subset.
Figure 9.
Comparison of the average test FROC curves for malignant cases for the FFDM and the SFM CAD systems. The FP cluster rates were estimated from the test sets with MCCs. (a) Cluster-based FROC curves, and (b) case-based FROC curves.
Figures 10(a) and 10(b) compare the average cluster-based and case-based test FROC curves for detection of malignant clusters for FFDM and SFM CAD systems when the data sets without MCCs were used for estimation of the FP cluster rates. The cluster-based FROC curves became very similar for the two systems. All malignant clusters were detected by the FFDM CAD system on at least one view (100% case-based sensitivity) at an average of 0.25 FP clusters/image. The SFM CAD system could not achieve 100% case-based sensitivity but the case-based FROC curve is slightly higher than that of the FFDM CAD system.
Figure 10.
Comparison of the average test FROC curves for malignant cases for the FFDM and the SFM CAD systems. The FP cluster rates were estimated from the test sets without MCCs. (a) Cluster-based FROC curves, and (b) case-based FROC curves.
4. Discussion
FFDM systems from several manufacturers have obtained FDA approval for clinical use. Several clinical trials have been conducted to compare FFDM with SFM in screening populations (Lewin et al., 2002; Skaane et al., 2003; Skaane and Skjennald, 2004; Pisano et al., 2005). Due to differences in various factors, such as the mammographic equipment, the study design, the sample sizes, and the reader experience, these clinical trials arrived at different conclusions about the advantages or disadvantages of FFDM in comparison to conventional SFM systems. Since the detection of cancers with a computerized program can also be affected by the image properties of the mammograms from different modalities, it is important to compare the performance between the CAD systems for FFDMs and for SFMs. We collected a case-matched data set of FFDMs and SFMs from the same patients to facilitate such comparisons.
In this study, our results showed that the FFDM CAD system detected more MCCs than the SFM CAD system when all clustered microcalcifications (malignant and benign) are considered. The difference in detection rates (table 2) and that in FROC performance (table 4(a)) were statistically significant. However, the difference was not statistically significant when malignant cases only were evaluated (see table 4(b)). Figures 11(a)-(d) show examples of clusters missed by the SFM CAD system but detected by the FFDM CAD system. These two clusters imaged on the SFMs appeared to be more subtle to the radiologist than on the FFDMs. An example of clusters missed by the FFDM CAD system but detected by the SFM CAD system is shown in figures 11(e) and 11(f). For this benign cluster, the ratings from the radiologist are very close to each other. The difference in the appearance of the clusters may be attributed to factors such as variations in positioning or differences in the image quality of the FFDMs and digitized SFMs. When the FP cluster rates were evaluated on the normal data sets, the difference between the performance of FFDM and SFM CAD system was smaller as shown in table 3 and figure 8.
Figure 11.
(a) A 10× 10mm2 malignant MCC with subtlety rated as 10 on SFM, (b) the same cluster as in (a) on FFDM with subtlety rated as 7. (c) A 28 × 26mm2 benign MCC with subtlety rated as 9 on SFM, (d) the same cluster as in (c) on FFDM with subtlety rated as 6. (e) A 10 × 10mm2 benign MCC with subtlety rated as 9 on SFM, (f) the same cluster as in (e) on FFDM with subtlety rated as 10. The subtlety of the MCCs was rated by experienced MQSA radiologists on a scale of 1 (obvious) to 10 (subtle) relative to the visibility range of microcalcifications encountered in clinical practice.
The CNN classifier in the SFM CAD system was trained with a different data set used in our previous study (Gurcan et al., 2002). We did not use the cross-validation SFM subsets for training in the current study because the ground truth locations of the individual MCs were not available for the current SFM data set and because a CNN can be trained using any independent data set with similar imaging properties. There might be a chance that the two subsets from the current SFM data set are more similar in their imaging properties than those between the current and the previous SFM data set, and thus using the previous SFM data set for training might introduce an unfavorable bias to the CNN classifier in the SFM CAD system. On the other hand, since the previous SFM data set for training the CNN was larger, it should allow the SFM CNN to be better trained, and thus better generalized to unknown data, than if the current data set was used. In this aspect, the SFM CNN may have an advantage (favorable bias) over the FFDM CNN. Figure 5 shows typical examples of ROIs containing a MC candidate with CNN score less than 0.4 from one of the test subsets for the SFM CAD system. These examples demonstrate that the MC candidates with low CNN scores were mostly fibrous structures or some linear artifacts on the mammograms. As the CNN scores increased, the MC candidates became more dot-like structures. There were also sharp and bright spots that might be caused by dust or film emulsion pick-off. The trained CNN appeared to be effective in recognizing the sharp white dots as FP signals. By choosing a threshold of 0.4, the MC candidates shown in figure 5 were eliminated as FPs by the CNN. The MC candidates with low CNN scores are similar to the FPs shown in our previous study (Chan et al., 1995). The SFM CNN thus was trained similarly even though the training sets used were different in these two studies.
To investigate if there was an observable bias, we compared in table 5 the FP cluster rates and FP reduction percentages of the FFDM and SFM CAD systems when the FP cluster rates were evaluated on the normal data set and the MCC data set at two different sensitivity levels. The FP reduction percentages of the FFDM CAD system were slightly better in the normal data set, which was an independent test set for the FFDM classifiers, than in the MCC data set, indicating that the FFDM CAD system was not over-trained in the two-fold cross-validation scheme. The FP reduction performances of the SFM and FFDM classifiers were, on average, within a few percents either in the normal or in the MCC data set and the overall difference was not statistically significant (paired t-test, p=0.47). However, the FP reduction percentages in the normal data set were significantly higher than those in the MCC data set considering both the FFDM and SFM CAD systems (paired t-test, p=0.03). This comparison provides some evidence that the FFDM CNN classifiers trained by the two-fold cross validation training scheme did not gain a favorable bias for the test results on the MCC data set. The differences in the average FP reduction percentages between the two systems were reasonably close in the MCC (about 2.5%) and the independent normal (about 3.5%) data sets. The smaller difference in the FP rates on the normal data sets before FP classification might be the reason that the performances of the FFDM and SFM CAD systems were closer when the FP rates were estimated using the normal data sets.
Although the same computer vision algorithms were used in both the FFDM and SFM CAD systems, the two important classifiers for FP reductions were trained separately with case samples for each modality. The two CNN classifiers have different performance ( Az = 0.96 and 0.91 for validation on FFDMs and SFMs, respectively). The features selected in the LDA classifiers have some overlap, but the coefficients in the linear discriminant functions are different. The differences in the performance of the FP classifiers led to the differences in the overall performances of the two systems.
There are several parameters in the CAD system that can be adjusted over a range. The choice of the CNN threshold or other parameters would affect the resulting FROC curves and we selected the parameter values empirically by training (Chan et al., 1987; Ge et al., 2006; Gurcan et al., 2002). We chose to fix the CNN threshold but to vary the LDA threshold in generating the final FROC curves based on two major reasons. First, the CNN values of the individual MC candidates were used to generate input features to the LDA classifier for reduction of false MCC candidates in the final step. If the CNN value was used as the threshold to generate FROC curves, we had to train a different LDA classifier for each point along the FROC curve. Second, we did not obtain a better FROC curve by varying the CNN threshold during the training process. Since the more complicated approach was not found to be advantageous, the LDA output was chosen as the decision threshold for our CAD systems.
We collected a case-matched data set for comparison of the performances of the FFDMs and SFMs. Although this approach reduced some of the variability in the case samples, the degree of subtlety of the clusters on the corresponding FFDM and SFM would differ due to the differences in positioning, compression, and exposure techniques in addition to the differences in the detector characteristics and the examination dates. Some of these variations can be reduced by averaging over a large data set, which may not have been achieved in the current study. Furthermore, the detector characteristics will depend on the detector manufacturer, the screen-film system, and the digitizer used. Further investigations are needed to evaluate the performances of MCC detection by CAD systems for the two modalities.
5. Conclusion
In this study, we compared the performance of our FFDM and SFM CAD systems for detection of MCCs on case-matched FFDM images and SFM images. The two CAD systems used the same computer vision techniques but their FP reduction classifiers were trained with samples from each modality. For cluster-based performance evaluation, FFDM CAD system achieved higher detection sensitivities than the SFM CAD system at the same FP cluster rates for the data set used. The difference was statistically significant with the AFROC analysis. The difference is smaller when the FP cluster rates were evaluated on the normal data sets, although the performance of the FFDM CAD system was still slightly better than that of the SFM CAD system. For malignant cases, the differences in the performance of the two CAD systems did not achieve statistical significance. Further study is underway to improve the performances of both systems.
Acknowledgments
This work is supported by USPHS grant CA95153 and U. S. Army Medical Research and Materiel Command grant DAMD17-02-1-0214. The content of this paper does not necessarily reflect the position of the government and no official endorsement of any equipment and product of any companies mentioned should be inferred. The authors are grateful to Charles E. Metz, Ph.D., for the LABROC and ROCKIT programs.
References
- Beam CA, Sullivan DC, Layde PM. Effect of human variability on independent double reading in screening mammography. Academic Radiology. 1996;3:891–7. doi: 10.1016/s1076-6332(96)80296-0. [DOI] [PubMed] [Google Scholar]
- Birdwell RL, Ikeda DM. Response to Letters to the Editor: 2006 Computer-aided detection with screening mammography: improving performance or simply shifting the operating point? Radiology. 239:917–8. doi: 10.1148/radiol.2393051392. [DOI] [PubMed] [Google Scholar]
- Brem RF, Baum JK, Lechner M, Kaplan S, Souders S, Naul LG, Hoffmeister J. Improvement in sensitivity of screening mammography with computer-aided detection: A multi-institutional trial. American Journal of Roentgenology. 2003;181:687–93. doi: 10.2214/ajr.181.3.1810687. [DOI] [PubMed] [Google Scholar]
- Burgess A. On the noise variance of a digital mammography system. Medical Physics. 2004;31:1987–95. doi: 10.1118/1.1758791. [DOI] [PubMed] [Google Scholar]
- Burnside ES, Sickles EA, Sohlich RE, Dee KE. Differential value of comparison with previous examinations in diagnostic versus screening mammography. American Journal of Roentgenology. 2002;179:1173–7. doi: 10.2214/ajr.179.5.1791173. [DOI] [PubMed] [Google Scholar]
- Chakraborty DP. Maximum likelihood analysis of free-response receiver operating characteristic (FROC) data. Medical Physics. 1989;16:561–8. doi: 10.1118/1.596358. [DOI] [PubMed] [Google Scholar]
- Chan H-P, Doi K, Galhotra S, Vyborny CJ, MacMahon H, Jokich PM. Image feature analysis and computer-aided diagnosis in digital radiography. 1. Automated detection of microcalcifications in mammography. Medical Physics. 1987;14:538–48. doi: 10.1118/1.596065. [DOI] [PubMed] [Google Scholar]
- Chan H-P, Doi K, Vyborny CJ, Schmidt RA, Metz CE, Lam KL, Ogura T, Wu Y, MacMahon H. Improvement in radiologists’ detection of clustered microcalcifications on mammograms. The potential of computer-aided diagnosis. Investigative Radiology. 1990;25:1102–10. doi: 10.1097/00004424-199010000-00006. [DOI] [PubMed] [Google Scholar]
- Chan H-P, Lo SCB, Sahiner B, Lam KL, Helvie MA. Computer-aided detection of mammographic microcalcifications: Pattern recognition with an artificial neural network. Medical Physics. 1995;22:1555–67. doi: 10.1118/1.597428. [DOI] [PubMed] [Google Scholar]
- Chan H-P, Niklason LT, Ikeda DM, Lam KL, Adler DD. Digitization requirements in mammography: Effects on computer-aided detection of microcalcifications. Medical Physics. 1994;21:1203–11. doi: 10.1118/1.597354. [DOI] [PubMed] [Google Scholar]
- Chan H-P, Sahiner B, Lam KL, Petrick N, Helvie MA, Goodsitt MM, Adler DD. Computerized analysis of mammographic microcalcifications in morphological and texture feature space. Medical Physics. 1998;25:2007–19. doi: 10.1118/1.598389. [DOI] [PubMed] [Google Scholar]
- Cole E, Pisano ED, Brown M, Kuzmiak C, Braeuning MP, Kim HH, Jong R, Walsh R. Diagnostic accuracy of Fischer SenoScan digital mammography versus screen-film mammography in a diagnositic mammography population. Academic Radiology. 2004;11:879–86. doi: 10.1016/j.acra.2004.04.003. [DOI] [PubMed] [Google Scholar]
- Destounis SV, DiNitto P, Logan-Young W, Bonaccio E, Zuley ML, Willison KM. Can computer-aided detection with double reading of screening mammograms help decrease the false-negative rate? Initial experience. Radiology. 2004;232:578–84. doi: 10.1148/radiol.2322030034. [DOI] [PubMed] [Google Scholar]
- Feig SA, Sickles EA, Evans WP, Linver MN. Re. Changes in breast cancer detection and mammography recall rates after the introduction of a computer-aided detection system. Journal of National Cancer Institute. 2004;96:1260–1. doi: 10.1093/jnci/djh257. [DOI] [PubMed] [Google Scholar]
- Freer TW, Ulissey MJ. Screening mammography with computer-aided detection: Prospective study of 12,860 patients in a community breast center. Radiology. 2001;220:781–6. doi: 10.1148/radiol.2203001282. [DOI] [PubMed] [Google Scholar]
- Ge J, Sahiner B, Hadjiiski LM, Chan H-P, Wei J, Helvie MA, Zhou C. Computer aided detection of clusters of microcalcifications on full field digital mammograms. Medical Physics. 2006;33:2975–88. doi: 10.1118/1.2211710. [DOI] [PubMed] [Google Scholar]
- Gur D, Sumkin JH, Rockette HE, Ganott MA, Hakim C, Hardesty LA, Poller WR, Shah R, Wallace L. Changes in breast cancer detection and mammography recall rates after the introduction of a computer-aided detection system. Journal of National Cancer Institute. 2004;96:185–90. doi: 10.1093/jnci/djh067. [DOI] [PubMed] [Google Scholar]
- Gurcan MN, Chan H-P, Sahiner B, Hadjiiski L, Petrick N, Helvie MA. Optimal neural network architecture selection: Improvement in computerized detection of microcalcifications. Academic Radiology. 2002;9:420–9. doi: 10.1016/s1076-6332(03)80187-3. [DOI] [PubMed] [Google Scholar]
- Harvey JA, Fajardo LL, Innis CA. Previous mammograms in patients with impalpable breast carcinomas: Retrospective vs blinded interpretation. American Journal of Roentgenology. 1993;161:1167–72. doi: 10.2214/ajr.161.6.8249720. [DOI] [PubMed] [Google Scholar]
- Helvie MA, Hadjiiski LM, Makariou E, Chan H-P, Petrick N, Sahiner B, Lo SCB, Freedman M, Adler D, Bailey J, Blane C, Hoff D, Hunt K, Joynt L, Klein K, Paramagul C, Patterson S, Roubidoux MA. Sensitivity of noncommercial computer-aided detection system for mammographic breast cancer detection - A pilot clinical trial. Radiology. 2004;231:208–14. doi: 10.1148/radiol.2311030429. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kopans DB. Breast Imaging. Lippincott-Raven Publishers; 227 East Washington Square, Philadelphia, PA: 1997. [Google Scholar]
- Lewin JM, D’Orsi CJ, Hendrick RE, Moss LJ, Isaacs PK, Karellas A, Cutter GR. Clinical comparison of full-field digital mammography and screen-film mammography for detection of breast cancer. American Journal of Roentgenology. 2002;179:671–7. doi: 10.2214/ajr.179.3.1790671. [DOI] [PubMed] [Google Scholar]
- Lewin JM, Hendrick RE, D’Orsi CJ, Isaacs PK, Moss LJ, Karellas A, Sisney GA, Kuni CC, Cutter GR. Comparison of full-field digital mammography with screen-film mammography for cancer detection: results of 4,945 paired examinations. Radiology. 2001;218:873–80. doi: 10.1148/radiology.218.3.r01mr29873. [DOI] [PubMed] [Google Scholar]
- Metz CE, Herman BA, Shen JH. Maximum-likelihood estimation of receiver operating characteristic (ROC) curves from continuously-distributed data. Statistics in Medicine. 1998;17:1033–53. doi: 10.1002/(sici)1097-0258(19980515)17:9<1033::aid-sim784>3.0.co;2-z. [DOI] [PubMed] [Google Scholar]
- O’Shaughnessy KF, Castellino RA, Muller SL, Benali K. Computer-aided detection (CAD) on 90 biopsy-proven breast cancer cases acquired on a full-field digital mammography (FFDM) system. Radiology. 2001;221(P):471. [Google Scholar]
- Pisano ED, Gatsonis C, Hendrick E, Yaffe M, Baum JK, Acharyya S, Conant EF, Fajardo LL, Bassett L, D’Orsi C, Jong R, Rebner M. Diagnostic performance of digital versus film mammography for breast-cancer screening. The New England Journal of Medicine. 2005;353:1773–83. doi: 10.1056/NEJMoa052911. [DOI] [PubMed] [Google Scholar]
- Skaane P, Balleyguier C, Diekmann F, Diekmann S, Piguet J-C, Young K, Niklason LT. Breast lesion detection and classification: Comparison of screen-film mammography and full-field digital mammography with soft-copy reading -- Observer performance study. Radiology. 2005a;237:37–44. doi: 10.1148/radiol.2371041605. [DOI] [PubMed] [Google Scholar]
- Skaane P, Skjennald A. Screen-film mammography versus full-field digital mammography with soft-copy reading: randomized trial in a population-based screening program -- The Oslo II Study. Radiology. 2004;232:197–204. doi: 10.1148/radiol.2321031624. [DOI] [PubMed] [Google Scholar]
- Skaane P, Skjennald A, Young K, Egge E, Jebsen I, Sager EM, Scheel B, Sovik E, Ertzaas AK, Hofvind S, Abdelnoor M. Follow-up and final results of the Oslo I study comparing screen-film mammography and full-field digital mammography with soft-copy reading. ACTA RADIOLOGICA. 2005b;46:679–89. doi: 10.1080/02841850500223547. [DOI] [PubMed] [Google Scholar]
- Skaane P, Young K, Skjennald A. Population-based mammography screening: comparison of screen-film and full-field digital mammography with soft-copy reading --- Oslo I Study. Radiology. 2003;229:877–84. doi: 10.1148/radiol.2293021171. [DOI] [PubMed] [Google Scholar]
- Warren Burhenne LJ, Wood SA, D’Orsi CJ, Feig SA, Kopans DB, O’Shaughnessy KF, Sickles EA, Tabar L, Vyborny CJ, Castellino RA. Potential contribution of computer-aided detection to the sensitivity of screening mammography. Radiology. 2000;215:554–62. doi: 10.1148/radiology.215.2.r00ma15554. [DOI] [PubMed] [Google Scholar]