Intracranial and Abdominal Aortic Aneurysms: Similarities, Differences, and Need for a New Class of Computational Models

Abstract

Intracranial and abdominal aortic aneurysms result from different underlying disease processes and exhibit different rupture potentials, yet they share many histopathological and biomechanical characteristics. Moreover, as in other vascular diseases, hemodynamics and wall mechanics play important roles in the natural history and possible treatment of these two types of lesions. The goals of this review are twofold: first, to contrast the biology and mechanics of intracranial and abdominal aortic aneurysms to emphasize that separate advances in our understanding of each disease can aid in our understanding of the other disease, and second, to suggest that research on the biomechanics of aneurysms must embrace a new paradigm for analysis. That is, past biomechanical studies have provided tremendous insight but have progressed along separate lines, focusing on either the hemodynamics or the wall mechanics. We submit that that there is a pressing need to couple in a new way the separate advances in vascular biology, medical imaging, and computational biofluid and biosolid mechanics to understand better the mechanobiology, pathophysiology, and treatment of these lesions, which continue to be responsible for significant morbidity and mortality. We shall refer to this needed new class of computational tools as Fluid-Solid-Growth (FSG) Models.

INTRODUCTION

The normal arterial wall consists of three layers: the intima, media, and adventitia. The innermost layer, or intima, consists of a monolayer of endothelial cells attached to a basement membrane composed of type IV collagen and laminin; the middle layer, or media, consists of smooth muscle cells embedded in an extracellular matrix composed of elastin, multiple types of collagen, and proteoglycans; the outermost layer, or adventitia, consists of fibroblasts embedded in an extensive plexus of type I collagen with admixed elastin. An aneurysm is defined as a focal dilatation of the arterial wall. Although the pathogenesis of aneurysms remains an enigma, the initial dilatation appears to be caused in part by degeneration of a portion of the arterial wall, often medial elastin and then smooth muscle. The two most common types of aneurysms are intracranial saccular aneurysms (ISAs) and abdominal aortic aneurysms (AAAs). ISAs occur in or near the circle of Willis, the major network of arteries that supplies blood to the brain; AAAs occur in the infrarenal aorta, the primary conduit that supplies blood to the legs. Genetics and risk factors play important roles in the natural history of aneurysms, but it is universally accepted that biomechanical factors (including increased pressures in hypertension) also play fundamental roles.

Advances in vascular biology, biomechanics, medical imaging, and computational methods collectively provide an unprecedented opportunity to develop and use mathematical models to understand better the progression of vascular diseases as well as to improve the design of medical devices and strategies for intervention. To realize this promise, however, there is a pressing need for a paradigm shift in our approach. Whereas the vast majority of prior modeling has focused on either the hemodynamics or the wall mechanics, and has focused on conditions at particular instants during disease progression or treatment, there is a need to develop coupled Fluid-Solid-Growth (FSG) Models of the evolving changes in vascular biology, geometry, wall properties, and hemodynamics. That is, most important vascular pathologies and most adverse responses to treatment manifest over extended periods, times during which the vascular wall grows and remodels in response to the altered mechanobiology. In this paper, we discuss the general need for FSG Models using as examples ISAs and AAAs. Toward that end, we briefly contrast the histopathology and mechanobiology of these aneurysms and review prior biomechanical analyses. We then outline a new approach for modeling these devastating lesions and conclude by suggesting particular needs for future research.

NATURAL HISTORY

Intracranial Saccular Aneurysm (ISA)

Two-to-five percent of people in the Industrialized World likely harbor an ISA, that is, a focal dilatation of a cerebral artery often characterized by a sac-like shape up to 30 mm in diameter (Figure 1). Histopathological and clinical studies reveal a higher prevalence in women (55–65%) than men and that multiple lesions occur in 15–30% of aneurysm patients. Although these lesions may remain dormant for years, the small percentage that rupture tend to do so during the 5^th to 7^th decades of life (mean ~52 years old; 1). Ruptured ISAs are the leading cause of non-traumatic subarachnoid hemorrhage, and thus its devastating sequela (cerebral vasospasm), which causes significant morbidity and mortality.

Figure 1.

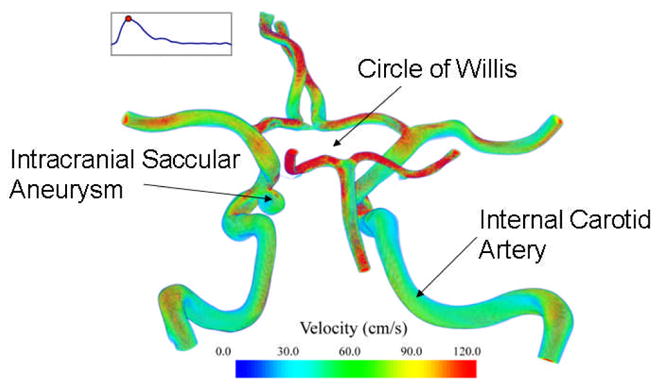
Computational model of a large portion of the human circle of Willis including an intracranial saccular aneurysm. Shown too are estimated velocity distributions based on a FSI simulation.

The natural history of ISAs consists of three phases: pathogenesis, enlargement, and rupture. The genesis is a subject of considerable debate, but it is generally accepted that mechanical factors play fundamental roles. Cerebral arteries do not have an external elastic lamina, they have sparse medial elastin, they lack supporting perivascular tissue, and they have structural irregularities at the apex of their bifurcations (2,3). These factors appear to render these arteries susceptible to a local weakening under the persistent action of hemodynamic loads, particularly in hypertension (4). One theme, in particular, is the internal elastic lamina and muscular media must be markedly fragmented or degraded for an ISA to form (5,6). Risk factors include cigarette smoking, heavy alcohol consumption, and long-term use of analgesics or oral contraceptives, but these may play a lesser role (7,8). Increased familial incidence, up to 12% in some populations, suggests that genetics is also important. For example, cerebral arteries in patients harboring an ISA tend to have less type III collagen (9), and it has long been thought that a genetic defect renders these vessels more susceptible (10,11). Yet, gene studies have failed to link mutations in COL3A1 and aneurysms (12). Indeed, diverse studies have similarly not found a strong link to a mutation in any of a number of prime candidates, as, for example, genes for fibronectin, fibrillin-2, lysyl oxidase, α1-antitrypsin, matrix metalloproteinases (MMP-1,3,9,12), tissue inhibitors of MMPs (TIMP-1,2,3), endothelial derived nitric oxide synthase, or prostacyclin-stimulating factor (13–18).

ISAs enlarge from an initially small out-pouching of the wall, often to have diameters of 5 to 10 mm as well as complex shapes and composition. It was long thought that these lesions could enlarge rapidly due to structural instabilities, namely, a limit point instability or resonance (19–22). Whereas these studies assumed linear or rubber-like properties of the wall, more appropriate nonlinear analyses suggest that such instabilities are unlikely (23,24). Rather, ISAs appear to enlarge via mechano-regulated growth and remodeling (G&R) processes common to diverse vascular adaptations (25,26). That is, as in other arterial adaptations (e.g., responses to sustained alterations in blood flow, blood pressure, or axial stretch; 27–29), there is a significant increase in MMP activity, synthesis of extracellular matrix proteins, and apoptosis in ISAs (4,6,17,30–32). Indeed, Peters et al. (33) said it well: “aneurysmal dilation results in a highly dynamic cellular environment in which extensive wound healing and tissue/extracellular matrix remodeling are taking place.”

Allcock & Canham (34) reported large variations in “growth” rates: some lesions enlarged markedly over a few months while others remained nearly the same size for years. Based on a detailed statistical analysis, Mitchell & Jakubowski (35) suggested that ISAs go through a brief period of high growth and rupture-potential soon after formation, but those that survive may subsequently pose a much lower risk of rupture for an extended period. They estimated this high risk period to be less than 41 weeks, which is consistent with half-lives of arterial collagen (70 days or less in normalcy and much less in disease; 28). Note, therefore, that lesion strength is due primarily to fibrillar collagens, despite occasional small patches of smooth muscle of stellate form and dispersed fibroblasts, macrophages, and cellular debris (2,36). Kosierkiewicz et al. (37) identified an intimal-type thickening in some small ISAs and advanced plaques with lipid-laden macrophages in some large lesions, yet atherosclerosis appears to result from, not cause, ISA development. Rather enlargement appears to result primarily from the turnover of fibrillar collagens (including significant degradation by MMPs; 31–32), with orientation, cross-linking, and volume fractions being key factors. See work by Canham and colleagues on the layered orientation of aneurysmal collagen, which they suggest lies along great circle trajectories and renders lesions less distensible than the parent arteries (38–40).

Rupture yields one of two outcomes: a catastrophic failure of a portion of the wall, with bleeding that is often lethal, or a transient leak, with less bleeding but clinical consequences nonetheless. Fortunately, the rate of rupture appears to be less than 0.1% per year. Failure mechanisms remain unknown, but rupture usually occurs at the fundus (pole) despite the neck often being thinner (2,41). Although this was long perplexing, finite element calculations suggest that the maximum biaxial stresses typically occur near the fundus, where intramural shear stress is small (23, 42–43). For this reason, it appears that a rupture criterion should be based on tensile, not shearing, stresses or strains. Several studies associate other physical factors with rupture potential. Asari and Ohmoto (44) suggested that the combination of lesion location (e.g., middle cerebral artery), shape (i.e., multilobular), and excess loading (hypertension) indicates a high risk of rupture. Hademenos et al. (45) similarly suggested that multilobular lesions are more prone to rupture, but that less prevalent posterior lesions are more likely to rupture. Ruiz et al. (46) suggested further that aneurysms of the posterior communicating artery may be more prone to rupture because of increased nonsymmetrical contact with perianeurysmal tissue (they also suggested that symmetrical contact constraints may be protective, consistent with modeling predictions by 47). Despite differing opinions based on clinical observations, it is likely that the location of a lesion relative to the inlet flow stream is critical to all aspects of the natural history, including rupture potential, for this dictates intra-aneurysmal hemodynamics and associated mechanobiological responses (48). For example, heterogeneities in wall shear stress could locally alter collagen production (endothelin-1 is a promoter of collagen synthesis and nitric oxide is an inhibitor; 49) and give rise to a local weakening.

Notwithstanding these diverse factors, most studies still base rupture potential primarily on the maximum dimension, with estimates of the critical size ranging from 5 to 10 mm (e.g., 50,51). From the perspective of mechanics, however, shape and wall thickness are more important determinants of stress in distended membranes than is overall size (23,43,52). Ujiie et al. (53) reported that 59% of ISAs are round, 24% oval, and 22% bar-like, but there has been little attempt to correlate rupture potential with specific shapes. That shape has not been considered is surprising since Crompton (54) showed long ago that saccular aneurysms in women tend to have a greater neck:height ratio and they are more likely to rupture. Lesion thickness can range from 30 to 500 μm in the unloaded configuration (55). It is believed that increasing thickness correlates primarily, but not exclusively, with continued enlargement (56).

Abdominal Aortic Aneurysm (AAA)

The normal adult human infrarenal aorta is approximately 12 cm long, 2 cm in diameter, and 2 mm thick. AAAs are typically defined by a 1.5 or more fold increase in diameter or simply a diameter greater than 3 cm; they tend to be diffuse, involving up to 9 cm of the infrarenal aorta (Figure 2). These lesions are six times more common in men, but three times more likely to rupture in women (57). Overall, AAAs affect 6 to 9% of people in the Industrialized World aged 65 and older. In addition to increasing age and male gender, risk factors include cigarette smoking, hypertension, chronic obstructive pulmonary disease, inflammation, and atherosclerosis. Some studies also suggest that up to 15% of the offspring of, and 13–32% of the siblings of, AAA patients also harbor a lesion (58). Of course, aging, smoking, hypertension, and atherosclerosis each correlate directly with increasing arterial wall stiffness (26), which in turn alters the hemodynamics. Like their intracranial counterparts, the natural history of AAAs includes pathogenesis, enlargement, and rupture.

Figure 2.

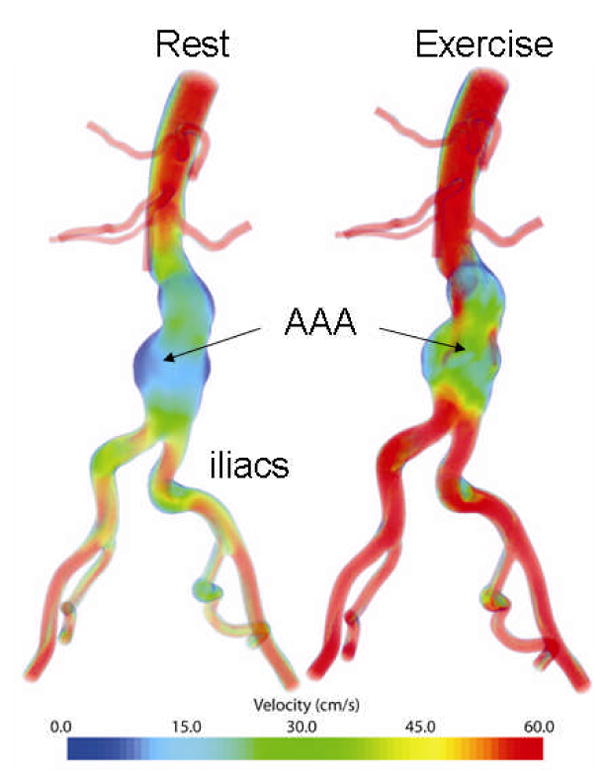
Computational model of a large portion of the human infrarenal aorta including an abdominal aortic aneurysm. Shown too are estimated velocity distributions based on a FSI simulation of both rest and exercise.

Again, there is considerable debate over pathogenesis. Some suggest that AAAs initiate due to inflammation and a local weakening of the wall (e.g., early loss of elastin), which in turn leads to atherosclerotic involvement and intraluminal thrombus; others suggest that AAAs are a consequence of a ruptured atherosclerotic plaque and associated formation of a thrombus and neovascularization from the vasa vasorum. See Alexander (59), Silverstein et al. (57), Sakalihasan et al. (60), Choke et al. (61), Thompson (62), and references therein. Regardless, AAAs expand at rates up to 0.25 to 0.75 cm per year, initially slower, then faster. If untreated, many lesions continue to enlarge until rupture (e.g., 50% of untreated AAAs in patients with high surgical risk will rupture, often within 1 year; 63). Whereas patients with a ruptured anterolateral wall often succumb to sudden death, those with a ruptured posterolateral wall can survive to hospitalization. Overall, the rate of rupture of AAAs has been estimated at 3 to 9% per year, significantly higher than that for ISAs, with mortality between 65 and 85%.

The normal human abdominal aorta consists of 45.5% collagen (60% type I and 22% type III), 30.1% elastin, and 22% smooth muscle by dry weight (64,65). The layered media contains abundant smooth muscle cells delimited by 28 to 30 concentric elastic laminae, less than would be expected of an elastic artery of its wall thickness. It is thought that this structure, combined with augmented pressures due to pulse wave reflections, may render the abdominal aorta more susceptible to aneurysms. Regardless, AAAs tend to have up to 90% less elastin, much of which is fragmented, and concomitantly few smooth muscle cells (66). Note, therefore, that normal elastin attenuates smooth muscle migration, proliferation, and apoptosis (67–69), but potentially reparative elastogenesis appears to be ineffective (59), consistent with reports that structurally significant vascular elastin is produced primarily during development (28,70). Among others, Freestone et al. (71) suggest that as the media attenuates and the aorta dilates, the adventitia experiences a stress-induced thickening via a turnover of fibrillar collagen that reinforces the wall. Zarins et al. (72) suggested that such turnover may be a response to altered loads, not just a consequence of altered genetics. The combination of decreased elastin and increased collagen and collagen cross-linking (66,73) increases wall stiffness and decreases distensibility to a degree that is evident clinically.

Whereas collagen turnover is likely a protective response to the loss of medial elastin and smooth muscle, localized imbalances between degradation and synthesis may be responsible in large part for eventual rupture (26,60). Key MMPs in AAAs are (59,74): MMP-1 (interstitial collagenase, acting primarily on fibrillar collagen), MMP-2 (gelatinase, acting primarily on elastin and cleaved collagen), MMP-9 (gelatinase, acting primarily on collagen IV), and MMP-3 (stromelysin, acting primarily on elastin). Although produced in latent forms and counteracted by TIMPS, MMPs are activated by plasmin, oxygen radicals, etc., and are significantly up-regulated in AAAs compared to normal aorta. Note, too, that MMP-9 is produced by inflammatory cells (e.g., macrophages and B-cells) that invade from the vasa vasorum or atherosclerotic intima.

Approximately 75% of AAAs have an intraluminal thrombus (61,75), yet the role of thrombus remains unclear. Stenbaek et al. (76) claim that rupture correlates best with the rate of growth of the thrombus and Kazi et al. (77) show dramatic differences in the portions of an AAA that are covered with a thrombus (e.g., thinner, less elastin, less smooth muscle, more T- and B-cells), yet Fillinger et al. (78) reported that the thickness of the thrombus does not correlate with rupture when based on matched overall diameters of the lesion. Nevertheless, thrombus appears to reduce overall wall stress slightly, it may be a barrier to the diffusion of oxygen and nutrients from the blood stream to the inner (avascular) portion of the wall, and it sequesters leukocytes and platelets that produce proteases and growth factors as well as control local levels of plasmin, which in turn activate MMPs (79,80). Hence, thrombus likely plays key chemo-mechanical roles in evolving AAAs and it must be understood and modeled better.

PRIOR BIOMECHANICAL ANALYSES

Intracranial Saccular Aneurysm (ISA)

Hemodynamics

There have been many in vitro experimental studies of fluid mechanics within and near an ISA, most using Newtonian fluids and rigid models of the arteries and aneurysms, with an emphasis on regions of elevated wall shear stress (e.g., 81,82). Alternatively, 3-D computational fluid dynamics (CFD) has been used increasingly to study cerebral blood flow, including flow in intracranial aneurysms (83–86). Indeed, there has been an important move to build computational models from in vivo medical imaging data in order to quantify patient-specific hemodynamics (87–95).

In contrast to the common hypothesis in experimental and CFD studies that locally elevated wall shear stress is important in pathogenesis, there has been no consensus as to which hemodynamic factors are important in enlargement or rupture. Cebral et al. (90) quantified flow velocity patterns in 62 patient-specific CFD models reconstructed from 3D rotational angiography and suggested that lesions most likely to rupture had complex or unstable flows and narrow jets and impingement sites. Increased flow complexity could be a sign of transition to turbulence and high-frequency pressure fluctuations, conditions thought to be responsible for post-stenotic dilatations (96). Alternatively, impingement due to a jet could cause steep gradients in wall shear stress and/or higher dynamic pressures on the wall. Yet, based on 26 patient-specific CFD simulations, Shojima et al. (97) reported that local rises in pressure due to flow impingement are less than 2 mmHg, which is small compared to nominal pressure levels in cerebral arteries, and concluded that dynamic pressures acting at bifurcations and on the walls of ISAs may be less significant to enlargement and rupture than previously assumed. In a longitudinal study of a basilar artery fusiform aneurysm, Acevedo-Bolton et al. (95) concluded that regions that continued to enlarge experienced low wall shear stress and speculated that this might be due to increased residence time of “particles that degrade the aneurysm wall.”

Finally, note that the wall shear stress in the cerebral vasculature (90,95) may normally be an order of magnitude higher than the 1 to 1.5 Pa value often cited as universal in large arteries (98). Of course, recent studies challenge the notion that wall shear stress is universally constant within large arteries within or across species (99,100). For example, Greve et al. (100) reported that wall shear stress τ_w in the abdominal aorta scales across mammalian species with body mass M according to the allometric relation τ_w ∝M^−0.38. Thus, interpretation of what constitutes a “high” or “low” wall shear stress should be based on nominal values for that region, and care should be taken when interpreting data from animal models or cell culture studies.

Wall Mechanics

The biomechanics of ISAs has been studied using Laplace’s equation: σ = Pa/2h, where σ is the uniform in-plane wall stress, P the transmural pressure, a the pressurized inner radius, and h the associated wall thickness. Examples range from Canham & Ferguson (101) who estimated a critical lesion diameter d_c = (4σ_cV / πP)^1/3 ~ 8.6 mm, with σ_c the critical wall strength (1–10 MPa) and V the volume of wall to Meng et al. (102) who suggested that the rupture potential of a daughter aneurysm depends solely on two geometric parameters related to the size of its orifice. Laplace’s relation has thus yielded useful insights, but it only holds for quasi-static inflations of spherical membranes and thereby cannot address elastodynamics, complex geometries, the propensity of rupture at the fundus, or how a lesion evolves. Conversely, early elasticity-based studies were limited by assumptions of linear or rubber-like behavior. In an attempt to address some of these shortcomings, Humphrey and colleagues began a series of nonlinear elasticity analyses in 1994 to analyze the then three primary biomechanical hypotheses: ISAs are materially unstable (21,22), they are dynamically unstable (19,20), and size alone is the critical predictor of rupture potential (7,50,54). Toward this end, one first needs information on the material behavior of human lesions.

Scott et al. (103) performed in vitro pressure-volume tests on 7 ISAs obtained at autopsy. Their data are fit well by a 2-D Fung-exponential strain energy function w (23):

$$w=c(e^Q-1),\text{where}Q=c_1{E}_{11}^2+c_2{E}_{22}^2+2c_3{E}_{11}{E}_{22},$$ (1)

c and c_i are material parameters, and E₁₁, E₂₂ are principal values of the Green strain. Yet, Scott’s data are global and essentially 1-D (i.e., pressure-volume), and thereby are not suitable to assess local properties or anisotropy. Whereas some investigators performed uniaxial stretching tests on strips of excised human aneurysms (5,56), Hsu et al. (104) developed a triplane video-based system to measure, in situ, local in-plane strains and curvatures at multiple pressures and Seshaiyer et al. (105) developed a sub-domain inverse finite element code (combining nonlinear finite elements with a Marquardt-Levenberg regression) to infer best-fit values of material parameters from these data. Based on data from 4 unruptured human lesions, they similarly found the Fung-exponential to be a reasonable descriptor, with typical values of the material parameters being c = 12.6 N/m, c₁ = 10.74, c₂, = 13.08, c₃, = 11.02 (which satisfy physical and mathematical constraints such as convexity). The meridional direction was often stiffer than circumferential, particularly away from the neck, thus suggesting a regional anisotropy.

Nonlinear finite element analyses (FEA) of idealized axisymmetric saccular aneurysms (23,42) confirmed that Laplace’s relation yields reasonable results only when lesions have a small neck and are nearly spherical. For this sub-class, however, one can prove analytically that lesions described by either Fung or Skalak-Tozeren-Zarda-Chien (STZC) type stress-strain relations cannot exhibit a limit point instability (23,106,107); this is in contrast to rubber-like spherical membranes, which typically exhibit limit points (22). Because static instabilities tend to organize dynamic instabilities, it was not surprising that one can also show both analytically (given small perturbations about various equilibria) and numerically (using methods of nonlinear dynamics and a Runge-Kutta solution of a new nonlinear differential equation of the elastodynamics) that nearly spherical lesions tend to be dynamically stable (107,108). Hence, at least for this sub-class of ISAs, and probably more generally, neither quasi-static nor dynamic instabilities appear to be responsible for enlargement.

Recall from above that although a “critical diameter” remains controversial, lesion size continues to be one of the most common clinical metrics used to predict rupture potential. For axisymmetric membranes, however, the principal (i.e., meridional and circumferential) Cauchy stress resultants T_i can be found in closed form (109) and shown to depend directly on transmural pressure P and principal curvatures κ and κ₂, not overall size:

$$T_1={\sigma }_{1}h=\frac{P}{2{\kappa }_2},T_2={\sigma }_{2}h=\frac{P}{{\kappa }_2}\left(1-\frac{{\kappa }_1}{2{\kappa }_2}\right).$$ (2)

Indeed, the continuing neglect of curvature is probably one reason why there is so much controversy over the elusive critical size (cf. 42,43). The significance of this general finding was illustrated, using FEA, for classes of axisymmetric lesions (23,42,47). For example, “small” lesions with a large neck:height ratio can have much higher stresses than “large” lesions with a small neck:height ratio; contact constraints due to interactions between a lesion and surrounding tissue can decrease the maximum stresses in an otherwise large lesion, however. Results also reveal that expected nonhomogeneous, non-equibiaxial distributions of stress in inflated, axisymmetric lesions can be restored to nearly homogeneous and equibiaxial (except for a boundary layer) by letting the material symmetry vary continuously from fundus to neck (25). These findings appear to be reasonable teleologically for they suggest that in response to local perturbations in properties (e.g., loss of elastin and smooth muscle), and thus geometry, ISAs can grow and remodel (via collagen turnover) so as to nearly recover the biaxial state of stress that was experienced by cells in the normal arterial wall. In summary, computations suggest that ISAs do not enlarge due to material or dynamic instabilities, and size is not the primary determinant of rupture potential. Rather, enlargement in response to an initial insult (first to elastin) appears to be yet another example of vascular G&R, one that seeks to alter structure locally so as to change the overall equilibrium geometry and thereby return stresses towards homeostatic values. Although idealized models are essential starting points, for they allow validation and they build intuition, there is a pressing need for geometrically and materially accurate finite element models of wall stress in saccular aneurysms. An important step in this direction was recently reported by Ma et al. (110).

Fluid-Solid Interactions

Following an earlier paper on the flow of a Newtonian fluid within 2-D, rigid saccular aneurysms, Low et al. (111) presented an important advance: a 3-D, fluid-solid interaction (FSI) model for two classes of lateral saccular aneurysms. Blood was modeled as a Casson fluid, the walls of the parent arteries and aneurysm were treated as linearly elastic, and flow was allowed to be unsteady. Among other conclusions, they found that “During the systolic acceleration phase where the aneurysm expands, inflow velocity near the downstream wall of the aneurysm is much higher in the distensible case, while at maximum flow rate, where the aneurysm already contracts, the inflow in the distensible case is significantly decreased.” Given this initial finding on the importance of wall distensibility, it is surprising that most studies continue to focus on rigid wall models. This assumption precludes wave propagation phenomena and fundamentally changes the character of resultant solutions (112) as well as negating possible fluid-solid interactions.

The common prescription of a pressure field at the outlets of a computational model is likewise unrealistic when modeling wave propagation phenomena, especially for FSI studies or treatment planning where this pressure is unknown and part of the desired solution. Moreover, it is not feasible to prescribe pressure waveforms at each of the outlet boundaries in multi-branched models since amplitude, shape, and phase depend on the solution in the modeled domain and cannot be assigned a priori. Consequences of the inattention to proper boundary conditions and wall deformability include uncertainty in global flow distributions, local velocity fields, and shear stresses. Indeed, although computed pressures are seldom reported, when they are reported the absolute values are inaccurate due to prescribed traction-free boundary conditions. For example, a number of papers on ISAs report elevated blood pressures within the lesion, yet closer inspection typically reveals values that differ only ~0.5 mmHg from those in nearby arteries. Such small differences would not be expected to be significant in the genesis and enlargement. Another unfortunate consequence of the inability to model well the pressure fields is, arguably, an over-emphasis on wall shear stress as the primary hemodynamic factor contributing to genesis, enlargement, and rupture. We conclude, therefore, that although the move to image-based, patient-specific models has yielded more realistic velocity and shear stress fields compared to idealized models, there has been little progress in measuring and then assigning physiologically realistic inlet flow waveforms, outlet boundary conditions, or wall properties.

Abdominal Aortic Aneurysms (AAA)

Hemodynamics

Many investigators have similarly used CFD to study blood flow in AAAs (e.g., 113–117). In many cases, regions of high pressure or high wall shear stress are singled out as potentially important to pathogenesis, though with little direct reference to the underlying mechanobiology. Bluestein et al. (118) pointed out that recirculation zones may also promote thrombus formation, which in turn may affect rupture potential. Overall, focus has been largely on pulsatile flows through rigid, idealized axisymmetric models, with blood modeled as an incompressible Newtonian fluid and outlet boundary conditions prescribed to be traction-free or constant pressure. Moreover, these studies do not include major branches immediately proximal to AAAs, such as the celiac, superior mesenteric, and renal arteries. These branches significantly influence conditions in the infrarenal aorta in normal subjects (119–121) and likely influence conditions in AAAs. In summary, while prior applications of CFD have increased our understanding of hemodynamics within AAAs, more realistic analyses will have to await more anatomically and physiologically accurate models and inclusion of wall properties. Progress towards addressing this latter limitation is discussed below following a brief review of mechanical properties of the aneurysmal wall.

Wall Mechanics

Despite general recognition of the importance of wall mechanics in the natural history of AAAs (e.g., 59, 63,122,123), there have been few studies of biomechanical properties. Early studies focused on gross measures of structural stiffness that can be useful in clinical correlations, but not biomechanical analyses. For example, Sumner et al. (124), MacSweeney et al. (125), and Lanne et al. (126) measured the pressure-strain modulus, E_p = d_s (p_s − p_d )/(d_s − d_d ), where p and d denote luminal pressure and inner diameter, respectively, and subscripts d and s denote diastolic and systolic. Values for this modulus range from 140 to 337 kPa in age-matched “normals” versus 313 to 504 kPa in AAAs. In contrast, He & Roach (65) reported 1-D stress-strain data for 8 AAAs and 8 age-matched controls (all axially oriented samples); although the nonlinear responses were interpreted within the context of a linearized strain, they showed that AAAs are stiffer than the normal aorta. Thubrikar et al. (127) reported similar findings, but also that the circumferential direction was stiffer than the axial direction and stiffness varied around the lesion: despite being thicker (e.g., 2.7 vs. 2.1 mm), posterior portions were less stiff than anterior or lateral portions. Raghavan & Vorp (128) performed 1-D tests on 69 human AAA specimens oriented along either the circumferential or the axial direction. They quantified data separately using a strain energy function of the form: W = c₁ (I_B −3) + c₂ (I_B −3)², where I_B = trB = tr(F·F^T ) and F is the deformation gradient. Mean values of the material parameters were c₁ = 186 kPa, c₂ = 2700 kPa in the circumferential and c₁ = 169 kPa, c₂ = 1570 kPa in the axial direction. Because 1-D data are not sufficient for determining multiaxial relations, Vande Geest et al. (129) performed biaxial tests on 26 AAAs and 8 age-matched controls (mean ages 72 and 71, respectively). The highly nonlinear responses were described well by a 2-D phenomenological Choi-Vito strain energy function, namely

$$W=c\left(exp[c_1{E}_{\theta \theta }^2]+exp[c_2{E}_{zz}^2]+exp[2c_3{E}_{\theta \theta }{E}_{zz}]-3\right)$$ (3)

where E_AB are principal values of Green strain E = 0.5(F^T·F − I). Mean values of the material parameters were c = 0.14 kPa, c₁ = 238.5, c₂ = 208.2, and c₃ = 204.1 for AAAs and c = 0.32 kPa, c₁ = 70.6, c₂ = 71.7, and c₃ = 64 for age-matched non-diseased aortic samples. These values confirm that AAAs are indeed stiffer and more anisotropic (stiffer in the circumferential direction) than the normal aorta.

There has been less attention to properties of the thrombus that often lines AAAs. DiMartino et al. (130) performed 1-D extension tests on 21 samples of thrombus obtained from 6 patients; the behavior was modeled as linearly elastic, despite finite strains, with a reported Young’s modulus of 130 kPa. Wang et al. (131) reported the most comprehensive study of the biomechanical properties of intraluminal thrombus from human AAAs. Briefly, each thrombus was removed from surgically resected human lesions and tested uniaxially within 24 hrs. Data from 50 specimens (mean lesion diameter of 5.6 cm) from 14 patients (69 years old) revealed that the behavior is mildly nonlinear over large strains, nearly isotropic (circumferential vs. axial), but highly nonhomogeneous (tissue from the luminal region was stiffer and stronger than that from the middle region). The data were fit well by a strain energy function of the form:

$$W=b_1({II}_B-3)+b_2{({II}_B-3)}^2$$ (4)

where 2II_B = (trB)² −trB². Mean values of the material parameters were b₁ = 30.4 kPa and b₂ = 30.1 kPa for the luminal region and b₁ = 21.4 kPa and b₂ = 21.7 kPa for the middle region. Measured strengths were on the order of 510 kPa for the luminal and 260 kPa for the middle regions, respectively.

The importance of wall stress in dictating the fate of individual lesions has also been recognized for decades. Most stress analyses have assumed idealized geometries, and are based on Laplace’s equation (132,133), axisymmetric membrane theory (134), or linear elastic finite element analyses (130,135–138). Values of the Young’s modulus range from 1 to 5 MPa. Linear analyses are inappropriate, however, due to the inherent nonlinear material behavior and large strains. In recent years, there has been increasing effort to develop more appropriate nonlinear FEA. The best models available (139,140,141) employ patient-specific geometries and treat the aneurysmal wall as nonlinearly elastic, albeit isotropic, homogeneous, uniformly thin, and unchanging. These authors acknowledge that many of their assumptions need to be relaxed, particularly that the in vivo diastolic geometry was assumed to be the stress-free reference. Nevertheless, Fillinger and colleagues showed, by comparing simulations for lesions that ruptured versus those that did not (100+ patients), that peak maximum normal stresses over ~440 kPa correlate strongly with rupture potential. This is an important finding; it reveals that computational models have real potential to improve our predictions of rupture potential (see the excellent review by Vorp (142) for more on the wall mechanics). In closing, it is noted that many investigators (e.g., 137,138,141) use the von Mises stress to assess the “maximum stress” in AAAs. The von Mises stress has utility in classical engineering analyses of ductile materials, which yield due to excessive shear stresses. Available data on aortic and other arterial tissue suggest, however, that maximum normal stresses, not shears, govern failure (e.g., 143–145). This issue of the most appropriate failure criteria must be addressed better.

Fluid-Solid Interactions

There has been increasing interest in FSI modeling of AAAs, yet most studies assume the arterial wall, AAA, and thrombus are linearly elastic, homogeneous, isotropic, nearly incompressible, and unchanging (146–148). Perhaps the most sophisticated FSI model to date is that by Wolters et al. (149). They used a shear thinning model for blood and a large strain, neo-Hookean model for the lesion (W = c₁ (I_B −3), with c₁ = 1 MPa). Nevertheless, the wall was assumed to be homogeneous, isotropic, uniformly thin (2 mm), and unchanging; outflow conditions were traction-free and wall deformation resulted from a uniform pressure boundary condition prescribed on the lateral surface rather than from the hemodynamic simulation. As such, this method cannot be regarded as fully coupled, and in particular, pressure fluctuations induced by turbulent or transitional flows in the lesion cannot be incorporated using this approach. Finally, as in most hemodynamic studies of AAAs, proximal branches of the abdominal aorta were neglected and a uniform velocity was prescribed in the infrarenal aorta.

NEED FOR A NEW CLASS OF COMPUTATIONAL TOOLS

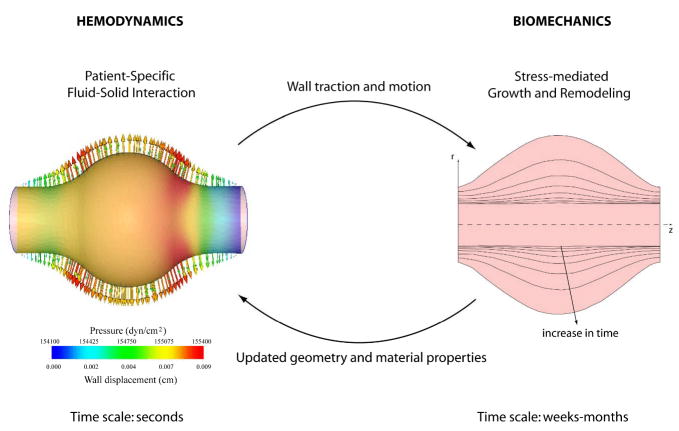
Based on this brief review of the literature, it is evident that computational biomechanical models have become increasingly sophisticated over the years and they have contributed significantly to our understanding of the natural history of aneurysms. There is a pressing need, however, for a new class of models that can describe the evolving geometry, nonlinear wall properties, and hemodynamics, which in turn dictate the evolving cell mechanobiology that is responsible for matrix turnover and the possible rupture of aneurysms. In contrast to using computational fluid dynamics (CFD) to study the hemodynamics or finite element analyses (FEA) to study wall stress, we submit that there is a need to couple fluid-solid interaction (FSI) models over a cardiac cycle with long-term growth and remodeling (G&R) models of the evolving wall (Figure 3). We shall refer to this new class of coupled computational tools for studying evolving vascular changes as Fluid-Solid-Growth (FSG) Models.

Figure 3.

Schema of the proposed Fluid-Solid-Growth (FSG) modeling approach: fluid-solid interaction (FSI) computations of the hemodynamics (time scale of seconds) provide updated information on wall tractions for the biosolid mechanics computations of G&R (time scale of days to weeks or years), which in turn provide updated information on changing geometry and material properties for the FSI code. The solution iterates between the hemodynamics and wall mechanics until either the vasculature achieves a steady state or a vessel or lesion ruptures. Modified from Figueroa et al. (190).

FSI During a Cardiac Cycle

Simulations of G&R of the vasculature require, as input, the mechanical forces (or tractions) that the fluid exerts on the wall. We contend that these tractions should be computed using FSI simulations, which in turn should be based on realistic anatomic models, refined discretizations to resolve complex hemodynamics, physiologically realistic fluid boundary conditions, appropriate models of wall stiffness, and robust, stable solvers for generally large systems of coupled fluid-solid equations. In particular, the only way to infer mechanisms of enlargement is to model actual geometries, hence we must exploit the tremendous advances in clinical magnetic resonance imaging or computed tomography. Toward this end, it is essential to image branches proximal and distal to a lesion because hemodynamic simulations can be very sensitive to inlet boundary conditions, unless the region of interest is many diameters from the inlets and there is sufficient dissipation in the system (150), and it can be difficult to prescribe outlet conditions where the flow remains disturbed from the complex geometry of the lesion.

Prakash & Ethier (151) discuss requirements for mesh generation and note that “suitable mesh convergence studies are rarely reported in the computational hemodynamics literature.” Unfortunately, this statement also characterizes the state-of-the art in aneurysm hemodynamics. As a result, many complex features observed in experimental studies of aneurysm flow (152,153) have not been replicated in computational simulations. Muller et al. (154) and Sahni et al. (155) recently described anisotropic adaptive finite element methods that are well suited for resolving complex, 3-D pulsatile flow dynamics as occur in aneurysms. A posteriori error estimators, based on the Hessian of the velocity magnitude (speed) field, yield directional information on the solution error. Because gradients in the velocity field are typically much greater in the radial than the circumferential direction in arterial flows, mesh generation strategies that exploit this feature can generate anisotropic meshes having an order of magnitude fewer degrees of freedom but results comparable to standard isotropic meshes (155). In summary, adaptive mesh generation can enable mesh-independent solutions for even the largest simulations of aneurysm hemodynamics given contemporary computing resources.

Simulations of fluid-solid interactions necessitate special considerations of inlet and outlet boundary conditions for both the velocity and the pressure fields need to be computed accurately to prescribe tractions on the vessel wall. Yet, prior simulations of hemodynamics in intracranial and abdominal aortic aneurysms have prescribed either zero outlet pressure (i.e., traction-free) conditions or, in a few cases, pressure waveforms at exits of the computational domain. We submit that impedance outlet boundary conditions are necessary for 3-D hemodynamic simulations to yield physiologic pressure and flow waves in distensible multi-vessel models. Decades of research show that vascular impedance can accurately represent the effects of a distal vascular bed (156–159). Impedance can be represented by a lumped parameter model (157) or computed using linear wave theory on randomly-branched distributed models (156). For example, Olufsen (160) showed that vascular impedance can be calculated efficiently on binary fractal tree models and provide appropriate outlet conditions for 1-D nonlinear wave propagation models. Vignon & Taylor (161) described a coupled multi-domain method based on Dirichlet-to-Neumann and variational multiscale methods that simplifies downstream domains and integrates them within image-based models as outlet boundary conditions. Vignon-Clementel et al. (162) extended this approach to include impedance outlet conditions for 3-D rigid-wall models whereas Figueroa et al. (163) described effects of various outlet conditions in 3-D FSI simulations. Findings show the effect of varying outlet conditions on flow, pressure, and displacement waveforms for a single artery model wherein a velocity profile is prescribed at the inlet. Only the impedance outlet boundary condition resulted in physiologic waveforms, noting in particular the unrealistic consequences of a prescribed constant outlet pressure on the upstream pressure and displacement waveforms.

Although models of the distal vasculature can be developed using distributed network or binary fractal tree approaches (156,160), it is preferable to use morphometric data to identify outlet boundary conditions. Such data are available for coronary and pulmonary circulations (164,165), but there is a pressing need for morphometric data for the cerebral and abdominal aortic vasculatures. Until such data are available, distributed and lumped models should be tuned numerically by constricting or dilating the distal vascular beds until the overall level of pressure and distribution of flow in the image-based model matches available measurements. Note that one advantage of distributed models is that physiologic variations are modeled easily for example, effects of lower extremity exercise on abdominal aortic blood flow can be modeled by changing the inflow waveform, dilating the vessels in the lower extremities, and constricting the beds that supply the abdominal organs (166). Finally, note that methods to couple 3-D and 1-D computational models of blood flow with the aim of minimizing wave reflections from the outlet of the 3-D domain (167) are inadequate unless the 1-D model is itself terminated with an impedance outlet condition. In our experience, coupling the 3-D model directly to an impedance outlet boundary condition is simpler and yields excellent results for FSI simulations.

Efficient coupling of fluid and solid domains is also fundamental to successful FSI simulations. Standard FSI techniques, such as the arbitrary Lagrangian-Eulerian (ALE) method, remain problematic for realistic anatomic and physiologic models of large portions of the vasculature. Hence consider a new method, the Coupled Momentum Method for Fluid Structure Interaction (CMM-FSI), which incorporates equations for the vascular wall at a variational level as a boundary condition for the fluid domain (163). Let three kinds of boundaries for an arbitrary geometry of a vessel be denoted as follows: Γ_g represents an inflow surface where a velocity field is prescribed; Γ_h represents an outlet surface where either impedance or resistance is prescribed; and Γ_s represents the lateral surface of the fluid domain, which interacts with the vessel wall. Whereas a Dirichlet condition of zero displacement (i.e., no-slip) is typically prescribed on Γ_s in rigid wall models, this is no longer appropriate when dealing with deformable vessels. Rather, letting Γ_s be subjected to a traction ${\mathbf{t}}_f^n$ originating from interactions with the vessel wall, the weak form of the governing equations for the fluid domain can be expressed as (163)

$$\begin{array}{l}{\int }_{\mathrm{\Omega }}\left\{\mathbf{w}·(\rho \mathbf{v}{,}_t+\rho \mathbf{v}·\nabla \mathbf{v}-\mathbf{g})+\nabla \mathbf{w}:(-p\mathbf{I}+\mathit{\tau })-\nabla q·\mathbf{v}\right\}d\mathbf{x}+{\int }_{{\mathrm{\Gamma }}_g}q{v}_{n}ds\\ +{\int }_{{\mathrm{\Gamma }}_h}\{-\mathbf{w}·\mathbf{h}+q{v}_n\}ds+{\int }_{{\mathrm{\Gamma }}_s}\left\{-\mathbf{w}·{\mathbf{t}}_f^n+q{v}_n\right\}ds+\text{stabilization}\text{terms}=0.\end{array}$$ (5)

Here, v and p are the fluid velocity and pressure (τ is the viscous Cauchy stress), g is a body force, h is a prescribed traction, and w and q are test functions. Details on the stabilization terms can be found in Taylor et al. (119) and Figueroa et al. (163). The traction ${\mathbf{t}}_f^n$ is unknown a priori, but can be related to a fictitious body force governing the motion of the vessel wall using a thin-wall approximation similar to that used by Womersley (168), who coupled blood flow and wall motion in an analytical solution for pulsatile flow in an axisymmetric, deformable cylinder. Using this approach, one can write the term containing the unknown traction as a function of the wall stress and inertial terms whereby the governing equation for the fluid domain becomes

$$\begin{array}{l}{\int }_{\mathrm{\Omega }}\left(\mathbf{w}·(\rho \mathbf{v}{,}_t+\rho \mathbf{v}·\nabla \mathbf{v}-\mathbf{g})+\nabla \mathbf{w}:(-p\mathbf{I}+\mathit{\tau })-\nabla q·\mathbf{v}\right)d\mathbf{x}+{\int }_{{\mathrm{\Gamma }}_g}q{v}_{n}ds-{\int }_{{\mathrm{\Gamma }}_h}\mathbf{w}·\mathbf{h}ds\\ +{\int }_{{\mathrm{\Gamma }}_h}q{v}_{n}ds+\zeta {\int }_{{\mathrm{\Gamma }}_s}\left(\mathbf{w}·{\rho }^s{\mathbf{v}}_{,t}+\nabla \mathbf{w}:\mathit{\sigma }(\mathbf{u})\right)ds-\zeta {\int }_{\partial {\mathrm{\Gamma }}_s}\mathbf{w}·{\mathbf{h}}^{s}dl+{\int }_{{\mathrm{\Gamma }}_s}q{v}_{n}ds+\\ +\text{stabilization}\text{terms}=0.\end{array}$$ (6)

Boundary terms, defined on Γ_s, can then be expressed in terms of fluid variables velocity and pressure – using a 2-D model of the vessel wall (e.g., a membrane model enhanced with transverse shear) since fluid responses depend only on the structural stiffness of the wall. For example, if one assumes a linearly elastic response, wall stress σ(u)can be derived easily from linearized wall strains and the usual stiffness tensor ℂ.

It is essential, however, to account for finite wall strains in G&R (as well as those due to usual in vivo deformations from a reference configuration). Because of the aforementioned increased stiffness and decreased distensibility of aneurysms, one can incorporate information from nonlinear wall mechanics during G&R into FSI simulations over a cardiac cycle by exploiting a theory of “small deformations superimposed on large.” Moreover, because timescales are so different between the cardiac cycle (seconds) and periods of G&R (days to years), one can solve the overall problem iteratively: determine tractions that are needed as inputs for the wall mechanics problem of finite deformation G&R by solving the hemodynamics problem assuming small deformations over a cardiac cycle, with each G&R solution providing an updated computational domain and structural stiffness of the wall for the next hemodynamic solution. Toward this end, Baek et al. (169) showed that complexities associated with an evolving aneurysm or artery (e.g., residual stress, nonlinear behavior, anisotropy, muscle tone, prior G&R, and finite deformations) can be so modeled. Let the position of a material point in an artery or aneurysm be given by x = x^o + u, where x^o represents a finite motion from a suitable reference to any intermediate configuration between diastole and systole, and u represents a small additional displacement during the cardiac cycle. The total deformation gradient is F = (I + H) · F^o, where H = ∂u/∂x^o is a small displacement gradient and F^o is the initial finite deformation. It can be shown that the Cauchy stress due to the additional small deformation σ^* is

$${\sigma }_{ij}^{\ast }=-p^{\ast }{\delta }_{ij}+{ℂ}_{\mathit{ijkl}}{\epsilon }_{kl}^{\ast }+{ℝ}_{\mathit{ijkl}}{\mathrm{\Omega }}_{kl}^{\ast },{{ℂ}_{\mathit{ijkl}}={\delta }_{ij}{\widehat{\sigma }}_{lj}^{\text{o}}+{\widehat{\sigma }}_{il}^{\text{o}}{\delta }_{jk}+4F_{iA}^{\text{o}}{F}_{jB}^{\text{o}}{F}_{kP}^{\text{o}}{F}_{lQ}^{\text{o}}\frac{{\partial }^{2}W}{\partial C_{AB}\partial C_{PQ}}\mid }_{C^{\text{o}}}$$ (7)

where ε^* and Ω^* are the linearized strain and rotation tensors, ℂ _ijkl is the “stiffness” matrix, and the over-hat denotes an extra stress. Although this stress response function has a form similar to that in linearized elasticity, the stiffness depends explicitly on the initial finite deformations and stress, which can include residual stress and G&R, and a strain energy W that describes complex nonlinear, anisotropic behaviors at any point or any instant. Hence, one can use a fully nonlinear analysis for G&R, but pass updated values of ℂ _ijkl and ℝ _ijkl to a usual FSI code to enable computationally efficient calculations of new hemodynamic loads for the adapting lesion and artery. We consider a method for finding appropriate strain energy functions for the wall in the next section. Finally, note that the variational FSI problem defined by equation (6) can be discretized using well-known, stabilized finite element techniques (e.g., 170,171) and the equations can be integrated in time using a modified version of the generalized-α method (172). This method provides an implicit, second-order accurate scheme with controllable numerical dissipation that shows excellent stability and has been applied to complex FSI problems with millions of degrees of freedom.

G&R Theory for Evolving Geometries and Material Properties

The last four decades have seen tremendous advances in vascular solid mechanics, from quantification of complex constitutive behaviors of tissues and cells to stress analyses of the same (26,173). Yet, most analyses have focused on geometries and properties at a particular instant, not how they evolve over time, and most constitutive relations have been phenomenological, describing overall behavior while assuming that the tissue or cell is materially uniform. An important advance, therefore, was the modeling of arterial development and adaptations to perturbed loads by Taber (174,175) and Rachev et al. (176,177). They employed the concept of kinematic growth introduced in 1981 by R. Skalak and showed that associated models can predict diverse manifestations of vessel growth. Two limitations, however, are the assumption that growth occurs in stress free configurations and that the tissue is materially uniform. Recall, for example, that the arterial wall consists of many different cell types and extracellular matrix proteins and proteoglycans, each of which can have individual material properties and rates of turnover in evolving, stressed configurations. A constrained mixture theory (178,179) can model evolving properties, turnover rates, and natural (i.e., stress-free) configurations of individual structural constituents that comprise a soft tissue, which is thereby modeled as materially nonuniform. Implementations of this G&R theory have predicted salient features of flow-, pressure-, and axial stretch-induced adaptations by carotid arteries (180–182) as well as enlargement of idealized intracranial aneurysms (183,184).

For illustrative purposes, consider an idealized thin-walled, axisymmetric aneurysm. Recall that intracranial aneurysms are largely devoid of elastin and smooth muscle, and thereby consist primarily of multiple families of collagen fibers. Because these fibers deform with the lesion, but are produced at different times and possibly with different orientations and natural configurations, they can be thought to constitute a constrained mixture (i.e., constituents co-exist within neighborhoods over which continuum averaging holds and deform together despite having different natural configurations). Analogous to continuum theories of membranes (26,52), Cauchy membrane stresses, or tensions T_i (= σ_ih), for a thin-walled intracranial aneurysm can be computed at any time t via (in principal directions 1 and 2)

$$\begin{array}{l}{T}_1(t)\frac{1}{{\lambda }_2(t)}\frac{\partial w}{\partial {\lambda }_1}=\frac{1}{{\lambda }_2(t)}\frac{\partial }{\partial {\lambda }_1}\left(\sum _k{w}^k\right)=\frac{1}{{\lambda }_2(t)}\sum _k\frac{\partial w^k}{\partial {\lambda }^k(t)}\frac{\partial {\lambda }^k(t)}{\partial {\lambda }_1(t)},\\ T_2(t)=\frac{1}{{\lambda }_1(t)}\sum _k\frac{\partial w^k}{\partial {\lambda }^k(t)}\frac{\partial {\lambda }^k(t)}{\partial {\lambda }_2(t)},\end{array}$$ (8)

where the strain energy function for the lesion (i.e., constrained mixture) w = Σw^k equals the sum of the energies stored in the k families of fibers, λ₁ and λ₂ are principal stretches experienced by the lesion, and

$${\lambda }^k(t)=\sqrt{{({\lambda }_{1}cos{\alpha }_o^k)}^2+{({\lambda }_{2}sin{\alpha }_o^k)}^2}$$ (9)

are stretches experienced by fibers in collagen family k relative to a common mixture reference configuration (with ${\alpha }_o^k$ the original angle between fiber family k and the 1-axis). To account for the constant deposition of new collagen fibers within evolving stressed configurations, it was assumed that there exists a target (homeostatic) deposition stretch $G_h^k$ (178), hence the stretch experienced by family k, relative to its unique natural configuration, is ${\lambda }_{n(\tau )}^k(t)=G_h^k{\lambda }^k(t)/{\lambda }^k(\tau )$, with t the current time and τ the past time at which family k was produced. Assuming locally parallel fibers within each family, a microstructurally-based constitutive relation for each family can be written in terms of the stored energy in a fiber (185), $W^k({\lambda }_{n(\tau )}^k)$, which depends on stretches experienced by the fiber relative to its individual natural configuration rather than a reference configuration for the lesion as a whole. Constituents only contribute to the overall structural integrity of the lesion until they are degraded, however, thus constituent stored energies per area can be written as (184)

$$w^k(t)=\frac{{\rho }^k(0)}{\rho }{Q}^k(t)W^k\left({\lambda }_{n(0)}^k(t)\right)+{\int }_0^t\frac{m^k(\tau )}{\rho }{q}^k(t-\tau )W^k\left({\lambda }_{n(\tau )}^k(t)\right)d\tau ,$$ (10)

where ρ^k (0) and Q^k (t) ∈ [0,1] represent the initial mass density, per unit area, and fraction of constituents produced prior to t = 0 that survive to current time t, and m^k (τ) and q^k (t−τ) ∈ [0,1] represent the mass density production rate and the fraction of constituents produced at time τ ∈[0,t] that survives to time t. Of particular note, the mass density productions and survival functions can be related to mass balance relations for each constituent, which in turn can incorporate chemical reaction kinetics (e.g., matrix synthesis or proteolytic degradation) naturally (186). In this way, it may be possible to build multi-scale models wherein global hemodynamics can be related to local wall stress, which in turn can be coupled to molecular-level biochemical reactions. Note, too, that the heredity integral contribution in equation (10) is similar to the concept of fading memory in nonlinear viscoelasticity; contributions to the overall structural integrity depend on the time since production. From equations (8)–(10), constituent principal Cauchy stress resultants are

$$\begin{array}{l}{T}_1^k(t)=\frac{1}{{\lambda }_2(t)}\left(\frac{{\rho }^k(0)Q^k(t)G_h^k}{\rho {\lambda }^k(0)}\frac{\partial W^k}{\partial {\lambda }_{n(0)}^k(t)}\frac{\partial {\lambda }^k(t)}{\partial {\lambda }_1(t)}+{\int }_0^t\frac{m^k(\tau )q^k(t-\tau )G_h^k}{\rho {\lambda }^k(\tau )}\frac{\partial W^k}{\partial {\lambda }_{n(\tau )}^k(t)}\frac{\partial {\lambda }^k(t)}{\partial {\lambda }_1(t)}d\tau \right),\\ T_2^k(t)=\frac{1}{{\lambda }_1(t)}\left(\frac{{\rho }^k(0)Q^k(t)G_h^k}{\rho {\lambda }^k(0)}\frac{\partial W^k}{\partial {\lambda }_{n(0)}^k(t)}\frac{\partial {\lambda }^k(t)}{\partial {\lambda }_2(t)}+{\int }_0^t\frac{m^k(\tau )q^k(t-\tau )G_h^k}{\rho {\lambda }^k(\tau )}\frac{\partial W^k}{\partial {\lambda }_{n(\tau )}^k(t)}\frac{\partial {\lambda }^k(t)}{\partial {\lambda }_2(t)}d\tau \right).\end{array}$$ (11)

In the case of axisymmetry, the sum over all k constituents yields the stress resultants for the lesion, which by equilibrium are given by (cf. equation 2)

$$T_1=\frac{P}{2{\kappa }_2}=\sum _k{T}_1^k,T_2=\frac{P}{{\kappa }_2}\left(1-\frac{{\kappa }_1}{2{\kappa }_2}\right)=\sum _k{T}_2^k$$ (12)

where the κ_i are principal curvatures. In cases of non-axisymmetry, equations for the full stress resultant tensor T can be computed similarly, though typically only via finite elements. Moreover, the Cauchy stress can be computed from the Cauchy stress resultant tensor via the deformed thickness. Illustrative examples of lesion G&R, independent of fluid-solid coupling, can be found in Baek et al. (183,184); see, too, the recent study by Kroon and Holzapfel (187).

Although Feng et al. (188) and Chatziprodromou et al. (189) support a similar FSG approach in principle, they assume the wall is linearly elastic and model changes in wall properties by simply prescribing decreases in a Young’s modulus that allow the wall to evolve. In contrast, we submit that there is a pressing need to embed rational growth and remodeling equations within a robust fluid-solid interaction model. This new paradigm was first presented by Figueroa et al. (190) and Baek et al. (191), but its full development must be our next focus. Indeed, although the overall theory is reasonably general, able to account for the evolution of properties, orientations, natural configurations, and mass fractions of multiple constituents, the primary challenge is to prescribe individual constitutive relations, particularly for the mass density productions, survival functions, and individual strain energy functions. Hence, there is further motivation for additional revealing experiments on both ISAs and AAAs.

CLOSURE

It is estimated that up to 12 million people harbor an intracranial aneurysm in the U.S.A. alone, over 30,000 of whom present yearly with a subarachnoid hemorrhage following rupture. It is expected that (a) advances in genetic research and a better understanding of risk factors will allow improved identification of patients at risk of developing saccular aneurysms and (b) advances in medical imaging will allow routine screening of high-risk patients, which together will result in a larger number of diagnosed unruptured lesions. Immediate prophylactic intervention for every diagnosed aneurysm will be unthinkable, however, because well less than 1% of these lesions rupture annually (1,51), and this low yearly risk appears to remain nearly constant as the patient ages (35,192). Rather, there will be an increasingly greater need to predict better which lesions will likely rupture, and thus require immediate intervention, and which will allow periodic monitoring. Such a decision can be aided by rational decision analysis algorithms (e.g., 193), but we must first understand better the biomechanics of enlargement that precedes rupture. Advances in neurointerventional technologies will similarly demand a better understanding of lesion stability. For example, the decision whether to perform a clip ligation, coil embolization, stenting, or any of a number of future endovascular techniques could be based in part on an assessment of an individual lesion and an understanding of how treatment may alter that lesion as well as the surrounding (adapting) vasculature. Computational FSG models have much to offer in this regard.

It is estimated that 175,000 people are diagnosed each year with an abdominal aortic aneurysm in the U.S.A. alone. Two current methods used to treat AAAs are (a) open surgical repair by replacing the diseased segment with a synthetic arterial graft or (b) endovascular repair by deploying a stent that is designed to shield the aneurysmal wall from the hemodynamic loads. Particularly provocative is the observation that some endovascularly treated AAAs actually regress, with decreases in size up to 8% (194,195). Given that an AAA actively grows and remodels during most of its natural history, this suggests that a stent can alter the applied loads in such a way that G&R may reverse the natural course of enlargement, which usually ends in rupture. Computational FSG models could help predict the rupture potential, help in the design of stents that exploit this advantageous regression, or predict if specific pharmacologic interventions could augment positive effects of a stent (59,60).

SUMMARY POINTS

1. Precise mechanisms by which intracranial and abdominal aortic aneurysms initiate, enlarge, or rupture remain unknown, but biomechanical factors play fundamental roles. Indeed, assessment of rupture-potential should include the geometry (shape, thickness), properties (anisotropy, strength), and applied loads (hemodynamic, perivascular), not be based primarily on the maximum dimension.

2. Following an early loss of elastin and subsequent loss of smooth muscle, a dynamic turnover of collagen can reinforce an aneurysm as it thins and enlarges; this turnover is controlled, in part, by cellular responses to changes in hemodynamic-induced wall shear and intramural stresses.

3. Atherosclerosis and intraluminal thrombus appear to play key roles in the development of AAAs whereas they appear to be a consequence of the development of some ISAs. That AAAs tend to be less stable biologically than ISAs suggests that the chronic inflammation associated with atherosclerotic lesions and intraluminal thrombus can be critical to the natural history.

FUTURE ISSUES

1. Continuing advances in vascular biology, medical imaging, biomechanics, and computational methods present a special opportunity to build integrated Fluid-Solid-Growth (FSG) Models that can account for 3-D patient-specific geometries, the full biofluid mechanics (shear and pressure), and the nonlinear mechanics of the wall (properties, biaxial stress), including cell-mediated changes in wall structure, properties, and geometry that will require multiscale modeling.

2. There is a pressing need for appropriate data and constitutive functions to enable us to exploit theoretical and computational advances. For example, there is a pressing need for morphological data on distal resistance beds. Moreover, amongst other substances, it is known that endothelin-1 and transforming growth factor-beta increase collagen synthesis by smooth muscle cells whereas nitric oxide and tissue necrosis factor-alpha decrease collagen synthesis, yet there are no quantitative descriptors of these relationships.