Quantifying the structural requirements of the folding transition state of Protein A and other systems

Abstract

The B-domain of protein A (BdpA) is a small 3-helix bundle that has been the subject of considerable experimental and theoretical investigation. Nevertheless, a unified view of the structure of the transition state ensemble (TSE) is still lacking. To characterize the TSE of this surprisingly challenging protein, we apply a combination of ψ-analysis (which probes the role of specific side chain to side chain contacts) and kinetic H/D amide isotope effects (which measures of hydrogen bond content), building upon previous studies using mutational φ-analysis (which probes the energetic influence of side chain substitutions). The second helix (H2) is folded in the TSE, while helix formation appears just at the carboxy and amino termini of the first and third helices, respectively. The experimental data suggest a homogenous, yet plastic TS with a native-like topology. This study generalizes our earlier conclusion, based on two larger α/β proteins, that the TSEs of most small proteins achieve ~70% of their native state’s relative contact order. This high percentage limits the degree of possible TS heterogeneity and requires a re-evaluation of the structural content of the TSE of other proteins, especially when they are characterized as small or polarized.

Introduction

The B-domain of protein A, BdpA, has been the focus of considerable experimental^{1; 2; 3; 4; 5; 6; 7; 8; 9} and theoretical investigation^{7; 10} due to its simple 3-helix bundle topology (Fig. 1A), small size (60 residues), two-state folding behavior, and fast folding rate. However, a consensus is still lacking concerning the structural content of its TSE.^{7; 10; 11} After extensive studies using φ-analysis, the participation of helices H1 and H3 in the TSE remains unclear.⁶ Similarly, the predicted helical content of the TS varies considerably among the theoretical treatments^{7; 10}. Some studies emphasize the presence of H1–H2 or H2–H3 microdomains, while others suggest the presence of all three helices.¹² To resolve these uncertainties, further information is required.

Fig. 1. Correlation between RCO and folding rate.

A) The locations of the biHis sites in BdpA^N are shown (each site is studied individually). B) Residues 12–51 of native BdpA represent an initial model of the TS that is drawn from the experimental results. C) Native and TS structures of Ub (76 residues) and Acp (98 residues) determined from previous ψ-analysis studies¹⁷; ²³. D) The RCO values of the three proteins studied using ψ-analysis span the RCO range. The definition of RCO is shown, where L is the length of the protein in amino acid residues, N is the number of contacts within 6 Å, and ΔSij is the number of residues separating the interacting pair of non-hydrogen atoms. Renderings created in PyMol.

We have developed ψ-analysis,¹³ in part to provide structural models of TSEs. This counterpart to mutational φ-analysis^{14; 15; 16} proceeds by introducing bi-Histidine (biHis) metal ion binding sites at specific positions on the protein surface. Upon addition of metal ions, these sites stabilize secondary and tertiary structures because an increase in the metal ion concentration stabilizes the interaction between the two histidine partners (appendix). The metal-induced stabilization of the TSE relative to the native state is represented by the ψ-value and directly reports the proximity of the two partners in the TSE. The ψ-value depends on the degree to which the biHis site is formed in the TSE. Values of zero or one indicate that the biHis site is absent or fully native-like in the TSE, respectively. Fractional values indicate that the biHis site recovers only part of the binding-induced stabilization of the native state. Examples of this partial recovery include sites having non-native ion binding affinity or sites being formed in a subpopulation of the TSE. The method is particularly well suited for identifying the side chain to side chain contacts that define the TS’s topology and structure. The mutational counterpart, φ-analysis, reports on the energetic influence of altering side chains and can underestimate the structural content of the TS^{13; 17; 18; 19} due to chain relaxation and accommodation or to non-native interactions.^{20; 21}

A second motivation for this study emanates from previous ψ-analyses of ubiquitin (Ub) and acyl phosphatase (Acp) (Fig. 1C) where we conjecture that the TSE’s of two-state proteins share a common and high fraction of their respective native topology.^{22; 23} This conjecture rests partly on the observation that the logarithm of the folding rate for these proteins strongly correlates with the structural complexity of the native state,^{24; 25; 26} for example, as defined by the relative contact order (RCO)²⁷ (Fig. 1D). In addition, ψ-analysis indicates that the TSEs of Ub and Acp have RCO^TS ~ 0.7–0.8 RCO^{N17; 22; 23}. These observations combine to suggest that TSs of other proteins obeying the known correlation of Fig. 1D also acquire a similar fraction of their native state’s RCO. However, Ub and Acp are both α/β proteins with intermediate to high RCOs (0.15 and 0.20, respectively). A test of the generality of this suggestion requires the determination of the RCO^TS of a helical protein with a low native RCO. BdpA is an excellent candidate, with an RCO of 0.10, lying at the lower end of the observed RCO range.

As reported in many previous studies of BdpA, we find that the TSE is challenging to characterize. Many ψ-values are fractional, as are the φ-values.⁷ However, remeasuring ψ in the background of additional mutations indicates that the fractional ψ-values do not arise from competing TSEs composed of either H1–H2 or H2–H3 microdomains, a possibility suggested by the symmetry of the protein and theoretical studies.¹¹ Furthermore, the kinetic amide H/D isotope effect^{28; 29; 30; 31; 32; 33} indicates that the TSE has ~70% of the native helical content. This critical information indicates that the TSE contains helix H2 along with half of both H1 and H3 docked against each other and H2 (Fig 1B). Folding from the TSE to the native state involves the extension of the H1 and H3 helices. The TS has an RCO that is ~ 60–70% of the native value. Finding this level for a small helical protein reinforces our conclusion that a high RCO^TS also applies for the other proteins that satisfy the empirical ln k_f - RCO correlation. In addition, we present a visualization of the TSE using constrained Langevin dynamics.

Results

ψ-analysis

Nine biHis sites were individually introduced with eight sites situated in i, i+4 positions along the three helices and one site replacing the E16-K50 salt bridge between H1 and H3 (Fig. 1A). The folding properties of each mutant were measured in the absence and presence of 1 mM zinc or nickel at 10°C, pH 7.7 (Table 1). ΔΔG_eq was determined from equilibrium denaturation measurements and the change in folding behavior according to

Table 1.

Equilibrium and kinetic parameters for divalent metal ion binding^a

Site	Mutationb	ΔΔGmut	$\mathrm{\Delta }\mathrm{\Delta }{\text{G}}_{\text{eq}}^{\text{equil}}(\mathrm{\Delta }\mathrm{\Delta }{\text{G}}_{\text{eq}}^{\text{kin}})$	$\mathrm{\Delta }\mathrm{\Delta }{\text{G}}_{\text{f}}^{‡}(\mathrm{\Delta }{\text{G}}_{\text{f}}^{‡})$	m0 ( ${\text{m}}_0^{\text{Me}}$)	mf/m0 ( ${\text{m}}_{\text{f}}^{\text{Me}}/{\text{m}}_0^{\text{Me}}$)	ψ0	Metal
	F14W			NA
p- WT	W15Y	NA	NA	(3.70 ± 0.02)	1.51 ± 0.02	0.72 ± 0.02	NA	NA
	H19N				(NA)	(NA)
			0.65 ± 0.01	0.27 ± 0.02
			(0.71 ± 0.04)	(3.50 ± 0.01)			0.24 ± 0.02	Zn
					1.46 ± 0.03	0.78 ± 0.01
	Q11H		NA	0.32 ± 0.12c	(1.33 ± 0.03)	(0.67 ± 0.01)
a	Y15H	−0.45 ± 0.10	(0.79 ± 0.05)c	NA			0.25 ± 0.01c	Znc
	(H1)
			1.46 ± 0.01	0.31 ± 0.03	1.46 ± 0.06	0.66 ± 0.02
			(1.68 ± 0.10)d	(3.48 ± 0.02)	(1.41 ± 0.05)d	(0.65 ± 0.03)d	0.039 ± 0.005d	Nid
			0.63 ± 0.01	0.32 ± 0.02	1.45 ± 0.05	0.63 ± 0.01
			(0.81 ± 0.07)	(3.35 ± 0.02)	(1.38 ± 0.05)	(0.63 ± 0.02)	0.23 ± 0.03	Zn
	Y15H
b	N19H	−0.89 ± 0.09
	(H1)		1.27 ± 0.01	0.43 ± 0.05	1.45 ± 0.08	0.63 ± 0.03
			(1.40 ± 0.12)	(3.35 ± 0.03)	(1.38 ± 0.14)	(0.62 ± 0.03)	0.11 ± 0.02	Ni
			1.20 ± 0.01	0.71 ± 0.03	1.58 ± 0.04	0.71 ± 0.01
			(1.19 ± 0.06)	(3.08 ± 0.02)	(1.39 ± 0.06)	(0.65 ± 0.01)	0.35 ± 0.03	Zn
	E25H
c	N29H	−0.76 ± 0.09
	(H2)		0.72 ± 0.01	1.01 ± 0.05	1.65 ± 0.09	0.75 ± 0.02
			(0.77 ± 0.07)	(3.19 ± 0.03)	(1.40 ± 0.06)	(0.69 ± 0.03)	1.71 ± 0.19	Ni
			ND	0.97 ± 0.06	1.61 ± 0.06	0.73 ± 0.01
	N29H		(1.30 ± 0.08)	(2.67 ± 0.03)	(1.48 ± 0.08)	(0.65 ± 0.02)	0.51 ± 0.05	Zn
d	Q33H	−0.97 ± 0.05
	(H2)		ND	1.50 ± 0.03	1.61 ± 0.06	0.73 ± 0.01
			(1.50 ± 0.04)	(2.67 ± 0.02)	(1.32 ± 0.05)	(0.65 ± 0.02)	0.99 ± 0.07	Ni
			0.45 ± 0.01	0.37 ± 0.02	1.52 ± 0.04	0.71 ± 0.01
			(0.28 ± 0.03)	(3.18 ± 0.01)	(1.32 ± 0.05)	(0.65 ± 0.01)	1.43 ± 0.18	Zn
	Q33H
e	D37H	−1.42 ± 0.06
	(H2)		1.39 ± 0.01	0.93 ± 0.03	1.52 ± 0.05	0.71 ± 0.01
			(1.28 ± 0.05)	(3.18 ± 0.02)	(1.31 ± 0.07)	(0.60 ± 0.02)	0.49 ± 0.04	Ni
			0.55 ± 0.02	0.37 ± 0.02	1.52 ± 0.03	0.73 ± 0.01
			(0.47 ± 0.03)	(3.06 ± 0.01)	(1.45 ± 0.03)	(0.75 ± 0.01)	0.71 ± 0.06	Zn
	A43H
f	A47H	−0.80 ± 0.05
	(H3)		1.39 ± 0.02	0.75 ± 0.09	1.52 ± 0.07	0.73 ± 0.02
			(1.16 ± 0.11)	(3.06 ± 0.02)	(1.27 ± 0.11)	(0.70 ± 0.02)	0.41 ± 0.04	Ni
			0.66 ± 0.01	0.49 ± 0.02	1.47 ± 0.04	0.76 ± 0.01
			(0.57 ± 0.09)	(3.19 ± 0.01)	(1.44 ± 0.08)	(0.74 ± 0.04)	0.78 ± 0.18	Zn
	A47H
g	K51H	−0.97 ± 0.05
	(H3)		1.86 ± 0.02	0.94 ± 0.06	1.47 ± 0.04	0.76 ± 0.01
			(1.53 ± 0.08)	(3.19 ± 0.01)	(1.34 ± 0.08)	(0.63 ± 0.01)	0.31 ± 0.02	Ni
			0.32 ± 0.01	0.05 ± 0.02	1.54 ± 0.04	0.78 ± 0.01
			(0.27 ± 0.11)	(3.43 ± 0.01)	(1.38 ± 0.03)	(0.73 ± 0.02)	0.15 ± 0.05	Zn
	K51H
h	A55H	−0.72 ± 0.10
	(H3)		1.40 ± 0.01	0.30 ± 0.04	1.54 ± 0.06	0.78 ± 0.01
			(1.21 ± 0.10)	(3.43 ± 0.02)	(1.45 ± 0.05)	(0.63 ± 0.02)	0.09 ± 0.01	Ni
i	E16H	−1.06 ± 0.35
			1.60 ± 0.01	0.32 ± 0.05	1.47 ± 0.09	0.74 ± 0.02	0.04 ± 0.01	Zn
			(1.68 ± 0.14)	(3.53 ± 0.03)	(1.37 ± 0.06)	(0.76 ± 0.07)
K50H
(H1–H3)			1.56 ± 0.01	−0.66 ± 0.08d	1.47 ± 0.16	0.74 ± 0.04
			(1.69 ± 0.16)d	(3.53 ± 0.03)	(1.59 ± 0.11)d	(0.70 ± 0.07)d	−0.04 ± 0.01d	Nid

^aTo minimize extrapolation errors, ΔΔG_f^‡ and ΔΔG_eq are calculated using the values determined at 2 and 6 M GdmCl, respectively, and are generated from a simultaneous fit to the two chevrons, with the parameter of interest being one of the fitting parameters. Units are kcal·mol⁻¹ (free energies) or kcal·mol⁻¹·M⁻¹ (m-values).

^bLocation of the biHis site is in noted parentheses.

^cFolding and unfolding rates were measured at 2.4M and 5.5 M GdmCl, respectively, as a function of [Zn²⁺] to obtain ΔΔG_f^‡ and ΔΔG_eq.¹⁷; ²³. The ψ_o-value is obtained from fitting a Leffler plot of ΔΔG_f^‡ vs ΔΔG_eq (Fig. 3B). The reported ΔΔG_eq are calculated using the parameters and equation in Fig. 3B at 1 mM Zn²⁺. The reported ΔΔG_f^‡ is then back-calculated using Eq. S1. The quoted error for ΔΔG_f^‡ is an overestimate as the covariance is not taken into account. In analyzing site a, the unfolding arms were fixed to the same slope.

^dMultiple phases were observed for sites a and i in the presence of Ni²⁺. Only the dominant phase is reported here. In the case of site a, the unfolding arms were fixed to the same slope.

$$\mathrm{\Delta }\mathrm{\Delta }{G}_{eq}([M{e}^{2+}])=-\mathit{RT}ln\left(\frac{k_f^{noMe}}{k_f^{Me}}/\frac{k_u^{noMe}}{k_u^{Me}}\right).$$ (Eq. 1)

The metal-induced stabilization and decrease in folding activation free energy reflect the difference between the ion binding affinity K_eq of the biHis site in the U(nfolded) state and in the N(ative) and TSs,

$$\mathrm{\Delta }\mathrm{\Delta }{G}_{eq}([{Me}^{2+}])=\mathit{RT}ln\left(1+\frac{[{Me}^{2+}]}{K_{eq}^N}\right)-\mathit{RT}ln\left(1+\frac{[{Me}^{2+}]}{K_{eq}^U}\right)$$ (Eq. 2a)

$$\mathrm{\Delta }\mathrm{\Delta }{G}_f^{‡}([{Me}^{2+}])=\mathit{RT}ln\left(1+\frac{[{Me}^{2+}]}{K_{eq}^{TS}}\right)-\mathit{RT}ln\left(1+\frac{[{Me}^{2+}]}{K_{eq}^U}\right).$$ (Eq. 2b)

The increase in stability due to metal ions is the same whether calculated from kinetic parameters or standard equilibrium chemical denaturation profiles (Table 1). This equivalence is derived assuming that metal ion binding equilibration is rapid relative to folding rates, a necessary condition for the application of ψ-analysis.

The limiting ψ-value from the extrapolation to zero metal ion concentration defines ψ_o. This quantity is obtained from the shifts in the folding and unfolding “chevron” arms in the dependence of relaxation rates on the denaturant in the presence and absence of metal ions (Fig. 2). The shifts provide $\mathrm{\Delta }\mathrm{\Delta }{G}_f^{‡}$ and $\mathrm{\Delta }\mathrm{\Delta }{G}_u^{‡}$, respectively, and ψ_o is calculated according to,

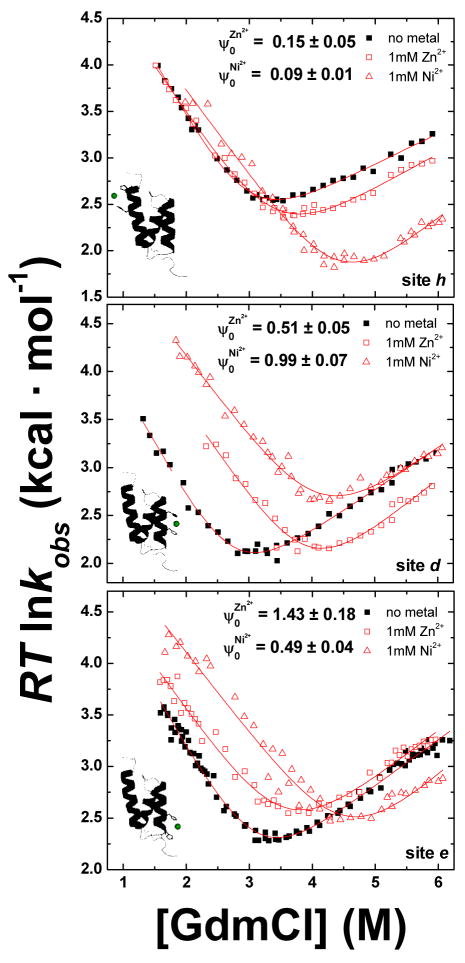
Fig. 2. Metal-dependent chevrons plots for BdpA.

Variants with different biHis sites respond differently to the presence of Zn²⁺ or Ni²⁺ producing low, intermediate, and high ψ_o-values. For many biHis sites (e.g., sites d and e), the different coordination geometries of Zn²⁺ and Ni²⁺ produce different ψ_o-values for the same site.

$$\mathrm{\Delta }\mathrm{\Delta }{G}_f^{‡}=\mathit{RT}ln\left((1-{\psi }_o)+{\psi }_o{e}^{\mathrm{\Delta }\mathrm{\Delta }{G}_{eq}/RT}\right),$$ (Eq. 3)

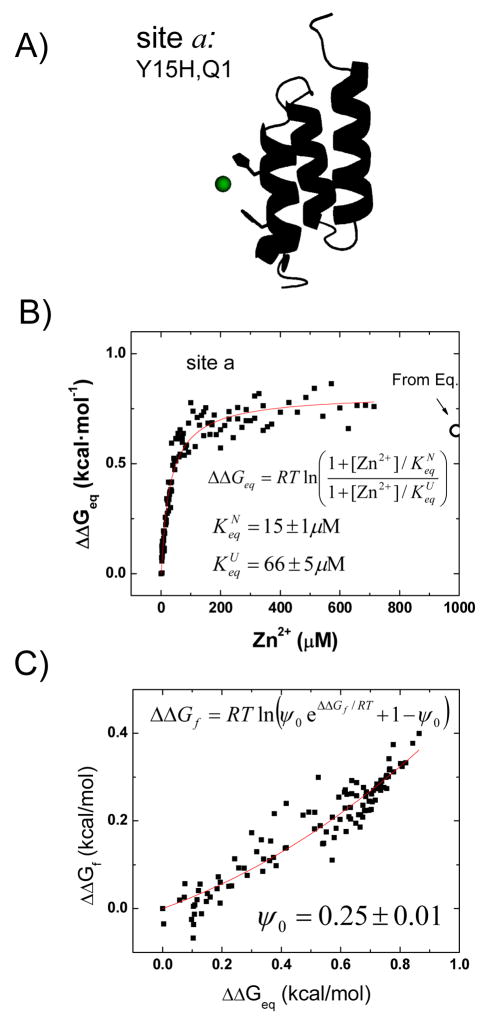
where $\mathrm{\Delta }\mathrm{\Delta }{G}_{eq}=\mathrm{\Delta }\mathrm{\Delta }{G}_f^{‡}-\mathrm{\Delta }\mathrm{\Delta }{G}_u^{‡}$. An independent determination of ψ_o for site a also is obtained from the fit of a Leffler plot of ΔΔG_f^‡ versus ΔΔG_eq using relaxation data taken under folding and unfolding conditions at dozens of Zn²⁺ concentrations (Fig. 3). The resulting ψ_o is in agreement with the value determined from the shift in the chevron arms (0.24 ± 0.02 versus 0.25 ± 0.01).

Fig. 3. Kinetics as a function of Zn²⁺ at fixed [GdmCl].

A) For the biHis mutant at site a located at the amino-terminus of H1, B) the change in stability ΔΔG_eq is calculated at different [Zn²⁺] by measuring the folding and unfolding rates at 2.4 M and 5.5 M GdmCl, respectively (data not shown). The values agrees with those obtained from two equilibrium denaturation profiles in the absence and presence of 1 mM Zn²⁺ (○) The unfolded and native state Zn²⁺ affinities, $K_{eq}^U$ and $K_{eq}^N$, are directly obtained from fitting to the equation shown. C) Corresponding Leffler plot showing the relationship between ΔΔG_f^‡ and ΔΔG_eq. The ψ_o is calculated directly from the fit using the given equation. The resultant ψ_o = 0.25 ± 0.01 is in good agreement with the value that is calculated by measuring two chevrons at zero and 1 mM Zn²⁺ (0.24 ± 0.02, Table 1).

The magnitude of ψ_o reflects the degree to which the biHis site is formed in the TSE. When metal binding only affects the unfolding rate k_u, the probed structure is absent in the TSE, and ψ_o is zero. Conversely, when the perturbation only affects k_f, the ion binding affinity in the TS is native-like ( $K_{eq}^N=K_{eq}^{TS}$) and ψ_o is unity. However, when both the folding and unfolding arms shift, ψ_o is fractional. The biHis site could be native-like in a fraction of the TSE at a level given by the ψ_o-value, or the site could have non-native binding affinity (e.g., a site with less favorable binding geometry, $K_{eq}^N<K_{eq}^{TS}$), or a combination of the two scenarios might be operative.^{17; 18}

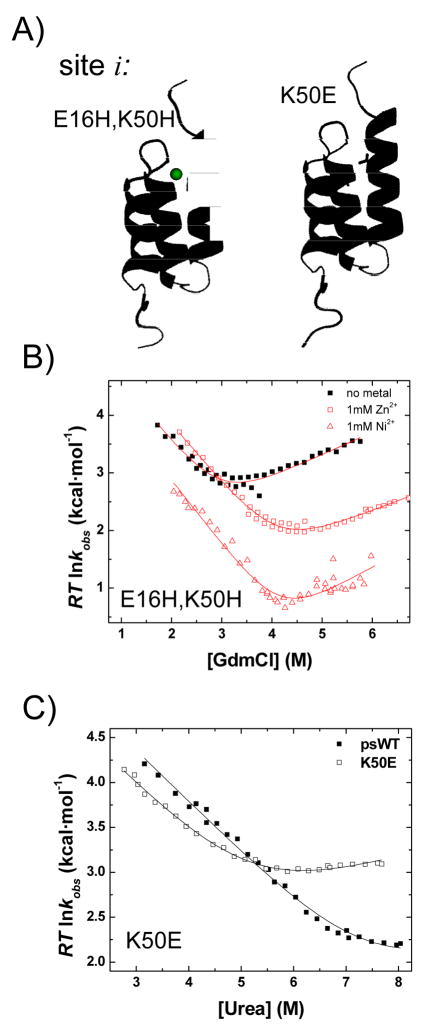
A large majority of the ψ_o are fractional for both Zn²⁺ and Ni²⁺, and they display a pattern similar to the mutational φ-values^{5; 7} (Table 1, Fig. 4). The helix H2 has the strongest presence in the TS, followed by the amino terminus of H3 and the carboxy terminus of H1. The other ends of H1 and H3 (the chain termini) have near zero ψ_o and φ. Site i, a biHis site across the E16-K50 salt bridge between H1 and H3, yields a nearly vanishing ψ_o (Fig. 5B), indicating an absence of this salt bridge in the TSE, a finding that is confirmed using φ-analysis of a K50E mutant at 15°C in low ionic conditions (φ^K50E ≤ 0.24 ±0.02, Fig. 5C).

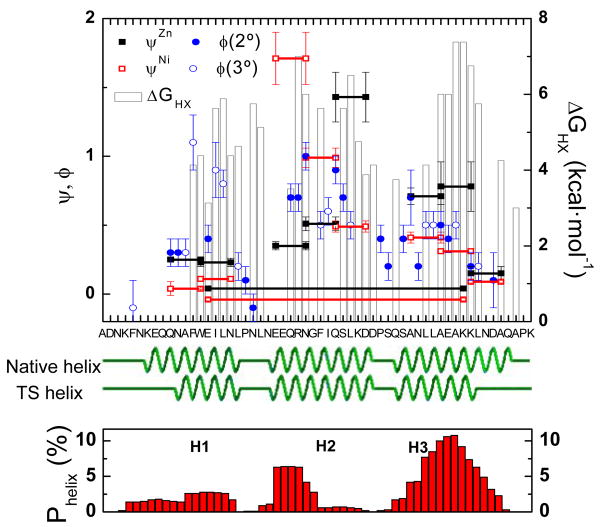
Fig. 4. ψ_o- and φ-values and hydrogen exchange data for BdpA.

The ψ_o-values in Zn²⁺ and Ni²⁺ are plotted alongside the φ-values⁷ for the residues on the helical surface, in turns (2°) and in the core (3°) and the ΔG_HX from hydrogen exchange (HX) for the native protein.⁵ Horizontal lines connect the two biHis partners. The native and proposed helical content of TSE are illustrated in green, while the bottom presents the AGADIR¹⁰⁶ predictions of the helical content for a chain devoid of tertiary structure.

Fig. 5. Absence of the E16-K50 salt bridge between H1–H3 contacts according to ψ- and φ-analysis.

A) The native E16-K50 salt bridge between H1–H3 is probed by separately inserting a biHis site (site i) and a K50E mutation. B) The biHis site is measured to be absent from the TS according to psi-values taken in Zn²⁺ (□) and Ni²⁺ (△). Multiphase behavior is observed in the presence of Ni²⁺; only the dominant phase is reported. Regardless, the metal has little effect on the TS. C) Similarly, a K50E substitution disrupts the salt bridge in the native state under low ionic conditions (50mM HEPES, urea rather than GdmCl) at 15°C. The φ^K50E is calculated assuming the unfolding arms have the same slope (m_u-value). Because of this assumption and the extrapolations involved, the φ-value at zero denaturant (0.24 ±0.02) should be considered an upper bound estimate. Overall, both methods indicate that E16-K50 contact is not well-formed in the TS.

Lack of TS heterogeneity

The extensive number of fractional ψ_o-values for BdpA contrasts with the findings for Ub,¹⁷ Acp,²³ and the cross-linked version of the GCN4 coiled coil¹³. These three proteins have obvious TS nuclei composed of multiple native-like biHis sites whose ψ_o equal unity. In BdpA, the abundance of fractional ψ-values may be indicative of structural heterogeneity in the TSE, as observed in the folding the dimeric version of the GCN4 coiled coil. In this protein, fractional ψ_o values are observed due to TS heterogeneity wherein nucleation occurs at multiple sites along the length of coiled coil.^{13; 34} The flux through each nuclei could be manipulated by mutation, e.g., a destabilizing Ala→Gly mutation at one site decreased the probability of nucleation occurring at this site, which increased the probability of nucleation occurring at the other sites. The change in the nucleation probability is accompanied with a change in the measured ψ_o values.

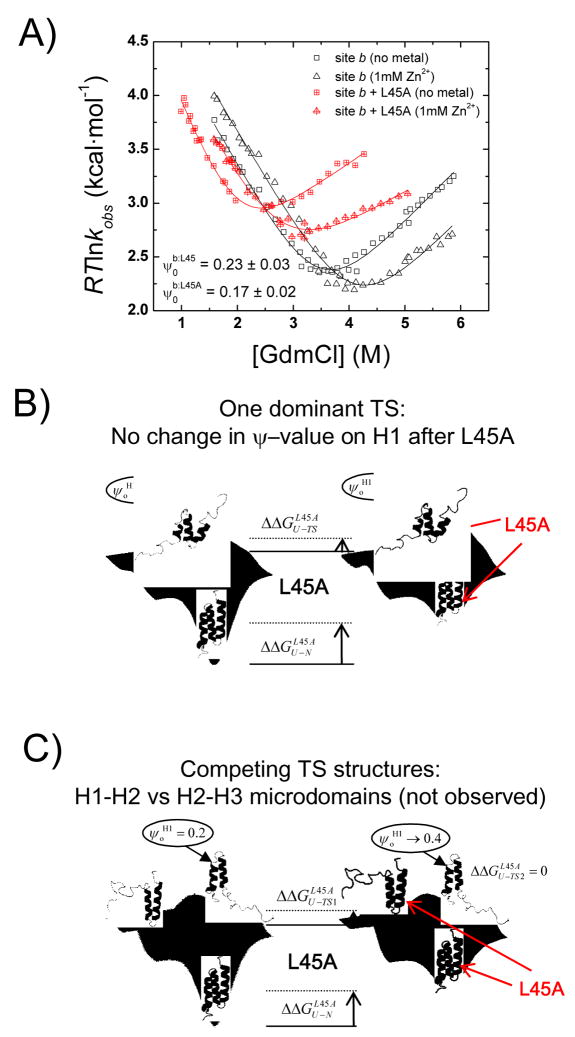
We use this strategy to investigate whether the TSE of BdpA is likewise heterogeneous. The two most plausible competing TS structures are the H1–H2 and H2–H3 microdomains, the two most frequently predicted species.¹¹ Because the ψ_o- and φ-values⁷ generally are higher in the H2-H3 microdomain, this species should be the more dominant. We sought to determine whether the population of the alternative species, the H1–H2 microdomain, would increase in response to a destabilization of the H2–H3 microdomain. Accordingly, we introduce a L45A mutation at the H2–H3 interface which is known to destabilize the native and the TS by 1.3 and 0.7 kcal·mol⁻¹, respectively (φ^L45A=0.5–0.6).⁷ We test for an increase in the population of the H1–H2 microdomain by remeasuring the ψ_o-value for Site b, located at the carboxy terminus of H1, in the background of the L45A substitution. This site spans the hydrophobic residues in the H1–H2 interface and is a representative site for the formation of this microdomain. In the heterogeneous scenario, the degree of H2–H3 destabilization upon introduction of the L45A mutation should increase the relative population of the minor H1–H2 species in the TS from 20% to at least 40%, according to the initial ψ_o-value for Site b (0.23 ± 0.03). However, ψ_o remained unchanged (0.17 ± 0.02) (Fig. 6A). This invariance after the significant destabilization in H2–H3 is inconsistent with a heterogeneous TSE containing the H1–H2 and H2–H3 microdomains as the major competing alternatives (Fig. 6C). Therefore, we conclude that the TSE is not composed of two distinct TS ensembles centered about H1–H2 or H2–H3 (Fig. 6B), in agreement with recent work based on the temperature invariance of φ-values.⁶

Fig. 6. Testing for competing TS composed of either H1-H2 or H2-H3 microdomains.

A) The ψ_o-value for site b, located on the carboxy-terminus of H1, is measured in the presence and absence of a destabilizing L45A mutation on H3. This mutation destabilizes the H2–H3 interaction in native and TS by 1.3 and 0.7 kcal·mol⁻¹, respectively.⁷ Nevertheless, the fractional ψ_o-value remains unchanged by the mutation. Hence, the fractional ψ_o-value does not result from a fractional population of the H1–H2 microdomain in the TSE. Had this been the case, the ψ_o-value would have increase from 0.2 to 0.4 upon destabilization of the H2–H3 microdomain. Therefore, both H1 and H3 participate in a singular TSE (Panel B), rather than a scenario where the TS contains two competing populations composed of either the H1–H2 or the H2–H3 microdomains (Panel C).

Given this lack of TS heterogeneity, the origin of the fractional ψ_o can be understood by their dependence on metal ion type. The different preferential coordination geometries of the metal ions³⁵ support the view that the fractional ψ_o emerge due to non-native binding affinity in the TS, for example $K_{eq}^{TS}/K_{eq}^N\approx 2$ (Table 2). If the site has a distorted geometry in a plastic TS, metals with different coordination geometries should stabilize the TS to different extents, relative to the stability each metal imparts to the native state. Hence, the use of different metal ions is likely to alter ψ_o, as observed in the present study. Overall, the appearance of metal-dependent, non-unity ψ_o indicates that the biHis sites have a non-native geometry in a malleable TS.

Table 2.

Relative metal binding affinities in the U, N and TSs

Site	Mutationa	ΔΔGeq (kinetic)	ψ0	$K_{eq}^U/K_{eq}^N$	$K_{eq}^{TS}/K_{eq}^N$ b	Metal
		0.71 ± 0.04	0.24 ± 0.02	3.6 ± 0.3	2.2 ± 0.2	Zn
a	Q11H Y15H (H1)	0.79 ± 0.05c	0.25 ± 0.01c	4.3 ± 0.4c	2.4 ± 0.3c	Znc
		1.68 ± 0.10	0.039 ± 0.005	19.8 ± 3.5	11.5 ± 2.2	Ni
b	Y15H N19H (H1)	0.81 ± 0.07	0.23 ± 0.03	4.2 ± 0.5	2.4 ± 0.4	Zn
		1.40 ± 0.12	0.11 ± 0.02	12.1 ± 2.7	5.6 ± 1.4	Ni
c	E25H N29H (H2)	1.19 ± 0.06	0.35 ± 0.03	8.2 ± 0.8	2.3 ± 0.3	Zn
		0.77 ± 0.07	1.71 ± 0.19	4.0 ± 0.5	0.7 ± 0.1	Ni
d	N29H Q33H (H2)	1.30 ± 0.08	0.51 ± 0.05	10.1 ± 1.4	1.8 ± 0.3	Zn
		1.50 ± 0.04	0.99 ± 0.07	14.4 ± 1.3	1.0 ± 0.1	Ni
e	Q33H D37H (H2)	0.28 ± 0.03	1.43 ± 0.18	1.7 ± 0.1	0.9 ± 0.1	Zn
		1.28 ± 0.05	0.49 ± 0.04	9.6 ± 0.9	1.9 ± 0.2	Ni
f	A43H A47H (H3)	0.47 ± 0.03	0.71 ± 0.06	2.3 ± 0.1	1.2 ± 0.1	Zn
		1.16 ± 0.11	0.41 ± 0.04	7.8 ± 1.6	2.1 ± 0.5	Ni
g	A47H K51H (H3)	0.59 ± 0.09	0.78 ± 0.18	2.8 ± 0.4	1.2 ± 0.3	Zn
		1.53 ± 0.08	0.31 ± 0.02	15.1 ±2.1	2.8 ± 0.5	Ni
h	K51H A55H (H3)	0.27 ± 0.11	0.15 ± 0.05	1.6 ± 0.3	1.5 ± 0.6	Zn
		1.21 ± 0.10	0.09 ± 0.01	8.6 ± 1.5	5.1 ± 1.0	Ni
i	E16H K50H (H1–H3)	1.68 ± 0.14	0.04 ± 0.01	19.8 ± 5.0	11.1 ± 3.1	Zn
		1.69 ± 0.16d	−0.04 ± 0.01d	20.0 ± 5.7d	64.5 ± 21.4	Ni

^aLocation of the biHis site is in parentheses.

^bDetermined by fitting $\mathrm{\Delta }\mathrm{\Delta }{G}_{eq}^{M^{2+}}$ assuming $\left[{Me}^{2+}\right]\gg K_{eq}^U,K_{eq}^N$.

^cValues directly calculated from measuring folding and unfolding rates at fixed GdmCl concentrations of 2.4 M and 5.5 M, respectively, as a function of [Zn²⁺] (Fig. S3B).

Amide H/D Kinetic Isotope Effect

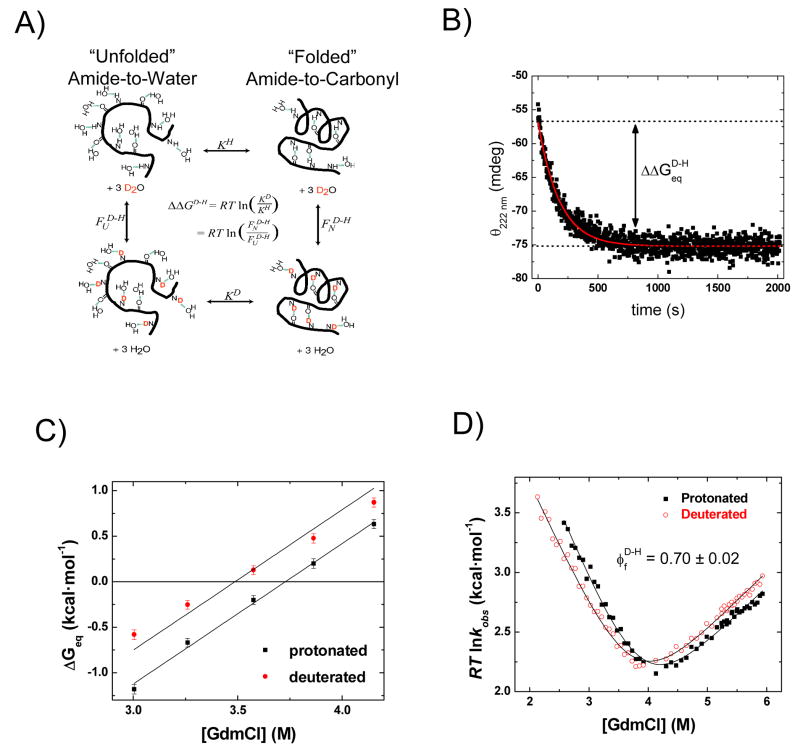
To further characterize the TS, we determined the fraction of formed helical hydrogen bonds (H-bonds) in the TS using backbone amide kinetic isotope effects.^{30; 32; 33} Folding rates of the protein with deuterated amide hydrogens were compared to the protonated version for the same bulk solvent conditions. The fraction ${\phi }_f^{D-H}$ of formed helical H-bonds in the TS was obtained from the ratio of the change in the folding activation free energy relative to the change in equilibrium stability, i.e. ${\phi }_f^{D-H}=\mathrm{\Delta }\mathrm{\Delta }{G}_f^{D-H}/\mathrm{\Delta }\mathrm{\Delta }{G}_{eq}^{D-H}$. We measured ${\phi }_f^{D-H}=0.70\pm 0.02$ from the difference in the kinetic parameters obtained from the chevron plots of the deuterated and protonated proteins in 11% D₂O (Fig. 7D). Also, the equilibrium isotope effect was determined from independent equilibrium denaturation measurements (Figs. 7A–C). The $\mathrm{\Delta }\mathrm{\Delta }{G}_{eq}^{D-H}$ from the equilibrium experiments agrees with the value obtained from the kinetic measurements (−0.39 ± 0.03 versus −0.37 ± 0.06 kcal·mol⁻¹).

Fig. 7. Amide H/D isotope effects.

A) Thermodynamics of D/H backbone amide substitution. The folded proteins are on the right (shown as a single α-helix and β-turn) and the unfolded proteins are on the left (hydrated random coil). The isotope effect on protein stability is represented by the equilibrium stability of protonated protein, K^H, as compared to the equilibrium stability of deuterated protein, K^D (horizontal arrows). Vertical arrows represent the complementary arms of the thermodynamic cycle. These arms are the fractionation factors, $F_N^{D-H}$ and $F_U^{D-H}$, for the folded and unfolded states, respectively, and represent the collective isotopic preference of the amide sites in each state relative to solvent. The equation (center) describes the mathematical relationship of $\mathrm{\Delta }\mathrm{\Delta }{G}_{\mathit{Equil}}^{D-H}$ and the four equilibrium constants defining the thermodynamic cycle. B) The equilibrium isotope effect is obtained by the change in circular dichroism (CD) signal at 222 nm in a separate experiment. The fully deuterated protein is diluted 100-fold into H₂O solvent under conditions where stability is determined prior to significant backbone amide exchange (pH 4.5, 10 °C).¹⁰⁷ The stability of the deuterated and the protonated protein is determined from the initial and final CD levels. C) The equilibrium isotope effect is obtained at five different denaturant concentrations. The stability of the deuterated and the protonated protein are fit using the average m_o-value obtained from the chevron data. D) In the kinetic isotope effect measurement, the different folding rates of protonated and deuterated proteins produce two offset chevrons. Their offset translates to a ${\phi }_f^{D-H}$ value of 0.70 ± 0.02, which equates to the fraction of backbone amide helical hydrogen bonds formed in the TSE. The m_f and m_o for protonated (deuterated) state are 1.17 ± 0.03 (1.06 ± 0.02) and 1.64 ± 0.04 (1.54 ± 0.03) kcal·mol⁻¹·M⁻¹, respectively, and $\mathrm{\Delta }{\text{G}}_{\text{f}}^{‡}=3.22\pm 0.01\text{kcal}·{\text{mol}}^{-1}$. The kinetic and equilibrium isotope effects are $\mathrm{\Delta }\mathrm{\Delta }{\text{G}}_{\text{f}}^{‡}=-0.27\pm 0.02\text{kcal}·{\text{mol}}^{-1}$ and $\mathrm{\Delta }\mathrm{\Delta }{\text{G}}_{\text{eq}}^{\text{D}-\text{H}}=-0.39\pm 0.03\text{kcal}·{\text{mol}}^{-1}$. Values for ΔΔG_f^‡ and ΔΔG_u^‡ are calculated at 2.75 and 5.5 M GdmCl.

The measured ${\phi }_f^{D-H}$ indicates that 70%, or ~23, of the 33 native helical hydrogen bonds are formed in the TS. This percentage equates to the fraction of surface burial in the TS, m_f/m₀ = 0.72±0.02, and is consistent with our proposal that roughly equal percentages of tertiary and secondary structure are formed in the TS.^{30; 32}

A preliminarily interpretation is that ${\phi }_f^{D-H}=0.70\pm 0.02$ indicates that 70% of the native H-bonds are formed in the TS, but other possible interpretations of the kinetic isotope data are now considered. All the H-bonds may be formed in the TSE, but with an average of 70% of the native isotope effect. A second possibility asserts that the 70% value might be due to all H-bonds either being formed 70% of the time, or being formed all of the time but in a distorted geometry with 70% of the equilibrium isotope effect. Both possibilities are inconsistent with the lack of helix formation at the amino and carboxy termini of H1 and H3, respectively, as indicated by the near zero values for the φ and ψ_o across these regions (Fig. 4).

The ensemble and time-averaged 70% isotope effect could also arise from intermediate scenarios. For example, the entire TSE might have 60% of the H-bonds formed all of the time and another 20% of the H-bonds formed half the time. In addition, the analysis of the kinetic isotope effect assumes that all helical H-bonds contribute equally to the global $\mathrm{\Delta }\mathrm{\Delta }{G}_{eq}^{D-H}$. This assumption is supported by the linear scaling of $\mathrm{\Delta }\mathrm{\Delta }{G}_{eq}^{D-H}$ with the total number of helical H-bonds in the protein.³⁰ Accordingly, we estimate that the percentage of H-bond may range from 60–80%. Our calculation below of the RCO of the TSE below accounts for these possibilities.

The ~70% helical H-bond content of the TSE reported by the analysis of ${\phi }_f^{D-H}$ apparently exceeds the fraction suggested by the ψ_o-values and the helix-probing φ^Ala→Gly values.⁷ The kinetic isotope effect data provide a more definitive conclusion because H/D substitution directly probes hydrogen bonding and only marginally perturbs the bonds. The low ψ_o are likely to arise from distorted helical geometries in the TSE. The φ-analysis only yields definite conclusions regarding H2. Seven sites on the surface of H1 and H3 have φ^Ala→Gly between 0.3–0.5. Four of these sites have ΔΔG_eq^Ala→Gly ~1.5–1.8 kcal·mol⁻¹, which is about 1 kcal·mol⁻¹ higher than the canonical value for context-free Ala→Gly helical substitutions.^{36; 37} We suggest that the fractional φ are consistent with helix formation, but within a context lacking the additional ~1 kcal·mol⁻¹ of tertiary stabilization present in the native state (i.e., $\mathrm{\Delta }\mathrm{\Delta }{G}_f^{{‡}^{\mathit{Ala}\to \mathit{Gly}}}\approx \mathrm{\Delta }\mathrm{\Delta }{G}_{\mathit{context}\mathit{free}}^{\mathit{Ala}\to \mathit{Gly}}$). Alternatively, the glycine substitution itself could reduce the helical content of the TS, producing a lower than expected φ. Because of these ambiguities in interpreting φ, kinetic isotope effect experiments are essential to enable the proper interpretation of the φ- and ψ-data.

Properties of the TS

The pattern of ψ and φ-values indicates that the H-bond content identified by the isotope effect data are best explained by the presence in the TS of a completely folded H2 with the adjoining portions of H1 and H3 also forming helical structure (e.g., a core composed of residues N12-K51, Fig. 1B). This H-bond content agrees extremely well with the native state hydrogen exchange data (Fig. 4).⁵ The H-bonds in our proposed model are observed to exchange only upon global unfolding (i.e., exchange only in molecules lying on the unfolded side of the kinetic barrier), while our model’s unstructured regions are found to fray prior to global unfolding.

Mutational studies by Fersht and coworkers⁷ demonstrate that the folded portions of the three helices dock against each other in the TSE. Moderate to high φ-values are observed when highly destabilizing core mutations are introduced directly between each of the pairs of helices (e.g., ${\phi }_{H1-H2}^{I17V}[\mathrm{\Delta }\mathrm{\Delta }{G}_{eq}=0.8\text{kcal}·{\text{mol}}^{-1}]=0.9,{\phi }_{H1-H3}^{L46A}[\mathrm{\Delta }\mathrm{\Delta }{G}_{eq}=1.9\text{kcal}·{\text{mol}}^{-1}]=0.5,{\phi }_{H2-H3}^{L45A}[\mathrm{\Delta }\mathrm{\Delta }{G}_{eq}=1.5\text{kcal}·{\text{mol}}^{-1}]=0.5$) as well as in the core between the three helices (e.g., ${\phi }_{H1-H2-H3}^{L35A}[\mathrm{\Delta }\mathrm{\Delta }{G}_{eq}=2.4\text{kcal}·{\text{mol}}^{-1}]=0.5,{\phi }_{H1-H2-H3}^{A49G}[\mathrm{\Delta }\mathrm{\Delta }{G}_{eq}=3.6\text{kcal}·{\text{mol}}^{-1}]=0.5$). Given these results, the TSE can be described as a mini-three helix bundle with frayed termini.

A TS model containing 70% of the formed H-bonds produces the RCO^TS/RCO^N ratio as 0.66–0.72, depending on the exact location of the native-like helical H-bond and assuming the remaining regions are unstructured. To test the robustness of this fraction, the RCO^TS is recalculated for models having 60–80% of the H-bonds formed. The calculated RCO ratios range from 0.61 – 0.72 when assuming a native-like geometry for the folded regions, as suggested by high inter-helical φ-values. The next section analyzes this assumption and the influence of chain relaxation in the TSE on the RCO^TS/RCO^N fraction.

Relaxing the TS model

All-atom implicit solvent Langevin dynamics (LD) simulations^{38; 39} are employed to investigate potential structural relaxation of the native-like TS models and the effect on their RCO values (Figs. 8, S1). This modeling is motivated by the mounting evidence that proteins undergo some chain relaxation along the folding trajectory, for example, minimizing energy through the formation of non-native hydrophobic interactions as observed in the intermediates of Rd-apocytochrome b₅₆₂,²¹ IM7,⁴⁰ and apomyoglobin,⁴¹ and in the TS of Ub.¹⁸ Specifically, the turns in BdpA between the helices yield low φ-values,⁷ indicating that the helices repack, being shifted or rotated relative to their native positions. Furthermore, the intermediate ψ-values reveal a level of plasticity in the TS in BpdA. Additional evidence for TS relaxation of BdpA is the preferential stabilization of the TS for G30 mutations.^{2; 4; 6}

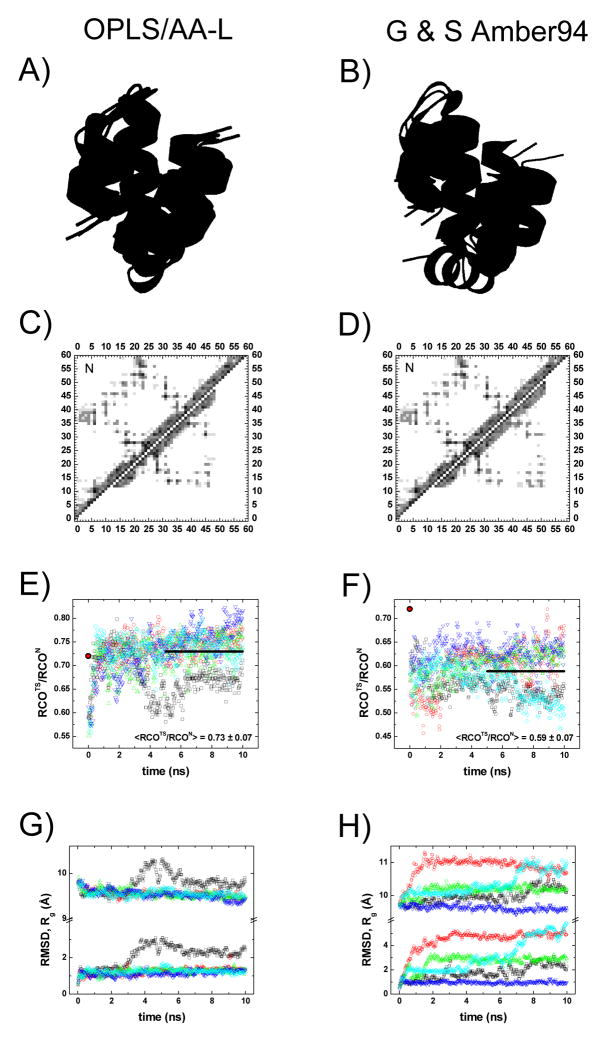
Fig. 8. Modeling the TS using Langevin Dynamics simulations.

Our initial model of the TS has native-like residues N12-K51 (black), representing 70% helical hydrogen bond formation, It is superimposed on representative structures taken from ten LD simulations using either the OPLS/AA-L (Panel A) or G–S Amber 94 force field (Panel B). The native helical residues for H1, H2, and H3 are colored blue, green, and red, respectively. Unstructured regions are not shown for clarity and are assumed to make no additional contacts. Average contact maps are calculated for five separate simulations (in different colors) from the structures appearing in the last 5 ns and are presented in the lower diagonals of Panels C–D, while the average contact map from the NMR ensemble (26 structures)⁷ are shown in the upper diagonals. Despite the increased motion of H3 in the G–S Amber 94 force field in D, the average contact map still exhibits native-like behavior with H1–H3 contacts. In the RCO plots (Panels E–F), the RCO^TS/RCO^N of the initial structural model is shown () along with the average value from the last 5 ns (solid line) of the trajectories. Changes in RMSD and R_g (Panels G–H) track with the observed changes in RCO. Renderings created in PyMol.

The robustness of the theoretical predictions are tested by running separate implicit solvent LD simulations employing two different force fields, OPLS/AA-L ^{42; 43} and Garcia and Sanbonmatsu’s modified version of Amber 94 (G–S Amber 94).⁴⁴ Beyond the standard terms in the force fields, the only additional constraints are posited for the H-bonds in the TSE. The O—H-N distances in these H-bonds are constrained to the native distances using a harmonic force constant of 100 kcal·mol⁻¹·A˚́⁻¹. The goal is to generate models of the TSE that are consistent with the experimental data rather than predict or test whether the model is a true transition state. Accordingly, simulations are conducted only using the folded residues (e.g., N12-K51) to avoid obtaining a trajectory that follows a possible downhill reaction towards the N or U states.

Figure 8 displays the results of ten 10 ns trajectories for a mini-bundle of N12-K51 starting with 70% H-bond formation (five trajectories with each force field). Trajectories with either force field indicate that the imposed O – H distance restraints provide enough stability that the three helices remain folded and in a native-like topology, although the structures do rearrange occasionally. Without the H-bond restraints, the three helices unfold and dissociate (data not shown).

During the initial 2 ns portion of the trajectories, H1 and H3 reposition themselves relative to the largely unperturbed H2. The three helices remain mostly in contact although H3 exhibits a low level of undocking with the G–S Amber 94 force field (compare Fig. 8A to 8B). Regardless, the average contact map over the last 5 ns of the trajectories still retains the native pattern (Figs. 8C,D). Because of the increased freedom of motion for H3, the structures calculated using the G–S Amber 94 force field retain a smaller fraction of the native RCO, ${\langle RC{O}^{TS}/RC{O}^N\rangle }_{5\mathit{trajectories}}^{5-10nsec}=59\pm 7\%$ (Fig 8F). The corresponding OPLS/AA-L trajectories predict the RCO as remaining much closer to the initial value, ${\langle RC{O}^{TS}/RC{O}^N\rangle }_{5\mathit{trajectories}}^{5-10nsec}=73\pm 7\%$ (Fig 8E). Very similar conclusions are obtained for models where the simulations begin with constraints applied for either 60% or 80% of the native helical H-bond content (Fig S1).

In summary, the LD simulations indicate that the RCO^TS/RCO^N ratio of 0.6–0.7 of our TS models is robust to the chain relaxation occurring in LD in addition to the modification in the assumed degree of helical H-bond content in the TSE.

Discussion

The TSE ensemble of BdpA is well-described as a mini-three helix bundle with frayed ends. This identification has been determined using a combination of ψ- and φ-analysis and kinetic isotope data. Beginning from this TS mini-bundle, folding to the native state proceeds by the extension of the two terminal helices and potentially by a mild readjustment of their relative orientation. The RCO for the TSE varies between 60–70% of the native value, with the uncertainty representing the extent of H-bonding and the degree of structural relaxation.

The folding of small proteins has been proposed by us^{45; 46; 47} and others^{48; 49} to be a nucleation process with the chain attaining a coarse version of the native topology in the TS. This proposal is supported by the well known correlation between ln k_f and the RCO, a metric of topological complexity.²⁷ For three proteins, BdpA, Ub, and Acp, whose topologies span the observed range of RCO values, we have shown that their TSEs share a common and high fraction of the native topology, RCO^TS ≈ 0.7·RCO^N. Accordingly, we contend that the TSEs of other proteins satisfying the RCO correlation should also exhibit RCOs sharing this high fraction.

As further support of our contention, Wallin and Chan use a C_α Gō-like model and find the TSEs of 13 proteins have 0.7·RCO^N.50 Similarly, all-atom simulations by Vendruscolo et al. for ten proteins find TSEs that share a common, albeit lower fraction, 0.5·RCO^N,⁵¹ potentially due to the incorporation in the analysis of φ-values that may underestimate chain-chain contacts. Likewise, Bai, Zhou and Zhou find that the use of a universal 78% value for the Total Contact Distance of the TS produces the best correlation between the critical nucleation size of the TS and ln k_f for 41 proteins.²⁵

We utilize the RCO metric to characterize a protein’s topology, in part, because of its broad usage. Other metrics ^{24; 25; 26} produce a similar conclusion. An advantage of the RCO metric is that topologically similar TS structures provide similar RCO values even when there is local “microscopic heterogeneity” such as frayed helices or hairpins²³ because the frayed portions in the simulations have contacts with approximately the same average sequence separation as their neighbors. Hence, the RCO, which is normalized to the number of contacts, remains unchanged upon fraying.

However, all such metrics are just proxies for the key properties of the TS. Any single parameter is likely to be insufficient to characterize a diverse set of protein folds. At the TS, the addition of more native-like structure pushes the system thermodynamically downhill. The chain is already pinned at enough points in the TS that further structure formation is thermodynamically favorable. The precise RCO at which this situation ensues varies according to the type and arrangement of secondary structure elements in any individual protein. Nevertheless, our results indicate that a native-like topology is expected to be a general property of the TS for many proteins.

Implications

The RCO^TS~0.7·RCO^N relationship provides a useful guide for interpreting previous studies and for modeling the TSs of other proteins. For example, a high RCO^TS/RCO^N fraction restricts the degree to which a TS can be small and polarized, as has been inferred from φ-data for some proteins that obey the RCO correlation^{52; 53; 54; 55; 56; 57; 58; 59; 60}. Using the published φ-values, we estimate that RCO^TS < 0.5·RCO^N, although the precise number depends on the threshold for which a φ-value is considered to be a contact. It seems unlikely that a universal RCO correlation would hold if some proteins have a small polarized TS containing only local structure and a low RCO, while others have a more extended TS with long-range contacts and a near-native RCO. Furthermore, the low degree of structure formation inferred from φ-values is inconsistent with the high surface burial in the TS that is observed for these proteins (m_f/m_o > 60%). Thus, it appears more likely that a contact threshold of φ > 0.5 is too stringent to identify structure in a TS, and a lower threshold is required.

However, even a lower threshold may still be inadequate¹⁹ because φ-values may reflect the ability of the TS to accommodate the new side chain rather than indicating the presence or absence of structure per se. Rigid, native-like regions in the TS should be more sensitive to a disruptive mutation and have higher φ compared to regions where the backbone can relax, or where the side-chains are solvent exposed, for example on the surface of an otherwise folded β-sheet. If the rigid regions are localized to one side of the protein, φ-analysis could misidentify the TS as structurally polarized.

The differences between φ and ψ-analysis can produce disparate conclusions. The strengths of ψ-analysis include the ability to report on chain-chain contacts, stabilization of the TS upon metal binding, extrapolation to zero perturbation, and generally to introduce less energetic and structurally perturbing mutations than φ-analysis (e.g. $\mathrm{\Delta }\mathrm{\Delta }{G}_{\mathit{surface}}^{\mathit{biHis}}<\mathrm{\Delta }\mathrm{\Delta }{G}_{\mathit{core}}^{\mathit{Leu}\to \mathit{Ala}}$). In Ub, the TS defined by unequivocal ψ_o=1 sites has RCO^TS ~ 0.7·RCO^N18. However, φ-analysis leads to the assignment of a small, polarized TS consisting of just the amino-terminal hairpin and helix^{18; 61} with an RCO fraction of only 30% of the native value (Fig. 1C). In particular, a vanishing φ is observed for the L67A substitution in the core of the TS,¹⁸ presumably due to backbone readjustment or side chain exposure. These possibilities are not as likely in the core of the hairpin-helix motif where higher φ are observed.

Our conclusion that φ-analysis underestimates the structural content of Ub’s TS is likewise consistent with Bulaj and Goldenberg’s findings of low φ in regions of native-like structure in BPTI intermediates.¹⁹ These concerns should be considered in the calculation of φ from folding simulations and in the interpretation of experimental data where a small, polarized TS has been identified. For example, high φ-values are located only on a single hairpin for Protein G^{62; 63} and Protein L⁶⁴. As noted by the authors, the participation of a third strand adjacent to the dominant hairpin in Protein G is suggested by three φ-values close to 0.4.⁶² Analogously in Protein L, two φ-values close to 0.3 suggest some interaction of a third strand and helix in the TSE.⁶⁴

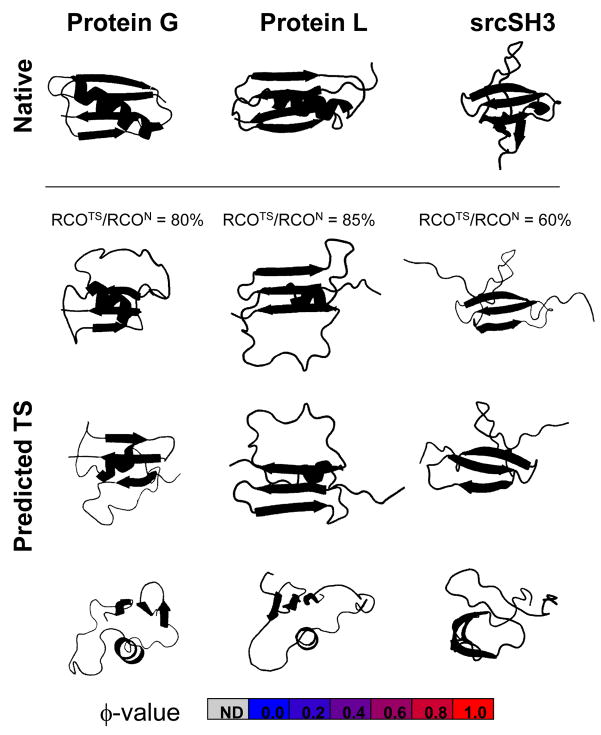
The Protein G and Protein L results highlight the inherent difficulty in defining thresholds for φ that are suitable to infer the presence of structure in the TS. With only a hairpin, and even part of the helix, these models the for TSE would predict a RCO fraction of only ~40%. Our RCO^TS ~ 0.7·RCO^N relationship requires that the TSEs of Proteins G and L include these additional long-range contacts, minimally with the adjoining β-strand, and potentially some docked^{62; 65} helical structure.³⁰ Such a configuration would produce a RCO ratio of ~80% (Fig. 9). Using these principles, a possible TS for srcSH3 also is created with an RCO in excess of 60%, by taking advantage of known information for φ,⁶⁶ψ_o,⁶⁷ and m_f/m_o.

Fig. 9. φ-values and model structures for the TS of other small domains.

Model TS structures are generated using experimental data for φ⁶²; ⁶³; ⁶⁴; ⁶⁶ in conjunction with the RCO^TS/RCO^N ~ 70% relationship. The models either leave regions in their native conformation or take them as unfolded but with allowable (φ, ψ) backbone dihedral angles. The Protein G and Protein L models yield a similar RCO fraction when the model lacks the helix. Kinetic isotope studies³⁰ and φ-values for positions on the sole helix’s hydrophobic face indicate some helical presence in the TS. A TS for srcSH3 is constructed using φ-values⁶⁶ and ψ-analysis.⁶⁷ Renderings created in PyMol.

TS and Pathway Diversity

The high degree of native topology in the TS implied by the RCO^TS~0.7·RCO^N relationship greatly limits the degree of TS heterogeneity. Experimentally, minimal evidence exists for TS heterogeneity as defined by the participation of different subsets of helices or strands^{17; 23; 68} (rather than local “microscopic heterogeneity”²³ such as frayed helices or hairpins).

Even when the TS is homogenous, the pathway to and from the TS could be diverse. However, a growing body of data indicates that elements of secondary structures, or “foldons”, form in a well-defined sequence after crossing the initial rate-limiting barrier to collapse.⁶⁹ This scenario is due to chain connectivity and sequential stabilization wherein pre-existing structures provide a foundation on which unfolded regions can dock. For many proteins, the addition of foldons after the TS only can be accomplished, or is strongly preferred, in a specific order due to the presence of a structural hierarchy.

On the way up to the TS from the denatured state, the issue is less clear. A multitude of unstable conformations are sampled, but some structures provide a more suitable base for the addition of other elements. Accordingly the uphill steps should involve a largely sequential accretion of structure,¹⁷ although the energetic biases may not be as pronounced as for the post-TS pathways.

Since smaller proteins such as BdpA have TSs with less structural hierarchy, they can exhibit more pathway diversity. Furthermore, the symmetry of BdpA permits independent association of H1 or H3 with H2. Hence, the path to the TS may begin with the formation of either the H1–H2 or H2–H3 microdomains. Likewise, after the TS, the folding of the frayed portions of H1 or H3 may occur in either order. This example illustrates the general result that when two foldons can be added along a pathway independently or with comparable energy, the pathway can temporarily bifurcate.^{17; 22; 70; 71}

Comparisons with Theoretical Studies

The TSE of BdpA is challenging to characterize because of the protein’s small size, symmetry, and lack of structural hierarchy. In theoretical studies, subtle changes in the energetic balance between secondary and tertiary structure formation can influence whether secondary structure or collapse is predicted to occur first or synchronously. Likewise, a slight error in the balance between enthalpy and entropy can shift the location of the TS. These properties have spawned a diverse set of predictions for the BdpA folding behavior^{7; 10}. One notable study by Galzitskaya and coworkers⁷² generates a TS model very similar to our mini three helix bundle. They create ensembles of unfolding pathways using an all-atom Ising-like model where residues are considered to be either folded and interacting or unfolded and non-interacting. Saddle points on the free energy surface are identified as part of the TSE.

Despite the presence of differences, considerable overlap exists between our model and many of the other theoretical studies. Typical discrepancies in prior descriptions include predictions of multiple, early or very late TSEs that contain either just the H1–H2 or H2–H3 microdomains, near-native helical content, or an undocked H3. The following briefly summarizes the diversity of the other prior predictions.

The TSs from two all-atom unfolding simulations by Daggett and coworkers find H1 disrupted in one trajectory while H2 is unfolded in another trajectory,¹² but the TS in a subsequent study appears to be very native-like with all three helices fully formed.⁷³ Biased sampling molecular dynamics studies by Brooks et al.^{74; 75} indicate that the H1-H2 interface forms in the TS and H3 only folds afterwards. In simulations for the folding of a C_α Gō-like model, Shea et al ⁷⁶ find high φ-values are located primarily in both turn regions. Linhananta and Zhou use an all-atom Gō-like model and identify a TS in which all three helices are fully formed but H1 is undocked from the H2–H3 microdomain.⁷⁷ All-atom simulations by Pak et al ⁷⁸ discern a TS involving the reorganization of all three fully formed helices. In an all-atom replica exchange molecular dynamics simulation, Garcia and Onuchic⁷⁹ identify a TS with a partially formed H1-H2 microdomain along with a nearly fully folded but undocked H3. Other all-atom Monte Carlo⁸⁰ and LD⁸¹ simulations by Shakhnovich et al. identify a TS containing the H2-H3 microdomain.⁸¹

All-atom integration of a model with stochastic difference equations by Scheraga et al. predict a folding pathway in which tertiary and secondary structure form in parallel but hydrogen bonds appear to form before the emergence of tertiary contacts.⁸² A later study using a “United Residue” (UNRES) model finds that H2 is the slowest to form⁸³ while all-atom simulations lead to the finding that this result is temperature dependent⁸⁴. Lee et al. use a UNRES model in Monte Carlo folding simulations and observe a folding pathway dominated by early collapse and formation of H3.^{85; 86} A coarse grained funnel-based simulation of the BdpA folding pathway provides the differing conclusion that the protein collapses and then passes through a wide variety of pathways characterized by very non-native intermediates.⁸⁷

Other theoretical studies have included comparisons with experimental φ-values. Itoh and Sasai predict temperature dependent φ that reflect a shift in populations between two TSEs composed of either H1–H2 or H2–H3 microdomains.¹¹ Experimentally, however, the φ-values are temperature invariant.⁶ Nelson and Grishin apply a similar technique but also account for the intermittency of contacts between the folded regions.⁸⁸ Their predicted φ are independent of temperature, while the TS consists of a fully formed H2 docked against the C-terminal region of H1 and a relatively unfolded and undocked H3. Liu and coworkers identify a very similar TS from distributed all-atom simulations guided by an index of topological similarity to the native fold.⁸⁹ A recent all-atom simulation by Shakhnovch et al. identifies a folded H1–H2 microdomain using an analysis based on P_fold calculations, but finds an undocked yet folded H3.⁹⁰ In a statistical analysis of the experimental φ-values, Weikl and Dill⁹¹ conclude that the TS contains a folded H2 which makes 50% of its tertiary contacts, while H3 is unformed but still makes 30% of its tertiary interactions. Ozkan et al. describe the folding of BdpA using a zipping and assembly method and observe the formation of the H2-H3 microdomain followed by the docking of H1.⁹²

Diffusion-collision (DC) mechanisms, introduced either by assuming that folding is limited by the collision of pre-formed helices^{1; 93} or when this behavior is observed in simulations,^{78; 94; 95; 96} predict that the H2–H3 microdomain plays the primary role because these two helices have the highest intrinsic helicity (Fig. 3). Although frequently cited as supporting evidence, the observation of helical content in the TS is insufficient to determine whether the structure forms before or after chain collision. A rare direct test of the DC model, demonstrates that helix formation occurs after initial chain collision for a coiled coil that is engineered to have negligible intrinsic helicity²⁸. Although it is difficult to falsify the DC model, we note that the structural content of the BdpA TS does not follow the pattern predicted by intrinsic helicity (e.g., H3 is unstructured at the carboxy terminus, although this half of the helix has higher intrinsic helicity than the folded regions of H1).

Conclusion

The small size and symmetry of BdpA makes it an attractive model system. Rather than simplifying the situation, however, these features along with minimal structural hierarchy render the determination of the TS particularly challenging. Nevertheless, we have characterized the TSE using a combination of methods.

A goal of the present study is to quantify the topological requirements of the TS. Our TS model for BdpA has an RCO that is ~ 60–80% of that for the native state. In conjunction with similar results for two more complex α/β proteins, Ub and Acp, we propose that the proteins satisfing the RCO correlation also have a TS that adopts 60–80% of the native topology, as defined by the RCO metric.

It remains to be determined whether the high level of structure in the TS is an intrinsic property of proteins that fold cooperatively and have a hydrophobic core. Alternatively, this behavior and the choice of protein folds with high RCO⁹⁷ could have been selected by evolution because such an organized and relatively late TS might reduce the presence of stably populated, partially unfolded states which could aggregate, e.g., into amyloidogenic fibers.

Regardless of the origin of the 60–80% RCO relationship, this high fraction places a strong restraint on possible structures and the degree of TS heterogeneity. By supplementing the considerations using data from φ-analysis and isotope exchange experiments, we propose alternative TS structures for proteins that have previously been reported to have small and polarized TSs based on φ-analysis. Our proposed structures can be used to test the generality of the 70% RCO relationship and the conjecture that φ-values often reflect the presence of rigid, native-like structure rather than the presence of structure per se.

Materials and Methods

Expression and Purification

BiHis variants in the pseudowild-type background⁷ (F14W W15Y H19N) were created using the QuikChange protocol (Stratagene) and prepared according to Ref.98.

Folding measurements

Unless indicated, data were collected at 10°C in 50mM HEPES, 0.1 M NaCl, pH 7.7. Kinetic measurements used a SFM-400 stopped-flow apparatus and a PTI A101 arc lamp. Fluorescence spectroscopy used λ_excite= 285 nm, and emission was observed at λ>310nm. Amide isotope effect measurements were conducted in 20mM sodium acetate 0.1M NaCl at pD_read 5.0. CD measurements used a Jasco 715 spectropolarimeter, with a 1 cm pathlength.

The zero and high Me²⁺ chevrons were simultaneously fit with ψ_o as one of the adjustable parameters assuming that the free energy changes $\mathrm{\Delta }{G}_f^{‡},\mathrm{\Delta }{G}_u^{‡}$, and ΔG_eq depend linearly on denaturant concentration. To minimize extrapolation errors, ΔΔG_f^‡ and ΔΔG_u^‡ were calculated for strongly folding and unfolding conditions, respectively. φ-values were determined from a simultaneous fit to the two chevrons, with φ being one of the fitting parameters.

Identification of Hydrogen Bonds

Amide helical hydrogen bonds were identified according to the presence of properly positioned (co-linear) NH and O=C moieties for i-i+4 residue pairs on H1 (11–20), H2 (28–38), and H3 (45–56).

Langevin Dynamics

LD simulations use the implicit solvent model developed in the Freed group^{39; 99} using a modified version¹⁰⁰ of the TINKER dynamics package.¹⁰¹ The model incorporates a non-linear, distance-dependent dielectric constant¹⁰² with the solute-solvent interaction free energy described by the Ooi-Scheraga solvent accessible surface area (SASA) potential¹⁰³ and the atomic friction coefficients calculated with the Pastor-Karplus scheme.¹⁰⁴ After an initial energy minimization step, trajectories are calculated for approximately 10 ns, with a structure being saved every 5 ps. The fractional surface burial (using a probe radii of 1.4 Å for water) is calculated from the difference between accessible surfaces from the average of an ensemble of 1000 unfolded structures¹⁰⁵ and the values obtained from LD simulations for the native and TS.

Abbreviations

Acp

acyl phosphatase

BdpA

B-domain of protein A

biHis

bi-histidine

CD

circular dichroism

G-S Amber 94

Garcia and Sanbonmatsu’s modified version of Amber 94

GdmCl

guanidinium chloride

$K_{eq}^D,K_{eq}^N,K_{eq}^{TS}$

metal ion binding affinity of the denatured, native and transition states, respectively

HX

hydrogen exchange

RCO

relative contact order

TSE

transition state ensemble

Ub

ubiquitin

ΔΔG_eq

change in equilibrium stability

ΔΔG_f^‡

change in activation free energy

Appendix

ψ-analysis

ψ-analysis uses engineered biHis sites to probe the fraction of native metal ion binding energy realized in the TS. The kinetic response as a function of metal ion concentration quantifies the degree to which the biHis site is present in the TSE (see Refs.²²; ²³ for detailed treatment). In a manner analogous to the φ-analysis performed using point mutations, the kinetic response due to metal binding can be obtained from the denaturant dependence of folding rates (“chevron analysis”) at zero and high metal ion concentrations.

When side chain substitution or metal binding only affects the unfolding rate k_u and not the free energy of the TS relative to the unfolded state, the structure probed is absent in the TSE, and the corresponding φ^mutation or ψ^metal vanishes. Conversely, when the perturbation only affects the folding rate, k_f, the structure probed is likely to be native-like in the TSE and the associated φ- or a ψ-value is unity. When both the folding and unfolding arms shift, the φ- or ψ-value is fractional, and the origin of a fractional value can be challenging to discern in both methods. Fractional φ may arise either due to partial structure formation in the TS or to the presence of multiple, distinct TS structures.¹³; ¹⁹; ³⁴; ⁶⁵; ¹⁰⁸; ¹⁰⁹; ¹¹⁰; ¹¹¹ A fractional ψ-value indicates the biHis site is either native-like in a subfraction of the TSE, or has non-native binding affinity in the entire TSE (e.g. a distorted site with less favorable binding geometry, or a flexible site that must be restricted prior to ion binding), or some combination thereof¹⁷; ¹⁸(D. Goldenberg, private communication).

ψ-analysis has the powerful capability of generating a large quantity of high quality kinetic data to accurately probe the degree to which a particular binding site is formed in the TSE. Each biHis variant enables the measurement of dozens of folding rates at increasing concentrations of metal ions. The binding of increasing concentrations of ions to the biHis site produces a nearly continuous increase in the stability of TS structures that contain the binding site. Hence, the stability is perturbed yet accomplished in an isosteric and isochemical manner. The resulting series of data can be justifiably combined, a process which may be inappropriate in traditional mutation studies where the perturbation can arise from multiple sources, including changes in backbone propensities as well as indeterminate non-local interactions.

The ψ-analysis data can be represented as a Leffler plot where the change in activation free energy is plotted relative to the change in the metal-induced stability¹¹² (Fig. 2B). If the biHis site is formed in the TSE, metal binding increases its stability, and folding rates increase. The associated Leffler plot has a positive slope as both ΔΔG^‡_f and ΔΔG_eq increase.

The starting point in the detailed interpretation of the Leffler plot involves fitting the data to a model with a single free parameter ψ_o, which is the slope at the origin in the absence of metal,

$$\mathrm{\Delta }\mathrm{\Delta }{G^{‡}}_f=\mathit{RT}ln\left((1-{\psi }_o)+{\psi }_o{e}^{\mathrm{\Delta }\mathrm{\Delta }{G}_{eq}/RT}\right)$$ (S1)

Along the curve, the instantaneous slope (or ψ-value) increases with additional binding energy as the fraction of the TSE with the biHis site grows. The instantaneous slope at any point on the curve as a function of binding stability (Fig. 2B) is given by

$$\psi =\frac{\partial \mathrm{\Delta }\mathrm{\Delta }{G}_f}{\partial \mathrm{\Delta }\mathrm{\Delta }{G}_{eq}}=\frac{{\psi }_o}{(1-{\psi }_o)e^{-\mathrm{\Delta }\mathrm{\Delta }{G}_{eq}/RT}+{\psi }_o}$$ (S2)

The interpretation of ψ-values is clear in the two cases where the Leffler plot is linear. When ψ_o is unity, the biHis site is present with native-like affinity in the TS ensemble. When ψ_o is zero, the site is absent with unfolded-like affinity. Otherwise, the Leffler plot displays curvature as ligand binding continuously increases the stability of the TS ensemble, i.e., ψ approaches unity with increasing metal concentration.

Assuming the metal ion binding affinity in the TS is either native-like or unfolded-like, the ψ-value obtained at any given metal concentration represents the fraction of the TS ensemble with the biHis site formed. The remainder of the TSE (quantified by 1-ψ) represents molecules crossing the rate-limiting barrier without the two histidines in a geometry capable of binding metal ions. Together, these two populations comprise the TSE.

This heterogeneous picture, rather than the scenario with a distorted site having non-native binding affinity, quantitatively describes the degree of TS heterogeneity in the folding of a dimeric α-helical coiled coil¹³, a system known to have multiple nuclei.³⁴

The complete ψ-analysis formalism takes into account the shifts in the native, unfolded and TS populations due to the binding of metal ions to each of these states. Folding rates are calculated assuming two classes of TSs depending on whether the biHis site is present (k^present) or absent (k^absent). The first class TS_present has the biHis site present in a native or near-native geometry with a dissociation constant $K_{TS}^{\mathit{present}}$. The second class TS_absent contains the biHis site as essentially absent but is assigned a nominal effective dissociation constant $K_{TS}^{\mathit{absent}}$. According to Eyring reaction rate theory,¹¹³ the overall reaction rate is taken to be proportional to the relative populations of the TS and U ensembles, k_f ∝ [TS]/[U]. The net folding rate is the sum of the rates proceeding down each of the two routes, k_f = k^present + k^absent, with

$$k_f\equiv \frac{1+[M]/K_{TS}^{\mathit{present}}}{1+[M]/K_U}{k}_o^{\mathit{present}}+\frac{1+[M]/K_{TS}^{\mathit{absent}}}{1+[M]/K_U}{k}_o^{\mathit{absent}}$$ (S3)

where $k_o^{\mathit{present}}\propto [{TS}_{\mathit{present}}]/[U],k_o^{\mathit{absent}}\propto [T{S}_{\mathit{absent}}]/[U]$ are the rates through each TS class prior to the addition of metal, and [M] is the divalent metal ion concentration. The pre-factors of these two rates in Eq. S3 represent the increase in the population of each class’s TS, relative to the increase in the population of the unfolded state, due to differential metal affinity in the TS and in the unfolded state. By examining shifts in populations and assuming metal binding is in fast equilibrium, this treatment avoids any assumptions about possible pathways connecting the different bound and unbound states.

Two major scenarios can be considered. In first scenario, the TS_present has the biHis site present with native-like affinity ( $K_{TS}^{\mathit{present}}=K_N$) while TS_absent has the site with the unfolded-like affinity ( $K_{TS}^{\mathit{absent}}=K_U$). Hence, only TS_present is stabilized with respect to the unfolded state upon the addition of metal ions. The height of the kinetic barrier associated with TS_present decreases by the same amount as the native state’s stability. Consequently, the rate increases down this pathway, $k^{\mathit{present}}=k_o^{\mathit{present}}{e}^{\mathrm{\Delta }\mathrm{\Delta }{G}_{eq}/RT}$. The instantaneous slope simplifies to the fraction of the TS ensemble which has the biHis site formed at a given metal ion concentration:

$$\psi =\frac{k^{\mathit{present}}}{k^{\mathit{present}}+k_o^{\mathit{absent}}}$$ (S4)

In the second scenario, curvature can also appear when the sole TS has binding affinity different than the native state (e.g. a distorted site with $K_{TS}^{\mathit{present}}>K_N$). The ψ_o-value is expressed strictly in terms of the binding affinities ( $K_{eq}^U,K_{eq}^N,K_{eq}^{TS}$), i.e.

$${\psi }_{\circ }=\frac{K_{eq}^N}{K_{eq}^{TS}}\frac{K_{eq}^U-K_{eq}^{TS}}{K_{eq}^U-K_{eq}^N}$$ (S5)

and then ψ is effectively a rescaling of the relative affinities to a value between 0 and 1, i.e. $K_{eq}^U>K_{eq}^{TS}>K_{eq}^N\Rightarrow 0<{\psi }_0<1$. It is important to emphasize again that for this and the other scenarios, the ψ = 0 and 1 values still imply that the biHis site is absent or 100% present in the TSE, respectively.