Predictions of fundamental frequency changes during phonation based on a biomechanical model of the vocal fold lamina propria

Abstract

This study examines the local and global changes of fundamental frequency (F₀) during phonation and proposes a biomechanical model of predictions of F₀ contours based on the mechanics of vibration of vocal fold lamina propria. The biomechanical model integrates the constitutive description of the tissue mechanical response with a structural model of beam vibration. The constitutive model accounts for the nonlinear and time dependent response of the vocal fold cover and the vocal ligament. The structural model of the vocal fold lamina propria is based on a composite beam model with axial stress. Results show that local fluctuations such as F₀ overshoots and undershoots can be characterized by the biomechanical model and might be related to the processes of stress relaxation of vocal fold tissues during length changes. The global changes of F₀ declination in declarative sentence production can also be characterized by the model. Such F₀ declination is partially attributed to the peak stress decay associated with stress relaxation of the vocal fold lamina propria and partially to neuromuscular control of the vocal fold length.

I. Introduction

The fundamental frequency (F₀) is a key characteristic of human phonation, which is produced by vibration of the vocal fold when air flows through the glottis. Extensive efforts have been made in signal processing to describe and predict the temporal contour of F₀ changes during speech or singing, e.g., Saitou et al [1] proposed a F₀ control model and showed several types of F₀ fluctuations in singing voice including pronounced over and undershoots at pitch changes; Kutik et al [2] reported a tendency for the fundamental frequency to drop towards the end of a declarative sentence, which is termed F₀ declination; Möbius [3] reported over and undershoots associated with syllables. However, few studies have been conducted to explain these local fluctuations and global changes of F₀ from a predictive point of view. In this study, a biomechanical model of the vocal fold lamina propria is proposed and used to predict the local and global changes of F₀ during speech. This model might provide a better understanding of the mechanisms underlying these phenomena, as opposed to signal processing models which focus on only the description of F₀ changes during phonation.

The biomechanical model of phonation starts with structural models of vocal fold vibration. The ideal string model [4] is the simplest model and is commonly used to predict F₀. e.g. [5]. However, the string model tends to underpredict the fundamental frequency [6], since the bending stiffness of the vocal fold lamina propria is neglected. Various beam models [6-9] have been proposed to characterize the vibration of the vocal fold. Titze and Hunter [7] developed a beam model, which considered the vocal ligament as the dominant load-carrying component of the lamina propria and idealized the tissue mechanical response as linear elastic. Descout et al [8] developed a multi-layer beam model also with linear elastic properties. Bickley [9] considered the vocal fold as a homogeneous beam without accounting for the effects of vocal fold stretch. A two-layer composite beam model of the vocal fold lamina propria is described in our previous study [6]. This model incorporates both the vocal fold cover and the vocal ligament. It accounts for vibration in the medial-lateral direction (i.e., the predominant direction of vocal fold vibration). Numerical solutions to the beam vibration equations under consideration of axial stress were well approximated by the sum of the closed form solution of the beam model for the unstretched state and the solution of the string model, both dependent on the geometrical properties of the vocal fold lamina propria and also the tissue mechanical response under stretch. To incorporate an accurate description of the vocal fold lamina propria, a constitutive model which can reliably characterize the mechanical response of vocal fold tissue must be utilized. Experimental studies [10, 11] have shown that vocal fold tissues, like other biological soft tissues, demonstrate both elastic and viscous mechanical behavior which is characterized by nonlinearity, hysteresis and time dependence of the stress-stretch response under cyclic deformation.

Extensive studies have been conducted on the mechanical properties of the vocal fold lamina propria. Min et al [12] proposed a nonlinear elastic model which captured the equilibrium stress-stretch response but failed to describe the hysteresis of the tissue. Viscoelastic models were employed by Hunter et al [13] and Chan et al [14, 15] to simulate the response of the vocal fold lamina propria under cyclic tensile or shear deformation. Our previous work [6] documents a two-network constitutive model to describe the stress-stretch response of the vocal fold lamina propria. The two-network model, which consists of a time-independent equilibrium network based on the Ogden's model of hyperelasticity [16] in parallel with a viscoplastic network, proved effective in characterizing the stress-stretch response of the vocal fold lamina propria [11]. The two-network model can describe the hysteretic response in individual load cycles but does not capture long-term viscous behavior. For example, during cyclic stretching and releasing of vocal fold tissues (a condition also termed “preconditioning”), the corresponding level of stress decreases with the number of cycle. Previous studies on brain tissues [17] indicate that such a transient response can be approximated by use of a double-exponential decay function.

The viscous response exhibited by the vocal fold tissues may help explain some phenomena in voice production. It is hypothesized that transient and time-dependent events in the fundamental frequency (over and undershoots as well as declinations) can be partially attributed to the time-dependent response of the vocal fold cover and the vocal ligament represented through the proposed constitutive model of the vocal fold tissue.

In this study, the two-layer composite beam model of vocal fold vibration [6] will be combined with the two-network constitutive model of the vocal fold lamina propria [11], with the constitutive model simulating the mechanical response and the structural model offering the predictions of F₀ under given stretch histories. These stretch histories are representative of transient changes of vocal fold length during phonation [18]. Length changes of the vocal fold are known to control fundamental frequencies and are driven by the activities of intrinsic laryngeal muscles, primarily the cricothyroid (CT) and the thyroarytenoid (TA) muscles [19]. Temporal correlation of muscle activation with syllable formation has also been documented [20]. To exemplify the approach, the constitutive model is applied to describe the mechanical response of cadaveric vocal fold tissues obtained from a 66-year-old male subject. With the tissue constitutive parameters determined, we employ the beam model for predictions of fundamental frequencies for several stretch histories each accounting for the contributions of active (neuromuscular) control.

II. Biomechanical Model of the Vocal Fold Lamina Propria

A. Constitutive Characterization of Vocal Fold Tissue

Vocal fold cover and vocal ligament were dissected from a 66-year-old male larynx excised 15 hours postmortem [10]. This larynx was used for the modeling throughout the present study. The subject was a nonsmoker and Caucasian, and free of head and neck disease and laryngeal pathologies. Experimental data on viscoelastic response of the vocal fold cover and the vocal ligament were obtained by use of a dual-mode servo control lever system (Aurora Scientific Model 300B-LR, Aurora, ON, Canada) with details given in Chan et al. [10].

The network model used to characterize the mechanical response of vocal fold tissue is motivated by the molecular structure of the vocal fold extracellular matrix (ECM). It is assumed that the fibrous proteins (collagen and elastin) provide a structural framework and a large part of the stiffness, whereas the interstitial proteins contribute to regulate the viscosity and elasticity of the ECM. A constitutive model, which consists of a time-independent equilibrium network (A) in parallel with a time-dependent network (B), is thus proposed to reflect the molecular structure of the vocal fold ECM. Following this parallel arrangement of networks, the applied deformation on the whole structure is identical to the deformation in each network, whereas the total stress is the sum of the stresses in these two networks. The time-independent equilibrium network is characterized by Ogden's hyperelastic model which provides a nonlinear correlation between stretch and stress. For uniaxial loading conditions with applied stretch λ_u the corresponding Cauchy stress σ is given as:

$${\sigma }_A=\frac{2{\mu }_A}{\alpha }\left({\lambda }_u^{\alpha }-{\lambda }_u^{-\alpha /2}\right)$$ (1)

where σ_A is the Cauchy stress and μ_A is the initial shear modulus of the equilibrium network (A), α is the corresponding dimensionless constant describing the nonlinearity of the elastic response, and λ_u is the applied stretch.

The second network describes a decomposition of deformation into a hyperelastic component (again described by the Ogden model) in series with a viscoplastic component characterized by a flow rule proposed by Bergström and Boyce [21]. The rate of equivalent plastic stretch is given by:

$${\stackrel{\dot{¯}}{\lambda }}_B^{\text{pl}}=Z{\left({\overline{\lambda }}_B^{\text{pl}}-1+\delta \right)}^c{\left({\overline{\sigma }}_B\right)}^m$$ (2)

in which ${\overline{\lambda }}_B^p$ is the effective inelastic stretch, m is a stress exponent characterizing the dependence of the inelastic deformation on the stress level in network (B), c is a stretch exponent characterizing the dependence of the rate of inelastic deformation on the current magnitude of inelastic deformation, Z is a viscosity scaling constant defining the absolute magnitude of the inelastic deformation, and δ is a small positive number (δ < 0.001) introduced to avoid singularities in the inelastic stretch rate when the inelastic stretch is close to unity. The procedure to determine the values of the constitutive parameters from the first cycle of the experimental stress-stretch curves is given in detail in Zhang et al. [11].

The peak stress values recorded during cyclic loading can be approximated by exponential decay functions of the form

$${\sigma }_{\text{p}}\left(t\right)={\sigma }_{\text{0}}\left[a_{\text{s}}+\sum _{k=1}^2{a}_k\cdot exp\left(-t/{\tau }_k\right)\right]$$ (3)

in which t is time, σ₀ is the value of the peak stress in the first cycle, (σ₀a_s) is the predicted stabilized peak stress level, and τ_k (k = 1,2) are characteristic time constants. Please note here t = 0 is the instance at which the peak load is reached in the first cycle. Values of a_s, a_k and τ_k (k = 1, 2) are determined by fitting experimental data to the double-exponential function (Matlab 7.0, Mathworks). After the values of the constitutive parameters are determined from the first cycle of stress-stretch curves, the stiffness of the time-independent equilibrium network (A) is made decrease asymptotically with time in the same manner as the double-exponential fit for the peak stress decay,

$${\mu }_A\left(t\right)={\mu }_{A,0}\left[a_{\text{s}}+\sum _{k=1}^2{a}_k\cdot exp\left(-t/{\tau }_k\right)\right]$$ (4)

with μ_A,0 being the initial shear modulus of the equilibrium network (A) determined from the first cycle, and all the other parameters remain unchanged.

B. Structural Model of Vocal Fold Vibration

The structural model of vocal fold vibration is motivated by the layered structure of the vocal fold lamina propria which is composed of the vocal fold cover (i.e., the epithelium and the superficial layer of the lamina propria) and the vocal ligament (i.e., the intermediate and the deep layer of the lamina propria). These two layers possess different geometrical (shape and cross-sectional area) and mechanical properties (stiffness and degree of nonlinearity) [5, 10]. In the two-layer composite beam model [6], the cross-section of the lamina propria is approximated by two adjacent rectangles that represent the cover and the ligament, respectively. The line connecting the centroid positions of the two rectangles is in the medial-lateral direction. Under the assumption of incompressible material response of vocal fold tissues, changes in cross-sectional areas with tensile deformation are accounted for. When the composite beam is under tension the partial differential equation governing its vibration is

$$\overline{\sigma }\frac{{\partial }^{2}v}{\partial x^2}-{\overline{E}}_0{\kappa }^2\frac{{\partial }^{4}v}{\partial x^4}=\rho \frac{{\partial }^{2}v}{\partial t^2}$$ (5)

where v is the medial-lateral displacement from the equilibrium position of an infinitesimal part of the beam with anterior-posterior distance x from one end of the beam, σ̄ is the homogenized Cauchy stress in the anterior-posterior direction, ρ is the tissue density, and Ē₀κ² is a measure of the bending stiffness for the composite beam with Ē₀ being the homogenized anterior-posterior modulus of the lamina propria and κ the radius of gyration of the composite cross-section. With clamped boundary conditions assumed at the vocal process (the posterior endpoint x = 0) and at the anterior commissure (the anterior endpoint x = l), the fundamental frequency of the composite beam can be calculated analytically for the unstretched and the stretched state separately. Furthermore, numerically predicted values of F₀ from Eq. (5) agreed very well with the two closed form analytical solutions in their respective ranges of validity [6]. Over a wide range of vocal fold stretch relevant to phonation, the numerical F₀ solution can be approximated by the sum of F₀ values as predicted from the well known string model and the beam model in the unstretched state

$$F_0\approx \frac{1}{2L{\lambda }_u}\sqrt{\frac{\overline{\sigma }}{\rho }}+\frac{3.5607}{L^2}\sqrt{\frac{{\overline{E}}_0{\kappa }^2}{\rho }}$$ (6)

where L is the in situ length (i.e., the stress-free length of the vocal fold), and λ_u is the longitudinal stretch applied on the vocal fold. Through the ratio between the areas of the cover and the ligament, the homogenized stress σ̄ in Eq. (6) is related to the stress in the vocal fold cover σ_c and the vocal ligament σ_l, which in turn are calculated by the two-network constitutive model. Further details about the structural model are given in Zhang et al. [6].

III. Results

The in situ length of the vocal fold dissected from the 66-year-old male subject was L = 20.425 mm, the initial cross-sectional area of the vocal fold cover was A_0,c = 0.098 cm², the initial cross-sectional area of the vocal ligament was A_0,l = 0.1189 cm². The aspect ratio (height to width) of the rectangles representing the cover and the ligament in the beam model was assumed to be three.

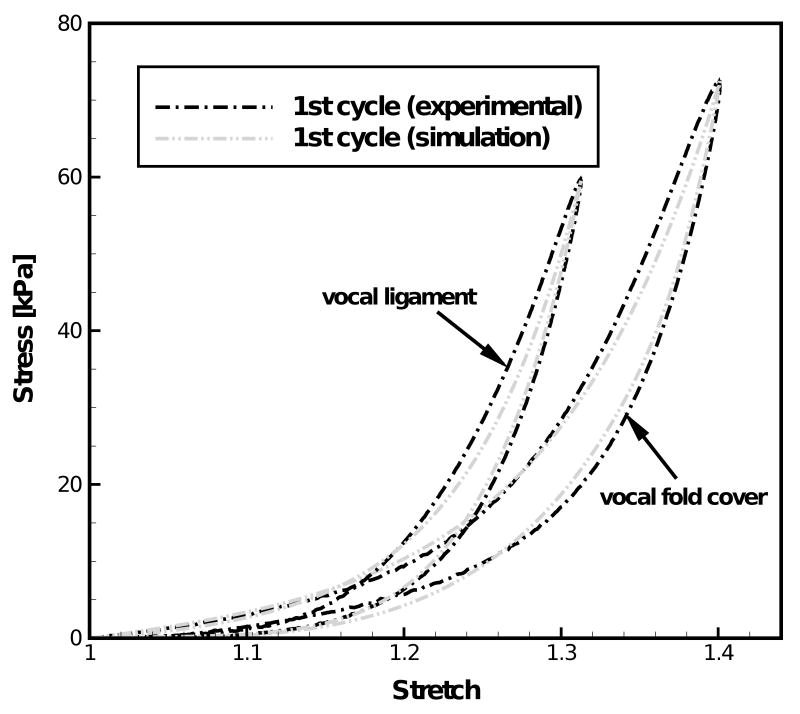
The first cycle of the stress-stretch curves was characterized by the two-network constitutive model. The following parameters characterize the constitutive response of the cover specimen, μ_A,0 = 4.50 kPa, μ_B = 130.0 kPa, α = 15.0, c = −1, m = 1.8, Z = 0.0025 sec⁻¹ (kPa)^−1.8. Another set of parameters were determined to describe the mechanical response of the ligament specimen, μ_A,0= 3.19 kPa, μ_B= 50.0 kPa, α = 20.0, c = −1, m = 1.3, Z = 0.004 sec⁻¹ (kPa)^−1.3. Based on these constitutive and geometrical parameter values one obtained Ē₀κ² = 0.01356 N·m. It can be seen from Figs. 1 and 3 that the vocal ligament is more compliant than the vocal fold cover at low stretch levels, which is confirmed by a lower stiffness μ_A of the equilibrium network. However, the vocal ligament possesses a larger nonlinearity constant α which plays a more significant role at high stretch levels, as can be seen in Figs. 1 and 3 that the stress level in the vocal ligament catches up and surpasses that in the vocal fold cover with the stretch increasing.

Figure 1.

Comparison between experimental data and simulation results of the first cycle of the tensile stress-stretch response at 1 Hz for the vocal fold cover and the vocal ligament of the 66-year-old male subject.

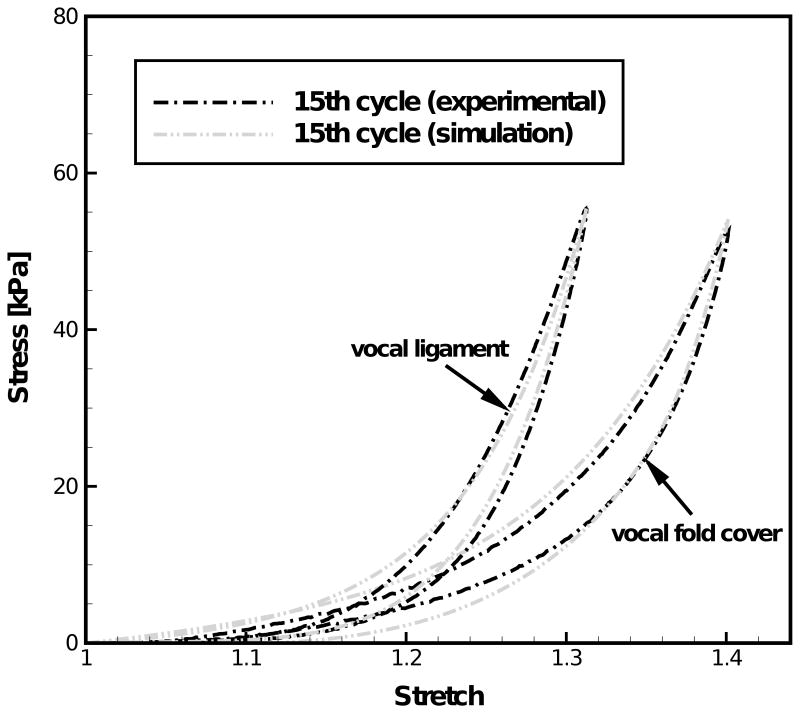
Figure 3.

Comparison between experimental data and simulation results by the improved constitutive model of the 15th cycle of the tensile stress-stretch response at 1 Hz for the vocal fold cover and the vocal ligament of the 66-year-old male subject.

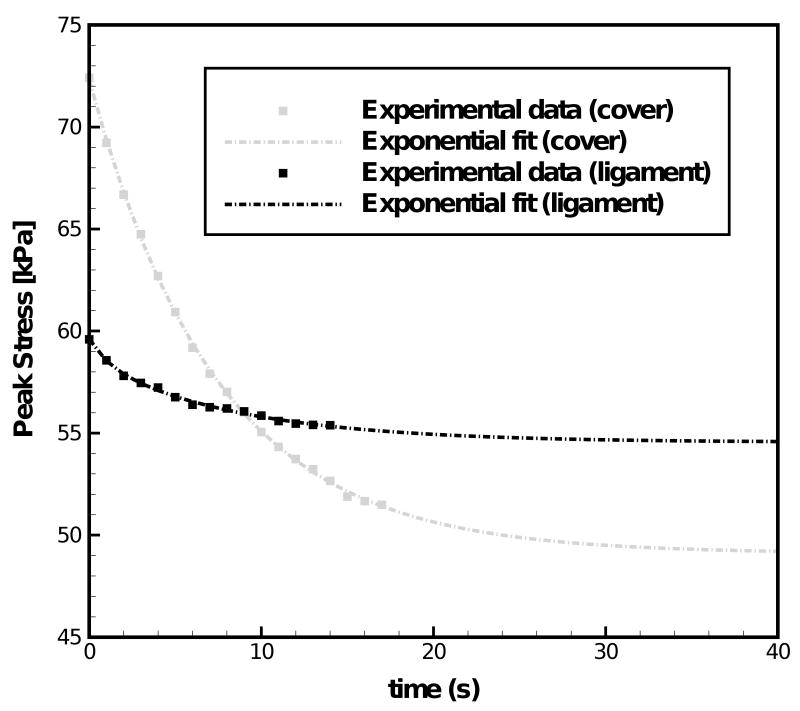
Figure 1 compares the experimental stress-stretch curve of the cover and the ligament to the constitutive model characterization. It can be seen from Fig. 1 that the nonlinear and hysteretic stress-stretch curves can be characterized very well by the two-network constitutive model both for the cover and the ligament specimen. Figure 2 exhibits the dependence of the experimentally determined peak values of stress σ_p for the vocal fold cover and the vocal ligament specimens upon the number of load cycles (or time). Figure 2 also shows the exponential fits obtained through curve-fitting for the cover and the ligament. Normalizing these fits by the values of peak stresses at t = 0 (72.3 kPa for the vocal fold cover and 59.6 kPa for the vocal ligament) yielded the long-term decay functions for the cover, σ_p,cover(t)/72.3 = 0.68 + 0.32·exp(−t/7.37), and the ligament, σ_p,ligament (t)/59.6 = 0.92 + 0.02·exp(−t/1.1) + 0.07·exp(−t/8.6). The stiffness of the time-independent equilibrium network evaluated from the first cycle of the stress-stretch curves was μ_A,0(cover) = 4.50 kPa for the cover, and μ_A,0(ligament) = 3.19 kPa for the ligament. These parameters were described to decrease with time after the first uploading by use of the exponential decay functions determined for the peak stress values for the cover μ_A,cover = 4.50·[0.68 + 0.32·exp(−t/7.37)] [kPa] and the ligament μ_A,ligament = 3.19·[0.92 + 0.02·exp(−t/1.1) + 0.07·exp(−t/8.6)] [kPa]. Figure 3 shows examples of simulation of the 15^th load cycle by the constitutive model including the decay in μ_A, in comparison to experimental data for the cover and the ligament, respectively. This figure indicates that the combination of the two-network model with a time dependent description of the stiffness of the equilibrium network can well capture both individual cycle hysteresis as well as long-term changes such as the peak stress decay observed during continuous cyclic loading.

Figure 2.

Comparison between experimental data and exponential fits of the peak stress decay with time for the vocal fold cover and the vocal ligament of the 66-year-old male subject.

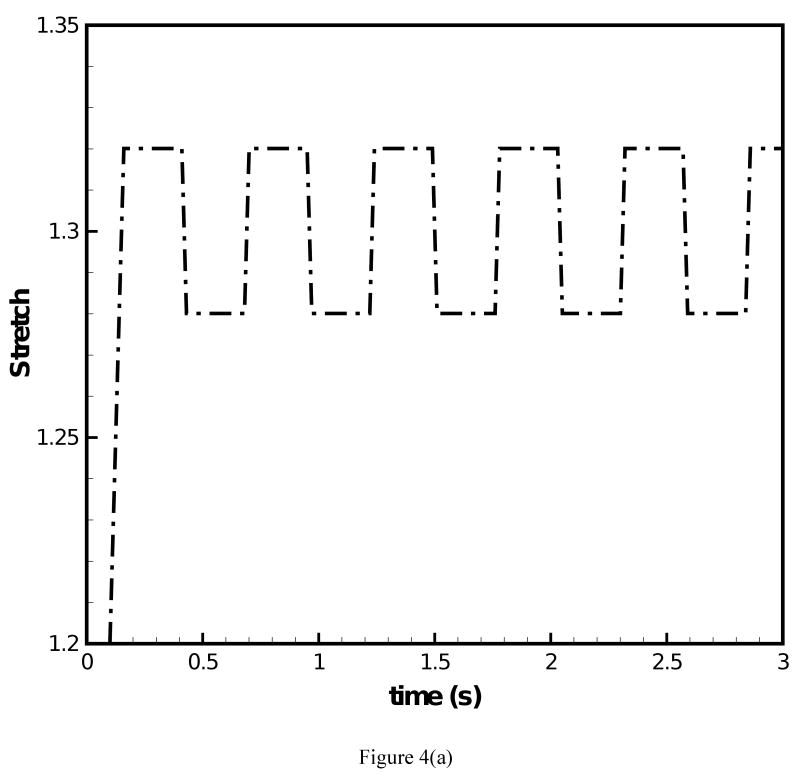
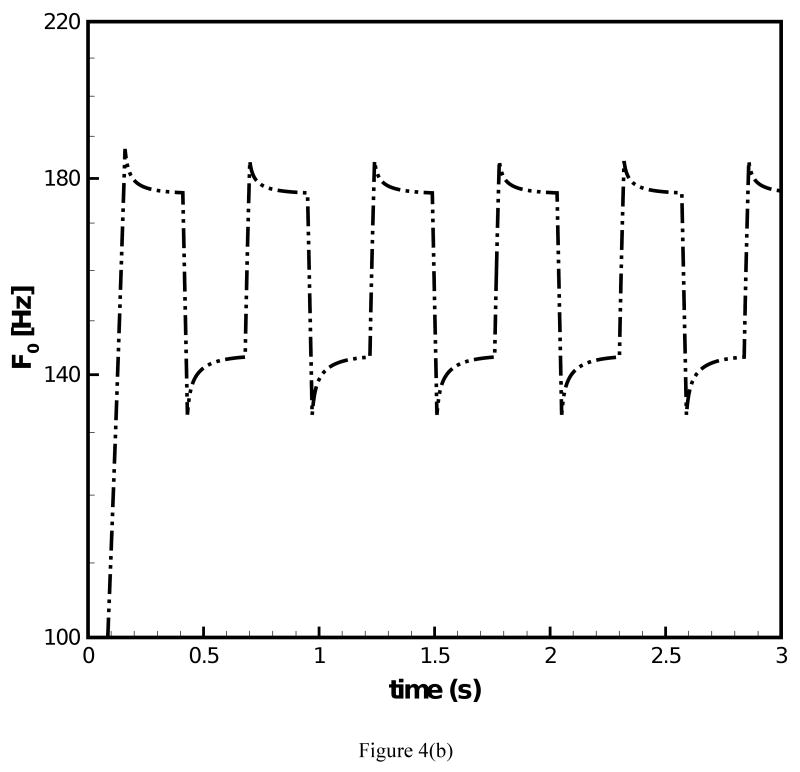
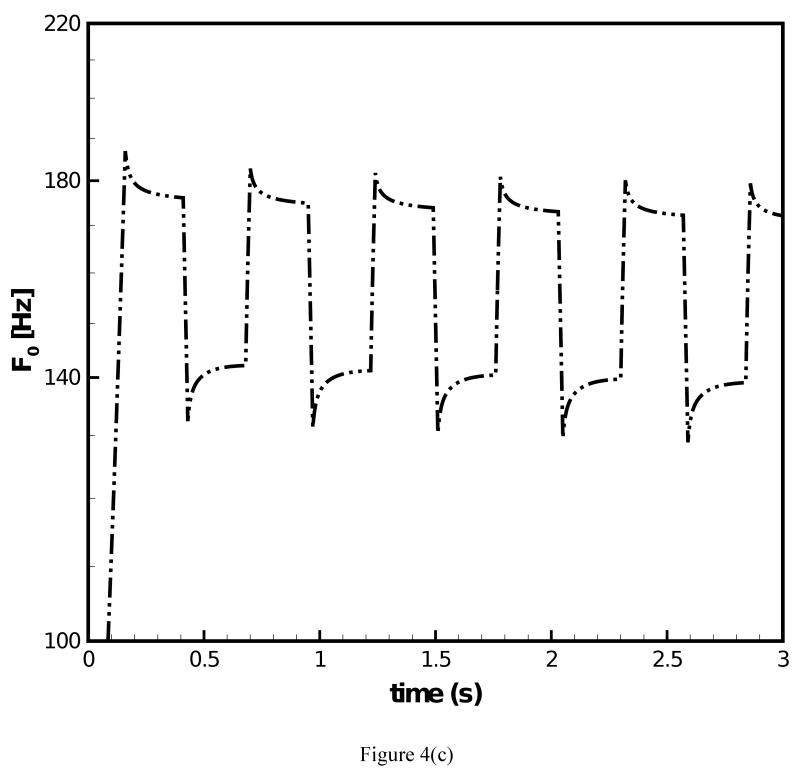
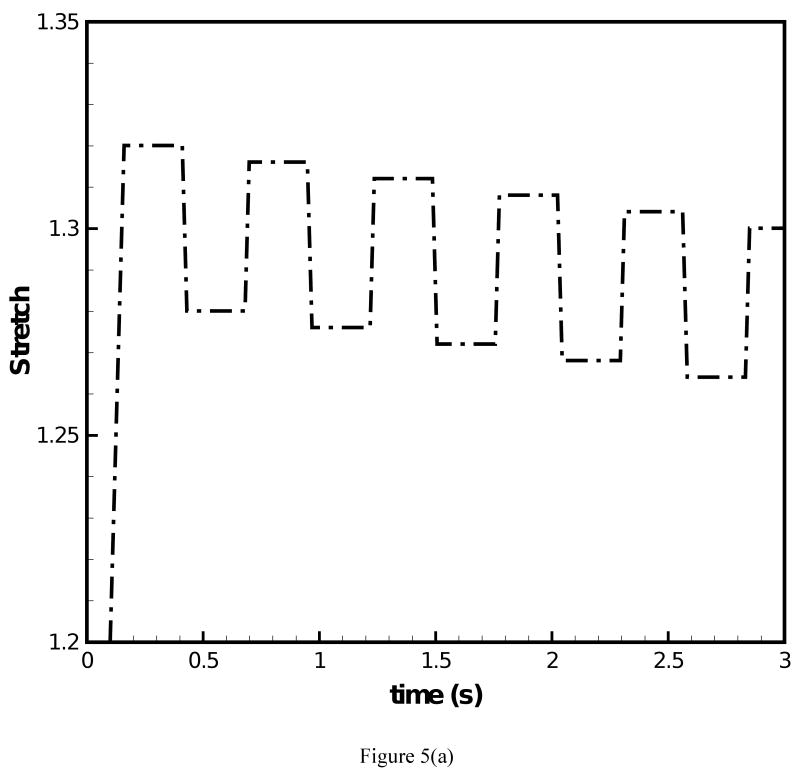
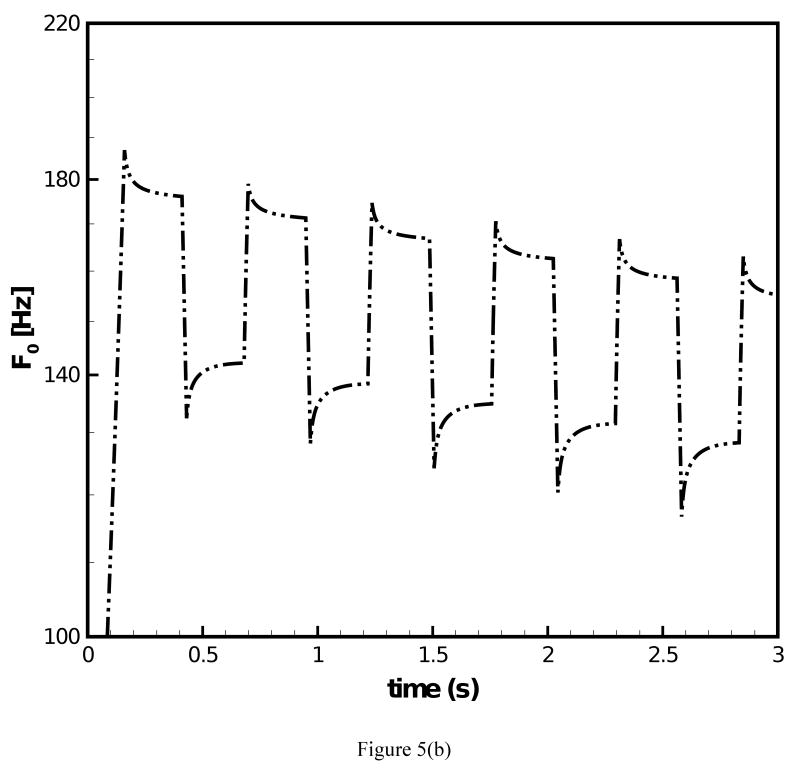
The fundamental frequency response under prescribed transient stretch histories was simulated with the data of the two-network constitutive model. Figure 4(a) depicts a transient stretch history with an initial increase in stretch and a subsequent square wave form under constant mean value of stretch. Figure 4(b) and (c) display the predicted F₀ contours under the conditions of (i) μ_A = const. and (ii) μ_A = f(t), respectively. For both simulations clear overshoot and undershoot events in fundamental frequency were predicted. Overshoots occurred at instances of steps in stretch increase. Thereby, F₀ quickly increased and a subsequent decreased slowly. Undershoots occurred at instances of steps in stretch decrease. Now F₀ quickly decreased and then steadily increased. Such findings are in good qualitative agreement with experimental data on F₀ [1]. It can be observed in Fig. 4(b) that for μ_A = const. the predicted peak values of F₀ remained constant at 184.1 Hz with exception of the first peak (186.9 Hz). Figure 4(c) shows that for μ_A = f(t) there was a gradual decrease of the predicted peak values of F₀, which reflects the decay of the stiffness in the equilibrium network. The percentage of peak F₀ decay was calculated to be 4.0%. However, the percentage of actual peak F₀ declination documented in experimental studies [2, 3] was about 25% for declarative sentences. To investigate on how such a level of peak F₀ decay could be achieved, the stretch history was modified to include a continuous decay in the mean value of stretch, Fig. 5(a). The corresponding predicted F₀ contour is given in Fig. 5(b). With the mean value of the stretch level diminishing with time, the percentage of peak F₀ decay was calculated to be 12.8%, closer to the 25% of decay in experimental studies [2, 3]. A stronger decay in stretch could be imposed such that a more significant decay in F₀ is predicted.

Figure 4.

(a) Stretch history under which F₀ contours are predicted; (b) F₀ contour predicted for the 66-year-old male subject with the original constitutive model employed; (c) F₀ contour predicted for the 66-year-old male subject with the improved constitutive model employed.

Figure 5.

(a) Stretch history under which F₀ contour is predicted; (b) F₀ contour predicted for the 66-year-old male subject with the improved constitutive model employed.

IV. Discussion

The objective of the present study is to propose a biomechanical model of the vocal fold lamina propria that predicts the local fluctuations and global changes of F₀ during phonation, under given stretch histories. These changes have been documented extensively [1-3] using signal processing methods to describe temporal F₀ contours. This paper aims to describe these changes from a different perspective. The biomechanical model of phonation is based upon a constitutive model for vocal fold tissues [11] and a structural model of vocal fold vibration [6] in our previous studies.

Experimental stress-stretch data were obtained from the vocal fold cover and the vocal ligament [10]. The constitutive model was utilized to characterize the large-strain, hyperelastic, and viscous response of the tissue components under tensile deformation in the anterior-posterior direction. The stiffness of the equilibrium network was prescribed to decrease synchronously with the peak stress to capture the peak stress decay observed in the preconditioning of vocal fold tissues. As can be seen from Figs. 1 and 3, the two-network model including a description of the stiffness decay in the equilibrium network can characterize experimental stress-stretch curves very well.

The model was employed to predict F₀ contours under different vocal fold stretch histories. Stretch histories are the active driving parameters in the present study. Real stretch histories in phonation are functions of the antagonistic activities of the cricothyroid (CT) muscle and the thyroarytenoid (TA) muscle. Vocal fold lengthening is primarily attributed to CT activation [5, 20]. It must be noted that the stretch histories implemented were hypothetical but reasonable since they were based upon previous studies [6, 18, 22-25] on the length changes of vocal fold during phonation. It can be seen from Figs. 4 and 5 that overshoots and undershoots of F₀ [1] (i.e., the local fluctuations F₀) can be characterized by our model corresponding to the step activation of stretch followed by hold periods in the stretch histories. The present model predicts that the overshoot and undershoot response is caused by stress relaxation in the vocal fold lamina propria. When the singer (or speaker) lengthens or shortens the vocal fold, and then keeps it at a constant length for a period of time, the stress in the vocal fold relaxes and causes the F₀ to drop or rise depending upon whether the vocal fold is lengthened or shortened. The global changes of F₀ are also characterized with the present biomechanical model of phonation. Under constant mean value of stretch the decay percentage of peak F₀ predicted in Fig. 4(c) is not enough compared to the actual decay percentage characteristic of declination in declarative utterances. This appears to indicate that the viscous response of the vocal fold lamina propria can only contribute partially to the fundamental frequency decay phenomenon in declarative utterances and that active linguistic and neuromuscular control of vocal fold stretch also plays a significant role in the formation of a declination.

The present constitutive model is not capable of characterizing some of the other phenomena associated with cyclic loading of vocal fold tissue (e.g., the gradual increase of the in situ (stress-free) length). A three-network constitutive model with two characteristic time constants has to be formulated to comprehensively characterize not only the short-term but also the long-term mechanical behaviors of the vocal fold lamina propria. Such a model is currently under investigation. In this sense, the current two-network model with an imposed exponential decay of the stiffness of the hyperelastic network is an intermediate model between the two-network model and the comprehensive three-network model. Limitations of the biomechanical model also originate from the structural model of vocal fold vibration, which only accounts for vibration in the medial-lateral direction. Physiologically, vocal fold vibration also involves motion in the inferior-superior direction. In this direction the vocal fold as a structure is more resistive than in the medial-lateral direction. Hence, the real F₀ of vocal fold vibration is probably higher than those predicted from the medial-lateral direction and thus much more complex to analyze.

V. Conclusion

The present study proposes a biomechanical model of phonation whose driving parameter is the stretch history as related to muscle activity. Since the model is based on parameters that describe actual tissue specimens it is in principle capable of predicting phonation differences between individual speakers. The contractions of the CT muscle and the TA muscle play antagonistic roles in regulating the vocal fold length changes. The vocal fold stretch histories employed in this study shift among different levels, which correspond to different syllables. The model demonstrates that the global (declination) and local changes (overshoot and undershoot) of fundamental frequency during phonation can in part be predicted by this biomechanical model as an outcome of the viscoplastic response of the tissue. Fundamental frequency changes over the time span of an utterance, however, appear to require additional active neuromuscular control of the vocal fold length. Such a model could be built by combining the present results with models involving active control, such as a body-cover model [5, 22].