Infrared micro-spectroscopy of human cells: Causes for the spectral variance of oral mucosa (buccal) cells

Abstract

We discuss the causes contributing to the variance of the spectra of individual human epithelial cells. This aspect has largely been ignored in previous studies, but needs to be understood for diagnostic applications of infrared micro-spectroscopy. We attribute the spectral variance to Mie scattering, and to variations of nuclear contributions to the overall spectra caused by different nuclear size.

1. Introduction

Infrared micro-spectroscopy (IR-MSP) of individual cells is a promising tool for automatic analysis and diagnosis of human cells. However, individual cell spectra show large spectral variations, both for cultured cells and cells exfoliated from human donors. Spectral variations observed for cultured cells have been the subject of studies in the authors’ laboratory for about 7 years, and have been attributed to different stages in the cell division cycle [1–4]. However, we also observe large spectral heterogeneity in exfoliated epithelial cells, which should be divisionally inactive, and relatively homogeneous. Therefore, variations due to cell division should be relatively uncommon in these samples.

An understanding of the spectral variations is essential if IR-MSP is going to be utilized as a diagnostic tool in medicine. We attribute the spectral variance to three distinct factors: Mie scattering, which may produce broad, undulating features superimposed on the spectra [5], changes in nuclear contributions to the spectra, and low wavenumber (<1400 cm⁻¹) variations most likely attributable to cell division [2]. In this paper, we shall discuss the first and second of these effects. For a discussion on recent results of spectral dependence on the cell cycle, the reader is referred to the literature [2]. In subsequent papers, we shall present multivariate statistical methods for the interpretation and classification of cellular spectra.

2. Methods

2.1. Cell collection and sample preparation

Oral mucosa (buccal) cells were harvested from volunteer graduate and undergraduate students in the department under a local IRB protocol. Before sample collection, the oral cavity was repeatedly rinsed with mouthwash. Subsequently, the inside of the cheek was gently swiped with a sterile polyester swab. Cells were shaken off the swabs in sterile saline solution, repeatedly centrifuged, washed with buffered saline solution (BSS), formalin-fixed, and eventually deposited on the sample substrate (see below). We estimate that a single swiping of the oral cavity results in about 10⁵ to 10⁶ exfoliated cells. Visual microscopic inspection of the cell samples produced indicates good homogeneity of the slides: over 99% of all cells are large squamous cells with small, well-delineated nuclei and a large cytoplasm. These cells typically are between 60 and 100 μm in diameter.

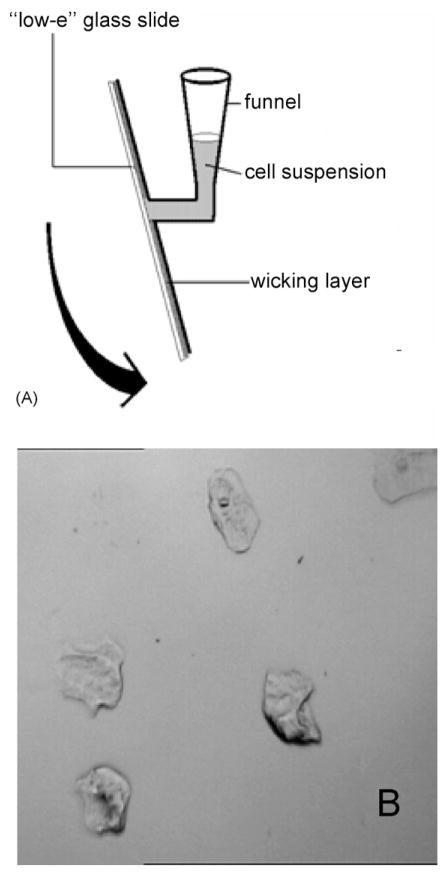
We deposit cells onto spectral substrates by one of two different methods developed originally for cytology: the CytoSpin^™ [6] or the ThinPrep^™ [7] methods. The aim of either deposition techniques is to produce sparse monolayers of cells such that all cells are well separated from their nearest neighbors to provide an unobstructed view (or measurement aperture) of each cell. This is quite different from the “smears” produced from cervical brushes, which were just smeared onto microscope slides. This procedure produces thick clumps of cells that are not suitable for visual or automatic analysis. All results presented here were collected from slides prepared by the CytoSpin^™ method using a CytoSpin4 centrifuge (Thermo Sheldon, Inc., Pittsburgh, PA). In the CytoSpec method, which is a “liquid-based” methods (since cells are deposited from a cell suspension, rather then from a brush or other exfoliation device), ca. 0.5 mL of cell suspension with a concentration of about 5 × 10⁴ cells/mL, are placed into a special, conical funnel, which is clamped against the microscope slide. Between the funnel and the slide is a layer of wicking paper with a 5 mm diameter hole (cf. Fig. 1A). The entire assembly is placed into a special rotor of a centrifuge, and spun between 800 and 1200 rpm for 6–8 min. The centrifugal force presses the liquid onto the slides, where it is wicked away by the absorbent layer of paper, leaving the cells on the substrate. After deposition of the cells, the sample is washed with deionized water and quick-dried in a dry air stream. A typical exfoliated cell sample prepared by this method is shown in Fig. 1B. The sampling area, 5 mm in diameter, contains about 10³ cells with more than a cell’s size distance between cells.

Fig. 1.

(A) Schematic of CytoSpin funnel used for the deposition of exfoliated cell samples on “low-e” slides. (B) Photomicrograph of a sample of exfoliated oral mucosa cells on a “low-e” slide. A typical cell measures about 50–60 μm along the longest dimension. The area shown represents about 800 μm on edge.

All IR-MSP spectra were collected in reflection mode from cells deposited on “low-e” slides (Kevley Technologies, Chesterland, OH), originally developed for skyscraper windows. They consist of thin layer of Ag atoms on glass, overcoated by a tin oxide layer. The coating is sufficiently thin to be transparent in the visible, but highly reflective in the infrared region. Thus, any cell on these slides can be inspected by visual microscopy, and IR spectral data can be collected, in reflectance, from these cells.

Spectra of exfoliated oral mucosa cells can be collected from fixed cell samples, or from unfixed cells after drying. Once deposited and dried, the cells were found to be stable for many days, which was established by examining spectra days or even weeks apart. Neither morphologic nor spectroscopic changes could be observed as a function of time. It is well known that “dry fixation” is a particularly mild form of fixation that preserves structure and composition of biological samples. The process of precipitating and drying proteins appears to have an effect similar to fixation in that it renders the protein matrix insoluble and relatively inert. On the other hand, formalin-fixation for about 30 s, using 5% buffered aqueous solution of formaldehyde, produces spectra that are indistinguishable from unfixed cells. This was demonstrated by analyzing data sets of hundreds of fixed and unfixed spectra by multivariate methods. These results will be discussed in a later paper.

2.2. Data acquisition

Spectra were collected using a Perkin-Elmer (Perkin-Elmer Corp., Sheldon, Connecticut) Spectrum One/Spotlight 300 FTIR micro-spectrometer in single point mode. This instrument is henceforth referred to as the PE300. It incorporates a 100 μm × 100 μm photoconductive HgCdTe (MCT) detector, operated at liquid nitrogen temperature, which covers the entire IR spectral range from 7000 to 650 cm⁻¹.

The objective provides an image magnification of 6× at a numerical aperture of 0.58. Visual image collection via a CCD camera is completely integrated with the microscope stage motion and IR spectra data acquisition. Visible images of the deposited cells are collected under white light LED illumination, and “quilted” together to give a pictures of the entire sample deposition area. Hundreds of individual cells are selected from this sample image on screen, and for each cell, an aperture size and orientation is defined. The aperture size is selected to straddle the cell, typically between 40 μm × 40 μm and 80 μm × 80 μm. Cell position and apertures are stored for each cell. Data acquisition of all stored positions proceeds automatically. For single cell spectra, 128–256 interferograms, collected at 4 cm⁻¹ spectral resolution, were co-added, requiring 1–2 min per spectrum.

The microscope and the optical bench are continuously purged with purified, dry air. In addition, the sample area in the focal plane of the microscope has been enclosed in a sample chamber, which is purged as well.

3. Results and discussion

In this section, we present spectral results for about 75 individual oral mucosa (buccal) cells from one donor, presumed healthy. We have collected similar data sets from about a dozen different donors, and have observed the same spectral patterns. Fig. 2 shows the un-normalized, raw spectra of these individual cells, along with their mean spectrum, and the standard deviation from the mean. We observed large variations in the overall amplitude of the spectra, at the wavenumber range of no absorption (Arrow A) as well as within strong bands (Arrow A′). In addition, broad undulating features are observed between the arrows marked B, and distinct spectral variations in the low wavenumber region, marked by the Arrow C in Fig. 2.

Fig. 2.

Raw infrared absorption spectra of ca. 150 oral mucosa cells. The region between the arrows marked A and A′ indicates the intensity variance of the spectra. The region delineated by arrows marked B represents the wavenumber range in which most of the Mie scattering contributions are observed for cellular nuclei. The region marked C indicated the “low wavenumber” range in which the effects of cellular activity are observed. The three heavy spectral traces represent (from top) the mean spectrum plus one standard deviation, the mean spectrum, and the mean spectrum minus a standard deviation.

We shall discuss these spectral observations in turn. The broad, undulating features observed relatively weakly in the spectra of entire cells were previously attributed to Mie scattering [5] of the cellular nuclei. For instrument apertures coinciding with the size of the nucleus, the Mie scattering due to the nucleus becomes more prevalent in the overall spectra (see Fig. 3). In spectra of entire cells, such as the ones shown in Fig. 2, the Mie scattering of the nuclei is averaged over the much larger area of the cell (nuclear area <100 μm², cellular area ca. 4000 μm²), and is observed with much lower amplitude as compared to the absorption features of the cell. Nevertheless, the broad background features contribute to the spectral background, and need to be explained properly.

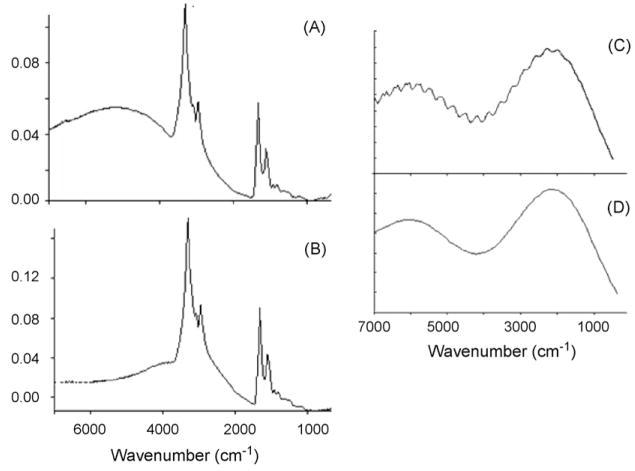
Fig. 3.

(A) and (B) Mie scattering contributions of cellular nuclei observed for two different oral mucosa cells. In both cases, the measurement aperture was selected to coincide with the nucleus. Notice the maximum of the scattering shifts with nuclear size, and that in these plots, the wavenumber scale is not linear but compressed by a factor of 2 above 2000 cm⁻¹). Comparison between Mie scattering contributions using exact (C) and approximate (D) theory, according to Eqs. (1) and (8), respectively.

3.1. Mie scattering of cellular nuclei

Examples of Mie-type scattering contributions of the nucleus, observed by setting the measurement aperture to straddle the nucleus rather than the entire cell, are shown in Fig. 3, Panels A and B. Dielectric spheres are known to scatter electromagnetic radiation if the wavelength of the light is comparable to the size of the dielectric sphere. Although the theory of this scattering process was first described theoretically by Mie [8], it is not well known in the chemist’s world. However, since the mathematics of Mie scattering is rather involved, only a short summary of the theory will be presented here.

Mie theory assumes a spherical scattering particle in the field of a plane electromagnetic wave. Therefore, it is best to express the wave in terms of spherical polar coordinates, resulting in complicated expressions of the electric and magnetic vectors in terms of Bessel (cylindrical coordinate) functions.

The scattering and extinction cross sections Q_sca and Q_ext of a dielectric sphere interacting with a plane electromagnetic wave can be written in terms of the scattering coefficients a_n and b_n [9]:

$$Q_{\text{sca}}=\left(\frac{1}{{\rho }^2}\right)\sum _{n=1}^{\infty }(2n+1)(\mid a_n{\mid }^2+\mid b_n{\mid }^2)$$ (1)

$$Q_{\text{ext}}=\left(\frac{1}{{\rho }^2}\right)\sum _{n=1}^{\infty }(2n+1)Re(a_n+b_n)$$ (2)

where the size parameter ρ is defined by

$$\rho =2\pi r\frac{m_0}{\lambda }$$ (3)

Here r is the radius of the sphere, λ the wavelength of the light, and m₀ is the refractive index of the surroundings.

The scattering coefficients a_n and b_n are complicated expressions in the Ricatti–Bessel functions Ψ, and Hankel functions ξ:

$$a_n=\frac{{\mathrm{\Psi }}_n(\rho ){\mathrm{\Psi }}_n(m\rho )-m{\mathrm{\Psi }}_n(m\rho ){\mathrm{\Psi }}_n(\rho )}{{\xi }_n(\rho ){\mathrm{\Psi }}_n(m\rho )-m{\mathrm{\Psi }}_n(m\rho ){\xi }_n(\rho )}$$ (4)

where Ψ_n(ρ) = (πρ/2)^1/2 J_n+(1/2) (ρ). The functions J_n+(1/2) (ρ) are the half-integer order Bessel (Ricatti–Bessel) functions of the first kind. The Hankel functions ξ_n(ρ) are the complex equivalents of Ψ_n(ρ). A similar expression holds for b_n. The Bessel functions account for the undulating wavelength dependence of Mie scattering.

The angle dependence of Mie scattering can be evaluated from the amplitude functions of the scattered electromagnetic fields (Poynting vectors) S₁ and S₂ [9]:

$$S_1(\theta )=\sum _{n=1}^{\infty }\frac{2n+1}{n(n+1)}[a_n{\tau }_n(cos\theta )+b_n{\pi }_n(cos\theta )]$$ (5)

$$S_2(\theta )=\sum _{n=1}^{\infty }\frac{2n+1}{n(n+1)}[b_n{\tau }_n(cos\theta )+a_n{\pi }_n(cos\theta )]$$ (6)

Here S₁ and S₂, respectively, describe the components that are polarized horizontally and vertically with respect to the scattering plane. The functions τ_n(cos θ) and π_n(cos θ) in Eqs. (5) and (6) are expressions in the Legendre polynomials, $P_n^{(l)}$:

$${\pi }_n(cos\theta )=\frac{P_n^{(l)}(cos\theta )}{sin\theta }\text{and}{\tau }_n(cos\theta )=\frac{\text{d}{P}_n^{(l)}(cos\theta )}{\text{d}\theta }$$ (7)

and account for the angular dependence of Mie scattering.

We have calculated the Mie scattering according to Eq. (1), using a program available as shareware [10]. We have also used an approximate formula, which was reported in the literature [11]:

$$Q_{\text{sca}}=2-\left(\frac{4}{\rho }\right)sin\rho +\left(\frac{4}{{\rho }^2}\right)(1-cos\rho )$$ (8)

with the size factor ρ defined previously. This approximation (which is the truncated form of the summation in Eq. (1)) reproduces the rigorous calculation to within 1%, but fails to reproduce the high frequency ripples on the Mie scattering curve. In Fig. 3, Panels C and D, we show the Mie scattering cross section, calculated for a sphere with refractive index of 1.33 and a radius of 5 μm, calculated using Eqs. (1) and (8). The rigorous calculations presented in Fig. 3C agrees quantitatively with previously reported Mie scattering curves [12], whereas the approximate calculations (Fig. 3D) do not reproduce the fine structure observed for perfect spheres.

A spectrum of a nucleus that includes a scattering background, collected from 650 to 7000 cm⁻¹, is shown in Fig. 4, Panel (B). The absorption spectrum is superimposed on a scattering contribution with a broad peak under the C–H stretching manifold. The onset of a second broad band appears at ca. 6000 cm⁻¹. The pure scattering spectrum, calculated for a nuclear radius of 4.2 μm, is shown in Fig. 4, Panel (A). Based on an approximate size of the nucleus (r ≈ 4.5 ± 0.5 μm, judged by the selected aperture), we may estimate the refractive index of the nucleus to be about 1.3 in the mid-to near IR spectral region.

Fig. 4.

Panel (A) Calculated Mie scattering contribution for a nucleus with radius of 4.2 μm and a refractive index of 1.3. Panel (B) Observed spectrum of a nucleus collected with an aperture of (r ≈ 4.5 ± 0.5 μm). The absorption spectrum is superimposed on a scattering contribution with a broad peak under the C–H stretching manifold. The onset of a second broad band appears at ca. 6000 cm⁻¹.

3.2. Overall intensity (amplitude) variations of observed cellular spectra

We now turn to the discussion of the overall intensity variations observed for spectra of cells. These variations can have various real and artificial reasons, both of which are related to aspects of the measurement area, and the thickness of the cell. An artifact will arise, for example, if spectra of cells of different sizes are acquired with a constant aperture. The spectrum of a cell is always averaged over the entire aperture area from which the data were acquired. Thus, if spectra are collected for one and the same cell with different measurement apertures, the overall intensity (amplitude) of the spectra varies. Similarly, if spectra of cells, whose dimensions varied greatly, are observed with a constant aperture, large intensity differences will be created. Therefore, we collected the cell spectra shown in Fig. 2 by matching the aperture to the size of the cell as closely as possible. Thus, it is unlikely that the variation in cell size contributes significantly to the variance in observed spectral intensities reported here.

The concentration of cellular components will affect the overall spectral intensities according to Beer–Lambert’s law. From a biochemical consideration, it is unlikely that for metabolically inactive superficial epithelial cells, the concentration of the major cellular components differ to an extent necessary to account for the observed spectral variations. Thus, we believe that the intensity variation in the observed spectra is due to two factors: the thickness of the cell, as well as the nucleus/cytoplasm (N/C) ratio.

The dried cytoplasm of an epithelial cell is very thin, as determined by confocal microscopic techniques [13], typically ca. 2–3 μm. In the cytoplasm, the amide I mode typically exhibits absorbance values of ca. 0.05 OD units. This was first reported, using truly confocal measurements based on synchrotron-based FTIR micro-spectroscopy [3]. In these measurement, the confocal geometry utilized minimizes diffraction effects of the cells’ edges. However, we found that the sampling geometry of the PE300 instrument used in these studies produces nearly identical results. Thus, we believe that diffraction from the cells’ edges does not contribute or falsify the observed spectra.

The nucleus of these tried cells maintains a more spherical shape, with an average thickness of about 7–10 μm, as determined by the Mie scattering properties discussed above. The variation in both these thickness themselves will produce significant variations in the absorption intensities of a cell. Therefore, the spectral contributions of the nucleus will affect the spectrum of a cell to a much greater extent than one might expect. This is demonstrated next.

Although the nucleus contains nearly the entire cellular DNA, the nuclear spectra are dominated by protein features, and often exhibit absorbance values of 0.3–0.5 OD units in the amide I band. The size of the nucleus will influence the overall amplitude of the spectral intensity of an entire cell in two ways: first, by an averaging process of the nuclear intensity over the entire area of the cell, and second, via an “optical density” argument similar to that employed to explain the absence of DNA signals in some nuclei.

To discuss the first aspect, let us assume that an oral mucosa cell on a substrate can be described by the cytoplasm, with an area of about 4000 μm², and the nucleus, with an area of about 100 μm². A simple calculation shows that the cross section of the nucleus, exhibiting an absorbance of 0.5 OD units, averaged over the cross section of a cell’s cytoplasm with an absorbance of 0.05 OD units, contributes about 20% of the total protein signal, although the area of the nucleus is only about 2.5% of the cell’s area. A small decrease in the nuclear size (for example, from 10 to 7 μm) will cause an overall change in protein signal by about 10%. Thus, small variations in nuclear size will influence the total protein intensity to a large extent.

Furthermore, very condensed histone proteins in very small nuclei may exhibit similar nonlinear absorption behaviour that was reported earlier for DNA [5,14]. For terminally differentiated and metabolically inactive cells, the nuclei become pyknotic, and the nuclear size decreases drastically. For such nuclei, the nuclear protein spectral intensity could be so high that the nucleus becomes opaque, and its spectral features would be lost. In this case, a large decrease in protein intensity would be observed. Thus, we believe that the nuclear size influences the overall protein spectral intensities of cells, and accounts in part for the variance in the overall intensity of cellular spectra, which we found for all exfoliated squamous epithelial cells. Even larger intensity variations were observed for cultured cervical cancer cells [4], for which large differences in cell morphology undoubtedly contributed to the spectral variance.

Thus, we believe that the large variations in spectral amplitudes of cells result from variations in the size of the nucleus as compared to the size of the entire cell. In cytology, this effect is referred to as the nuclear/cytoplasmic ratio (N/C), which is a commonly applied measure of a cell’s health and activity. We found that in spite of these intensity variations, cellular spectra can be analyzed by multivariate statistical methods that emphasize common features and de-emphasize irrelevant variations in the spectra. Results of these studies will be reported shortly.

Furthermore, we conclude that spectroscopy of cells is very different from normal “chemical” spectroscopy in as far as sample-to-sample variations are much larger for cells than for chemical analytes. IR spectra of a chemical analytes, collected at different laboratories, at different times, and using different instruments, will be highly reproducible. Any differences can be attributed to physical factors such as temperature, purity and instrumental response. For such analytes, a “true” spectrum of the analyte exists. For cells, a true spectrum does not exist per se, but has to be viewed as a most probable spectrum from a class of spectra with large variance, caused by variations in the dimensions of the nucleus. This aspect is new in the field of spectroscopy, and may have contributed to spurious results reported in the literature, since the statistical nature of spectral results of cells was not recognized. Furthermore, the fact that two near-identical cells may present quite different spectral patterns points to the fact that sophisticated methods of multivariate statistics need to be employed in this research to yield useful results.

The causes for variations of spectral patterns in the low wavenumber (<1400 cm⁻¹) region, observed for very few cells, are not understood at this time, but may be due to pyknosis or necrosis of the cells. These effects are being studied in detail in the authors’ laboratory.

4. Conclusions

In this and subsequent papers, we lay the groundwork for the application of cell spectroscopy for medical diagnostic purposes. We find that spectra of very homogeneous cell samples produce very heterogeneous results. We presented mechanisms to explain this spectral heterogeneity.