Abstract
Depression-related differences in memory for emotional material are well established, but recognition memory and lexical decision tasks often fail to produce consistent results. The null results from these tasks could be due to inadequacies in traditional analyses rather than the absence of effects. In particular, analyses of accuracy or mean reaction times rely on only a fraction of the behavioural data and are sensitive to individual differences in response biases. The diffusion model addresses these limitations by incorporating all of the behavioural data and separating out response biases. We applied the diffusion model to data from lexical decision and recognition memory tasks and showed consistent effects, specifically a positive emotional bias in non-dysphoric subjects and even-handedness in dysphoric subjects. This pattern was not apparent with comparisons of reaction times or accuracy, consistent with previous null findings. These results suggest a relationship between dysphoria and the internal representation of emotional information.
INTRODUCTION
The effect of depressive states on memory for emotional information has been extensively researched. For studies of memory and perceptual processing, the common finding is a processing advantage (often termed a bias) for mood congruent information (Bower, 1981). Numerous studies have shown a negative emotional bias in clinical depression, even-handedness (i.e., no emotional bias) in dysphoria, and a positive emotional bias in non-depressed individuals (Bradley & Mathews, 1983, 1988; Colombel, Gilet, & Corson, 2004; Gotlib & McCann, 1984; Kuiper, Olinger, MacDonald, & Shaw, 1985). While this pattern of differences is fairly robust in paradigms like recall or primed lexical decision, other related tasks often produce null effects. In particular, recognition memory and unprimed lexical decision tasks have failed to consistently show depression-related mood congruency. There are two interpretations of the null results from these tasks. It could be that these tasks are too insensitive to produce consistent effects in this domain (e.g., Coles & Heimberg, 2002), leaving open the possibility that underlying differences still exist. An alternative explanation is that the inconsistent results across tasks reflect the bounded nature of mood congruent memory, suggesting that certain aspects or levels of processing (and thus certain tasks) do not show mood congruency (e.g., Watkins, 2002). The goal of this study was to test these interpretations by using a cognitive model to increase analysis sensitivity. As such, we explored whether applying the diffusion model (Ratcliff, 1978) to data from lexical decision and recognition memory tasks could demonstrate consistent dysphoria-related differences in memory for emotional material. Finding such differences would challenge some of the presumed boundaries in mood congruent memory and support the claim that the null results in these tasks were due to variability in the data rather than the absence of an effect. Before the model is described, we present a brief review of studies failing to find emotional memory differences using lexical decision and recognition memory tasks, followed by a discussion of the inadequacies of traditional analyses in these tasks.
Depression-related mood congruency has been considered robust in recall tasks (Blaney, 1986), but several studies using recognition tasks have failed to produce significant results (Danion, Kauffmann-Muller, Grange, Zimmerman, & Greth, 1995; Dietrich et al., 2000; Nikendei, Dengler, Wiede-mann, & Pauli, 2005). Further, at least two studies that have failed to show differences in recognition tasks have shown significant results in recall measures (Kurtz & Morey, 1999; Neshat-Doost, Taghavi, Moradi, Yule, & Dalgleish, 1998). The basic (unprimed) lexical decision task has also failed to reveal consistent depression-related differences in memory for emotional material, whereas primed lexical decision tasks have been more successful. Greater repetition priming of depression-related words has been shown in clinically depressed compared to non-depressed individuals (Bradley, Mogg, & Williams, 1995) and dysphoric compared to non-depressed individuals (Bradley, Mogg, & Millar, 1996; Colombel, Gilet, & Corson, 2004). Although none of these studies reported comparisons of the basic (unprimed) conditions, their data suggest that the differences would not be significant. In addition, Scott, Mogg, and Bradley (2001) found significant differences in semantic priming, but not in the repetition priming or basic lexical decision task. Thus primed lexical decision tasks have demonstrated mood congruency, but basic lexical decision tasks have not. There is some evidence, however, that there are depression-related differences in the basic lexical decision task, even though the behavioural measures do not reflect it. For example, Canli and colleagues failed to produce behavioural differences in a lexical decision task, but did show differences through fMRI analyses, where depressed subjects relative to non-depressed had reduced activity for positive words (Canli et al., 2004).
Recall measures and primed lexical decision measures, which involve retrieval based on the associative strength between words, have produced fairly consistent differences in this area, but recognition and unprimed lexical decision tasks, which involve the internal representation of the word, often produce null results. This fundamental distinction between these tasks provides support for boundaries in depression-related mood congruent memory, implying that depression is associated with differential associative strength for emotional information, but not differential strength of the internal representations of such information. This distinction is consistent with many contemporary theories of depression. For example, Neshat-Doost et al. (1998) stated that the failure to find mood congruency in their recognition task was “not surprising because none of the current theories in the adult literature predicts a bias in recognition memory associated with depression” (p. 647).
In a related vein, Watkins (2002) has reported evidence that conceptually based implicit memory tasks show mood congruency (though not always), but perceptually based tasks do not. He takes these results as evidence that mood congruent memory does not occur at all levels of processing, noting that the relation between conceptual elaboration and depressive rumination might account for the need to use conceptual tests to produce an effect. However, while Watkins considered the null results from perceptually based tasks to support boundaries in mood congruency, he suggested that some of the null findings in conceptual tasks might be due to error variance. Given that perceptual tasks consistently fail to produce effects, whereas conceptual tasks do show effects, this is a reasonable interpretation. However, it is also possible that the null results in perceptual tasks could be due to noisy data as well. The same explanation could hold for the presumed boundaries between associative and representation based tasks, namely that sources of error variance are obscuring small effects in representation based tasks. In the next section, we discuss potential sources of noise in data from these tasks and then introduce a method for reducing it through analyses.
Variability in speeded cognitive tasks
Both lexical decision and recognition memory tasks are choice reaction time (RT) tasks that involve fast, one-process decisions, and the collection of three dependent measures, accuracy and correct and error reaction times. This class of paradigms has been used extensively to assess memory for emotional material in depressive states, as well as the effects of depressive states outside of emotional memory (e.g., Bulbena & Berrios, 1993; Ferguson, Wesnes, & Schwartz, 2003; Hindmarch, 1998). When analysing data from choice RT tasks, researchers typically focus on either accuracy or mean (or median) correct RTs for analyses. Unfortunately, there are several limitations to this approach. The first limitation is that individual differences in response biases can greatly affect results. Subjects can be biased toward one response or the other, or they can be biased to have a conservative or liberal response style. This problem can be illustrated through a well-established phenomenon in these tasks, the speed/accuracy trade-off: an individual who responds quickly will tend to make more errors than one who responds slowly. Because RTs and accuracy are affected by response style, differences in either measure do not necessarily reflect the construct of interest (e.g., memory or lexical processing). As such, extraneous noise is introduced into the analyses, decreasing their sensitivity. Many researchers ignore this problem, but when it is addressed the common approach is to compare group means on accuracy and RTs to identify differences in speed/accuracy settings. Unfortunately, this method averages over individual differences in criterion settings and thus does not properly address the issue.
The second major limitation of traditional analyses is that they use only a portion of the available data. Analyses of lexical decision data usually focus on correct RTs and ignore accuracy values and error RTs, provided that there aren’t large group or condition differences in accuracy, whereas analyses of recognition memory data usually focus on accuracy and ignore RTs. In fact, in studies on depression and memory for emotional material, we only found one lexical decision study that analysed error rates (Canli et al., 2004) and one recognition memory study that analysed RTs (Dietrich et al., 2000). In addition, RTs for error responses are almost never analysed, even though they should presumably arise from the same process as correct responses. This practice becomes problematic because effects of independent variables manifest in all three dependent measures. By focusing on only one of the dependent measures, researchers exclude informative data.
These limitations can significantly decrease sensitivity and obscure underlying differences, which could be partially responsible for the null findings in lexical decision and recognition tasks. Fortunately, current sequential sampling decision models (e.g., Ratcliff & Smith, 2004) can address these issues by incorporating all of the behavioural data and parsing it into separate components of processing. In the present study we focus on the diffusion model (Ratcliff, 1978; Ratcliff & Rouder, 1998; Ratcliff, Van Zandt, & McKoon, 1999), a successful member of this class of models. It uses the RT distributions and accuracy from behavioural data to estimate the contribution to performance of each of the components involved in making a simple decision.
THE DIFFUSION MODEL
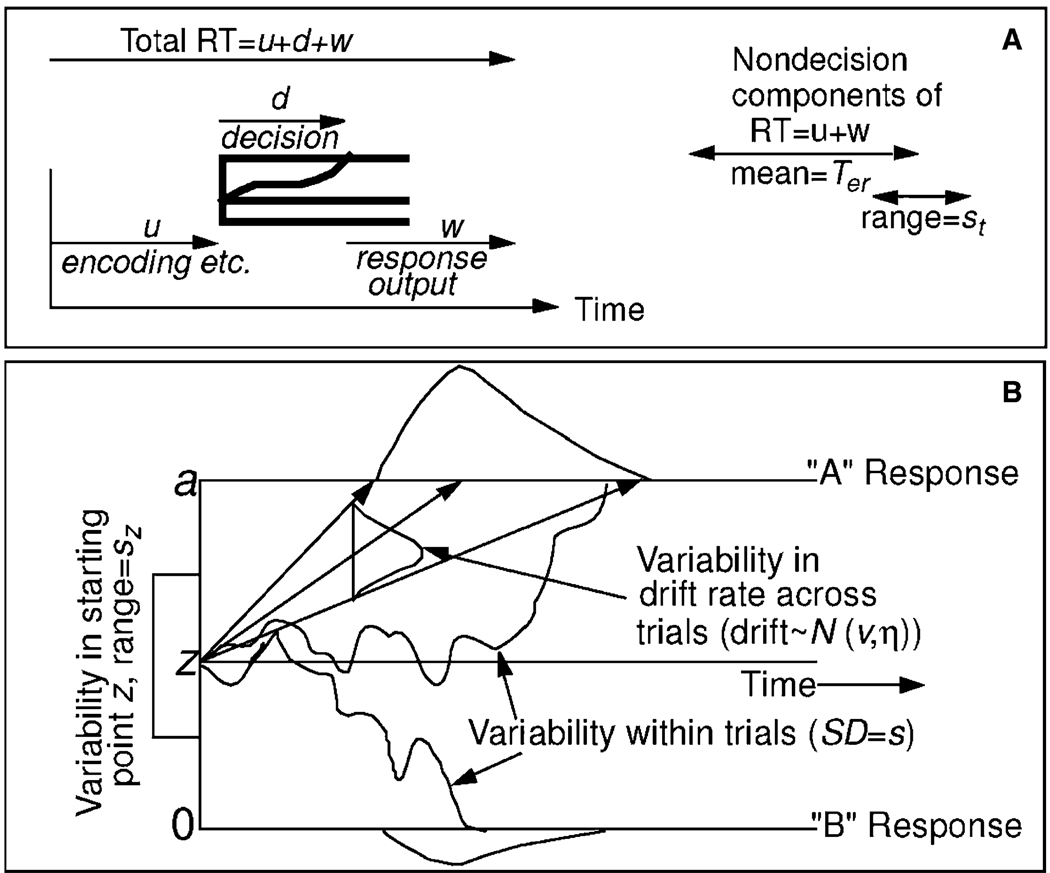
The diffusion model (Ratcliff, 1978) is a decision process model that accounts for the entire process involved in making a simple decision. In a choice RT task, subjects must encode the stimulus (e.g., visually), use the information to make a decision, and then make a motor response (e.g., press a button). For the decision component of this process, the diffusion model assumes that decisions are made by a noisy process that accumulates information over time from a starting point to one of two response boundaries, shown in Panel B of Figure 1, where the starting point is labelled z and the boundaries are labelled a and 0. A response is initiated when one or the other boundary is reached. Components of processing not involved in the decision process, including stimulus encoding and response execution (u and w in Panel A of Figure 1) are combined into one component with mean Ter.
Figure 1.
An illustration of the diffusion model. Panel A shows the total response process, including encoding and response output. Panel B shows the diffusion process for the decision component of the response process. Parameters of the model are: α, boundary separation; z, starting point: Ter, mean value of the non-decision component of reaction time; η, SD in drift across trials; sz, range of the distribution of starting point (z) across trials; ν, drift rate; p0, proportion of contaminants; st, range of the distribution of non-decision times across trials; and s, SD in variability in drift within trials.
In the decision process the mean rate of accumulation of information is called the “drift rate”, υ, and it is determined by the quality of the information extracted from the stimulus. For a lexical decision task, drift rate represents the match between the test string and lexical memory, with a high frequency (i.e., familiar) word producing a high value of match with lexical memory and therefore a higher drift rate than a low-frequency word. For a recognition memory task, drift rate represents the match between a test word and memory, meaning a strongly learned word will have a higher drift rate than a weakly learned word. Within each trial, there is noise (variability) in the process of information accumulation, represented by the non-monotonic line in Figure 1B, so that processes with the same mean drift rate do not always terminate at the same time (producing RT distributions), or at the same boundary (producing errors). The geometry of the model predicts the positively skewed RT distributions that are found in empirical data (Ratcliff & Rouder, 1998).
The distance between boundaries, a (i.e., a – 0), indexes response conservatism. A large boundary separation indicates a conservative response style, which leads to slower but more accurate responses. A small boundary separation indicates a liberal response style, which leads to faster but less accurate responses. The location of the starting point (z) relative to the two boundaries indexes an individual’s bias towards one response or the other. If an individual has a starting point that is closer to boundary a than 0, that person is biased towards that response. By estimating the values of boundary separation and starting point for an individual, the diffusion model directly addresses speed/accuracy tradeoffs and response biases, allowing for unbiased estimates of an individual’s rate of evidence accumulation from stimuli (i.e., drift rate).
In summary, the primary parameters of the diffusion model correspond to the components of the decision process as follows: z is the starting point of evidence accumulation; a represents the distance between boundaries; Ter is the non-decision time (encoding and motor response); and υ is the drift rate for each condition. It is assumed that easy conditions in an experiment have large numerical values of drift rate, and difficult conditions have lower numerical values of drift rate. The secondary parameters, which are important to provide good fits to the data, are as follows: η is the standard deviation in mean drift rate across trials; sz is the range of the starting point across trials; and st is the range of Ter. For the interested reader, these variability parameters are described in the Ratcliff and Tuerlinckx (2002).
The diffusion model has been applied to data from recognition memory tasks (Gronlund & Ratcliff, 1991; Ratcliff, 1978, 1988; Ratcliff, Thapar, & McKoon, 2004d) and lexical decision tasks (Ratcliff, Gomez, & McKoon, 2004a; Ratcliff, Perea, Coleangelo, & Buchanan, 2004b; Ratcliff, Thapar, Gomez, & McKoon, 2004c), supporting its use in the present study. The methodology of a diffusion-model analysis provides advantages that lead to increased sensitivity. First, the model incorporates all of the behavioural data, including the accuracy values and correct and error RT distributions for each condition. Thus no data are discarded, and all manifested differences are captured. The second major advantage of the diffusion model methodology is the control of extraneous variability. This can be especially important in experiments with a limited number of stimuli, including studies of mood congruency. To control for differences in response style, experiments are designed to include many filler observations, in this case emotionally neutral words. When the behavioural data is modelled, these filler conditions (along with the emotional conditions) are used to estimate values of response criterion for each individual. Because there are more fillers than emotional words, the fillers dominate in estimating response criteria. Then, the drift rates estimated for the emotional conditions take into account each subject’s values for conservatism, bias, and non-decision time. Thus the resulting drift rates are not subject to the effects of these components, and therefore are less noisy than the behavioural data.
Another advantage of the diffusion model is that is allows for between-group comparison of the different processing components. Ratcliff et al. (2004c) used the diffusion model to investigate the effects of aging, and showed that the slower lexical decision RTs for older subjects (age 65–75) were mainly due to more conservative decision criteria and slower non-decision time, and did not reflect a deficit in extracting information from the stimuli. By decomposing the general cognitive slowing associated with aging into different processing components, the model provided a more precise and different interpretation of the cause of the slowdown.
EXPERIMENTS
Three experiments were designed to assess differences in memory for emotional material between dysphoric and non-dysphoric subjects. In all three experiments there were positively and negatively valenced words presented sporadically among many emotionally neutral words. Experiment 1 was a lexical decision task and Experiment 2 and Experiment 3 were recognition memory tasks.
We expected to find differences in memory for emotionally valenced words between dysphoric and non-dysphoric subjects, specifically a positive emotional bias in non-dysphoric subjects and no emotional bias (even-handedness) in dysphoric subjects. Accordingly, positively valenced words should provide a better match to memory than negatively valenced words for non-dysphoric subjects, but not for dysphoric subjects. Although a typical mood congruency effect might predict a negative bias for dysphoric individuals, there is substantial evidence for even-handedness associated with dysphoria (Bradley & Mathews, 1983; Gotlib & McCann, 1984; Matt, Vasquez, & Campbell, 1992). The diffusion model also allows us to examine differences in response conservatism, response bias, and non-decision time, though we have no a priori expectations that there will be differences in these components.
Experiment 1
Method
Stimuli
The stimuli were emotionally valenced words, emotionally neutral high and low-frequency words, and non-words. Emotional words were taken from previous studies that examined memory bias and negative self-schemata (Bradley & Mathews, 1983; Mathews, Mogg, May, & Eysenck, 1989). Two 30-word pools were created, one positive and one negative, that were matched for letter length (average 7 letters) and word frequency, with positive emotional words having frequencies of 1–202 per million (M=30.83, SD=43.3; Kucera & Francis, 1967) and negative emotional words having frequencies of 1–195 per million (M=30.63, SD=43.7).
The emotionally neutral word pools consisted of 366 high frequency (HF) words with frequencies from 78 to 10,600 per million (M=287.49, SD=476) and 599 low-frequency words (LF) with frequencies of 4 and 5 per million (M=4.41, SD=0.17). Non-words were created by randomly replacing all of the vowels with other vowels (except for u after q) from the original neutral word pools (for further details see Ratcliff et al., 2004a). The neutral word pools did not contain words that were emotionally valenced or closely related to an emotional word (e.g., “fortune” and “fortunate”). Stimuli were chosen randomly from the pools without replacement for use in the experiments.
Measures
Level of dysphoria was assessed using the Center for Epidemiological Studies Depression Scale (CES-D; Radloff, 1977). Cut-off scores were chosen to roughly capture the upper and lower third of CES-D scores. This method was chosen over a median split to produce groups that were more differentiated in terms of level of dysphoria. Subjects who scored 18 or higher were classified as dysphoric, and those who scored 8 or lower were classified as non-dysphoric.
Subjects
All subjects were Ohio State University students who participated for course credit in an introductory psychology course. All available students were allowed to participate in the experiments, but only those who had a CES-D score of greater than 18 or less than 8 were included for analyses. In Experiment 1, 19 subjects (9 female) were non-dysphoric (CES-D M=5.4, SD=3.1) and 19 (10 female) were dysphoric (CES-D M=23.6, SD=4.4).
Design
In Experiment 1 a standard lexical decision procedure was used. Subjects were shown strings of letters and instructed to decide for each whether it was a word or non-word. Each string of letters was displayed until a response was made. Subjects were instructed to press the “/” key if the string was a word, and the “z” key if it was not a word, and to perform the task quickly and accurately. Each string of letters was displayed until a response was made with a 200 ms delay between response and presentation of the next letter string. After completing a practice block of 24 trials (6 high- and 6 low-frequency words, 12 non-words), subjects completed 15 blocks of 72 trials. Each block consisted of 17 high-frequency words, 17 low-frequency words, 34 non-words, and 4 emotionally valenced words (2 positive, 2 negative). Neutral words and non-words were presented randomly within each block. Emotionally valenced words were displayed no earlier than the tenth trial in each block and were separated from each other by at least 5 trials. To control for potential sequential effects, each emotionally valenced word was preceded by a high-frequency word. The entire experiment lasted approximately 45 minutes.
The stimuli were displayed on a CRT of a Pentium II class PC, and RTs and accuracy were collected from the keyboard. To discourage guessing, if a subject responded incorrectly the word “ERROR” was displayed for 750 ms. Subjects were provided opportunities to rest between each block and completed a CES-D questionnaire after all blocks were completed. The CES-D was not available to the subjects until they had completed all blocks.
Fitting the diffusion model to experimental data
This section provides more technical details about the modelling process itself and the fit quality. A major issue in modelling concerns the quality of the fits to the data, since the extracted parameter values are meaningless unless the model provides a good description of the data. The information included in this section is not necessary to understand the results and conclusions, so readers who are primarily interested in the dysphoria-relevant findings may wish to go directly to the results section. A more detailed description of the fit quality is provided in the appendix.
The diffusion model was fit to each individual subject’s data to obtain the values of each processing component that best fit the data, then these parameter values were averaged across subjects. For all subjects, RTs less than 250 ms or greater than 3 s were excluded to eliminate fast guesses and long outliers (less than 0.5% of the data). The model was fit to the data by minimising a chi-square value with a general SIMPLEX minimisation routine that adjusted the parameters of the model to find the values that gave the minimum chi-square value (for a full description of the fitting method see Ratcliff & Tuerlinckx, 2002). The data entered into the minimisation routine for each experimental condition were the RTs for each of five quantiles for correct and error responses, the accuracy values, and the number of observations. The .1, .3, .5 (median), .7, and .9 quantiles were used to approximate the shape of the RT distributions.
The chi-squared values used in the minimisation routine provided a quantitative measure of the quality of fit. Goodness of fit was assessed with degrees of freedom equal to (K×11) – M, where K was the number of conditions and M was the number of parameters (for additional details see Ratcliff & Tuerlinckx, 2002). For Experiment 1 the chi-square test had 53 degrees of freedom and a critical value of 71. The mean chi-square value was 102 for all subjects, suggesting significant misses between the model and data. However, the number of observations was very large and the power of the chi-squared statistic increases with number of observations, so even a small difference in the proportions of observed and expected frequencies (e.g., .01) becomes significant as N grows (see Ratcliff et al., 2004c).
The fit quality was comparable to previous applications of the diffusion model (e.g., Ratcliff et al., 2004c) and showed that the model fit the data well. Based on this, the parameter values from the model can be interpreted. The parameters of interest in the present study correspond to drift rate (υ), decision criteria (boundary separation, a, and starting point, z), and non-decision components (Ter). The other parameter values are important for fitting the model but do not directly apply to our main hypotheses and thus are not included in the analyses.1 Visual inspection shows that none of them varied meaningfully across experiments or groups.
Results
Because the focus of this study is on memory for emotional stimuli, responses to filler stimuli will not be included in the analyses. However, the filler stimuli were important to constrain the model parameters (see Advantages and limitations of the diffusion model), so the data and parameter estimates for these conditions are reported. Traditional analyses of mean RTs and accuracy will be presented along with drift-rate analyses to allow comparison between measures. Table 1 shows the behavioural data and Table 2 shows the corresponding diffusion-model parameters.
TABLE 1.
Behavioral data for each experiment
| Dysphoric |
Non-dysphoric |
|||||||
|---|---|---|---|---|---|---|---|---|
| Exp. & condition |
Accuracy | Mean correct RT |
Mean error RT |
No. of observ. |
Accuracy | Mean correct RT |
Mean error RT |
No. of observ. |
| Exp. 1 | ||||||||
| HF | .968 | 638 | 612 | 5744 | .971 | 569 | 561 | 6119 |
| LF | .845 | 764 | 771 | 5688 | .847 | 681 | 706 | 6118 |
| Non-word | .873 | 699 | 785 | 11,080 | .935 | 667 | 705 | 11,264 |
| Negative | .954 | 692 | 685 | 566 | .952 | 643 | 672 | 600 |
| Positive | .949 | 653 | 704 | 563 | .952 | 583 | 576 | 600 |
| Exp. 2 | ||||||||
| HF old | .730 | 830 | 922 | 1525 | .702 | 800 | 934 | 1526 |
| HF new | .602 | 920 | 855 | 1966 | .693 | 875 | 890 | 1984 |
| LF old | .793 | 778 | 915 | 1221 | .823 | 766 | 938 | 1223 |
| LF new | .772 | 852 | 880 | 1977 | .845 | 838 | 929 | 1986 |
| Negative | .785 | 795 | 926 | 507 | .809 | 797 | 946 | 509 |
| Positive | .801 | 798 | 900 | 508 | .815 | 797 | 881 | 508 |
| Exp. 3 | ||||||||
| HF old | .676 | 781 | 825 | 2981 | .680 | 849 | 929 | 3019 |
| HF new | .662 | 849 | 798 | 1919 | .669 | 897 | 941 | 2588 |
| LF old | .782 | 742 | 780 | 2655 | .818 | 779 | 973 | 1940 |
| LF new | .810 | 808 | 797 | 1930 | .837 | 860 | 985 | 1938 |
| Negative | .681 | 854 | 800 | 714 | .755 | 895 | 909 | 717 |
| Positive | .687 | 821 | 851 | 715 | .714 | 886 | 890 | 720 |
Notes: SEs for dysphoric subjects are in the range of 50–85 ms across subjects for error responses and 60–95 ms for correct responses. SEs for non-dysphoric subjects are in the range of 40–85 ms for error responses and 45–85 ms for correct responses. RT=response time; HF=high-frequency words; LF=low-frequency words; Negative=negative emotional words; Positive=positive emotional words; No. of observ.=total number of observations for each group.
TABLE 2.
Average model parameters from fits of the diffusion model for each experiment
| Drift rates | Filler | Emotional | ||||
|---|---|---|---|---|---|---|
| Exp. 1 (Lex) | HF word | LF word | Non-word | Pos | Neg | |
| Non-dysphoric | 0.503 (0.19) | 0.212 (0.08) | −0.308 (0.10) | 0.453 (0.23) | 0.336 (0.12) | |
| Dysphoric | 0.396 (0.09) | 0.182 (0.05) | −0.248 (0.12) | 0.363 (0.13) | 0.333 (0.12) | |
| Exp. 2 (Rn) | HF old | HF new | LF old | LF new | Pos old | Neg old |
| Non-dysphoric | 0.106 (0.06) | −0.167 (0.09) | 0.198 (0.07) | −0.263 (0.08) | 0.234 (0.08) | 0.171 (0.10) |
| Dysphoric | 0.101 (0.07) | −0.091 (0.10) | 0.168 (0.08) | −0.214 (0.09) | 0.132 (0.07) | 0.158 (0.12) |
| Exp. 3 (Rn) | HF old | HF new | LF old | LF new | Pos new | Neg new |
| Non-dysphoric | 0.092 (0.08) | −0.118 (0.09) | 0.248 (0.09) | −0.0301 (0.10) | −0.181 (0.09) | −0.256 (0.14) |
| Dysphoric | 0.089 (0.07) | −0.112 (0.07) | 0.173 (0.11) | −0.214 (0.11) | −0.102 (0.10) | −0.108 (0.11) |
| Response criteria | Boundary sep. (a) | Starting point (z) | Bias (z/a) | Non-decision time (Ter) | ||
| Exp. 1 (Lex) | ||||||
| Non-dysphoric | .128 (.02) | .064 (.01) | .506 (.03) | .428 (.04) | ||
| Dysphoric | .149 (.05) | .069 (.02) | .525 (.05) | .432 (.05) | ||
| Exp. 2 (Rn) | ||||||
| Non-dysphoric | .138 (.03) | .058 (.02) | .579 (.05) | .576 (.06) | ||
| Dysphoric | .137 (.02) | .059 (.01) | .576 (.05) | .538 (.07) | ||
| Exp. 3 (Rn) | ||||||
| Non-dysphoric | .150 (.03) | .064 (.01) | .573 (.06) | .571 (.06) | ||
| Dysphoric | .126 (.03) | .054 (.01) | .563 (.08) | .515 (.10) | ||
Notes: Standard deviations are shown in parenthesis. Lex=lexical decision task; Rn=recognition memory task; HP=high frequency; LF=low frequency; Pos=positively valenced words; Neg=negatively valenced words; old=studied words; new=unstudied words; a=boundary separation; Ter=non-decision component; z=starting point; Bias=relative distance between starting point and boundaries (see text for details). Negative drift rates correspond to the “non-word” boundary in Exp. 1 and the “new” boundary in Exps 2 and 3. For a boundary separation of.10: drift rates of.1, .2, and .3 correspond to accuracy of .70, .85, and .93, respectively.
For analyses of emotional memory, 2×2 mixed ANOVAs were performed on each dependent measure (i.e., accuracy, mean RTs, drift rates), with Group (dysphoric, non-dysphoric) as the between factor and Valence (positive, negative) as the within factor. For accuracy comparisons there were no significant main effects or interactions (all Fs<1). For comparisons of mean RTs, the main effect of Valence was significant, F(1, 36)=22.93, MSE=2089, p<.001, with faster responses to positively valenced words. There was no main effect of Group, F(1, 36)=2.75, MSE=19816, p=.101, or interaction between Group and Valence, F(1, 36)=1.04, MSE=2089, p=.315. For drift rate comparisons there was a main effect of Valence, F(1, 36)=11.48, MSE=0.010, p=.002, with higher drift rates for positively valenced words. The main effect of Group was not significant, F(1, 36)=1.82, MSE=0.037, p=.186, but the interaction between Group and Valence did reach significance, F(1, 36)=4.44, MSE=0.010, p=.042. Subsequent paired t-tests showed that non-dysphoric subjects had higher drift rates for positively compared to negatively valenced words, t(18)=3.12, p=.005, and the difference was not significant for dysphoric subjects, t(18)=1.35, p=.193.
Differences in response criteria were assessed by between-group t-tests. Response conservatism was assessed by comparing boundary separation (a), response bias was assessed by comparing the relative position of the starting point of information accumulation (z) between the two boundaries, and encoding and motor reaction time was assessed by comparing the non-decision component (Ter). Table 2 shows the corresponding parameter values. The dysphoric group showed evidence of greater conservatism, but the difference did not reach significance, t(36)=1.768, p=.085. There were no differences in response bias or non-decision time (both ts < 1.3).
Discussion of Experiment 1
Comparisons of drift rates showed a difference in memory for emotional material between dysphoric and non-dysphoric subjects, with the latter showing preferential memory for positively valenced words, and the former showing even-handedness. Reaction time differences were in the expected direction but did not reach significance. Although there was a hint of increased conservatism in the dysphoric group, the difference was not significant, and none of the other processing components differed between the groups.
Experiments 2 and 3
Experiment 2 and Experiment 3 are presented together because they were both recognition memory tasks that differed only in whether emotional words were targets or lures. Because each emotional word pool contained only 30 words, splitting them into target and lure responses within an experiment would leave a small number of observations that would result in noisier estimates of RTs, accuracy, and drift rates. Thus rather than include emotional words as targets and lures within an experiment, we chose to use the words only as targets in Experiment 2 and only as lures in Experiment 3. The same stimuli and CES-D cut-offs were used as in Experiment 1.
Methods
Design
Experiment 2 and Experiment 3 used a standard recognition memory procedure in which subjects studied a list of words and then were tested on a list of words and instructed to respond “old” (“it was studied”) by pressing the “/” key, or “new” (“it was not studied”) by pressing the “z” key. Subjects were instructed to respond quickly and accurately. The only difference between Experiment 2 and Experiment 3 was the placement of emotional words, with emotional words presented only as targets (old) in Experiment 2 and lures (new) in Experiment 3.
In both experiments, subjects completed a practice list of 8 study words and 16 test words, followed by 10 study/test lists. Each study list contained 26 words presented once. In Experiment 2 there were 11 high-frequency, 9 low-frequency, and 6 emotionally valenced words (3 positive, 3 negative) in each study list. Test lists consisted of 52 words: the 26 studied words and 26 new words, the latter consisting of 13 high-frequency and 13 low-frequency words. In Experiment 3, study lists contained 13 high-frequency and 13 low-frequency words. Test lists consisted of the 26 studied words and 26 new words, the latter consisting of 10 high-frequency words, 10 low-frequency words, 3 positively valenced words, and 3 negatively valenced words.
For both experiments, neutral words were presented randomly in the study and test lists. To avoid primacy and recency effects, there was a buffer of at least four neutral words at the beginning and end of all study and test lists. To avoid potential priming effects, emotionally valenced words were separated by at least 3 words in the study lists and 5 words in the test lists. Study words were presented for 1200 ms, and each test word was presented until a response was made, with a 200 ms delay between response and presentation of the next test word. Both experiments lasted approximately 40 minutes and subjects did not fill out the CES-D until all lists were completed.
Subjects
In Experiment 2, 17 subjects (7 female) were non-dysphoric (CES-D M=6.4, SD=2.8), and 17 (9 female) were dysphoric (CES-D M=26.4, SD=6.1). In Experiment 3, 24 subjects (12 female) were non-dysphoric (CES-D M=6.84, SD=2.4), and 24 (11 female) were dysphoric (CES-D M=24.2, SD=5.8).
Hypotheses
Our hypotheses for Experiment 2 and Experiment 3 were similar to those for Experiment 1. We expected positive emotional words to provide a better match to memory than negative emotional words for the non-dysphoric subjects, which would produce opposing effects in Experiment 2 and Experiment 3 because of the different task requirements. A better memory match would enhance the ability to correctly retrieve the studied words, thus we expected to see an advantage for positive emotional words in the non-dysphoric group in Experiment 2. On the contrary, when the emotional words are presented as unstudied lures, a better match to memory would impair the ability to correctly reject them (i.e., they would seem more familiar), thus we expected to see a disadvantage for positive emotional words in the non-dysphoric group in Experiment 3. The even-handedness we observed for the dysphoric subjects in Experiment 1 suggests that they would show no preferential memory for positive or negative emotional words in either experiment.
Results
The quality of model fits was comparable to Experiment 1. The average chi-square values were 93 in Experiment 2 and 112 in Experiment 3, with a critical value of 71 for both experiments. Comparisons of emotional memory were performed using 2×2 mixed ANOVAs for each dependent measure, with Group as the between factor and Valence as the within factor. Behavioural data are shown in Table 1, diffusion-model parameters in Table 2.
For Experiment 2 (emotional words “old”), accuracy comparisons showed no significant main effects or interactions (all Fs<1). Comparisons of RTs also showed no significant differences (all Fs<.05). Drift rate comparisons showed a main effect of Group, F(1, 32)=5.64, MSE=0.009, p=.024, with higher drift rates for the non-dysphoric group. There was no main effect of Valence on drift rates, F(1, 32)=0.06, MSE=0.007, p=.808, but the interaction between Group and Valence was significant, F(1, 32)=4.64, MSE=0.007, p=.039. Subsequent paired t-tests showed that non-dysphoric subjects had higher drift rates for positively compared to negatively valenced words, t(16)=2.15, p=.048, and the difference was in the opposite direction but not significant for dysphoric subjects, t(16)=−0.898, p=.382.
For Experiment 3, comparisons of accuracy showed that the main effect of Group did not quite reach significance, F(1, 46)=3.03, MSE=0.021, p=.088, and there was no main effect of Valence, F(1, 46)=1.11, MSE=0.007, p=.297, or interaction between Group and Valence, F(1, 46)=1.83, MSE=0.007, p=.183. Although the interaction did not reach significance, we ran the subsequent t-tests and found that the non-dysphoric subjects showed lower accuracy for positive compared to negative emotional words that neared significance, t(23)=1.91, p=.068, and there was no difference for dysphoric subjects, t(23)=−0.193, p=.849. Comparisons of RTs showed a borderline effect for Valence, with slower overall responses to negative emotional words, F(1, 46)=4.04, MSE=4212, p=.051. Neither the main effect of Group nor the Group by Valence interaction reached significance (both Fs<1.75). Drift rate comparisons showed main effects for Group, F(1, 46)=16.58, MSE=0.018, p <.001, and Valence, F(1, 46)=7.12, MSE=0.006, p=.01. Overall, non-dysphoric subjects had higher drift rates than dysphoric subjects, and drift rates for negative emotional words were higher than for positive emotional words. The interaction between Group and Valence was significant for drift rates, F(1, 46)=5.22, MSE=0.006, p=.027. Subsequent paired t-tests showed that non-dysphoric subjects had lower drift rates for positive compared to negative emotional words, t(23)=3.04, p=.005, and there was no difference for dysphoric subjects, t(23)=0.332, p=.743.
Comparisons of diffusion-model parameters from Experiment 2 showed no significant differences in conservatism, bias, or non-decision time (all ts<1.7). In Experiment 3, the non-dysphoric subjects were significantly more conservative than dysphoric subjects, t(46)=2.96, p=.005, and had longer non-decision time, t(46)=2.46, p=.018, but there was no difference in response bias, t(46)=0.482, p=.632.
Discussion of Experiments 2 and 3
The results of the two recognition memory tasks were informative. Comparisons of drift rates showed significant interactions between group and valence in both experiments. When the emotional words were studied targets, non-dysphoric subjects showed an advantage for positive emotional words. When the emotional words were unstudied lures, non-dysphoric subjects showed a disadvantage for positive emotional words. This pattern is consistent with the results of Experiment 1, suggesting that positive emotional words are more strongly represented than negative emotional words for non-dysphoric subjects, resulting in a bias to respond “old”. Dysphoric subjects, on the other hand, consistently showed even-handedness in their responses to positive and negative emotional words. This pattern of results was only significant in comparisons of drift rates, though the accuracy comparison in Experiment 3 showed a non-significant trend in the expected direction.
There were two other results of interest from Experiments 2 and 3. First, there were main effects of group in both experiments, showing higher drift rates overall for non-dysphoric subjects. We might expect that this reflects an emotion-specific deficit in the dysphoric subjects, but we ran ANOVAs on the filler conditions and found an overall performance deficit that was significant for drift rates and borderline for accuracy, suggesting that the deficit was not specific to emotional words. The other interesting result was that non-dysphoric subjects were more conservative and had longer non-decision time than dysphoric subjects in Experiment 3. However, the fact that it only happened in 1 of 3 experiments suggests that might be specific to that particular subject group.
GENERAL DISCUSSION
The three experiments in the present study show a consistent pattern of differences between dysphoric and non-dysphoric subjects. Although the lexical decision and recognition memory tasks involve different processes, the results can easily be explained within a unified framework. In this framework, different processes operate on the stimulus representation to produce a match value, which then serves as evidence to drive a common decision process. The results suggest that positive emotional words are more strongly represented than negative emotional words in the non-dysphoric subjects. A stronger representation would lead to greater perceptual fluency and match to lexical memory, and thus a preferential advantage in the lexical decision task. For the recognition memory tasks, a stronger representation would be similar to greater familiarity, which would increase the likelihood that a word would be labelled as “studied”, subsequently increasing performance for targets but decreasing performance for lures. The dysphoric subjects, on the other hand, lacked the stronger representation seen in the non-dysphoric subjects, which was reflected by null differences between positive and negative emotional words.
The primary aim of this study was to determine if differential emotional memory could be shown in lexical decision and recognition memory tasks. The results support the claim that these differences do exist in the tasks, but are weak enough to be obscured by variability in the data. Drift rates proved to be a more sensitive measure of performance than accuracy or RTs, allowing the underlying differences to emerge. Accordingly, it appears as though the previous null results from these tasks reflect insensitivity inherent in the traditional methodology rather than a true boundary of mood congruency.
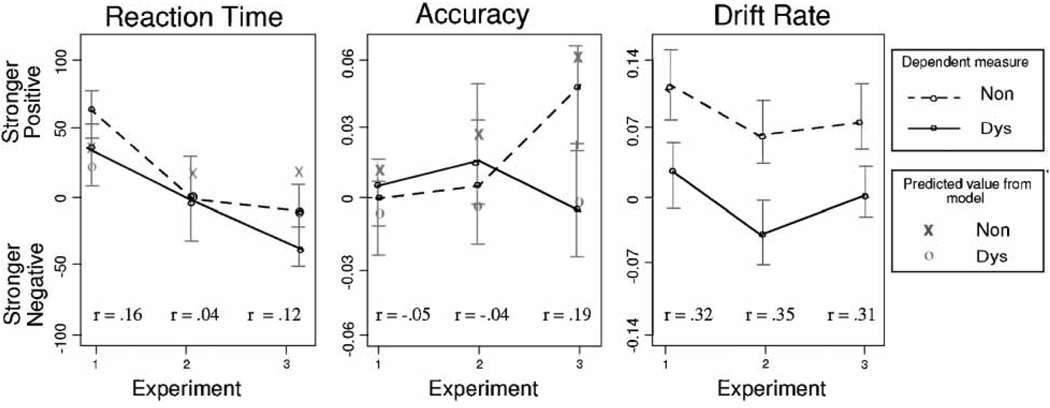
The advantage of drift rates over RTs and accuracy can best be shown by simultaneously displaying the results from all three experiments. Figure 2 displays the differences between positively and negatively valenced words for each dependent measure. Effect-size correlations are listed at the bottom of each graph (computed from Cohen’s d), indicating the magnitude of the difference between dysphoric and non-dysphoric subjects (i.e., the Group × Valence interaction). Positive effect size indicates a difference in the hypothesised direction. In the figure, “stronger positive” indicates evidence that positively valenced words were more strongly represented than negatively valenced (i.e., better performance in Experiments 1 and 2 but worse performance in Experiment 3). Overall, Figure 2 shows consistent, significant differences in drift rates that are not present for accuracy or reaction times. Further, the effect size in drift rates is much larger and more consistent than in RTs or accuracy. The dark “o” symbols are the average data for each group, and the grey “x” and “o” symbols represent the predicted values from the diffusion-model parameters for the non-dysphoric and dysphoric groups, respectively. All of the predicted values fall within two standard errors of the behavioural data and capture the basic trend of the behavioural data, showing small, insignificant differences.
Figure 2.
Comparisons of memory for emotional words across experiments from differences in mean reaction time, accuracy, and drift rates between positively and negatively valenced words. The dashed lines represent non-dysphoric subjects and the solid lines represent dysphoric subjects. Positive values correspond to stronger information from positively valenced words and negative values correspond to stronger information from negatively valenced words. Error bars represent 1 SE; r= effect-size correlation (from Cohen’s d). See text for details on computing the differences.
The design of these experiments allows us to make important claims about the differences in retrieving emotional words from memory, namely that the effects occur quickly and automatically. This study differs from many others in this domain because the emotional words occurred randomly, with an average lag of at least 3 items between them. Because of this, the words were unlikely to prime each other, and subjects were unlikely to notice them as stimuli of interest, suggesting that the processing differences between dysphoric and non-dysphoric were not the result of strategic influences or associative priming.
In addition to drift rate comparisons of memory for emotional material, applying the diffusion model to the data allowed comparison of conservatism, response criteria and non-decision components. Although we had no a priori expectations of differences in these components, the diffusion-model analysis allowed us to investigate the possibility. Unsurprisingly, there were no consistent differences between dysphoric and non-dysphoric subjects in response bias, conservatism, or non-decision components. The non-dyspho-ric group was more conservative and had longer non-decision time in Experiment 3, but the failure to replicate this in the other two experiments suggests that the differences are not consistent across groups. So, even though there were no consistent differences in response criteria between dysphoric and non-dysphoric subjects, the diffusion model provides a precise method to further explore the issue.
Associative strength vs. strength of representation
The consistent dysphoria-related differences found in semantic priming and recall measures support differential associative strength of emotional information associated with dysphoria. The results of the present study suggest that dysphoria also affects the strength of the internal representation of such information. The effect sizes in the present study (rs=.31–.35) are comparable, though slightly smaller, than the effect sizes found in many of the associative tasks (rs=.37–.41; e.g., Bradley et al., 1995, 1996; Neshat-Doost et al., 1998). Given the different subject characteristics, stimuli, and methodologies among the present study and the reported associative tasks, this slight discrepancy in effect size is unlikely to be meaningful, suggesting comparable effects in both types of task.
Limitations of present study
There are several limitations of this study that must be addressed. The study would benefit from the inclusion of a clinically depressed sample. As it currently stands, the results can only be taken as support for differential emotional representation between dysphoric and non-dysphoric individuals. The empirical question remains unanswered of whether major depressives would show even-handedness similar to dysphorics, or perhaps a negative emotional bias in these tasks. In a related vein, the CES-D cut-offs that were chosen excluded about one third of subjects who participated in the experiment. Although this resulted in smaller samples and thus less statistical power, it was done because there could be substantial overlap among individuals in the middle third of CES-D scores. For example, a score of 12 might not be sufficiently different from a score of 13, which could have obscured group differences if we had used a median split. One way to address this problem is to assess the correlation between CES-D score and positive bias (i.e., the difference between positive and negative emotional words for a given measure). This correlation was significant for drift rates in Experiment 1, r(55)=−.31, p=.041, but not for RTs or accuracy, supporting the findings from the group comparisons. Unfortunately, the unanalysed data from Experiments 2 and 3 were accidentally discarded, preventing such analyses for those experiments.
Another limitation of the present study is that the results have been couched in terms of mood congruent processing, even though the CES-D is not an explicit measure of mood. While this is true, CES-D depressive symptoms have been shown to strongly correlate (r=.66) with a measure of negative affect in unselected college samples (Rzeznikiewicz, 2004), derived from the Positive and Negative Affect Schedule (PANAS; Watson, Clark, & Tellegen, 1988). Lastly, we did not assess level of anxiety, so we cannot address how or if level of anxiety relates to these findings.
While these are legitimate limitations, we do not believe they take away the significance of these findings. Given the design and methodology of the present study, the results support the following claim: For individuals with low levels of dysphoria, positive emotional words are more strongly represented than negative emotional words. For dysphoric individuals this advantage for positive emotional words is absent, leading to more even-handed representations of positive and negative emotional words. It could be argued that a typical mood congruency effect would reveal a negative emotional bias associated with higher levels of dysphoria, but this asymmetrical finding of a positive emotional bias in non-dysphorics and even-handedness in dysphorics remains an important distinction that is well established with other paradigms (e.g., Bradley & Mathews, 1983; Gotlib & McCann, 1984; Matt et al., 1992). Further, these results are consistent with Canli et al. (2004), who found that relative to non-depressed, depressed subjects had reduced brain activity for positive emotional words (as opposed to increased activity for negative emotional words).
Advantages and limitations of the diffusion model
The most important benefit of using the diffusion model is extracting measures from RTs and accuracy that represent components of processing. The two most salient for the present study are decision criteria and strength of information. Because both accuracy and RTs can be affected by task difficulty as well as an individual’s criteria settings, it is important to identify the contribution of both measures at the individual level so as to allow examination of individual differences (Ratcliff et al., 2004d,c). The resulting drift rates provide a measure that is less noisy, and thus more sensitive, than RTs and accuracy.
Another benefit of the diffusion model is that it incorporates all of the behavioural data, which accounts for all of the possible effects in the data. RTs and accuracy are rarely, if ever, combined into one measure of performance, which means that informative data are not utilised. Further, the diffusion model incorporates error responses, which contain valuable information. For example, in Experiment 3 the differences in memory strength were shown by a decreased ability to reject the emotional words, which corresponds directly to increased errors in those conditions. Failing to include the RTs from the errors in this situation would be disadvantageous, but applying the diffusion model eliminates this problem.
One limitation of the diffusion model is that conditions with few observations can lead to variable drift rate estimates. However, this limitation equally applies to traditional analyses. For RTs, accuracy, and drift rates, the stability of the measure increases with the number of observations. This issue was prevalent in the present study, which relied on a limited number of emotional words. As previously mentioned, an advantage that the diffusion model has over traditional analyses is that filler responses can be used to increase the stability of drift rates for small conditions. By fitting all of the data simultaneously, the filler conditions (high- and low-frequency words, non-words) constrained the decision criteria and duration of non-decision components of processing so that each participant’s response tendencies were taken into account when the drift rates for emotional words were estimated, thus reducing the noise introduced by differences in response style. This methodological advantage is only available with the diffusion model, as it is not apparent how the filler conditions could be used to constrain the accuracy or RTs of the emotional conditions.
Another limitation of applying the diffusion model is perhaps the most salient to researchers. We do not hide the fact that modelling is a more difficult and involved process than traditional methods of analysis, which raises the question of whether the benefits outweigh the costs. We believe that they do. The benefits of applying the model have already been addressed, and the additional work needed to employ the model is less intense than might be expected. Researchers who conduct choice RT experiments need only compute the quantiles of each RT distribution and response proportion for each condition to prepare the data for modelling. Further, the model has recently become available in a MATLAB package (Vandekerckhove & Tuerlinckx, 2007), providing a readily available and user-friendly approach to applying it.
Because the diffusion model produces a more sensitive measure of performance in addition to allowing comparison of individual differences in decision criteria, we argue that it should be preferred over traditional analyses. Further, with advances like the MATLAB package, the additional work needed to understand and apply the model is becoming increasingly small.
CONCLUSION
The present study shows how this type of modelling can aid researchers. We had two groups of subjects that hypothetically should have differed in their responses to emotional stimuli. Each individual in the study had their own settings for processing components like response criteria, bias for a response, and encoding time. Because an individual’s settings on these components affect their responses, and the effects of experimental manipulations manifest in reaction times and accuracy, we did not see the expected differences from traditional analyses, consistent with previous studies. By applying the diffusion model, we incorporated all of the data to estimate values for these response settings. Once each subject’s response settings had been identified and controlled, we were able to see the expected differences between dysphoric and non-dysphoric subjects. It is apparent from these experiments that relying solely on either accuracy or mean correct RT can lead to contradictory or null results. Decision-process models like the diffusion model provide a theoretically grounded method to incorporate all of the behavioural data and produce interpretable and meaningful parameter values. This approach is readily extendable to the study of other psychological disorders, and should be considered an optimal alternative to traditional analyses.
By applying the diffusion model, we demonstrated that recognition memory and lexical decision tasks can reveal dysphoria-related differences in memory for emotional material. The consistent differences in drift rates, coupled with the null results in RTs and accuracy values, suggest that previous failures to find mood congruency in these tasks reflect insensitive analyses and not the absence of an effect. As such, researchers should be cautious when interpreting differential across-task findings. By challenging such differential findings, we were able to show that the internal representation strength of emotional words, not just the associative strength between them, is related to an individual’s level of dysphoria.
APPENDIX
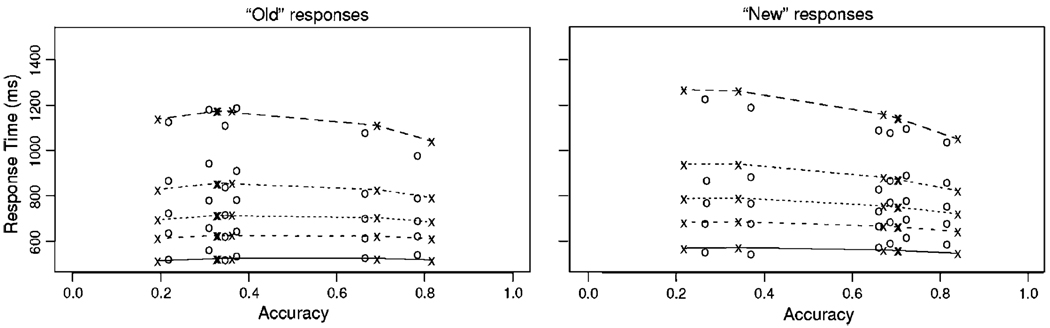
The model fits can be assessed qualitatively through visual displays of the predicted and observed values in a quantile probability function shown in Figure A1. A quantile probability function is a plot of the quantile RTs against the response proportions. The position of a point on the x-axis is determined by the proportion of responses for that experimental condition, and the position on the y-axis is determined by the .1, .3, .5 (median), .7, and .9 quantile RTs for that condition. Thus the function simultaneously plots accuracy and the correct and error RT quantiles for each condition. Figure A1 shows the function from Experiment 3, though the results were similar for all three experiments. Experiment 3 had six conditions (HF old, HF new, LF old, LF new, positive new, negative new), each corresponding to a column in the plot. The plots are split into “old” and “new” responses because bias for one response can obscure the fits when all responses are presented together. Responses on the right side of each plot (> .5) represent the proportion of correct responses, whereas responses on the left (<.5) represent errors. In each figure, the o symbols are the quantiles from the data and the x symbols are the quantiles predicted from the model. As Figure A1 shows, the predicted values are very close to the actual data, showing that the diffusion model fit all aspects of the behavioural data. Simultaneously capturing the accuracy and RT distributions proves a stringent test of any model, and these results strongly support the diffusion model.
Figure A1.
Quantile probability plots for Experiment 3. The lines and x symbols represent the theoretical fits of the diffusion model, and the circles represent the empirical quantile reaction times (RTs). The lines in order from the bottom to the top are for the .1, .3, .5, .7, and .9 quantile RTs.
Footnotes
Full terms and conditions of use: http://www.informaworld.com/terms-and-conditions-of-access.pdf
This article may be used for research, teaching and private study purposes. Any substantial or systematic reproduction, re-distribution, re-selling, loan or sub-licensing, systematic supply or distribution in any form to anyone is expressly forbidden.
Publisher's Disclaimer: The publisher does not give any warranty express or implied or make any representation that the contents will be complete or accurate or up to date. The accuracy of any instructions, formulae and drug doses should be independently verified with primary sources. The publisher shall not be liable for any loss, actions, claims, proceedings, demand or costs or damages whatsoever or howsoever caused arising directly or indirectly in connection with or arising out of the use of this material.
These secondary parameter values are available from the authors upon request.
REFERENCES
- Blaney PH. Affect and memory. A review. Psychological Bulletin. 1986;99:229–246. [PubMed] [Google Scholar]
- Bower GH. Mood and memory. American Psychologist. 1981;86:129–148. doi: 10.1037//0003-066x.36.2.129. [DOI] [PubMed] [Google Scholar]
- Bradley B, Mathews A. Mood and the self-reference bias in recall. Behaviour Research and Therapy. 1983;21:233–239. doi: 10.1016/0005-7967(83)90204-8. [DOI] [PubMed] [Google Scholar]
- Bradley BP, Mogg K, Millar N. Implicit memory bias in clinical and non-clinical depression. Behaviour Research and Therapy. 1996;34:865–879. doi: 10.1016/s0005-7967(96)00074-5. [DOI] [PubMed] [Google Scholar]
- Bradley BP, Mogg K, Williams R. Implicit and explicit memory for emotion-congruent information in clinical depression and anxiety. Behaviour Research and Therapy. 1995;33:755–770. doi: 10.1016/0005-7967(95)00029-w. [DOI] [PubMed] [Google Scholar]
- Bradley BP, Mathews A. Memory bias in recovered clinical depressives. Cognition & Emotion. 1988;2:235–245. [Google Scholar]
- Bulbena A, Berrios GE. Cognitive function in the affective disorders: A prospective study. Psychopathology. 1993;26:6–12. doi: 10.1159/000284794. [DOI] [PubMed] [Google Scholar]
- Canli T, Sivers H, Thomason ME, Whitfield-Gabrieli S, Gabrieli JDE, Gotlib IH. Brain activation to emotional words in depressed vs. healthy subjects. Neuroreport: For Rapid Communication of Neuroscience Research. 2004;15:2585–2588. doi: 10.1097/00001756-200412030-00005. [DOI] [PubMed] [Google Scholar]
- Coles ME, Heimberg RG. Memory biases in the anxiety disorders: current status. Clinical Psychology Review. 2002;22:587–627. doi: 10.1016/s0272-7358(01)00113-1. [DOI] [PubMed] [Google Scholar]
- Colombel F, Gilet A-L, Corson Y. Implicit mood congruent memory bias in dysphoria: Automatic and strategic activation. Current Psychology of Cognition. 2004;22:607–634. [Google Scholar]
- Danion J-M, Kauffmann-Muller F, Grange D, Zimmerman M, Greth P. Affective valence of words, explicit and implicit memory in clinical depression. Journal of Affective Disorders. 1995;34:227–234. doi: 10.1016/0165-0327(95)00021-e. [DOI] [PubMed] [Google Scholar]
- Dietrich DE, Emrich HM, Waller C, Wieringa BM, Johannes S, Munte TF. Emotion/cognition-coupling in word recognition memory of depressive patients: An event-related potential study. Psychiatry Research. 2000;96:15–29. doi: 10.1016/s0165-1781(00)00187-6. [DOI] [PubMed] [Google Scholar]
- Ferguson JM, Wesnes KA, Schwartz GE. Reboxetine versus paroxetine versus placebo: Effects on cognitive functioning in depressed patients. International Clinical Pharmacology. 2003;18:9–14. doi: 10.1097/00004850-200301000-00002. [DOI] [PubMed] [Google Scholar]
- Gotlib IH, McCann CD. Construct accessibility and depression: An examination of cognitive and affective factors. Journal of Personality and Social Psychology. 1984;47:427–439. doi: 10.1037//0022-3514.47.2.427. [DOI] [PubMed] [Google Scholar]
- Gronlund SD, Ratcliff R. Analysis of the Hockley and Murdock decision model. Journal of Mathematical Psychology. 1991;35:319–344. [Google Scholar]
- Hindmarch I. The behavioural toxicity of antidepressants: Effects on cognition and sexual function. International Clinical Psychopharmacology. 1998;13:S5–S8. [PubMed] [Google Scholar]
- Kucera H, Francis W. Computational analysis of present-day American English. Providence, RI: Brown University Press; 1967. [Google Scholar]
- Kuiper NA, Olinger LJ, MacDonald MR, Shaw BF. Self-schema processing of depressed and non-depressed content: The effects of vulnerability to depression. Social Cognition. 1985;3:77–93. [Google Scholar]
- Kurtz JE, Morey LC. Verbal memory dysfunction in depressed outpatients with and without borderline personality disorder. Journal of Psychopathology and Behavioral Assessment. 1999;21:141–156. [Google Scholar]
- Mathews A, Mogg K, May J, Eysenck M. Implicit and explicit memory bias in anxiety. Journal of Abnormal Psychology. 1989;98:236–240. doi: 10.1037//0021-843x.98.3.236. [DOI] [PubMed] [Google Scholar]
- Matt GE, Vazquez C, Campbell WK. Mood-congruent recall of affectively toned stimuli. A meta-analytic review. Clinical Psychology Review. 1992;12:227–255. [Google Scholar]
- Neshat-Doost HT, Taghavi MR, Moradi AR, Yule W, Dalgleish T. Memory for emotional trait adjectives in clinically depressed youth. Journal of Abnormal Psychology. 1998;107:642–650. doi: 10.1037//0021-843x.107.4.642. [DOI] [PubMed] [Google Scholar]
- Nikendei C, Dengler W, Wiedemann G, Pauli P. Selective processing of pain-related word stimuli in subclinical depression as indicated by event-related brain potentials. Biological Psychology. 2005;70:52–60. doi: 10.1016/j.biopsycho.2004.11.012. [DOI] [PubMed] [Google Scholar]
- Radloff LS. The CES-D scale: A self-report depression scale for research in the general population. Applied Psychological Measurement. 1977;1:385–401. [Google Scholar]
- Ratcliff R. A theory of memory retrieval. Psychological Review. 1978;85:59–108. [Google Scholar]
- Ratcliff R. Continuous versus discrete information processing: Modeling the accumulation of partial information. Psychological Review. 1988;95:238–255. doi: 10.1037/0033-295x.95.2.238. [DOI] [PubMed] [Google Scholar]
- Ratcliff R, Gomez P, McKoon G. Diffusion model account of lexical decision. Psychological Review. 2004a;111:159–182. doi: 10.1037/0033-295X.111.1.159. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ratcliff R, Perea M, Coleangelo A, Buchanan L. A diffusion model account of normal and impaired readers. Brain and Cognition. 2004b;55:374–382. doi: 10.1016/j.bandc.2004.02.051. [DOI] [PubMed] [Google Scholar]
- Ratcliff R, Rouder JN. Modeling reaction times for two-choice decisions. Psychological Science. 1998;9:347–356. [Google Scholar]
- Ratcliff R, Smith PL. A comparison of sequential sampling models for two-choice reaction time. Psychological Review. 2004;111:333–367. doi: 10.1037/0033-295X.111.2.333. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ratcliff R, Thapar A, Gomez P, McKoon G. A diffusion-model analysis of the effects of aging in the lexical-decision task. Psychology and Aging. 2004c;19:278–289. doi: 10.1037/0882-7974.19.2.278. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ratcliff R, Thapar A, McKoon G. A diffusion-model analysis of the effects of aging on recognition memory. Journal of Memory and Language. 2004d;50:408–424. [Google Scholar]
- Ratcliff R, Tuerlinckx F. Estimation of the parameters of the diffusion model: Approaches to dealing with contaminant reaction times and parameter variability. Psychonomic Bulletin and Review. 2002;9:438–481. doi: 10.3758/bf03196302. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ratcliff R, Van Zandt T, McKoon G. Connectionist and diffusion models of reaction time. Psychological Review. 1999;106:261–300. doi: 10.1037/0033-295x.106.2.261. [DOI] [PubMed] [Google Scholar]
- Rzeznikiewicz AE. Unpublished master’s thesis. Baton Rouge, LA, USA: Louisiana State University; 2004. A cross-sectional study comparing the psychological correlates for overconcern with body size and shape in men and women. [Google Scholar]
- Scott KM, Mogg K, Bradley BP. Masked semantic priming of emotional information in subclinical depression. Cognitive Therapy and Research. 2001;25:505–524. [Google Scholar]
- Vandekerckhove J, Tuerlinckx F. Fitting the Ratcliff diffusion model to experimental data. Psychonomic Bulletin and Review. 2007;14:1011–1026. doi: 10.3758/bf03193087. [DOI] [PubMed] [Google Scholar]
- Watkins PC. Implicit memory bias in depression. Cognition and Emotion. 2002;16:381–402. [Google Scholar]
- Watson D, Clark LA, Tellegen A. Development and validation of brief measures of positive and negative affect: The PANAS scales. Journal of Personality and Social Psychology. 1988;54:1063–1070. doi: 10.1037//0022-3514.54.6.1063. [DOI] [PubMed] [Google Scholar]