Origin of Substituent Effects in Edge-to-Face Aryl-Aryl Interactions

Abstract

Substituent effects in the edge-to-face configuration of the benzene dimer have been studied using modern density functional theory. An accurate interaction potential energy curve has been computed for the unsubstituted dimer using ab initio methods with large basis sets. The recommended binding energy for the edge-to-face benzene dimer is 2.31 kcal mol^-1, estimated at the counterpoise-corrected CCSD(T)/aug-cc-pVTZ level of theory. For both edge-ring and face-ring-substituted dimers, interaction energies correlate with σ_m for the substituents, indicating that substituent effects can be understood qualitatively in terms of simple electrostatic effects, although in the latter case dispersion results in some scatter in the data. In contrast to prevailing models of substituent effects in benzene dimers, polarization of the π-system of the substituted ring does not induce substituent effects. For edge-ring-substituted dimers, substituent effects arise from differential electrostatic interactions between the hydrogens on the substituted ring and the π-cloud of the face ring and direct interactions of the substituents with the unsubstituted ring. For face-ring-substituted dimers, substituent effects arise from direct electrostatic and dispersion interactions of the substituents with the edge ring. Substituents with σ_m > 0.12 favor edge ring substitution while for σ_m < 0.12 substitution on the face ring is preferred.

I. Introduction

Aryl-aryl interactions are key to understanding myriad chemical phenomena including stereoselective organic reactions [1-3], host-guest chemistry [4], and supramolecular self-assembly [5], yet are perhaps the least well-understood [6] among non-covalent interactions [7-10]. π-π interactions are also pivotal in numerous biochemical processes. For example, the intercalation of mutagenic and tumorigenic polycyclic aromatic diol epoxides into DNA, which constitutes a key step in DNA damage by polycyclic aromatic hydrocarbons [11], is mediated by π-stacking interactions with DNA. Similarly, face-to-face and edge-to-face interactions of aromatic amino acid side-chains with DNA bases are key to binding in anti-DNA autoantibodies [12], which are involved in the pathogenesis of systemic lupus erythematosus [13].

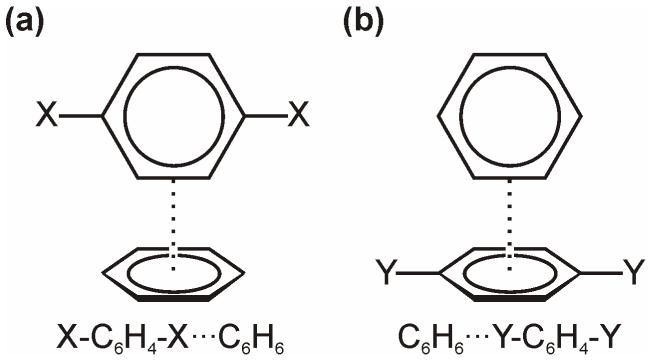
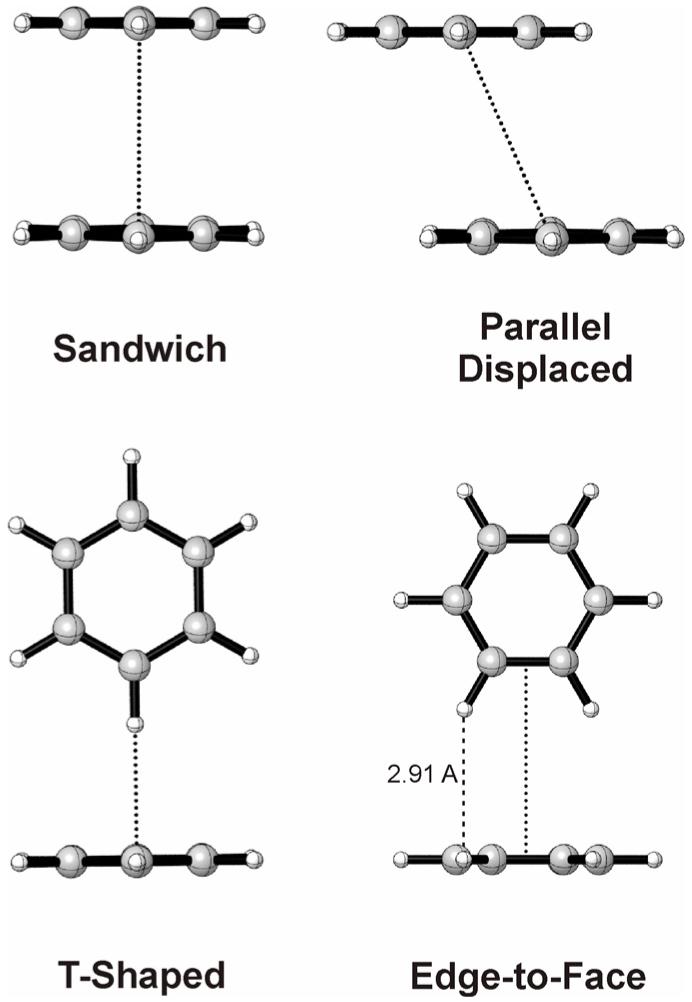
Vital to many applications of aryl-aryl stacking interactions in drug design and materials science is the ability to modulate the strength of these subtle interactions through the exploitation of substituent effects. Four prototypical benzene dimer structures [7] can be considered as models for substituent effects in general aryl-aryl interactions (see Fig. 1). The sandwich and parallel displaced structures feature face-to-face arrangements, while the C_2v-symmetric T-shaped and edge-to-face configurations are perhaps more aptly described as aromatic CH/π interactions [14]. Our understanding of effects governing general aryl-aryl interactions should rest on a sound understanding of these simple model systems. In this work we will focus solely on substituent effects in the edge-to-face configuration [15].

Figure 1.

Prototypical benzene dimer configurations.

For monosubstituted edge-to-face benzene dimers, substituents can be introduced in a number of unique positions on the edge ring (X) or the face ring (Y). We will focus exclusively on the edge-ring-substituted and face-ring-substituted systems depicted in Fig. 2a, since experimental results are available for similarly substituted systems. This configuration is also most relevant to understanding edge-to-face interactions in biological systems, including anti-DNA autoantibodies [12]. Hunter and co-workers [16-18] presented experimental binding free energies for substituted edge-to-face aryl-aryl interactions measured using chemical double mutant cycles [19] in hydrogen-bonded molecular zipper complexes. Following a Hammett analysis of nine binding free energies for different disubstituted complexes, Hunter et al. [16-18] introduced a model of substituent effects in edge-to-face aromatic interactions in which differences in interaction energies are due to changes in:

1. electrostatic interactions between the positively charged hydrogens on the edge ring and the π-cloud of the face ring; and

2. electrostatic interactions between the global dipoles of the two substituted rings. Since monosubstituted dimers have one ring with no dipole moment, this model predicts that substituent effects in monosubstituted dimers must arise entirely from (a). Alternatively, if source (b) is extended to include higher-order multipole interactions, then in the case of monosubstituted edge-to-face dimers one can consider the contribution of differential dipole-quadrupole and quadrupole-quadrupole interactions, for example. Regardless, for monosubstituted dimers this proposed model is similar to prevailing electrostatic models of substituent effects in the parallel displaced and sandwich configurations of the benzene dimer [8,20,21].

Figure 2.

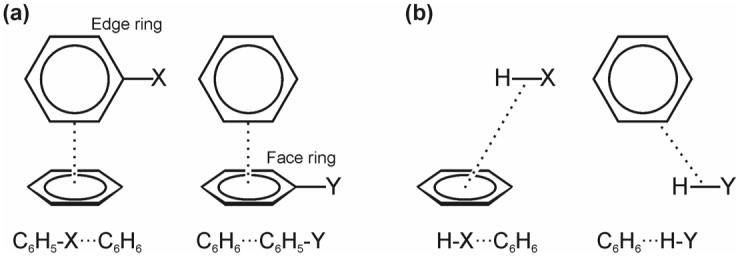
(a) Monosubstituted edge-to-face benzene dimers and (b) truncated structures used to quantify the role of direct interactions of substituents with the other ring.

The last decade has witnessed the publication of a bevy of theoretical studies of substituent effects in the benzene dimer [20,22-35]. Sherrill and co-workers [22,25,28,29,36] and Lee et al. [26,27] have studied substituent effects in a number of benzene dimer configurations. Beg and co-workers [23] studied the effect of multiple halogen substitutions on the sandwich configuration while Gung and Amicangelo [24] have examined substituent effects in C₆H₅-X^...C₆F₆. Both Sinnokrot and Sherrill [25] and Lee and co-workers [26,27] published benchmark CCSD(T) (coupled cluster theory with single, double, and perturbative triple excitations) results for the unsubstituted and substituted T-shaped dimer. For substituted T-shaped dimers, Lee et al. found [27] that π-electron donating substituents (defined in terms of Hammett σ_p constants) favor substitution on the face-ring, while electron donors stabilize axial-ring-substituted dimers. They also found that substituent effects in axially-substituted dimers are dominated by electrostatic effects while the effects in face-ring-substituted dimers arise primarily from a combination of dispersion and exchange-repulsion. In the former case, these differential electrostatic interactions were attributed to changes in the partial positive charges of the hydrogens on the substituted ring. To our knowledge, there has been no systematic theoretical study of substituent effects in the related edge-to-face benzene dimer.

The role of direct interactions of substituents with the other ring in the benzene dimer has also been addressed in several studies [22,28,32,35]. Wheeler and Houk [32] showed that direct interactions of the substituents with the other ring account for nearly all of the predicted substituent effects in the sandwich configuration of the benzene dimer. Rashkin and Waters [35] also concluded that direct substituent interactions were involved in a model system for substituted parallel displaced dimers. Arnstein and Sherrill [22] surmised that direct interactions were responsible for features in computed potential energy curves for substituted parallel displaced benzene dimers while Ringer, Sinnokrot, and Sherrill [28] invoked direct interactions between substituents in certain positions around the ring with the unsubstituted ring to explain non-additivity of substituent effects in the T-shaped dimer.

The simple, intuitive model of substituent effects in edge-to-face aromatic interactions presented by Hunter et al. [16-18] is compelling. However, in light of recent findings regarding the dominant role of direct interactions of substituents with the unsubstituted ring in the sandwich configuration of the benzene dimer [32], we have investigated this system using carefully calibrated density functional theory methods. It has also recently been shown [37] that the enhanced binding in activated CH/π complexes of halogen-substituted methanes with benzene is due to direct interactions between the halogens and the aromatic ring. Since the dominant interactions in the edge-to-face configuration of the benzene dimer are similar to those in CH/π interactions [14], a careful re-examination of the physical underpinnings of the model espoused by Hunter et al. [16-18] is warranted.

Studies of substituent effects in edge-ring and face-ring-substituted benzene dimers can help discern the importance of changes in the π-system of substituted benzenes in non-covalent interactions. The attraction in the edge-to-face dimer arise from the interplay of a number of non-bonded effects (electrostatics, dispersion, polarization, etc.) The dominant favorable electrostatic interaction is between the positively charged periphery of the edge ring and the π-electron cloud on the face ring [7]. There will also be favorable electrostatic interactions between the π-cloud of the edge ring and the face ring hydrogens. These latter interactions will be much smaller, however, due to the significantly larger distance between the face ring hydrogens and the center of the edge ring (5.62 Å), compared to a distance of 3.16 Å between the two closest edge ring hydrogens and the center of the face ring. Neglecting “direct” interactions between the substituents and the unsubstituted ring (vide infra), the electrostatic component of substituent effects in edge-ring-substituted dimers should reflect changes in the partial charge of the edge ring hydrogens, while substituent effects in face-ring-substituted dimers should reflect changes in the face ring π-system.

II. Theoretical Methods

The proper description of π-stacking interactions using ab initio methods demands large one-particle basis sets and rigorous treatments of electron correlation via coupled cluster theory [29] due to the preponderant role of dispersion interactions in these complexes. However, the recapitulation of substituent effects in aromatic interactions is less sensitive to method [25-29] and is often achievable using smaller basis sets and more modest treatments of electron correlation. While most density functional theory (DFT) functionals fail to adequately describe dispersion-dominated non-covalent complexes [38,39], the M05-2X functional [40] has been shown [40-44] to provide an accurate description of the benzene dimer at a drastically reduced computational cost compared to ab initio methods. Also, we have previously shown [45] that M05-2X, when paired with the small 6-31+G(d) basis set, accurately reproduces the CCSD(T) relative interaction energies of Sherrill and co-workers[25,29,36] for substituted sandwich dimers.

Benchmark computations were executed for the unsubstituted edge-to-face benzene dimer using CCSD(T) [46-49] paired with the aug-cc-pVDZ basis set [50] across a series of inter-ring separations. The resulting potential energy curve was further refined by appending a correction for basis set incompleteness based on the difference between MP2/aug-cc-pVTZ and MP2/aug-cc-pVDZ energies. The result is a reliable estimate of the CCSD(T)/aug-cc-pVTZ interaction energy curve. For comparison, the interaction potential was also computed using spin-component-scaled MP2 (SCS-MP2) approach of Grimme [51] paired with the aug-cc-pVTZ basis set. In each case, the inter-ring distance (R) was scanned at 0.1 Å intervals with the monomers frozen at MP2/aug-cc-pVDZ optimized geometries. The equilibrium separation (R_e) was then located by scanning the region around the energy minimum at 0.05 Å intervals. All ab initio calculations were corrected for basis set superposition error via the counterpoise approach of Boys and Bernardi [52]. For brevity, the aug-cc-pVXZ basis sets [50] will be denoted by AVXZ below.

For the substituted dimers, M05-2X/6-31+G(d) was used exclusively. A diverse set of 24 substituents was considered, ranging from strong electron donors (NHCH₃, σ_m = -0.30) to strong electron acceptors (NO₂, σ_m = 0.71). The substituents considered are listed in Tables 2 and 3, along with Hammett σ_m constants [53]. Traditionally, σ_m values were determined by the effect of substituents on the pK_a’s of meta-substituted benzoic acids, and provide a measure primarily of the inductive (non-resonance) electron-donating or withdrawing character of each substituent. Other related substituent constants have been defined and measured that seek to more clearly partition resonance and inductive/field effects. However, σ_m is used here as a means to order and classify substituents and to provide a qualitative understanding of the underlying causes governing substituent effects.

Table 2.

Predicted interaction energies (E_int, kcal mol^-1), relative to the unsubstituted case, for edge-ring-substituted dimers (C₆H₅-X^...C₆H₆), the corresponding truncated structures (H-X^...C₆H₆), and edge-ring-disubstituted dimers (X-C₆H₄-X^...C₆H₆)

X	σmX	σpX	Eint(C6H5-X...C6H6)	Eint(H-X...C6H6)	Eint(X-C6H4-X...C6H6)
NH2	-0.16	-0.66	0.04	-0.13	0.03
CH3	-0.07	-0.17	0.05	0.02	0.15
H	0.00	0.00	0.00a	0.00b	0.00a
CH2OH	0.00	0.00	-0.01	-0.14	0.04
SiH3	0.05	0.10	-0.29	-0.16	-0.46
OH	0.12	-0.37	-0.26	-0.45	-0.24
CCH	0.21	0.23	-0.30	0.03	-0.52
SH	0.25	0.15	-0.41	-0.40	-0.70
BF2	0.32	0.48	-0.51	-0.21	-0.93
F	0.34	0.06	-0.41	-0.37	-0.83
CHO	0.35	0.42	-0.62	-0.24	-1.10
COOCH3	0.37	0.45	-0.52	-0.24	-0.83
COOH	0.37	0.45	-0.60	-0.29	-0.82
COCH3	0.38	0.50	-0.76	-0.63	-0.88
CF3	0.43	0.54	-0.73	-0.51	-1.50
SiF3	0.54	0.69	-0.90	-0.53	-1.67
CN	0.56	0.66	-0.90	-0.55	-1.80
NO	0.62	0.91	-0.79	-0.39	-1.43
NO2	0.71	0.78	-1.11	-0.66	-2.17

^aAbsolute E_int = -1.88 kcal mol^-1.

^bAbsolute E_int = -0.03 kcal mol^-1.

Table 3.

Predicted interaction energies (E_int, kcal mol^-1), relative to the unsubstituted case, for, face-ring-substituted dimers (C₆H₆ ^...C₆H₅-Y), corresponding truncated structures (C₆H₆^...H-Y). and face-ring-disubstituted dimers (C₆H₆ ^...Y-C₆H₄-Y)

Y	σmY	σpY	Eint(C6H6 ...C6H5-Y)	Eint(C6H6...H-Y)	Eint(C6H6 ...Y-C6H4-Y)
NHCH3	-0.3	-0.84	-0.68	-0.58	-0.85
NH2	-0.16	-0.66	-0.70	-0.59	-1.40
N(CH3)2	-0.15	-0.83	-0.69	-0.47	-1.34
CH3	-0.07	-0.17	-0.29	-0.11	-0.48
NHOH	-0.04	-0.34	-0.49	-0.31	-0.89
H	0.00	0.00	0.00a	0.00b	0.00a
CH2OH	0.00	0.00	-0.29	-0.01	-0.52
SiH3	0.05	0.10	-0.34	-0.10	-0.32
OH	0.12	-0.37	-0.25	-0.15	-0.47
OMe	0.12	-0.27	-0.29	-0.24	-0.60
SCH3	0.15	0.00	-0.61	-0.42	-1.23
CCH	0.21	0.23	-0.17	0.02	-0.38
SH	0.25	0.15	-0.54	-0.29	-1.06
BF2	0.32	0.48	0.28	0.36	0.54
F	0.34	0.06	0.08	0.23	0.16
CHO	0.35	0.42	0.16	0.24	0.28
COOCH3	0.37	0.45	0.05	0.21	0.18
COOH	0.37	0.45	0.13	0.29	0.24
COCH3	0.38	0.50	0.10	0.14	0.11
OCF3	0.38	0.35	0.05	0.19	-0.03
CF3	0.43	0.54	-0.14	0.04	-0.26
SiF3	0.54	0.69	-0.29	-0.19	-0.47
CN	0.56	0.66	0.13	0.30	0.20
NO	0.62	0.91	0.22	0.26	0.42
NO2	0.71	0.78	0.38	0.46	0.64

^aAbsolute E_int = -1.88 kcal mol^-1.

^bAbsolute E_int = -0.23 kcal mol^-1.

The inter-ring distance was scanned at 0.05 Å intervals to locate the minimum energy structure, with the substituted monomers frozen at their respective M05-2X/6-31+G(d) geometries. For many of the dimers considered there are multiple unique rotameric states, of which we only report the lowest lying conformation. Interaction energies [E_int = E(C₆H₅-X^...C₆H₆) - E(C₆H₆) - E(C₆H₅-X), for example] are all given relative to the corresponding unsubstituted case (X or Y = H). For substituents on the edge ring that extend towards the face ring [N(CH3)₂, NHCH₃, NHOH, OCF₃, OCH₃, and SCH₃], an inordinate amount of direct interaction of the substituent with the face ring would be expected. We have excluded such substituents on the edge ring from the present study.

The contribution to the interaction energies due to direct interactions of the substituents with the unsubstituted ring was determined by considering “truncated” structures derived from the equilibrium geometries of the corresponding substituted dimers (see Fig. 2b). These model systems were constructed by replacing the substituted phenyl ring with a hydrogen. In each case, the hydrogen was placed along the X-C (or Y-C) bond and the placement of the hydrogen along this bond optimized with the remainder of the structure held fixed. The binding energies of these systems—relative to X = H or Y = H—were computed using M05-2X/6-31+G(d).

All M05-2X computations were carried out using NWChem [54,55], while Molpro2006.1 [56] was used for the MP2, SCS-MP2, and CCSD(T) energies. For the M05-2X computations, a fine DFT integration grid was used (70 radial and 590 angular points), since meta-GGAs are known to be sensitive to integration grid size for non-covalent complexes [38,57,58].

III. Results and Discussion

A series of substituted benzene dimers has been studied using modern density functional theory to unravel the provenance of substituent effects in edge-to-face aryl-aryl interactions. First, a benchmark coupled cluster interaction potential is presented to provide an accurate binding energy for the unsubstituted edge-to-face benzene dimer and to assess the performance of the M05-2X DFT functional for this model system across a range of inter-ring distances. We then consider mono- and disubstituted edge-to-face dimers, focusing on quantifying the contribution of direct interactions to the overall dimerization energy. The present results are then compared with substituent effects in other dimer configurations.

A. Benchmark Edge-to-Face Interaction Potential

Potential energy curves for the edge-to-face benzene dimer are shown in Fig. 3, computed at the counterpoise-corrected MP2/AVTZ, SCS-MP2/AVTZ, CCSD(T)/AVDZ, and estimated CCSD(T)/AVTZ levels of theory. Predicted interaction energies (E_int) and equilibrium inter-ring distances (R_e, measured from ring-center to ring center) are listed in Table 1. The estimated CCSD(T)/AVTZ dimerization energy is -2.31 kcal mol^-1, which is slightly higher than a similarly computed interaction energy of -2.62 kcal mol^-1 for the T-shaped dimer, reported by Sinnokrot and Sherrill [25]. This is unsurprising given the similarity of the T-shaped and edge-to-face configurations (see Fig. 1). The CCSD(T)/AVTZ predicted R_e value is 5.05 Å, corresponding to the edge ring hydrogens positioned 2.91 Å above the plane of the face ring. The CCSD(T)/AVDZ and SCS-MP2/AVTZ results are similar to the benchmark CCSD(T)/AVTZ result, while MP2/AVTZ significantly over-binds the edge-to-face benzene dimer as has been observed in other benzene dimer configurations [29]. CCSD(T)/AVDZ and SCS-MP2/AVTZ slightly overestimate the benchmark R_e value of 5.05 Å, while MP2/AVDZ predicts a somewhat shorter distance.

Figure 3.

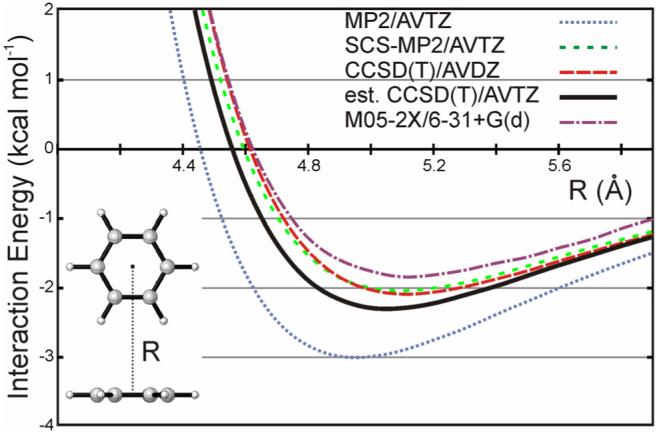
Potential energy scans at the MP2/AVTZ, SCS-MP2/AVTZ, CCSD(T)/AVDZ, estimated CCSD(T)/AVTZ, and M05-2X/6-31+G(d) levels of theory.

Table 1.

Predicted equilibrium inter-ring separations (R_e, Å) measured from ring-center to ring-center and interaction energies (E_int, kcal mol^-1) for the edge-to-face benzene dimer. All ab initio results include counterpoise corrections

Method	Re	Eint
MP2/AVTZ	4.95	-3.01
SCS-MP2/AVTZ	5.10	-2.05
CCSD(T)/AVDZ	5.10	-2.10
Est. CCSD(T)/AVTZ	5.05	-2.31
M05-2X/6-31+G(d)	5.10	-1.88

Also included in Fig. 3 is the interaction potential computed using M05-2X/6-31G+(d). Overall, the M05-2X/6-31+G(d) interaction curve is remarkably similar to the estimated CCSD(T)/AVTZ result. Moreover, the M05-2X/6-31+G(d) potential is closer to the benchmark curve than MP2/AVTZ, though it performs slightly worse than CCSD(T)/AVDZ and SCS-MP2/AVTZ. While the final predicted interaction energy (-1.88 kcal mol^-1, see Table 1) is 0.43 kcal mol^-1 higher than the estimated CCSD(T)/AVTZ result, M05-2X/6-31+G(d) provides a qualitatively correct description of the edge-to-face interaction potential. The M05-2X-predicted R_e value of 5.10 Å is also in general agreement with the benchmark coupled cluster result. Additionally, M05-2X/6-31+G(d) is expected to yield very accurate relative interaction energies for substituted edge-to-face dimers compared to reliable ab initio benchmarks, as is the case for the sandwich structure [45]. M05-2X/6-31+G(d) will be used exclusively below to study substituent effects in the edge-to-face benzene dimer. The relatively low computational cost of M05-2X/6-31+G(d) enables the study of a large number of substituents, which is vital to glean meaningful generalizations from trends in substituent effects.

B. Substituent Effects in Monosubstituted Dimers

Interaction energies (E_int), relative to the unsubstituted case, for 43 monosubstituted edge-to-face dimers have been predicted using M05-2X/6-31+G(d), as described above. These energies are plotted against the corresponding Hammett sigma meta constants (σ_m^X and σ_m^Y for the edge-ring-substituted and face-ring-substituted dimers, respectively) in Fig. 4. The relative interaction energies are given in Tables 2 and 3. For both configurations, predicted substituent effects on the interactions are substantial compared to the binding energy in the unsubstituted dimer, with predicted dimerization energies spanning over 1 kcal mol^-1.

Figure 4.

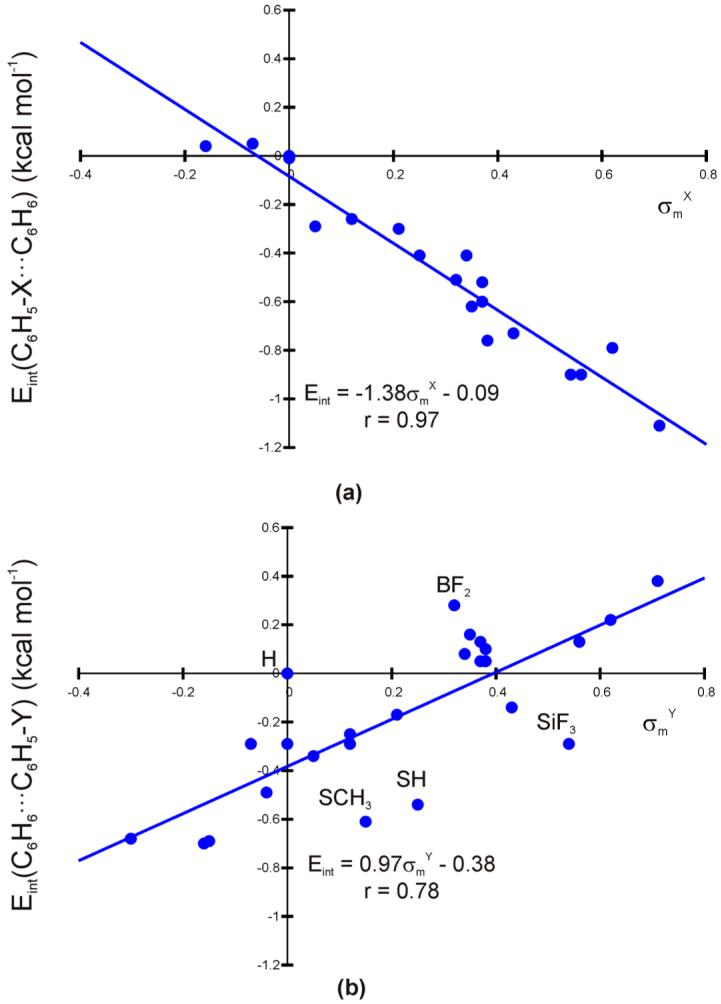
(a) Relative interaction energies for edge-ring-substituted dimers [E_int(C₆H₅-X^...C₆H₆)] plotted against σ_m^X; and (b) relative interaction energies for face-ring-substituted dimers [E_int(C₆H₆^...C₆H₅-Y)] plotted against σ_m^Y. Obvious outliers (H, BF₂, SCH₃, SH, and SiH₃) are labeled in the lower plot. Removing these outliers from the least-squares-fit yields E_int = 1.09σ_m^Y - 0.38 (r = 0.95).

For the edge-ring-substituted dimers, there is a strong correlation (r = 0.97) between E_int and σ_m^X, suggesting that trends in substitutent effects in this system can be understood in terms of the inductive electron withdrawing or donating character of the substituents. Electron withdrawing substituents (σ_m^X > 0) are predicted to enhance the binding relative to X = H while donors quench the attractive interaction. The intercept of the best-fit line is essentially zero, indicating that there are no appreciable σ_m-independent interactions driving substituent effects in this system.

The contributions to the relative interaction energies due to direct interactions of the substituents with the unsubstituted ring were estimated using the truncated structures depicted in Fig. 2b. The resulting energies [E_int(H-X^...C₆H₆)] are listed in Table 2 and plotted against the relative interaction energies for the corresponding edge-ring-substituted dimers [E_int(C₆H₅-X^...C₆H₆)] in Fig. 5a. There is a reasonable correlation between these two sets of data (r = 0.85). The slope of the linear least squares fit line of 0.49 indicates that direct interactions account for about half of the overall substituent effects in edge-ring-substituted benzene dimers. As mentioned above, apart from direct interactions, substituent effects in edge-ring-substituted dimers reflect changes in the partial charges of the edge ring hydrogens. Electron withdrawing groups increase the partial positive charge on the hydrogens, enhancing the attractive interaction with the π-cloud of the face ring. Electron donors hinder the interaction through the opposite mechanism. This effect is only responsible for half of the predicted substituent effects in edge-ring-substituted dimers. Direct electrostatic interactions between the substituents and the face ring, which account for the other half, are most simply understood in terms of local multipole interactions. The local dipole due to the σ-withdrawing effects of the substituents interacts favorably (in the case of electron withdrawing groups) or unfavorably (for donors) with the z² component of the quadrupole moment of the face ring.

Figure 5.

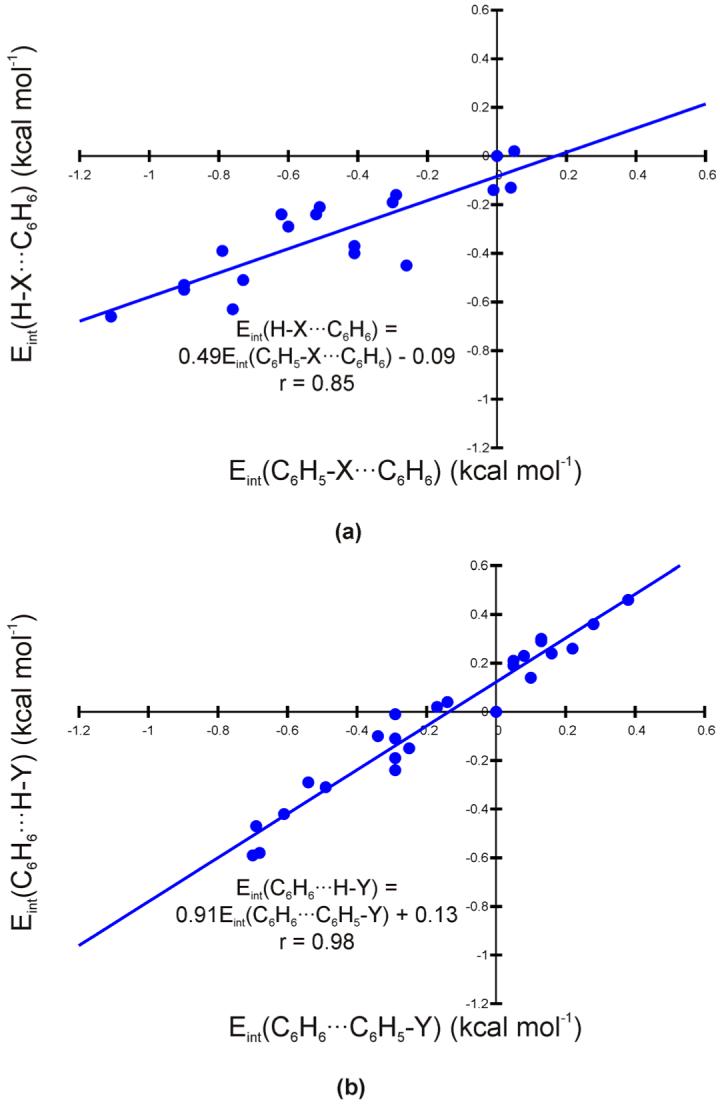
(a) Relative interaction energies for truncated edge-ring-substituted dimers [E_int(H-X^...C₆H₆)] plotted against E_int(C₆H₅-X^...C₆H₆); and (b) relative interaction energies for truncated face-ring-substituted dimers [E_int(C₆H₆^...H-Y)] plotted against E_int(C₆H₅^...C₆H₅-Y).

For the face-ring-substituted dimers, there is also a correlation with σ_m, though in this case the correlation coefficient is only 0.78, indicating that σ_m-independent effects also contribute to substituent effects in face-ring-substituted dimers. There are five substituents that are clear outliers in the data plotted in Fig. 4b (H, BF₂, SCH₃, SH, and SiF₃). If these five points are not considered in the least-squares fit, then the results correlate very well with σ_m^Y (r = 0.95). Electron donors (σ_m < 0) are predicted to enhance the binding in the face-ring-substitued dimers relative to the unsubstituted case. For inductive electron withdrawing substituents the picture is murkier, since some result in a destabilization of the dimer relative to the unsubstituted case while some enhance the binding. The intercept of the best-fit line is -0.4 kcal mol^-1, which, by analogy with the sandwich configuration of the benzene dimer [32], is attributed to stabilizing dispersive interactions between the substituents and the edge ring. These interactions are, on average, greater for the substituted benzene dimers than the unsubstituted case, resulting in an overall lowering of the energies of substituted dimers compared to the Y = H case. That the three outliers falling significantly below the best-fit line (SCH₃, SH, and SiF₃) all contain second-row atoms is also consistent with this hypothesis, since they would be expected to have larger polarizabilities and result in a greater dispersive interaction. This postulated dispersive interaction is partially responsible for the present prediction that some electron withdrawing groups enhance the binding while others destabilize face-ring-substitued dimers relative to Y = H. The results for CH₂OH (σ_m = 0.00) are particularly instructive, since the introduction of this substituent onto the face ring stabilizes the benzene dimer by 0.3 kcal mol^-1 (see Table 3), despite being neither an electron donor nor electron acceptor. If CH₂OH is taken as the σ_m^Y = 0.0 reference, rather than H, then we see that all donors stabilize the face-ring-substituted dimer while electron-withdrawing substituents (except for SCH₃, SH, and SiF₃) hinder the binding, relative to C₆H₆^...C₆H₅-CH₂OH.

Direct interactions of substituents with the edge ring have been quantified using the truncated structures shown in Fig. 2b. Relative interaction energies [E_int(C₆H₆^...H-Y)] are shown in Table 3 and plotted against the face-ring-substituted dimerization energies [E_int(C₆H₆^...C₆H₅-Y)] in Fig. 5b. This time, there is a very strong correlation between these two sets of data (r = 0.98) and the slope of the best-fit line (0.91) is close to unity; for these face-ring-substituted dimers, substituent effects are accounted for almost entirely by direct interactions of the substituents with the edge-ring. The interactions are between the local dipoles induced by the substituents and the positively charged periphery of the edge ring, giving rise to the opposite trend in substituent effects compared to the edge-ring-substituted and sandwich dimers. Since the face ring is not necessary to reproduce the computed substituent effects, the polarization of the substituted benzene π-system must not play an appreciable role in the substituent effects in the face-ring-substituted benzene dimer.

For all of the face-ring-substituted dimers studied, the relative interaction energy of the truncated system is slightly higher (less negative or more positive E_int) than for the corresponding C₆H₆^...C₆H₅-Y dimer. This is most apparent for CCH and CF₃, for which computations on the dimer indicate an enhanced interaction upon substitution while the truncated models indicate a slight weakening of the interaction. The largest such deviation (0.27 kcal mol^-1) occurs for C₆H₆^...C₆H₅-CH₂OH. Apparently there is some additional effect, largely independent of σ_m, that stabilizes the face-ring-substituted dimers not accounted for by the truncated models. Regardless, this deviation is, on average, only about 0.1 kcal mol^-1.

In the edge-to-face dimer, the electrostatic attraction arises primarily from the interaction of the positively charged edge ring hydrogens with the π-cloud of the face ring [7]. Substituent effects could potentially arise from either the polarization of the face ring π-system or changes in the partial charges of the edge ring hydrogens. Apparently, only the latter effect is operative, since substituent effects in face-ring-substituted dimers are accounted for entirely by model systems in which the face ring is not present.

C. Disubstituted Dimers

Computed relative interaction energies for para-substituted edge-ring and face-ring-disubstituted dimers (see Fig. 6) are plotted against the corresponding monosubstituted results in Fig. 7. The correlation in both cases is excellent (r = 0.97 and 0.98). The slopes of the best fit lines of 1.9 and 1.8 indicate a nearly exact additivity of substituent effects in the edge-to-face dimer. If the global dipole moment were the primary determinant of the dimerization energy in substituted dimers one would anticipate little or no substituent effects in these symmetrically disubstituted dimers since the dipoles of the substituents largely cancel to yield small or zero overall dipole moments. Instead, consideration of the interaction of local dipole moments induced by substituents with the other ring yields a more accurate predictive model of substituent effects in edge-to-face benzene dimers.

Figure 6.

Symmetrically disubstituted benzene dimers: (a) edge-ring-disubstituted and (b) face-ring-disubstituted.

Figure 7.

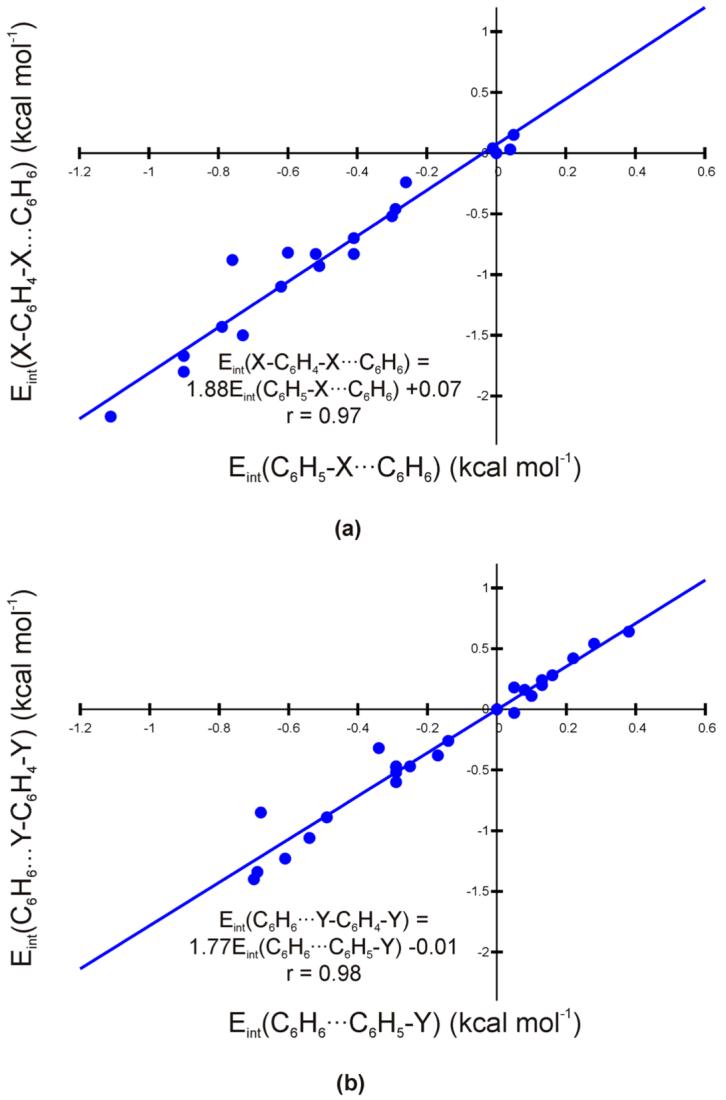
(a) Relative interaction energies for edge-ring-disubstituted dimers [E_int(X-C₆H₄-X^...C₆H₆)] plotted against E_int(C₆H₅-X^...C₆H₆); and (b) relative interaction energies for face-ring-disubstituted dimers [E_int(C₆H₆^...H-C₆H₄-Y)] plotted against E_int(C₆H₆^...C₆H₅-Y).

Unlike the sandwich configuration, there are a number of symmetry-unique positions on both the edge ring and face ring in the edge-to-face benzene dimer. We have considered only the simple case of symmetrically disubstituted dimers depicted in Fig. 6. The additivity demonstrated in this case is not expected to continue for additional substitutions. Direct interactions with the unsubstituted ring will differ depending on which site of the ring is substituted. Similarly, in the case of multiple substitution of the edge-ring, the changes in partial charges of the ring hydrogens closest to the face ring would differ depending on the substitution pattern.

Ringer et al. [28] examined the effects of multiple substitution in the sandwich and T-shaped configurations of the benzene dimer. While these effects were nearly perfectly additive in the sandwich dimer, substituent effects in the T-shaped dimer increased irregularly, depending on the position of the substituent relative to the unsubstituted ring. These irregularlities were explained by direct interactions between the substituents and the unsubstituted ring for some substituted T-shaped dimers. Our findings for the closely related edge-to-face dimer suggest that there will be a prominent role of direct interactions for all substituted T-shaped dimers, though the exact magnitude of this interaction will vary depending on the relative distance and orientation of the substituent and the unsubstituted ring.

D. Comparison with Other Benzene Configurations

Direct comparison of substituent effects in the edge-to-face dimer with substituent effects in the sandwich configuration is straightforward since data are available for the same set of substituents [32]. Substituent effects in edge-ring-substituted dimers are similar in trend and magnitude to those in the sandwich dimer. Inductive electron donors hinder the interaction while electron acceptors enhance it. Unlike the sandwich dimer, however, there appears to be little net effect of dispersion interaction in the edge-ring-substituted dimers. Also, in the edge-ring-substituted dimers direct interactions between substituents and the unsubstituted ring do not fully account for the observed substituent effects, while such interactions are the dominant cause of substituent effects in the sandwich dimer. That only direct substituent effects are important in the sandwich dimer is consistent with the present conclusion that the polarization of the π-system of a substituted ring has no appreciable effect on the binding energy in face-ring-substituted dimers. The lack of appreciable dispersion interactions between the substituents and the face ring in the edge-ring-substituted dimers arises from the increased distance between the substituents and the other ring compared to the sandwich configuration. For example, in the edge-to-face dimer C₆H₅-F^...C₆H₆, the distance between the fluorine and the center of the face ring is 5.74 Å compared to 4.80 Å in the sandwich dimer of fluorobenzene and benzene.

For the face-ring-substituted dimers the trends in substituent effects are opposite to those in the sandwich dimers and of slightly smaller magnitude. However, the almost exclusive role of direct interactions and presence of direct dispersion interactions is similar. The dispersion interactions between the substituents and the edge ring in the face-ring-substituted dimers is consistent with the proximity of the substituents and the hydrogens of the edge ring. The reversal of substituent effects is due to the interaction of the substituents with the positively charged ring-hydrogens in the face-ring-substituted dimers rather than with the π-electrons of the unsubstituted ring as in the sandwich dimer.

Qualitatively, the presently predicted substituent effects in the edge-to-face dimer are the same as those reported by Lee et al. [27] for the T-shaped dimer. Substituent effects in the edge-ring-substituted dimers are primarily electrostatic with little contribution from dispersion, while interactions in the face-ring-substituted dimers is a more complex mélange of effects, including electrostatics and dispersion. However, the present results indicate that direct interactions play a vital role in substituent effects in both edge-ring and face-ring-substituted dimers, particularly in the latter case. These direct interactions are presumably also operative in the T-shaped dimers studied by Lee and co-workers [27].

Arnstein and Sherrill [22] found direct electrostatic interactions between the substituents and the unsubstituted ring in parallel displaced benzene dimers at non-equilibrium configurations. At these geometries the substituents were located nearly directly above the other ring. The present results indicate that in the edge-to-face dimers such direct interactions are significant even at equilibrium geometries in which the substituents are positioned above the periphery of the unsubstituted ring. These direct substituent interactions are also likely present in substituted parallel displaced benzene dimers, even at equilibrium geometries.

IV. Conclusions

Attractive interactions between substituted aromatic rings play a central role in disparate chemical and biochemical phenomena and constitute a powerful tool in the design of novel materials and for host-guest chemistry [1-5,7-10]. However, our understanding of the effect of substituents even in simple model systems based on the benzene dimer continues to evolve [22,25-29,31,32,36]. We have presented the first theoretical study of substituent effects in edge-to-face aromatic interactions. In contrast to nearly all previous studies of substituent effects in the benzene dimer [20,22-31,33-35], the contribution to interaction energies attributed to direct interactions between the local dipoles induced by the substituents and the unsubstituted ring has been explicitly evaluated. The result is a new qualitative model of substituent effects in the edge-to-face dimer, depicted in Fig. 8.

Figure 8.

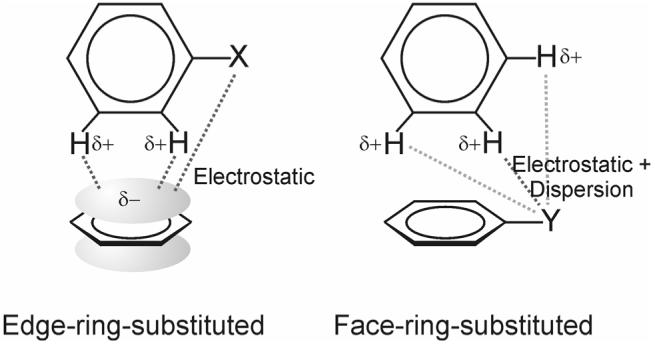
Primary origins of substituent effects in monosubstituted edge-to-face benzene dimers. In edge-ring-substituted dimers, substituent effects arise from the direct, primarily electrostatic, interaction of the substituent with the face ring and differential interactions between the edge ring hydrogens and the π-cloud of the face ring. In face-ring-substituted dimers, substituent effects are dictated by direct electrostatic and dispersion interactions between the substituent and the edge ring hydrogens.

The attractive interaction in the unsubstituted edge-to-face dimer is due to a blend of electrostatic, dispersion, polarization, and exchange-repulsion interactions. The intuitive model of substituent effects espoused by Hunter and co-workers[16-18] is not supported by the present theoretical results. Instead, substituent effects in the edge-to-face benzene dimer are due in large part to direct interactions between the local dipoles induced by the substituents and the other ring. For edge-ring-substituted dimers there is a strong correlation between E_int and σ_m, indicating that the substituent effect is dominated by differential electrostatic interactions. However, half of the observed trend is due to the direct interaction of the substituents with the face ring, with the remainder due to the modulation of the interaction between the edge ring hydrogens and the face ring π-electrons. Upon substitution, the attractive electrostatic interaction between the edge ring hydrogens and the face ring in the unsubstituted dimer are either enhanced or diminished by the inductive effects of the substituents, complemented by additional electrostatic interactions between the substituents and the face ring. Dispersion interactions between the substituents and the face ring contribute little, if any, to the substituent effect.

For the face-ring-substituted dimer, the substituent effects arise from direct electrostatic and dispersion interactions between the substituents and the periphery of the edge ring, analogous to the sandwich configuration of the benzene dimer [32]. The effects present in the unsubstituted dimer remain largely unperturbed—substituent effects arise from the additional, direct interactions of the substituents with the edge ring. Apart from several obvious outliers, the predicted substituent effects in the face-ring-substituted dimer correlate with σ_m. There are dispersion interactions between the substituents themselves and the edge ring that preferentially stabilize substituted dimers compared to the unsubstituted case. As a result, CH₂OH is a more suitable σ_m = 0.0 reference than H, since this system accounts at least approximately for the average stabilization of face-ring-substituted dimers due to dispersion. The abovementioned outliers (substitution by H, BF₂, SCH₃, SH, and SiF₃) correspond to cases with unusually large or small dispersive interactions. Overall, inductive electron withdrawing groups hinder the interaction relative to C₆H₆^...C₆H₅-CH₂OH, while inductive electron donors enhance the interaction.

Strong inductive electron donors clearly favor formation of the face-ring-substituted dimer, while strong electron acceptors favor edge-ring-substitution. The crossover point for this preference is the phenol-benzene edge-to-face dimer (σ_m^OH = 0.12); for C₆H₅-OH the edge-ring and face-ring-substituted configurations are isoenergetic. Apart from two outliers (SH and SCH₃), for substituents with σ_m > 0.12 the edge-ring-substituted dimer is lower in energy while for σ_m < 0.12 face ring substitution is favored. This trend is skewed towards the face-ring-substituted dimers due to the attractive dispersive interactions in this configuration that are mostly absent in the edge-ring-substituted dimers.