Abstract
It has recently been discovered that guests combining a nonpolar core with cationic substituents bind cucurbit[7]uril (CB[7]) in water with ultra-high affinities. The present study uses the Mining Minima algorithm to study the physics of these extraordinary associations and to computationally test a new series of CB[7] ligands designed to bind with similarly high affinity. The calculations reproduce key experimental observations regarding the affinities of ferrocene-based guests with CB[7] and β-cyclodextrin and provide a coherent view of the roles of electrostatics and configurational entropy as determinants of affinity in these systems. The newly designed series of compounds is based on a bicyclo[2.2.2]octane core, which is similar in size and polarity to the ferrocene core of the existing series. Mining Minima predicts that these new compounds will, like the ferrocenes, bind CB[7] with extremely high affinities.
I. INTRODUCTION
Host-guest systems - receptors of low molecular weight that bind specific molecules - have a range of potential applications in chemical sensing, separations, materials science, catalysis, and pharmaceutics. They are also compact yet informative molecular recognition cases with the potential to deepen our understanding of noncovalent association in more complex biomolecular systems. Indeed, host-guest binding resembles protein-ligand binding in important ways. Both rely on nonbonded interactions like hydrogen-bonds, van der Waals (vdW) interactions, and for aqueous systems, the hydrophobic effect. Both also are governed by the same laws of statistical mechanics, with its implications for preorganization, strain and entropy, and both display the same empirical pattern of entropy-enthalpy compensation1,2 (Figures 1 and 2). One might therefore expect, a priori, that host-guest and protein-ligand systems would have similar distributions of binding affinities.
FIG. 1.
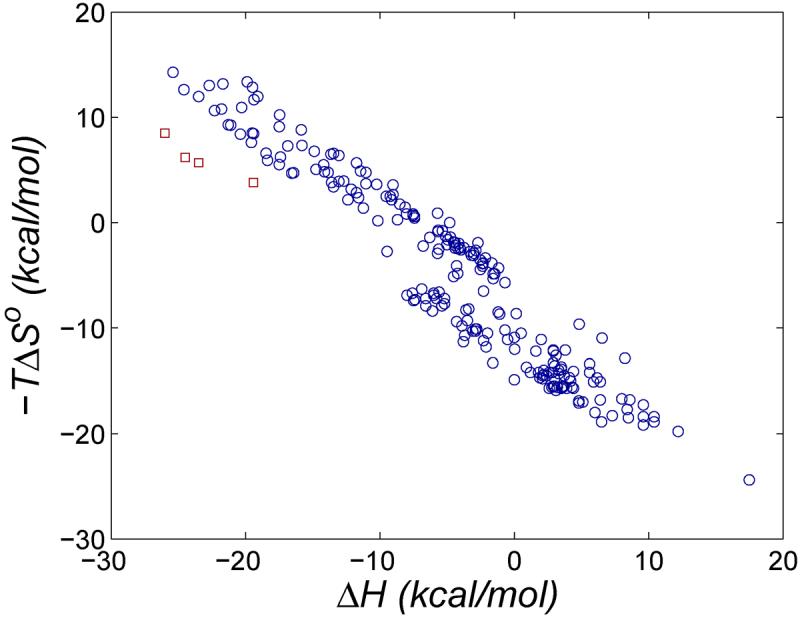
Changes in entropy versus enthalpy for protein-ligand binding data in the BindingDB database44-46 (blue circles) and for biotin with avidin wild type and mutants47 (red squares) from calorimetric studies.
FIG. 2.
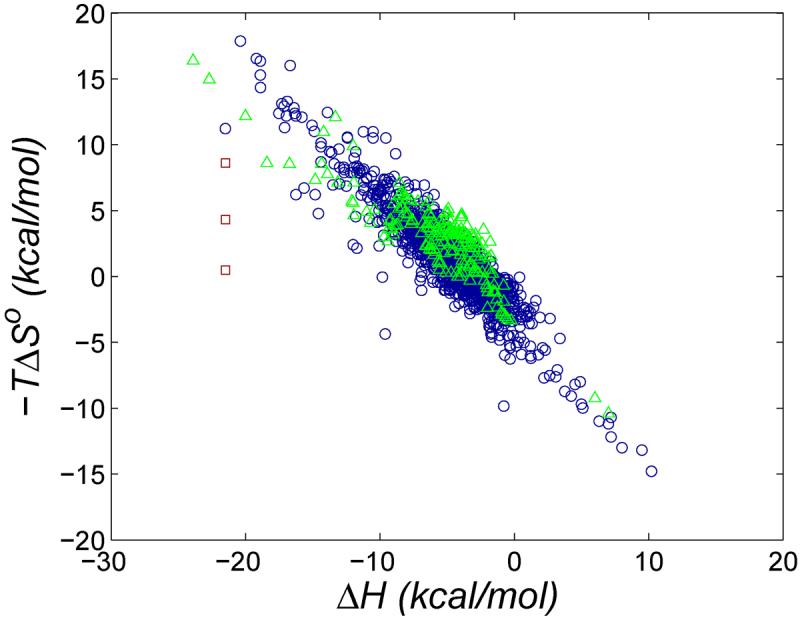
Change in entropy versus enthalpy for cyclodextrin-guest systems48 (blue circles), non-aqueous host-guest systems1 (green triangles), and CB[7] with ferrocene derivatives F1, F3, and F6 (red squares)12.
However, reported host-guest affinities tend to be considerably weaker than protein-small molecule affinities:1 Figure 3 shows that protein-ligand binding free energies drawn from the medicinal chemistry literature peak about 8 kcal/mol lower than published host-guest binding free energies. One physical reason for this difference may be that a protein's binding pocket has more surface area than does the binding site of a typical chemical host and therefore can more completely enfold a ligand, as previously noted1. A protein's many degrees of freedom also may allow the shape of its binding site to conform better to the shape of a ligand. In addition, the seemingly inert bulk of a protein away from the binding pocket might contribute to binding, perhaps through effects on configurational entropy or solvation.
FIG. 3.
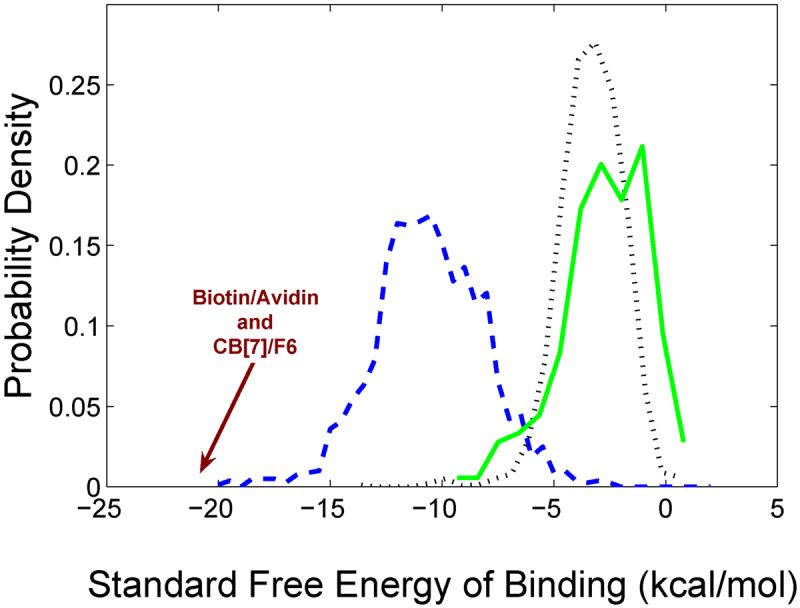
Distributions of measured binding free energies, showing data for protein-ligand affinities from the medicinal chemistry literature (dashed blue line), as collected in BindingDB44-46 and computed as RT ln Ki, where Ki is an enzymatic inhibition constant; synthetic, aqueous host-guest systems (solid green line)1, and aqueous cyclodextrin-guest systems1 (dotted black line). The measured binding free energies of biotin with avidin47 and of CB[7] with F612 are also indicated.
On the other hand, the statistical differences between protein-ligand and host-guest affinities may be more historical than scientific in origin, since many protein-ligand systems have been extensively optimized by natural selection or by drug-design projects, far more so than for host-guest systems. Moreover, computational tools for the design of host-guest systems are fewer and less developed than those for computer-aided drug-design. Recent developments in host-guest modeling include the HostDesigner3,4 and ConCept5 programs for automated host design, and the Mining Minima algorithm (M2) for calculation of host-guest affinities6,7. The latter has yielded promising agreement with experiment in a series of retrospective studies6,8,9.
Host-guest systems have now been discovered whose affinities rival those of the tightest binding protein-ligand systems: the 7-unit cucurbitural host (CB[7]), Figure 4, binds cationic adamantyl10 and ferrocene11,12 derivatives with binding constants of 109 - 1013M-1. The higher values here reach the affinity level of biotin with avidin13 (Figure 3), and CB[7]-based systems are being evaluated as replacements for these widely used biomolecular linkers14. M2 calculations for these systems reproduce their high affinities and concur with calorimetric measurements that the high affinities are associated with unusually small entropic penalties12.
FIG. 4.
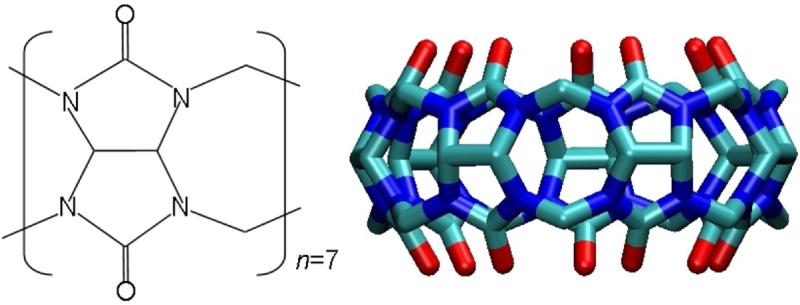
Chemical structure of the 7-unit cucurbitural host (CB[7]).
Here we use the M2 method to study the balance of forces in these remarkable CB[7]-ligand systems in greater detail, with particular attention to electrostatics and entropic effects, and to test how well M2 calculations match experiments showing that the same ferrocene-based guests bind only weakly to β-cyclodextrin (βCD), Figure 5. We then propose new metal-free compounds designed to bind CB[7] with high affinity and apply the M2 method to assess their affinities in advance of experiment. These studies bear on the usefulness of M2 as a design tool and also on whether guests without a metal atom can achieve the ultra-high affinities of the ferrocene-based guests. The Discussion section puts the present results into context, reviews sources of error in the M2 method, and analyzes the challenge of overcoming energy-entropy compensation in protein-ligand systems.
FIG. 5.
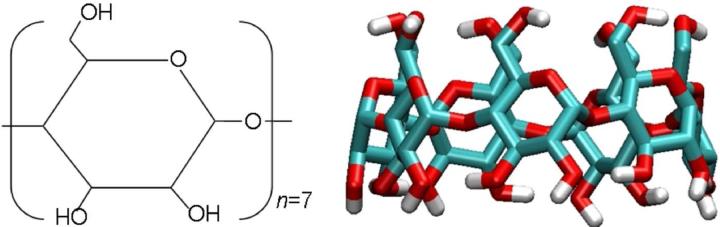
Chemical structure of the β-cyclodextrin host (βCD).
II. METHODS
A. Computational Approach
The M2 method has been detailed previously, and so is only summarized here. The free energy of host-guest binding is computed as
| (1) |
where , and are the standard chemical potentials of the complex, host, and guest molecules, respectively. The standard chemical potential of a molecule in solution is approximated as a sum over M local energy minima:
| (2) |
| (3) |
where R, T, Cο, E(r), and Zi are, respectively, the gas constant, the absolute temperature, the standard concentration, the energy as a function of the internal coordinates r, and the configuration integral over internal coordinates in energy well i. (Factors that will cancel in the final free energy difference have been omitted.) Local energy minima are identified with the Tork search algorithm15, and local configuration integrals are computed with the Harmonic Approximation/Mode Scanning (HA/MS) method7. Because the Tork search can arrive at the same conformation more than once, duplicate conformations are eliminated with a symmetry-aware algorithm to prevent double-counting16.
The energy E(r) can be decomposed into the sum of the potential energy, U(r), and the solvation energy, W(r), both functions of the conformation17,18. The CHARMM force field19-22 is used here for the potential energy function. During conformational search and HA/MS calculations, a generalized Born model23 is used for the solvation energy. Solvation energies are subsequently corrected toward the Poisson-Boltzmann/Surface Area model24,25, based upon one finite-difference solution of the linearized Poisson-Boltzmann equation and one surface area calculation for each energy minimum i, as previously described6.
The M2 calculations also yield the change in the Boltzmann-averaged sum of the potential and the solvation energies on binding, Δ〈U + W〉, which can be combined with the change in binding free energy to yield the change in configurational entropy17, which accounts for changes in the mobility of the host and guest on binding, :
| (4) |
The change in configurational entropy includes changes in the rotational, translational, conformational, and vibrational entropy of the host and guest molecules upon binding, but it does not include the change in solvent entropy. The change in mean energy on binding can be decomposed into Boltzmann-averaged terms
| (5) |
representing, respectively, the changes in valence energy (bond stretches, angle bends, and dihedral rotations), van der Waals (vdW) interactions, Coulombic interactions, electrostatic solvation free energy, and nonpolar solvation free energy.
B. Molecular Models and Computational details
The force field parameters of ferrocene and its derivatives (Table 1) were generated as previously described12. For the other compounds, CHARMM force field parameters other than partial charges were assigned by Quanta. Partial atomic charges were generated by the VC/2004 charging method as implemented in the program Vcharge26. Poisson-Boltzmann calculations were carried out with the program UHBD27. The interior and solvent dielectric constants are set, respectively, to 1 and that of water (80 at 300K). The boundary between the low-dielectric interior and the high-dielectric exterior is defined by the Richards molecular surface28 with a 1.4Å solvent probe. Each atom's dielectric cavity radius is set to the Rmin value for its CHARMM Lennard-Jones parameter, except that hydrogen radii are set to 1.2 Å. The parameters are included in supporting information (SI). Three gedanken experiments to examine the role of electrostatic interactions in the association of CB[7] with F6 were done by recomputing affinities with 1) all the partial charges of every atom of the diaminoferrocene derivative, F6, set to zero; 2) all partial atomic charge of every atom of CB[7] set to zero; and 3) all partial charges of both molecules set to zero.
TABLE 1.
Chemical structures of ferrocene core and derivatives
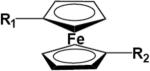
| R1 | R2 | |
|---|---|---|
| F | -H | -H |
| F1 | -CH2OH | -H |
| F2 | -H | |
| F3 | -H | |
| F4 | -CH2N(CH3)2(CH2)3Br+ | -H |
| F5 | -COO- | -H |
| F6 |
The starting structure of CB[7] was taken from the crystal structure11, and the starting structures of βCD and the various guest molecules were constructed with the program Quanta29. All initial structures were refined by an initial energy minimization in Quanta using CHARMM first by the method of conjugate gradients with a root-mean-square (RMS) gradient tolerance of 0.01 kcal/mol, and then by the Newton-Raphson method with an RMS gradient tolerance of 0.001 kcal/mol. Initial structures of the host-guest complexes were generated by using the program Vdock30,31 to rigidly fit the initial minimized guest structure into the initial minimized host structure.
A Tork conformational search for a given molecule or complex yielded an initial set of local energy minima. The corresponding local configuration integrals were computed with the HA/MS method, for T = 300K, and their solvation energies were corrected as noted above. The corrected configuration integrals were used to compute an initial estimate of the standard chemical potential via Eq 2. The six conformations of lowest chemical potential were then used to initiate six new Tork searches and configuration integrations. This cycle was iterated until a cycle changed the free energy less than 0.1 kcal/mol. Some of the present results differ slightly from those previously reported12 due to recalculation with slightly tighter tolerances in a procedure for converting from internal to Cartesian coordinates. The present calculations use lengthy searches, which took ~2 days on a 3.4 GHz Pentium® processor, to lower the likelihood of missing a global energy minimum.
III. RESULTS
A. Binding of ferrocene-based guests to CB[7] and βCD
1. Overview of results
The calculated binding free energies of the ferrocene guests (Table 1) with CB[7] and βCD are listed in Table 2, along with the available experimental binding free energies. The calculations correctly reproduce the key experimental observations that all the ferrocene derivatives have unremarkable affinities for βCD. The anionic derivative, F5, essentially does not bind CB[7] but does bind βCD; the monocationic derivatives bind CB[7] tightly (~-14 kcal/mol); and the dicationic derivative, F6, binds CB[7] extremely tightly (~-21 kcal/mol). The root-mean-square deviation (RMSD) between calculation and experiment is 2.1 kcal/mol overall, and the RMSD values for the CB[7] and βCD subsets are 1.9 and 2.1 kcal/mol respectively. Linear regression of calculation against experiment yields a slope of 1.02 and a correlation coefficient of R2 = 0.97.
TABLE 2.
Thermodynamic analysis of binding of ferrocene guests with βCD and CB[7]. Q1, Q2: ionic charge of R1 and R2 groups (Table 1). From left to right, the remaining columns show the measured binding free energy, when available; calculated binding free energy; calculated changes in mean potential plus solvation energy, configurational entropy, mean van der Waals energy, mean Coulombic energy, mean total electrostatic energy (ΔEel = ΔUC + ΔWel), valence energy and nonpolar solvation energy; and the energy efficiency. Units: kcal/mol. The Boltzmann average of energy term signs are omitted for brevity
| Changes in Mean Energy Terms |
||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Q1,Q2 | Δ(U + W) | ΔUvdw | ΔUC | ΔWel | ΔEel | ΔUval | ΔWnp | |||||
| Cucurbit [7] uril | ||||||||||||
| F | 0, 0 | -11.4 | -19.8 | 8.4 | -25.6 | -3.2 | 9.8 | 6.6 | 1.9 | -2.5 | 0.57 | |
| F1 | 0, 0 | -12.9 | -10.5 | -25.3 | 14.8 | -27.0 | -17.0 | 19.8 | 2.8 | 1.5 | -2.6 | 0.42 |
| F2 | +1, 0 | -16.8 | -14.6 | -32.5 | 17.9 | -29.9 | -77.9 | 75.8 | -2.0 | 2.3 | -2.9 | 0.45 |
| F3 | +1, 0 | -17.2 | -14.5 | -31.1 | 16.6 | -33.0 | -70.2 | 74.8 | 4.6 | 0.2 | -3.0 | 0.47 |
| F4 | +1, 0 | -12.8 | -31.1 | 18.3 | -34.3 | -71.2 | 76.7 | 5.5 | 0.8 | -3.1 | 0.41 | |
| F5 | -1, 0 | NB | -0.9 | -8.4 | 7.5 | -5.3 | -9.0 | 7.0 | -2.0 | -0.1 | -0.9 | 0.1 |
| F6 | +1,+1 | -21.0 | -21.0 | -38.8 | 17.8 | -39.2 | -133.2 | 136.2 | 3.0 | 0.8 | -3.4 | 0.54 |
| β-Cyclodextrin | ||||||||||||
| F | 0, 0 | -8.6 | -17.2 | 8.7 | -17.6 | -0.1 | 3.4 | 3.4 | -0.7 | -2.3 | 0.50 | |
| F1 | 0, 0 | -4.8 | -16.1 | 11.3 | -18.1 | 0.2 | 4.6 | 4.8 | 0.4 | -2.4 | 0.30 | |
| F2 | +1, 0 | -3.1 | -19.3 | 16.3 | -20.7 | -15.0 | 17.1 | 2.1 | 1.9 | -2.6 | 0.16 | |
| F3 | +1, 0 | -4.7 | -2.0 | -8.7 | 6.7 | -13.0 | 3.2 | 4.4 | 7.7 | -1.3 | -2.1 | 0.23 |
| F4 | +1, 0 | -3.1 | -12.2 | 9.1 | -14.0 | 2.8 | 2.2 | 5.0 | -1.1 | -2.1 | 0.26 | |
| F5 | -1, 0 | -4.6 | -4.1 | -19.7 | 15.6 | -16.6 | -19.6 | 18.2 | -1.4 | 0.7 | -2.4 | 0.21 |
| F6 | +1,+1 | ≥ 0 | ||||||||||
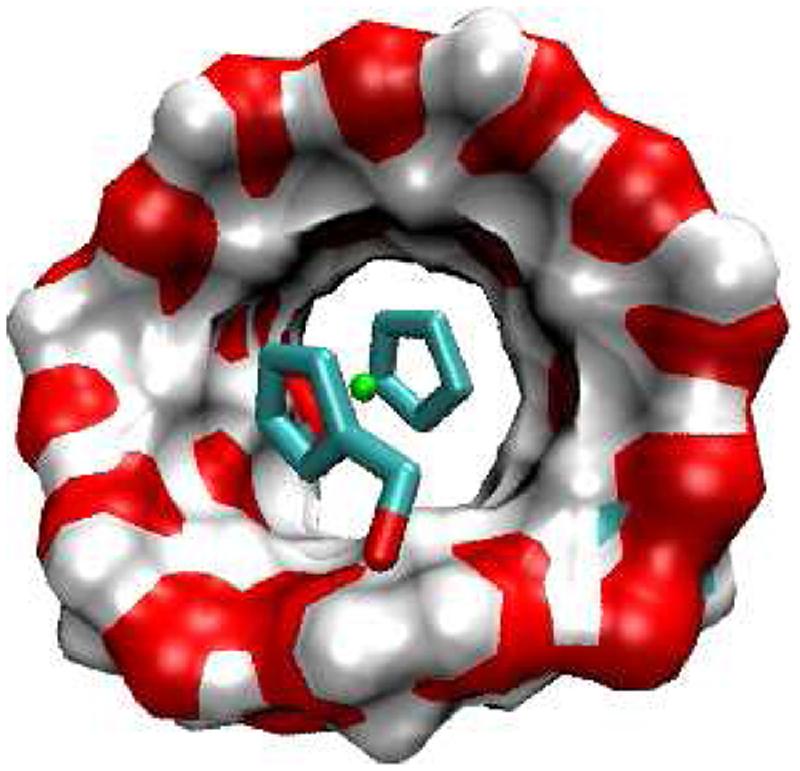
Figures 6-11 show the most stable computed complex of each host with several different guest molecules. For the monocationic ferrocenes, the nonpolar ferrocene moiety is held within the nonpolar cavity of CB[7] or βCD and the cationic moiety lies at the polar portals of the respective hosts. However, CB[7] holds these guests more snugly than βCD does and provides a ring of carbonyls to stabilize the cationic groups of the guests. As previously shown12, the diaminoferrocene is able to place each amino group at one of the electronegative portals of CB[7] (Figure 11). On the other hand, the anionic F5 is predicted to be unstable inside the CB[7] cavity, presumably because its anionic carboxyl group would necessarily lie at the electronegative portal and generate a repulsive electrostatic interaction; in consequence, F5 is predicted to bind CB[7] with an essentially negligible binding free energy (Table 2), consistent with experiment. In contrast, βCD accommodates the anionic F5 comfortably, the carboxylate remaining well solvated near the cyclodextrin's flexible hydroxyls (Figure 8). On the other hand, the diamino ferrocene derivative, F6, which binds CB[7] with outstanding affinity, is predicted not to bind to βCD. Conformations where F6 is in the binding cavity of βCD lead to substantial desolvation of the cationic groups and hence a large value of ΔWel, which is only partly compensated by favorable Coulombic interactions.
FIG. 6.
Most stable conformation computed for complex of F1 with βCD.
FIG. 11.
Most stable conformation computed for complex of F6 with CB[7].
FIG. 8.
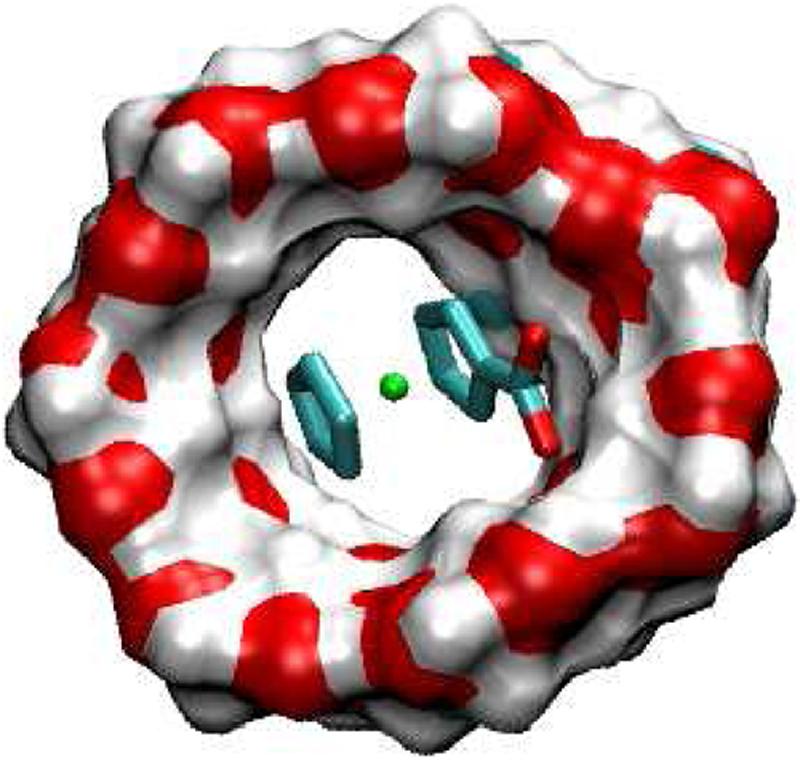
Most stable conformation computed for complex of F5 with βCD.
2. Balance between energy and entropy
The present calculations allow the binding free energy to be broken into the change in configurational entropy, , and the change in mean energy, Δ〈U + W〉, where U is potential energy and W is solvation free energy. These quantities are listed in the fifth and sixth data columns of Table 2. In all cases, the calculated binding free energies are balances of large, favorable changes in potential and solvation energy, and large, unfavorable changes in configurational entropy.
The neutral and monocationic ferrocene guests incur larger configurational entropy penalties, , on binding the CB[7] than on binding βCD; the averages across these hosts are 15 kcal/mol for CB[7] and 11 kcal/mol for βCD. Nonetheless, these guests bind CB[7] much more strongly than βCD (Table 2): the mean binding free energies are -13 and -4 kcal/mol, respectively. We surmise that the comparatively flexible βCD loses more internal entropy on binding than does the rigid CB[7], while CB[7] leads to a greater loss of rotational and translational entropy on binding because it holds the ferrocene guests so tightly. Because the overall entropy penalties are generally greater for CB[7] than for βCD, the greater affinities for CB[7] must trace to more favorable changes in mean energy, Δ〈U + W〉: this quantity averages -28 kcal/mol for CB[7] and -16 kcal/mol for βCD. This energy difference is discussed in Section III A 3.
The difference between CB[7] and βCD is even more marked for the diamino guest, which binds CB[7] with ultra-high affinity (ΔGο = -21 kcal/mol) and is predicted to have negligible affinity for βCD. The difference between the association of the diamino and monoamino derivatives with CB[7] is entirely energetic in origin; the loss of configurational entropy, ~ 18 kcal/mol, is basically equivalent to that of the monoamino guests, ~18 kcal/mol, but the energy change goes from ~ -32 kcal/mol for the monoamino case to ~-39 kcal/mol for the diamino.
The energy efficiency, , is a quantity which captures the degree to which attractive forces are effective in generating binding free energy, rather than being canceled by entropy losses9; a larger value indicates that the host-guest system overcomes energy-entropy compensation to a larger degree. As shown in Table 2, the energy efficiencies are roughly twice as large for binding to CB[7] versus βCD. The largest efficiencies, ~0.57, are observed for CB[7] with plain ferrocene (F) and for the ultra-high affinity diamino derivative. These CB[7] efficiencies are 2-3× larger than those previously computed for a series of designed peptide receptors9.
Figure 12 puts the present results in the context of prior studies which indicate a rather consistent relationship between energy gain and entropy loss on binding9. The ferrocene-βCD interactions fit the prior pattern, and linear regression of the combined data set yields an energy-entropy relationship of
| (6) |
as shown in the figure. The ferrocene-CB[7] interactions, in contrast, are markedly left-shifted relative to this trendline, toward less entropy loss per unit energy gain, consistent with the greater energy efficiency and higher affinity of these binding interactions. We can examine how tightly the diamino ferrocene (F6) would bind if it followed the usual trend by artificially shifting its data point in Figure 12 up to the trendline. This shift corresponds to an increase in its entropy penalty from 18 kcal/mol to 32 kcal/mol and a resulting reduction of the binding free energy from -21 kcal/mol to -7 kcal/mol. We conclude that this system would not achieve its ultra-high affinity if it did not overcome the usual entropy-energy pattern.
FIG. 12.
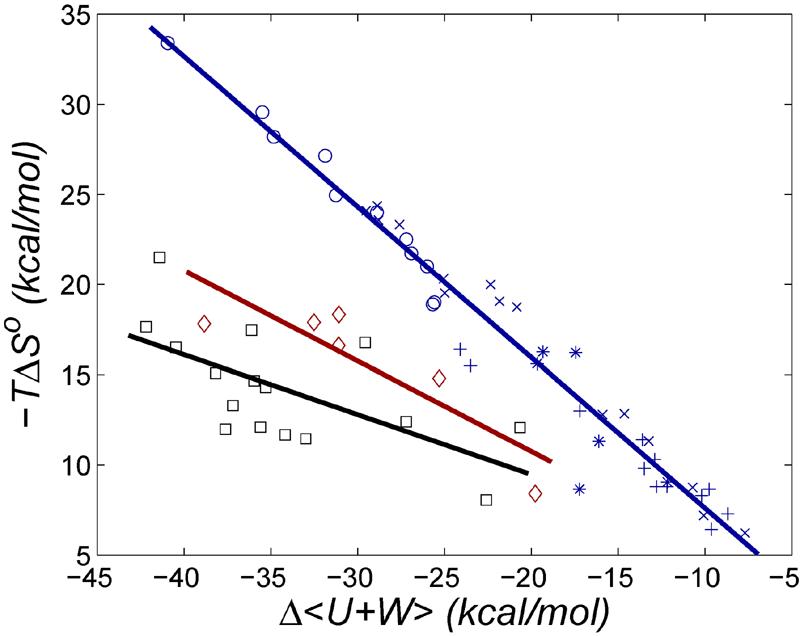
Computed changes in configurational entropy versus changes in mean energy Δ(U +W), for βCD with ferrocene derivatives (blue stars), designed RGD receptors9 (blue circles), aqueous cyclodextrins with various guests8 (blue “x”s), various host-guest systems in chloroform6 (blue “+”s), CB[7] with ferrocene derivatives (red diamonds), and CB[7] with bicyclo[2.2.2]octane derivatives (black squares).
3. Energetics and electrostatics
As shown by the crystal structure of the CB[7]-diaminoferrocene complex12 and the present calculations (Figures 10 and 11), the cationic ferrocene derivatives studied here position their cationic groups at the portals of CB[7], which are highly electronegative due to the convergence of multiple carbonyl oxygens. It might therefore be expected that much of the energetic driving force for binding would be attributable to electrostatic interactions and, in fact, we find strongly attractive Coulombic interactions for these complexes (Table 2): ΔUC is about -73 kcal/mol for the monocations and -133 kcal/mol for the dication. However, these favorable Coulombic interactions are canceled with striking precision by unfavorable electrostatic solvation penalties, ΔWel, (Table 2). As a consequence, the net electrostatic driving force for binding, ΔEel = ΔUC + ΔWel, contributes at best -2 kcal/mol to the binding free energy and is found to oppose binding by 3-5 kcal/mol in most cases. Overall, then, strongly favorable Coulombic host-guest interactions are canceled by the large energy cost of stripping polarized water from the cationic groups of the ligands and from the carbonyls at the CB[7] portals. Such electrostatic compensation has been noted previously9,32,33.
FIG. 10.
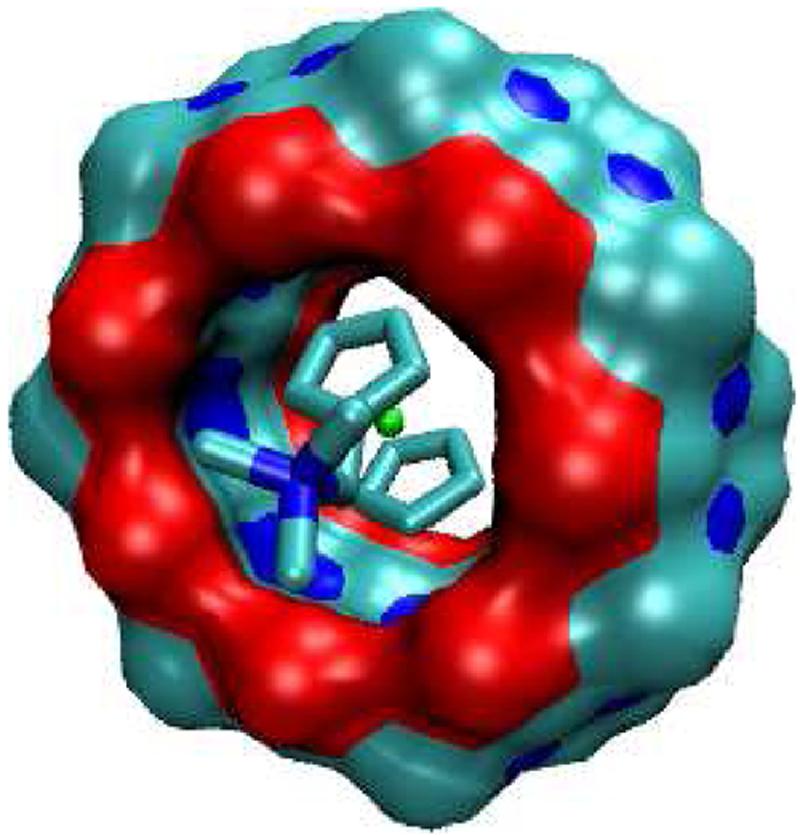
Most stable conformation computed for complex of F3 with CB[7].
Furthermore, electrostatic interactions do not account for the large differences between the binding energies, Δ〈U + W〉, of βCD and CB[7] for the cationic ferrocenes (Section III A 2). Indeed, the net electrostatic contributions to binding, ΔEel, are very similar for the two hosts, averaging ~3.5 and ~4 kcal/mol for CB[7] and βCD, respectively. However, this quantity partitions very differently for the two hosts: in contrast with CB[7], βCD does not form especially strong Coulombic interactions with the cationic guests, but it also leaves them relatively well-solvated, so both 〈UC〉 and 〈Wel〉 are small and their sum is similar to that observed for binding to CB[7]. The near-cancelation of electrostatic terms for both hosts leaves the van der Waals energy component, 〈UvdW〉, as the main net contributor to the affinities of the ferrocenes for both hosts. It is also the chief energetic reason for the difference in affinities for CB[7] versus βCD: the change in van der Waals energy averages about -32 kcal/mol for binding to CB[7], but only -17 kcal/mol for βCD. This difference is traceable to the more complementary fit of the ferrocene core to the cavity of CB[7] versus βCD (Figures 6-11).
We further examined the roles of electrostatics and van der Waals interactions with gedanken experiments in which electrostatic interactions between the two molecules were zeroed by artificially making the host, the guest, or both, entirely nonpolar. These calculations treat one or both molecules essentially as nonpolar alkanes. Neutralizing both molecules yields a computed binding free energy of -21 kcal/mol, much as found for the fully charged molecules, even though we have now forced all electrostatic interactions to zero. This result is consistent with the dominant role of van der Waals interactions, which are essentially unaffected by changing the polarity of these rigid molecules. When only one of the molecules is made nonpolar, however, the computed binding free energies become greater than zero, implying negligible affinity. These unfavorable binding free energies reflect the free energy cost of stripping solvent from the solitary polar molecule without the benefit of attractive Coulombic interactions between the two molecules. In the full calculation where both molecules are treated as polar (Section III A 1), the attractive Coulombic interactions successfully balance the electrostatic desolvation penalty, leaving the attractive van der Waals interaction as the chief force driving binding.
The anionic guest, F5, binds βCD about as well as the neutral and cationic guests do, but, unlike the other guests, does not bind CB[7] with appreciable affinity. Its low affinity for CB[7] probably results from the fact that the ferrocene moiety cannot insert into the cavity of CB[7] without positioning the anionic acid at the carbonyl-rich portal of CB[7] and thereby generating severe electrostatic repulsions. Indeed, the calculations indicate that the guest prefers to bind outside the cavity. As a consequence, the electrostatics listed in Table 2 are not unfavorable (〈ΔUC + ΔWel〉 = -2.0 kcal/mol), but the change in van der Waals is only about -5 kcal/mol, compared with about -32 kcal/mol for the other guests. Once the entropy loss is factored in, the net result is a negligible binding affinity.
B. High-affinity, non-ferrocenyl CB[7] guests
1. Design
We conjecture that guests without a ferrocenyl moiety can also achieve ultra-high affinity for CB[7]. In fact, the agreement of the above M2 calculations with experiment suggests that this is possible, because the M2 calculations do not include any special nonbonded interaction terms for the iron atom. Instead, the ferrocene moiety appears to function only as a rigid, nonpolar core that affords favorable van der Waals interactions with CB[7] at a low cost in configurational entropy, while simultaneously positioning cationic groups at the host's electronegative portals. The similarly rigid, nonpolar adamantyl group can play a similar role, yielding binding affinity of 1012 M-1 with CB[7] for monoammonium derivatives10. However, adding a second ammonium group to the adamantyl core was found to weaken binding for CB[7]10, rather than strengthening it as in the ferrocene case, presumably because the second cationic group is not optimally positioned.
A bicyclo[2.2.2]octane core (Table 3) is a promising alternative to the ferrocene group for the present purpose. It is similarly rigid and nonpolar and possesses an axial symmetry that matches the symmetry of CB[7] better than either ferrocene or adamantane and therefore may do a better job of positioning cationic groups at the host's electronegative portals. This section reports the results of M2 calculations for bicyclo[2.2.2]octane itself, as well as a series of neutral and cationic derivatives (Table 3) which probe the possibility of gaining binding affinity by placing additional positive charge at and beyond the portal of CB[7]. This series is motivated by a prior experimental study showing a monotonic rise in affinity of the CB[6] host for a series of linear amines of increasing charge34.
TABLE 3.
Chemical structures of bicyclo[2.2.2]octane core and derivatives

| R1 | R2 | |
|---|---|---|
| B | -H | -H |
| B1 | -CH2OH | -H |
| B2 | -CH2OH | -CH2OH |
| B3 | -CH2OCH3 | -H |
| B4 | -H | |
| B5 | ||
| B6 | -H | |
| B7 | ||
| B8 | -H | |
| B9 | ||
| B10 | -H | |
| B11 | ||
| B12 | -H | |
| B13 |
2. Overview of computed affinities
The calculations yield high affinities for the bicyclo[2.2.2]octane compounds with CB[7] (Table 4). The computed binding free energies range up to -26 kcal/mol, and their mean binding free energy is computed to be about 7 kcal lower (greater affinity) than that of the neutral and cationic ferrocenes. Structurally, the bicyclo[2.2.2]octane core fits the cavity of CB[7] well (Figure 13). Indeed, the plain bicyclo[2.2.2]octane core, B, is predicted to bind CB[7] more tightly (-14.5 kcal/mol) than the plain ferrocene core, F (-11.4 kcal/mol). This difference is attributable exclusively to more favorable energetics, largely in the form of van der Waals interactions, as the computed entropy losses are indistinguishable (Tables 2 and 4). In addition, the bicyclo[2.2.2]octane core correctly positions the ammonium groups that are proximate to the core at the portals of CB[7] (Figure 13), and adding one such cationic group to each end of the core, as in B5, leads to a boost of up to ca. -10 kcal/mol in binding free energy relative to the plain core, B. On the other hand, elongating the substituents and adding more positive charge to them does not increase the computed affinity beyond that of the simplest dicationic guest, B5, even though the extended chains are predicted to wrap back and interact with the CB[7] host, as illustrated for B13 (Figure 14). This result differs from experimental observations for the similar series with CB[6], mentioned in Section III B 1.
TABLE 4.
Thermodynamic analysis of binding of bicyclooctane-based guests with CB[7]. See Table 3 for definitions
| Changes in Mean Energy Terms |
|||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Q1,Q2 | ΔUvdW | ΔUC | ΔWel | ΔEel | ΔUval | ΔWnp | |||||
| B | 0, 0 | -14.5 | -22.6 | 8.1 | -28.9 | 1.0 | 7.8 | 8.8 | -0.3 | -2.2 | 0.64 |
| B1 | 0, 0 | -14.8 | -27.2 | 12.4 | -31.6 | -3.3 | 9.7 | 6.4 | 0.4 | -2.5 | 0.54 |
| B2 | 0, 0 | -12.8 | -29.6 | 16.8 | -34.6 | -8.1 | 14.3 | 6.2 | 1.4 | -2.7 | 0.43 |
| B3 | 0, 0 | -8.6 | -20.7 | 12.1 | -32.0 | -1.1 | 13.9 | 12.8 | 1.1 | -2.6 | 0.42 |
| B4 | +1, 0 | -22.5 | -34.2 | 11.7 | -30.0 | -78.0 | 75.1 | -2.9 | 1.2 | -2.5 | 0.66 |
| B5 | +1,+1 | -25.6 | -37.6 | 12.0 | -31.8 | -162.1 | 155.3 | -6.8 | 3.8 | -2.7 | 068 |
| B6 | +1, 0 | -21.3 | -36.0 | 14.7 | -36.1 | -68.2 | 71.0 | 2.8 | 0.1 | -2.8 | 0.59 |
| B7 | +1,+1 | -24.5 | -42.2 | 17.7 | -41.9 | -138.0 | 140.4 | 2.4 | 0.6 | -3.3 | 0.58 |
| B8 | +2, 0 | -23.5 | -35.6 | 12.1 | -34.2 | -123.2 | 122.1 | -1.0 | 2.3 | -2.8 | 0.66 |
| B9 | +2,+2 | -21.0 | -35.3 | 14.3 | -38.5 | -244.2 | 245.5 | 1.3 | 5.2 | -3.3 | 0.59 |
| B10 | +2, 0 | -23.1 | -38.2 | 15.1 | -35.2 | -123.7 | 118.9 | -4.8 | 4.7 | -2.9 | 0.61 |
| B11 | +2,+2 | -19.9 | -41.4 | 21.5 | -42.0 | -241.1 | 232.0 | -9.1 | 13.5 | -3.8 | 0.48 |
| B12 | +3, 0 | -21.5 | -33.0 | 11.5 | -34.8 | -163.1 | 159.9 | -3.2 | 7.9 | -2.9 | 0.65 |
| B13 | +3,+3 | -18.7 | -36.1 | 17.5 | -37.3 | -313.9 | 313.0 | -0.9 | 5.3 | -3.2 | 0.52 |
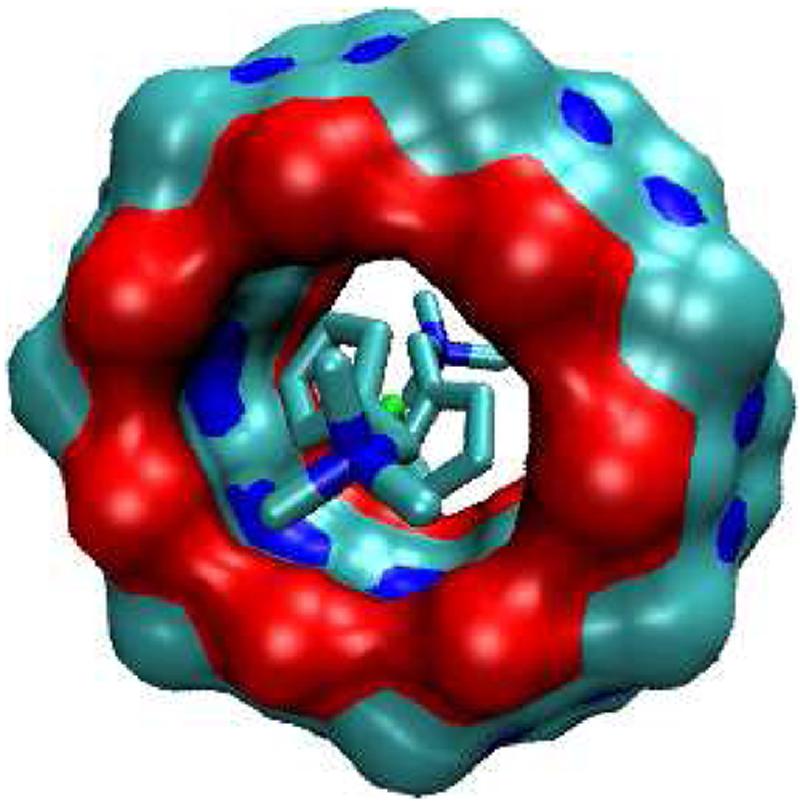
FIG. 13.
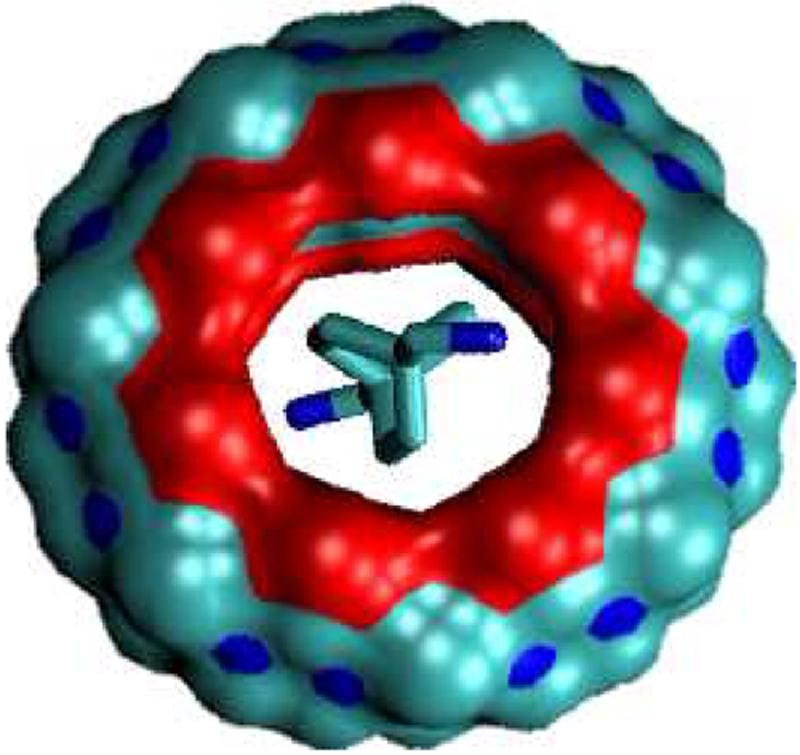
Most stable conformation computed for complex of B5 with CB[7].
FIG. 14.
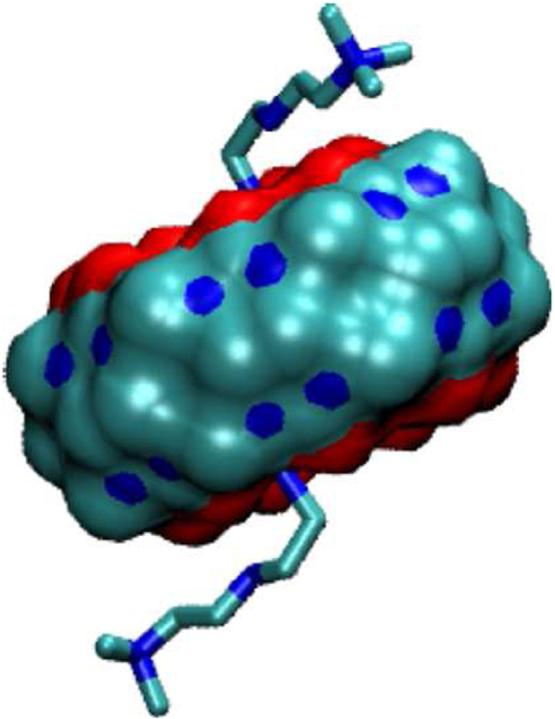
Most stable conformation computed for complex of B13 with CB[7].
3. Analysis of entropy and energy changes on binding
The thermodynamic breakdowns for the bicyclooctane compounds (Table 4) are generally similar to those for the ferrocene compounds (Table 2), with large favorable energy changes, Δ〈U + W〉 partly compensated by large unfavorable entropy changes, We again observe massive cancellation of the Coulombic and electrostatic solvation energies, ΔUC and ΔWel, so that the van der Waals energy, ΔUvdW, remains as the largest uncanceled contributions to binding. The greater affinities of the bicyclooctanes relative to the ferrocenes are traceable primarily to their more favorable energy changes, because the changes in configurational entropy for both series are rather similar. As a consequence, the computed energy efficiencies range higher for the bicyclooctanes than for the ferrocenes, up to nearly 0.6 as opposed to nearly 0.5, and the bicyclooctanes fall even further below the “standard” entropy-energy compensation regression line (Figure 12).
Bicyclooctane B5 is computed to bind CB[7] 4-5 kcal/mol more strongly than the tightest-binding ferrocene, F6, as noted above. The difference results from the smaller predicted entropy penalty for B5, 12 kcal/mol, relative to F6, 18 kcal/mol. This difference cannot be directly attributed to the different nonpolar cores, because the cores themselves, guests B and F, are predicted to have very similar entropy losses (Tables 2 and 4). In fact, guests B5 and F6 differ not only in their nonpolar cores but also in their cationic substituents: B5 has a primary ammonium, while F6 has a quaternary ammonium. It is thus of interest that guest B7, which has quaternary ammonium, is predicted to have the same binding entropy as F6. Put differently, replacing the primary ammonium of B5 with the quaternaries of B7 increases the computed entropy loss by about 6 kcal/mol. The greater entropy losses for the bulkier quaternary ammoniums of F6 and B7 appear to result from steric restriction in the narrow portals of CB[7] (although the binding energy is enhanced by 4.6 kcal/mol, minimizing the decrease of ΔGο to only 1 kcal/mol).
Extending the R1 and R2 chains linked to the bicyclooctane core is predicted not to increase affinity for CB[7], as noted above, despite the addition of considerably more positive charge. As shown in Figure 14, the longer guests are predicted to wrap back onto the CB[7] host. The resulting contacts lead to generally stronger van der Waals interactions than for the shorter guests. In addition, the added charges of the long chains lead to very large, favorable Coulombic interactions, but these are largely canceled by unfavorable electrostatic solvation terms. Meanwhile, the greater flexibility of the extended chains in their free state, combined with their tendency to wrap onto the host in the bound state, leads to greater entropic penalties on binding and greater valence energy penalties associated with distortion away from energetically favored trans rotamers. For example, extending both the R1 and R2 substituents of B5 to generate B13 leads to little change in the binding energy, Δ〈U + W〉, but a greater entropy loss, so that the predicted affinity is somewhat lower for the longer B13 guest (Table 4).
IV. DISCUSSION
The present study bears on the potential for design and discovery of new ultra-high affinity guests for CB[7], the reliability of the M2 methodology, and the physical determinants of binding affinity, as now discussed.
A. Designed high-affinity guests for CB[7]
Using a bicyclooctane core in place of the previously studied ferrocene moiety is predicted to yield new guest molecules with extremely high affinity for the CB[7] host. The new guests are predicted to bind CB[7] with somewhat higher affinities than those observed to date for the ferrocene series, and the difference of ~ -6.0 kcal/mol may be genuine, since it is larger than the ~2 kcal/mol root-mean-square deviation of M2 versus experiment for the ferrocene series. On the other hand, extending the cationic chains of these ligands is not predicted to enhance their affinities for CB[7]. This result is unexpected in light of experimental data showing that extended cation chains lead to greater affinities of linear polyamines for the similar CB[6] host34.
B. Validity of the M2 method
The M2 calculations reproduce the chief affinity trends of the ferrocene guests with CB[7] and βCD. This observation supports the utility of the M2 method as a tool for host-guest design. It also supports, though it cannot prove, the validity of the physical interpretations provided by the method. On the other hand, the root-mean-square-deviation relative to experiment of ~2 kcal/mol, is somewhat higher than found in previous applications6,8,35. This might reflect a lack of transferability of the conventional force field parameters used to the metal-containing ferrocene moiety. It seems equally likely, however, that it is broadly representative of the level of accuracy that can be expected from the method at its present stage of development.
The chief potential sources of error in the M2 method deserve note. One is the force field, which yields the potential energy as a function of conformation, U(r). Force field errors may arise from the parameters, such as van der Waals radii and partial charges, assigned to the host and guest. They may also derive from approximations inherent in the force field's functional form, such as the lack of an explicit treatment of electronic polarization. A second source of error is the continuum treatment of the solvent. It is actually somewhat surprising that the M2 method proves to be as accurate as it is, given that it completely neglects the molecular nature of the aqueous solvent. A third source of error is that we have no way of being certain to discover the most stable conformation of a molecule or complex, although we have sought here to minimize this risk by carrying out lengthy searches. A more subtle issue arises from the filtering of duplicate conformations to avoid double-counting. The filtering process requires application of a similarity threshold - a root-mean-square-deviation in Å- below which two conformations are deemed identical. This threshold is still somewhat arbitrary, and shifts within a reasonable range of 0.1 to 0.4Å sometimes cause the computed chemical potential to shift by ~ 1 kcal/mol. Some error may derive from the approximation that the energy wells are, for the most part, harmonic in form, although the mode-scanning part of the procedure should correct for most anharmonicity7. Finally, the use of a simplified version of the implicit solvent model during conformational sampling and of a single-conformation correction with the Poisson-Boltzmann/surface area model might limit accuracy. Depending upon the outcome of further comparisons with experiment, one might wish to mitigate some of these potential problems by the use of more detailed models. For example, the present force field model could be replaced by a polarizable force field, as these become more stable and accepted.
C. Use of host-guest affinity data to test and improve models
More generally, experimental host-guest affinities form a large data set that can be of enormous value for testing and validating not only the M2 method, but also a wide range of computational approaches and models. Force fields and algorithms are routinely tested against pure liquid properties and experimental solvation energies for small organic molecules. However, such data cover only a very limited range of chemistries, especially in relation to the range of compounds that are encountered in medicinal applications. Moreover, modeling the solvation of small molecules arguably is not a stringent or informative test of a computational method. Indeed, a variety of different models perform reasonably well against experimental solvation data, but it is not clear whether these successes bear on the adequacy of the same models for treating complex biomolecular systems. One can also test physical models of binding by comparing with protein-small molecule or protein-protein affinity data, but such tests can be problematic because it is almost impossible to be confident that the calculations have adequately sampled the thermodynamically accessible conformations of the system. Host-guest systems arguably lie in a very useful place between the uninformative simplicity of small molecule solvation and liquid state data, and the excessive computational complexity of proteins. They are sufficiently complex and chemically varied to provide nontrivial and informative tests, yet simple enough to allow thorough conformational sampling so that one can be fairly confident of learning something about one's model and not about convergence problems.
D. Electrostatics and entropy in host-guest and protein-ligand binding
Although the present calculations make certain approximations, as just discussed, they are rooted in a coherent and complete statistical thermodynamic framework. This, combined with their ability to reproduce the experimentally observed affinity trends, suggests that they can provide meaningful insights regarding the physical chemistry of molecular recognition.
A perhaps unexpected observation is that, despite the evident electrostatic complementarity of the cationic guests and the electronegative carbonyl portals of CB[7], electrostatic interactions are not found to provide a significant net driving force for binding. This is because the strong Coulombic attractions between the guests and CB[7] are precisely balanced by the energetic cost of stripping solvating water from the cationic guests and the polar host upon binding. Indeed, artificially making both molecules completely nonpolar has virtually no effect on their computed binding affinity. However, it would be difficult to actually carry out our gedanken experiments in the laboratory, even if one possessed nonpolar molecules having the same shapes as CB[7] and its ferrocene guests, because these large, nonpolar molecules would be virtually insoluble in water. A host must be polar to be water-soluble, but then any guest that it binds must have a complementary pattern of polar groups so that the energy cost of desolvating the host's polar groups can be compensated by attractive Coulombic interactions. In this view, then, polarity affords solubility and binding specificity, but usually little affinity. (However, theory predicts that electrostatics can contribute to affinity when the charges on both molecules are laid out just right36,37.)
The calculations also indicate that the extraordinary affinity of some of the CB[7]-guest systems results from their paying an entropy penalty that is unusually small in relation to the favorable energetics of binding, as indicated by their high energy efficiencies and their falling below the energy-entropy trendline observed for less remarkable host-guest systems. This property is related to the rigidity of CB[7] and its high-affinity guests, but rigidity alone is not enough: the two molecules must also be mutually complementary in their preferred conformations. Other host-guest systems may be equally rigid and therefore lose little entropy on binding, but if there is not a strong binding energy, Δ〈U + W〉, they will still not overcome entropy-energy compensation and their affinity will be unremarkable. Alternatively, two flexible molecules may achieve a highly favorable binding energy because they are free to conform to each other; but their flexibility will lead to a large entropy penalty so, again, they will not overcome entropy-energy compensation and their affinity, again, will not be remarkable. The systems studied here are special because they are highly preorganized into highly complementary conformations.
It is of interest to inquire whether proteins, too, can achieve extraordinary affinity by overcoming entropy-energy compensation. One challenge to achieving this goal comes from the likelihood that a protein - a linear polymer whose 3-dimensional shape is maintained by soft nonbonded interactions - is unlikely ever to be as rigid as a covalently linked ring of rings like CB[7]. Perhaps, however, this challenge could be overcome by a rigid ligand, or one whose natural motions match those of the binding site. We analyze this problem by considering four highly simplified binding models:
In the worst case scenario for maximizing affinity, both molecules are flexible when free but become locked on binding. Consider a receptor whose binding site, in the free state, can adopt any of 10 different conformations with equal probability, so its entropy is Rln 10. Say the free ligand also has 10 equally probably conformations, for an entropy of Rln 10. If, on binding, both the receptor and ligand are locked into a single conformation, for an entropy of Rln 1 = 0, then the resulting entropy change is -2Rln 10.
In the best case scenario, exemplified by the high-affinity CB[7] systems studied here, both the free molecules and their complex possess only one accessible conformation, so the entropy of each species is Rln 1 = 0, so the entropy change on binding is 0.
What if both molecules are flexible, but they retain flexibility after binding? This situation is modeled by considering the free receptor, the free ligand, and the complex all to have 10 different conformations of equal probability. In the complex, the ligand and receptor are envisioned to move in synchrony while remaining bound. The entropy before binding is 2Rln 10, and the entropy after is Rln 10, for a net entropy loss of Rln 10. This is better than the worst case, but not as good as the best one.
Can we reduce the entropy loss on binding to the same flexible receptor by using a rigid ligand? The ligand is now considered to possess only one conformational state, so it locks the receptor, too, into a single conformation upon binding. In this case, the entropy loss is only that of the receptor, Rln 10. This is no better or worse than the previous case in which the flexible ligand retained its flexibility upon binding.
These models are crude; they neglect, for instance, the residual translational motion of the bound ligand in the binding site. However, they make the fundamental point that, if the binding site is flexible, there is an irreducible amount of entropy loss upon binding, which is incurred either by forcing the motions of a flexible ligand to correlate with the motions of the receptor (Case 3), or by locking down the receptor with a rigid ligand (Case 4). Although a more detailed treatment may reveal unforeseen subtleties, it appears at first blush as though a flexible receptor, such as a protein, may be unable to overcome entropy-energy compensation as effectively as a rigid one, such as CB[7]. This analysis also may help explain why, although making a ligand more rigid may be expected to reduce its configurational entropy loss on binding38,39, it often leads to little improvement in affinity40-43.
If there is always a significant entropy penalty for binding a flexible receptor, then it may be difficult for a protein-ligand system to overcome entropy-energy compensation in the manner of some of the CB[7]-guest systems studied here. Presumably, then, a protein-ligand system with very high affinity achieves this by some other means, such as by maximizing the size of the protein-ligand interface1. This view would be consistent with the observation that biotin and avidin are not far from the typical entropy-enthalpy trend for a large number of other protein-ligand systems, as shown with the experimental data in Figure 1. This contrasts with the experimental data for CB[7] with several ferrocene derivatives, which fall well below the corresponding trendline (Figure 2).
Supplementary Material
FIG. 7.
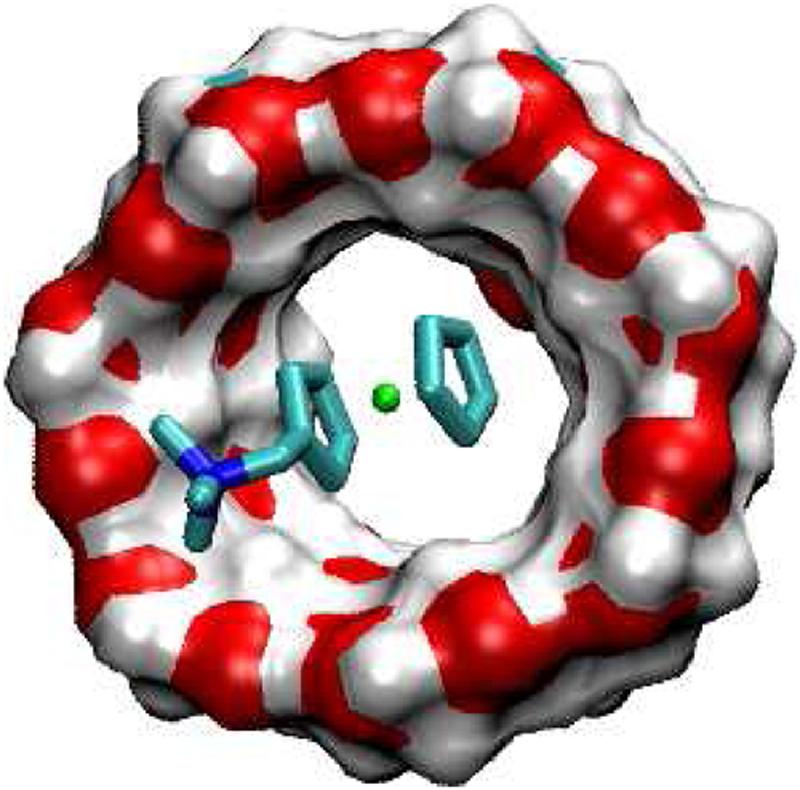
Most stable conformation computed for complex of F3 with βCD.
FIG. 9.
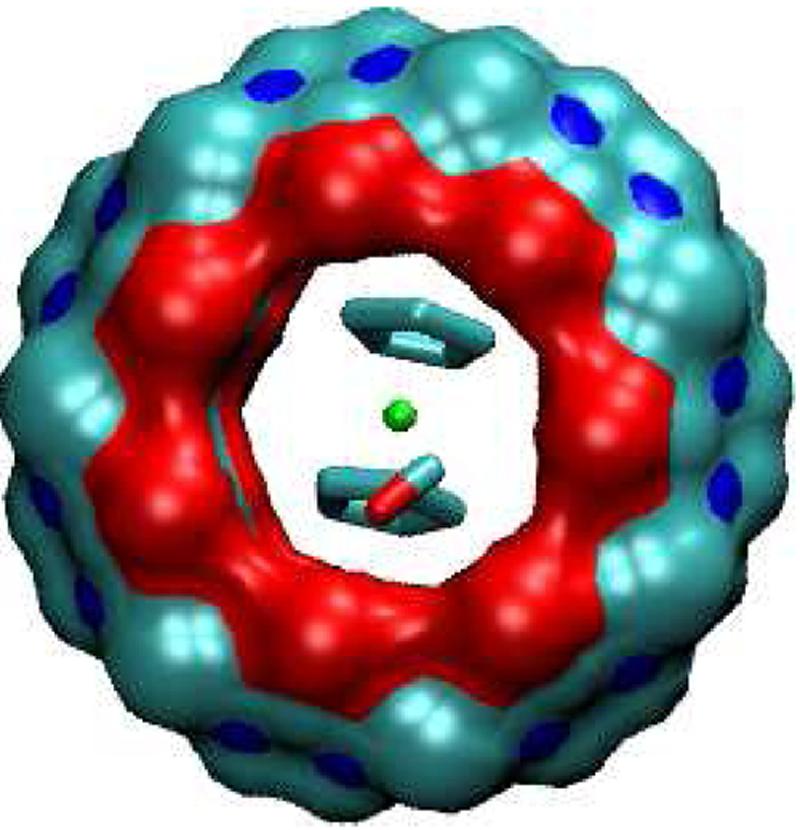
Most stable conformation computed for complex of F1 with CB[7].
V. ACKNOWLEDGEMENTS
We thank Dr. K. Houk for providing the host-guest data displayed in Figure 3. This publication was made possible by grant no. GM61300 from the National Institute of General Medical Sciences of the National Institutes of Health. Its contents are solely the responsibility of the authors and do not necessarily represent the official views of the National Institute of General Medical Sciences. YI thanks the Japan Science and Technology Agency for the support of this work through the Collaborative Development of Innovative Seeds program.
Footnotes
VI. SUPPORTING INFORMATION AVAILABLE The force field parameters used in these calculations are provided in supporting information (SI), as is the complete form of reference 21. This information is available free of charge via the Internet at http://pubs.acs.org/.
References
- 1.Houk KN, Leach AG, Kim SP, Zhang XY. Ang. Chem. Int. Ed. 2003;42:4872–4897. doi: 10.1002/anie.200200565. [DOI] [PubMed] [Google Scholar]
- 2.Inoue Y, Wada T. Adv. Supramolec. Chem. 1997;4:55–96. [Google Scholar]
- 3.Bryantsev VS, Hay BP. J. Am. Chem. Soc. 2006;128:2035–2042. doi: 10.1021/ja056699w. [DOI] [PubMed] [Google Scholar]
- 4.Hay BP, Firman TK. Inorg. Chem. 2002;41:5502–5512. doi: 10.1021/ic0202920. [DOI] [PubMed] [Google Scholar]
- 5.Chen W, Gilson MK. J. Chem. Inf. Model. 2006;47:425–434. doi: 10.1021/ci600233v. [DOI] [PubMed] [Google Scholar]
- 6.Chang C-E, Gilson MK. J. Am. Chem. Soc. 2004;126:13156–13164. doi: 10.1021/ja047115d. [DOI] [PubMed] [Google Scholar]
- 7.Chang C-E, Potter MJ, Gilson MK. J. Phys. Chem. B. 2003;107:1048–1055. [Google Scholar]
- 8.Chen W, Chang C-E, Gilson MK. Biophysical Journal. 2004;87:3035–3049. doi: 10.1529/biophysj.104.049494. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Chen W, Chang C-E, Gilson MK. J. Am. Chem. Soc. 2006;128:4675–4684. doi: 10.1021/ja056600l. [DOI] [PubMed] [Google Scholar]
- 10.Liu S, Rupic C, Mukhpadhayay P, Chakrabarti S, Zavalij PY, Isaacs L. J. Am. Chem. Soc. 2005;127:15959–15967. doi: 10.1021/ja055013x. [DOI] [PubMed] [Google Scholar]
- 11.Jeon WS, Moon K, Park SH, Chun H, Ko YH, Lee JY, Samal S, Selvapalam N, Rekharsky MV, Sindelar V, Sobransingh D, Inoue Y, Kaifer AE, Kim K. J. Am. Chem. Soc. 2005;127:12984–12989. doi: 10.1021/ja052912c. [DOI] [PubMed] [Google Scholar]
- 12.Rekharsky MV, Mori T, Yang C, Ko YH, Selvapalam N, Kim H, Sobransingh D, Kaifer AE, Liu S, Isaacs L, Chen W, Moghaddam S, Gilson MK, Kim K, Inoue Y. Proc. Natl. Acad. Sci. USA. 2007;104:20737–20742. doi: 10.1073/pnas.0706407105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Green NM. Biochem. J. 1963;89:585–591. doi: 10.1042/bj0890585. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Hwang I, Baek K, Jung M, Kim Y, Park KM, Lee DW, Selvapalam N, Kim K. J. Am. Chem. Soc. 2007;129:4170–4171. doi: 10.1021/ja071130b. [DOI] [PubMed] [Google Scholar]
- 15.Chang C-E, Gilson MK. J. Comput. Chem. 2003;24:1987–1998. doi: 10.1002/jcc.10325. [DOI] [PubMed] [Google Scholar]
- 16.Chen W, Huang J, Gilson MK. J. Chem. Inf. Comput. Sci. 2004;44:1301–1313. doi: 10.1021/ci049966a. [DOI] [PubMed] [Google Scholar]
- 17.Chang C-E, Chen W, Gilson MK. Proc. Natl. Acad. Sci. USA. 2007;104:1534–1539. doi: 10.1073/pnas.0610494104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Head MS, Given JA, Gilson MK. J. Phys. Chem. 1997;101:1609–1618. [Google Scholar]
- 19.Polar hydrogen parameter set for CHARMm. Molecular Simulations Inc.; Waltham, MA: [Google Scholar]
- 20.Brooks BR, Bruccoleri RE, Olafson BD, States DJ, Swaminathan S, Karplus M. J. Comput. Chem. 1983;4:187–217. [Google Scholar]
- 21.MacKerell A, et al. J. Phys. Chem. B. 1998;102:3586–3616. doi: 10.1021/jp973084f. [DOI] [PubMed] [Google Scholar]
- 22.MacKerell AD, Jr., Wiókiewicz-Kuczera J, Karplus M. J. Am. Chem. Soc. 1995;117:11946–11975. [Google Scholar]
- 23.Qiu D, Shenkin PS, Hollinger FP, Still WC. J. Phys. Chem. 1997;101:3005–3014. [Google Scholar]
- 24.Gilson MK, Honig B. Prot. Struct. Func. Gen. 1988;4:7–18. doi: 10.1002/prot.340040104. [DOI] [PubMed] [Google Scholar]
- 25.Sitkoff D, Sharp KA, Honig B. J. Phys. Chem. 1994;98:1978–1988. [Google Scholar]
- 26.Gilson MK, Gilson HSR, Potter MJ. J. Chem. Inf. Comput. Sci. 2003;43:1982–1997. doi: 10.1021/ci034148o. [DOI] [PubMed] [Google Scholar]
- 27.Davis ME, Madura JD, Luty BA, McCammon JA. Comput. Phys. Commun. 1991;62:187–197. [Google Scholar]
- 28.Richards FM. Ann. Rev. Biophys. Bioeng. 1977;6:151–176. doi: 10.1146/annurev.bb.06.060177.001055. [DOI] [PubMed] [Google Scholar]
- 29.Quanta. Accelrys, Inc.; San Diego, CA: [Google Scholar]
- 30.David L, Luo R, Gilson MK. J. Comput. Aided Mol. Des. 2001;15:157–171. doi: 10.1023/a:1008128723048. [DOI] [PubMed] [Google Scholar]
- 31.Kairys V, Gilson MK. J. Comput. Chem. 2002;23:1656–1670. doi: 10.1002/jcc.10168. [DOI] [PubMed] [Google Scholar]
- 32.Gilson MK, Honig B. Proc. Natl. Acad. Sci. USA. 1989;86:1524–1528. doi: 10.1073/pnas.86.5.1524. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Hendsch ZS, Tidor B. Prot. Sci. 1994;3:211–226. doi: 10.1002/pro.5560030206. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Rekharsky MV, Ko YH, Selvapalam N, Kim K, Inoue Y. Supramolec. Chem. 2007;19:39–46. [Google Scholar]
- 35.Chen W, Chang C-E, Gilson MK. J. Am. Chem. Soc. 2006;128:4675–4684. doi: 10.1021/ja056600l. [DOI] [PubMed] [Google Scholar]
- 36.Kangas E, Tidor B. J. Chem. Phy. 1998;109:7522–7545. [Google Scholar]
- 37.Lee LP, Tidor B. J. Chem. Phys. 1997;106:8681–8690. [Google Scholar]
- 38.Rao J, Lahiri J, Weis RM, Whitesides GM. J. Am. Chem. Soc. 2000;122:2698–2710. [Google Scholar]
- 39.Burger A, Abraham DJ. Burger's Medicinal Chemistry and Drug Discovery. Wiley Press, University of Michigan; 2003. [Google Scholar]
- 40.de Mol NJ, Catalina MI, Dekker FJ, Fischer MJE, Heck AJR, Liskamp RMJ. ChemBioChem. 2005 [Google Scholar]
- 41.Dekker FJ, de Mol NJ, Bultinck P, Kemmink J, Hilbersa HW, Liskamp RMJ. Bioorganic & Medicinal Chemistry. 2003;11:941–949. doi: 10.1016/s0968-0896(02)00536-9. [DOI] [PubMed] [Google Scholar]
- 42.Burke TR, Barchi JJ, George C, Wolf G, Shoelson SE, Yan X. J. Med. Chem. 1995;38:1386–1396. doi: 10.1021/jm00008a017. [DOI] [PubMed] [Google Scholar]
- 43.Plake HR, Sundberg TB, Woodward AR, Martin SF. Tetrahedron Letters. 2003;44:1571–1574. [Google Scholar]
- 44.Chen X, Lin Y, Liu M, Gilson MK. Bioinformatics. 2002;18:130–139. doi: 10.1093/bioinformatics/18.1.130. www.bindingdb.org. [DOI] [PubMed] [Google Scholar]
- 45.Chen X, Liu M, Gilson MK. Biopolymers/Nucleic Acid Sci. 2002;61:127–141. doi: 10.1002/1097-0282(2002)61:2<127::AID-BIP10076>3.0.CO;2-N. www.bindingdb.org. [DOI] [PubMed] [Google Scholar]
- 46.Liu T, Lin Y, Wen X, Jorissen RN, Gilson MK. Nucl. Acid Res. 2007;35:D198–D201. doi: 10.1093/nar/gkl999. www.bindingdb.org. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Chilkoti A, Stayton PS. J. Am. Chem. Soc. 1995;117:10622–10628. [Google Scholar]
- 48.Rekharsky MV, Inoue Y. Chem. Rev. 1998;98:1875–1917. doi: 10.1021/cr970015o. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


