Statistical learning of phonetic categories: Insights from a computational approach

Abstract

Recent evidence (Maye, Werker & Gerken, 2002) suggests that statistical learning may be an important mechanism for the acquisition of phonetic categories in the infant's native language. We examined the sufficiency of this hypothesis and its implications for development by implementing a statistical learning mechanism in a computational model based on a Mixture of Gaussians (MOG) architecture. Statistical learning alone was found to be insufficient for phonetic category learning—an additional competition mechanism was required in order to successfully learn the categories in the input. When competition was added to the MOG architecture, this class of models successfully accounted for developmental enhancement and loss of sensitivity to phonetic contrasts. Moreover, the MOG with competition model was used to explore a potentially important distributional property of early speech categories -- sparseness -- in which portions of the space between phonetic categories is unmapped. Sparseness was found in all successful models and quickly emerged during development even when the initial parameters favored continuous representations with no gaps. The implications of these models for phonetic category learning in infants are discussed.

Infants face a difficult problem in acquiring their native language because the acoustic/phonetic variability in the input far exceeds the limited number of distinctive differences that define language-specific phonemes. How do infants attend to the relevant information that distinguishes words? Recent evidence suggests that phonemic categories may be induced, in whole or in part, by a rapid statistical learning mechanism that is sensitive to the distributional properties of phonetic input (Maye, Werker & Gerken, 2002; Maye, Weiss & Aslin, 2008). This evidence suggests that the detailed frequency-of-occurrence of tokens along continuous speech dimensions plays a crucial role in the formation and modification of phonemic categories.

The present paper describes a computational model of statistical speech category learning that examines the necessary and sufficient mechanisms needed to account for known empirical data from infants, and the implications of those mechanisms for early speech categories. We demonstrate that statistical learning alone is insufficient: competition is also required. However, once this feature is added to the model, it can account for a number of developmental trajectories in speech category learning. Finally, we examine the possibility that early speech categories are independent and sparsely distributed; that is, they do not fully cover all values along a phonetic dimension.

Statistical Learning and Development

The classic view of speech perception in both adults (cf., Liberman, Harris, Hoffman & Griffith, 1957) and infants (cf., Eimas, Siqueland, Jusczyk & Vigorito, 1971; see Jusczyk, 1997) is that stop consonants are perceived categorically. However, more recent evidence confirms within-category sensitivity in both adults (Pisoni & Tash, 1974; Carney, Widen & Viemeister, 1979; Miller, 1997) and infants (Miller & Eimas, 1996; McMurray & Aslin, 2005). Nevertheless, adults and infants have a bias to group acoustically similar sounds into categories, and these categories begin to match their native language by 6 to 12 months of age. This matching process can take a number of forms. For some dimensions infants are initially able to distinguish a number of contrasts not found in their native language followed by a loss of the unnecessary contrasts (Werker & Tees, 1984; see Werker & Curtin, 2005 and Kuhl, 2004 for recent reviews). For others, contrasts are initially indiscriminable and enhanced over development (Eilers & Minifie, 1975; Eilers, Wilson & Moore, 1977).

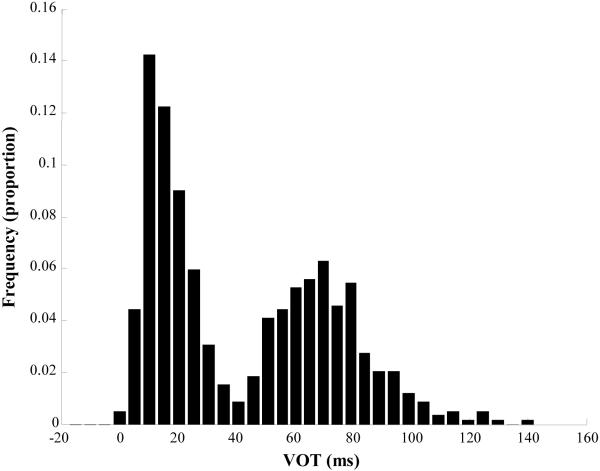
Speech exemplars tend to cluster statistically along continuous acoustic/phonetic dimensions. For example, Figure 1 shows measurements of Voice Onset Times (VOTs: distinguishing voiced from voiceless sounds) from English speakers, illustrating two clusters corresponding to voiced and voiceless categories (Lisker & Abramson, 1964; Allen & Miller, 1999). These clusters approximate Gaussian distributions, one centered at 0 ms (voiced) and one at 60 ms (voiceless). While the incidence of tokens near 0 and 60 ms is frequent, few are attested at 30, 100, and -20 ms.. Similar clustering is seen for the cues to vowels (Peterson & Barney, 1951; Hillenbrand, Getty, Clark & Wheeler, 1995) and approximants (Espy-Wilson, 1992).

Figure 1.

The bimodal distribution of voice-onset-time VOT in English. Shown is relative frequency as a function of VOT collapsed across all three places of articulation. Two clusters are clearly visible: one centered around 10-15 ms (Voiced) and one centered around 65-75 ms (Voiceless). Data are from Allen & Miller (1999).

This suggests that the frequency of occurrence of tokens along a given speech dimension could allow listeners to induce phonetic categories from the clusters of tokens in the input. This has been explicitly tested behaviorally with adults (Maye & Gerken, 2000) and infants (Maye et al., 2002, 2008). Listeners who were exposed to a series of speech sounds for which the frequency of any VOT was distributed bimodally (characteristic of two categories) were able to discriminate two exemplars that straddled the category boundary, whereas listeners exposed to a unimodal (single category) distribution could not. Thus, a few minutes of exposure to statistically structured input biases perception in a way that is consistent with statistical learning.

Existing Models

A variety of computational models implement category learning via clustering algorithms. Connectionist models (Elman & Zipser, 1986; Guenther & Gjaja, 1996; Nakisa & Plunkett, 1998; see also McCandliss, Fiez, Protopapas, Conway & McClelland, 2002) have demonstrated the feasibility of input-driven learning mechanisms, but such models incorporate other features that make it difficult to isolate statistical learning. Elman and Zipser (1986) used nonlinear activation functions and competition (dimensionality reduction); Guenther and Gjaja (1996) employed topographic competition; and Nakisa and Plunkett (1998)'s genetic algorithm produced an array of specialized architectures and learning rules. In these models, statistical learning is one of many mechanisms involved in speech category development.

To better isolate the clustering mechanism, we simulated statistical learning in a model that uses a simple architecture; makes few theoretical assumptions; and only adds constraints when needed to account for the data. Many models start with a theoretical paradigm (e.g., connectionism or dynamical systems theory), and ask whether the principles of this paradigm are sufficient to solve a problem. Our goal was to start with the computational problem the system is trying to solve (learning the mapping between continuous inputs and categories), and use current theory (distributional learning) to arrive at an architecture suited to that problem.

This led us to use the Mixture of Gaussians (MOG) approach. This is a classic tool from statistics and computer science used for estimating the parameters of a set of probabilistic clusters (Titterington, Smith & Makov, 1985). While this requires certain architectural assumptions, these are made with respect to the problem being solved, not due to any paradigmatic approaches to development. This approach allows us to isolate and evaluate statistical learning as a mechanism for forming categories.

The Mixture of Gaussians Model

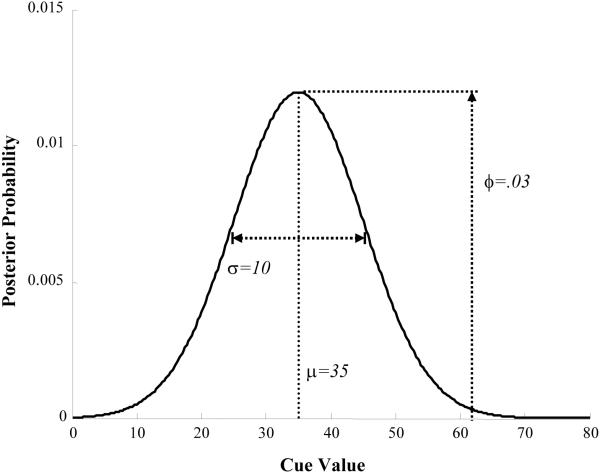
The MOG approach to speech categorization estimates the probability ( M[VOT] ) of obtaining any individual cue-value (e.g., a specific VOT) as the sum of probabilities from some number (K) of overlapping Gaussians, each with some prior likelihood. The model represents each potential or actual category (e.g. voiced or voiceless) with a single Gaussian (G_i) that has a set of parameters that describe the frequency of that category (ϕ), its location in the input-space (μ), and its variability in the input-space (σ) (see Figure 2, Equation 1 for an example along the VOT dimension).

Figure 2.

The parameters of the Gaussian distributions used to represent each speech category. The mean (μ) refers to the location (in cue-space) of the prototype, the SD (σ), refers to the width of the category, and the height (ϕ) to its frequency (or posterior probability).

$$G_i\left(\mathit{vot}\right)={\varphi }_i\frac{1}{\sqrt{2\pi {{\sigma }_i}^2}}\exp \left(\frac{{(\mathit{vot}-{\mu }_i)}^2}{2{{\sigma }_i}^2}\right)$$ (1)

Each Gaussian computes the likelihood of hearing a specific VOT if that category was the intended production. The MOG estimates the likelihood of a given input (e.g. a specific VOT) as the sum of the likelihood that that input was obtained from each of the K Gaussians.

$$M\left(\mathit{vot}\right)=\sum _{i=1}^K{G}_i\left(\mathit{vot}\right)$$ (2)

For example, the probability of obtaining a VOT of 40 ms from a mixture of K=2 Gaussians is the sum of the likelihood that it was generated by either category: the low probability that it arose from the voiced category (e.g. μ=0, σ=10), plus the higher probability that it arose from a voiceless category (e.g. μ=50, σ=20). Category membership is simply a matter of determining which Gaussian in the mixture was most likely for a given input.

The MOG approach can fit any continuous cue that forms clusters in the input, and it only assumes that each input category creates a different probability distribution. Speech category learning is simply a matter of estimating the number of categories and their parameters from the input. Multiple contrasts (e.g., voicing and place) can be learned by estimating the parameters of multiple mixtures simultaneously, and Toscano and McMurray (in press) have shown that this framework can be extended to weight multiple cues for the same category. The MOG assumes that the psychological representation of such categories is Gaussian. This is not unreasonable, given the prevalence of Gaussian tuning curves in auditory cortex, and the fact that speech categories exhibit considerable gradiency within categories that takes a more or less Gaussian form (Miller & Volaitis, 1989; McMurray, Tanenhaus & Aslin, 2002).

The MOG approach has been used by De Boer and Kuhl (2003) demonstrate that a MOG can learn a small number of vowel categories, and that infant-directed speech (Kuhl, Andruski, Chistovich & Chistovich, 1997) can facilitate acquisition. Their model, however, learned with Expectation Maximization (EM), which employs a complex, multi-stage procedure and estimates parameters after receiving a large batch of input. Infants, however, must learn iteratively (i.e., learning occurs after each input). Additionally, the model was incapable of learning the number of categories needed for a given contrast (the number was specified a priori). Since different languages have different numbers of categories, the model must be able to determine this on the basis of the input. Thus, we developed an iterative approach to learning that was simple, plausible, and capable of learning the correct number of categories to fit the native language structure.

The Learning Algorithm

Our learning algorithm is based on Maximum Likelihood Estimation (MLE) by stochastic gradient descent. MLE is a standard way to estimate the parameters of any function by maximizing the likelihood of the parameters given the data. Gradient descent is a general optimization technique which virtually all connectionist learning rules (as well as classic learning theory) implement in some way (see Barto, 1995, for an overview). Gradient descent simply adjusts parameters of the likelihood function (equation 2) along the derivative of the likelihood function (with respect to the parameter). When the derivatives become 0, no further change in the parameters is possible - the function has reached maximum likelihood. This can be a local maximum (for example if the model overgeneralized to a single category), or a global maximum, the best parameter-set for the data.

Our model uses gradient descent to adjust μ, σ, and ϕ as it encounters individual VOTs (or other cues). This, then maximizes the likelihood of the input given the particular parameter-set. This allows us to model learning, as it happens, in the moment (see McMurray, Horst, Toscano & Samuelson, in press, for a theoretical discussion). Thus, our learning rules are as follows:

$$\Delta {\varphi }_{\mathrm{i}}={\eta }_{\varphi }\cdot \frac{{\mathrm{G}}_{\mathrm{i}}\left(\mathrm{vot}\right)}{\mathrm{M}\left(\mathrm{vot}\right)}$$ (3)

After updating ϕ, the vector of all ϕ's is normalized to sum to 1 since ϕ represents a prior probability which must be between 0 and 1.

$$\Delta {\mu }_i={\eta }_{\mu }\cdot \left(\frac{G_i\left(\mathit{vot}\right)}{M\left(\mathit{vot}\right)}\right)\frac{(\mathit{vot}-{\mu }_i)}{{\sigma }_i^2}$$ (4)

$$\Delta {\sigma }_i={\eta }_{\sigma }\cdot \left(\frac{G_i\left(\mathit{vot}\right)}{M\left(\mathit{vot}\right)}\right)\left({\sigma }_i^{-3}{(\mathit{vot}-{\mu }_i)}^2-{\sigma }_i^{-1}\right)$$ (5)

In all three equations, η is a learning rate parameter and μ_i, σ_i and ϕ_i represent the parameters of Gaussian i (G_i). As before M(vot) is the sum of all G_i's. These learning rules are applied to each Gaussian after each input. By updating each parameter in small increments (η), the system gradually moves to a set of Gaussians whose parameters are more optimal for the dataset. After sufficient learning, these parameters will typically be truly optimal (a global minimum). However, occasionally the model will converge on a local minimum in which the parameters are not optimal, but cannot be further improved. In all of the simulations that were run, a local minimum were only seen when the model incorrectly estimated the the number of Gaussian with non-zero ϕ's: either over-generalizing (too few Gaussians) or under-generalizing (too many).

The model was trained as follows. First, an array of K Gaussians is randomly generated to serve as the initial state. K is relatively high (e.g., 10-20) since the model does not know how many categories (Gaussians) it will need. The μs of these Gaussians are randomly selected, σs are set to a small constant value¹, and ϕs to 1/K. After initializing the model, it is exposed to a set of inputs. On each generation, a single value of a speech cue is selected. For these simulations, VOT was generally used, but this is arbitrary—a MOG can be applied to any continuous cue. These cue values are randomly generated from a bimodal (2-category) Gaussian distribution (whose means and standard deviations are based on the means and standard deviations reported by speech production measurements such as Lisker & Abramson, 1964). After this cue-value is selected, the three parameters (ϕ, μ and σ) of each of the K Gaussians are adjusted according to the learning rules in Equations 3-5. This is repeated until the model converges on a solution (the parameters reach asymptote), usually several thousand iterations².

Tests of the Model

Simulation 1: Statistical learning requires competition

The first simulations determined if these learning rules were sufficient to learn speech categories. 100 models were initialized (parameters in Table 1, Sim 1) and trained for 100,000 generations on a random sampling from a dataset based on Lisker and Abramson's (1964) estimates of English VOTs. We then determined if (1) the model converged on the correct number of categories (i.e., the frequency parameter, ϕ, was much greater than .01 for the correct number of Gaussians) and (2) if those categories approximated the training distribution (had correct values for μ and σ).

Table1.

Initial parameters for simulations.

	Starting State				Learning Rates			Input Language
Sim. #	K	σ	μ	ϕ	η μ	η σ	η ϕ	μ	σ	ϕ
1a: learning	25	2	Rand.	1/K	1	1	.0001	[0 50]	[5 15]	[.5 .5]
1b: learning + competition	25	2	Rand.	1/K	1	1	.0001	[0 50]	[5 15]	[.5 .5]
2: Pruning	10	5	Rand.	1/K	.2	.2	.0005	[0 50]	[5 10]	[.5 .5]
3: Enhancement	10	20	Rand.	1/K	.2	.2	.0005	[0 50]	[20 20]	[.5 .5]
4: Sparseness	4-50	1-60	Rand.	1/K	.2	.2	.004	[0 50]	[12 12]	[.5 .5]

None of the models converged on a reasonable solution, averaging 11.9 (SD=1.8) active Gaussians, and no model reached the true two-category solution. Thus while the model suppressed some Gaussians (K was 25), it never arrived at the correct number. Nonetheless, the model could have approximated the training distribution across a set of Gaussians (a distributed representation). To test this, each active Gaussian was categorized as belonging to either the voiced or the voiceless category (which ever it was closest to), and the parameters of the corresponding sets of Gaussians were analyzed to determine if they collectively approximated the input. First, we considered whether ϕ was estimated correctly. Since multiple Gaussians were above-threshold for each category, the sum of their ϕs should be .5. However, only 57 of the 100 models were between .45 and .55. μ and σ were equally inaccurate. The average RMS difference of each Gaussian's μ from the closest input category was 6.14 ms of VOT (SD=.9), and for σ this value was 3.68 ms (SD=.9). Thus, even a representation distributed across multiple Gaussians did not match the input distribution.

To improve the model, a simple change was introduced: winner-take-all competition. The model used the same learning rules, with the exception that ϕ was changed only for the single Gaussian that had the highest likelihood for the current input. This is psychologically plausible, since only the frequency of one category should be adjusted for a given input. Computationally, it approximates Rumelhart and Zipser's (1986) competitive learning, which McMurray and Spivey (1999) applied to bimodal Gaussian distributions.

We implemented 100 new models and found that 97 arrived at the correct two-category solution. For these 97 models, ϕ was always between .45 and .55 for the two categories, μ averaged .52 ms of VOT (SD=.28) from that of the closest input category, and σ averaged .69 ms from that of the nearest input category (SD=.63). Thus, competition allowed the MOG to learn the correct number of categories and to align them nearly perfectly with the input.

The discreteness of winner-take-all competition, however, may oversimplify what is most likely an underlyingly continuous process. Thus, we attempted three additional competition schemes: simple linear normalization, quadratic normalization, and the softmax function (with and without winner-take-all). As Table 2 shows, without competition, quadratic normalization and softmax outperformed the original implementation. However, when competition is included, these two schemes offered no additional benefit over the original model. Thus, this form of statistical learning is only successful with competition, and, of the competition methods examined, winner-take-all seems to yield the best performance.

Table 2.

Average number of categories after 100,000 generations of learning as a function of competition rules. Numbers in parentheses are standard deviations. Numbers on second line refer to the proportion (of 100 simulations) which correctly extracted two categories.

	Implementation of ϕ (frequency)
	ϕ (original)	$\frac{{\varphi }_{\mathrm{i}}}{\underset{\mathrm{j}\in \mathrm{k}}{\Sigma }{\varphi }_{\mathrm{j}}}$ (normalized)	$\frac{{{\varphi }_{\mathrm{i}}}^2}{\underset{\mathrm{j}\in \mathrm{k}}{\Sigma }{{\varphi }_{\mathrm{j}}}^2}$ (quadratic normalized)	$\frac{\exp \left(\mathrm{T}{\varphi }_{\mathrm{i}}\right)}{\underset{\mathrm{j}\in \mathrm{k}}{\Sigma }\exp \left(\mathrm{T}{\varphi }_{\mathrm{j}}\right)}$ (softmax)
No competition	11.9 (1.8) 0%	10.6 (2.3) 0%	3.8 (1.3) 16%	3.5 (1.5) 33%
Winner take all	1.97 (.17) 97%	1.99 (.1) 99%	1.93 (.26) 93%	1.89 (.31) 89%

A number of unsupervised connectionist architectures show the same property. Competitive Hebbian learning (e.g. Rumelhart & Zipser, 1986) uses winner-take-all competition; Hebbian Normalized Recurrence uses quadratic normalization and cannot learn speech categories without it (McMurray et al., in press); and self-organizing feature maps (Guenther & Gjaja, 1992) employ a topographic excitation/inhibition rule. These architectures buttress the current point: competition is required for distributional category learning.

Modeling the Developmental Timecourse

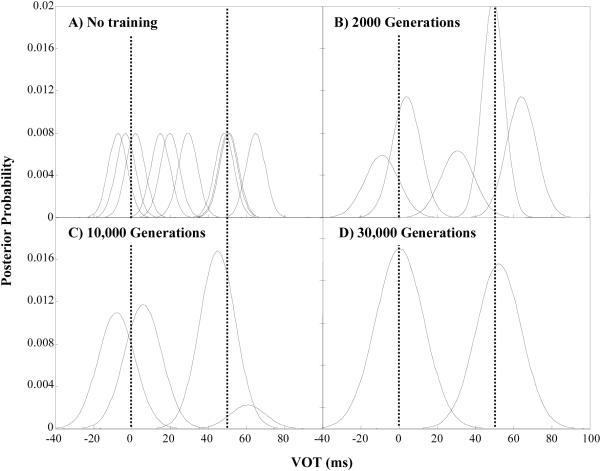
Using the hybrid model (learning + competition) we now ask whether it accounts for the developmental timecourse of phonetic category formation. Figure 3 shows a characteristic run of the model. Over the course of development, unnecessary Gaussians are eliminated and the remaining ones adjust to fit the input from the training distribution. Thus, at 2,000 training generations (Panel B), the model has a large number of categories that are not aligned to the training data. At this point, any two VOTs are likely to fall under different categories and be easily discriminable. However, after 30,000 generations (Figure 3D), the model successfully represents the input and many (within-category) contrasts will fall under the same Gaussian and be indiscriminable.

Figure 3.

A single MOG over the course of training on a distribution with means of 0 and 50 and equal standard deviations of 15. Dashed vertical lines represent the means of the two training categories. A) With no input, all K (8) Gaussians are equally likely. B and C) After a few thousand exposures, the model suppresses some of the unnecessary Gaussians, until D) by the end of training, only the two correct Gaussians remain.

This simplistic analysis assumes that infants only discriminate tokens that fall completely into different categories. However, early in development, inputs may fall under a number of overlapping categories. Discrimination could occur for differences between any of these Gaussians. We developed a discrimination measure to account for this. Each of the two VOTs that were to be compared were converted to K-length vectors of the probabilities of each Gaussian (category). The RMS distance of these vectors was used to compare the two VOTs in “category-space”. A small RMS would arise if baseline and comparison stimuli are represented with a similar set of categories. On the other hand, a large RMS indicates largely different sets of categories.

Simulation 2: Pruning

Many phonetic dimensions exhibit an overgeneration/pruning pattern over the course of development: infants are initially sensitive to a wide range of phonetic contrasts, and lose sensitivity to contrasts that are not used (e.g. Werker & Tees, 1984). To model this, we exposed 30 models to the Lisker and Abramson (1964) distribution of English VOTs for 30,000 epochs using the parameters described in Table 1 (Simulation 2). They were tested every 500 epochs on three VOT contrasts: 0 vs. 40 ms (tokens from opposite categories), 30 vs. 70 ms (a within-category difference that should be lost), and 50 vs. 90 ms (still within-category, but the difference is between a prototypical and non-prototypical token; e.g., Miller & Eimas, 1996).

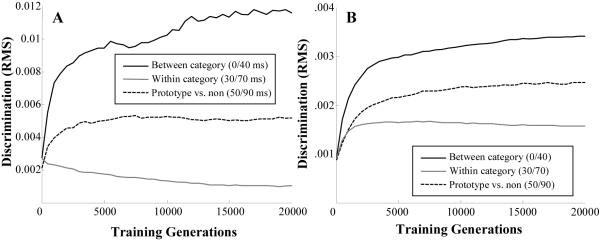
Figure 4A shows discrimination performance of the model (RMS) over the course of training. Initially, the model is equally good at all three. Over the course of training, between-category discriminability increases, while within-category discrimination is lost. Discriminability between prototype/non-prototype distinctions also increases (as the model extracts the structure of the category), but never approaches between-category discriminability. Thus, the model starts with some ability to discriminate all three contrasts and loses the ones it does not need.

Figure 4.

Changes in the RMS discrimination metric over the course of training. Models were tested every 500 generations on three comparisons: discrimination between 0 and 40 ms tokens that crossed the category boundaries (black lines), discrimination between the 30 and 70 ms tokens in the same category (gray lines), and discrimination between a prototypical (50 ms) and a non-prototypical (90 ms) exemplar (dashed lines). A) The average of 30 models that started with small σ's and were given as input the distribution of VOT in English. B) The average of 30 models that started with large σ's and were given as input the highly overlapping distribution of exemplars that simulate English fricatives.

Simulation 3: Enhancement

A small number of speech contrasts (e.g. s/z and f/θ, Eilers & Minifie, 1975; Eilers, Wilson & Moore, 1977) show developmental enhancement: infants initially lack the ability to discriminate a meaningful speech contrast and develop it later.

To simplify this problem to a single dimension, we assumed that the underlying cue for fricative discrimination was sensitivity to the spectral mean of the frication noise. Since these spectral-mean detectors have Gaussian tuning curves, and many frequencies are present at once for a fricative, the starting categories (σ_initial) and statistical distributions are quite broad. Thirty additional simulations were run using a hypothetical training distribution based on these estimated spectral means. These simulations were identical to the prior ones for VOT except that the model's σs (σ_initial) started out broad (σ=20), and the distributions of the input were highly overlapping (Table 1, sim 3).

Again the model started with relatively equal abilities to discriminate the three contrasts (Figure 4B). As in the previous simulation, the between-category contrast was enhanced over the course of learning, as was the contrast between the prototypical and non-prototypical exemplars. In addition, the within-category contrast was enhanced slightly. While this seems counterintuitive, if we assume that within-category contrasts are difficult to discriminate in adulthood, this upward trend would imply that everything is indiscriminable early.

Simulation 4: Sparseness

The MOG model can account for the developmental trends in speech categorization along several different acoustic/phonetic dimensions. However, it also provides novel insights about development. One non-obvious implication of this model is that infants do not learn category boundaries; rather, they learn the distribution of exemplars that define a category. Since each category is defined independently of any others they are not required to completely encompass the phonetic space, and there may be regions of the phonetic space that are not mapped to any category (a gap).

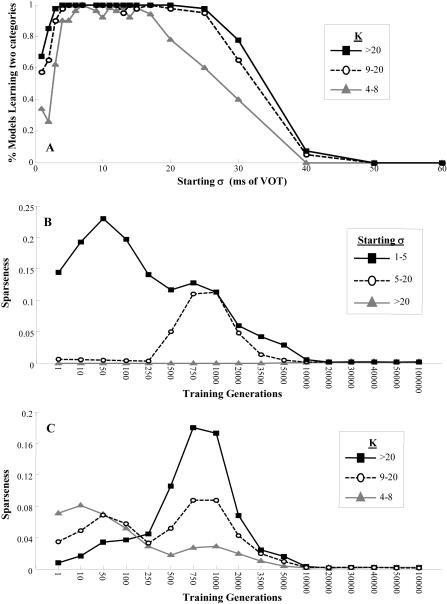
McMurray and Aslin (2005) provided evidence that is suggestive of such a sparse representation. After being exposed to a series of words with syllable-initial VOTs near 3-4 ms, infants discriminated them from tokens with VOTs near 12 ms (and these were not different from 40 ms). This could be explained by a category boundary between 3-4 and 12 ms, though there is no evidence for such a boundary in any language or age group. Alternatively, there may be no category at all in the middle region of the VOT dimension. To test this conjecture, a series of simulations evaluated the amount of input space that was uncategorized over the course of learning. Since this sparseness value is likely to be related to the number of categories available to fill this space (K), and to the width of the initial categories (σ_initial), a range of 21 σs (from 1-60) and 13 Ks (from 4 to 50) were selected. Fourteen models were trained with each combination of these parameters (Table 1, Simulation 4).

As in the prior simulations, the number of categories learned (i.e., ϕ > .01 after training) was used to measure success. Both K and σ_initial were related to success. While the model was successful over a large range of σs, it tended to fail when σ_initial exceeded 25 (Figure 5A), half the distance between the category means (50 ms). In a sense, it was easier for the model to work from small to large categories than to divide initially large categories. Large Ks could mitigate this effect, but not eliminate it: even with K=50, no model was able to learn when σ_initial was greater than 40.

Figure 5.

Results of Simulation #4: Sparseness. A) The effect of starting σ and K on the probability of success (learning the correct 2-category solution). B) Sparseness coefficient, SC (the proportion of the input space not mapped onto a category) over the course of training for small, medium and large initial σ's. C) SC over the course of training for small, medium and large values of K.

To estimate the amount of input space that the model left uncategorized between 0 to 50 ms (the two prototype VOTs), we computed a sparseness coefficient (SC). At each VOT, the posterior probabilities of each of the K Gaussians was computed. If any of these was higher than 10% of the maximum posterior³, that point was said to have been categorized, otherwise it was uncategorized. The SC was the percentage of these 51 VOTs (between 0 and 50 ms) that were left uncategorized.

Figure 5B displays the SC as a function of training epochs and starting σ. Not surprisingly, models starting with large σs were not sparse—these wide categories encompassed most of the cue-space. Also not surprisingly, small initial σs (1-4) yielded early sparseness that gradually decreased. Interestingly, however, medium σs (5-20) showed an initial lack of sparseness, followed by a rapid increase between 250 and 1000 generations, and finally a decrease to complete representations. Most of the models with large σs (71%) failed at learning the input (compared to 98% and 76% for medium and small σs, respectively), implying that sparseness arises naturally for most of the successful starting states.

The same pattern was seen with respect to K (Figure 5C). Ks greater than 20 had quite complete representations initially, while medium and small Ks started out sparser. However, all Ks showed an increase (and decrease) in sparseness between 250 and 3500 generations. Moreover, the largest increases occurred for the largest values of K. As before, this increase in sparseness appeared to be related to success: large Ks were associated with the greatest success rate (83%) compared to medium (79%) and small (69%) Ks. Thus, again, optimal starting parameters led (developmentally) to sparse representations of the input, even where the optimal K led to an initially complete representation.

A hierarchical logistic regression was used to determine if sparse representations led to successful learning. Success was regressed against K, σ_initial, and SC (between 250 and 3000 generations). In the first step of the regression, significant main effects of both σ_initial (B=-.105, Wald(1)=815.2, p<.001) and K (B=.04, Wald(1)=91.2, p<.001) were found. Here, σ_initial was inversely correlated with success (lower σs led to greater success), while K was positively correlated. In the second step, the K × σ interaction was significant (B=-.002, Wald(1)=48.4, p<.001): higher Ks allowed the model to overcome larger σs. In the third step, SC was added and was highly significant, over and above the other two factors (χ²_change(1)=67.4, p<.0001; B=14.2, Wald(1)=43.5, p<.0001). Thus, while K and σ influenced sparseness, SC had a positive effect on success beyond that of K and σ (and their interaction). Models that arrived at sparse representations were more likely to succeed after further input than those that did not.

Conclusions

The MOG approach to the statistical learning of speech categories highlights a number of important points. First, statistical learning is insufficient to accomplish the task: competition of some kind is required. Competition is a property of many models in many domains, including unsupervised connectionist architectures and models of adult word recognition (McClelland & Elman, 1986; Luce & Pisoni, 1998). Moreover, once competition is incorporated into the model, it accounts for both developmental trajectories observed empirically: overgeneration/pruning and enhancement. Here, the specific trajectory does not arise from differences in developmental mechanisms, but rather from differences in how the cues are perceived and in their statistical distributions.

An alternative to the competition/distributional learning account presented here might make sole use of the counts of each VOT. Such an alternative would simply track the frequency of individual VOTs, perhaps recording these counts by warping perceptual space. However, for this set of frequency statistics to create a set of categories, a decision criterion must be employed. This or any other decision process would invariably involve competition. As a result, we agree with Remez (2005)—simple counts of token frequency may not be sufficient for category learning. However, across a range of architectures (the MOG as well as the connectionist architectures discussed), competition can transform these counts into useful categories.

Second, the MOG model implies that infants are not learning phonological distinctions (e.g., voicing), but rather that the process of category acquisition is one in which isolated regions of these dimensions are gradually grouped together. Categories are independent of one another and do not need to completely encompass a given dimension (at least early in learning). Our simulations demonstrate that even models that do not start out sparse go through a sparse stage and sparseness is correlated with later success. By not categorizing certain regions of the input (typically the more ambiguous regions), the model is, in a sense, waiting for more data before committing to a mutually exclusive category structure⁴.

Finally, the implications of sparseness suggest a different understanding of classic data concerning the seemingly counterintuitive ability of young infants to discriminate non-native phonetic contrasts. Colloquially, this ability is often described as infants “having” non-native categories. However, the MOG model suggests that discrimination could also occur when one input is categorized and one falls into a sparse region of the space (no category).

This computational work provides further evidence for the plausibility of unsupervised learning of speech categories via a statistical learning mechanism. Our implementation suggests that statistical learning alone is not sufficient for robust learning. However, when combined with another core mechanism (competition), the MOG yields not only successful data-driven learning that approximates the developmental timecourse, but also novel insights about the sparse nature of early speech categories.