Modulation of leg muscle function in response to altered demand for body support and forward propulsion during walking

Abstract

A number of studies have examined the functional roles of individual muscles during normal walking, but few studies have examined which are the primary muscles that respond to changes in external mechanical demand. Here we use a novel combination of experimental perturbations and forward dynamics simulations to determine how muscle mechanical output and contributions to body support and forward propulsion are modulated in response to independent manipulations of body weight and body mass during walking. Experimentally altered weight and/or mass was produced by combinations of added trunk loads and body weight support. Simulations of the same experimental conditions were used to determine muscle contributions to the vertical ground reaction force impulse (body support) and positive horizontal trunk work (forward propulsion). Contributions to the vertical impulse by the soleus, vastii and gluteus maximus increased (decreased) in response to increases (decreases) in body weight; whereas only the soleus increased horizontal work output in response to increased body mass. in addition, soleus had the greatest absolute contribution to both vertical impulse and horizontal trunk work, indicating that it not only provides the largest contribution to both body support and forward propulsion, but the soleus is also the primary mechanism to modulate the mechanical output of the leg in response to increased (decreased) need for body support and forward propulsion. The data also showed that a muscle’s contribution to a specific task is likely not independent of its contribution to other tasks (e.g., body support versus forward propulsion).

Introduction

Determining the functional roles of individual muscles during activities such as walking has been the focus of several recent studies (e.g., Neptune et al. 2001; Anderson and Pandy 2003; Gottschall and Kram 2003; Neptune et al. 2004; Stewart et al. 2007; McGowan et al. 2008). By understanding the relative contribution of specific muscles to the various tasks performed during walking (e.g., body support, forward propulsion or leg swing), we have gained important insight into the neuromotor control of walking. To date, the majority of these studies have focused on determining muscle function during steady-state walking (e.g., Neptune et al. 2001; Anderson and Pandy 2003; Gottschall and Kram 2003; McGowan et al. 2008). However, activities of daily living often require tasks such as carrying a load, accelerating, or walking on an incline which alter the mechanical energetic demands on the musculoskeletal system. Understanding how the nervous system modulates neuromotor patterns and mechanical outputs to meet changes in energetic demands may help researchers develop more effective rehabilitation strategies and prosthetic/orthotic devices that improve impairments caused by lower limb disabilities.

In a recent study, we examined the functional roles of the plantar flexors during walking using a novel experimental design that independently manipulated body weight and/or body mass via combinations of added trunk loads and body weight support (McGowan et al. 2008). The rationale for that study was that the activity of muscles which contribute to body support would be sensitive to changes in body weight, while the activity of muscles that contribute to forward propulsion would be sensitive to changes in body mass. Based on the analysis of electromyographic (EMG) activity, we concluded that both the gastrocnemius (GAS) and soleus (SOL) provide body support and that SOL is the primary contributor to forward propulsion (McGowan et al. 2008). A necessary assumption in our previous study and other similar perturbation analyses (e.g., Gottschall and Kram 2003; Gottschall and Kram 2005) is that that by increasing or decreasing the mechanical demand for a specific task (e.g., body support or forward propulsion), EMG activity in muscles that normally perform those tasks would increase or decrease proportionally in response to the perturbation. While this may be a reasonable assumption, analysis of EMG alone provides little insight into the changes in mechanical output from individual muscles or how these changes influence walking dynamics.

Computer modeling and forward dynamics simulation studies provide another approach that has been used to explore individual muscle function (e.g., Neptune et al. 2001; Anderson and Pandy 2003; Neptune et al. 2004; Liu et al. 2006). These studies use detailed musculoskeletal models and computer simulations to emulate experimentally measured kinematic and kinetic patterns. Unlike experimental studies, simulations provide predictions for the mechanical output from individual muscles and can quantify how muscles adapt to changes in mechanical demands (e.g., Zajac et al. 2002; Zajac et al. 2003).

In this study, we combined experimental perturbations with forward dynamics simulations to examine how individual muscles are modulated to meet changes in mechanical demand produced by manipulations of body weight and/or body mass. Expanding on the conclusions from our previous work (McGowan et al. 2008), the goal of this study was to examine the relative changes in mechanical output from the plantar flexors and determine how these changes influence walking dynamics during experimentally perturbed conditions. Specifically, we tested the hypothesis that both GAS and SOL would increase/decrease mechanical output in response to changes in weight and that SOL would increase mechanical output in response to increased mass, consistent with previously measured changes in EMG. In addition, we examined the mechanical output and modulation of the other major proximal leg muscles. Studies have shown that the uniarticular hip and knee extensors (gluteus maximus and vasti) contribute substantially to body support (e.g., Winter 1990; Anderson and Pandy 2003; Neptune et al. 2004). However, it is not known how the mechanical output of these muscles changes in response to altered weight and/or mass or how lower extremity muscles combine to meet changes in mechanical demands on the body.

Methods

Experimental data

The experimental apparatus, protocol, and data processing were previously described in detail in McGowan et al. (2008) and will be summarized here. The data were collected at the University of Colorado at Boulder from ten healthy subjects (5 male/5 female; height = 1.74 ± 0.09 m; mass = 67.1 ± 8.5 kg; age = 27.7 ± 7.7 yrs) walking at 1.3 ms⁻¹ on a dual belt force measuring treadmill. Subjects walked normally (control) and with increased trunk loads (increased weight and mass), weight support (decreased weight only), and an equal combination of increased trunk load and weight support (increased mass only). Each perturbation was preformed at 25% and 50% of the subject’s body weight for a total of seven conditions. Trunk loads were applied by adding thin lead strips to a padded belt worn tight around the hips. Weight support was provided by a nearly constant upward vertical force applied to a waist harness. And added mass only was achieved by applying a trunk load and weight support simultaneously. Sagittal plane kinematics and 3D ground reaction forces were collected at 200 Hz and 2000 Hz, respectively, and a standard inverse dynamics approach was used to calculate joint moments and powers. Average data for a stride were calculated for each subject (average of 10 strides) during each condition and these data were averaged across subjects to provide group average kinematic and kinetic data for each condition.

Musculoskeletal model and simulations

Forward dynamics simulations were developed for the seven experimental walking conditions: normal (control), body weight and mass increased by 25% and 50% (+25W&M and +50W&M), body mass increased by 25% and 50% (+25M and +50M), and body weight decreased by 25% and 50% (−25W and −50W).

The musculoskeletal model was developed using SIMM (MusculoGraphics, Inc.) and has been described in detail elsewhere (e.g., Neptune et al. 2000; Neptune et al. 2001; Neptune et al. 2004; Sasaki et al. 2008). Briefly, the model has 13 degrees of freedom including flexion/extension at the hip, knee, ankle, mid-foot and toes of each leg, and horizontal and vertical translation and pitch rotation at the trunk. Foot-ground contact was modeled using 31 visco-elastic elements with Coulomb friction (Neptune et al. 2000) distributed over the three foot segments. The dynamical equations-of-motion were generated using SD/FAST (PTC, Needham, MA) and forward dynamics simulations were developed using Dynamics Pipeline (MusculoGraphics, Inc.).

The model was driven by 25 Hill-type musculotendon actuators per leg combined into 11 functional groups based on anatomical classifications (Fig. 1) with muscles in each group receiving the same excitation pattern. Individual muscle excitations were modeled using block patterns characterized by an onset, duration and magnitude, with the magnitude defined with up to six nodes. The minimum number of nodes that characterized the experimental EMG pattern of each muscle was used. Activation-deactivation dynamics were modeled with a first-order differential equation (Raasch et al. 1997) with activation and deactivation time constants of 12 and 48 ms, respectively.

Figure 1.

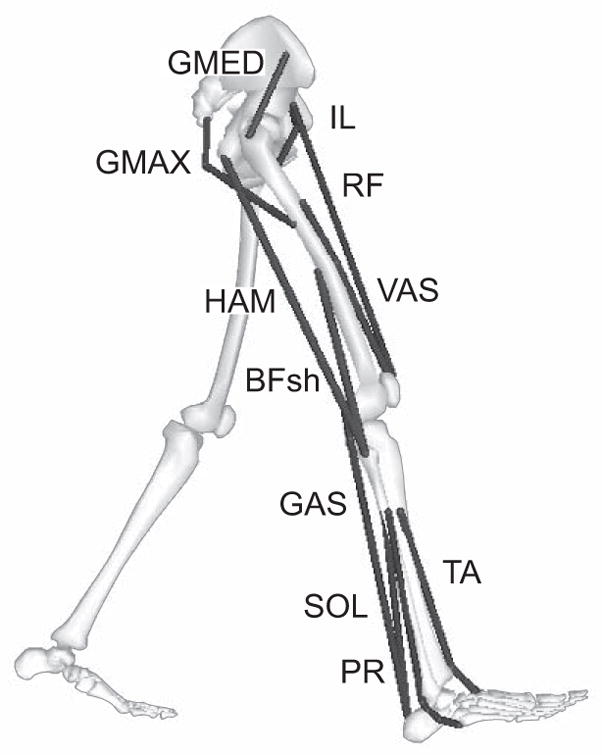
The model consisted of rigid segments representing a trunk (head, torso and arms) and two legs, each consisting of a thigh, shank, patella, rear-foot, mid-foot and toes. The 11 muscle groups were defined as IL (illiacus, psoas), GMAX (gluteus maximus, adductor magnus), GMED (gluteus medius), VAS (3-component vastus), RF (rectus femoris), HAM (medial hamstrings, biceps femoris long head), BFsh (biceps femoris short head), GAS (medial and lateral gastrocnemius), SOL (soleus, tibialis posterior, flexor digitorum longus, flexor hallucis longus), TA (tibialis anterior, extensor digitorum longus, extensor hallucis longus) and PR (peroneus longus).

For the added load conditions, the mass and inertial characteristics of the trunk segment were increased by 25% and 50% of the control (nominal) model. For the weight support conditions, a constant upward vertical force was applied to the trunk center-of-mass equal to 25% and 50% of the control model weight. Finally, for the increased mass only condition, mass and inertia of the trunk segment were increased as in the added load condition while simultaneously applying an equal constant upward force to the trunk center-of-mass.

Dynamic optimization

Walking simulations of a complete gait cycle were generated for each condition from left heel-strike to the following left heel-strike. A simulated annealing algorithm (Goffe et al. 1994) was used to fine-tune the muscle excitation patterns and initial joint velocities to minimize the difference between the simulated and experimental data for each condition. Muscle stress and activation were also minimized to ensure equal recruitment of agonist muscles and limit co-contraction of antagonist muscles. The timing of muscle excitations (onset and offset) were constrained such that muscle activations occurred in periods of the gait cycle consistent with experimental EMG data. The variables tracked included the left and right hip, knee and ankle angles, trunk translations (horizontal and vertical) and the horizontal and vertical ground reaction forces. The optimizations were continued until all tracking variables were within two standard deviations of the group averaged experimental data.

Assessing muscle function

Added load and weight support were used to manipulate the requirements for body support whereas added mass was used to increase the demand for forward propulsion independent of body support. To assess how the musculoskeletal system was modulated in response to body support manipulations, vertical ground reaction forces for each condition were decomposed into individual muscle force contributions (e.g., Neptune et al. 2004; Neptune et al. 2008). To examine how individual muscles were modulated in response to increased demands for trunk propulsion, a segmental power analysis (Fregly and Zajac 1996) was used to quantify how the mechanical energy generated by each muscle contributed to horizontal trunk motion. The power delivered to the trunk segment in the horizontal direction was calculated throughout the gait cycle for each muscle and integrated with respect to time to determine the work done by each muscle on the trunk segment. Horizontal trunk power was chosen over the horizontal ground reaction force to examine forward propulsion because the segment power analysis is able to separate muscle contributions to trunk propulsion (where the increased mass was applied) versus other segments (e.g., accelerating the leg forward).

Results

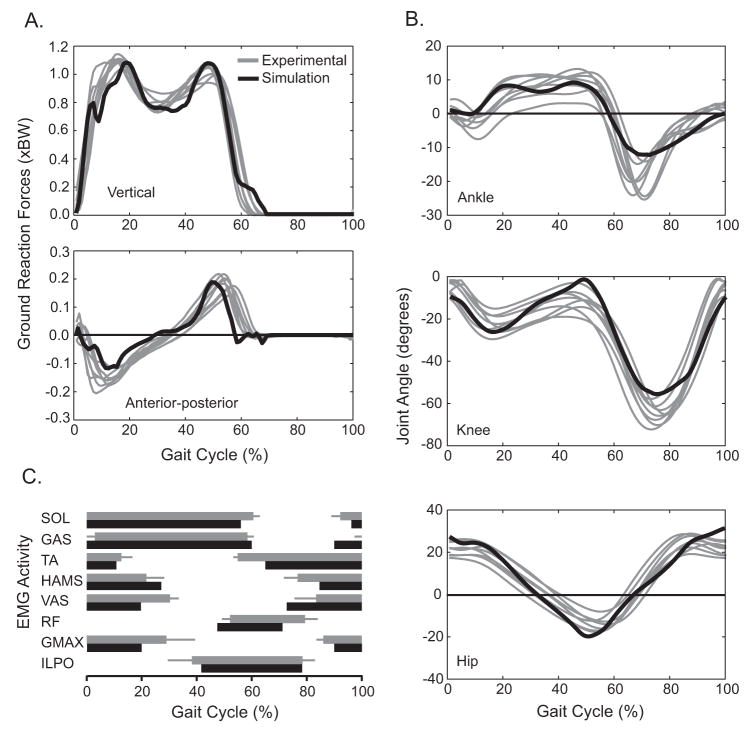
Data from the simulations agreed well with the experimental data for all of the conditions (Fig. 2, Table 1). The average tracking error for normalized ground reaction forces (Fig. 2A), joint angles (Fig. 2B) and timing of EMG activity (Fig. 2C) were all within 2 S.D. of the group averaged experimental data (Table 1). The simulations maintained constant walking speed (1.3 ms⁻¹) and accounted for minor differences in contact time and duty factor seen in the experimental data within ± 5%. In addition, the relative changes in the time integrated simulation excitation patterns for the SOL and GAS were similar to the relative changes in integrated EMG activity observed experimentally (Fig. 3).

Figure 2.

The results from the control simulation (black) show close agreement with the experimental data (grey). Grey lines represent individual averages for each subject’s A) ground reaction forces and B) joint angles. C) Grey horizontal bars represent group average EMG timing (± 1 s.d.) normalized to the gait cycle.

Table 1.

Average tracking error

Condition	Ground reaction forces		Kinematics
	Vertical ×BW	Horizontal ×BW	Hip degrees	Knee degrees	Ankle degrees
Control (Exp. s.d.)	−0.030 (0.068)	0.023 (0.023)	−0.19 (3.53)	2.96 (4.69)	−0.26 (2.65)
+25W (Exp. s.d.)	−0.033 (0.105)	0.023 (0.033)	−2.21 (3.80)	2.21 (5.96)	1.25 (3.02)
+50W (Exp. s.d.)	0.006 (0.086)	0.012 (0.029)	−2.00 (3.52)	4.30 (5.58)	−0.36 (2.94)
+25W&M (Exp. s.d.)	−0.029 (0.068)	0.021 (0.022)	1.73 (3.62)	3.83 (5.27)	−3.15 (3.23)
+50W&M (Exp. s.d.)	−0.029 (0.071)	0.033 (0.021)	3.09 (2.91)	5.23 (3.48)	−1.76 (2.42)
−25W (Exp. s.d.)	−0.042 (0.059)	0.027 (0.016)	3.52 (3.56)	2.32 (5.25)	0.55 (3.37)
−50W (Exp. s.d.)	−0.001 (0.051)	0.001 (0.012)	2.15 (3.22)	−3.84 (3.66)	−2.71 (3.84)

Exp. s.d. = One deviation for experimental data.

Figure 3.

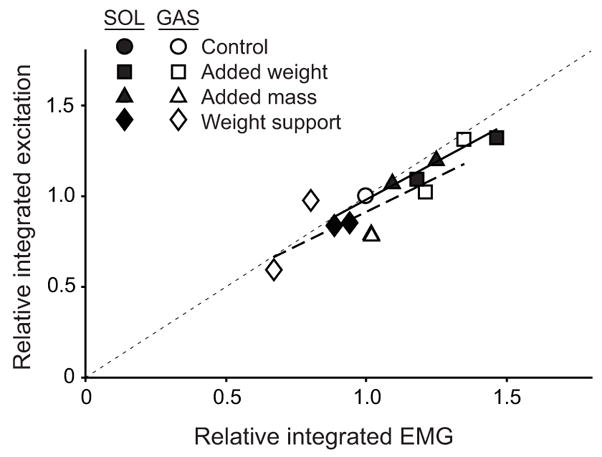
A comparison of the relative changes (normalized to control values) in integrated EMG activity and the integrated simulation excitation patterns for soleus (SOL) and gastrocmeius (GAS). The dotted line indicates a one-to-one correlation. SOL R² = 0.95. GAS R² = 0.63.

Vertical ground reaction force

Added loads increased the vertical impulse, weight support decreased the vertical impulse and added mass had no effect (Fig. 4). The relative muscle contributions to the total vertical impulse were nearly constant for all conditions, ranging from 67% to 73% (Fig. 4). The remainder of the vertical impulse was produced by non-muscular sources (i.e., gravity, velocity dependent forces and passive structures) in the model.

Figure 4.

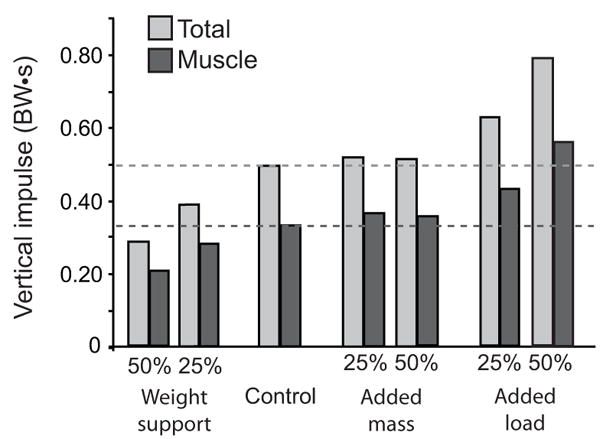
Total vertical impulse and total muscular contributions to all of the simulated conditions during stance. Non-muscular contributions to vertical impulse were due to gravity, velocity dependent forces and passive structures in the model. Dotted lines indicate the magnitude of the control values.

SOL, GAS, VAS and GMAX all contributed to the vertical impulse in all conditions, with SOL having the greatest contribution (Fig. 5). The remaining muscles (HAM, RF, IL, GEMD and PR) had relatively small contributions to the vertical impulse and were summed (Fig. 5, Other muscles). Those muscles that had small negative contributions to the vertical impulse (BFsh and TA) were also grouped (Fig. 5., Other muscles).

Figure 5.

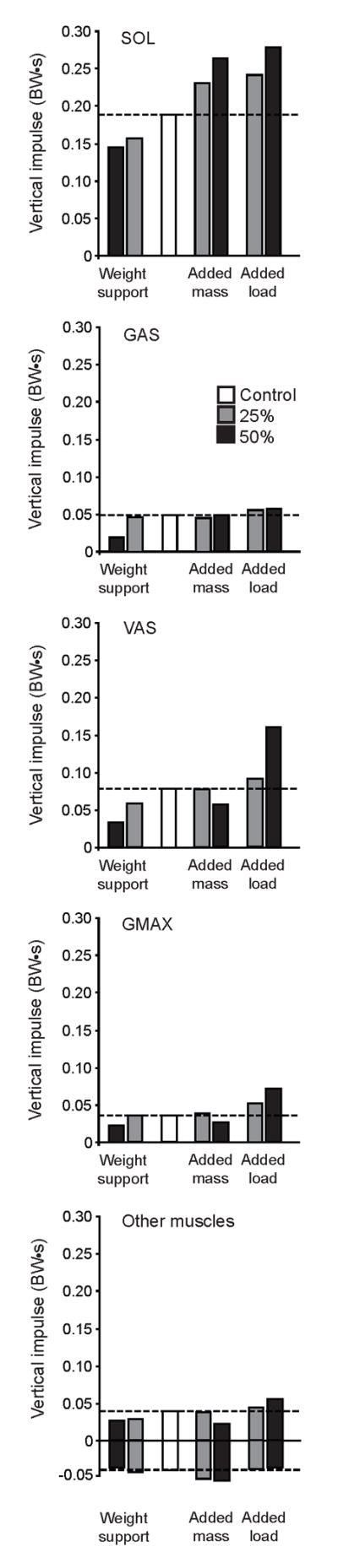
Individual muscle contributions to vertical impulse by SOL, GAS, VAS, GMAX and the sum of the other muscles for the control (white) for the 25% (grey) and 50% (black) conditions. The sum of the other muscles includes HAM, RF, IL, GMED and PR. Muscles that made negative contributions to the vertical impulse (IL and BFsh) were excluded. Dotted lines indicate the magnitude of the control values.

SOL exhibited the greatest absolute changes in contributions to the vertical impulse across experimental conditions (Fig. 5). Added loads resulted in nearly proportional increases in vertical impulse, whereas weight support produced only 16% and 23% decreases for −25W and −50W conditions, respectively. The added mass only condition produced large increases in vertical impulse by SOL despite there being no increased demand for weight support. GAS had a similar contribution to vertical impulse in all experimental conditions except 50% weight support, where the impulse was reduced by 60%, relative to the control (Fig. 5). VAS had the second largest contribution to the vertical impulse in all conditions. Added load produced a small increase in VAS impulse (+17%) with +25W&M, but the impulse more than doubled (+105%) during +50W&M. Yet it should be noted that the absolute contribution by VAS was still less than that of SOL (Fig. 5). Weight support conditions produced reductions in VAS vertical impulse of 25% and 58% for −25W and −50W conditions, respectively. Added mass alone had no effect on VAS vertical impulse with +25M, but +50M produced a reduction in vertical impulse of 28% (Fig. 5). In the control condition, GMAX contribution to vertical impulse was small, and similar to that of GAS. Both 25% and 50% added loads produced large increases in vertical impulse by GMAX (+40% and +101%, respectively), relative to the control condition. Added mass and weight support resulted in no changes with +25M and −25W conditions, but produced small decreases in GMAX vertical impulse with +50M and −50W conditions. The remaining muscles that contribute positively to the vertical impulse collectively tended to increase with added load and decrease with weight support, although the absolute changes in the impulse were relatively small. Added mass resulted in a slight increase (+10%) in the impulse with +25M, and a large decrease (−42%) with +50M.

Horizontal segmental work

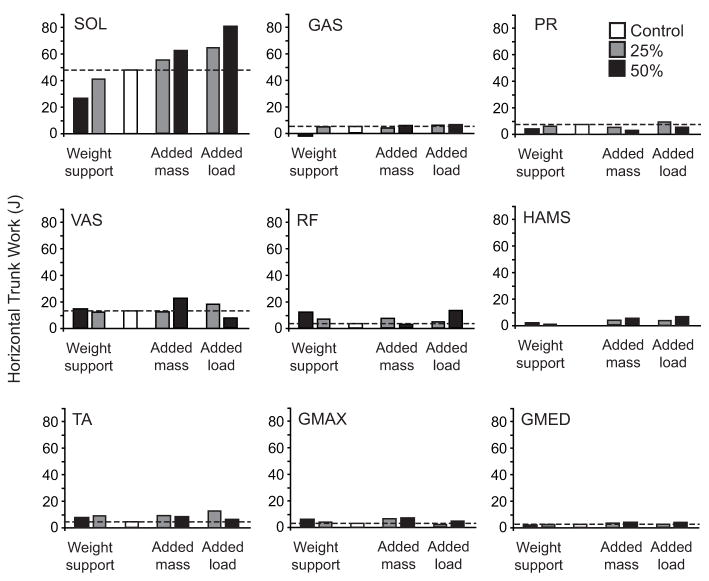
Increasing body weight and mass (+W&M) increased the mechanical demands for forward propulsion. SOL contributed the most work to propel the trunk forward (Fig. 6). In addition, SOL exhibited the greatest changes in horizontal work in response to changes in mechanical demand. As expected, both added mass and load produced proportional increases in SOL horizontal work. Interestingly, weight support also produced proportional decreases in SOL horizontal work, despite there being no change in the demand for forward propulsion. Of the remaining muscles, only VAS contributed substantially to positive horizontal work during most conditions. However, there was not a clear trend with increased mass or altered weight (Fig. 6). The sum of all non-SOL muscles tended to increase across conditions, but again there was no clear trend with changes in mass or weight.

Figure 6.

Individual muscle contributions per leg to the horizontal trunk mechanical work. Positive values indicate the muscle acts to accelerate the trunk in the direction of motion. Muscles that had a net negative contribution horizontal trunk work are not shown (IL and BFsh). Dotted lines indicate the magnitude of the control values.

Discussion

The goal of this study was to combine experimental perturbations with computer modeling and simulations to examine how individual muscles are modulated in response to changes in external mechanical demand. The results of this study show that SOL not only provides the largest contribution to both body support (vertical impulse; Fig. 5) and forward propulsion (horizontal work; Fig. 6), but also plays the greatest role in modulating the muscular response to altered demands for these walking sub-tasks. The results for the control walking condition are consistent with previous studies, which have shown SOL to be a major contributor to body support (e.g., Ferris et al. 2001; Neptune et al. 2001; Anderson and Pandy 2003; Hof and Otten 2005; Stewart et al. 2007; McGowan et al. 2008) and the primary contributor to trunk forward propulsion (e.g., Neptune et al. 2001; Hof and Otten 2005; McGowan et al. 2008).

It is important to note that individual muscle contributions to body support and forward propulsion are not independent and could not be decoupled during the different experimental conditions. For example, during the added mass only conditions the demand for forward propulsion was increased while the demand for body support was not changed. The mechanical output by SOL increased to meet the demands for forward propulsion (Fig. 6), but in doing so also increased its contribution to the vertical impulse (Fig. 5). Therefore, other muscles which contribute primarily to body support and less to forward propulsion had to reduce their mechanical output (i.e., VAS and GMAX; Fig. 5).

In our previous analysis of the experimental data set used in the current study, relative changes in EMG activity and inverse dynamics were used to examine the relative contributions of the plantar flexors to body support and forward propulsion (McGowan et al. 2008). The assumption in that analysis was that if walking kinematics remained similar in all conditions, then increases or decreases in EMG activity should be proportional to increases or decreases in mechanical output by the muscles. In general, the results from our current analysis of mechanical output support this assumption. The contributions by SOL and GAS to body support and the contributions by SOL to forward propulsion were consistent with our previous conclusions. However, EMG measurements alone could not provide information about absolute contributions to mechanical output by individual muscles, or the relative contributions within a given condition. For example, our previous analysis of EMG (McGowan et al. 2008) identified both GAS and SOL as contributors to body support, but could not determine that the relative contribution by SOL to body support was much greater than the contribution by GAS. Further, because the absolute values for the vertical impulse were substantially greater for SOL, relative changes with each condition represented much greater absolute changes compared to those for GAS. Therefore, even though the relative changes in EMG were approximately proportional to the relative changes in vertical impulse, SOL (not GAS) was the primary mechanism for modulating the vertical impulse in response to changes in mechanical demand.

In our experiments, relative changes in EMG activity provided a reasonable proxy for relative changes in mechanical output. However, it is important to note that this result should not be generalized for all locomotor tasks. For example, joint kinematics may not always accurately reflect muscle fiber length changes as muscle fibers may shorten even when the whole muscle-tendon unit is being stretched (e.g., Lichtwark and Wilson 2006). Further, the relationship between muscle activity and mechanical output depends on a number of nonlinear intrinsic properties (i.e., force-length-velocity relationships) that make the relationship difficult to predict. Thus, it is likely that during activities involving rapid movements, large joint angular excursions or high forces, these musculotendon interactions and intrinsic properties would produce significant confounding effects on the relationship between EMG activity and muscle mechanical output.

As with previous studies (e.g., Ferris et al. 2001; Neptune et al. 2001; Anderson and Pandy 2003; Hof and Otten 2005; Stewart et al. 2007; McGowan et al. 2008), our work highlights the importance of the ankle plantar flexors for providing body support and forward propulsion during normal walking. Further, our results suggest that the uni-articular SOL is the dominant contributor to these walking sub-tasks and is also the primary muscle involved in modulating mechanical output in response to changing energetic demands. Individuals with various neuromuscular pathologies often exhibit ankle plantar flexor weakness that limits their ability to walk normally. The results from this study suggest that rehabilitation of SOL would produce the greatest improvement in walking performance. This is consistent with a recent study suggesting that the use of powered ankle-foot orthoses, which are analogous to uni-articular plantar flexors, may be effective in gait rehabilitation because they enable patients to improve ankle push off kinematics during walking (Sawicki et al. 2006).

The potential limitations of the walking simulations and analyses used have been addressed in detail in previous studies (e.g., Neptune et al. 2001; Zajac et al. 2003). Briefly, the modeling framework requires assumptions regarding anatomy, muscle physiology and structural and mechanical properties including the interaction between the model and the ground. Further, the simulations relied on simplified excitation patterns and did not include any feedback modulation that would be required for sustained steady state walking. Despite these assumptions, the same basic model and simulation framework was used for all conditions and our results were consistent with the relative changes in experimentally measured variables between the conditions. Therefore, we are confident that, while altering model or simulation parameters may affect the magnitude of specific quantities, it would not substantially impact the conclusions drawn.

In conclusion, we found that soleus is the primary muscle involved in both providing and modulating body support and forward propulsion in response to changes in external mechanical demand. The relative changes in mechanical output predicted by our simulations agreed well with the relative changes in EMG activity reported in our previous experimental perturbation study. However, our results revealed that while relative changes in EMG were indicative of relative changes in mechanical output from a given muscle, EMG was not able to provide information regarding the absolute contributions or relative contributions within each condition. Therefore, we suggest that EMG be used in conjunction with other analysis techniques (e.g., modeling and simulation, imaging techniques) to assess individual muscle function. Finally, our data show that for muscles that contribute to multiple tasks (e.g., body support and forward propulsion) the muscle’s contribution to one task is not independent of its contributions to the other tasks and the relative contributions to each task may not scale equally in response to changes in mechanical demand.