How Accurate are the Extremely Small P-values Used in Genomic Research: An Evaluation of Numerical Libraries

Abstract

In the fields of genomics and high dimensional biology (HDB), massive multiple testing prompts the use of extremely small significance levels. Because tail areas of statistical distributions are needed for hypothesis testing, the accuracy of these areas is important to confidently make scientific judgments. Previous work on accuracy was primarily focused on evaluating professionally written statistical software, like SAS, on the Statistical Reference Datasets (StRD) provided by National Institute of Standards and Technology (NIST) and on the accuracy of tail areas in statistical distributions. The goal of this paper is to provide guidance to investigators, who are developing their own custom scientific software built upon numerical libraries written by others. In specific, we evaluate the accuracy of small tail areas from cumulative distribution functions (CDF) of the Chi-square and t-distribution by comparing several open-source, free, or commercially licensed numerical libraries in Java, C, and R to widely accepted standards of comparison like ELV and DCDFLIB. In our evaluation, the C libraries and R functions are consistently accurate up to six significant digits. Amongst the evaluated Java libraries, Colt is most accurate. These languages and libraries are popular choices among programmers developing scientific software, so the results herein can be useful to programmers in choosing libraries for CDF accuracy.

1. Introduction

In the era of high-dimensional biology (HDB), modern technologies, such as the gene expression microarray and the genome-wide single-nucleotide-polymorphism (SNP) array, produce hundreds of thousands to over a million measurements per sample. In analyzing these data, one conducts at least as many tests of hypothesis which, after adjusting for multiple testing, might require very small significance levels. For example, one might test each hypothesis (after a Bonferroni correction) at a significance level of α =0.05/2.0×10⁶ = 2.5×10⁻⁸, for a study with two million independent measurements per array. If one further decided to examine all pair-wise SNP×SNP interactions in a genome-wide association study, this might entail on the order of 2.5×10¹² tests and a corresponding significance level of 0.05/(2.5×10¹²) or 2.5×10⁻¹⁴. Published papers are already and increasingly reporting p-values as small as or smaller than these levels. For a number of examples, refer to Table 1 where we show a selected subset of recent papers that report such p-values. This makes the accuracy of the calculation of small tail areas in statistical distributions (the basis for the p-value) an important question that will only grow in importance as the use of HDB technology becomes more widespread and the technology itself improves.

Table 1. A selected subset of published papers that report “small” p-values.

Reported P-Value	Reference
9.3×10−142	M. Ashburner et al. An Exploration of the Sequence of a 2.9-Mb Region of the Genome of Drosophila melanogaster: The Adh Region. Genetics, Vol. 153, 179–219, September 1999.
5.4×10−140	Cauchi S, El Achhab Y, Choquet H, Dina C, Krempler F, Weitgasser R et al. TCF7L2 is reproducibly associated with type 2 diabetes in various ethnic groups: a global meta-analysis. J Mol Med 2007; 85: 777–782.
2.42×10−134	The Wellcome Trust Case Control Consortium, 2007. Genome- wide association study of 14,000 cases of seven common diseases and 3,000 shared controls. Nature 447(7145) 661–678.
1.0×10−131	Castillo-Davis C. I, Hartl D. L. Genome Evolution and Developmental Constraint in Caenorhabditis elegans. MBE 19: 728:735, 2002.
2.0×10−100	Brockert et al. Phenotypic Switching and Mating Type Switching of Candida glabrata at Sites of Colonization. Infect. Immun. 71 (12): 7109–7118, 2003
3.0×10−35	Frayling, TM, et al., 2007. A Common Variant in the FTO Gene Is Associated with Body Mass Index and Predisposes to Childhood and Adult Obesity. Science, 316(5826) 889–894.
2.51×10−19	Liu Y, Helms C, Liao W, Zaba LC, Duan S, et al., 2008. A Genome-Wide Association Study of Psoriasis and Psoriatic Arthritis Identifies New Disease Loci. PLoS Genet 4(3): e1000041.
3.3×10−18	Tomlinson, IP, et al., 2008. A genome-wide association study identifies colorectal cancer susceptibility loci on chromosomes 10p14 and 8q23.3. Nat Gen 10.1038/ng.111.
9.7×10−13	Ober C, Tan Z, Sun Y, et al. Effect of variation in CHI3L1 on serum YKL-40 level, risk of asthma, and lung function. N Engl J Med 2008; 358:1682–1691.

Numerical libraries provide the foundation for any numerical software tool and the best libraries should consistently calculate accurate tail areas. Herein, we measure and show the accuracy of cumulative distribution functions (CDF) of statistical distributions provided by numerical libraries using the LRE metric described in [12], demonstrate the importance of having separate CDF for the lower and upper tail areas to avoid complementation error [12] [8], and make recommendations on how to choose numerical libraries from the perspective of the scientific programmer.

The reliability of statistical software is an important topic that has been examined with increasing interest in the past decade [1] [9] [11] [12] [13]. The sources of error (complementation or cancellation errors) in numerical computation, a straightforward way to measure accuracy, and the use of benchmark datasets with known answers that can be used to assess software accuracy are introduced and discussed by McCullough in [12]. The importance of accuracy of tail areas and percentiles in statistical distribution using the ELV program by Knusel [10] and the DCDFLIB library by Brown [3] is also discussed in [12]. The output of the algorithms implemented in these programs is currently considered the benchmark for comparison of accuracy in CDF implementations [12] [13] [24].

In general, we would like to choose a high-quality numerical library based on criteria like accuracy, performance, and ease-of-use. There are resources available for assessing performance [2]; however, even after a thorough literature search, we could not find a paper assessing the accuracy of numerical libraries. Therefore, in this paper we specifically examined the accuracy of CDF implementations of commercial and free or open-source libraries that are likely to be of interest to researchers and developers of custom scientific software, including several popular Java and C libraries. We have also evaluated R because it is a popular tool among statisticians and its methods are frequently and critically examined by statistical programmers.

Accuracy can be defined in terms of the absolute or relative error of an approximate quantity with respect to its true value. In IEEE double precision floating point, rounding of operations occurs at the 15^th or 16^th significant digit to accommodate the results of numerical computation in a fixed number of bits [8]. Thus it makes sense for users of numerical libraries to pay as much, if not more, attention to accuracy as to other criteria, such as rich application programming interface (API) and user friendliness. This paper treads a path similar to [9], [11], and [12] in evaluating numerical accuracy by comparing calculated tail areas of statistical distributions (or p-values in the context of hypothesis testing) to true tail areas. Specifically we evaluate values obtained using the CDF of Chi-square and t-distribution which are important distributions for many hypothesis tests.

2. Log Relative Error (LRE) as a Measure of Accuracy

If a is the calculated value and a′ is the true value, then LRE is given by,

$$\mathit{LRE}=-{log}_{10}\frac{\mid a-a^{\prime }\mid }{\mid a^{\prime }\mid }$$ (1)

The LRE is a measure of accuracy and represents the number of correct significant digits with respect to a′. The interpretation of LRE is discussed in [8] and practical implementation is discussed in [12].

3. Obtaining Exact Tail Areas of Distributions (a′)

In any assessment of accuracy in CDF implementations, the question of how to obtain the exact tail area is clearly very important. One option is to use software that applies symbolic methods to calculate these areas with arbitrary precision; the Mathematica software is examined by McCullough and used, in conjunction with ELV, to test the accuracy of CDF in MS Excel [15] [24].

Other options include software that calculates these tail areas by a high-quality numerical approximation. ELV is a DOS program widely considered to be the standard for comparison when evaluating CDF accuracy and was used to test accuracy in MS Excel and to test SAS [11] [13]. DCDFLIB is a C library with CDF implementations for many statistical distributions and is described in [12] as an alternative to using ELV for calculating exact tail areas. We found in our own testing that DCDFLIB consistently returned accurate tail areas to six significant digits when compared against ELV and use it to make our comparisons because (a) it is more straightforward to call a C library than a DOS program from our testing framework, allowing us to test a wider range of values, and (b) the design of ELV is limited to returning values no smaller than 1.0×10⁻¹⁰⁰ [10] [24].

4. Methods

Our methods of assessing accuracy are based largely on the application of guidelines described in [12] [14]. For each numerical library under consideration, we reviewed the application programming interface (API) documentation and identified the CDF call that returns the upper tail area in the statistical distribution of interest. We focus our testing on that tail because p-values from typical hypothesis testing are obtained from the upper tail areas of a distribution, making the accuracy of extreme values in those tails the target of our evaluation. For example, in the Colt (Java) library, there is a class cern.jet.stat.Probability with function chiSquareComplemented(double v, double x) that returns “the area in the right hand tail (from x to infinity) of the Chi-square probability density function with v degrees of freedom” [4].

For those libraries that did not have a CDF for that tail, we identified the lower tail CDF and obtained the upper tail area by complementation. For example, in the JMSL (Java) library, there is a class com.imsl.stat.Cdf with a function chi(double chsq, double df) that returns a “value representing the probability that a Chi-squared random variable takes a value less than or equal to chsq” [23]. For this library, we calculate the upper tail area as 1 − chi(chsq, df). In other words, we attempt to use the CDF that returns P{X≥x} directly; if this function is not available, we use the CDF that returns P{X≤x} and calculate P{X≥x} as 1 − P{X≤x}. As we show in the results, taking 1 − P{X≤x} introduces a substantial amount of inaccuracy when P{X≤x} is near one, as two nearly equal numbers are subtracted leading to complementation or cancellation error [8] [12].

Once the upper tail CDF is identified, we call that function with a vector of x values of interest chosen to correspond to extreme upper tail areas. For example, we evaluate a Chi-square distribution with 1 degree of freedom (df) and x from 1 to 450; this results in a vector of tail areas as extreme as 1.0×10⁻¹⁰⁰. We then compare this vector of calculated tail areas to the vector of exact tail areas obtained from DCDFLIB and calculate a vector of LRE values that represent the measured accuracy of the calculated tail area versus the exact tail area at each x value.

For the open-source and free libraries, the CDF from the latest version (the exact version numbers are documented in the supplementary material) available as of early 2008 was used to calculate the tail areas. For the commercial JMSL library, version 4.0 was used. The custom source code written to call the Java libraries was run in the Java 6 Runtime Environment (JRE). The C code was compiled using the GCC compiler version 3.4.4 with default switches. The R code was run using version 2.6.2. The results from all of the libraries were combined and tabulated using a custom set of scripts written in Java to automate the process and eliminate the element of human error in managing and organizing the considerable amount of data that were generated. All of these programming tasks were performed on a dual Intel Xeon workstation with 2 GB of RAM running the Windows Server 2003 SP2 operating system.

5. Results

The LRE of upper tail areas for the Chi-square distribution was plotted against the x values supplied to the CDF for each library under consideration (Fig. 1). In our test framework, the comparison to DCDFLIB is set up so that the highest possible value for LRE is 6. In other words, LRE values lower than 6 are not “perfectly” accurate and values close to 0 are very inaccurate. We note that the value returned by a function call may have more than six digits; however, because the algorithms used by ELV and DCDFLIB can only guarantee a relative error ≤10⁻⁶ [10], corresponding to six correct significant digits, we round the values returned by each function call to six digits before comparison.

Figure 1.

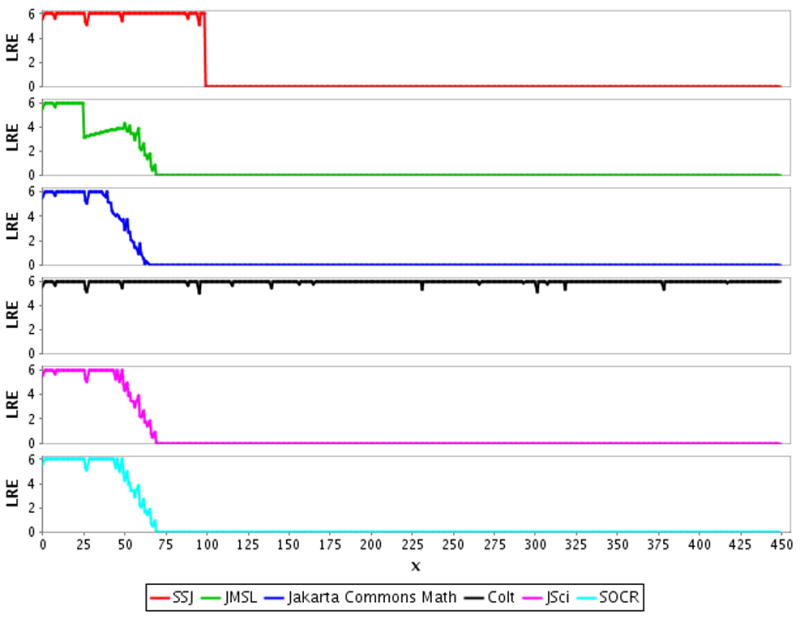
Log relative error (LRE) plotted against the x supplied to the CDF call of the tested numerical libraries to obtain the upper tail P{X>=x} for the Chi-square distribution with df=1.

Amongst the Java libraries for the Chi-square distribution, SSJ performs well until around x = 100; because SSJ provides a direct (not calculated by complementation) upper tail CDF, this inaccuracy in more extreme tails is likely due to poor algorithm performance [16]. The JMSL, Jakarta Math, SOCR and JSci libraries perform comparatively poorly, with accuracy steadily decreasing from about x = 50 and dropping to zero at x = 66 and x = 71. This poor performance is likely due to complementation error as none of these libraries provide a direct CDF for the upper tail area, which had to be obtained by complementation [18] [21] [22] [23]. The Colt library does very well, with only minor inaccuracies across the entire range of x values; it is unclear why the accuracy is not perfect, but this may be due to an implementation bug as the choice of algorithm appears sound [4]. The LRE curves for the GSL library and the R statistical language are not plotted because the CDF tail areas were perfectly accurate with respect to the exact values from DCDFLIB; both GSL and R provide separate functions to directly compute both tail areas and the algorithms implemented in these functions are accurate across the entire range of x values we tested [7] [17].

To illustrate the degree of inaccuracy introduced by complementation, we plot the LRE for the Chi-square upper tail area using both the direct upper tail function and the upper tail by complementation of the lower tail function in the GSL (Fig. 2). This plot shows that had GSL only provided a lower tail CDF for the Chi-square distribution, forcing the end user to obtain upper tail areas by complementation, accuracy would steadily decrease until around 1×10⁻¹⁷, at which point complementation error causes the calculated value to equal zero, resulting in an LRE of zero. This “steadily decreasing to zero” LRE curve is what we observe in Fig. 1 for JMSL, Jakarta Math, SOCR and JSci, libraries that did not provide direct upper tail CDF. Tables 2 and 3 provide information about the magnitude of p-value when LRE first drops to 0 for the Chi-square and t-distribution.

Figure 2.

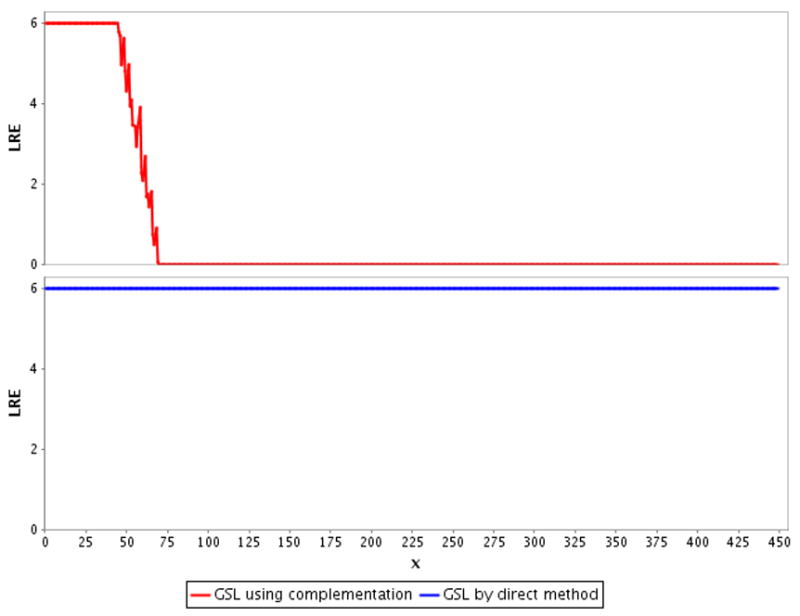
Log relative error (LRE) plotted against the x supplied to the CDF call of GSL to obtain the upper tail P{X>=x} for the Chi-square distribution with df=1. Illustrates how complementation error affects the accuracy if the tail area is computed by complementation instead by the direct method.

Table 2. Magnitude of p-value when LRE first drops to 0 for Chi-square distribution with df=1.

Table 2 describes the magnitude of p-values when LRE first drops to 0. Specifically, we have tabulated the smallest p-value for which the library can represent a value with LRE > 0.

Library	Language	Magnitude of p-value when LRE First drops to 0	Method to Obtain Upper Tail CDF
GSL	C	None	Direct
Package Stats	R	None	Direct
Colt	Java	None	Direct
SSJ	Java	1E-23	Direct
JSci	Java	1E-17	Complementation
Jakarta Math	Java	1E-16	Complementation
SOCR	Java	1E-17	Complementation
JMSL	Java	1E-17	Complementation

Table 3. Magnitude of p-value when LRE first drops to 0 for t distribution with df=50.

Table 3 describes the magnitude of p-values when LRE first drops to 0. Specifically, we have tabulated the smallest p-value for which the library can represent a value with LRE > 0.

Library	Language	Magnitude of p-value when LRE First drops to 0	Method to Obtain Upper Tail CDF
GSL	C	None	Direct
Package Stats	R	None	Direct
Colt	Java	None	Complementation
SSJ	Java	1E-16	Complementation
JSci	Java	1E-16	Complementation
Jakarta Math	Java	1E-16	Complementation
SOCR	Java	1E-16	Complementation
JMSL	Java	1E-16	Complementation

Unfortunately, none of the Java libraries provided direct methods to compute the upper tail area for the t-distribution. That means for df=1, the smallest p-value for which all of these libraries have an LRE of 6 was 1E-4. Similarly, for df=50 the smallest p-value was 1E-93, and these libraries had an LRE of 0 after x near 12 due to complementation error. In other words, increasing the degrees of freedom changes the point at which inaccuracy is introduced, but does not change the fact that complementation error occurs. The plot of LRE for the upper tail CDF for the t-distribution for other degrees of freedom is comparable to what is shown in Fig. 1 and therefore not plotted again here.

7. Discussion

In this paper we applied a method for assessing the accuracy of tail areas calculated for the Chi-square and t-distribution in functions provided by Java and C numerical libraries and the R statistical language. The results show that, in the range of x values we evaluated, GSL and R are as accurate as ELV and DCDFLIB and with further, more comprehensive testing, these libraries may be equally appropriate as alternative standards of comparison. For the Java libraries tested, the LRE curves provide up-to-date and practical guidance as to what libraries the reader should choose based on CDF accuracy.

While most scientific programmers understand the need for choosing a CDF that implements an accurate algorithm, the degree of inaccuracy that is introduced by CDF complementation to obtain the opposite tail area is not as well-understood. There is also confusion created by the often incomplete or inaccurate API documentation that accompanies numerical libraries; for example, some may not clearly document that the upper tail CDF simply returns the complement of the lower tail CDF, so programmers may be unwittingly using complementation. Because complementation steadily erodes accuracy as x increases, completely erasing accuracy at around 1×10⁻¹⁷, and many interesting papers are reporting p-values as small or more extreme than that, we hope that this paper raises awareness regarding the importance of avoiding the cancellation error caused by complementation.

This is arguably a trickier issue for those tail areas at approximately 1×10⁻⁸ to 1×10⁻¹⁷ (in the Chi-square distribution example) because the function call will return a seemingly reasonable number whose inaccuracy may not be apparent to the average programmer. Problems in the more extreme tail areas are easier to detect because the complementation will cause “catastrophic” cancellation error [5], resulting in a tail area of zero, which is a much clearer signal that something is amiss than an answer that may appear similar to what was expected. This creates a somewhat counter-intuitive situation where inaccuracies in more extreme tail areas (larger exponent) are more obvious than those in less extreme tail areas (smaller exponent).

We also note that four out of five of the Java libraries tested do not provide a direct upper tail CDF, even for distributions as common as Chi-square and t. This means that the inaccuracy introduced by complementation error may be especially relevant to scientific programmers developing in Java. Because p-values for typical hypothesis testing are obtained from the upper tail, programmers using those libraries are forced to obtain the upper tail area by complementation.

It is our intent that the methods and results presented in this paper underscore that a well-written numerical API for the calculation of tail areas must have both a separate lower tail and upper tail CDF, where the function implementation for each tail often requires a different algorithm to control relative error [10], as well as up-to-date and complete API documentation describing the choice of algorithm and limits of accuracy. This high standard is well-met by many of the libraries that did well in our testing and by none that did poorly.

Addendum

Since initial submission of this paper, we contacted Visual Numerics (VNI), the developers of the JMSL library, to check and confirm our results primarily because of the unexpectedly poor performance of JMSL in our findings given that it is one of the only commercial numerical libraries available to Java programmers and the only library we tested written to meet commercial standards. We are pleased and very much encouraged to report that engineers at VNI have not only confirmed our results, but also implemented a number of improvements to address the problems we describe in this paper, including adding upper tail CDF implementations for the Chi-square, t, and F distributions to a newly released version 5.0.1 of the JMSL (Dr. Ed Stewart, personal communication, May 5 2008).