Nonlinear Random Effects Mixture Models: Maximum Likelihood Estimation via the EM Algorithm

Abstract

Nonlinear random effects models with finite mixture structures are used to identify polymorphism in pharmacokinetic/pharmacodynamic phenotypes. An EM algorithm for maximum likelihood estimation approach is developed and uses sampling-based methods to implement the expectation step, that results in an analytically tractable maximization step. A benefit of the approach is that no model linearization is performed and the estimation precision can be arbitrarily controlled by the sampling process. A detailed simulation study illustrates the feasibility of the estimation approach and evaluates its performance. Applications of the proposed nonlinear random effects mixture model approach to other population pharmacokinetic/pharmacodynamic problems will be of interest for future investigation.

1. Introduction

There is substantial variability in the way individuals respond to medications, in both treatment efficacy and toxicity. The sources of a drug’s underlying pharmacokinetic and pharmacodynamic variability can include demographic factors (such as age, sex, weight), physiological status (such as renal, liver, cardiovascular function), disease states, genetic differences, interactions with other drugs and environmental factors. In their seminal work, Sheiner, Rosenberg and Melmon (1972) proposed a parametric nonlinear mixed-effects modeling framework for quantifying both within and between subject variability in a drug’s pharmacokinetics, and developed an approximate maximum likelihood solution to the problem. Since the introduction by Beal and Sheiner (1979) of the general purpose software package NONMEM implementing this approach, other approximate maximum likelihood algorithms have been introduced to solve the nonlinear random and mixed effects modeling problem (see Davidian and Giltinan (1995) for an extensive review). An exact maximum likelihood (i.e., no linearization) solution to the parametric population modeling problem based on the EM algorithm has also been proposed by Schumitzky (1995) and fully developed and implemented by Walker (1996). The population modeling framework has had a significant impact on how pharmacokinetic (and pharmacodynamic) variability is quantified and studied during drug development, and on the identification of important covariates associated with a drug’s inter-individual kinetic/dynamic variability.

While population models incorporating measured covariates have proven to be useful in drug development, it is recognized that genetic polymorphisms in drug metabolism and in the molecular targets of drug therapy, for example, can also have a significance influence on the efficacy and toxicity of medications (Evans and Relling, 1999). There is, therefore, a need for population modeling approaches that can extract and model important subpopulations using pharmacokinetic/pharmacodynamic data collected in the course of drug development trials and other clinical studies, in order to help identify otherwise unknown genetic determinants of observed pharmacokinetic/pharmacodynamic phenotypes. The nonparametric maximum likelihood approach for nonlinear random effects modeling developed by Mallet (1986), as well as the nonparametric Bayesian approaches of Wakefield and Walker (1997) and Rosner and Mueller (1997), and the smoothed nonparametric maximum likelihood method of Davidian and Gallant (1993) all address this important problem. In this paper we propose a parametric approach using finite mixture models to identify subpopulations with distinct pharmacokinetic/pharmacodynamic properties.

An EM algorithm for exact maximum likelihood estimation of nonlinear random effects finite mixture models is introduced, extending the previous work of Schumitzky (1995) and Walker (1996). The EM algorithm has been used extensively for linear mixture model applications (see McLachlan and Peel (2000) for a review). The algorithm for nonlinear mixture models presented below has an analytically tractable M step, and uses sampling-based methods to implement the E step. Section 2 of this paper describes the finite mixture model within a nonlinear random effects modeling framework. Section 3 gives the EM algorithm for the maximum likelihood estimation of the model. Section 4 addresses individual subject classification, while an error analysis is presented in section 5. A detailed simulation study of a pharmacokinetic model is presented in section 6. Section 7 contains a discussion.

2. Nonlinear Random Effects Finite Mixture Models

A two-stage nonlinear random effects model that incorporates a finite mixture model is given by

$${\mathbf{Y}}_i\mid {\mathbf{\theta }}_i,\mathbf{\beta }\sim N({\mathbf{h}}_i({\mathbf{\theta }}_i),{\mathbf{G}}_i({\mathbf{\theta }}_i,\mathbf{\beta })),i=1,\dots ,n$$ (1)

and

$${\mathbf{\theta }}_i,\dots ,{\mathbf{\theta }}_n{\sim }_{i.i.d}\sum _{k=1}^K{w}_{k}N({\mathbf{\mu }}_k,{\mathbf{\sum }}_k),$$ (2)

where i=1,…,n indexes the individuals and k=1,…,K indexes the mixing components.

At the first stage represented by (1), Y_i = (y_1i,…,y_mii)^T is the observation vector for the ith individual (Y_i ∈ R^mi); h_i (θ_i) is the function defining the pharmacokinetic/pharmacodynamic (PK/PD) model, including subject specific variables (e.g., drug doses), and θ_i is the vector of model parameters (random effects) (θ_i ∈ R^p). In (1) G_i (θ_i, β) is a positive definite covariance matrix (G_i ∈ R^mi×mi) that may depend upon θ_i as well as on other parameters β (fixed effects) (β ∈ R^q).

At the second stage given by (2), a finite mixture model with K multivariate normal components is used to describe the population distribution. The weights {w_k}are nonnegative numbers summing to one, denoting the relative size of each mixing component (subpopulation), for which μ_k (μ_k ∈ R^p) is the mean vector and Σ_k (Σ_k ∈ R^p×p) is the positive definite covariance matrix.

Letting φ represent the collection of parameters, {β,(w_k, μ_k, Σ_k),k = 1,…,K}, the population problem involves estimating φ given the observation data{Y₁,…,Y_n}. The maximum likelihood estimate (MLE) can be obtained by maximizing the overall data likelihood L with respect to φ. Under the i.i.d. assumption of the individual parameters {θ_i}, L is given by the expression

$$L(\phi )=\prod _{i=1}^n\int p({\mathbf{Y}}_i\mid {\mathbf{\theta }}_i,\mathbf{\beta })\sum _{k=1}^K{w}_{k}p({\mathbf{\theta }}_i\mid {\mathbf{\mu }}_k,{\mathbf{\sum }}_k)d{\mathbf{\theta }}_i.$$ (3)

The MLE of φ is defined as φ_ML with L(φ_ML) ≥ L(φ) for all φ in the parameter space.

3. Solution via the EM Algorithm

The EM algorithm, originally introduced by Dempster, Laird and Rubin (1977), is a widely applicable approach to the iterative computation of MLEs. It was used by Schumitzky (1995) and Walker (1996) to solve the nonlinear random effects maximum likelihood problem for a second stage model consisting of a single normal distribution. The EM algorithm is typically formulated in terms of “complete” versus “missing” data structure. Consider the model given by (1) and (2) for the important case

$${\mathbf{G}}_i({\mathbf{\theta }}_i,\mathbf{\beta })={\sigma }^2{\mathbf{H}}_i({\mathbf{\theta }}_i)$$ (4)

where H_i (θ_i) is a known function and β = σ². The component label vector z_i is introduced as a K dimensional indicator such that z_i (k) is one or zero depending on whether or not the parameter θ_i arises from the kth mixing component. The individual subject parameters (θ₁,…,θ_n) are regarded as unobserved random variables. The “complete” data is then represented by Y_c = {(Y_i, θ_i, z_i),i = 1,…,n} with {θ_i, z_i} representing the “missing” data.

The algorithm starts with φ⁽⁰⁾ and moves from φ^(r) to φ^(r+1) at the rth iteration. At the E-step, define

$$Q(\phi ,{\phi }^{(r)})=E\{log{L}_c(\phi )\mid \mathbf{Y},{\phi }^{(r)}\},$$

where log L_c (φ) is the complete data likelihood given by

$$log{L}_c(\phi )=\sum _{i=1}^n\sum _{k=1}^K{z}_i(k)logp({\mathbf{Y}}_i,{\mathbf{\theta }}_i\mid {\sigma }^2,{\mathbf{\mu }}_k,{\mathbf{\sum }}_k).$$ (5)

Now

$$E\{z_i(k)\mid \mathbf{Y},\phi \}=pr\{z_i(k)=1\mid \mathbf{Y},\phi \}={\tau }_i(k),$$

and by Bayes’ Theorem,

$${\tau }_i(k)=\frac{w_{k}p({\mathbf{Y}}_i\mid {\sigma }^2,{\mathbf{\mu }}_k,{\mathbf{\sum }}_k)}{{\displaystyle \sum _{k=1}^K}{w}_{k}p({\mathbf{Y}}_i\mid {\sigma }^2,{\mathbf{\mu }}_k,{\mathbf{\sum }}_k)}=\frac{w_k\int p({\mathbf{Y}}_i\mid {\sigma }^2,{\mathbf{\theta }}_i)p({\mathbf{\theta }}_i\mid {\mathbf{\mu }}_k,{\mathbf{\sum }}_k)d{\mathbf{\theta }}_i}{{\displaystyle \sum _{k=1}^K}{w}_k\int p({\mathbf{Y}}_i\mid {\sigma }^2,{\mathbf{\theta }}_i)p({\mathbf{\theta }}_i\mid {\mathbf{\mu }}_k,{\mathbf{\sum }}_k)d{\mathbf{\theta }}_i}.$$

Introducing the notation

$$g_{ik}({\mathbf{\theta }}_i,\phi )=\frac{w_{k}p({\mathbf{Y}}_i\mid {\sigma }^2,{\mathbf{\theta }}_i)p({\mathbf{\theta }}_i\mid {\mathbf{\mu }}_k,{\mathbf{\sum }}_k)}{{\displaystyle \sum _{k=1}^K}{w}_k\int p({\mathbf{Y}}_i\mid {\sigma }^2,{\mathbf{\theta }}_i)p({\mathbf{\theta }}_i\mid {\mathbf{\mu }}_k,{\mathbf{\sum }}_k)d{\mathbf{\theta }}_i},$$

then

$${\tau }_i(k)=\int g_{ik}({\mathbf{\theta }}_i,\phi )d{\mathbf{\theta }}_i.$$

The expected value of (5) is given by

$$Q(\phi ,{\phi }^{(r)})=\sum _{i=1}^n\int g_{ik}({\mathbf{\theta }}_i,{\phi }^{(r)})logp({\mathbf{Y}}_i,{\mathbf{\theta }}_i\mid {\sigma }^2,{\mathbf{\mu }}_k,{\mathbf{\sum }}_k)d{\mathbf{\theta }}_i,$$

where

$$logp({\mathbf{Y}}_i,{\mathbf{\theta }}_i\mid {\sigma }^2,{\mathbf{\mu }}_k,{\mathbf{\sum }}_k)=C-\frac{m_i}{2}log({\sigma }^2)-\frac{1}{2{\sigma }^2}{({\mathbf{Y}}_i-{\mathbf{h}}_i({\mathbf{\theta }}_i))}^T{\mathbf{H}}_i{({\mathbf{\theta }}_i)}^{-1}({\mathbf{Y}}_i-{\mathbf{h}}_i({\mathbf{\theta }}_i))-\frac{1}{2}{({\mathbf{\theta }}_i-{\mathbf{\mu }}_k)}^T{{\mathbf{\sum }}_k}^{-1}({\mathbf{\theta }}_i-{\mathbf{\mu }}_k)-\frac{1}{2}log\mid {\mathbf{\sum }}_k\mid$$

for some constant C.

The M-step takes φ^(r) → φ^(r+1) where φ^(r+1) is the unique optimizer of Q(φ, φ^(r)) such that ${\phi }^{(r+1)}=\underset{\phi }{argmax}Q(\phi ,{\phi }^{(r)})$. Let φ′ = {β,(μ_k, Σ_k), k=1,…, K}, then the optimizer of Q(φ, φ^(r)) relative to φ′ occurs at interior points, and the corresponding components of φ^(r+1) are the unique solution to

$${\frac{\partial }{\partial {\phi }^{\prime }}Q(\phi ,{\phi }^{(r)})\mid }_{{\phi }^{(r+1)}}=0.$$ (6)

From the expression of log p(Y_i, θ_i | σ², μ_k, Σ_k),

$$\frac{\partial }{\partial {\mathbf{\mu }}_k}log{L}_c(\phi )=\sum _{i=1}^n\sum _{k=1}^K{z}_i(k)\{{({\mathbf{\sum }}_k)}^{-1}({\mathbf{\theta }}_i-{\mathbf{\mu }}_k)\},$$

so

$$E\{\frac{\partial }{\partial {\mathbf{\mu }}_k}log{L}_c(\phi )\mid \mathbf{Y},{\phi }^{(r)}\}=\sum _{i=1}^n\int g_{ik}({\mathbf{\theta }}_i,{\phi }^{(r)})\{{{\mathbf{\sum }}_k}^{-1}({\mathbf{\theta }}_i-{\mathbf{\mu }}_k)\}d{\mathbf{\theta }}_i.$$

Also,

$$\frac{\partial }{\partial {\mathbf{\sum }}_k}log{L}_c(\phi )=\sum _{i=1}^n\sum _{k=1}^K{z}_i(k)\{\frac{1}{2}{{\mathbf{\sum }}_k}^{-1}({\mathbf{\theta }}_i-{\mathbf{\mu }}_k){({\mathbf{\theta }}_i-{\mathbf{\mu }}_k)}^T{{\mathbf{\sum }}_k}^{-1}-\frac{1}{2}{{\mathbf{\sum }}_k}^{-1}\}$$

and

$$\frac{\partial }{\partial ({\sigma }^2)}log{L}_c(\phi )=\sum _{i=1}^n\sum _{k=1}^K{z}_i(k)\{-\frac{m_i}{2}\frac{1}{{\sigma }^2}+\frac{1}{2}\frac{{({\mathbf{Y}}_i-{\mathbf{h}}_i({\mathbf{\theta }}_i))}^T{\mathbf{H}}_i{({\mathbf{\theta }}_i)}^{-1}({\mathbf{Y}}_i-{\mathbf{h}}_i({\mathbf{\theta }}_i))}{{\sigma }^4}\}.$$

The unique solution of (6) is thus given by

$${\mathbf{\mu }}_k^{(r+1)}=\frac{{\displaystyle \sum _{i=1}^n}\int {\mathbf{\theta }}_i{g}_{ik}({\mathbf{\theta }}_i,{\phi }^{(r)})d{\mathbf{\theta }}_i}{{\displaystyle \sum _{i=1}^n}\int g_{ik}({\mathbf{\theta }}_i,{\phi }^{(r)})d{\mathbf{\theta }}_i},$$ (7)

$${\mathbf{\sum }}_k^{(r+1)}=\frac{{\displaystyle \sum _{i=1}^n}\int ({\mathbf{\theta }}_i-{{\mathbf{\mu }}_k}^{(r+1)}){({\mathbf{\theta }}_i-{{\mathbf{\mu }}_k}^{(r+1)})}^T{g}_{ik}({\mathbf{\theta }}_i,{\phi }^{(r)})d{\mathbf{\theta }}_i}{{\displaystyle \sum _{i=1}^n}\int g_{ik}({\mathbf{\theta }}_i,{\phi }^{(r)})d{\mathbf{\theta }}_i},$$ (8)

and

$${({\sigma }^2)}^{(r+1)}=\frac{{\displaystyle \sum _{i=1}^n}{\displaystyle \sum _{k=1}^K}\int {({\mathbf{Y}}_i-{\mathbf{h}}_i({\mathbf{\theta }}_i))}^T{\mathbf{H}}_i{({\mathbf{\theta }}_i)}^{-1}({\mathbf{Y}}_i-{\mathbf{h}}_i({\mathbf{\theta }}_i))g_{ik}({\mathbf{\theta }}_i,{\phi }^{(r)})d{\mathbf{\theta }}_i}{{\displaystyle \sum _{i=1}^n}{m}_i}.$$ (9)

The updated estimates {w_k^(r+1)} are calculated independently. If z_i were observable, then the MLE of w_k would be ${\widehat{w}}_k=\frac{1}{n}{\displaystyle \sum _{i=1}^n}{z}_i(k)$. By replacing each z_i by its conditional expectation from the E step, the updating for w_k is given by (see McLachlan and Peel, 2000):

$${w_k}^{(r+1)}=\frac{1}{n}\sum _{i=1}^n{\tau }_i(k)=\frac{1}{n}\int g_{ik}({\mathbf{\theta }}_i,{\phi }^{(r)})d{\mathbf{\theta }}_i.$$ (10)

Dempster et al. (1977) showed that the resulting sequence {φ^(r+1)} has the likelihood improving property L (φ^{(r +1)}) ≥ L(φ^(r)). It can be shown that the above updates are well-defined, that is for all 1 ≤ k ≤ K, if $w_k^{(0)}>0$ then $w_k^{(r+1)}>0$ so that ${\displaystyle \sum _{i=1}^n}\int g_{ik}({\mathbf{\theta }}_i,{\phi }^{(r)})d{\mathbf{\theta }}_i>0$ and ${\mathbf{\sum }}_k^{(r+1)}$ are positive definite. Wu (1983) and Tseng (2005) gave the sufficient conditions for the convergence of φ^(r) to a stationary point of the likelihood function L(φ). A number of starting positions are suggested, however, in an effort to ensure convergence to a global maximum.

In order to implement the algorithm all the integrals in (7)–(10) must be evaluated at each iterative step. For the non-mixture problem involving a relatively simple pharmacokinetic model, Walker (1996) proposed Monte Carlo integration to evaluate the required integrals. We and others (Ng et al., 2005) have found that importance sampling is preferable to the Monte Carlo integration for approximating the integrals in the EM algorithm for a number of representative models of interest in PK/PD. We have also applied importance sampling to the current mixture model.

We note that all the integrals above have the following form

$$\int f({\mathbf{\theta }}_i)g_{ik}({\mathbf{\theta }}_i,\phi )d{\mathbf{\theta }}_i=\frac{\int f({\mathbf{\theta }}_i)w_{k}p({\mathbf{Y}}_i\mid {\sigma }^2,{\mathbf{\theta }}_i)p({\mathbf{\theta }}_i\mid {\mathbf{\mu }}_k,{\mathbf{\sum }}_k)d{\mathbf{\theta }}_i}{{\displaystyle \sum _{k=1}^K}\int w_{k}p({\mathbf{Y}}_i\mid {\sigma }^2,{\mathbf{\theta }}_i)p({\mathbf{\theta }}_i\mid {\mathbf{\mu }}_k,{\mathbf{\sum }}_k)d{\mathbf{\theta }}_i}.$$

For each mixing component, a numbers of samples are taken from an envelope distribution, ${\mathbf{\theta }}_{i(k)}^{(1)},\dots ,{\mathbf{\theta }}_{i(k)}^{(T)}{\sim }_{i.i.d.}{p}_{e(k)}({\mathbf{\theta }}_i)$, and used to approximate the integrals as follows

$$\int f({\mathbf{\theta }}_i)g_{ik}({\mathbf{\theta }}_i,\phi )d{\mathbf{\theta }}_i\cong \frac{{\displaystyle \sum _{l=1}^T}f\left({\mathbf{\theta }}_{i(k)}^{(l)}\right)w_{k}p({\mathbf{Y}}_i\mid {\sigma }^2,{\mathbf{\theta }}_{i(k)}^{(l)})p({\mathbf{\theta }}_{i(k)}^{(l)}\mid {\mathbf{\mu }}_k,{\mathbf{\sum }}_k)/p_{e(k)}({\mathbf{\theta }}_{i(k)}^{(l)})}{{\displaystyle \sum _{k=1}^K}{\displaystyle \sum _{l=1}^T}{w}_{k}p({\mathbf{Y}}_i\mid {\sigma }^2,{\mathbf{\theta }}_{i(k)}^{(l)})p({\mathbf{\theta }}_{i(k)}^{(l)}\mid {\mathbf{\mu }}_k,{\mathbf{\sum }}_k)/p_{e(k)}({\mathbf{\theta }}_{i(k)}^{(l)})}.$$ (11)

For each mixing component for each subject, the envelope distribution is taken to be a multivariate normal density using the subject’s previously estimated conditional mean and conditional covariance as its mean and covariance. Therefore all the random samples are independent and individual specific. For details of the importance sampling approach in general, see Geweke (1989). The number of independent samples, T, will depend on the complexity of the model and the required accuracy in the integral approximations.

4. Classification of Subjects

It is of interest to assign each individual subject to a subpopulation. Such a classification will allow further investigation into the genetic basis of any identified PK/PD polymorphism. The quantity τ_i (k) = E{z_i (k) | Y, φ} in the E step is the posterior probability that the ith individual belongs to the kth mixing component. The classification involves assigning an individual to the subpopulation associated with the highest posterior probability of membership. For example, for each i, (i =1,…,n), set

$${\widehat{z}}_i(k)=1\text{if}k=arg\underset{c}{max}{\tau }_i(c),$$

or to zero otherwise. No additional computation is required since all the τ_i (k) are evaluated during each EM step.

5. Standard Errors

Assuming the regularity conditions from Philppou and Roussas (1975), it can be shown that asymptotically as n → ∞,

$$\mathit{Cov}({\phi }_{ML})\approx {(\sum _{i=1}^n{\mathbf{V}}_i({\phi }_{ML}))}^{-1},$$

where ${\mathbf{V}}_i(\phi )=(\frac{\partial }{\partial \phi }logp({\mathbf{Y}}_i\mid \phi )){(\frac{\partial }{\partial \phi }logp({\mathbf{Y}}_i\mid \phi ))}^T$.

Now

$$\frac{\partial }{\partial \phi }logp({\mathbf{Y}}_i\mid \phi )=\sum _{k=1}^K\int \{\frac{\partial }{\partial \phi }logp({\mathbf{Y}}_i,{\mathbf{\theta }}_i\mid \phi )\}{g}_{ik}({\mathbf{\theta }}_i,\phi )d{\mathbf{\theta }}_i,$$

and the gradient components are calculated for k=1,…,K as

$$\begin{array}{c}{\mathbf{s}}_{{\mathbf{\mu }}_k}=\frac{\partial }{\partial {\mathbf{\mu }}_k}logp({\mathbf{Y}}_i\mid \phi )=\int g_{ik}({\mathbf{\theta }}_i,\phi )\{{{\mathbf{\sum }}_k}^{-1}({\mathbf{\theta }}_i-{\mathbf{\mu }}_k)\}d{\mathbf{\theta }}_i,\\ {\mathbf{s}}_{{\mathbf{\sum }}_k}=\frac{\partial }{\partial {\mathbf{\sum }}_k}logp({\mathbf{Y}}_i\mid \phi )=\int g_{ik}({\mathbf{\theta }}_i,\phi )\{(-\frac{1}{2}){{\mathbf{\sum }}_k}^{-1}+\frac{1}{2}{{\mathbf{\sum }}_k}^{-1}({\mathbf{\theta }}_i-{\mathbf{\mu }}_k){({\mathbf{\theta }}_i-{\mathbf{\mu }}_k)}^T{{\mathbf{\sum }}_k}^{-1}\}d{\mathbf{\theta }}_i,\\ {\mathbf{s}}_{{\sigma }^2}=\frac{\partial }{\partial {\sigma }^2}logp({\mathbf{Y}}_i\mid \phi )=\sum _{k=1}^K\int g_{ik}({\mathbf{\theta }}_i,\phi )\{-\frac{1}{2}\frac{m_i}{{\sigma }^2}+\frac{1}{2}\frac{{({\mathbf{Y}}_i-{\mathbf{h}}_i({\mathbf{\theta }}_i))}^T{{\mathbf{H}}_i}^{-1}({\mathbf{\theta }}_i)({\mathbf{Y}}_i-{\mathbf{h}}_i({\mathbf{\theta }}_i))}{{\sigma }^4}\}d{\mathbf{\theta }}_i,\end{array}$$

and for k=1,…,K−1,

$$s_{w_k}=\frac{\partial }{\partial w_k}logp({\mathbf{Y}}_i\mid \phi )=\frac{1}{w_k}\int g_{ik}({\mathbf{\theta }}_i,\phi )d{\mathbf{\theta }}_i-\frac{1}{w_K}\int g_{iK}({\mathbf{\theta }}_i,\phi )d{\mathbf{\theta }}_i.$$

Introduce the notation s_ϖk = ((s_Σk)_1,1, (s_Σk)_2,1 …, (s_Σk)_{p, p}), where (s_Σk)_{i, j} is the component of the lower triangular part of s_Σk in the (i, j) position. Put these results together to produce the vector

$${\mathbf{s}}_i=({\mathbf{s}}_{{\mathbf{\mu }}_1},\dots ,{\mathbf{s}}_{{\mathbf{\mu }}_K},{\mathbf{s}}_{{\varpi }_1},\dots ,{\mathbf{s}}_{{\varpi }_K},s_{w_1},\dots ,s_{w_{K-1}},s_{{\sigma }^2}),$$

so

$$\mathit{Cov}({\phi }_{ML})={(\sum _{i=1}^n{\mathbf{s}}_i{{\mathbf{s}}_i}^T)}^{-1}.$$

All the computations can be performed during the importance sampler calculation at the final iteration of the EM algorithm.

6. Example

In this section a simulation study is conducted to evaluate the proposed algorithm for calculating the exact MLEs for a population finite mixture model. A one compartment pharmacokinetic model is used, with the observations of plasma concentration given by

$$y_{ji}=\frac{D}{V_i}exp(-k_i\ast t_j)(1+{\epsilon }_{ji}),$$

where D is a bolus drug administration with 100 units of dose, V represents the volume of distribution and k is the elimination rate constant. For all the individuals, m_i = 5 with t₁ = 1.5, t₂ = 2, t₃ = 3, t₄ = 4 and t₅ = 5.5. The within-individual error is assumed to be i.i.d. with variance 0.01. Data sets were simulated from this model for each of 100 subjects sampled from the following population model:

$$\begin{array}{c}{V}_i{\sim }_{i.i.d}N(20,2^2),\\ k_i{\sim }_{i.i.d}0.8N(0.3,{0.06}^2)+0.2N(0.6,{0.06}^2),\end{array}$$

where V_i and k_i are assumed to be independent. A total of 200 such population data sets were generated. This model represents the pharmacokinetics of a drug with an elimination that can be characterized by two distinct subpopulations.

The formulation of Section 2 has been modified to accommodate the important case where a subset of parameters are modeled by a multivariate normal distribution and the remaining parameters follow a mixture of normals (see modified updating formulas in the Appendix). The MLEs were obtained for each of the 200 population sets using the EM algorithm with importance sampling described above. For each of the estimated parameters φ, its percent prediction error was calculated for each population data set as:

$${\text{pe}}_j=100\times ({\phi }_j^{\text{ML}}-{\phi }_j)/{\phi }_j,j=1,\dots ,200.$$

These percent prediction errors were used to calculate the mean prediction error and root mean square prediction error for each parameter. In addition, for each population data set, the calculated standard errors were used to construct 95% confidence intervals for all estimated parameters. The percent coverage of these confidence intervals was then tabulated over the 200 population data sets. Finally, the individual subject classification accuracy was evaluated for each population data set.

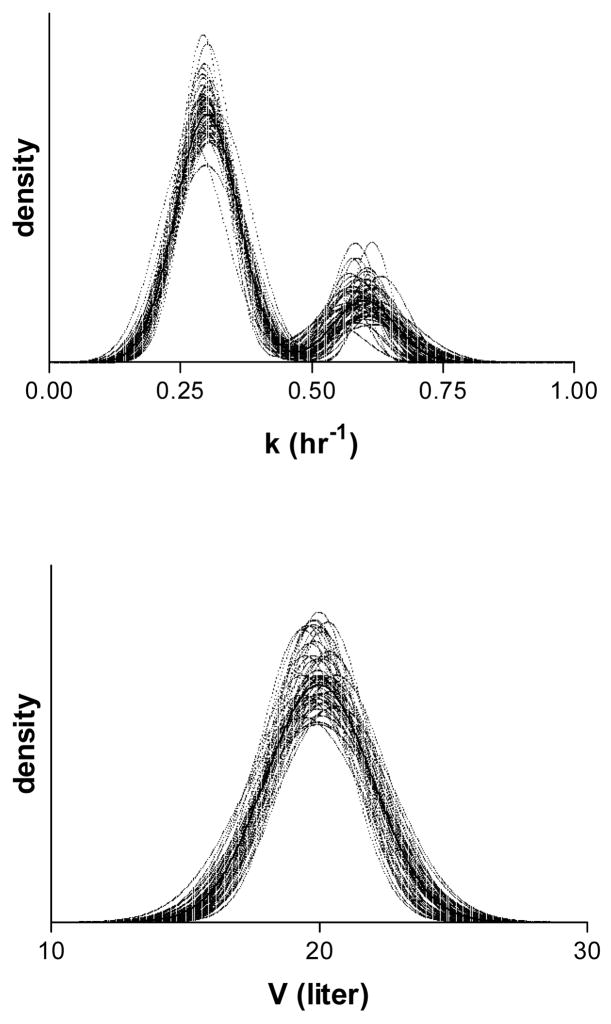
Figure 1 provides a graphical illustration of the results showing the true population distributions of V and k along with the estimated distribution obtained from the 200 simulated population data sets. Quantitative results are presented in Table 1, which gives mean and root mean square prediction errors (RMSE) as well as the percent coverage of the calculated confidence intervals for each of the estimated parameters. The parameter estimates, overall, match the population values and the percent coverage of confidence intervals is reasonable. The estimates of population variance have relatively greater biases and RMSE. Over the 200 population data sets, on average 1.54 out of 100 subjects were classified in the wrong subpopulation. The largest number of subjects misclassified was 4, while all the subjects were correctly classified in 83 of the 200 population data sets.

Fig. 1.

True (solid line) and estimated (dotted line) population densities of k (upper panel) and V (lower panel) from the population simulation analysis.

Table 1.

Mean of parameter estimates (over 200 simulations); Mean percent prediction error (PE) and root mean square percent prediction error (RMSE); Percent coverage of 95% confidence interval

Parameter	Population Values	Mean of Estimates	Mean PE (%)	RMSE (%)	Coverage of 95% CI (%)
μV	20	19.978	0.043586	1.0399	94.5
μk1	0.3	0.29982	−0.09045	1.6491	96.5
μk2	0.6	0.60029	0.10042	2.6455	90.5
w1	0.8	0.80448	0.55991	5.4248	94.5*
σV2	4	3.7605	−5.0867	23.822	94.5
σk12	0.0036	0.003573	−1.0539	14.88	91.0
σk22	0.0036	0.003195	−10.857	40.236	83.5
σ	0.1	0.099931	−0.06857	4.0618	95.5

^*The coverage of the transformed variable $\frac{w_1}{1-w_1}$ is shown.

Central to the calculation of the MLEs is the computation of the integrals in (7)–(9), as approximated by importance sampling in our implementation. Using one of the 200 population data sets we examined the influence of the number of samples (T) used in the importance sampler, as well as the number of EM iterations required to achieve two digits of accuracy for each of the estimated parameters. Table 2 presents the parameter estimates from 50 EM iterations by using 1000, 2000 and 3000 samples in the important sampling. Accuracy to two digits was obtained with 1000 samples. Based on this experience, T was taken to be 1000 in this simulations study and 50 EM iterations were run on each data set.

Table 2.

Parameter estimates by importance sampling with 1000, 2000 and 3000 samples

Parameter	T=1000	T=2000	T=3000
μV	19.85039	19.84843	19.85201
μk1	0.30840	0.30837	0.30853
μk2	0.60038	0.60029	0.60079
w1	0.75164	0.75157	0.75269
σV2	5.73544	5.72227	5.70365
σk12	0.00327	0.00323	0.00328
σk22	0.00202	0.00203	0.00200
σ	0.09706	0.09687	0.09692

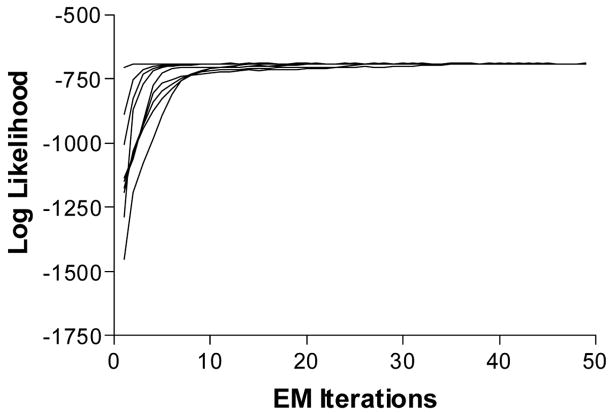
Error! Reference source not found

demonstrates the convergence of log-likelihood values for a particular data set by starting the 50 EM iterations from 9 different positions. The log-likelihood values were approximated via Monte Carlo integration

$$log\{L(\phi )\}\cong \sum _{i=1}^{n}log\{\frac{1}{T}\sum _{k=1}^K\sum _{l=1}^T{w}_{k}p({\mathbf{Y}}_i\mid {\sigma }^2,{\mathbf{\theta }}_{i(k)}^{(l)})p({\mathbf{\theta }}_{i(k)}^{(l)}\mid {\mathbf{\mu }}_k,{\mathbf{\sum }}_k)/p_{e(k)}({\mathbf{\theta }}_{i(k)}^{(l)})\},$$

where ${\mathbf{\theta }}_{i(k)}^{(1)},\dots ,{\mathbf{\theta }}_{i(k)}^{(T)}{\sim }_{i.i.d.}{p}_{e(k)}({\mathbf{\theta }}_i)$. In any particular example, of course, the number of EM iterations, the number of samples T used to approximate integrals, as well as the use of different starting guess will depend on the experiment design and complexity of the model.

7. Discussion

In this paper, an EM algorithm for maximum likelihood estimation of nonlinear random effects mixture models is presented that has application in pharmacokinetic/pharmacodynamic population modeling studies. It extends the previous work on the use of the EM algorithm for MLE of nonlinear random effects models, to the case of finite mixture models, and reinforces the practicability of using exact (no linearizing approximation) MLE estimation in PK/PD modeling studies (see also, Kuhn and Lavielle (2005) for a stochastic EM variation). The parametric mixture model MLE approach presented also complements previous work on nonparametric Bayesian and smoothed nonparametric MLE, in addressing the increasingly important problem of identifying subpopulations with distinct PK/PD properties in drug development trials. We note that approximate maximum likelihood methods using mixture models are also available in NONMEM.

The EM algorithm has been used extensively for fitting linear mixture models in numerous applications in diverse fields of study. Even for linear problems involving mixture of normal components, a number of challenges attend the use of the EM algorithm for maximum likelihood estimation (McLachlan and Peel (2000)) that are also relevant to the nonlinear random effects problem. These include: potential unboundness of the likelihood for heteroscedastic covariance components; local maxima of the likelihood function; and choice of the number of mixing components. Application of the algorithm for nonlinear random effects mixture models presented here can be guided by the extensive work related to these issues for linear mixture modeling.

We have investigated the possible unboundness of the likelihood for the example considered in this paper. If, for example, in the first component of the mixture, μ₁ satisfies h_i (μ₁) = Y_i for any i and Σ₁ → 0, then the likelihood will tend to infinity, and the global maximizer will not exist. By restricting the covariance matrices Σ_k, k = 1,…, K to be equal (homoscedastic components), as is often done in mixture modeling, the unboundness of the likelihood will be eliminated. In our example with heteroscedastic variance components, each individual has five error-associated observations, while the parameter space is of dimension two. The condition for likelihood singularity is therefore very unlikely to be satisfied.

Future work is also needed to extend the algorithm to include important practical cases involving more general error variance models and random effects covariates.

Fig. 2.

Convergence of log-likelihood by starting the EM algorithm from 9 positions.

Appendix

For the example in Section 6, as in other PK/PD problem, it is often reasonable to assume that the mechanism of genetic polymorphism applies to only part of the system, for example, drug metabolism or drug target. It is therefore desirable to partition the parameter θ_i into two components, one (α_i) that follows a mixture of multivariate normals and the second (β_i) defined by a single multivariate normal distribution: θ_i = {α_i, β_i}, where α_i and β_i are independent. The EM updates for this special case are given by:

$$\begin{array}{c}{(\mathbf{\mu }\_\mathbf{\alpha })}_k^{(r+1)}=\frac{{\displaystyle \sum _{i=1}^n}\int {\mathbf{\alpha }}_i{g}_{ik}({\mathbf{\theta }}_i,{\phi }^{(r)})d{\mathbf{\theta }}_i}{{\displaystyle \sum _{i=1}^n}\int g_{ik}({\mathbf{\theta }}_i,{\phi }^{(r)})d{\mathbf{\theta }}_i},\\ {(\mathbf{\sum }\_\mathbf{\alpha })}_k^{(r+1)}=\frac{{\displaystyle \sum _{i=1}^n}\int ({\mathbf{\alpha }}_i-{{(\mathbf{\mu }\_\mathbf{\alpha })}_k}^{(r+1)}){({\mathbf{\alpha }}_i-{{(\mathbf{\mu }\_\mathbf{\alpha })}_k}^{(r+1)})}^T{g}_{ik}({\mathbf{\theta }}_i,{\phi }^{(r)})d{\mathbf{\theta }}_i}{{\displaystyle \sum _{i=1}^n}\int g_{ik}({\mathbf{\theta }}_i,{\phi }^{(r)})d{\mathbf{\theta }}_i},\text{for}1\le k\le K;\\ {(\mathbf{\mu }\_\mathbf{\beta })}^{(r+1)}=\frac{{\displaystyle \sum _{i=1}^n}\{{\displaystyle \sum _{k=1}^K}\int {\mathbf{\beta }}_i{g}_{ik}({\mathbf{\theta }}_i,{\phi }^{(r)})d{\mathbf{\theta }}_i\}}{n},\end{array}$$

and

$${(\mathbf{\sum }\_\mathbf{\beta })}^{(r+1)}=\frac{{\displaystyle \sum _{i=1}^n}\{{\displaystyle \sum _{k=1}^K}\int ({\mathbf{\beta }}_i-{(\mathbf{\mu }\_\mathbf{\beta })}^{(r+1)}){({\mathbf{\beta }}_i-{(\mathbf{\mu }\_\mathbf{\beta })}^{(r+1)})}^T{g}_{ik}({\mathbf{\theta }}_i,{\phi }^{(r)})d{\mathbf{\theta }}_i\}}{n}.$$

The updates for {w_k, 1 ≤ k ≤ K} and σ² are the same as in Section 3.