Improving the performance of predictive process modeling for large datasets

Abstract

Advances in Geographical Information Systems (GIS) and Global Positioning Systems (GPS) enable accurate geocoding of locations where scientific data are collected. This has encouraged collection of large spatial datasets in many fields and has generated considerable interest in statistical modeling for location-referenced spatial data. The setting where the number of locations yielding observations is too large to fit the desired hierarchical spatial random effects models using Markov chain Monte Carlo methods is considered. This problem is exacerbated in spatial-temporal and multivariate settings where many observations occur at each location. The recently proposed predictive process, motivated by kriging ideas, aims to maintain the richness of desired hierarchical spatial modeling specifications in the presence of large datasets. A shortcoming of the original formulation of the predictive process is that it induces a positive bias in the non-spatial error term of the models. A modified predictive process is proposed to address this problem. The predictive process approach is knot-based leading to questions regarding knot design. An algorithm is designed to achieve approximately optimal spatial placement of knots. Detailed illustrations of the modified predictive process using multivariate spatial regression with both a simulated and a real dataset are offered.

1. Introduction

Recent advances in Geographical Information Systems (GIS) and Global Positioning Systems (GPS) enable accurate geocoding of locations where scientific data are collected. This has encouraged collection of large spatial datasets in many fields and has generated considerable interest in statistical modeling for location-referenced spatial data. This trend is particularly apparent in large-scale natural resource inventories and environmental monitoring initiatives. The data collected in these settings are commonly multivariate, with several spatial variables observed at each location. Given these data, researchers and resource analysts are typically interested in modeling how variables are associated both within and across locations. Specific interest lies in obtaining full inference for model parameters and subsequent predictions along with estimates of associated uncertainty.

Here, we focus upon the setting where the number of locations yielding observations is too large for fitting desired hierarchical spatial random effects models using Markov chain Monte Carlo methods. That is, such fitting involves matrix decompositions whose complexity increases as O(n³) in the number of locations, n, at every iteration of the MCMC algorithm, hence the infeasibility or “big n” problem for large datasets. This computational burden is exacerbated in multivariate settings with several spatially dependent response variables as well as when spatial data are collected over time.

In an effort to maintain the richness of desired hierarchical spatial modeling specifications in the presence of large datasets, Banerjee et al. (2008), proposed a class of models based upon the idea of a spatial predictive process (motivated by kriging ideas). The predictive process projects the original process onto a subspace generated by realizations of the original process at a specified set of locations (or knots). The approach is in the same spirit as process model approaches using basis functions and kernel convolutions, that is, specifications which attempt to facilitate computation through lower-dimensional process representations. A shortcoming of the original formulation of the predictive process is that it induces a positive bias in the non-spatial error term of the models. Further, Banerjee et al. (2008), identified several open questions regarding the spatial design for placement of knots.

The contribution of this paper is to address both of these issues. In particular, we extend the univariate modified predictive process offered in Finley et al. (in press), by detailing the multivariate modified predictive process that effectively partitions and removes the bias in the non-spatial error terms. Further, we offer an algorithm that places a specified number of knots such that spatially averaged prediction variance is minimized, noting that a predictive process with smaller predictive variance might be viewed as better approximation to the parent process.

The remainder of this manuscript evolves as follows. Section 2 reviews the multivariate predictive process, introduces our proposed bias reducing modification, and describes the Bayesian implementation of the proposed multivariate models. Section 3 illustrates the proposed methods with a simulated dataset and a dataset that couples forest inventory data from the USDA Forest Service Bartlett Experimental Forest with imagery from the Landsat sensor and other variables to map predicted forest biomass by tree species. Section 4 outlines our proposed improved knot design algorithm and provides a simulation study. Finally, Section 5 concludes with a brief discussion including future work.

2. Predictive process models

Geostatistical settings typically assume, at locations s ∈ D ⊆ ℜ², a response variable Y(s) along with a p × 1 vector of spatially-referenced predictors x(s) which are associated through a spatial regression model such as,

$$Y(\mathbf{s})={\mathbf{x}}^{\mathrm{T}}(\mathbf{s})\mathit{\beta }+w(\mathbf{s})+\epsilon (\mathbf{s}),$$ (1)

where w(s) is a zero-centered Gaussian Process (GP) with covariance function C(s, s′) and $\epsilon (\mathbf{s})\stackrel{\mathit{\text{iid}}}{~}N(0,{\tau }^2)$ is an independent process modeling measurement error or micro-scale variation (see, e.g., Cressie (1993)). In applications, we often specify C(s, s′) = σ² ρ(s, s′; θ) where ρ(·; θ) is a correlation function and θ includes decay and smoothness parameters, yielding a constant process variance. The likelihood for n observations Y = (Y(s₁),…,Y(s_n))^T from (1) is Y ~ N(X β, Σ_Y), with Σ_Y = C(θ) + τ²I_n, where $X={[{\mathbf{x}}^{\mathrm{T}}({\mathbf{s}}_i)]}_{i=1}^n$ is a matrix of regressors and $C(\mathit{\theta })={[C({\mathbf{s}}_i,{\mathbf{s}}_j;\mathit{\theta })]}_{i,j=1}^n$. Evidently, both estimation and prediction require evaluating the Gaussian likelihood, hence, evaluating the n × n matrix ${\Sigma }_{\mathbf{y}}^{-1}$. While explicit inversion to compute the quadratic form in the likelihood is replaced with faster linear solvers, likelihood evaluation remains expensive for big n, even more so with repeated evaluation as needed in MCMC algorithms.

Recently, Banerjee et al. (2008) proposed a class of models based upon a predictive process that operates on a specified lower-dimensional subspace by projecting the original or parent process. The lower-dimensional subspace is chosen by the user by selecting a set of “knots” ${𝓈}^{*}=\{{\mathbf{s}}_1^{*},\dots ,{\mathbf{s}}_m^{*}\}$, which may or may not form a subset of the entire collection of observed locations 𝓈. The predictive process w̃(s) is defined as the “kriging” interpolator

$$\tilde{w}(\mathbf{s})=E[w(\mathbf{s})|{\mathbf{w}}^{*}]={\mathbf{c}}^{\mathrm{T}}(\mathbf{s};\mathit{\theta })C^{*-1}(\mathit{\theta }){\mathbf{w}}^{*},$$ (2)

where ${\mathbf{w}}^{*}={[w({\mathbf{s}}_i^{*})]}_{i=1}^m~\mathit{\text{MVN}}(\mathbf{0},C^{*}(\mathit{\theta }))$ comprises the parent process realization over the knots in ${𝓈}^{*},C^{*}(\mathit{\theta })={[C({\mathbf{s}}_i^{*},{\mathbf{s}}_j^{*};\mathit{\theta })]}_{i,j=1}^m$ is the corresponding m × m covariance matrix, and $\mathbf{c}(\mathbf{s};\mathit{\theta })={[C(\mathbf{s},{\mathbf{s}}_j^{*};\mathit{\theta })]}_{j=1}^m$.

The predictive process w̃(s) ~ GP(0, C̃(·)) defined in (2) has non-stationary covariance function,

$$\tilde{C}(\mathbf{s},\mathbf{s}\prime ;\mathit{\theta })={\mathbf{c}}^{\mathrm{T}}(\mathbf{s};\mathit{\theta })C^{*-1}(\mathit{\theta })\mathbf{c}(\mathbf{s}\prime ,\mathit{\theta }),$$ (3)

and is completely specified by the parent covariance function. Realizations associated with Y are given by $\tilde{\mathbf{w}}={[\tilde{w}({\mathbf{s}}_i)]}_{i=1}^n~{\mathit{\text{MVN}}(\mathbf{0},c}^{\mathrm{T}}(\mathit{\theta }{)C}^{*-1}(\mathit{\theta })c(\mathit{\theta }))$, where c^T(θ) is the n × m matrix whose ith row is given by c^T(s_i; θ). The attractive theoretical properties of the predictive process including its role as an optimal approximator have been discussed in Banerjee et al. (2008).

The predictive process in (2) immediately extends to multivariate Gaussian process settings. For a q × 1 multivariate Gaussian parent process, w(s), the corresponding predictive process is

$$\tilde{\mathbf{w}}(\mathbf{s})=\text{Cov}(\mathbf{w}(\mathbf{s}),{\mathbf{w}}^{*}{)\text{Var}}^{-1}({\mathbf{w}}^{*}){\mathbf{w}}^{*}={𝒞}^{\mathrm{T}}(\mathbf{s};\mathit{\theta }){𝒞}^{*-1}(\mathit{\theta }){\mathbf{w}}^{*},$$ (4)

where ${\Gamma }_{\mathbf{w}}(\mathbf{s},\mathbf{s}\prime )=\text{Cov}(\mathbf{w}(\mathbf{s}),\mathbf{w}(\mathbf{s}\prime ))={[{\text{Cov}(w}_l(\mathbf{s}),w_m(\mathbf{s}\prime ))]}_{l,m=1}^q$ is the cross-covariance matrix (see, e.g., Banerjee et al. (2004)), ${𝒞}^{\mathrm{T}}(\mathbf{s};\mathit{\theta })=[{\Gamma }_{\mathbf{w}}(\mathbf{s},{\mathbf{s}}_1^{*};\mathit{\theta }),\dots ,{\Gamma }_{\mathbf{w}}(\mathbf{s},{\mathbf{s}}_m^{*};\mathit{\theta })]$ is q × mq and ${𝒞}^{*}(\mathit{\theta })={[{\Gamma }_{\mathbf{w}}({\mathbf{s}}_i^{*},{\mathbf{s}}_j^{*};\mathit{\theta })]}_{i,j=1}^m$ is the mq × mq dispersion matrix of ${\mathbf{w}}^{*}={[\mathbf{w}({\mathbf{s}}_i^{*})]}_{i=1}^m$. Eq. (4) shows w̃(s) is a zero mean q × 1 multivariate predictive process with cross-covariance matrix given by Γ_w̃(s, s′) = 𝒞^T(s; θ)𝒞^*−1(θ)𝒞(s′; θ). This is especially important for the applications we consider, where each location s yields observations on q dependent variables given by a q × 1 vector $\mathbf{Y}(\mathbf{s})={[Y_l(\mathbf{s})]}_{l=1}^q$. For each Y_l(s), we also observe a p_l × 1 vector of regressors x_l(s). Thus, for each location we have q univariate spatial regression equations which can be combined into the following multivariate regression model:

$$\mathbf{Y}(\mathbf{s})={\mathbf{X}}^{\mathrm{T}}(\mathbf{s})\mathit{\beta }+\mathbf{w}(\mathbf{s})+\epsilon (\mathbf{s}),$$ (5)

where X^T(s) is a q × p matrix $(p={\displaystyle {\sum }_{l=1}^q{p}_l)}$ having a block-diagonal structure with its lth diagonal being the 1 × p_l vector ${\mathbf{x}}_l^{\mathrm{T}}(\mathbf{s})\text{and}\mathit{\epsilon }(\mathbf{s})\stackrel{\mathit{\text{iid}}}{~}\mathit{\text{MVN}}(\mathbf{0},\Psi )$. Note that β = (β₁,…,β_p)^T is a p × 1 vector of regression coefficients with β_l being the p_l × 1 vector of regression coefficients corresponding to ${\mathbf{x}}_l^{\mathrm{T}}(\mathbf{s})$. Likelihood evaluation from (5) that involves nq × nq matrices can be reduced to mq × mq matrices by simply replacing w(s) in (5) by w̃(s).

Further computational gains in computing 𝒞^*−1(θ) can be achieved by adopting “coregionalization” methods (Wackernagel, 2003; Gelfand et al., 2004; Banerjee et al., 2008) that model ${\Gamma }_{\mathbf{w}}(\mathbf{s},\mathbf{s}\prime )=A(\mathbf{s})\text{Diag}{[{\rho }_l(\mathbf{s},\mathbf{s}\prime ;\mathit{\theta })]}_{l=1}^q{A}^{\mathrm{T}}(\mathbf{s}\prime )$, where each ρ_l(s, s′; θ) is a univariate correlation function satisfying ρ_l(s, s′; θ) → 1 as s → s′. Note that Γ_w(s, s) = A(s)A^T(s), hence $A(\mathbf{s})={\Gamma }_{\mathbf{w}}^{1/2}(\mathbf{s},\mathbf{s})$ can be taken as any square-root of Γ_w(s, s). Often we assume A(s) = A and assign an inverse-Wishart prior on AA^T with A a computationally efficient square-root (e.g., Cholesky or spectral). It now easily follows that 𝒞^*(θ) = (I_m ⊗ A) Σ^*(θ)(I_m ⊗ A^T), where Σ^*(θ) is an mq × mq matrix partitioned into q × q blocks, whose (i, j)th block is the diagonal matrix ${\text{Diag}[{\rho }_l({\mathbf{s}}_i^{*},{\mathbf{s}}_j^{*};\mathit{\theta })]}_{l=1}^q$. This yields a sparse structure and can be computed efficiently using specialized sparse matrix algorithms. Alternatively, we can write Σ^* as an orthogonally transformed matrix of an m × m block-diagonal matrix, $P^{\mathrm{T}}[{\oplus }_{l=1}^q{[{\rho }_l({\mathbf{s}}_i^{*},{\mathbf{s}}_j^{*};{\theta }_l)]}_{i,j=1}^m]P$, where ⊕ is the block-diagonal operator and P is a permutation (hence orthogonal) matrix. Since P⁻¹ = P^T, we need to invert qm × m symmetric correlation matrices rather than a single qm × qm matrix. Constructing the nq × mq matrix $\tilde{\Sigma }(\mathit{\theta })={[\text{Diag}{[{\rho }_l({\mathbf{s}}_i,{\mathbf{s}}_j^{*};\mathit{\theta })]}_{l=1}^q]}_{i,j=1}^{n,m}$, we further have

$${\text{Var}(\tilde{\mathbf{w}})=𝒞}^{\mathrm{T}}(\mathit{\theta }){𝒞}^{*-1}(\mathit{\theta })𝒞(\mathit{\theta })=(I_n\otimes A)\tilde{\Sigma }(\mathit{\theta }){\Sigma }^{*-1}(\mathit{\theta }){\tilde{\Sigma }}^{\mathrm{T}}(\mathit{\theta })(I_m\otimes A^{\mathrm{T}}),$$ (6)

where the Kronecker structures and sparse matrices render easier computations.

2.1. Modified predictive process and its implementation

The predictive process systematically underestimates the variance of the parent process w(s) at any location s. This follows immediately since we have var(w̃(s)) = c^T(s, θ)C^*−1(θ)c(s, θ), var(w(s)) = C(s, s) and that 0 ≤ var(w(s)|w^*) = C(s, s)−c^T(s, θ)C^*−1(θ)c(s, θ). In practical implementations, this often reveals itself by overestimating the nugget variance in predictive process versions of models such as (1), where the estimated τ² roughly captures the τ² + E(C(s, s) − c^T(s)C^*−1(θ)c(s)). (Here, E(C(s, s) − c^T(s)C^*−1(θ)c(s)) denotes the averaged bias underestimation over the observed locations.) Indeed, Banerjee et al. (2008) observed that while predictive process models employing a few hundred knots excelled in estimating most parameters in several complex high-dimensional models for datasets involving thousands of data points, reducing this upward bias in τ² was especially problematic.

To remedy this problem, we propose a modified predictive process, defined as ẅ(s) = w̃(s) + ε̃(s), where $\tilde{\epsilon }(\mathbf{s})\stackrel{\mathit{\text{indep}}}{~}N(0,C(\mathbf{s},\mathbf{s})-{\mathbf{c}}^{\mathrm{T}}(\mathbf{s},\mathit{\theta })C^{*-1}(\mathit{\theta })\mathbf{c}(\mathbf{s},\mathit{\theta }))$ is a process of independent variables but with spatially adaptive variances. It is now easy to see that var(ẅ(s)) = C(s, s) = var(w(s)), as desired. Furthermore, E[ẅ(s) | w^*] = w̃(s) which ensures that ẅ(s) inherits the attractive properties of w̃(s) (Banerjee et al., 2008). The adjustment for the multivariate predictive process is analogous: following (6), we have ẅ(s) = w̃(s) + ε̃(s), where ε̃(s) ~ MVN(0, Γ_w(s, s) − 𝒞^T(s, θ)𝒞^*−1(θ)𝒞(s, θ)).

For estimating the modified predictive process model corresponding to (5), we have the data likelihood from the set 𝓈 = {s₁,…,s_n} as

$$\begin{array}{ccc}\mathbf{Y}=\mathbf{X}\mathit{\beta }+{𝒞}^{\mathrm{T}}(\mathit{\theta }){𝒞}^{*-1}(\mathit{\theta }){\mathbf{w}}^{*}+\tilde{\mathit{\epsilon }}+\mathit{\epsilon };& \tilde{\mathit{\epsilon }}~N(\mathbf{0},{\Sigma }_{\tilde{\epsilon }}),& \mathit{\epsilon }~N(\mathbf{0},I_q\otimes \Psi ),\end{array}$$ (7)

where $\mathbf{Y}={[\mathbf{Y}({\mathbf{s}}_i)]}_{i=1}^n$ is the nq × 1 response vector, $\mathbf{X}={[{\mathbf{X}}^{\mathrm{T}}({\mathbf{s}}_i)]}_{i=1}^n$ is the nq × p matrix of regressors, β is the p × 1 vector of regression coefficients and ${𝒞}^{\mathrm{T}}(\mathit{\theta })={[{\Gamma }_{\mathbf{w}}({\mathbf{s}}_i,{\mathbf{s}}_j^{*};\mathit{\theta })]}_{i,j=1}^{n,m}$ is nq × mq. In addition, ${\Sigma }_{\tilde{\epsilon }}=\text{Diag}{[{\Gamma }_{\mathbf{w}}({\mathbf{s}}_{i,}{\mathbf{s}}_i)-{𝒞}^{\mathrm{T}}({\mathbf{s}}_i,\mathit{\theta }){𝒞}^{*-1}𝒞({\mathbf{s}}_i,\mathit{\theta })]}_{i=1}^n$. Given priors, model fitting employs a Gibbs sampler with Metropolis–Hastings steps using the marginalized likelihood MVN(Xβ, 𝒞^T(θ)𝒞^*−1(θ)𝒞(θ) + Σ_ε̃+ε(θ)), where ${\Sigma }_{\tilde{\epsilon }+\epsilon }(\mathit{\theta })=\text{Diag}{[\Psi +{\Gamma }_{\mathbf{w}}({\mathbf{s}}_{i,}{\mathbf{s}}_i)-{𝒞}^{\mathrm{T}}({\mathbf{s}}_i,\mathit{\theta }){𝒞}^{*-1}𝒞({\mathbf{s}}_i,\mathit{\theta })]}_{i=1}^n$. Computing the marginalized likelihood for the predictive process likelihood now requires the inverse and determinant of 𝒞^T(θ)𝒞^*−1(θ)𝒞(θ) + Σ_ε̃+ε(θ). The inverse is computed using the Sherman–Woodbury–Morrison formula, ${\Sigma }_{\tilde{\epsilon }+\epsilon }^{-1}(\mathit{\theta })-{\Sigma }_{\tilde{\epsilon }+\epsilon }^{-1}(\mathit{\theta }){𝒞}^{\mathrm{T}}(\mathit{\theta }){[{𝒞}^{*}(\mathit{\theta })+𝒞(\mathit{\theta }){\Sigma }_{\tilde{\epsilon }+\epsilon }^{-1}(\mathit{\theta }){𝒞}^{\mathrm{T}}(\mathit{\theta })]}^{-1}𝒞(\mathit{\theta }){\Sigma }_{\tilde{\epsilon }+\epsilon }^{-1}(\mathit{\theta })$, requiring mq × mq inversions instead of nq × nq inversions, while the determinant is computed as |Σ_ε̃+ε(θ)||𝒞^*(θ) + 𝒞(θ)Σ_ε̃+ε(θ)𝒞^T(θ)|/|𝒞^*(θ)|. In particular, with coregionalized models 𝒞^T(θ)𝒞^*−1(θ)𝒞(θ) can be expressed as in (6), while

$${\Sigma }_{\tilde{\epsilon }}(\mathit{\theta })=\text{Diag}[A{A}^{\mathrm{T}}-({\mathbf{1}}_m^{\mathrm{T}}\otimes A)[{\oplus }_{j=1}^m[{\oplus }_{k=1}^m{\rho }_k({\mathbf{s}}_i,{\mathbf{s}}_j^{*};\mathit{\theta })]]{\Sigma }^{*-1}(\mathit{\theta })[{\oplus }_{j=1}^m[{\oplus }_{k=1}^m{\rho }_k({\mathbf{s}}_i,{\mathbf{s}}_j^{*};\mathit{\theta })]]({\mathbf{1}}_m\otimes A^{\mathrm{T}})].$$

To complete the hierarchical specifications, customarily we set β ~ MVN(µ_β, Σ_β), while Ψ could be assigned an inverse-Wishart prior. More commonly, independence of pure error for the different responses at each site is adopted, yielding a diagonal $\Psi =\text{Diag}({\tau }_i^2{)}_{i=1}^q\text{with}{\tau }_i^2~\mathit{\text{IG}}(a_i,b_i)$. Also we model AA^T with an inverse-Wishart prior. Assigning priors to parameters within θ will again depend upon the choice of correlation function. A particularly flexible choice is the Matérn correlation function, which allows control of spatial range and smoothness (see, e.g., Stein (1999)) and is given by

$$\begin{array}{cc}\rho (\mathbf{s},\mathbf{s}\prime ;\varphi ,\nu )=\frac{1}{2^{\nu -1}\Gamma (\nu )}{(\Vert \mathbf{s}-\mathbf{s}\prime \Vert \varphi )}^{\nu }{𝒦}_{\nu }(\Vert \mathbf{s}-\mathbf{s}\prime \Vert ;\varphi );& \varphi >0,\nu >0.\end{array}$$ (8)

In (8), 𝒦_ν is a modified Bessel function of the third kind with order ν and ‖s−s′‖ is the Euclidean distance between the sites s and s′. ϕ controls the decay in spatial correlation and ν is interpreted as a smoothness parameter with higher values yielding smoother process realizations. The spatial decay parameters are generally weakly identifiable and, reasonably informative priors are needed for satisfactory MCMC behavior. Priors for the decay parameters are set relative to the size of D, e.g., prior means that imply the spatial ranges to be a chosen fraction of the maximum distance. The smoothness parameter ν is typically assigned a prior support of (0, 2) as the data can rarely inform about smoothness of higher orders.

We obtain L samples, say ${\{{\Omega }^{(l)}\}}_{l=1}^L$, from p(Ω | Data) ∝ p(β)p(A)p(θ)p(Y | β, A, θ, Ψ), where Ω = (β, A, θ, Ψ). Sampling proceeds by first updating β from an MVN(µ_β|·, Σ_β|·) distribution with ${\Sigma }_{\mathit{\beta }|·}={[{\Sigma }_{\mathit{\beta }}^{-1}+{({\mathbf{X}}^{\mathrm{T}}{𝒞}^{\mathrm{T}}(\mathit{\theta }){𝒞}^{*-1}(\mathit{\theta })𝒞(\mathit{\theta })+{\Sigma }_{\tilde{\epsilon }+\epsilon })}^{-1}\mathbf{X}]}^{-1}$ and mean µ_β|· = Σ_β|·X^T(𝒞^T(θ)𝒞^*−1(θ)𝒞(θ) + Σ_ε̃+ε)⁻¹Y. The remaining parameters are updated using Metropolis steps, possibly with block-updates (e.g. all the parameters in Ψ in one block and those in A in another). Typically, random walk Metropolis with (multivariate) normal proposals is adopted; since all parameters with positive support are converted to their logarithms, some Jacobian computation is needed. For instance, while we assign an inverted Wishart prior to AA^T, in the Metropolis update we update A, which requires transforming the prior by the Jacobian $2^k{\displaystyle {\prod }_{i=1}^k{a}_{ii}^{k-i+1}}$. Uniform priors on the spatial decay parameters will require a Hastings step due to the asymmetry in the priors.

Once the posterior samples from $P(\Omega |\mathit{\text{Data}}),{\{{\Omega }^{(l)}\}}_{l=1}^L$, have been obtained, posterior samples from P(w^* | Data) are drawn by sampling w^*(l) for each Ω^(l) from P(w^* | Ω^(l), Data). This composition sampling is routine because P(w^* | Ω, Data) is Gaussian; in fact, from (7) we have this distribution as

$$\begin{array}{c}\mathit{\text{MVN}}[{({𝒞}^{*-1}(\mathit{\theta })+{𝒞}^{*-1}(\mathit{\theta })𝒞(\mathit{\theta }){\Sigma }_{\tilde{\epsilon }+\epsilon }^{-1}{𝒞}^T(\mathit{\theta }){𝒞}^{*-1}(\mathit{\theta }))}^{-1}{𝒞}^{*-1}(\mathit{\theta })𝒞(\mathit{\theta }){\Sigma }_{\tilde{\epsilon }+\epsilon }^{-1}(\mathbf{Y}-\mathbf{X}\mathit{\beta }),\hfill \\ {({𝒞}^{*-1}(\mathit{\theta })+{𝒞}^{*-1}(\mathit{\theta })𝒞(\mathit{\theta }){\Sigma }_{\tilde{\epsilon }+\epsilon }^{-1}{𝒞}^T(\mathit{\theta }){𝒞}^{*-1}(\mathit{\theta }))}^{-1}].\hfill \end{array}$$

In some instances (e.g., prediction) we desire to recover ε̃, in which case we again use composition sampling to draw ε̃^(l) from the distribution

$$\mathit{\text{MVN}}[{({\Sigma }_{\tilde{\epsilon }}^{-1}+(I_n\otimes {\Psi }^{-1}))}^{-1}(I_n\otimes {\Psi }^{-1})(\mathbf{Y}-\mathbf{X}\mathit{\beta }-{𝒞}^{\mathrm{T}}(\mathit{\theta }){𝒞}^{*-1}(\mathit{\theta }){\mathbf{w}}^{*}),{({\Sigma }_{\tilde{\epsilon }}^{-1}+(I_n\otimes {\Psi }^{-1}))}^{-1}].$$

Once w^* and ε̃ are recovered, prediction is carried out by drawing Y^(l)(s₀), for each l = 1,…, L from a q × 1 multivariate normal distribution with mean X^T(s₀)β^(l) + 𝒞^T(θ^(l))𝒞^*−1(θ^(l))W^*(l) + ε̃^(l) and variance Ψ^(l).

3. Illustrations

We present two simulated data examples followed by an analysis of forest biomass data from a USDA Forest Service experimental forest. Our modified predictive process implementations were written in C++, leveraging threaded and processor optimized BLAS, sparse BLAS, and LAPACK routines for the required matrix computations. The most demanding model (involving 6000 spatial effects) took approximately 5 h to deliver its entire inferential output involving three chains of 25,000 MCMC iterations on two Quad-Core 3.0 GHz Intel Xeon processors with 32.0 GB of RAM running Fedora Linux. Convergence diagnostics and other posterior summarizations were implemented within the R statistical environment (http://cran.r-project.us.org) employing the CODA package.

3.1. Simulated illustrations

We start this section with an example that demonstrates the bias introduced when using the unmodified predictive process; then, a second example of a computationally demanding analysis of a large multivariate dataset that would require 6000 dimensional matrix computations.

For the first example, we generate 2000 locations within a [0, 100] × [0, 100] square and then generate the dependent variable from model (1) with an intercept as the regressor, an exponential covariance function with range parameter ϕ = 0.06 (i.e., such that the spatial correlation is ~0.05 at 50 distance units), scale σ² = 1 for the spatial process, and with nugget variance τ² = 1. We then fit the predictive process and modified predictive process models using a holding-out set of randomly selected sites, along with a separate set of regular lattices for the knots (m = 49, 144 and 900). Table 1 shows the posterior estimates and the root mean square prediction error (RMSPE) based on the prediction for the hold-out dataset. The overestimation of τ² by the unmodified predictive process is apparent and we also see how the modified predictive process is able to adjust for the τ². Not surprisingly, the RMSPE is essentially the same under either process model.

Table 1.

Parameter estimates for the predictive process and modified predictive process models in the univariate simulation

	µ	σ2	τ2	RMSPE
True	1	1	1
m = 49
Predictive process	1.365 (0.292, 2.610)	1.367 (0.652, 2.371)	1.177 (1.067, 1.230)	1.2059
Modified process	1.363 (0.511, 2.392)	1.042 (0.522, 1.915)	0.936 (0.679, 1,140)	1.2048
m = 144
Predictive process	1.363 (0.524, 2.324)	1.387 (0.764, 2.442)	1.095 (0.959, 1.244)	1.1739
Modified process	1.332 (0.501, 2.240)	1.141 (0.643, 1.784)	0.932 (0.764, 1.223)	1.1718
m = 900
Predictive process	1.306 (0.235, 2.545)	1.121 (0.853, 1.581)	0.993 (0.851, 1.155)	1.1685
Modified process	1.307 (0.230, 2.632)	1.045 (0.763, 1.493)	0.984 (0.872, 1.210)	1.1679

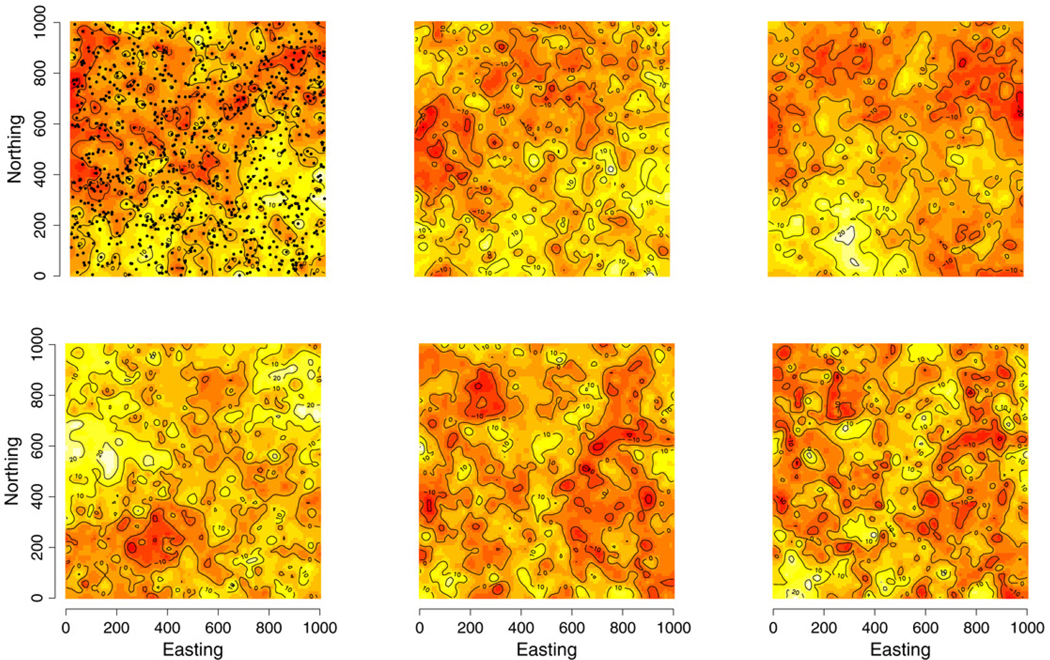
For the second example, we simulated a response vector Y(s) of length q = 6 for each of 1000 irregularly scattered locations over a [0, 1000] × [0, 1000] square domain using (5) and associated parameter values given in Table 2. Spatial association was assumed to follow the Matérn correlation function (8), with response-specific range, ϕ, and smoothness, ν, parameters indexed with subscript 1,…, 6 in Table 2. The simulated locations and interpolated surfaces of the resulting univariate responses are displayed in Fig. 1. Given these data, we considered sub-models of (5) including the non-spatial (i.e., (5) without w(s)) and spatial non-separable (i.e., coregionalized) models with several knot intensities. For the spatial models, Ψ and Γ_w are considered full q × q cross-covariance matrices. The iterative inversion of the 6000 dimension matrix (i.e., q × n = 6 × 1000) makes fitting the full spatial models computationally challenging. Therefore, the candidate spatial models employ the modified predictive process and consider three knot intensities of 64, 100 and 225. Knots were located on a uniform grid over the domain. We judge the performance of these models based on the ability to recover the true parameter values, prediction of a hold-out set of 1000 locations, and visual similarity between the predicted and true response surfaces.

Table 2.

Simulated data generated with these parameter values and model (5)

Parameter	Value	Parameter	Value	Parameter	Value
Γw;1,1	50	Ψ1,1	25	β0	1
Γw;1,2	25	Ψ1,2	0	β1	1
Γw;1,3	25	Ψ1,3	0	β2	1
Γw;1,4	−25	Ψ1,4	0	β3	1
Γw;1,5	0	Ψ1,5	0	β4	1
Γw;1,6	0	Ψ1,6	0	β5	1
Γw;2,2	50	Ψ2,2	50	ϕw1	0.004
Γw;2,3	25	Ψ2,3	0	ϕw2	0.004
Γw;2,4	−25	Ψ2,4	0	ϕw3	0.004
Γw;2,5	0	Ψ2,5	0	ϕw4	0.004
Γw;2,6	0	Ψ2,6	0	ϕw5	0.015
Γw;3,3	50	Ψ3,3	25	ϕw6	0.015
Γw;3,4	−25	Ψ3,4	0	νw1	0.5
Γw;3,5	0	Ψ3,5	0	νw2	0.5
Γw;3,6	0	Ψ3,6	0	νw3	0.5
Γw;4,4	50	Ψ4,4	50	νw4	0.5
Γw;4,5	0	Ψ4,5	0	νw5	0.5
Γw;4,6	0	Ψ4,6	0	νw6	0.5
Γw;5,5	50	Ψ5,5	25	Rangew1	750
Γw;5,6	45	Ψ5,6	0	Rangew2	750
Γw;6,6	50	Ψ6,6	50	Rangew3	750
				Rangew4	750
				Rangew5	200
				Rangew6	200

Fig. 1.

Interpolated surfaces of the simulated multivariate response values over 1000 sites. Response variables ordered 1–3, top row and 4–6, bottom row. Site locations overlaid on top left panel.

Prior distributions are assigned to model parameters to complete the Bayesian specification. As is customary, a flat prior was assigned to each intercept parameter β. The cross-covariance matrices Ψ and Γ_w each receives an inverse-Wishart, IW(df, S), with the degrees of freedom set to q + 1. For Ψ and Γ_w, the scale matrix, S, was constructed with zeros on the off-diagonal elements and diagonal elements taken as the nugget and partial-sill values, respectively, from univariate semi-variograms fit to the residuals of the non-spatial multivariate model. For each response variable, the Matérn correlation function decay parameter ϕ follows a U(0.003, 3) which, when ν = 0.5, corresponds to about 1 to 1000 distance units for the effective spatial range (i.e., −log(0.05)/ϕ is the distance at which the correlation drops to 0.05). As previously noted in Section 2, ν is typically poorly identified by the data and therefore we fix it at 0.5.

For each model, we ran three initially over-dispersed chains for 25,000 iterations. Convergence diagnostics revealed 5000 iterations to be sufficient for initial burn-in and so the remaining 20,000 samples from each chain were used for posterior inference. The non-separable model with 255 knots required the most computing resources, taking approximately 5 h to complete the MCMC sampling; the non-spatial and separable models required substantially less time to collect the specified samples.

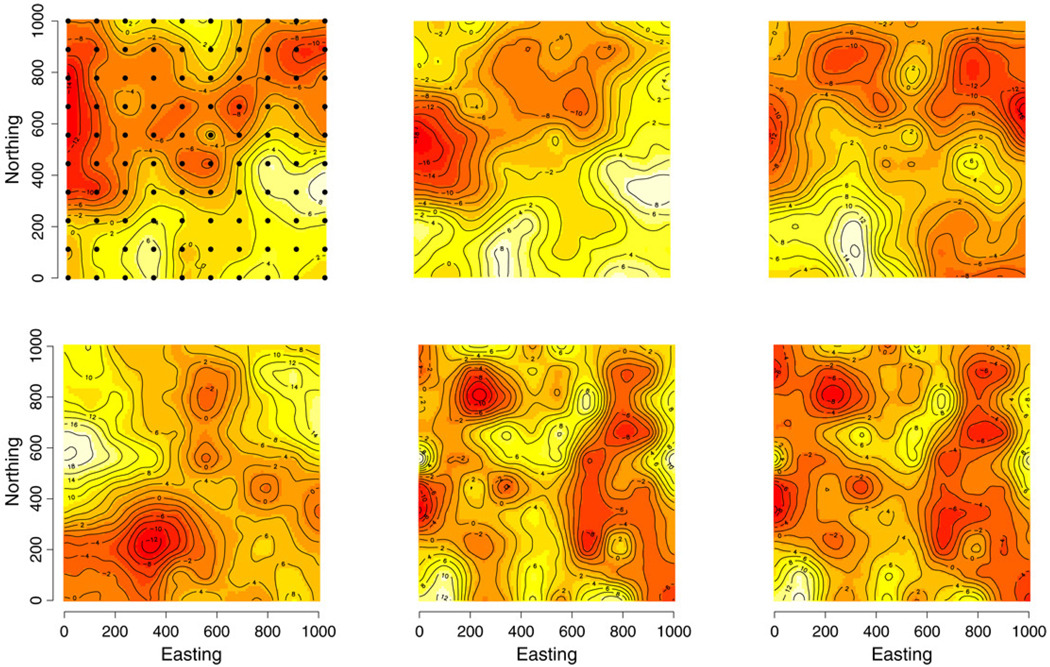
For the three knot intensities, there was negligible difference among the parameter estimates. Further, in only two instances, at the 64 knot intensity, did the estimated 95% credible interval not cover the true parameter’s value. Table 3 presents the parameter estimates for the 64 knot grid. At the 100 knot intensity and greater, all 95% credible intervals cover the true parameter values and there is a marginal tightening of the spatial range parameters. We now turn our attention to prediction of the hold-out set. The empirical coverage of 95% prediction interval for the three knot intensities 64, 100, and 255 were 91%, 93%, and 96%, respectively. There was no perceptible tightening of the prediction intervals as knot intensity increased; however, increasing the knot intensity allowed estimates of w̃ to better approximate the local trends in the residual spatial surface. Fig. 2 offers an interpolated surface for the median of the posterior predictive distribution from the 100 knot model. These prediction surfaces closely approximate the true response surfaces in Fig. 1.

Table 3.

Simulated data parameter estimates for the 64 knot non-separable modified predictive process model

Parameter	50% (2.5%, 97.5%)	Parameter	50% (2.5%, 97.5%)	Parameter	50% (2.5%, 97.5%)
Γw;1,1	41.09 (24.81, 51.56)	Ψ1,1	23.56 (20.83, 27.09)	β0	−2.19 (−7.52, 3.07)
Γw;1,2	21.94 (18.71, 25.34)	Ψ1,2	−0.22 (−1.01, 0.36)	β1	−0.54 (−5.85, 4.87)
Γw;1,3	22.42 (16.80, 25.31)	Ψ1,3	0.01 (−0.77, 0.59)	β2	−2.54 (−8.67, 2.60)
Γw;1,4	−22.98 (−25.97, −17.70)	Ψ1,4	−0.18 (−0.75, 0.51)	β3	5.09 (0.34, 10.20)
Γw;1,5	−0.12 (−1.92, 0.76)	Ψ1,5	0.39 (−0.34, 1.73)	β4	0.95 (−1.97, 3.79)
Γw;1,6	0.31 (−1.74, 2.17)	Ψ1,6	−0.42 (−1.04, 0.13)	β5	1.01 (−1.71, 3.52)
Γw;2,2	45.19 (35.86, 64.79)	Ψ2,2	50.83 (45.22, 56.46)	ϕw1	0.003 (0.003, 0.004)
Γw;2,3	24.06 (22.02, 28.40)	Ψ2,3	0.03 (−0.64, 1.35)	ϕw2	0.004 (0.003, 0.006)
Γw;2,4	−24.27 (−27.75, −22.59)	Ψ2,4	0.81 (−0.06, 1.62)	ϕw3	0.004 (0.003, 0.007)
Γw;2,5	−0.30 (−2.06, 0.86)	Ψ2,5	0.31 (−1.32, 1.97)	ϕw4	0.007 (0.004, 0.011)
Γw;2,6	−0.04 (−1.01, 0.97)	Ψ2,6	−0.22 (−1.07, 1.27)	ϕw5	0.010 (0.008, 0.012)
Γw;3,3	53.92 (42.78, 74.91)	Ψ3,3	21.12 (18.19, 24.15)	ϕw6	0.015 (0.005, 0.028)
Γw;3,4	−24.88 (−28.52, −21.90)	Ψ3,4	0.25 (−0.39, 1.07)	Rangew1	911.85 (717.70, 996.68)
Γw;3,5	−0.45 (−3.07, 1.21)	Ψ3,5	0.07 (−0.55, 1.40)	Rangew2	738.92 (487.80, 974.03)
Γw;3,6	0.46 (−0.58, 1.45)	Ψ3,6	−0.10 (−1.79, 0.33)	Rangew3	672.65 (412.65, 964.63)
Γw;4,4	55.71 (46.88, 75.40)	Ψ4,4	43.94 (34.50, 52.04)	Rangew4	439.24 (272.73, 826.45)
Γw;4,5	0.24 (−1.18, 2.93)	Ψ4,5	0.34 (−0.21, 1.82)	Rangew5	301.20 (244.50, 372.67)
Γw;4,6	−0.52 (−1.42, 1.19)	Ψ4,6	0.00 (−0.98, 2.68)	Rangew6	204.36 (107.68, 551.47)
Γw;5,5	58.53 (49.95, 74.85)	Ψ5,5	20.30 (16.23, 25.94)
Γw;5,6	49.10 (44.55, 56.00)	Ψ5,6	−0.16 (−1.60, 0.47)
Γw;6,6	49.35 (45.98, 53.66)	Ψ6,6	54.39 (48.18, 62.49)

Bold values identify those 95% credible intervals that do not include the true parameter values given in Table 2.

Fig. 2.

Interpolated surfaces of the median predicted multivariate response values over a grid of 1000 hold-out sites. The order of panels corresponds to Fig. 1. Predictions based on the 100 knot locations overlaid on top left panel.

3.2. Forest biomass prediction and mapping

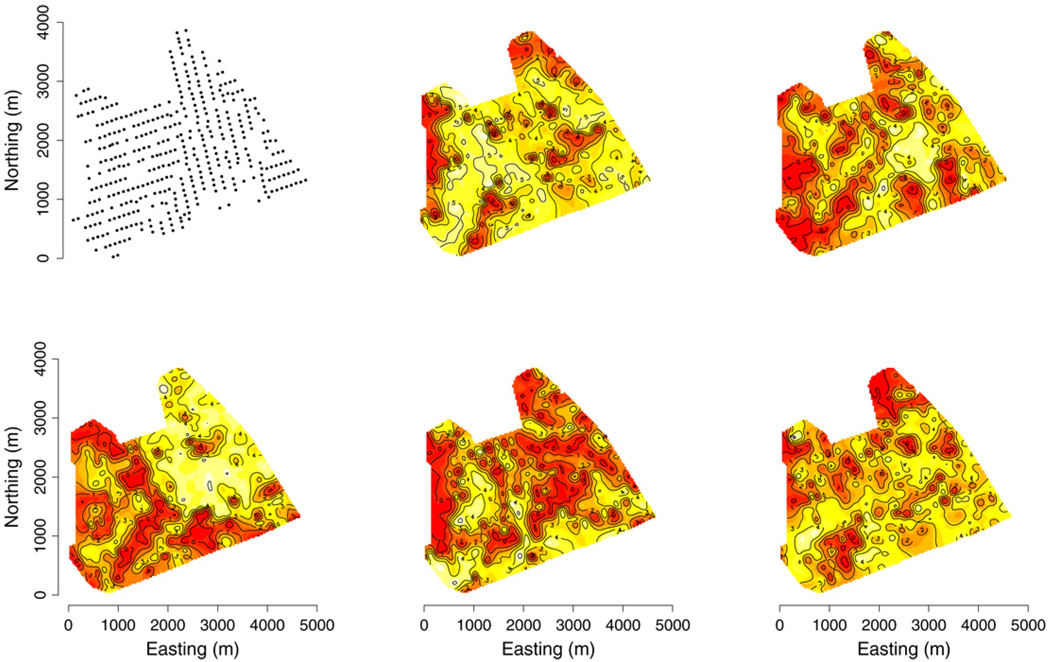
Spatial modeling of forest biomass and other variables related to measurements of current carbon stocks and flux have recently attracted much attention for quantifying the current and future ecological and economic viability of forest landscapes. Interest often lies in detecting how biomass changes across the landscape (as a continuous surface) by forest tree species. We consider point-referenced biomass (log-transformed) data observed at 437 forest inventory plots across the USDA Forest Service Bartlett Experimental Forest (BEF) in Bartlett, New Hampshire. Each location yields measurements of metric tons of above-ground biomass per hectare for American beech (BE), eastern hemlock (EH), red maple (RM), sugar maple (SM), and yellow birch (YB) and five covariates: TC1, TC2, and TC3 tasseled cap components (see Huang et al. (2002)) derived from a spring date of mid-resolution Landsat 7 ETM+ satellite imagery from the National Land Cover Database (www.mrlc.gov/mrlc2k_nlcd.asp), and; elevation (ELEV) and slope (SLOPE) derived from a digital elevation model data (see http://seamless.usgs.govfor metadata). Fig. 3 offers interpolated surfaces of the response variables. Covariates were measured on a 30 × 30 m pixel grid and are available for every location across the BEF. Interest lies in producing pixel-level prediction of biomass by species across large geographic areas. Because data layers such as these serve as input variables to subsequent forest carbon estimation models, it is crucial that each layer also provides a pixel-level measure of uncertainty in prediction. Following our discussion in Section 2.1, we see that basing prediction on a predictive process could substantially reduce the time necessary to estimate the posterior predictive distributions over a large array of pixels. A similar analysis was conducted by Finley et al. (2008); however, due to computational limitations they were only able to fit models using half of the available data and pixel-level prediction was still infeasible.

Fig. 3.

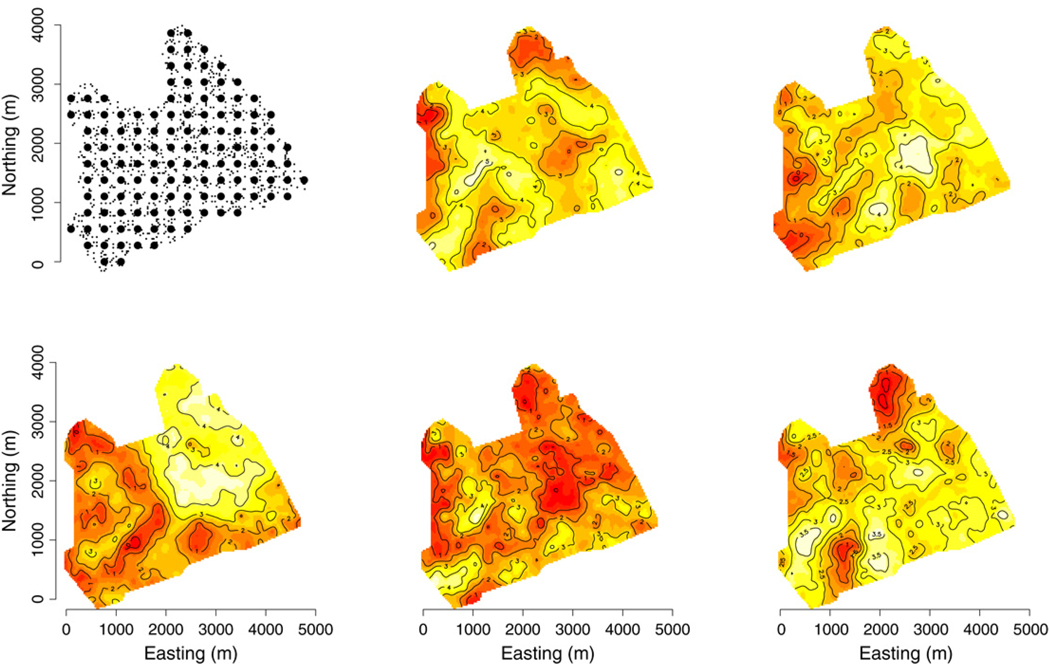
Interpolation surfaces of log-transformed metric tons of biomass per hectare by species measured on forest inventory plots across the BEF. Response variables ordered BE, EH, top row and RM, SM, YB, bottom row. The set of 437 forest inventory plots is represented as points in the top left panel.

Here we considered sub-models of (5) including the non-spatial and spatial non-separable models with the modified predictive process and three knot intensities of 51, 126, and 206. For all models Ψ and Γ_w are considered full q × q cross-covariance matrices where q = 5. Predictive process knots were located on a uniform grid within the BEF. We judge the performance of these models based on prediction of a hold-out set of 37 inventory plots, and visual similarity between the predicted and observed response surfaces.

We assigned a flat prior to each of the 30 β parameters (i.e., $p={\sum }_{l=1}^5{P}_l=30$ with each p_l including an intercept, TC1, TC2, TC3, ELEV, and SLOPE). The cross-covariance matrices Ψ and Γ_w each receives an inverse-Wishart, IW(df, S), with the degrees of freedom set to q + 1 = 6. Again, diagonal elements in the IW hyperprior scale matrix for Ψ and Γ_w were taken from univariate semi-variograms fit to the residuals of the non-spatial multivariate model. The decay parameter ϕ in the Matérn correlation function spatial follows a U(0.002, 0.06) which corresponds to an effective spatial range between 50 and 1500 m. Again, the smoothness parameter, ν, was fixed at 0.5, which reduces (8) to the common Exponential correlation function. For each model, we ran three initially over-dispersed chains for 35,000 iterations. Unlike in the simulation analysis, substantial effort was required to select tuning values that achieved acceptable Metropolis acceptance rates. Ultimately, we resorted to univariate updates of elements in Ψ^1/2 and ${\Gamma }_w^{1/2}$ to gain the control necessary to maintain an acceptance of approximately 20%. Convergence diagnostics revealed 5000 iterations to be sufficient for initial burn-in and so the remaining 30,000 samples from each chain were used for posterior inference. The 206 knot model required approximately 2 h to complete the MCMC sampling with the 106 and 51 knot models requiring substantially less time to collect the specified number of samples.

For the three knot intensities, there was negligible difference among the β parameter estimates. The estimated diagonal elements of Ψ and Γ_w for the three models were also nearly identical. Further, all of the 95% credible intervals for the off-diagonal elements in Ψ and Γ_w overlapped between the 126 and 206 knot models; however, the 206 knot model had several more significant off-diagonal elements (i.e., indicated by a credible interval that does not include zero). For the 51 knot model, off-diagonal elements of Γ_w were generally closer to zero and the corresponding elements in Ψ were significantly different from zero, suggesting that the coarseness of this knot grid could not capture the covariation among the residual spatial processes.

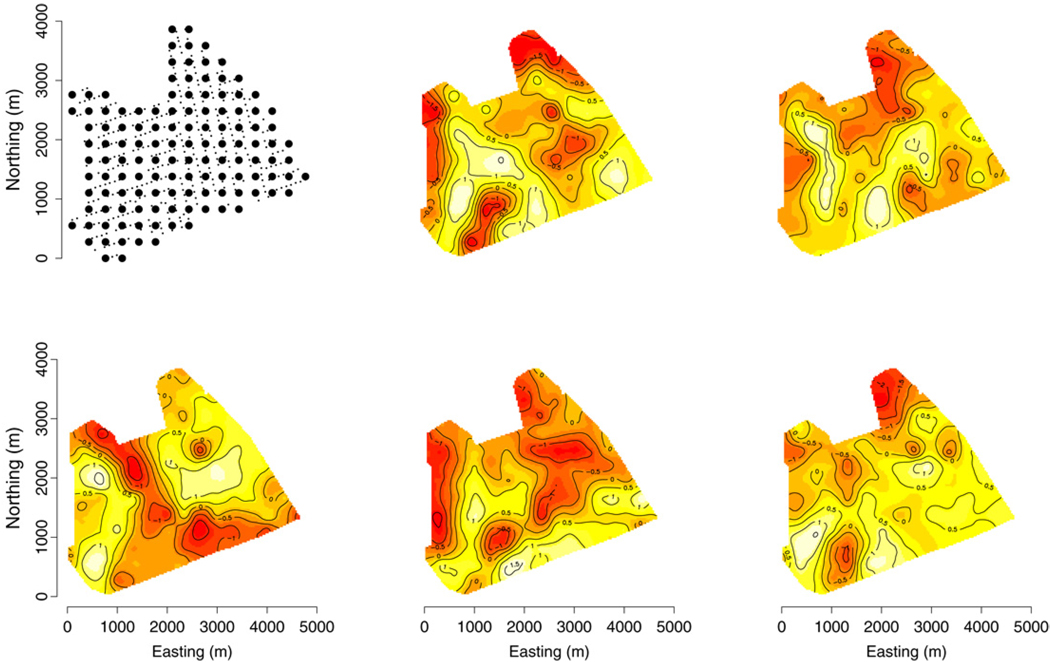
Table 4 presents the parameter estimates of Γ_w, Ψ, and ϕ for the 126 knot model. For brevity we have omitted β estimates but note that 15 were significant at the 0.05 level. Significant off-diagonal elements Γ_w;2,3 and Γ_w;1,5 in Table 4 correspond the spatial correlations between BE and YB and between EH and RM. These associations can also be seen in the interpolated surface of w̃ depicted in Fig. 4, where surface patterns are similar between BE and YB and between EH and RM.

Table 4.

BEF biomass parameter estimates for the 126 knot modified predictive process model

Parameter	50% (2.5%, 97.5%)	Parameter	50% (2.5%, 97.5%)	Parameter	50% (2.5%, 97.5%)
Γw;1,1	1.97 (1.93, 2.02)	Ψ1,1	1.95 (1.92, 1.98)	ϕw1	0.0056 (0.0033, 0.01)
Γw;1,2	0.0044 (−0.0029, 0.019)	Ψ1,2	−0.01 (−0.031, −0.0002)	ϕw2	0.0048 (0.0037, 0.0144)
Γw;1,3	−0.014 (−0.034, −0.004)	Ψ1,3	−0.0069 (−0.018, 0.001)	ϕw3	0.0028 (0.0021, 0.0053)
Γw;1,4	0.011 (−0.0004, 0.027)	Ψ1,4	0.01 (−0.0026, 0.019)	ϕw4	0.0051 (0.0035, 0.0085)
Γw;1,5	0.012 (0.0009, 0.018)	Ψ1,5	−0.0048 (−0.022, 0.013)	ϕw4	0.0059 (0.0032, 0.0102)
Γw;2,2	1.96 (1.89, 2.00)	Ψ2,2	1.92 (1.88, 1.97)	Rangew1	536.75 (296.06, 903.66)
Γw;2,3	0.017 (0.0043, 0.032)	Ψ2,3	0.0081 (−0.0001, 0.015)	Rangew2	624.72 (208.76, 806.32)
Γw;2,4	0.0032 (−0.01, 0.013)	Ψ2,4	−0.0048 (−0.012, 0.0019)	Rangew3	1085.68 (563.5, 1453.63)
Γw;2,5	0.0031 (−0.0058, 0.041)	Ψ2,5	0.011 (0.0042, 0.038)	Rangew4	586.02 (350.93, 846.24)
Γw;3,3	1.98 (1.9, 2.01)	Ψ3,3	1.97 (1.95, 1.98)	Rangew5	506.06 (293.25, 934.23)
Γw;3,4	−0.0058 (−0.015, 0.012)	Ψ3,4	−0.013 (−0.045, −0.0002)
Γw;3,5	0.016 (−0.0017, 0.029)	Ψ3,5	0.0018 (−0.0089, 0.016)
Γw;4,4	2.03 (1.99, 2.065)	Ψ4,4	1.94 (1.90, 1.98)
Γw;4,5	0.0064 (−0.0091, 0.016)	Ψ4,5	0.0044 (−0.003, 0.012)
Γw;5,5	1.91 (1.84, 2.026)	Ψ5,5	1.96 (1.93, 1.98)

Subscripts 1–6 correspond to BE, EH, RM, SM, and YB species.

Fig. 4.

Interpolated surfaces of the 126 knot model’s median w̃ at each inventory plot. Top left panel shows forest inventory plots (small points) under the 126 knots (large points). The order of response variables in the subsequent panels corresponds to Fig. 3.

Turning to prediction, it appears that the covariates and spatial proximity of observed inventory plots explain a significant portion of the variation in the response variables, perhaps leading to overfitting. We note that for our 37 hold-out plots the 95% prediction intervals are quite broad yielding a 100% empirical coverage for all three knot intensities. Finally, comparing the surface of pixel-level prediction for 1000 randomly selected pixels (Fig. 5) to the observed (Fig. 3) we see that the model can capture landscape-level variation in biomass and spatial patterns in biomass by species.

Fig. 5.

Interpolated surfaces of the 126 knot model’s median predicted response value over a random subset of 1000 pixels in the BEF. Top left panel shows the subset of prediction pixels (small points) under the 126 knots (large points). The order of response variables in the subsequent panels corresponds to Fig. 3.

As described in Finley et al. (2008), the goal of these types of modeling exercises, that couple remotely sensed covariates and georeferenced forest inventory, is to enable fine resolution prediction of forest attributes (e.g., biomass) at the landscape scale. Ideally, the remotely sensed covariates would explain all of the variation in the response variable; however, this is rarely the case and we are often left with substantial spatial dependence in the residuals, as seen here. As noted above, the computational burden of the full multivariate geostatistical model forced Finley et al. (2008) to use only half the available forest inventory plot data. Although, we considered only a subset of the covariates used in Finley et al. (2008) and worked with a log-transformed response variable, we see several common trends in the residual spatial process (e.g., significance among several cross-covariance terms). Ultimately, the predictive process model makes this analysis and subsequent pixel-level prediction trivial for even a common single processor workstation.

4. Optimal knot design

4.1. A brief review of spatial design

As with any knot-based method, selection of knots is a challenging problem with choice in two dimensions more difficult than in one. Suppose for the moment that m is given. We are essentially dealing with a problem analogous to a spatial design problem, with the difference being that we already have samples at n locations. There is a rich literature in spatial design which is summarized in, e.g., the recent paper of Xia et al. (2006). One approach would be the so-called space-filling knot selection following the design ideas of Nychka and Saltzman (1998). Such designs are based upon geometric criteria, measures of how well a given set of points covers the study region, independent of the assumed covariance function. Instead, a number of authors have investigated the problem of optimal spatial sampling design assuming a particular spatial model. Model-based design often involves the minimization of a prediction-driven design criterion which depends on the particular prediction objectives. See, for example, McBratney and Webster (1981), Ritter (1996), and Zhu (2002). A recent work by Zhu and Stein (2005) and Zimmerman (2006) considers designs to achieve good prediction and accounts for covariance parameter estimation uncertainty using the likelihood. Diggle and Lophaven (2006) discuss a Bayesian design criterion which minimizes the spatially averaged prediction variance. Their Bayesian design approach naturally combines the goal of efficient spatial prediction while allowing for uncertainty in the values of model parameters. Application-specific numerical methods are often used to find optimal solutions. For example, Zhu and Stein (2005) implement the optimization using a simulated annealing algorithm. Xia et al. (2006) consider algorithms such as sequential selection, block selection and stochastic search.

4.2. Proposed approach

For a given set of observations, our goal is to construct a knot selection strategy such that the induced predictive process is a better approximation to the parent process. For a selected set of knots, w̃(s) = E[w(s)|w^*] is considered as an approximation to the parent process. Given θ, the associated predictive variance of w(s) conditional on the predictive process w^* on 𝓈^* can be written as V_θ(s, 𝓈^*) = VAR[w(s)|w(·), 𝓈^*, θ] = C(s, s) − c^T(s, θ)^TC^*−1c(s, θ), which measures how well we approximate w(s) by the predictive process w̃(s).

One possible criterion in knot selection is then defined as a function of V_θ(s, 𝓈^*). One commonly used criterion is:

$$V_{\mathit{\theta }}({𝓈}^{*})={\displaystyle {\int }_A{V}_{\mathit{\theta }}(\mathbf{s},{𝓈}^{*})g}(\mathbf{s})\mathrm{d}\mathbf{s}={\displaystyle {\int }_A\text{VAR}[w(\mathbf{s})|\mathbf{w}(·),{𝓈}^{*},\mathit{\theta }]}g(\mathbf{s})\mathrm{d}\mathbf{s},$$

where g(s) is the weight assigned to location s. In this paper we only consider the simple case for which g(s) ≡ 1. V_θ(𝓈^*) is referred to as spatially averaged predictive variance. In our case, we compute the spatially averaged prediction variance over all the observed locations, i.e.,

$$V_{\mathit{\theta }}({𝓈}^{*})=\frac{{\displaystyle \sum _{i=1}^n\text{VAR}[w({\mathbf{s}}_i)|\mathbf{w}(·),{𝓈}^{*},\mathit{\theta }]}}{n}.$$

We ultimately reduce the problem of knot performance to the minimization of a design criterion which is the function V_θ(𝓈^*).

It can be proved that: (1) V_θ({𝓈^*, s₀})−V_θ(𝓈^*) < 0 for a new site s₀, (2) V_θ({𝓈^*, s₀})−V_θ(𝓈^*) → 0 when $\Vert {\mathbf{s}}_0-{\mathbf{s}}_i^{*}\Vert \to 0$, where ${\mathbf{s}}_i^{*}$ is any point of the knots, (3) V_θ({s₁,…, s_n}) = 0, where {s₁,…, s_n} are the original observed locations. The variance covariance matrix under the parent process model in Section 2 is Σ_Y = C + τ²I, and the variance covariance matrix from the corresponding predictive process is given by Σ_pred = c^TC^*−1c + τ²I. The Frobenius norm between Σ_Y and Σ_pred is ‖Σ_Y − Σ_pred‖ ≡ tr(C − c^TC^*−1c)². Since C − c^TC^*−1c is positive definite, the Frobenius norm $\Vert {\Sigma }_{\mathbf{Y}}-{\Sigma }_{\mathit{\text{pred}}}\Vert \equiv {{\displaystyle \sum \lambda }}_i^2$, where λ_i is the ith eigenvalue of Σ_Y − Σ_pred. Also, the averaged predictive variance V = tr(Σ_Y − Σ_pred)/n = ∑ λ_i/n.

In practice, the values of covariance parameters have to be estimated under the assumed model. An option is to obtain the parameter estimations by using a subset of original data or fitting the predictive process model based on a regular lattice of knots. (That is what we do.) Another option is to adopt a Bayesian criterion, which places a prior on θ and then minimizes E_θ(V_θ(𝓈^*)) (see, Diggle and Lophaven (2006)).

Suppose the values of the parameters and the knot size m are given. We consider the following sequential search algorithm approach to find the approximately optimal design:

• Initialization: specify allowable sampling locations of size N; possible choices include a fine grid, the observed locations or the union of these two sets.

• Specify a set of locations of size n₀ as starting points for knot selection; possible choices include a regular grid, or a subset of the observed locations chosen randomly or deterministically.

• At step t + 1,

  • For each sample point s_i in the allowable sample set, evaluate V({𝓈^*(t), s_i}).
  • Remove the sample point with maximum decrease in V from the allowable sample set and add it to the knot set.

• Repeat the above procedure until we obtain m points in knot set.

The sequential evaluation of V is achieved using a very efficient algorithm incorporating block-matrix computation. We have successfully implemented the sequential algorithm in a simulation study shown in Section 4.3. We remark that the sequential algorithm does not necessarily achieve the global optimization solution. Alternative computational approaches are available to be used in finding approximately optimal designs such as stochastic search and block selection (see Xia et al. (2006)).

As for the choice of m, the obvious answer is “as large as possible”. Evidently, this is governed by computational cost and sensitivity to choice. So, in principle, we will have to implement the analysis over different choices of m and consider run time along with stability of predictive inference; in our case, the value of minimized V under different choices of m.

Finally, we can perform a two-step analysis by combining this knot selection procedure with the modified predictive process in a natural way: (1) choose a set of knots to minimize the averaged predictive variances; (2) then use the modified process in the model fitting.

4.3. A simulation example using the two-step analysis

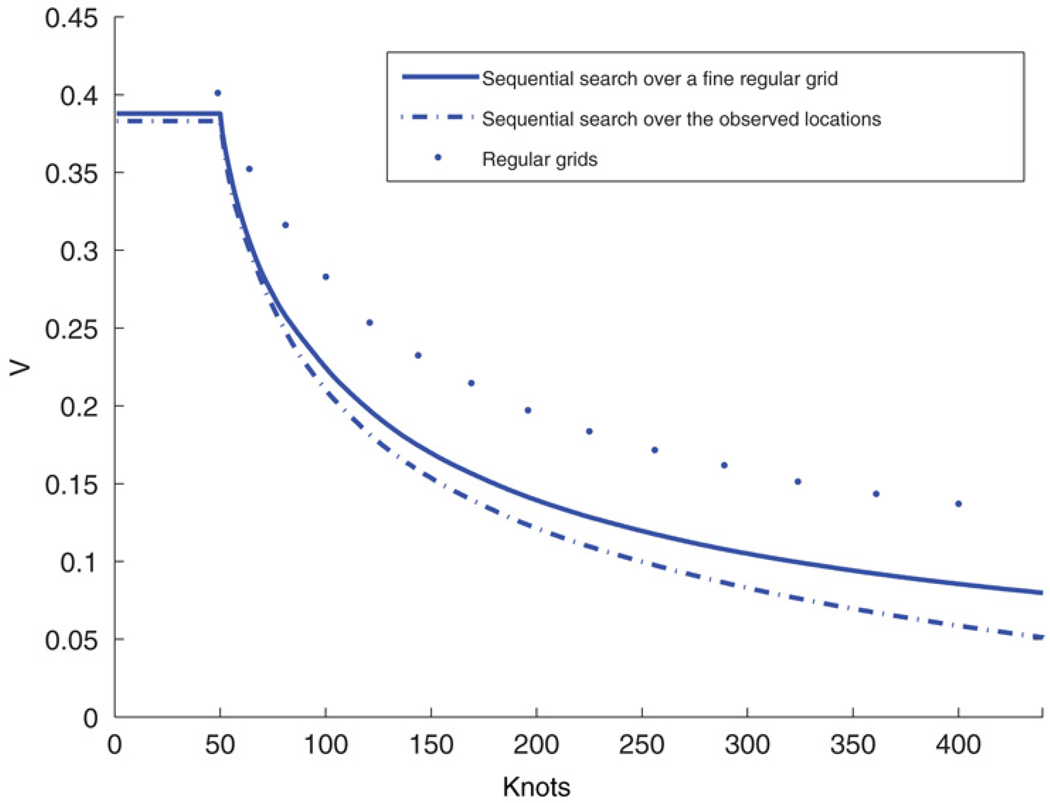
We generated 1000 data points in a [0, 100] × [0, 100] square and then generated the dependent variable from model (1) with an intercept µ = 1 as a regressor, an exponential covariance function with range parameter ϕ = 0.06 (i.e., an effective range of ~50 units), scale σ = 1 for the spatial process, and with nugget variance τ² = 1. We illustrate a comparison among three design strategies, including regular grids, sequential search over all the observed locations and sequential search over a fine regular lattice. In Fig. 6, we plot the averaged predictive variances under each strategy. Sequential search algorithm is clearly better than choosing a regular grid as knots. For instance, with 180 sites selected, sequential search over the observed locations yielded an averaged predictive variance approximately 0.15. For the regular grids, roughly 150 additional sites are needed to achieve the same level of performance.

Fig. 6.

Averaged prediction variance (V) versus number of knots (m). Solid dots denote results for regular grids; dash-dotted line denotes results for the sequential search over the observed data locations (starting with 49 randomly chosen sites from the observed locations), and; solid line denotes results for the sequential search over a 60 × 60 regular grid (starting with a 7 × 7 regular grid).

5. Summary and future work

Treating the “big N problem” for spatial data is currently an active research area and, with increased data collection and storage capability, will become even more of an issue. With our proposed modification and approximately optimal knot design, predictive process models offer an attractive tool for handling this problem.

Future work will extend these models to handling space–time datasets, where, with high temporal resolution, additional computational challenges exist. A related problem is scalability of spatial models. Spatial modeling is often done on small scales to achieve high resolution or at large scales, sacrificing resolution. Strategies that implement predictive processes offer the possibility of studying high resolution over large regions.