Abstract
Many self-incompatible plant species exist in continuous populations in which individuals disperse locally. Local dispersal of pollen and seeds facilitates inbreeding because pollen pools are likely to contain relatives. Self-incompatibility promotes outbreeding because relatives are likely to carry incompatible alleles. Therefore, populations can experience an antagonism between these forces. In this study, a novel computational model is used to explore the effects of this antagonism on gene flow, allelic diversity, neighborhood sizes, and identity-by-descent. I confirm that this antagonism is sensitive to dispersal levels and linkage. However, the results suggest that there is little to no difference between the effects of gametophytic and sporophytic SI on unlinked loci. More importantly both GSI and SSI affect unlinked loci in a manner similar to obligate outcrossing without mating types. This suggests that the primary evolutionary impact of self-incompatibility systems may be to prevent selfing, and prevention of biparental inbreeding might be a beneficial side effect.
Keywords: self-incompatibility, isolation-by-distance, local dispersal, recombination, neighborhood size, genetic structure
Introduction
Both local dispersal and self-incompatibility systems are common in plant species. Local dispersal of seeds creates spatial population structures in plant populations such that relatives are likely to be found near one another. Furthermore, local dispersal of pollen creates pollen pools containing relatives when coupled with local dispersal of seeds. Therefore, local dispersal can facilitate inbreeding and geographic differentiation within a population. Many plant taxa have also evolved self-incompatibility systems that prevent selfing. Because these systems involve genetic mating types, relatives are likely to be incompatible. Therefore, self-incompatibility systems promote outbreeding in addition to requiring outcrossing. Clearly, if a plant population has both local dispersal and self-incompatibility systems, then an antagonism can exist between their evolutionary effects. This study seeks to investigate the effects of this antagonism on gene dispersal, allelic diversity, neighborhood sizes, and identity-by-descent via a novel spatially explicit, individual-based computational model.
Local Dispersal and Isolation-by-Distance
Species that inhabit a geographically contiguous region with no physical barriers to gene flow may not be panmictic. Physical distances separating two individuals could prevent them from mating freely, and instead individuals would be more likely to mate with nearby individuals than individuals that are far away. Wright (1943) referred to this as “isolation-by-distance” and subsequently developed the concept of neighborhood size to compare how different mating systems affect isolation-by-distance (Wright, 1946). Neighborhood size, Nb, is calculated from dispersal and effective population size via Nb ≡ 4πσ2 d, where d is the effective density of individuals per unit area and 2σ2 is the second moment of dispersal distance (Crawford, 1984; Fenster et al., 2003; Rousset, 2000; Vekemans and Hardy, 2004).
Because individuals near one another are expected to be more closely related than individuals farther apart, isolation-by-distance generates fine-scale spatial genetic structure, in which individuals that are close geographically are more likely to have identical alleles. Therefore, alleles can often show a patchy distribution with respect to geography (Epperson, 1990; Rohlf and Schnell, 1971; Sokal and Wartenberg, 1983; Turner et al., 1982). Neighborhood size partially quantifies fine-scale spatial genetic structure because it is an important component of the relationship between identity-by-descent (Malécot, 1975) and isolation-by-distance (Rousset, 1997, 2000, 2008; Sawyer, 1977).
Self-Incompatibility Systems
Self-fertilization is the most extreme form of inbreeding. While many taxa of angiosperms are physically unable to self (e.g. via dioecy), other, hermaphroditic taxa prevent self-fertilization via molecular self-incompatibility systems (SI). Over half of all angiosperm species exhibit some form of self-incompatibility (Hiscock and Kües, 1999). SI systems are typically controlled by a single, highly polymorphic Mendelian locus, the S locus, which contains several tightly linked genes that function together as a haplotype. The function of the S locus is to prevent pollen from fertilizing flowers of genetically similar plants. The primary result is that self-fertilization is impossible, and the secondary result is that matings between relatives are reduced. S loci evolve under negative, frequency-dependent (balancing) sexual selection, resulting in high fitness for rare and novel alleles (Wright, 1939). In other words, plants with rare alleles can pollinate more plants than plants with common alleles.
Two types of self incompatibility, gametophytic and sporophytic, have been extensively studied both theoretically and experimentally. In gametophytic self-incompatibility (GSI), the mating-type of pollen is determined by the pollen haplotype, and styles reject any pollen bearing either one of their haplotypes. In sporophytic self-incompatibility (SSI), the mating types of individuals are determined by their diploid genotypes, and stigmas reject any pollen that matches their phenotypes. Although there are several forms of SSI typically studied (Bateman, 1952; Billiard et al., 2007; Schierup et al., 1997; Vekemans et al., 1998), we will study the effects of two forms: SSIcod and SSIdomcod. SSIcod models assume that both pollen and stigma phenotypes have codominance, while SSIdomcod models assume that the pollen phenotype has dominance, while the stigma phenotype has codominance. For simplicity, I will refer to the SSIcod model as SSI and SSIdomcod as BSI because it is an approximation of the Brassicaceae system.
The genes of S specify both the male and female mating-type determinants. Because these determinants must work in unison, they are tightly linked. This tight linkage results from both close physical association on the chromosome and reduced recombination rate in the area (Kamau and Charlesworth, 2005). Because recombination rates are reduced and S experiences strong balancing selection, genes near S exhibit more allelic diversity than they would otherwise (Awadalla and Charlesworth, 1999; Charlesworth, 2006a; Charlesworth et al., 2006; Hagenblad et al., 2006; Kamau and Charlesworth, 2005; Schierup et al., 2000a).
In self-incompatibility systems, female fecundity can be impacted by pollen availability and compatibility (Charlesworth, 2006b; Larson and Barrett, 2000). This results in (fecundity) selection for females with rare genotypes since they are compatible with most of the pollen they receive and thus have more offspring than females that do not have compatible pollen donors available. Vekemans et al. (1998) found that when both males and females experience selection related to a self-incompatibility system different dynamics can occur than when only males experience selection. Fecundity selection reinforces frequency-dependent selection, increasing the number of haplotypes that are maintained in the population. However, as population sizes increase, the effects of fecundity selection decrease because mate availability becomes less of a problem for stigmas. (See Billiard et al. 2007 for more discussion.)
Antagonism
Self-incompatibility systems promote outbreeding while local dispersal can facilitate inbreeding; therefore, an antagonism exists between these two processes (Brooks et al., 1996; Schierup et al., 2006). When a species is both self-incompatible and has local dispersal, it will likely experience this antagonism to some degree. Schierup et al. (2006) confirmed the existence of this antagonism in an Icelandic population of Arabidopsis lyrata by finding that matings between adjacent individuals were reduced by self-incompatibility. This antagonism will manifest differently in markers linked to S loci than in markers that are unlinked. Because recombination is reduced near self-incompatibility loci (Casselman et al., 2000; Kamau et al., 2007; Kamau and Charlesworth, 2005; Kawabe et al., 2006; Tomita et al., 2004), a large section of the genome could be affected by this antagonism.
Several studies looked at the effect of population subdivision on allelic diversity of S loci. Wright (1939) proposed that subdivided populations will contain more S haplotypes than panmictic populations because each deme will have its own distinct set of haplotypes. However, the interaction of migration and negative frequency-dependent selection is more complicated. The number of alleles maintained is actually a convex function of the migration rate (Muirhead, 2001; Schierup, 1998). Intermediate levels of migration maintain fewer S haplotypes and have lower effective population sizes than panmixia or complete isolation. Because rare S haplotypes are favored, they migrate more successfully than neutral haplotypes. Therefore, except at very low, unrealistic levels of migration, little haplotype differentiation exists among demes (Muirhead, 2001; Schierup et al., 2000b). And thus, the reduction of diversity due to smaller demes is not offset by increased differentiation among them.
Schierup et al. (2000a) found that, within demes, haplotype diversity of linked markers increases with increasing linkage to S and increasing migration (for the most part), reflecting an increase in the effective deme size of linked loci. As populations become more subdivided, hitch-hiking increases the diversity of a larger area of the genome around S, reflecting a decrease in effective recombination rates in demes as they became more isolated. For very low, unrealistic migration rates, unlinked loci can actually have more genetic diversity than some linked loci, and thus hitch-hiking affects less loci at the total population level. They also found that population structure decreased with increasing linkage. This effect was noticeable even at intermediate migration rates. Interestingly, they also noticed that self-incompatibility slightly lowered levels of structure for unlinked loci. Ultimately, they confirmed that neutral loci are affected by both migration and linkage to S. Linkage increases diversity at neutral markers through associative balancing selection, whereas subdivision increases diversity by increasing the effective size of the total population. However, linkage also increases the effective migration rate of neutral markers, decreasing diversity by decreasing effective population sizes. For intermediate levels of linkage, the decrease in diversity due to facilitated migration can outweigh the increase due to associative balancing selection.
Three studies have investigated the effects of isolation-by-distance on self-incompatibility systems. Brooks et al. (1996) used a model similar to the one in this paper to study variance in S-haplotype frequencies due to seed dormancy, limited dispersal, and variable plant size. They found that local dispersal slightly increases haplotype frequency variance. When they compared their results to a torus model with no edge effects, they found that a considerable part of the effects of local dispersal are due to edge effects. Neuhauser (1999) developed a frequency-dependent selection model on ancestral selection graphs (Fearnhead, 2001; Krone and Neuhauser, 1997) and applied it to the fine-scale spatial structure of GSI haplotypes. She found that, in a continuous population, limited dispersal increases the rate of loss of haplotypes and maintains fewer haplotypes in the population. In addition, increasing pollen dispersal decreases extinction, while increasing seed dispersal decreases spatial correlations. Wagenius et al. (2007) also used a spatially explicit, individual-based model to explore the effects of habitat fragmentation on self-incompatible populations. They showed that self-incompatibility increases the Allee effect caused by habitat fragmentation because obligate outcrossing decreases pollen pools.
This study explores the interaction of isolation-by-distance and self-incompatibility systems on exponentially linked loci, focusing on how the antagonism manifests in gene dispersal, allelic diversity, neighborhood size, and identity-by-descent. I develop and employ a novel, spatially explicit, individual-based computational model to simulate the antagonism under various configurations. Expanding previous studies, I investigate the joint effects of dispersal, self-incompatibility, and linkage, with attention to differences among five different models of (in)compatibility. I expect that self-compatible populations will have higher levels of identity-by-descent and lower levels of dispersal than self-incompatible populations. Additionally, because the strength of balancing selection varies among PSI, BSI, GSI, and SSI (lowest to highest), I hypothesize that they will behave differently due to differences in half-sib compatibility and expected pollen pool sizes. Stronger selection should increase neighborhood sizes and allelic diversity and decrease identity-by-descent. Furthermore, increasing dispersal should decrease the effects of self-incompatibility and population structure. And finally, the influence of S loci will only manifest in GSI, SSI, and BSI models and should be stronger on tightly linked than on weakly linked or unlinked loci.
Methods
Model
This model is similar to the isolation-by-distance S-loci models of Brooks et al. (1996) and Wagenius et al. (2007) but has several important differences in how geography and biology are modeled. In this model the population lives on a rectangular lattice, where each cell is a hermaphroditic, diploid individual. Each individual is a diploid organism with 1 chromosome per haploid set (2n = 2). The chromosomes contain multiple neutral markers and an S locus, ordered such that S is to the left of all the markers. One crossover occurs each time a gamete is produced, hitting the marker region 50% of the time. Each marker has a recombination rate with S of 2n—m—1, where n is the marker number and m is the total number of markers. The right-most marker, U, is unlinked, having a recombination rate of 50% with S. The second-to-right-most locus,M [m-1], has a recombination rate of 25% with S, etc. For the initial generation, K alleles are assigned uniformly to each of the chromosomes. During simulations, mutations occur to each locus via the infinite alleles model at a per-locus mutation rate of μ.
The model implements five different types of mating-systems: no (NSI), physical (PSI), gametophytic (GSI), codominant sporophytic (SSI), and dominant-codominant sporophytic (BSI) self-incompatibility. Under NSI, all individuals are compatible with themselves and all other individuals. This model does not include a parameter for selfing, instead selfing occurs when pollen does not disperse out of its cell. Thus in this model, selfing is influenced by dispersal and edge effects, which is different than typical mixed-mating models. Under PSI, individuals are obligate outcrossers, but there are no genetic mating-types; selfing is prevented but biparental inbreeding is always allowed. BSI, GSI, and SSI were discussed above. Castric and Vekemans (2004) reviewed some situations that would complicate the above models of compatibility: S haplotypes might not be selectively equivalent because they could be linked to recessive, deleterious mutations (Uyenoyama, 1997, 2003), and S haplotypes can violate Mendel’s laws by segregating unevenly (Bechsgaard et al., 2004). I model neither of these situations in the present study.
In this model, there are two different types of dispersal—male gametes (in pollen) and embryos (in seeds)—both of which have a uniform direction and an exponential distance (Brooks et al., 1996; Wagenius et al., 2007). Exponential dispersal is leptokurtic, which is common for plant dispersal; although, natural kurtoses are usually larger (Kot et al., 1996). Under this model the probability density of dispersal in polar coordinates is
where 2σ2 is the second moment of dispersal distance (Crawford, 1984; Rousset, 2000), θ is the angle of dispersal from the positive x-axis, and r is the dispersal distance. The model allows for seeds and pollen to have different parameters of dispersal: σs for seeds and σp for pollen.
Seeds and pollen are assumed to be infinite, which allows for dispersal to be simulated backwards. For each cell, a mother is drawn from the previous generation based on seed dispersal centered on the cell and repeated until a valid mother is found. (Invalid mothers are cells that are not contained in the population.) Once a mother is found, a pollen grain is drawn from the previous generation based on pollen dispersal centered on the mother, Mendel’s laws, and mutation. Gametes that contain multiple mutations do not occur. If the pollen grain comes from an invalid (out-of-habitat) father or if it is incompatible with the mother, the parent pair is rejected and the process repeats until a valid, compatible pair is chosen, a form of fecundity selection (Billiard et al., 2007; Vekemans et al., 1998). At this point, the chosen pollen grain is combined with a random, possibly mutant gamete from the mother to form the offspring cell. Under the BSI implementation, the dominance levels of novel S-loci haplotypes are assigned randomly between 0 and 1, where higher values are considered dominant over lower values.
Simulation and Analysis
Simulations of this model were run using twenty-five different parameter sets: five different SI systems—NSI, PSI, BSI, GSI, or SSI—by five different pollen dispersal levels—σp = 2, 6, 10, 14, or 18. Seed dispersal was fixed at σs = σp/4 to decrease parameter space. The population size was 50×50 = 2500 individuals, and the initial number of alleles was 20. The per locus-generation-individual mutation rate was μ = 10-5, which is equivalent to 1 mutation per locus in the population every 20 generations. A single mutation rate for all loci is a simplification because S loci typically have lower mutation rates than marker loci. I also ran single-marker simulations in which the mutation rate of S loci was lower than the unlinked marker mutation rate (10-6 or 10-7 vs. 10-5). They produced similar results and are not shown.
Several population statistics were measured every 2500 generations from a random sample of 500 individuals, for five million generations after a burn-in of fifty thousand generations. This produced 2000 equilibrium samples of each population statistic for each parameter set, from which I estimated their means. At each locus and for each statistic, I performed pairwise t-tests in R (R Development Core Team, 2008), comparing the 25 parameter sets to one another, under the null hypothesis that the difference in means was zero. When calculating the t-tests, standard deviations were not pooled and variances were not assumed to be equal. P-values were corrected for multiple tests on a per-locus-per-statistic basis via Holm correction (Holm, 1979; Wright, 1992). I consider a p-value to show significant evidence that the two distributions of summary statistics have different means if they are less than 0.05/16. Unreported pairwise Wilcoxon rank sum tests were also calculated and have results similar to the t-tests.
The number of alleles was measured for each locus, and the gene dispersal coefficient, σ2, was measured from the distances of the sampled individuals from their parents. Effective population size was calculated from allelic diversity via (Ewens, 2004), and combined with σ2 to estimate neighborhood size of each locus, where Nb = 4πσ2Ne/A and A = 2500 was the habitat area of the population. To study inbreeding levels, the simulation tested every locus in every individual for identity-by-descent (Malécot, 1975) and calculated probabilities of identity-by-descent for each locus in the population. A locus was considered identical-by-descent if both of the copies in an individual were descended from the same grandparent copy, regardless of mutation.
Results
Dispersal
I simulated the model under 25 different parameter schemes and measured gene dispersal, allelic diversity, neighborhood sizes, and identity-by-descent to test for differences among the schemes. When considering dispersal, it is important to note that there are two concepts of dispersal in this model: “gamete-progeny” dispersal occurs when pollen and seeds disperse in the habitat and is a part of the model. “Gene” dispersal occurs when “gamete-progeny” dispersal is successful—pollen grain fertilizes an embryo and an embryo establishes in a cell—and is a result of the model. Figure 1 reports the mean levels of gene dispersal for each simulation and whether they are significantly different from one another. All levels of gameteprogeny dispersal produce gene dispersals that are distinct from one another, and NSI is significantly different from the other mating systems at all levels. Because NSI allows selfing, pollen can disperse a distance of 0, which is not present in the other mating systems, and thus NSI will have lower average gene dispersal. At high levels of gamete-progeny dispersal PSI, BSI, GSI, and SSI are not distinguishable, and as gamete-progeny dispersal decreases, PSI becomes distinguishable, followed by SSI. Simulations with low gamete-progeny dispersal show significant differences among PSI, BSI, GSI and SSI due to differences between their promotion of outbreeding.
Figure 1. Comparisons of Gene Dispersal.
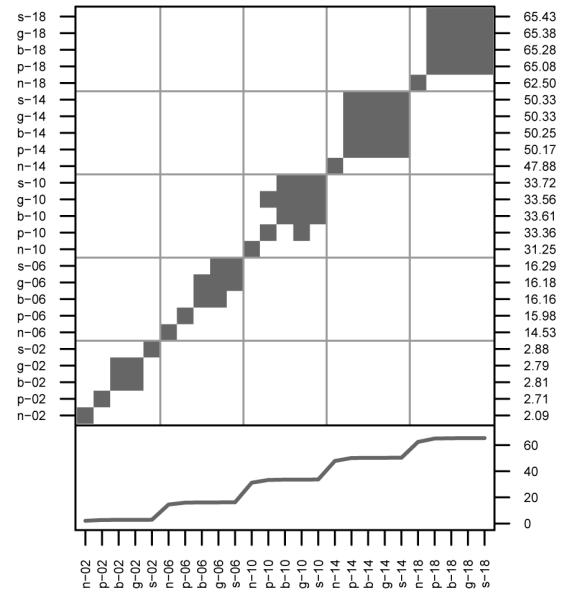
In the upper panel, shaded cells denote simulation pairs with means that were not significantly different from one another. The left and bottom axes identify the parameters sets specific to each cell. The right axes identifies the mean of each simulation. The bottom panel is a plot of the means. Each simulation is identified as ‘i—j,’ where ‘i’ represents NSI, PSI, BSI, GSI, or SSI and ‘j’ represents σp.
It is also important to note that the level of gene dispersal is different than the level of gamete-progeny dispersal. In my simulations, the level of gamete-progeny dispersal is expected to be , ignoring edge effects (Crawford, 1984). However, the level of gene dispersal will depend on the interaction of gamete-progeny dispersal with habitat size and mating system. At σp = 2, gameteprogeny dispersal only reaches a few cells, and thus the gene dispersal of NSI is below due to rounding to the nearest cell. Additionally, at low levels of gamete-progeny dispersal, gene dispersal of self-incompatible mating systems will be larger than gamete-progeny dispersal because discarded self-pollen makes up a large proportion of the pollen pool. Gene dispersal increases as gamete-progeny dispersal increases; however, more pollen and seed disperse off lattice, which reduces the gene dispersal compared to gamete-progeny dispersal. When σp > 2, gene dispersals are all lower than the associated, expected levels of gamete-progeny dispersal in an infinite habitat.
Allelic Diversity
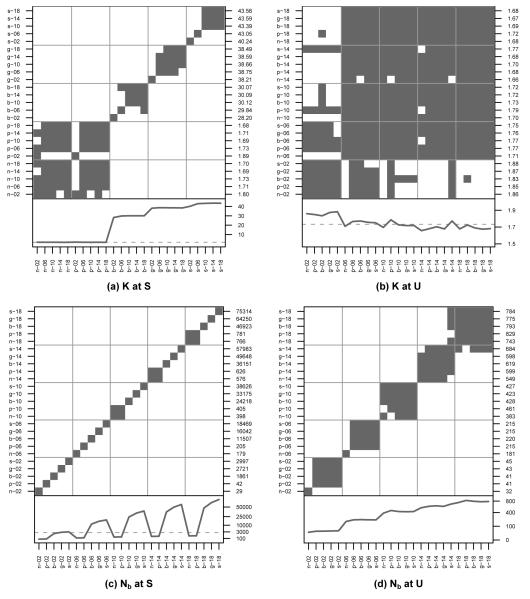
Figure 2a shows the average number of alleles maintained by S in each simulation at equilibrium. (Note that the order of cells in Figure 2a is different than the other subfigures.) At every level of dispersal, the number of alleles maintained follows the strength of balancing selection expected in the mating system. NSI and PSI are not significantly different and maintain the fewest number of alleles. BSI maintains significantly more alleles than NSI and PSI and the neutral expectation, but significantly less than GSI, which maintains significantly fewer alleles than SSI. Allelic diversity is equivalent among high levels of 10, while low levels of dispersal σp ≥ 10, while low levels of dispersal tend to maintain different levels of diversity than high levels, σp = 2 more so than σp = 6.
Figure 2. Comparisons of K and Nb at Loci S and U.
Identification of simulation pairs with significantly different means (white cells) of allelic diversity (a,b) and of neighborhood size (c,d) at the self-incompatibility locus, S, and the neutral marker unlinked to it, U. Note that the order of cells in (a) is different than the other subfigures. For the lower panels of (a) and (b), the dashed line is equal to 1.73, the expected neutral level of diversity. For the lower panels of (c) and (d), the dashed line is equal to 2500, or the total census size of the simulated population. See Figure 1 for more details on the layout of each subfigure.
For NSI and PSI, σp = 2 shows an increase in the number of alleles, as expected in a subdivided population with low migration rates. Although low dispersal increases drift locally, it also decreases genetic drift globally because local populations fix different alleles. Additionally, low dispersal decreases reproductive variance which also increases Ne. The genetic mating systems show an opposite effect, with σp = 2 preserving significantly lower levels of diversity than higher dispersal levels. This follows the results of Schierup (1998) and Schierup et al. (2000b), who found that low levels of migration reduce allelic diversity in the population at loci under balancing selection. Although drift increases locally, local populations no longer fix different alleles because the effective migration rates of novel S-loci haplotypes are still high. Additionally, low dispersal decreases pollen pools and increases relatedness inside the pools. This results in increased variance of fecundity and decreased Ne as locally rare S-locus genotypes produce more offspring.
Figure 2b shows that the average number of alleles maintained by U in each simulation at equilibrium is roughly 5% of the diversity maintained by S. Additionally, for this unlinked locus, allelic diversity does not significantly differ among mating systems. As in S, the lowest level of dispersal, σp = 2, does maintain significantly higher levels of allelic diversity than other levels of dispersal, except that BSI, GSI, and SSI now behave like NSI and PSI. Figures S.1 and S.2 show that between these two endpoints, the allelic diversity of marker loci monotonically decreases as linkage to S decreases. Around M8, 0.4 cM from S, all five mating systems maintain nearly indistinguishable levels of allelic diversity.
Neighborhood Sizes
Figure 2c shows the average Nb of S in each simulation, calculated from the measured levels of allelic diversity and dispersal. As expected, Nb increases as dispersal increases. Additionally, the balancing selection of BSI, GSI, and SSI increases Nb even further, over 20 times the census size of the population when σp = 18. Although this appears to be counter intuitive, the effective density of these simulations is high, which causes Nb to be greater than the census size. Interestingly, although most simulations appear to be significantly different from one another, NSI and PSI are not significantly different at high levels of dispersal (σp ≥ 10). This is in opposition to the finding in Figure 1 that NSI has significantly different of dispersal than PSI.
Figure 2d shows a similar pattern for U; Nb increases as dispersal increases. However, the Nb sizes are smaller and the impact of genetic mating systems is no longer seen. PSI, BSI, GSI, and SSI all behave similarly, with NSI being significantly different at low levels of dispersal. In Figures S.3 and S.4, we can see that Nb decreases monotonically as linkage to S decreases. These neighborhood sizes are similar to those found for several self-incompatible taxa (Clauss and Mitchell-Olds, 2006; Vekemans and Hardy, 2004).
Inbreeding and Identity-by-Descent
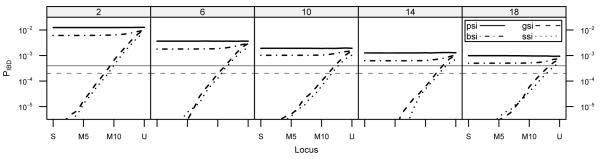
The antagonism between local dispersal and self-incompatibility is demonstrated in Figures 3, 4, S.5, and S.6. For clarity, NSI values were omitted from Figure 3 because selfing makes them much larger than other mating systems. For U, NSI had probabilities of identity-by-descent (PIBD ) of 15.6%, 6.0%, 4.0%, 3.1%, and 2.6% as σp increases from 2 to 18. (Other loci showed similar levels.) In contrast, a randomly mating population of size 2500 should have a PIBD of 0.040% (0.020% if selfing is prevented). Across all mating systems, increasing dispersal reduces PIBD.
Figure 3. Probability of Identity-by-Descent.
The average probabilities of grandparental IBD of each locus is plotted for self-incompatible mating systems. NSI values are listed in Results. Each panel represents a different dispersal regime. The solid gray line is approximately at 2/2500, the expected level under random mating, the dashed gray line is at 1/2500, the expected level if selfing were prohibited. Measurements above the lines can be considered inbred and measurements below outbred.
Figure 4. Comparisons of PIBD at Locus U.
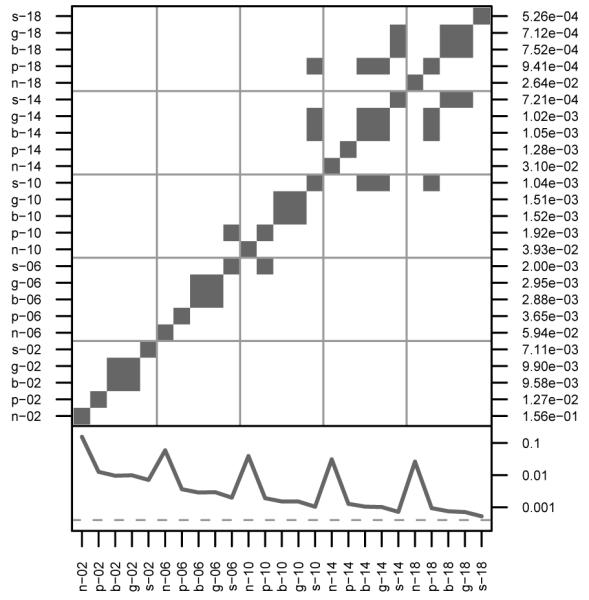
Identification of simulation pairs with significantly different means of probability of IBD at unlinked locus U (white cells). In the lower panel, the solid line is approximately at 2/2500, the expected level under random mating. See Figure 1 for more details on the layout.
Interestingly, BSI behavesmore like NSI and PSI and less like the other genetic mating systems. These results indicate that BSI does not prevent biparental inbreeding, although its levels of PIBD are lower than the levels of NSI and PSI. The dominance of the BSI mating system prevents some half-sib matings, but apparently not enough to cause outbreeding in spite of local dispersal. Furthermore, the influence of BSI on linked loci shows a different pattern than the influences of GSI and SSI. Under BSI, PIBD appears flat until around M11, about 3.1 cM from S, at which point it increases slightly until U. In these populations, S predictably shows lower levels of PIBD than expected under random mating. Under GSI and SSI, the mating system has a stronger effect on S than local dispersal, and inbreeding is prevented by forcing outbreeding. Loci tightly linked to S also show outbreeding, and as linkage decreases, PIBD increases. The effect of SSI appears to be stronger than that of GSI. Eventually loci become inbred as the effect of local dispersal becomes stronger than the effect of the mating system, and the transitions between inbreeding and outbreeding depend on the interaction of dispersal and mating system.
For U, BSI, GSI, and SSI surprisingly reduce PIBD compared to PSI, and SSI is reduced further than BSI and GSI, which show similar levels. Such distinctions are not seen in dispersal, allelic diversity, or neighborhood sizes. Genetic mating systems appear to reduce inbreeding at unlinked loci, while not significantly affecting equilibrium allelic diversity or levels of dispersal.
Discussion
I have developed a novel, spatially explicit, individual-based model of a continuous plant population to measure the antagonism between local dispersal and self-incompatibility. My results—gene dispersal, allelic diversity, neighborhood sizes, and identity-by-descent—confirm several of my hypotheses. As expected, an antagonism exists between local dispersal and self-incompatibility, demonstrated by the significant differences among statistics of self-compatible (NSI) and self-incompatible (PSI, BSI, GSI, and SSI) populations (cf. Brooks et al., 1996; Schierup et al., 2006). This antagonism manifested most clearly in the measurements of identity-by-descent, which increased when dispersal became more local and decreased when self-incompatibility became stronger. Additionally, the results confirm that markers linked to S are affected differently than unlinked loci under gametophytic and sporophytic self-incompatibility. As linkage decreased, allelic diversity and Nb decreased while PIBD increased (cf. Schierup et al., 2000a). However, unlike Schierup et al. (2000a), I did not find different levels of population structure of unlinked loci among self-incompatible mating systems, which may be due to different sensitivities of Fst and Nb. Furthermore, I found only monotonic effects of linkage and dispersal rates on my population statistics, unlike Muirhead (2001), Schierup (1998), and Schierup et al. (2000a,b), which included unrealistic migration rates in island models that are not part of my simulations.
For unlinked loci, self-incompatible populations show minor differences among their probabilities of identity-by-descent, yet few significant or important differences in gene dispersal, allelic diversity, or neighborhood sizes. This similarity suggests that studies of plant populations may be able to ignore the specific genetics of self-incompatibility when studying other aspects of plant biology. Specifically, computational population models can safely assume obligate outcrossing (PSI) without the need to model the genetics of self-incompatibility in reasonable instances. However, ecological models dependent on pollen limitation and seed set, like invasive species colonization, should still model the genetics of self-incompatibility because some mating systems are more susceptible to pollen limitation than others (Burd, 1994; Busch and Schoen, 2008; Knight et al., 2005).
The similarity among my self-incompatible models was unexpected and suggests that self-incompatibility systems, while they may affect unlinked loci slightly differently on short time scales, do not exhibit long term effects beyond the prevention of selfing. This is consistent with Wilkins (2004), who found that coalescence in a continuous population can often be modeled as a two-phase process. In the recent past, the first phase (“scattering”) operates and depends on the sample locations. In the distant past, the first phase asymptotically converges to the second phase (“collecting”) at a rate dependent on sample locations. The second phase operates independently of sample locations and can be represented by standard coalescence models. This transition is possible because with enough dispersal, spatial correlations among ancient lineages can eventually break up. Because local genetic correlations reveal differences among my self-incompatibility models, long-term processes lose such differences as they lose local genetic correlations.
Furthermore, when Nb > 4π ≈ 12.57, certain models of isolation-by-distance produce lineages that tend to disperse faster than they coalesce and isolation-by-distance does not affect Ne (Maruyama, 1972; Wilkins, 2004). (But note the criticisms of similar models by Felsenstein 1975.) However, in my simulations, σp = 2 had neighborhood sizes that were 2.5–4 times larger than this threshold but still showed that isolation-by-distance had increased Ne. One possible explanation for this difference is that my model included edge effects, which certainly caused Nb to vary across the habitat. At low dispersal, some regions were probably below the Nb threshold, which increased the Ne of the population as a whole. This argument suggests that edge effects and regional habitat variation can strengthen isolation-by-distance, and thresholds developed on classic, toroid models are unsurprisingly too conservative.
The observation that for unlinked loci, self-incompatible populations are only subtly distinguishable from one another but very distinguishable from self-compatible populations suggests that the primary evolutionary advantage for self-incompatible taxa may only extend to the prevention of selfing and not the prevention of biparental inbreeding (contra Charlesworth and Charlesworth, 1987). Any reduction of inbreeding with relatives is a beneficial side-effect. This observation has important and obvious consequences for research into the origin and evolution of self-incompatibility systems. More work needs to be done to establish the strength of this hypothesis. Importantly, this conclusion is tentative because my model lacked inbreeding depression, which would provide a selective advantage for avoiding inbreeding. However, models can be developed to investigate the differences among how PSI, BSI, GSI, and SSI can rescue a population from inbreeding depression, whether on their own or in competition. If PSI proves to be competitive with genetic mating systems, then avoiding selfing—but not biparental inbreeding—is likely to be one of the forces driving the evolution of self-incompatibility systems.
Supplementary Material
Figure S.1: Mean Numbers of Alleles at Equilibrium. Each figure panel is a separate simulation, with different parameters. Within each panel, the mean number of alleles is plotted for each locus separately. The horizontal line is at K = 1.73, which is the expected number of alleles maintained at a neutral locus in an equivalent panmictic population.
Figure S.2: Pairwise Comparisons of K at Each Locus. This is an extension of Figure 2, reporting the comparisons at all loci.
Figure S.3: Neighborhood Sizes at Equilibrium. Each figure panel is a separate simulation, with different parameters. Within each panel, the mean neighborhood size is plotted for each locus separately. The horizontal line is at N = 2500, the census size of the population.
Figure S.4: Pairwise Comparisons of Nb at Each Locus. This is an extension of Figure 2, reporting the comparisons at all loci.
Figure S.5: Probability of Identity-by-Descent at Equilibrium. Each figure panel is a separate simulation, with different parameters. Within each panel, the probability of grandparental IBD is plotted for each locus separately. The solid horizontal line is at PIBD ≈ 2/2500, the level of grandparental IBD in an equivalent, panmictic population.
Figure S.6: Pairwise Comparisons of PIBD at Each Locus. This is an extension of Figure 4, reporting comparisons at all loci.
Acknowledgments
This work was supported by an NSF Predoctoral Fellowship and N.I.H. grant GM070806. The author would like to thank W. Anderson, S. Chang, J. Hamrick, J. Kissinger, R. Pulliam, J. Ross-Ibarra, F. Rousset, P. Schliekelman, E. Stone, J. Thorne, J. Wares, and anonymous reviewers for their helpful suggestions.
References
- Awadalla P, Charlesworth D. Recombination and selection at Brassica self-incompatibility loci. Genetics. 1999;152:413–425. doi: 10.1093/genetics/152.1.413. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bateman AJ. Self-incompatibility systems in angiosperms I. Theory. Heredity. 1952;6:285–310. [Google Scholar]
- Bechsgaard J, Bataillon T, Schierup MH. Uneven segregation of sporophytic self-incompatibility alleles in Arabidopsis lyrata. Journal of Evolutionary Biology. 2004;17:554–561. doi: 10.1111/j.1420-9101.2004.00699.x. [DOI] [PubMed] [Google Scholar]
- Billiard S, Castric V, Vekemans X. A general model to explore complex dominance patterns in plant sporophytic self-incompatibility systems. Genetics. 2007;175:1351–1369. doi: 10.1534/genetics.105.055095. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brooks RJ, Tobias AM, Lawrence MJ. The population genetics of the self-incompatibility polymorphism in Papaver rhoeas. XI. The effects of limited pollen and seed dispersal, overlapping generations and variation in plant size on the variance of S-allele frequencies in populations at equilibrium. Heredity. 1996;76:367–376. [Google Scholar]
- Burd M. Bateman’s principle and plant reproduction: The role of pollen limitation in fruit and seed set. Botanical Review. 1994;60:83–139. [Google Scholar]
- Busch JW, Schoen DJ. The evolution of self-incompatibility when mates are limiting. Trends in Plant Science. 2008;13(3):128–136. doi: 10.1016/j.tplants.2008.01.002. [DOI] [PubMed] [Google Scholar]
- Casselman AL, Vrebalov J, Conner JA, Singhal A, Giovannoni J, Nasrallah ME, Nasrallaha JB. Determining the physical limits of the Brassica S locus by recombinational analysis. Plant Cell. 2000;12:23–33. doi: 10.1105/tpc.12.1.23. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Castric V, Vekemans X. Plant self-incompatibility in natural populations: a critical assessment of recent theoretical and empirical advances. Molecular Ecology. 2004;13:2873–2889. doi: 10.1111/j.1365-294X.2004.02267.x. [DOI] [PubMed] [Google Scholar]
- Charlesworth D. Balancing selection and its effects on sequences in nearby genome regions. PLoS Genetics. 2006a;2(4):379–384. doi: 10.1371/journal.pgen.0020064. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Charlesworth D. Evolution of plant breeding systems. Current Biology. 2006b;16(17):R726–R735. doi: 10.1016/j.cub.2006.07.068. [DOI] [PubMed] [Google Scholar]
- Charlesworth D, Charlesworth B. Inbreeding depression and its evolutionary consequences. Annual Review Of Ecology And Systematics. 1987;18:237–268. [Google Scholar]
- Charlesworth D, Kamau E, Hagenblad J, Tang C. Trans-specificity at loci near the self-incompatibility loci in Arabidopsis. Genetics. 2006;172:2699–2704. doi: 10.1534/genetics.105.051938. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Clauss MJ, Mitchell-Olds T. Population genetic structure of Arabidopsis lyrata in Europe. Molecular Ecology. 2006;15:2753–2766. doi: 10.1111/j.1365-294X.2006.02973.x. [DOI] [PubMed] [Google Scholar]
- Crawford TJ. The estimation on neighbourhood parameters for plant populations. Heredity. 1984;52:273–283. [Google Scholar]
- Epperson BK. Spatial autocorrelation of genotypes under directional selection. Genetics. 1990;124:757–771. doi: 10.1093/genetics/124.3.757. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ewens W. Mathematical Population Genetics I. Theoretical Introduction. Springer Science+Buisness Media, Inc.; New York: 2004. [Google Scholar]
- Fearnhead P. Perfect simulation from population genetic models with selection. Theoretical Population Biology. 2001;59:263–279. doi: 10.1006/tpbi.2001.1514. [DOI] [PubMed] [Google Scholar]
- Felsenstein J. A pain in the torus: Some difficulties with models of isolation by distance. American Naturalist. 1975;109(967):359. [Google Scholar]
- Fenster CB, Vekemans X, Hardy OJ. Quantifying gene flow from spatial genetic structure data in a metapopulation of Chamaecrista fasciculata (Leguminosae) Evolution. 2003;57:995–1007. doi: 10.1111/j.0014-3820.2003.tb00311.x. [DOI] [PubMed] [Google Scholar]
- Hagenblad J, Bechsgaard J, Charlesworth D. Linkage disequilibrium between incompatibility locus region genes in the plant Arabidopsis lyrata. Genetics. 2006;173:1057–1073. doi: 10.1534/genetics.106.055780. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hiscock SJ, Kües U. Cellular and molecular mechanisms of sexual incompatibility in plants and fungi. International Review of Cytology. 1999;193:165–295. doi: 10.1016/s0074-7696(08)61781-7. [DOI] [PubMed] [Google Scholar]
- Holm D. A simple sequentially rejective multiple test procedure. Scandinavian Journal of Statistics. 1979;6:65–70. [Google Scholar]
- Kamau E, Charlesworth B, Charlesworth D. Linkage disequilibrium and recombination rate estimates in the self-incompatibililty region of Arabidposis lyrata. Genetics. 2007;176:2357–2369. doi: 10.1534/genetics.107.072231. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kamau E, Charlesworth D. Balancing selection and low recombination affect diversity near the self-incompatibility loci of the plant Arabidopsis lyrata. Current Biology. 2005;15:1773–1778. doi: 10.1016/j.cub.2005.08.062. [DOI] [PubMed] [Google Scholar]
- Kawabe A, Hansson B, Forrest A, Hagenblad J, Charlesworth D. Comparative gene mapping in Arabidopsis lyrata chromosomes 6 and 7 and A. thaliana chromosome IV: evolutionary history, rearrangements and local recombination rates. Genetical Research. 2006;88:45–56. doi: 10.1017/S0016672306008287. [DOI] [PubMed] [Google Scholar]
- Knight TM, Steets JA, Vamosi JC, Mazer SJ, Burd M, Campbell DR, Dudash MR, Johnston MO, Mitchell RJ, Ashman T-L. Pollen limitation of plant reproduction: Pattern and process. Annual Review of Ecology, Evolution, and Systematics. 2005;36(1):467–497. [Google Scholar]
- Kot M, Lewis MA, van den Driessche P. Dispersal data and the spread of invading organisms. Ecology. 1996;77:2027–2042. [Google Scholar]
- Krone SM, Neuhauser C. Ancestral processes with selection. Theoretical Population Biology. 1997;51:210–237. doi: 10.1006/tpbi.1997.1299. [DOI] [PubMed] [Google Scholar]
- Larson BMH, Barrett SCH. A comparative analysis of pollen limitation in flowering plants. Biological Journal of the Linnean Society. 2000;69:503–520. [Google Scholar]
- Malécot G. Heterozygosity and relationship in regularly subdivided populations. Theoretical Population Biology. 1975;8:212–241. doi: 10.1016/0040-5809(75)90033-7. [DOI] [PubMed] [Google Scholar]
- Maruyama T. Rate of decrease of genetic variability in a two-dimensional continuous population of finite size. Genetics. 1972;70:639–651. doi: 10.1093/genetics/70.4.639. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Muirhead C. Consequences of population structure on genes under balancing selection. Evolution. 2001;55:1532–1541. doi: 10.1111/j.0014-3820.2001.tb00673.x. [DOI] [PubMed] [Google Scholar]
- Neuhauser C. The ancestral graph and gene genealogy under frequency-dependent selection. Theoretical Population Biology. 1999;56:203–214. doi: 10.1006/tpbi.1999.1412. [DOI] [PubMed] [Google Scholar]
- R Development Core Team . R: A Language and Environment for Statistical Computing. R Foundation for Statistical Computing; Vienna, Austria: 2008. ISBN 3-900051-07-0. [Google Scholar]
- Rohlf FJ, Schnell GD. An investigation of the isolation-by-distance model. American Naturalist. 1971;105:295–324. [Google Scholar]
- Rousset F. Genetic differentiation and estimation of gene flow from F-statistics under isolation by distance. Genetics. 1997;145:1219–1228. doi: 10.1093/genetics/145.4.1219. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rousset F. Genetic differentiation between individuals. Journal of Evolutionary Biology. 2000;13:58–62. [Google Scholar]
- Rousset F. Demystifying Moran’s I. Heredity. 2008;100:231–232. doi: 10.1038/sj.hdy.6801065. [DOI] [PubMed] [Google Scholar]
- Sawyer S. Asymptotic properties of the equilibrium probability of identity in geographically structured populations. Advances in Applied Probability. 1977;9:268–282. [Google Scholar]
- Schierup MH. The number of self-incompatibility alleles in a finite, subdivided population. Genetics. 1998;149:1153–1162. doi: 10.1093/genetics/149.2.1153. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schierup MH, Bechsgaard JS, Christiansen FB. Selection at work in self-incompatible Arabidopsis lyrata: mating patterns in a natural population. Genetics. 2006;172:477–484. doi: 10.1534/genetics.105.045682. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schierup MH, Charlesworth D, Vekemans X. The effect of hitch-hiking on genes linked to a balanced polymorphism in a subdivided population. Genetical Research. 2000a;76:63–73. doi: 10.1017/s0016672300004547. [DOI] [PubMed] [Google Scholar]
- Schierup MH, Vekemans X, Charlesworth D. The effect of subdivision on variation at multi-allelic loci under balancing selection. Genetical Research. 2000b;76:51–62. doi: 10.1017/s0016672300004535. [DOI] [PubMed] [Google Scholar]
- Schierup MH, Vekemans X, Christiansen FB. Evolutionary dynamics of sporophytic self-incompatibility alleles in plants. Genetics. 1997;147:835–846. doi: 10.1093/genetics/147.2.835. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sokal RR, Wartenberg DE. A test of spatial autocorrelation analysis using an isolation-by-distance model. Genetics. 1983;105:219–237. doi: 10.1093/genetics/105.1.219. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tomita RN, Suzuki G, Yoshida K, Yano Y, Tsuchiya T, Kaked K, Muka Y, Kowyama Y. Molecular characterization of a 313-kb genomic region containing the self-incompatibility locus of Ipomoea trifida, a diploid relative of sweet potato. Breeding Science. 2004;54:165–175. [Google Scholar]
- Turner ME, Stephens JC, Anderson WW. Homozygosity and patch structure in plant populations as a result of nearest-neighbor pollination. Proceedings of the National Academy of Sciences USA. 1982;79:203–207. doi: 10.1073/pnas.79.1.203. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Uyenoyama MK. Genealogical structure among alleles regulating self-incompatibility in natural populations of flowering plants. Genetics. 1997;147:1389–1400. doi: 10.1093/genetics/147.3.1389. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Uyenoyama MK. Genealogy-dependent variation in viability among self-incompatibility genotypes. Theoretical Population Biology. 2003;63:281–293. doi: 10.1016/s0040-5809(03)00020-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vekemans X, Hardy OJ. New insights from fine-scale spatial genetics structure analyses in plant populations. Molecular Ecology. 2004;13:921–935. doi: 10.1046/j.1365-294x.2004.02076.x. [DOI] [PubMed] [Google Scholar]
- Vekemans X, Schierup MH, Christiansen FB. Mate availability and fecundity selection in multi-allelic self-incompatibility systems in plants. Evolution. 1998;52:19–29. doi: 10.1111/j.1558-5646.1998.tb05134.x. [DOI] [PubMed] [Google Scholar]
- Wagenius S, Lonsdorf E, Neuhauser C. Patch aging and the S-Allee effect: breeding system effects on the demographic response of plants to habitat fragmentation. American Naturalist. 2007;169(3):383–397. doi: 10.1086/511313. [DOI] [PubMed] [Google Scholar]
- Wilkins J. A separation-of-timescales approach to the coalescent in a continuous population. Genetics. 2004;168:2227–2244. doi: 10.1534/genetics.103.022830. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wright S. The distribution of self-sterility alleles in populations. Genetics. 1939;24:538–552. doi: 10.1093/genetics/24.4.538. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wright S. Isolation by distance. Genetics. 1943;28:114–138. doi: 10.1093/genetics/28.2.114. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wright S. Isolation by distance under diverse systems of mating. Genetics. 1946;31:39–59. doi: 10.1093/genetics/31.1.39. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wright SP. Adjusted p-values for simultaneous inference. Biometrics. 1992;48(4):1005–1013. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Figure S.1: Mean Numbers of Alleles at Equilibrium. Each figure panel is a separate simulation, with different parameters. Within each panel, the mean number of alleles is plotted for each locus separately. The horizontal line is at K = 1.73, which is the expected number of alleles maintained at a neutral locus in an equivalent panmictic population.
Figure S.2: Pairwise Comparisons of K at Each Locus. This is an extension of Figure 2, reporting the comparisons at all loci.
Figure S.3: Neighborhood Sizes at Equilibrium. Each figure panel is a separate simulation, with different parameters. Within each panel, the mean neighborhood size is plotted for each locus separately. The horizontal line is at N = 2500, the census size of the population.
Figure S.4: Pairwise Comparisons of Nb at Each Locus. This is an extension of Figure 2, reporting the comparisons at all loci.
Figure S.5: Probability of Identity-by-Descent at Equilibrium. Each figure panel is a separate simulation, with different parameters. Within each panel, the probability of grandparental IBD is plotted for each locus separately. The solid horizontal line is at PIBD ≈ 2/2500, the level of grandparental IBD in an equivalent, panmictic population.
Figure S.6: Pairwise Comparisons of PIBD at Each Locus. This is an extension of Figure 4, reporting comparisons at all loci.