Evaluation of dental composite shrinkage and leakage in extracted teeth using X-ray microcomputed tomography

Abstract

Objective

Use X-ray microcomputed tomography (μCT), to test the hypothesis that composite shrinkage and sites of potential leakage in human teeth are non-uniformly distributed and depend on cavity geometry and C-factor.

Methods

Two holes of equal volume but different dimensions were drilled into the exposed dentin of extracted human molars. The cavities were filled with composite and teeth were scanned, before and after curing, using μCT. Three-dimensional (3D) reconstructions of the data were prepared and analyzed using image analysis software.

Results

3D reconstructions showed that cavity geometry did not affect the polymerization shrinkage. The shrinkage for all restorations was 2.66 ± 0.59 %, and cavity dimensions did not affect the volume lost, either in quantity or location on the sample. Potential leakage sites were identified by gap formations and found to be non-uniformly distributed along the tooth-composite interface. Leakage in regions calculated by μCT was confirmed by visualization of sectioned samples with confocal laser scanning microscopy.

Significance

μCT evaluation will add tremendous value as part of a suite of tests to characterize various properties of dental materials. The non-uniform distribution of potential leakage sites about the cavities that was determined by μCT emphasizes the inadequacy of traditional methods of determining leakage, which are capable of analyzing only limited areas. Additionally, μCT evaluation can produce quantitative analyses of shrinkage and leakage, compared to the conventional methods, which are qualitative or semi-quantitative. Finally, experimentally determined shrinkage and leakage of composite in extracted teeth agrees with the results of similar experiments in model cavities, confirming the validity of those models.

Introduction

Dental caries is the most prevalent childhood disease in the United States and continues to be present at high levels among all age groups [1]. The standard treatment for a carious lesion is placement of a filling after removal of the infected, demineralized tooth structure. Longevity of the restoration varies according to a number of factors such as the material (e.g., amalgam, composite, glass ionomer) and location of the restoration; however, the most common reason for replacement of dental restorations is secondary caries [2] as perceived by the clinician. The precise connection between secondary (recurrent) caries and the occurrence of microleakage at the margins of restorations is controversial. The integrity of a restoration’s margins is believed to be a highly important indicator of its potential clinical performance [3]: poor margins are thought to suggest a tendency to leak, allowing oral fluids that carry bacteria, enzymes, and acids into direct contact with exposed dentin. For this reason, it has long been clinical practice to replace restorations with imperfect margins. The main sources of contention regarding the link between microleakage and secondary caries are: first, the difficulty in ascertaining whether the infection is indeed a new area of demineralization; and second, the challenge presented by the difficulty of diagnosis. Concerning the first issue, the question is whether the caries lesion is caused by agents admitted via leakage, or is in fact remnants of the original lesion that were not removed when preparing the cavity before placing the restoration. With regard to the latter problem, it is often difficult to differentiate between active and arrested caries, and some practitioners also state that color change in the tooth tissue surrounding a restoration is not necessarily an indication of secondary caries [3]. Tools that impart a greater understanding of microleakage and its relationship to secondary caries would provide the insight needed to improve upon existing treatments.

Several in vitro methods are available to evaluate microleakage caused by polymerization shrinkage, including dye and tracer penetration and the use of air pressure. Dye and tracer penetration methods typically involve soaking a prepared tooth in a suitable solution, sectioning through the restoration, and assessing the leakage that has occurred using light microscopy, scanning electron microscopy, or autoradiography [4]. The extent of leakage may be quantified using a length scale, but is often more subjectively evaluated using a system whereby the degree of leakage is graded by operators using a predetermined range of values. Microleakage may also be detected by submerging the restored tooth in water and subjecting it to air pressure - if bubbles appear, there are gaps that have permitted the passage of air [4]. All of the aforementioned methods are destructive since they may involve sectioning the tooth. Additionally, these methods are semi-quantitative at best, relying on visual assessment by the operator to decide the extent of dye penetration, while the air pressure method is simply qualitative. The biggest drawback to all of these methods is that none is capable of quantitatively assessing the extent of leakage along the entire tooth-composite interface: dye and tracer samples can only be examined in the plane through which they were sectioned, while air pressure cannot give any spatial information about the microleakage that has occurred. A method that can provide precise information about leakage and its distribution along the interface would be of great value.

In X-ray microcomputed tomography (μCT), X-rays are passed through the specimen along a plane or “slice” and collected by a detector; this operation is repeated along the length of the subject, slice-by-slice. This two-dimensional information is processed using specific algorithms and ultimately a three-dimensional (3D) reconstruction is generated. Differences in radiopacity between the subject of interest and the background give rise to contrast. In dental research, μCT has been proven useful for studying tooth [5] and root canal morphology [6, 7]. Some attempts have also been made to investigate leakage of dental restorative materials using contrast agents, such as silver nitrate; however, these have met with only limited success [8, 9]. Our previous studies have demonstrated that μCT can accurately determine regions of polymerization shrinkage [10] and leakage [11] in 3D model cavities, that shrinkage and leakage are not uniformly distributed, and that shrinkage values are not significantly affected by volume or C-factor in these model cavities [10].

In this study we present a μCT-based method to measure the shrinkage and locations of potential leakage in restorations that have been placed in extracted human teeth. It has been demonstrated that 3D imaging and image analysis produce quantitative, spatially resolved information on position changes due to polymerization, from which leakage is inferred. This study investigates composite shrinkage and the spatial distribution of leakage in extracted teeth, in order to evaluate the material in a more clinically relevant setting. Additionally, the effect of cavity geometry and C-factor (defined as the ratio of bonded area to unbonded area) on composite shrinkage and potential leakage are examined.

Materials and Methods^*

Caries- and restoration-free, extracted human molars (N = 6) were obtained according to protocols approved by the National Institute of Standards and Technology’s Institutional Review Board (IRB). Teeth were sterilized by γ-irradiation (24 kGy) and stored in deionized water at 4 ºC until used. The occlusal surface of each tooth was ground flat to expose the dentin, after which two cavities of approximately the same volume (3 mm³) but different dimensions were drilled, using a drill press, into each tooth. One cavity (C₁) measured 2 mm (diameter, d) × ≈ 2.25 mm (height, h) and the other (C₂) measured. 3 mm (d) × ≈ 1 mm (h). Excess water was removed with a Kimwipe and the cavities were filled with a commercial restorative composite (TPH³, DENTSPLY/Caulk, Milford, DE), placed as a single layer filling the entire cavity and then condensed. The teeth were not etched, nor was a bonding agent used. The filled tooth was placed, occlusal surface facing upwards, in a sample holder designed to hold a small amount of deionized water, so that the samples would remain hydrated throughout the experiment without being completely submerged (Figure 1A).

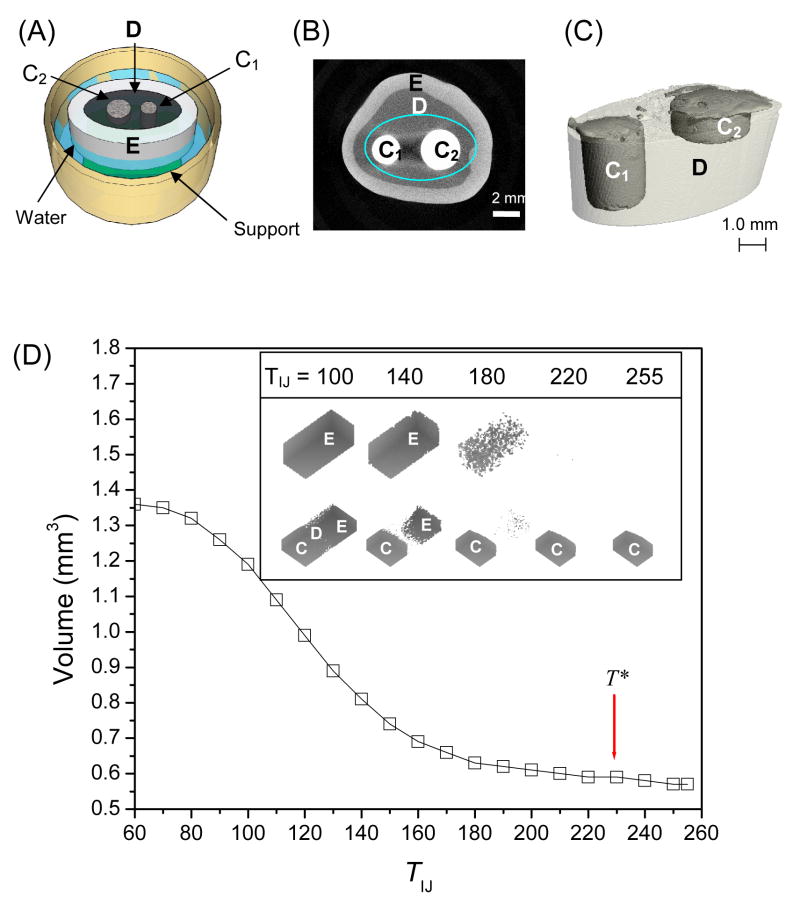
Figure 1.

(A) A sketch of a prepared tooth disk partially submerged in the water secured on a support in the sample holder. C₁ and C₂ are composite filled cavities with different geometries; D is dentin; E is enamel. (B) One slice of μCT scan of a filled tooth. (C) A three-dimensional reconstruction of composite in dentin (area enclosed by the ellipse in (B)). (D), the volume of an object containing dentin, enamel, and composite as a function of threshold value. T* is the optimal threshold. Inset shows ImageJ reconstructions of enamel only and an object containing enamel, dentin, and composite analyzed at increasing thresholds.

Each tooth was scanned individually using μCT (Scanco μCT 40; Scanco Medical, Bassersdorf, Switzerland) at a resolution of 15 μm, I = 114 μA, E = 70 kVp, integration time of 300 ms (previous studies [10] have scanned at 16 μm resolution). The composite was cured with a 600 mW/cm² Spectrum 200R (DENTSPLY/Caulk, Milford, DE) quartz tungsten halogen curing light for 60 s, and the tooth was scanned again using the identical conditions after a 30-min wait to allow polymerization stress to plateau. Reconstruction of three-dimensional (3D) images and image analysis was carried out using the manufacturer’s software and ImageJ [12] software. In the μCT software, the segmentation parameters sigma and support were set at 1.2 and 2, respectively. A threshold for image reconstruction with the μCT software (T_CT) was the average value of the six samples determined by adaptive thresholding (taken before and after photopolymerization). As a separate segmentation procedure, the threshold in ImageJ (T_IJ) was determined by generating a series of reconstructions utilizing increasing thresholds and obtaining the calculated volumes. The resulting function was graphed, and the maximum value at which the composite volume remained constant and the dentin and enamel were invisible was deemed the appropriate threshold value. Overall shrinkage was computed by subtracting the total volume of composite after photopolymerization from the total volume of composite before polymerization. 3D reconstructions of objects before and after composite polymerization were compared to predict leakage locations after aligning those images in ImageJ using the TransformJ plug-in [13]. TransformJ allows multi-dimensional manipulation of image stacks such as translation along and rotation about the x, y, and z axes, all of which were necessary adjustments if the sample moved between scans. Slice-by-slice analysis was done by calculating the area of each slice, converting it to a volume, and subtracting the value of each “after” slice from that of its corresponding “before” slice—thus permitting the localization of shrinkage along the depth of the sample. Visualization of areas of potential leakage was accomplished using ImageJ’s “Image Calculator” function. The “after” image was subtracted from the “before” image and projected in 3D in a contrasting color, then combined with a 3D projection of the composite alone.

In order to validate the results obtained from μCT, teeth were prepared for confocal microscopy in reflectance mode (Zeiss LSM 510). Using a diamond blade, teeth were bisected along a plane through both composite fillings with an Isomet precision saw (Buehler Ltd., Lake Bluff, IL), then rinsed with distilled water for 60 s. Air was gently blown over the surface for 10 s to remove debris. Excitation was at λ = 488 nm with an argon ion laser.

Statistical analysis was performed using One-Way Analysis of Variance (ANOVA) and Student’s t test, where appropriate, at a significance level of 0.05 given the standard uncertainty.

Results

Figure 1B shows a typical x-y image slice of a composite-filled tooth, where the composite (“C₁” and “C₂”) is surrounded by dentin (D, dark gray), which is enclosed by enamel (E, light gray). After determination of a suitable threshold T*, grayscale images of the filled teeth were converted into binary images and reconstructed into 3D objects. It was possible to visualize composite restorations both independently and within the tooth (as shown in Figure 1C). Detailed thresholding and alignment procedures will be discussed further.

The procedure of determining T* is critical. T*_CT, calculated by the instrument software, was obtained by averaging values that were computed by the program’s adaptive thresholding feature. For composite, T*_CT = 825 before curing, T*_CT = 834 after curing, on the instrument’s scale of −1000 to 1000. A modest increase in T upon polymerization reflects the densification of the composite after curing. T*_IJ was obtained by plotting the volumes of a block contain dentin, enamel and composite calculated at a series of increasing thresholds within ImageJ’s scale (ranging from 0 to 255) and determining the highest value at which the composite volume remained constant but neither dentin nor enamel was visible; T*_IJ = 230.

Using the appropriate segmentation parameters (sigma, support, and threshold), the object of interest is separated from the background for accurate calculation of volume and to determine its precise location. The object in this study is composite and the background is tooth tissue (dentin, enamel). At the optimized threshold (T*), the background voxels are quantitatively removed while the object volume (voxels) remains constant. The volume of an object containing enamel, dentin, and composite was plotted as a function of T obtained using ImageJ software (Figure 1D). The point at which changes in volume were minimized was identified as the optimum threshold value, T*_IJ = 230. Inset of Figure 1D illustrates the effect of T_IJ on object volume: the top row shows an enamel block which is completely visible at T_IJ = 100. Decreased volume is observed at T_IJ = 140; further increase to T_IJ = 160 removes a significant volume of the enamel structure. The enamel is nearly entirely removed at T_IJ = 220. The bottom row shows an object composed of dentin, enamel, and composite. The dentin was not completely intact even at T_IJ = 100. At higher T values (T_IJ > 220), only the composite remains. Due to varying mineral content among individual teeth, the T value may fluctuate slightly; nevertheless, this method of establishing a threshold can be applied when evaluating samples that are composed of two (or more) materials of different density.

Composite shrinkage determined using T*_IJ was compared with that computed using average values of optimum thresholds calculated by the manufacturer’s adaptive thresholding feature (Table 1). Composite volumes before and after curing, in addition to shrinkage, were determined using each of the two methods and compared using Student’s t test. No significant differences in volume between C₁ and C₂ samples at any of the threshold values (p > 0.05) were found. Comparison of shrinkage values revealed no significant differences between C₁ and C₂ samples, or between image analysis methods for each type of sample.

Table 1.

Composite volumes and shrinkage values assessed by different software.

Values shown are mean plus or minus one standard deviation. The variations in reported volumes before and after polymerization are due to sample variation (C₁, N=5; C₂, N=6), and do not represent measurement or analytical uncertainty.

	C1			C2
	Before (mm3)	After (mm3)	% Shrinkage	Before (mm3)	After (mm3)	% Shrinkage
ImageJ	9.18 (1.28)	8.95 (1.23)	2.48 (0.31)	8.47 (0.81)	8.23 (0.76)	2.84 (0.38)
μCT	9.26 (1.29)	8.99 (1.23)	2.91 (0.44)	8.50 (0.89)	8.22 (0.84)	3.25(0.39)

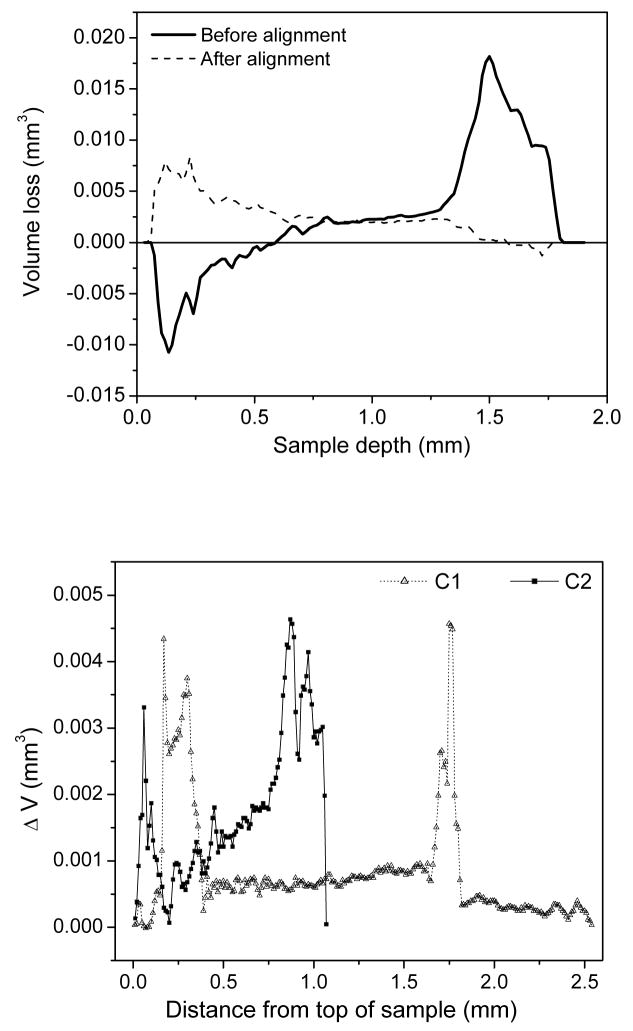
A slice-by-slice analysis was performed in ImageJ to evaluate shrinkage as a function of sample depth. Initial analysis indicated that some samples shifted between scans; this was implied by the apparent “growth” of sample volume. Areas of enamel (relative positions of which do not change when the composite is polymerized) were used as fiduciary markers to realign 3D images by translating along and rotating about the x, y, and z axes as necessary such that the initial positions corresponded to the post-polymerized positions. As shown in Figure 2A, the shrinkage profile of one sample before alignment showed that the composite appeared to increase in volume (negative volume loss) at the top, while the greatest part of the shrinkage appeared to occur at the bottom. After alignment, shrinkage of this sample occurred primarily near the top surface and gradually decreased with increased depth. In Figure 2B, profiles typical of C₁ and C₂ restorations from the same, representative sample are compared. Both cavity geometries exhibit similar patterns of volume loss, i.e. a substantial decrease in volume at the top of the sample, smaller but steady loss along most of the length, then another spike in loss at or near the bottom of the sample. As a validation, the total shrinkage volume obtained by summing all slices is consistent with results shown in Table 1.

Figure 2.

(A) Slice-by-slice analysis of volume loss before and after alignment of a representative sample. (B) Slice-by-slice analysis of C₁ and C₂ composite restorations from a representative sample reveals similar shrinkage profiles, with large volume loss at the top, some loss occurring along the walls, and an additional spike in shrinkage at or near the bottom of the sample.

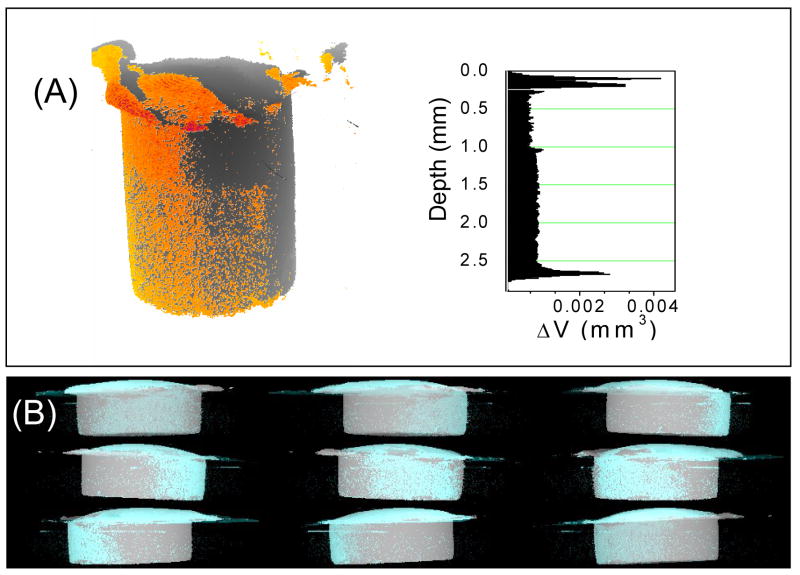
Figure 3A shows the 3D leakage profiles predicted by ImageJ for a C₂ cavity geometry restoration where the leakage locations (shown in orange) are superimposed over the original composite; the corresponding slice-by-slice shrinkage profile is adjacent to the image. Results from the slice-by-slice analysis show appreciable shrinkage from the top surface (free shrinkage), on the bottom surface, as well as along the side, as in Figure 2B. The 3D leakage profile indicates that much of the potential leakage tended to be along one side of the sample rather than being uniformly distributed. This leakage profile is consistent with previous results, [11] regardless of cavity dimensions. The montage of images in Figure 3B represents a 3D reconstruction of a C₂ sample rotated about the y axis, shown at 60° intervals. The composite is light gray, while areas in which volume has been lost are shown in cyan. The non-uniform distribution of the potential leakage is clearly visible as discrete patches of cyan.

Figure 3.

(A) The orange represents areas in which volume has been lost due to photopolymerization for a C₁ sample; the corresponding slice-by-slice analysis illustrates the magnitude of volume loss as a function of depth. (B) A 3D reconstruction of a C₂ sample. The montage of images represents positions at 60° intervals as the sample is rotated on the y axis; the composite is light gray, while areas in which volume has been lost are shown in cyan.

Confocal microscopy images revealed that gaps that measured 15 μm to 20 μm between the composite and the cavity wall arose in areas where μCT imaging indicated the occurrence of potential leakage (Figure 4A). Conversely, areas in which the μCT imaging did not suggest leakage showed the composite and dentin to be in close contact (Figure 4B).

Figure 4.

Cut-plane visualization of restorations with confocal microscopy. (A) Large gaps between dentin (D) and composite (C) indicated by the white arrowheads. (B) dentin (D′) and composite (C′) are in close contact consistent with μCT predictions.

Discussion

In the current study, we prepared cavities of a near constant volume (≈ 3 mm³) but different dimensions and therefore C-factors (2.33 and 3.56) to investigate the effect that C-factor has on composite shrinkage within an extracted tooth. One cavity of each configuration was prepared on the same tooth so that effects due to tooth-to-tooth variations in mineral content would be minimized. Two additional key issues that were addressed in the experimental design included the need to maintain sample hydration and the development of a suitable analysis protocol. μCT data acquisition can take several hours, during which time the geometry of a progressively dehydrated tooth could become altered enough to produce gaps at the tooth-composite interface not due to composite shrinkage. To this end, we designed a holder for the tooth that contained enough water to hydrate the sample, but did not submerge it (Figure 1A). The tooth was positioned securely near the top opening of the tube to allow easy access for the curing probe.

It was necessary to develop a specific protocol for image analysis in order to handle variations in mineral content, both within each tooth and between teeth, and to resolve tooth tissue from composite as accurately as possible. The first step in determining an object’s volume using reconstructed μCT images is to establish the optimal threshold T*. When a histogram of voxel signal intensity is constructed (on a scale of 0 to 255), T* is defined as the T at which the voxels that represent the object in question remain visible and constant while the background—surrounding objects and unoccupied spaces–is removed. During the thresholding process, we found that in histograms of voxel intensity for images containing dentin, composite and enamel, the peak that represented dentin was easily resolved, but the peaks of voxel signal intensity for composite and enamel were broad and partially overlapped. Both composite and enamel are highly scattering materials; separating the two objects by thresholding is more challenging and potentially leads to a greater uncertainty. For these reasons, we chose to place the composite restorations in exposed dentin to eliminate interference that might arise from enamel in the immediate vicinity of the composite.

Although precautions were taken to immobilize the samples during the μCT scanning process – any movement during a scan will render the results incomparable for determination of potential leakage sites – movement between scans did occasionally occur. The ImageJ program permits stacks of images to be translated along and rotated about the x, y, and z axes; this proved necessary in order to align the “before” and “after” images for leakage identification and visualization. Images were aligned using reference locations or fiduciary markers in each sample, such as pieces of enamel, which would not change in size, shape, or relative position upon curing. Figure 2A is a clear demonstration of the necessity of proper alignment: when the sample images are not positioned properly, a slice-by-slice analysis suggests that the sample increases in volume near the top and loses a larger than expected volume at the bottom. Volume loss occurred in the expected manner once the image stacks are brought into alignment. Information obtained from slice-by-slice analysis is particularly valuable for 3D localization of shrinkage; these data inform whether the majority of shrinkage occurs at a particular depth along the sample, or is evenly distributed throughout.

Proper alignment is also necessary for visualization of the samples in 3D. Potential leakage is defined as the difference when a reconstructed image of a sample after polymerization is subtracted from that of the same sample before polymerization (Figure 3). Slice-by-slice analysis combined with 3D image reconstructions provide comprehensive information related to leakage location and magnitude. Total volume loss due to polymerization is independent of cavity dimensions for the dimension studied, and there is no discernible difference in the general leakage profile. As in the image reconstructions, peak volume loss occurs at the top of the samples, where there is a large free and unconstrained area. A smaller, uniform loss occurs along the cavity walls, then there is a slight peak in volume loss again at the bottom of the sample as the surface area increases. Distributions of potential leakage areas obtained from reconstructions are in good agreement with those obtained from previous studies in model cavities[11].

Computation of overall shrinkage using both T*_CT and T*_IJ indicated that the cavity geometry, and hence C-factor, did not affect the shrinkage magnitude (Table 1). The slice-by-slice analysis performed in ImageJ also showed that the regions of greatest shrinkage were similarly distributed along the depth of each sample, as described previously, regardless of cavity geometry. Finally, 3D reconstructions revealed that the areas of potential leakage were comparably distributed.

Visualization of the samples by confocal microscopy served to validate the μCT predictions of leakage: gaps measuring 15 μm to 20 μm were observed between the cavity wall and the composite in areas in which leakage was indicated by μCT analysis. Conversely, in regions where the μCT suggested no leakage, the images collected by confocal microscopy revealed that the composite and cavity wall were in close contact. We note that dye was not used in the cross-section imaging. Trial experiments indicated that exposed dentin adjacent to the composite absorbed dye such that the composite was completely surrounded, rather than dye penetration of the putative leaking area only.

While the preceding results are in good agreement with earlier investigations [10, 11], we acknowledge that the size of the gaps determined by confocal microscopy is close to the limit of the resolution of this particular experimental setup. The “patchy” appearance of areas of potential leakage in 3D reconstructions is likely a result of this. At higher resolutions we are confident that such areas will appear interconnected, as they do when examined by optical microscopy. This study demonstrates that when applied to extracted teeth, μCT imaging and analysis produces results that are reliably similar to model cavities. Higher-resolution μCT instruments are available, although at higher resolutions the file sizes become substantially larger, and data acquisition and analysis times can greatly increase.

The use of μCT for assessing the shrinkage and leakage of dental composites is nondestructive and allows 3D visualization and quantification of potential leakage sites. This technique presents many advantages over existing methods for evaluating leakage that typically involve sectioning and microscopy (with or without dye penetration). As noted previously, the traditional methods have many drawbacks. Chief among the disadvantages is that the shrinkage and leakage may only be evaluated in the plane through which the sample is sectioned; furthermore, the sectioning procedure itself may cause a break in the interface. On the other hand, shrinkage and leakage occur in three dimensions, so the true magnitude of leakage cannot be determined via sectioning. Additionally, ground sections are limited by the width of the blade used to cut the section, meaning that restorations of a clinically relevant size and shape may yield only one sample. The sectioning itself can be hit-or-miss—for example, if a band of leakage is particularly narrow, or if there are multiple bands, one slice through a restoration may well miss such regions entirely. Often, measurements obtained by these means are subjective, depending on an observer’s judgment. Finally, this method is by its very definition destructive, further tests cannot be performed on samples investigated in this manner, eliminating the possibility of establishing clear relationships between shrinkage/leakage and, for example, mechanical properties, which would be very helpful in the prediction of clinical performance of dental materials. Imaging via μCT provides a means to bypass all the undesirable properties of traditional leakage measurements.

3D imaging and image analysis also permits the evaluation of restorations of clinically relevant preparation geometries, such as multifacial restorations or those with bevels or retention grooves, from all angles. As noted previously, a bonding agent was not used in this study; we did this so as to keep the system as simple as possible in order to observe unambiguously the behavior of the composite. We acknowledge that the use of a bonding agent will provide results of enhanced clinical relevance, and this is planned for future studies.

Conclusions

In this study, 3D imaging and image analysis via μCT quantified shrinkage and potential leakage of composites placed in extracted human teeth. We found that neither overall shrinkage nor its spatial distribution is affected by cavity geometry or C-factor for the two geometries considered, in agreement with results previously observed in model cavities [10]. The use of μCT in the assessment of dental composite shrinkage and corresponding spatially resolved leakage is a powerful tool. With this method, it is possible to not only to visualize composites in situ, before and after polymerization, but the potential leakage that may occur from polymerization shrinkage can also be seen and and its location precisely identified. Quantitative 3D analysis is also achievable with μCT; overall volume loss can be easily calculated, and the distribution of positional information regarding this loss is obtainable through slice-by-slice analysis. Finally, μCT is a nondestructive method that can evaluate an entire sample, permitting further tests to be performed as part of a “test suite” that will greatly improve prediction of the clinical performance of dental restorative materials.