The Origins of Diverse Domains of Mathematics: Generalist Genes but Specialist Environments

Abstract

The authors assessed 2,502 ten-year-old children, members of 1,251 pairs of twins, on a Web-based battery of problems from 5 diverse aspects of mathematics assessed as part of the U.K. national curriculum. This 1st genetic study into the etiology of variation in different domains of mathematics showed that the heritability estimates were moderate and highly similar across domains and that these genetic influences were mostly general. Environmental factors unique to each twin in a family (rather than shared by the 2 twins) explained most of the remaining variance, and these factors were mostly specific to each domain.

The domain of mathematics is extremely complex, including such distinct areas as arithmetic, algebra, and geometry, with each of these areas consisting of many subdomains and encompassing many cognitive processes. For elementary school children, standardized achievement tests assess a wide range of arithmetic skills, including such diverse cognitive processes as learning, remembering, and retrieving arithmetic facts; executing calculation procedures; using problem-solving strategies that involve executive function and working memory (Geary, 2004; Landerl, Bevan, & Butterworth, 2004); and implementing general semantic memory and visuospatial processes (Geary, 1993; Mazzocco & Myers, 2003). Although standardized achievement tests often assess diverse mathematical skills, this information frequently is aggregated into a global score of mathematical achievement that essentially averages information about children’s patterns of strengths and weaknesses.

Although relatively little is known about the phenotypic (observed) relationships among mathematics skills, even less is known about the genetic and environmental origins of these relationships. The few univariate twin and adoption studies of mathematics performance have reported a wide range of heritabilities, from .20 to .90 (reviewed in Oliver et al., 2004), using global assessments of mathematics. In a recent report, three different aspects of mathematics ability and disability in 7-year-olds were assessed by teachers using U.K. national curriculum criteria during the 2nd year of elementary school (Oliver et al., 2004). The results showed substantial genetic influence (.69–.74) for the three measures. However, it is important to note that the average phenotypic correlation among the three measures was very high (.81) in this study, which might be partly because of the teachers’ bias toward rating the three aspects of mathematics as if they were more similar than they are. Although several multivariate genetic studies addressed the etiology of covariation between mathematics and other cognitive skills (reviewed in Kovas, Harlaar, Petrill, & Plomin, 2005), we could find no published reports of multivariate analyses that addressed the heterogeneity within the domain of mathematics.

The purpose of the present study is to provide the first multivariate genetic analysis of the etiological relationship among five aspects of mathematics that are part of the U.K. national curriculum. Our focus is on individual differences in mathematics ability for a representative sample of children rather than on mathematics disability, for which much more has been written about possible subtypes (e.g., Geary, 2004; Geary, Hamson, & Hoard, 2000; Landerl et al., 2004; Mazzocco & Myers, 2003; Miranda Casas & García Castellar, 2004; Temple & Sherwood, 2002). Nonetheless, genetic research suggests that individual differences in mathematical ability are relevant to mathematical disability because, rather than having a unique etiology, common disability appears to be the quantitative extreme of the same genetic and environmental factors responsible for typical variation in ability (Oliver et al., 2004; Plomin & Kovas, 2005). For example, for each of many genes associated with a specific ability, a “good” and a “bad” variant may exist, and the relative number of good and bad variants (together with other relevant factors) influences a person’s position on a continuum of ability. In other words, when genes are found that are associated with mathematics ability, the same genes are expected to be associated with mathematics disability.

Rather than focusing on genetic and environmental contributions to the variance of a single trait (univariate genetic analysis), multivariate genetic analysis investigates the genetic and environmental contributions to the covariance between traits (Martin & Eaves, 1977; Plomin, DeFries, McClearn, & McGuffin, 2001), as described in detail in the Method section of the current investigation. Multivariate genetic analysis yields a statistic called the genetic correlation, which indexes the extent to which genetic effects on one trait correlate with genetic effects on another trait independently of the heritability of the two traits. The genetic correlation can be roughly interpreted as the extent to which the same genes affect the two traits; a genetic correlation of 1.00 indicates that the same genes affect both traits, and a genetic correlation of .00 signifies that different genes are involved.

Although no multivariate genetic research has addressed the issue of heterogeneity within the domain of mathematics, multivariate genetic research in other cognitive areas demonstrates a surprisingly high degree of genetic overlap among such diverse aspects of ability as grammar, vocabulary and phonology in language (average genetic correlations ~ .60), and reading of words and nonwords (genetic correlation ~ .80; reviewed in Plomin & Kovas, 2005). Moreover, substantial genetic overlap has been found for whole cognitive areas, such as reading, language, and general cognitive ability (Plomin & Kovas, 2005), and a recent analysis included mathematics in this network of genetic links (Kovas et al., 2005). Such multivariate genetic research has led to the hypothesis that a single set of genes is largely responsible for genetic effects on diverse cognitive and learning abilities and disabilities (Plomin & Kovas, 2005). This generalist genes hypothesis predicts that when genes are found that are associated with a particular cognitive ability, the same genes will also be associated with other cognitive abilities. The generalist genes hypothesis leads us to predict substantial genetic overlap within the domain of mathematics, a hypothesis that we can test directly using multivariate genetic analysis. In the present study, our prediction is that genetic correlations will be substantial among five aspects of mathematics ability.

A practical problem in conducting genetic research on mathematics ability is that large samples of twins must be assessed, but it is expensive to test such large samples in person, especially when their home residences are distributed over a wide area. Our previous research circumvented this problem by using teacher assessments based on U.K. national curriculum criteria (Kovas et al., 2005; Oliver et al., 2004). Although teacher assessments are a valuable source of information about children’s progress, the criteria used were broad and not amenable to multivariate genetic analysis. Even if more specific ratings were obtained, it is possible that teachers would not be able to adequately discriminate a child’s strengths and weaknesses in different aspects of mathematics.

In the current research, we address this problem by the use of Web-based tests, which make it possible to assess large samples efficiently and economically. To increase the relevance of the multivariate research to current educational practice, we decided to base our testing on the U.K. national curriculum, which focuses on five aspects of mathematics when children are 10 years of age: (a) using mathematics in a problem-solving situation; (b) understanding the numerical and algebraic process to be applied when solving problems; (c) retrieving and computing facts; (d) interpreting information from diagrams, graphs, tables, charts, and scales; and (e) understanding nonnumerical mathematical processes and concepts. We designed a Web-based battery of tests using these subtypes to investigate the etiology of variance and covariance for these aspects of mathematics in a sample of 1,251 pairs of 10-year-old twins.

Method

Participants

Participants were part of the Twins’ Early Development Study (TEDS), a longitudinal study involving a representative sample of all twins born in England and Wales in 1994, 1995, and 1996 (Trouton, Spinath, & Plomin, 2002). Data from 2,690 children born between January 1994 and August 1995 were analyzed for this study. The families in our database were contacted by post, receiving an invitation to participate in the Web-based study. They received the log-in information and were welcomed to call the usual toll-free telephone number if they had any questions or required technical assistance. We monitored the testing progress online and made follow-up calls to relevant families.

The following exclusion criteria were used: specific medical syndromes, such as Down’s syndrome and other chromosomal anomalies, cystic fibrosis, and cerebral palsy; hearing loss; autism spectrum disorder; organic brain damage; extreme outliers for birth weight; gestational age; maternal alcohol consumption during pregnancy; and special care after birth. Finally, 72 children (36 pairs) for whom English was not the first language spoken at home were excluded from the sample. After exclusions, the sample consisted of 2,502 children: 470 pairs of monozygotic (MZ) twins and 781 pairs of dizygotic (DZ) twins (399 same-sex pairs, 382 opposite-sex pairs). All cotwins in this sample shared the same household.

Zygosity was ascertained by parental ratings, with an error rate not exceeding 5%, as validated by DNA typing (for details, see Freeman et al., 2003). We have previously reported analyses of representativeness of the TEDS sample and its subsamples against U.K. population data and against the participants lost to attrition (Harlaar, Spinath, Dale, & Plomin, 2005; Spinath, Walker, Saudino, & Plomin, in press). These analyses showed that the TEDS sample continues to be representative of the U.K. population in terms of demographic characteristics, despite attrition.

Measures

To assess mathematics knowledge and problem-solving ability, we developed a Web-based battery that included questions from five different components of mathematics. The items were based on the National Foundation for Educational Research 5–14 Mathematics Series (nferNelson Publishing Co., 1994a, 1994b, 1994c, 1994d, 1999a, 1999b), which is linked closely to curriculum requirements in the U.K. and the English Numeracy Strategy. From Booklets 6, 7, 8, 9,10, and 11 (referring to age of students), 134 target items were chosen. The items were organized by mathematical category (see below) and level of difficulty. The level of difficulty was based on the national curriculum level and the standardization sample percentage correct for each item (reported in the Group Record Sheets; nferNelson Publishing Co., 1994a, 1994b, 1994c, 1994d, 1999a, 1999b). A set of adaptive branching and discontinuation rules was developed separately for each of the five categories, so that all the children started with the same items but then were branched to easier or harder items depending on their performance. The presentation of items was streamed, so that items from different categories were mixed, but the data recording and branching were done within each category. Participants could attempt each item only once.

As with many psychological tests that use branching (e.g., Wechsler Intelligence Scale for Children; Wechsler, 1992), the generic scoring rules were as follows: One point was recorded for each correct response, for each unadministered item preceding the child’s starting point, and for each item skipped through branching to harder items. After a certain number of failures, a discontinue rule was applied within each category, and no points were recorded for any items after discontinuation. Thus, for each of the 134 items in the test, a score of 1 or 0 was recorded for each child. For example, in the Computation and Knowledge category (total number of items = 31), all children started at Item 10. The following rules were then applied:

If Items 10, 11, and 12 were all answered incorrectly, the child was branched to Item 1 and had to continue with the test attempting all remaining items or working until the discontinuation criterion was met.

If Items 10, 11, and 12 were all answered correctly, the child received credit for all preceding items (1–9) and was branched to Item 24. If Items 24, 25, and 26 were all answered incorrectly, the child was branched back to Item 13 and had to continue with the test (skipping all items previously administered), attempting all remaining items or until the discontinuation criterion was met. If Items 24, 25, and 26 were not all answered incorrectly, the child received credit for all preceding items (13–23) and then continued with the test, attempting Items 27, 28, 29, 30, and 31 or working until the discontinuation criterion was met.

If Items 10, 11, and 12 were not all answered incorrectly or correctly, the child received credit for all preceding items (1–9) and then had to continue with the test, attempting all remaining items or working until the discontinuation criterion was met.

The discontinuation criterion was three incorrect answers in a row (did not apply across branching points).

Not only were the items of increasing difficulty, but also the branching points corresponded with expected grades. Children started with age-appropriate difficulty levels and branched to below or above their expected grade difficulty level. As with other psychological tests that contain items of increasing difficulty and use similar rules, this scoring system is equivalent to that in which all children attempt all items, which allowed us to calculate the total number and proportion of correct responses for each child for each category as well as test the internal consistency of each category (see the Results section). Specific branching and discontinuation rules and the number of skipped (credited) items for each category are available on request.

The items were drawn from the following five categories:

1. Mathematical Application (24 items) is a broad category testing the ability to use mathematics in problem-solving situations, which requires that the student determine the needed operation from the context before performing the calculation (if any). This category tests the application of acquired skills and concepts. For example, “The time is 7:40. Matthew has set his alarm for 8:30. How much longer can he sleep?” Another example is, “There are ten coins in your purse. You have three friends. You give each friend one coin. How many coins will be left in your purse?”

2. Understanding Number (27 items) requires an understanding of the numerical and algebraic process to be applied when solving problems (e.g., understanding that multiplication and division are inverse operations). For example, “Look at the number 6085. Change the order of the figures around to make the biggest number possible.” Another example is, “Type the missing number in the box: 27 + 27 + 27 + 27 + 27 + 27 = 27×—.”

3. Computation and Knowledge (31 items) assesses the ability to perform straightforward computations using well-rehearsed pencil-and-paper techniques and the ability to recall mathematical facts and terminology. These questions either are mechanistic or rely on memorization of mathematical facts and terminology. The operation is stated or is relatively unambiguous. Three examples follow: “Type in the answer: 76 – 39.” “All 4-sided shapes are called? Click on the answer (Squares Rectangles Parallelograms Kites Quadrilaterals).” “Type in the answer: 149 + 785 = ?”

4. Mathematical Interpretation (33 items) involves the ability to interpret information from diagrams, graphs, tables, charts, and scales. A calculation may be involved. Two examples that do not require calculation follow. “The graph shows the weight of a baby girl in the first 8 weeks of her life. How heavy was the baby when she was 8 weeks old? Click on the answer.” A second example is, “This shows entrance prices for a nature reserve. How much does it cost for an 8 year-old child on a Saturday? Click on the answer.”

5. Non-Numerical Processes (19 items) does not rely solely on memory but rather requires understanding of nonnumerical mathematical processes and concepts, such as rotational or reflective symmetry and other spatial operations. The questions do not have any significant numerical content that pupils need to consider. Three examples follow: “Which is the longest drinking straw? Click on it.” “One of these shapes has corners that are the same. Click on this shape.” “Which card appears the same when turned upside down? Click on it.”

It must be noted that in creating this battery we aimed to choose tests that would, among them, cover a wide range of mathematical abilities of 10-year-old children, without subscribing to a particular theoretical position on the structure of mathematical domain. Some overlap in what these tests measure is inevitable, as they each make demands on overlapping cognitive and performance factors (attention, motivation, memory) and as it is never possible to achieve a completely pure measure of any of these components. Although one can never entirely control for the multiple influences on performance on a mathematical test, it is nevertheless possible to choose tests that stress one component of mathematics more than another. For example, solving problems in the Mathematical Application component requires determining the needed operation from the context. If actual performance of this operation were required, the operation would be relatively simple. In this way, the main source of variance in this component is the ability to formulate a problem using contextual information. On the contrary, in the Computation and Knowledge component, such ability is not tested, because the operation or a question about mathematical facts is clearly stated. The main source of variance in this category can be attributed to the ability to perform the required mathematical operation or to retrieve the necessary mathematical fact. The questions in the NonNumerical Knowledge category do not require any computation, and the required operations are explicitly stated.

Most important, the five aspects of mathematics that we assessed were not arbitrarily chosen: These are used in the U.K. national curriculum to assess aspects of mathematics. The categories used in this study include items that were statistically discriminated and trialed as part of the development of the tests by the nferNelson Publishing Co. (1994a, 1994b, 1994c, 1994d, 1999a, 1999b). Further information on standardization, reliability, and validity of the test scores can be found in the teacher’s guides for each year. One of the main reasons for using the assessment based on the U.K. national curriculum is to increase the relevance of our study to education. In addition, curriculum-based assessment alleviates some of the potential biases associated with other achievement tests (Good & Salvia, 1988).

The use of Web-based assessment allows data from large, widely dispersed samples to be collected quickly, inexpensively, and reliably. Web-based data collection is less error prone because it does not require human transcription and data entry (Kraut et al., 2004; Naglieri et al., 2004). Another positive aspect of Web testing is that the social pressure and embarrassment that might be present in face-to-face testing are reduced, making it easier for participants to stop whenever they feel discomfort (Birnbaum, 2004; Kraut et al., 2004).

Several recent empirical studies have found that Web-based findings generalize across presentation formats and are consistent with findings from traditional methods (e.g., Gosling, Vazire, Srivastava, & John, 2004).

An empirical study (Gosling et al., 2004) designed to test several misconceptions that are associated with Web testing found that (a) Internet samples were usually more diverse than traditional samples, (b) Internet users did not differ from nonusers on markers of adjustment and depression, (c) Internet findings replicated across different presentation formats, and (d) Internet-based findings were consistent with findings based on traditional methods. In TEDS, 80% of the families had daily access to the Internet (on the basis of a pilot with 100 randomly selected TEDS families), which is similar to market surveys of U.K. families with adolescents. Most children without access to the Internet at home had access in their school and local libraries.

In designing our Web battery, we took precautions against potential problems associated with research on the Internet. The Web site and testing were administered by a secure server in the TEDS office (the TEDS Web site can be accessed at www.teds.ac.uk). We used a secure site for data storage; identifying information was kept separate from the data. Appropriate safeguards were in place that prevented children from answering the same item more than once. We provided technical support and other advice to parents and children, who were advised to call our toll-free telephone number in case of any problems or questions.

Testing Procedures

Informed consent was obtained from all of the families who agreed to take part in the study. Parents supervised the testing by coming online first with a user name and password for the family, examining a demonstration test, and completing a consent form. Then parents allowed each twin to complete the test in turn. Parents were urged not to assist the twins with answers and to ensure that each twin completed the tests separately and that the twins were not in the same room at the time of testing. We are confident that most parents complied with this requirement. First, the parents and the twins had participated in TEDS for 10 years and were familiar with TEDS’s research needs. Second, during the development of Web-based testing, we asked parents about this issue, and they indicated that they had no reason not to comply with our requirement because the children’s scores were for research purposes only. Finally, we tested the validity of our measures and found them satisfactory (see the Results section).

Analyses

Phenotypic analyses

The data were first explored with descriptive statistics analyses in SPSS. Analysis of variance was performed to assess the effects of sex and zygosity on mathematical ability in our sample. Phenotypic relationships among the five categories were explored with Pearson correlation and principal-components factor analysis.

Before assessing genetic and environmental influences on variance and covariance among the five aspects of mathematics, we explored the phenotypic structure of interrelationships between them. We used a phenotypic Cholesky decomposition analysis to test the shared and unique influences on the five aspects of mathematics. The phenotypic Cholesky is analogous to a hierarchical multiple regression analysis in which the first four categories are entered sequentially and the fifth category is the dependent variable (see Tiu, Wadsworth, Olson, & DeFries, 2004, for details of this procedure). We used a five-factor model in which the first factor represented shared variance for the five aspects of mathematics. The second factor represented the shared variance among the remaining four categories after we accounted for the variance in common with the first test. The third factor represented the shared variance among the remaining three categories after we accounted for the shared variance with the first and second tests. The fourth factor represented the proportion of variance in common for the remaining variables after we accounted for the shared variance with the first three tests. Finally, the fifth factor estimated the proportion of the variance that was unique to the fifth test. In other words, we used this procedure to test the independent effect of one variable (e.g., influences on Mathematical Interpretation) on another variable (e.g., Non-Numerical Processes) after controlling for influences that were also important for the preceding aspects of mathematics (Mathematical Application, Understanding Number, and Computation and Knowledge).

Genetic analyses

The twin method addresses the origins of individual differences by estimating the proportion of variance that can be attributed to genetic, shared environment, and nonshared environment factors (Plomin, DeFries, et al., 2001). In the case of complex traits that are likely to be influenced by multiple factors, the genetic component of variance refers to the influence of alleles at all gene loci that affect the trait. The similarity between twins for any particular trait can be due to a common set of genes. It may also be due to the shared environment, which refers to environmental influences that vary among families but not within families and that contribute to the similarity between cotwins. For example, twins experience similar conditions during gestation, have the same socioeconomic status, live in the same family, and usually go to the same school. These factors could reasonably be expected to increase similarity between cotwins. Nonshared environment refers to any aspect of environmental influence that makes cotwins different from each other, including measurement error. Such influences involve aspects of environment that are specific to an individual, such as traumas and diseases, idiosyncratic experiences, different peers, differential treatment by the parents and teachers, and different perceptions of such influences.

Genetic influence is estimated via comparison of the covariance between identical (MZ) twins, who are genetically identical, and fraternal (DZ) twins, who share 50% of the same genes, on average. If the MZ twin correlation exceeds the DZ twin correlation, then genetic influences (or heritability) are implicated. Shared environmental effects are implied to the extent that MZ and DZ correlations are similar beyond heritability. Nonshared environment is the extent to which the MZ twin correlation is not 1.00.

Structural equation model fitting is a comprehensive way of estimating variance components on the basis of these principles. For example, variations on the so-called ACE model can be used for analyses of individual differences; this model apportions the phenotypic variance into genetic (A), shared environmental (C), and nonshared environmental (E) components, assuming no effects of nonadditive genetics or nonrandom mating. The researcher can estimate the ACE parameters and their confidence intervals by fitting the models to variance–covariance matrices using the model-fitting program Mx (Neale, 1997; Neale, Boker, Xie, & Maes, 2002).

These principles can be extended to investigate the etiology of the covariance between traits. Multivariate genetic analysis assesses the extent to which genetic and environmental factors are responsible for the phenotypic correlation between two traits. For twin studies, multivariate genetic analysis is based on cross-trait twin correlations for two or more traits. For example, one twin’s Computation and Knowledge score is correlated with the cotwin’s Non-Numerical Processes score. Similar to the univariate case described above, the phenotypic covariance between two traits is attributed to genetic overlap to the extent that the MZ cross-trait twin correlation exceeds the DZ cross-trait twin correlation. Shared environmental influences are indicated to the extent that the DZ cross-twin correlation is more than half of the MZ correlation.

As with univariate analysis, structural equation modeling represents a more comprehensive way of estimating the proportion of covariance. In particular, we fitted a multivariate Cholesky decomposition model (with five variables) to the variance–covariance matrices derived from the twin data to test for common and independent genetic and environmental effects on variance in the five aspects of mathematics. The Cholesky procedure is similar to hierarchical regression analyses in nongenetic studies, whereby the independent contribution of a predictor variable is assessed after its shared variance with other predictor variables is accounted for (see Tiu et al., 2004, and Neale et al., 2002, for more detail). The order in which the variables were entered in the analysis was determined by the logical assumption that Mathematical Application is the most general ability of the five and is therefore likely to have shared etiology with the other abilities to a large extent. Thus, Mathematical Application was entered in the analysis first, followed by increasingly more specific categories (see Loehlin, 1996, for a discussion of the Cholesky procedure). This order, however, is by no means the only possible logical order. For example, because one could argue that Mathematical Application is a higher order skill, it may not be an optimum base factor. Instead, the Computation and Knowledge category may be a better candidate, as children might have a better grounding in this aspect and it may underpin more of the other categories. However, if the generalist genes hypothesis is true for the five aspects of mathematics, the order of entry into the analysis should not make a difference. We tested this hypothesis by rerunning this analysis with the five tests in different orders.

As with the phenotypic analysis, we used a five-factor model in which the first factor assessed genetic and shared and nonshared environmental influences on Mathematical Application, some of which also influenced the Understanding Number, Computation and Knowledge, Mathematical Interpretation, and Non-Numerical Processes categories. The second factor represented genetic and shared and nonshared environmental influences on Understanding Number that were not shared with Mathematical Application but were shared with the Computation and Knowledge, Mathematical Interpretation, and Non-Numerical Processes categories. The third factor represented genetic and shared and nonshared environmental influences on Computation and Knowledge that were not shared with Mathematical Application and Understanding Number but were shared with the Mathematical Interpretation and Non-Numerical Processes categories. The fourth factor represented genetic and shared and nonshared environmental influences on Mathematical Interpretation that were not shared with Mathematical Application, Understanding Number, and Computation and Knowledge but were shared with the Non-Numerical Processes category. Finally, the fifth factor estimated genetic and shared and nonshared environmental influences that were unique to the Non-Numerical Processes category. The model also allowed us to estimate the proportions of the total variance attributable to genetic and environmental factors for each of the categories (univariate estimates).

In addition, we transformed the paths from the model to obtain estimates of genetic, shared environmental, and nonshared environmental correlations between each pair of factors. Genetic correlations index the extent to which the sum of genetic influences on one measure correlates with the sum of genetic influences on a second measure, regardless of the heritabilities of the traits. Put another way, it is the extent to which the heritabilities described in Table 3 are influenced by the same genetic factors. We also estimated the proportion of the phenotypic (observed) covariance among the math measures that could be attributed to genetic covariance between Trait 1 and Trait 2, which is bivariate heritability, the genetic correlation weighted by the product of the square roots of the heritabilities of the two traits and divided by the phenotypic correlation between them (Plomin & DeFries, 1979). Shared and nonshared environmental correlations, which index the extent to which the same shared and nonshared environmental influences are important for the two aspects of mathematics, and environmental contributions to the phenotypic correlation were also estimated. Details of the estimation of these statistics are provided elsewhere (e.g., Plomin & DeFries, 1979; Posthuma et al., 2003; Tiu et al., 2004). In summary, we used a Cholesky decomposition to estimate the genetic, shared environmental, and nonshared environmental contributions to the variance of the measures and the covariance among the measures.

Table 3.

Individual-Differences Univariate Model Fitting for the Five Aspects of Mathematics—Genetic (A), Shared Environmental (C), and Nonshared Environmental (E) Parameter Estimates

	A		C		E
Measure	Estimate	CI	Estimate	CI	Estimate	CI
Applic	0.30	0.16, 0.46	0.30	0.16, 0.41	0.41	0.35, 0.47
Underst	0.42	0.24, 0.57	0.15	0.03, 0.29	0.44	0.37, 0.51
Comput	0.42	0.24, 0.54	0.10	0.01, 0.24	0.48	0.41, 0.56
Interp	0.35	0.21, 0.46	0.08	0.01, 0.21	0.56	0.50, 0.63
Non-Num	0.45	0.27, 0.58	0.11	0.01, 0.26	0.44	0.38, 0.51

Note. Three fit indexes are reported: chi-square, Akaike’s information criterion (AIC; Akaike, 1987), and root-mean-square error of approximation (RMSEA). Model fit: χ² (65, N = 756) = 83.197, p = 0.06 (AIC = −46.803, RMSEA = 0.028). The univariate estimates were obtained from the multivariate model fitting, which is reflected in the degrees of freedom. CI = confidence interval; Applic = Mathematical Application category; Underst = Understanding Number category; Comput = Computation and Knowledge category; Interp = Mathematical Interpretation category; Non-Num = Non-Numerical Processes category.

The overall fit of the model can be evaluated with several indexes. The chi-square statistic, for which degrees of freedom equal the number of observed correlations minus the number of estimated parameters, indicates the fit of the full model, with a low value indicating good fit. However, the chi-square statistic is inflated with large sample sizes. Two other indexes—Akaike’s information criterion (equal to χ² − 2df; Akaike, 1987) and the root-mean-square error of approximation—give more interpretable estimates of fit for large samples, with lower values representing good fit.

Results

Validity of Measures

In terms of validity, we were able to compare children’s overall Web-based performance in mathematics at 10 years with their overall mathematics performance as assessed by their teachers on the national curriculum criteria when the children were 9 years old, and we found a correlation of .54 (p < .001). Only 1 twin from each pair was randomly selected for this analysis; a similar correlation of .50 was found for the other half of the sample. In addition, on the basis of the Web results, we identified 20 children from different bands of the distribution and invited them to do the battery again using paper and pencil. The correlation between the scores obtained on the Web and on paper-and-pencil tests was .95. The internal consistency of the Web-administered measures was examined and yielded high Cronbach’s alpha coefficients (Mathematical Application: α = .88; Understanding Number: α = .88; Computation and Knowledge:α = .92; Mathematical Interpretation: α = .92; Non-Numerical Processes: α = .77).

Descriptive Statistics and Further Exclusions

Descriptive statistics for the five categories (Mathematical Application, Understanding Number, Computation and Knowledge, Mathematical Interpretation, and Non-Numerical Processes) are summarized in Table 1. As the results for same-sex and opposite-sex DZ twins were very similar, the data from all DZ twins were collapsed into one group. We also repeated all analyses performed in this study using same-sex twins only and obtained almost identical results (available from Y. Kovas). It can be seen that MZ and DZ twins had almost identical means and standard deviations (percentage of correct responses scores). Analysis of variance revealed no significant main effect of zygosity for any of the variables. A significant main effect of sex was found for two categories, Mathematical Application and Understanding Number, with boys, on average, performing better than girls. However, the effect size was very small, accounting for less than 1% of the variance. Only one Sex × Zygosity interaction was significant; however, in light of the negligible effect size, this interaction was only significant because of the large sample. The five means (and standard deviations) were very similar, suggesting that the categories were of similar difficulty. For subsequent analyses, we separately standardized the five tests using the means and standard deviations of the entire sample (after medical and ethnic exclusions described in the Method section) so that each test had zero mean and unit variance for the total sample of 2,574 twins.

Table 1.

Means, Standard Deviations, Sample Size, and Analysis of Variance (ANOVA) Results by Sex and Zygosity (Zyg) for the Five Aspects of Mathematics

																ANOVA
	All			MZ			DZ			Boys			Girls			Sex		Zyg		Sex × Zyg
Measure	M	SD	n	M	SD	n	M	SD	n	M	SD	n	M	SD	n	p	η2	p	η2	p	η2
Applic	0.70	0.20	1,748	0.70	0.20	643	0.70	0.20	1,105	0.72	0.21	751	0.69	0.19	997	.000	.007	.714	.000	.144	.002
Underst	0.78	0.18	1,748	0.78	0.16	643	0.78	0.18	1,105	0.80	0.18	751	0.77	0.17	997	.004	.005	.917	.000	.163	.002
Comput	0.84	0.18	1,748	0.84	0.18	643	0.84	0.19	1,105	0.84	0.18	751	0.83	0.18	997	.111	.001	.706	.000	.017	.005
Interp	0.84	0.17	1,748	0.84	0.17	643	0.85	0.17	1,105	0.85	0.18	751	0.84	0.17	997	.057	.002	.529	.001	.270	.002
Non-Num	0.72	0.17	1,748	0.71	0.17	643	0.72	0.16	1,105	0.72	0.17	751	0.71	0.16	997	.072	.002	.728	.000	.088	.003

Note. Descriptive statistics are reported on the whole sample after the medical exclusions, N = 2,574. The analysis was first conducted for the same-sex and opposite-sex DZ twins separately, with very similar results for the two groups. Number of individuals without missing data = 1,748. Eta-squared indicates the proportion of the total variance that is attributed to an effect (calculated as the ratio of the effect variance to the total variance). All distributions are unimodal and positively skewed. In the ANOVA analysis, zygosity had three levels: MZ, DZ same-sex, and DZ opposite-sex. No significant effect of zygosity was found. The sex effect was significant for the Mathematical Application and Understanding Number categories, favoring boys. However, sex explained less than 1% of the variance in both cases. MZ = monozygotic twins; DZ = dizygotic twins; Applic = Mathematical Application category; Underst = Understanding Number category; Comput = Computation and Knowledge category; Interp = Mathematical Interpretation category; Non-Num = Non-Numerical Processes category.

The results were corrected so that age and sex differences did not contribute to twin resemblance, which is standard in analyses of twin data (McGue & Bouchard, 1984). This was done by means of regression, in which the sex-appropriate mean was subtracted from the scores of each individual and the linear component of age was regressed out from each score. The following analyses were carried out on the residual scores. The scores were also residualized for age because, although the children were tested at 10 years of age, the results could be affected even by small differences in age or months of school at the time of testing, and members of a twin pair were exactly the same age.

In addition to exclusions described in the Method section, we also excluded from further analyses all pairs in which one or both twins had missing data; we did this separately for each category. To avoid the possibility that our results would be affected by very extreme scores, we excluded from each category all pairs in which one or both twins scored three or more standard deviations below or above the mean (16 pairs for Mathematical Application, 14 pairs for Understanding Number, 12 pairs for Computation and Knowledge, 25 pairs for Mathematical Interpretation, and 22 pairs for Non-Numerical Processes). All further phenotypic and genetic analyses were performed on the sample of 300 MZ and 500 DZ pairs for the Mathematical Application category, 299 MZ and 502 DZ pairs for the Understanding Number category, 301 MZ and 502 DZ pairs for the Computation and Knowledge category, 294 MZ and 498 DZ pairs for the Mathematical Interpretation category, and 292 MZ and 501 DZ pairs for the Non-Numerical Processes category.

Univariate Analyses

Twin intraclass correlations for the five aspects of mathematics are shown in Table 2. The results for all categories are similar and are consistent with those previously reported for teacher-assessed global measures of mathematics in the same sample when the children were 7 years old (Kovas et al., 2005; Oliver et al., 2004). The twin correlations of between .51 and .63 for MZ twins and between .29 and .46 for DZ twins suggest at least moderate genetic influences, with environmental factors being primarily of a nonshared nature. Correlations for same-sex and opposite-sex DZ twins were similar, suggesting the absence of sex differences in genetic and environmental parameter estimates. We repeated all subsequent analyses using a combined DZ twins group (same-sex and opposite-sex twins) and a same-sex-only DZ twins group. The results were very similar for the combined and the same-sex groups (available from Y. Kovas). We report the model-fitting results from the combined group only because of the increased power that the larger sample affords.

Table 2.

Intraclass Correlations (Number of Pairs) for the Five Aspects of Mathematics

	MZ		DZ		DZss		DZos
Measure	ICC	n	ICC	n	ICC	n	ICC	n
Applic	.63*	300	.46*	500	.42*	263	.49*	237
Underst	.60*	299	.37*	502	.33*	265	.41*	237
Comput	.55*	301	.32*	502	.31*	265	.32*	237
Interp	.51*	294	.29*	498	.27*	262	.31*	236
Non-Num	.59*	292	.35*	501	.34*	266	.38*	235

Note. The numbers are after the exclusion of all pairs in which at least one twin was an outlier or had missing data. MZ = monozygotic; DZ = dizygotic; DZss = same-sex twins; DZos = opposite-sex twins; ICC = intraclass correlation; Applic = Mathematical Application category; Underst = Understanding Number category; Comput = Computation and knowledge category; Interp = Mathematical Interpretation category; Non-Num = Non-Numerical Processes category.

^*p < .01.

The Cholesky decomposition model was fitted to the variance–covariance matrices derived from the data. As can be seen from the model-fit statistics shown in the note to Table 3, the full model provided an adequate fit to the data. Additionally, Table 3 presents the proportions of the total variance for each of the five tests due to genetics (A), shared environment (C), and nonshared environment (E). The univariate estimates of genetic influence were moderate for all five tests, with estimates from 0.30 to 0.45. Environmental influences were primarily of a nonshared nature, with the exception of the Mathematical Application category, for which the shared environmental estimate was 0.30.

Multivariate Analyses

Phenotypic analyses

Table 4 presents the results of phenotypic explorations of the data, showing substantial correlations between each pair of tests (rs = .45–.68, n = 810, p <.01). The smallest correlation was observed between the Computation and Knowledge and Non-Numerical Processes categories; the highest correlation was observed between the Mathematical Application and Understanding Number categories. For these and the following factor analyses and phenotypic Cholesky analyses, only the data from 1 randomly selected twin from each pair were used to avoid any distortion of the results due to nonindependence of 2 twins in a pair. The results for the second half of the sample were almost identical. Principal-components factor analysis of the five test scores yielded a general factor (unrotated first principal component) that explained 67% of the total variance. All the tests showed high loadings (.75–.86) on this general factor, suggesting that most of the covariance among the tests was well described by a single factor.

Table 4.

Phenotypic Correlations Among the Five Aspects of Mathematics

Measure	1	2	3	4	5
1. Applic	—	.68*	.56*	.65*	.60*
2. Underst		—	.57*	.66*	.61*
3. Comput			—	.54*	.45*
4. Interp				—	.57*
5. Non-Num					—

Note. Because the twins in a pair are not independent, the analysis was done on one twin in a pair. All children who were outliers or had missing data on any of the measures were excluded from the analysis. n = 811 individuals. Applic = Mathematical Application category; Underst = Understanding Number category; Comput = Computation and Knowledge category; Interp = Mathematical Interpretation category; Non-Num = Non-Numerical Processes category.

^*p <.01.

Results of the phenotypic Cholesky analysis are presented in Table 5. As expected from the substantial intercorrelations in Table 4 and the factor analysis, the first factor loaded significantly on all five tests; the loadings suggest that at least a third of the variance for each of the five tests could be accounted for by this common factor. The other four factors indicate that the remaining variance for the tests was unique to each test, as seen in the diagonal of Table 5. For example, for the Non-Numerical Processes test, 35% of the variance was explained by the common factor, and 55% of the variance was unique to this test.

Table 5.

Standardized Phenotypic Cholesky Squared Path Estimates for the Five Aspects of Mathematics Indicating the Proportion of Variance for Each Trait That Is Shared With or Independent of Other Traits

Path	Applic	Underst	Comput	Interp	Non-Num
Factor 1	1.00	.46	.32	.43	.35
Factor 2		.54	.07	.09	.08
Factor 3			.62	.02	.00
Factor 4				.47	.02
Factor 5					.55

Note. The model is saturated. Because the twins in a pair are not independent, the analysis was done on one twin in a pair. All children who were outliers or had missing data on any of the measures were excluded from the analysis. n = 811 individuals. Applic = Mathematical Application category; underst = Understanding Number category; Comput = Computation and Knowledge category; Interp = Mathematical Interpretation category; Non-Num = Non-Numerical Processes category.

Genetic analyses

The main results of the present study concern the etiological relationships among the diverse aspects of mathematics. Cross-trait twin correlations for the five categories are presented in Table 6. The average MZ cross-trait twin correlation (.52) was almost as great as the average phenotypic correlation (.59) in Table 4, suggesting nearly complete familial overlap among the traits. The MZ cross-trait twin correlations were greater than for DZ twins for all pairings (.34 on average), suggesting genetic overlap among the five aspects of mathematics. Consistent with the univariate results, only modest shared environmental influence was indicated for most pairings, in that cross-trait twin correlations for DZ twins were only slightly greater than half the cross-trait twin correlations for MZ twins.

Table 6.

Cross-Trait Twin Correlations (Number of Pairs) for the Five Aspects of Mathematics

	MZ		DZ		DZss		DZos
Twin and measure	r	n	r	n	r	n	r	n
Twin 1 Underst–Twin 2 Applic	.56*	297	.32*	501	.24*	263	.42*	238
Twin 1 Comput–Twin 2 Applic	.47*	301	.34*	502	.35*	264	.33*	238
Twin 1 Interp–Twin 2 Applic	.54*	297	.33*	499	.31*	262	.36*	237
Twin 1 Non-Num–Twin 2 Applic	.53*	302	.42*	501	.36*	263	.49*	238
Twin 1 Comput–Twin 2 Underst	.45*	294	.24*	502	.26*	267	.22*	235
Twin 1 Interp–Twin 2 Underst	.54*	292	.30*	499	.35*	265	.25*	234
Twin 1 Non-Num–Twin 2 Underst	.55*	296	.37*	501	.36*	266	.38*	235
Twin 1 Interp–Twin 2 Comput	.48*	298	.33*	499	.30*	263	.37*	236
Twin 1 Non-Num–Twin 2 Comput	.58*	303	.38*	501	.35*	264	.42*	237
Twin 1 Non-Num–Twin 2 Interp	.51*	297	.34*	500	.29*	263	.39*	237

Note. The numbers are after the exclusion of all pairs in which at least one twin was an outlier or had missing data. MZ = monozygotic; DZ = dizygotic; DZss = DZ same-sex twins; DZos = DZ opposite-sex twins; underst = Understanding Number category; Applic = Mathematical Application category; Comput = Computation and Knowledge category; Interp = Mathematical Interpretation category; Non-Num = Non-Numerical Processes category.

^*p <.01.

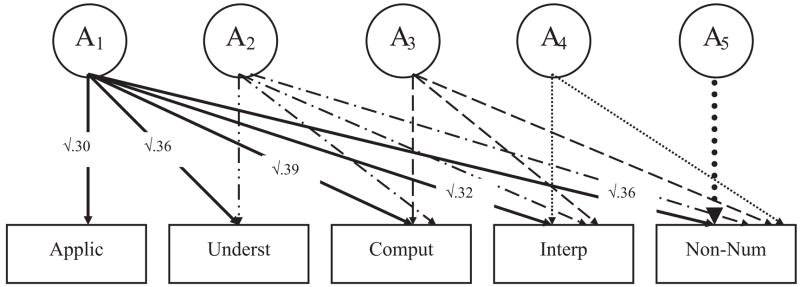
The Cholesky decomposition model was fitted to the variance–covariance matrices derived from the data several times to test whether the pattern of results was affected by the ordering of the variables (see the Method section). The order made no difference to the pattern of results, and only the results from the order described in the Method section are reported. The main results from the multivariate model fitting are presented in Table 7, which partitions the total variance of the five tests into common and independent ACE influences. Figure 1 illustrates the Cholesky results, concentrating just on the genetic influences (Rows A₁ A₂, A₃, A₄, and A₅ in Table 7). The first latent factor (A₁) showed significant genetic effects on Mathematical Application (√.30), some of which also affected the Understanding Number (√.36), Computation and Knowledge (√.39), Mathematical Interpretation (√.32), and Non-Numerical Processes categories (√.36). The other four latent genetic factors (A₂, A₃, A₄, A₅) showed no significant additional shared or independent genetic effects on any of the categories (the confidence intervals for all estimates included zero). Another way of looking at these results is that the Cholesky model divided the genetic influence on the last category entered (Non-Numerical Processes) into five components: .36 + .03 + .06 + .00 + .00 = .45, which add up to the heritability of the Non-Numerical Category shown in Table 3. That is, 80% (.36/.45 = .80) of the genetic influence on Non-Numerical Processes was explained by a common genetic factor encompassing all five tests. It can be seen from Table 7 that the shared environmental influences on all five aspects of mathematics were small, as shown in the univariate analyses earlier. The path coefficients in the model were therefore also small, as they showed the proportion of total variance that could be attributed to shared environment for these measures. The shared environmental influences on individual differences in Mathematical Application were the largest of the five (30%), and some of these influences were shared with other aspects of mathematics. Nonshared environmental influences were almost exclusively unique to each of the mathematical categories and explained 38%–47% of the variance.

Table 7.

Standardized Cholesky Squared Path Estimates for the Five Aspects of Mathematics Indicating Proportions of Genetic, Shared Environmental, and Nonshared Environmental Influences on Each Trait That Are Shared With or Independent of Other Traits

	Applic		Underst		Comput		Interp		Non-Num
Path	Estimate	CI	Estimate	CI	Estimate	CI	Estimate	CI	Estimate	CI
A1	.30	.16, .46	.36	.18, .55	.39	.20, .53	.32	.16, .45	.36	.17, .55
C1	.30	.16, .41	.13	.03, .25	.08	.01, .18	.07	.01, .16	.08	.01, .19
E1	.41	.35, .47	.05	.03, .09	.03	.01, .05	.07	.04, .11	.02	.01, .05
A2			.05	.00, .15	.01	.00, .14	.02	.00, .12	.03	.00, .21
C2			.02	.00, .10	.02	.00, .10	.02	.00, .08	.00	.00, .12
E2			.38	.33, .45	.01	.01, .02	.02	.01, .04	.00	.00, .02
A3					.02	.00, .14	.01	.00, .07	.06	.00, .17
C3					.01	.00, .08	.00	.00, .04	.03	.00, .12
E3					.45	.39, .52	.01	.00, .02	.00	.00, .01
A4							.00	.00, .07	.00	.00, .11
C4							.00	.00, .04	.00	.00, .11
E4							.47	.42, .52	.00	.00, .02
A5									.00	.00, .11
C5									.00	.00, .09
E5									.41	.35, .47

Note. All pairs for which at least one twin was an outlier or had missing data on any of the five measures were excluded from this analysis. n (monozygotic) = 282; n (dizygotic) = 474. Applic = Mathematical Application category; Underst = Understanding Number category; Comput = Computation and Knowledge category; Interp = Mathematical Interpretation category; Non-Num = Non-Numerical Processes category; A = genetic influences; C = shared environmental influences; E = nonshared environmental influences.

Figure 1.

Genetic results from the Cholesky decomposition of the five aspects of mathematics. The five measured variables (rectangles) are the five aspects of mathematics, and the latent variables (circles) represent additive genetic (A) estimates. The proportions of shared genetic influence on each of the aspects of mathematics (squared Cholesky path estimates) are shown for the first factor as an illustration. All other shared and independent influences were negligible. Applic = Mathematical Application; Underst = Understanding Number; Comput = Computation and Knowledge; Interp = Mathematical Interpretation; Non-Num = Non-Numerical Processes.

Table 8 shows the genetic, shared environmental, and nonshared environmental correlations and their confidence intervals for the five aspects of mathematics, estimated from the Cholesky model fitting. For example, we can estimate the shared genetic effects between Category 1 (Mathematical Application) and Category 2 (Understanding Number) by multiplying the paths from A₁ (see Figure 1 or Table 7). Thus, the genetic contribution to the phenotypic correlation between these two measures is .33 (i.e., √.30 × √.36). We can then estimate the genetic correlation between them: The genetic contribution to the phenotypic correlation (.33) mentioned above is the product of the square roots of the two heritabilities and the genetic correlation (Plomin & DeFries, 1979). Because we know the heritabilities of both variables (.30 for Mathematical Application and .42 for Understanding Number; see Table 3), we can solve for the genetic correlation [.33/(√.30 × √.42) = .92], which is within a rounding error of the genetic correlation between these two measures reported in Table 8. It can be seen that the bivariate correlations indicate substantial genetic overlap among the five aspects of mathematics, with genetic correlations ranging from .75 to .98. Shared environmental bivariate correlations were also very high (.61–.99), suggesting that whatever small effects of shared environment there were, they were shared to a large extent for all aspects of mathematics. The nonshared environmental bivariate correlations were modest (.13–.35), suggesting that the substantial effects of the nonshared environment were primarily specific to each trait.

Table 8.

Genetic (A), Shared Environmental (C), and Nonshared Environmental (E), Correlations for the Five Aspects of Mathematics and Proportion of Phenotypic Correlation (r_p) Among These Variables Mediated by A, C, and E

	Underst × Applic		Comput × Applic		Interp × Applic		Non-Num × Applic		Comput × Underst		Interp × Underst		Non-Num × Underst		Interp × Comput		Non-Num × Comput		Non-Num × Interp
Statistics	r	CI	r	CI	r	CI	r	CI	r	CI	r	CI	r	CI	r	CI	r	CI	r	CI
Correlation
rA	.94	.77, 1.00	.96	.78, 1.00	.95	.77, 1.00	.90	.68, 1.00	.85	.72, 1.00	.98	.88, 1.00	.93	.77, 1.00	.84	.70, .99	.75	.53, 1.00	.98	.84, 1.00
rC	.93	.67, 1.00	.86	.50, 1.00	.90	.55, 1.00	.84	.40, 1.00	.97	.43, 1.00	.99	.63, 1.00	.79	−.01, 1.00	.99	.39, 1.00	.61	−.33, 1.00	.72	−.21, 1.00
rE	.35	.26, .43	.23	.14, .32	.35	.28, .43	.23	.14, .32	.18	.08, .28	.29	.20, .37	.17	.07, .27	.22	.13, .31	.13	.02, .23	.20	.12, .29
Mediation of rP
A (axayrA/rP)	.49	.30, .70	.57	.35, .79	.50	.31, .69	.57	.35, .80	.64	.39, .86	.60	.38, .78	.70	.46, .90	.61	.37, .80	.73	.44, .97	.70	.47, .86
C (cxcyrC/rP)	.29	.11, .45	.26	.07, .44	.23	.06, .39	.26	.06, .45	.21	.03, .41	.18	.03, .35	.17	.00, .37	.17	.02, .37	.15	−.05, .38	.12	−.01, .32
E (exeyrE/rP)	.22	.15, .29	.17	.10, .25	.27	.20, .35	.17	.10, .25	.15	.06, .25	.23	.15, .31	.13	.05, .22	.22	.13, .32	.13	.03, .24	.18	.10, .27

Note. All pairs for which at least one twin was an outlier or had missing data on any of the five measures were excluded from this analysis. n (monozygotic) = 282; n (dizygotic) = 474. Underst = Understanding Number category; Applic = Mathematical Application category; Comput = Computation and Knowledge category; Interp = Mathematical Interpretation category; Non-Num = Non-Numerical Processes category; CI = 95% confidence interval.

Table 8 also shows the proportion of phenotypic correlations between these variables mediated by A, C, and E (bivariate heritabilities and environmentalities), as derived from the results of the Cholesky analysis. For example, the bivariate heritability between Mathematical Application and Understanding Number was .49 (confidence interval = .30, .70), which we obtained by dividing the genetic contribution to the phenotypic correlation between the two measures (.33) by the phenotypic correlation (.68). This means that 49% of the phenotypic correlation of .68 between these two aspects of mathematics was mediated genetically. It can be seen that these phenotypic correlations were primarily mediated by genetic factors for all aspects of mathematics, with bivariate heritabilities ranging from .49 to .73 (61% on average). Shared and nonshared environmental factors contributed more modestly to the phenotypic correlations (.12–.29 and .13–.27, respectively).

Discussion

The study reported in this article had two major goals. The first goal was to investigate whether the etiology of individual differences was quantitatively similar for various aspects of mathematics. Previously, only the etiology of individual variation in a single broad measure of mathematical achievement had been investigated. The results of the present study suggest that etiologies of aspects of mathematics, such as mathematical application, understanding of numbers, computation and knowledge, mathematical interpretation, and nonnumerical processes, are similar, with heritabilities ranging from .30 to .45, shared environmental influences ranging from .08 to .30, and nonshared environmental influences ranging from .41 to .56. The only measure that seemed to stand out was Mathematical Application, in that it showed stronger shared environmental influences than other measures. However, the shared environmental estimate for Mathematical Application was not significantly different from the other four tests, indicating that more research is needed to determine whether these differences can be replicated and to identify the possible reasons for these differences.

Consistent with previous research, we found that most environmental influences on diverse aspects of mathematics were nonshared. That is, on average across the five tests, 76% of the environmental variance could be attributed to nonshared environment rather than shared environment. This means that environmental factors that shape individual differences in mathematics were not shared between the cotwins (even MZ twins) in the same family. In other words, having the same parents, being of the same socioeconomic status, and going to the same school did not contribute to the similarity between the two children beyond the similarity in their genetic make-up. To assess whether being in the same class and having the same teacher increased similarity between cotwins and affected the genetic findings, we reran our correlational analyses, splitting the data by same versus different teacher. The two groups were approximately equal in size. For example, for the Mathematical Application category, 51% of the twin pairs were in the same class (vs. 49% in different classes). The results (available upon request) showed that being in the same class and having the same teacher did not significantly increase similarity between cotwins in their performance on the Web-based battery of tests—average MZ and DZ twin correlations were .58 and .38, respectively, for twins in the same classroom and .57 and .33, respectively, for twins in different classrooms. Thus, ACE parameter estimates were also similar for twins in the same and different classrooms. We also ran analyses splitting the sample into pairs taught by the same or a different teacher when the twins were 7 and 9 years of age. The results for the two groups were also highly similar at both ages, suggesting that early shared classroom experiences did not increase similarity between cotwins on a mathematical test at 10 years of age. Overall, these findings suggest that teachers and classroom environments affect mathematical ability in different children (even twins) in different ways (and therefore these effects are subsumed under the nonshared environmental estimate).

The average correlation for MZ twins was only .58—what made them different could only be nonshared environment (and error of measurement). Nonshared environment could be explained by pre-, peri-, and postnatal factors that contribute to the differential development of mathematical ability within pairs of MZ twins. These factors could include childhood illnesses, differential parental influence, or differential effects of curricula and other school factors on children. If, as our findings suggest, three quarters of the environmental variation on mathematical ability is nonshared, it is important to identify the nonshared environmental factors that lead to differences in mathematical ability even within pairs of MZ twins growing up in the same family and attending the same school. If these nonshared environmental factors can be identified, they could lead to more individualized curricula, although much more research is necessary to clarify whether such a move toward individualization in education is necessary or feasible practically.

It should be emphasized that quantitative genetic research such as ours describes genetic and environmental influences that exist in a particular population at a particular time. Our results suggesting that most of the individual differences in mathematics performance at 10 years were due to genetic and nonshared environmental influences describe the factors that were at work at this time in our U.K. sample. Even if heritability were 1.00, new environmental interventions could have a major effect. Moreover, results could differ in different populations. For example, having a common national curriculum, as in the United Kingdom, with its guidance on the methods and the content at each age, might decrease environmental variation and thus increase the relative impact of genetic variation. In a country without a national curriculum, greater environmental variation could emerge if differences in school curriculum made a difference in children’s learning of mathematics skills. These environmental differences would be expected to be shared environmental influences to the extent that children attending the same school experienced this school-level effect similarly. Heritability would also be lower, as environmental influences would account for relatively more variance. An interesting avenue for research is to investigate whether the relative contribution of genes and environments changes as a function of changes introduced to the national curriculum.

The second goal of this study was to go beyond these univariate analyses to conduct the first multivariate genetic study into heterogeneity of mathematical ability, assessing the extent to which individual differences in diverse aspects of mathematics are influenced by the same genetic and environmental factors. Our phenotypic explorations of the data showed that correlations among the five aspects of mathematics ranged from .45 to .68. The highest correlation was between Mathematical Application and Understanding Number; the smallest correlations were between Computation and Knowledge and Non-Numerical Processes and between Computation and Knowledge and Mathematical Interpretation. These phenotypic differences in correlations seem to make sense: The highest correlation, between the Mathematical Application and Understanding Number categories, might reflect the fact that these two categories seem to be the most general, requiring some meta-understanding of mathematical information in addition to the ability to retrieve a mathematical fact from memory. The smallest correlations might reflect the relative specificity of simple computation versus spatial judgments and interpretation. However, the results of the phenotypic Cholesky analysis indicate that the best fitting model was one in which the variance in all five aspects of mathematics was due to factors shared among all of them in addition to factors unique to each aspect.

Next, we applied multivariate genetic analysis to determine the extent to which the five aspects of mathematics were related etiologically. The results showed that these diverse aspects of mathematics were influenced largely by the same genetic factors. On average, genetic overlap accounted for over 60% of the phenotypic correlation among the five aspects of mathematics (Table 8). Moreover, the average genetic correlation among the five aspects of mathematics was .91 (Table 8), which indicates that the same genes largely affected all five aspects of mathematics. These findings represent additional support for the generalist genes hypothesis, which proposes that genetic influences within and between cognitive abilities and disabilities largely overlap (Plomin & Kovas, 2005).

What are the processes by which genetic influences have such broad effects? In genetics, the word pleiotropy is used to refer to manifold effects of genes. It is possible that many cognitive processes might also be pleiotropic. Fundamental cognitive mechanisms—spatial attention, for example—might contribute both to calculation (attention to space on a number line) and to mental rotation. Indeed, spatial and numerical representations seem to have overlapping brain correlates (Hubbard, Piazza, Pinel, & Dehaene, 2005; Pinel, Piazza, Le Bihan, & Dehaene, 2004). Moreover, many behavioral protocols have shown a close connection between numbers and space, in which small numbers are represented on the left side of space and large numbers on the right. It is also possible that the adult competence for arithmetic arises from this fundamental number sense (Hubbard et al., 2005), which might be linked to the general space sense. Both abilities also involve many nonspecific mechanisms, such as memory and speed of processing. These commonalties and many other examples of this sort might reflect pleiotropic genetic influences.

The finding that most genetic effects are general charts the course for future molecular genetic research that aims to identify genes that account for heritability. Rather than focusing on specific aspects of mathematics, attempts to identify genes would profit from focusing on what is in common among different aspects of mathematics. When such genes are found, it might be possible to use them to identify children at genetic risk for mathematical disability early enough to prevent the problem from arising (Plomin & Walker, 2003).

The finding that genetic influences on diverse aspects of mathematics were largely general suggests that differentiation of mathematical abilities and disabilities was due to environmental rather than genetic factors. Moreover, most of this environmental heterogeneity was due to nonshared environmental influences. However, we have little idea about the sorts of mathematics-relevant environments that are nonshared and that are specific to each aspect of mathematics. A discouraging prospect is that these nonshared environmental influences might reflect many idiosyncratic experiences of very small effect, multiple gene–environment and environment–environment interactions, and other factors (e.g., in utero environment and diseases) over which we have little control. However, until research is conducted on nonshared environment specific to mathematics, it is far too early to accept such a gloomy hypothesis (Plomin, Asbury, & Dunn, 2001).

It is possible that even more specific aspects of mathematical ability may indeed have unique genetic etiology. However, the large genetic overlap among different aspects of mathematics observed in this study speaks against this prediction. Future genetic studies using a wider range of more specific mathematical tasks can clarify this issue. Our research also suggests that if the aim of the national curriculum classification is to identify more specific strengths and weaknesses in children’s mathematical ability, this classification may need reassessment. For example, more in-depth assessment of spatial abilities may be contrasted with more specific fact retrieval ability, whereas some other distinctions might be less informative.

Another future direction for research is to investigate whether most of the variance in the diverse aspects of mathematics can be explained by factors that also influence reading and general cognitive ability. For example, one might be tempted to say that what is in common among these different aspects of mathematics is intelligence. However, our view is that this does not take us much farther in terms of understanding mechanisms, because we do not know what intelligence is any more than we know what causes the general factor that influences different aspects of mathematics. Although many brain and cognitive processes are likely to contribute to the phenotypic overlap among the subdomains of mathematics, the point of the present results is that the same set of genes is largely responsible for genetic influence in these domains (for more discussion on this issue, see Plomin & Kovas, 2005). We have collected data on reading and general cognitive ability in addition to mathematics as part of a large Web-based battery. The next step for our research is to include these variables in multivariate genetic analyses. From previous research (e.g., Kovas et al., 2005) and the present study, we predict substantial overlap among genetic influences on mathematics, reading, and general cognitive ability but also some unique genetic influences on mathematics.

Finally, despite the large sample of this study, an even larger sample is needed to assess whether the small quantitative differences in etiology of the five aspects of mathematics found in this study are statistically significant. We are planning to investigate this issue when the data from the second TEDS cohort are available. Increasing the sample size will also allow us to investigate sex differences in the etiology of individual differences in mathematical ability.