ergm: A Package to Fit, Simulate and Diagnose Exponential-Family Models for Networks

Abstract

We describe some of the capabilities of the ergm package and the statistical theory underlying it. This package contains tools for accomplishing three important, and interrelated, tasks involving exponential-family random graph models (ERGMs): estimation, simulation, and goodness of fit. More precisely, ergm has the capability of approximating a maximum likelihood estimator for an ERGM given a network data set; simulating new network data sets from a fitted ERGM using Markov chain Monte Carlo; and assessing how well a fitted ERGM does at capturing characteristics of a particular network data set.

1. Introduction

The ergm package for R (R Development Core Team 2007), a cornerstone of the statnet suite of packages for statistical network analysis, provides tools for modeling networks based on a well-studied class of models called exponential-family random graph models (ERGMs) or p-star models (Holland and Leinhardt 1981; Wasserman and Pattison 1996; Robins, Pattison, Kalish, and Lusher 2007a). In particular, the package allows users to obtain approximate (or, in some cases, exact) maximum likelihood estimates (MLEs); simulate random networks from a specified ERGM; and perform graphical goodness-of-fit checks of the type described by Hunter, Goodreau, and Handcock (2008). This article describes some of the technical background and algorithms that drive the ergm package.

1.1. Obtaining ergm

Because the ergm package is part of the statnet suite of packages, it may be obtained and loaded by loading the statnet suite as described in Goodreau, Handcock, Hunter, Butts, and Morris (2008a) or at the statnet project Web site at http://statnetproject.org/. Alternatively, a user may choose to install and load just the ergm package itself in R via

R> install.packages(“ergm”)R> library(“ergm”)

(Throughout this article, R input is represented by italicized typewriter font beginning with the R> prompt, or the + prompt if it is a continuation of a previous line.) Because the ergm package depends on the network package (Butts 2008), the lines above will automatically install (if necessary) and load the network package as well. All of these packages are available from the Comprehensive R Archive Network (CRAN) at http://CRAN.R-project.org/, and further information about them may be obtained from the statnet Web site at http://statnetproject.org/.

1.2. License and citation information

The ergm package is free and open-source, and released under GPL-3 with attribution requirements for the software and its source code. To obtain license information go to http://statnetproject.org/attribution/.

Please cite the ergm package when you use it for research that is published or otherwise publicly distributed. Citation information is provided on our Web site at http://statnetproject.org/citation.shtml, and can be obtained by typing citation(“ergm”).

1.3. ERGMs in a nutshell

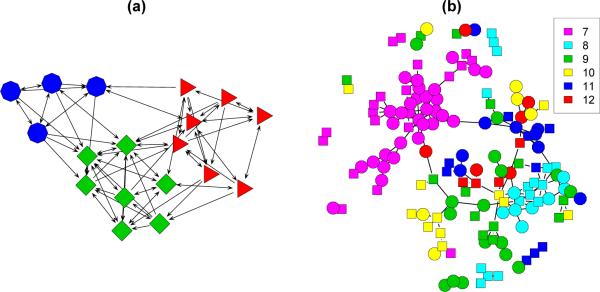
The purpose of ERGMs, in a nutshell, is to describe parsimoniously the local selection forces that shape the global structure of a network. To this end, a network dataset, like those depicted in Figure 1, may be considered like the response in a regression model, where the predictors are things like “propensity for individuals of the same sex to form partnerships” or “propensity for individuals to form triangles of partnerships”. In Figure 1(b), for example, it is evident that the individual nodes appear to cluster in groups of the same numerical labels (which turn out to be students’ grades, 7 through 12); thus, an ERGM can help us quantify the strength of this intra-group effect. The information gleaned from use of an ERGM may then be used to understand a particular phenomenon or to simulate new random realizations of networks that retain the essential properties of the original. Handcock, Hunter, Butts, Goodreau, and Morris (2008) say more about the purpose of modeling with ERGMs; yet in this article, we focus primarily on technical details.

Figure 1.

The (a) samplike and (b) faux.mesa.high networks described in Section 2. The values of nodal covariates may be indicated using various colors, shapes, and labels of nodes.

In the remainder of the article, we introduce the two network datasets of Figure 1 that will be used for illustrative purposes (Section 2), provide a brief technical summary of what an ERGM is (Section 3), and list a few examples of ERGMs along with numerous references in which these models are developed more fully (Section 4). Section 5 describes the algorithm for producing approximate maximum likelihood estimates used by the ergm package, while Sections 6 and 7 describe the simulation and goodness-of-fit capabilities, respectively, of the package. The focus of this article is restricted to the technical aspects of modeling using ERGMs, so it does not provide a proper discussion of the purpose of ERGMs nor how best to construct ERGMs in practice. There is a large body of literature on these topics, and the interested reader might turn to the special issue of Social Networks (Robins and Morris 2007), which contains several related articles and which provides extensive lists of references. Additional aid on the practical use of the statnet suite of packages is given by Goodreau et al. (2008a) in the form of a short tutorial.

2. Network datasets in ergm

Several network datasets are included with the ergm package. To see a list of them, type:

R> data(package = “ergm”)

In this article, we use the samplike and faux.mesa.high networks, depicted in Figure 1, to illustrate various aspects of the ergm package functionality. To learn more about these particular datasets, or any of the datasets included with the ergm package, it is possible to view their corresponding documentation files by using the help function, or, equivalently, the question mark, as follows:

R> help(“samplike”)R> ? “faux.mesa.high”

In the samplike dataset of Figure 1(a), each node represents a monk within a particular monastery and a directed edge from one to another indicates that the first named the second as one of the three monks he likes the most, at any of the three distinct time points when the survey was administered; type help(“sampson”) for more details. Three groups, identified by Sampson (1968) after analyzing the trends in the pattern of ties over time, are indicated by the three different shapes and colors of nodes. Note that the definition of group membership in this case is endogenous: membership is not a measured attribute of the node, like age, that is independent of the relational structure, but instead a latent cluster defined by the structure of relations. The default behavior of the plotting function for a directed network like samplike is to place arrows at one end of each line segment, indicating the direction of each edge.

In the faux.mesa.high dataset of Figure 1(b), each node represents a student in grades seven through twelve at a hypothetical yet realistic school (or middle school-high school pair) in the United States, and each edge indicates a mutual friendship in which each node named the other as one of his or her top five male or top five female friends; see the appendix in Goodreau et al. (2008a) for the origin of this data set. Boys are depicted by square nodes and girls by many-sided polygons that appear circular; the label for each node indicates the grade in school (seventh through twelfth). In contrast to the samplike network, the nodal attributes in this case, grade and sex, are exogeneous. This difference means they can serve as predictors in a generative model for the friendships. Since the edges indicate mutual friendships, this is an undirected network.

In both figures 1(a) and 1(b), it is evident that the colors used for displaying the nodes are related to the clustering of the nodes. However, the plotting function does not consider these colors in any way when positioning the nodes; it only considers the pattern of edges and non-edges that exist in the network. Since the colors in the samplike are derived from the pattern of edges, the clustering by color is tautological. The fact that the nodes from faux.mesa.high cluster by grades, however, is different. In this case the clustering reveals a qualitative fact about this network, and the ergm package allows us to analyze properties like this quantitatively. The exact R code used to produce both of these plots is given in Appendix A—note that, because the algorithm used for the plots has a random element, this code will not produce exactly the same layouts as in Figure 1.

3. ERGM specification

Let the random matrix Y represent the adjacency matrix of an unvalued (binary) network and let Y denote the support of Y. Then we may think of Y as the set of all obtainable networks. Typically, as in this article, one fixes the number n of individuals, so that y is a subset of all n × n matrices whose entries are all zero or one and whose diagonal entries are all zero—since the (i, j) entry indicates an edge from i to j, forcing the diagonal to be zero means that self-partnerships are disallowed. In the undirected case, Y contains only symmetric matrices.

3.1. The model

The distribution of Y can be parameterized in the form

$${\mathsf{P}}_{\theta ,\mathcal{Y}}(\mathbf{Y}=\mathbf{y})=\frac{\exp \left\{{\theta }^{\mathsf{T}}\mathbf{g}\left(\mathbf{y}\right)\right\}}{\kappa (\theta ,\mathcal{Y})},\mathbf{y}\in \mathcal{Y},$$ (1)

where $\theta \in \Omega \subset {\mathbb{R}}^q$ is the vector of model coefficients and g(y) is a q-vector of statistics based on the adjacency matrix y (Frank and Strauss 1986; Wasserman and Pattison 1996). Model (1) may be expanded by replacing g(y) with g(y,X) to allow for additional covariate information X about the network, as described in Section 4.3. The denominator,

$$\kappa (\theta ,\mathcal{Y})=\sum _{\mathbf{z}\in \mathcal{Y}}\exp \left\{{\theta }^{\mathrm{T}}\mathbf{g}\left(\mathbf{z}\right)\right\},$$ (2)

is the normalizing factor that ensures that Equation 1 is a legitimate probability distribution. Specification of Y, including the number of nodes, n, is an important yet often overlooked aspect of model (1). If, for instance, an edge denotes a heterosexual sexual relationship, then each element of Y should contain certain structural zeros, namely, all Y_ij for which both i and j represent nodes of the same sex. At its largest, for a fixed n, Y may contain up to N = 2ⁿ⁽ⁿ⁻¹⁾ networks, a very large number even for moderate-sized n, which makes calculation of κ(θ,y) the primary barrier to inference using this model.

3.2. Change statistics

An alternative specification of the model (1) clarifies the interpretation of the coefficients. To articulate this alternative, we first introduce the notion of a vector of change statistics. Such a vector is a function of three things: A particular choice g(·) of statistics defined on a network, a particular network y, and a particular pair of different nodes (i, j) that is either ordered or unordered, respectively, according to whether y is directed or undirected. We define the vector of change statistics as

$${\delta }_{\mathbf{g}}{\left(\mathbf{y}\right)}_{ij}=\mathbf{g}\left({\mathbf{y}}_{ij}^{+}\right)-\mathbf{g}\left({\mathbf{y}}_{ij}^{-}\right),$$

where ${\mathbf{y}}_{ij}^{+}$ and ${\mathbf{y}}_{ij}^{-}$ represent the networks realized by fixing y_ij = 1 or y_ij = 0, respectively, while keeping all the rest of the network exactly as in y itself. In other words, δ_g(y)_ij is the change in the value of the network statistic g(y) that would occur if y_ij were changed from 0 to 1 while leaving all of the rest of y fixed.

In terms of the change statistic vector, model (1) may be shown to imply the following distribution of the Bernoulli variable Y_ij, conditional on the rest of the network:

$$\mathrm{logit}[{\mathsf{P}}_{\theta ,\mathcal{Y}}(Y_{ij}=1\mid {\mathbf{Y}}_{ij}^c={\mathbf{y}}_{ij}^c)]={\theta }^{\mathsf{T}}{\delta }_{\mathbf{g}}{\left(\mathbf{y}\right)}_{ij},$$ (3)

where the logit function is defined by logit(p) = log[p/(1 − p)] and ${\mathbf{Y}}_{ij}^c$ represents the rest of the network other than the single variable Y_ij. When the network statistics involve covariates X in addition to y, as we will describe in Section 4.3, we may add X to the notation and write δ_g(y,X)_ij.

Equation 3 reveals two facts: First, the probability on the left hand side depends on ${\mathbf{y}}_{ij}^c$ only through the change statistics δ_g(y)_ij, not on g(${\mathbf{y}}_{ij}^{+}$) or g(${\mathbf{y}}_{ij}^{-}$) themselves. In many cases, it is much easier to calculate δ_g(y)_ij than it is to calculate g(${\mathbf{y}}_{ij}^{+}$) or g(${\mathbf{y}}_{ij}^{-}$), and this fact can lead to efficient computational algorithms. As an example of this phenomenon, the Erdös-Rényi model of Section 4.1 implies that δ_g(y)_ij = 1 for all y and for all i and j.

Second, Equation 3 says that each component of the δ vector may be interpreted as the increase in the conditional log-odds of the network, per unit increase in the corresponding component of g(y), resulting from switching a particular Y_ij from 0 to 1 while leaving the rest of the network fixed at ${\mathbf{Y}}_{ij}^c$. For examples of these kinds of interpretations for an actual dataset, refer to Sections 4 and 6 of Goodreau et al. (2008a).

The specific statistics that may be included in the g(y) vector in the ergm package are listed and described in Morris, Handcock, and Hunter (2008). In the next section, we illustrate the use of only a small fraction of the available terms on the samplike and faux.mesa.high datasets. It is important to remember that because samplike is directed and faux.mesa.high is undirected, there are certain types of model terms that may not be used with one or the other of these datasets. A summary of these restrictions may be found in the table in Appendix A of Morris et al. (2008).

4. Examples of ERGMs

Here, we offer a brief glimpse at some important categories of ERGMs. We also give numerous references for readers interested in delving more deeply into the intricacies of building ERGMs, which is a subject that we cannot adequately cover given the limited space available and the limited scope of this article.

4.1. Bernoulli and Erdös-Rényi models

In the remainder of this article, we take

$$\Omega =\{\theta \in {\mathbb{R}}^q:\kappa (\theta ,\mathcal{Y})<\infty \}$$

to be the parameter space. The dimension q of Ω is at most N − 1 (for the “saturated” model), although it is typically much smaller than this. For example, if the dyads Y_ij = Y_ji of an undirected network are mutually independent and Y consists of the set of all possible undirected networks, the model can be written

$$\log \left[{\mathsf{P}}_{\theta ,\mathcal{Y}}(\mathbf{Y}=\mathbf{y})\right]=\underset{i<j}{\sum \sum }{\theta }_{ij}{y}_{ij}-\log \kappa (\theta ,\mathcal{Y}),\mathbf{y}\in \mathcal{Y},$$ (4)

where θ_ij = logit [P θ,_Y(Y_ij = 1)] is the log-odds of a tie in the (i, j) dyad and

$$\log \kappa (\theta ,\mathcal{Y})=\underset{i<j}{\sum \sum }\log [1+\exp \left\{{\theta }_{ij}\right\}].$$

[Recall that the logit, or log-odds, function is defined by logit p = log p − log(1 − p).] Thus, for model (4), q = n(n − 1)/2 and the elements of the vector g(y) are just y_ij. This model is often called a Bernoulli network. The special case where the dyads have a common probability implies that q = 1, g(y) = $\sum {\sum }_{i<j}{y}_{ij}$ is the number of partnerships in the network, and the single coefficient θ can be interpreted as the common log-odds of partnership formation within any dyad. The mathematical properties of this homogeneous Bernoulli network model, also known as the Erdös-Rényi model, have been extensively studied—see Albert and Barabási (2002) and the many references therein—but the simplicity and homogeneity that make it tractable also make it less useful as a realistic model for social phenomena.

Consider the samplike dataset, which is contained in the ergm package and which may be accessed, once ergm is loaded, by typing

R> data(“sampson”)

Some information about the dataset may be obtained by typing help(“sampson”) or help(“samplike”). To obtain summary statistical information, we may type either samplike or summary(samplike):

R> samplike

Network attributes:

• vertices = 18

• directed = TRUE

• hyper = FALSE

• loops = FALSE

• multiple = FALSE

• total edges= 88

• ...

A directed network with eighteen vertices (nodes) could have up to 18 × 17 = 306 edges. Since this network has 88, we should expect the maximum likelihood estimator for δ in an Erdös-Rényi model to equal logit (88/306) = −.90716. To verify this fact using the ergm package, we may use the following commands:

R> model1 <- ergm(samplike ~ edges)R> model1$coefedges−0.9071582

Note that the ergm command requires the formula format in R, much like other regression-like functions such as lm for linear regression or glm for generalized linear models. For ergm, the formula should be of the form

network object ~ <model term 1> + <model term 2> + ...

where the model terms determine the elements of the g(y) vector. The ergm function allows many possible model terms other than edges; a complete catalog is given in Morris et al. (2008).

4.2. The p₁ model

Holland and Leinhardt (1981) appear to be the first to propose log-linear models for social networks. Suppose that we take y to be the set of all directed graphs, with independent dyads [i.e., the pairs (Y_ij, Y_ji) are independent for different choices of {i, j}] and the following model for tie probabilities:

$${\mathsf{P}}_{\theta ,\mathcal{Y}}(Y_{ij}=x,Y_{ij}=y)=\{\begin{array}{cc}{m}_{ij}\hfill & \mathrm{if}x=y=1\hfill \\ a_{ij}\hfill & \mathrm{if}x=1,y=0\hfill \\ n_{ij}\hfill & \mathrm{if}x=y=0.\hfill \end{array}\phantom{\}}$$

In this specification, each dyad has its own probability distribution. This model can represent arbitrary nodal indegree and outdegree marginal distributions and strength of reciprocity (or mutuality) within dyads. It can be written in log-linear form as

$$\log \left[{\mathsf{P}}_{\theta ,\mathcal{Y}}(\mathbf{Y}=\mathbf{y})\right]=\underset{i<j}{\sum \sum }{\rho }_{ij}{y}_{ij}{y}_{ji}+\underset{i\ne j}{\sum \sum }{\varphi }_{ij}{y}_{ij}-\log \kappa (\rho ,\varphi ,\mathcal{Y}),\mathbf{y}\in \mathcal{Y},$$ (5)

which is a special case of Equation 1 with q = 3n(n − 1)/2. Holland and Leinhardt (1981) refer to this as the p₁ model, though they point out that it has too many coefficients to be useful statistically and instead consider a simplified version of model (5) in which all of the ρ_ij are equal (to ρ) and ϕ_ij = θ + α_i + β_j. In this model, ρ may be considered the mutuality effect; α_i and β_j are the sender and receiver effects, respectively, of the ith and jth nodes; and θ is the overall edge effect, analogous to the intercept in a linear regression. We may fit this model using maximum likelihood estimation as follows (because ergm uses a complex algorithm to fit this model, as described in Section 5.1, the ergm command may take a few minutes):

R> model2 <- ergm(samplike ~ edges + sender + receiver + mutual,+ seed = 2345, verbose = TRUE)R> summary(model2)==========================Summary of model fit==========================Formula: samplike ~ edges + sender + receiver + mutualNewton-Raphson iterations: 88MCMC sample of size 10000

Monte Carlo MLE Results:
	Estimate Std.	Error	MCMC s.e.	p-value
edges	−2.54244	0.14724	0.011	< 1e-04	***
sender2	−0.85810	0.72326	0.032	0.236495
sender3	−0.29592	0.72313	0.017	0.682705
... <output edited for length>
receiver17	−1.45863	0.34780	0.005	< 1e-04	***
receiver18	−1.17712	0.32407	0.005	0.000336	***
mutual	3.71983	0.12621	0.002	< 1e-04	***

---Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Null	Deviance:	424.21	on	306	degrees of freedom
Residual	Deviance:	224.11	on	270	degrees of freedom
	Deviance:	200.09	on	36	degrees of freedom

AIC: 296.11 BIC: 430.16

The seed argument is used here and elsewhere in the article to make the output exactly reproducible, since the fitting algorithm is random; however, we have noticed that there exist some differences among the output produced by some platforms for some of the examples nonetheless. We obtained these results using R version 2.6.2 on a Windows machine using ergm version 2.1 and network version 1.3. The verbose = TRUE argument results in a lot of output as the algorithm proceeds. The control = control.ergm(check.degeneracy = TRUE) option would have invoked a check for degeneracy that takes quite a bit of time for this particular model due to the fact that it contains 36 parameters. Model degeneracy is discussed briefly by Handcock et al. (2008) in this volume, and in more detail by Handcock (2003b,a).

Note that summary(model1) produced a lot of information besides the coefficient estimates. The standard errors and loglikelihood values on which the deviance, AIC and BIC values are based use stochastic approximations discussed in Hunter and Handcock (2006). Also note that there are only 17 sender effects (sender2 through sender18) and 17 receiver effects, even though there are 18 nodes. This is because inclusion of all 18 effects would result in a linear dependency among the statistics of g(y), which should be avoided here, as in all statistical models.

The estimates above are approximate maximum likelihood estimates obtained using a stochastic algorithm based on Markov Chain Monte Carlo (MCMC); hence, the results will not be exactly the same for all runs. However, if exact reproducibility of coefficient estimates is important, it is possible to seed the random number generator manually using the seed argument to the ergm function; type ?ergm for more details. In this particular case, the formula in Equation 1 simplifies considerably and it is possible using numerical methods to find the exact maximum likelihood estimator, i.e., without resorting to a stochastic MCMC-based algorithm. Holland and Leinhardt (1981) do this, but unfortunately it is not possible to compare their results directly with ours because they use a slightly different dataset.

These early simple ERGMs, which have no exogeneous covariates and assume independence across dyads, have been substantially extended and generalized in subsequent social network literature. Based on developments in spatial statistics (Besag 1974), Frank and Strauss (1986) introduce forms of dependence with Markov structure. Wasserman and Pattison (1996) incorporate exogeneous and endogenous nodal attributes (Pattison and Wasserman 1999) and make a distinction between explanatory and response variables (Robins, Pattison, and Wasserman 1999), resulting in social influence (Robins, Pattison, and Elliott 2001b) and social selection (Robins, Elliott, and Pattison 2001a) models. These generalizations essentially allow analysis of networks with “colors” on the nodes, where “color” is used to indicate the attribute values conceptually as Figure 1 does literally. Recent developments include new forms of dependency structures, to take into account more general neighborhood effects. These models relax the one-step Markovian dependence assumptions, allowing investigation of longer range configurations, such as longer paths in the network or larger cycles (Pattison and Robins 2002). Models for bipartite (Faust and Skvoretz 1999) and tripartite (Mische and Robins 2000) network structures have also been developed.

4.3. Exogenous covariates and dyadic independence

Attribute information is easily incorporated into an ERGM (Fienberg and Wasserman 1981). Suppose we wish to examine the impact of p exogenous attributes represented by an n × n × p array, X, whose ijkth element is the value of the kth attribute for the potential edge represented by the Bernoulli random variable Y_ij. Note that this construction allows the attributes to be functions of nodal covariates. For instance, X_ijk might be the absolute difference in ages between nodes i and j, say, |age_i − age_j|. As a practical matter, note in this example that it is not actually necessary to store the entire X array; it is much simpler to store only the vector giving the age of each node along with a rule for how to calculate X_ijk when needed.

To modify the ERGM of Equation 1 to allow X to influence the probability distribution of Y, we replace g(y) by g(y,X), indicating that the statistics depend on the attribute information in addition to the relationship information. As an example, suppose that g(y,X) includes the following terms (where the equivalent ergm-package codings are given in square brackets):

• # of edges in y [ergm code: edges]

• # of edges between students of the same grade, counted separately for each possible grade [nodematch(“Grade”, diff = TRUE)]

• # of edges involving males, with male-male edges counted twice [nodefactor(“Sex”)]

We might say that this model contains terms for the overall number of edges, a differential homophily effect for grade, and a main effect for sex. We may fit this model using the faux.mesa.high dataset as follows:

R> data(“faux.mesa.high”)R> model3 <- ergm(faux.mesa.high ~ edges + nodematch(“Grade”, diff = TRUE) ++ nodefactor(“Sex”))R> summary(model3)...

	estimate	s.e.	p-value	MCMC s.e.
edges	−5.6784	0.1820	< 1e-04	NA
nodematch.Grade.7	2.7869	0.1981	< 1e-04	NA
nodematch.Grade.8	2.9969	0.2395	< 1e-04	NA
nodematch.Grade.9	2.4074	0.2643	< 1e-04	NA
nodematch.Grade.10	2.6208	0.3744	< 1e-04	NA
nodematch.Grade.11	3.3627	0.2971	< 1e-04	NA
nodematch.Grade.12	3.6628	0.4578	< 1e-04	NA
nodefactor.Sex.M	−0.3743	0.1047	0.000351	NA

...

We see that in each grade, students are more likely to make friends with those in their own grade than those in other grades. Furthermore, girls are more likely than boys to make friends in this network. These coefficients may be interpreted as described in Section 3.2, and these interpretations will be familiar to practitioners of logistic regression. For instance, we can say that if all other covariate values are the same, then an individual female's odds of forming a tie with a particular student are exp{0.3743} = 1.454 times those of an individual male, conditional on the rest of the network. See Goodreau et al. (2008a) for further interpretation of output such as this.

The output above is not based on a stochastic MCMC algorithm, so the code should always produce exactly the same values. This is not true of the stochastically obtained summary of model2 in Section 4.2. Before explaining the difference, we emphasize that a dyad in a network is the random variable representing the state of the relationship(s) between two given nodes. In other words, a dyad in an undirected network is simply a single Y_ij, whereas a dyad in a directed network is a pair (Y_ij, Y_ji). We now articulate the idea of dyadic independence via a couple of definitions. To understand Definition 1, it may be helpful to review the definition of the change statistic vector δ_g(y,X)_ij in Section 3.2.

Definition 1 A dyadic independence term is a term in an ERGM for which the corresponding network change statistic(s) in the δ_g(y,X)_ij vector—or δ_g(y)_ij if there are no covariates—may always be calculated, regardless of the values of i and j, without knowing anything about y except possibly (in the case of a directed network) the value of y_ji.

The table in Appendix A of Morris et al. (2008) indicates which of the terms currently available in statnet are dyadic independence terms. Examples include each of the terms used in model2 and model3: edges, receiver, sender, mutual, nodematch. and nodecov.

Definition 2 A dyadic independence ERGM is an ERGM all of whose terms are dyadic independence terms.

In the case of dyadic independence models for undirected networks, the conditional probability ${\mathsf{P}}_{\theta ,\mathcal{Y}}(Y_{ij}=1\mid {\mathbf{Y}}_{ij}^c={\mathbf{y}}_{ij}^c)$ in Equation 3 may be replaced by the unconditional, or marginal, probability P_δ,Y(Y_ij = 1). This results in an enormous simplification of the likelihood function, as described in Section 5.2, allowing the exact calculation of the maximum likelihood estimator. The output from fitting model3 is a case in point.

The situation is almost this simple for dyadic independence ERGMs for directed networks. However, a dyad in a directed network consists of two edges, so even in a dyadic independence model, it is possible that P_θ,Y(Y_ij = 1) depends on Y_ji. This is exactly the situation of the p₁ model of Section 4.2, which is why ergm employs a stochastic MCMC algorithm in the model2 example. Currently, there are only two terms in statnet—mutual and asymmetric—that require a dyadic independence model to use MCMC. See Morris et al. (2008) or type ?ergm.terms for full descriptions of these terms. Any dyadic independence ERGM for a directed network not containing either of these two terms exploits the same exact maximum likelihood calculation used for model3 above.

To conclude this section, we draw an important distinction between dyadic independence and linear independence. It is always important to ensure that there are no linear dependencies among the terms in an ERGM, and linear dependencies can arise with either dyadic independence or dyadic dependence terms. For instance, it was to avoid linear dependence that the sender1 and receiver1 statistics are eliminated from model2 of Section 4.2, even though both sender and receiver are dyadic dependence terms, whether or not we include sender1 and receiver1 statistics in g(y). Many other statnet terms eliminate (or can be made to eliminate) certain statistics in order to avoid linear dependencies; for examples, see all terms that use the base argument in the summary table of Appendix A in Morris et al. (2008).

4.4. Dyadic dependence models

One commonly used class of dyadic dependence models—i.e., models that do not satisfy Definition 2—exhibit Markov dependence in the sense defined by Frank and Strauss (1986). For these models, dyads that do not share a node are conditionally independent, an idea analogous to the nearest neighbor concept in spatial statistics. Sometimes, a homogeneity condition is also added so that all isomorphic networks have the same probability under the model. Frank and Strauss (1986) show that homogeneous Markov network models are exactly those having the triangle parameterization, in which $\theta \in \Omega ={\mathbb{R}}^n$ and

$$\mathbf{g}\left(\mathbf{y}\right)=[S_1\left(\mathbf{y}\right),\dots ,S_{n-1}\left(\mathbf{y}\right),T_1\left(\mathbf{y}\right)],$$

where

$$S_k\left(\mathbf{y}\right)=\frac{1}{k!}\underset{i_0,\dots ,i_k}{\sum \cdots \sum }{y}_{i_0{i}_1}\cdots y_{i_0{i}_k},k=1,\dots ,n-1;$$

and

$$T_1\left(\mathbf{y}\right)=\frac{1}{6}\sum _{i=1}^n\sum _{j=1}^n\sum _{k=1}^n{y}_{ij}{y}_{jk}{y}_{ki}.$$

In this parameterization, S_k(y) counts the so-called k-stars for 1 ≤ k ≤ n − 1 and T₁(y) is a count of triangles (or cyclic triads in the directed case). An equivalent form is the degree distribution parameterization, in which

$$\mathbf{g}\left(\mathbf{y}\right)=[D_1\left(\mathbf{y}\right),\dots ,D_{n-1}\left(\mathbf{y}\right),T_1\left(\mathbf{y}\right)],$$ (6)

where D_k(y) equals the number of individuals with exactly k relationships, 1 ≤ k ≤ n − 1. The degree distribution parameterization has the advantage that the degree statistics are directly interpretable in terms of concurrency of partnerships; i.e., D_m(y) for m > 0 counts the number of individuals with m concurrent partners.

In practice, these models have often been simplified further, reducing the terms to edges, two-stars and triangles, and assuming isomorphic homogeneity. Unfortunately, we now know that such simple Markov models rarely produce reasonable networks. The reason has to do with the problem of degeneracy (Handcock 2003a,b), which is discussed in the context of the ergm package by Handcock et al. (2008). For a lengthy case study of degeneracy in a model that contains the triangle term, see Section 5 of Goodreau et al. (2008a). The shortcomings of the simplified Markov model may be addressed by allowing for some heterogeneity via the inclusion of covariate-dependent model terms as described in Subsection 4.3, and by the use of triad-based curved exponential family terms in place of the triangle count as described below.

4.5. Curved exponential-family models

This section details some of the technical considerations underlying a recently-developed class of network statistics that has been shown to work well in many social network contexts (Snijders, Pattison, Robins, and Handcock 2006; Robins, Snijders, Wang, Handcock, and Pattison 2007b; Goodreau, Kitts, and Morris 2008b). As an example of this type of statistic, consider the quantity

$$u(\mathbf{y};{\varphi }_s)=e^{{\varphi }_s}\sum _{i=1}^{n-1}\left\{1-{\left(1-e^{-{\varphi }_s}\right)}^i\right\}{D}_i\left(\mathbf{y}\right).$$ (7)

Evidently, u(y; ϕ_s) is a scalar for a fixed network y and parameter ϕ_s, obtained by a linear combination of the degree statistics D_i(y) that depends on the tuning parameter ϕ_s (Hunter 2007). Because of the geometric series used in the linear weights, u(y; ϕ_s) is referred to as the geometrically weighted degree (GWD) statistic. If the edges term is also included in g(y), then u(y; ϕ_s) may be shown to be equivalent in a certain sense to the alternating k-star statistic of Snijders et al. (2006).

The ergm package has the capability of fitting models that include the GWD statistic, via the gwdegree term and several other related terms. In addition, two other geometrically weighted statistics, the geometrically weighted edgewise shared partner (GWESP) and the geometrically weighted dyadwise shared partner (GWDSP) statistics, are also supported by ergm. The first of these, GWESP, is equal to

$$v(\mathbf{y};{\varphi }_t)=e^{{\varphi }_t}\sum _{i=1}^{n-2}\left\{1-{\left(1-e^{-{\varphi }_t}\right)}^i\right\}{\mathrm{EP}}_i\left(\mathbf{y}\right),$$ (8)

where EP_i(y) is the number of edges in y between two nodes that share exactly i neighbors in common, i.e., the number of edges that serve as the common base for exactly i distinct triangles (Hunter 2007). The GWDSP statistic is similar, except EP_i(y) is replaced by DP_i(y), which is the number of pairs (i, j) such that i and j share exactly i neighbors in common, whether or not y_ij = 1.

From a modeling perspective, these geometrically weighted terms are useful because they are not merely counts of local network configurations, like the degree of k-star statistics; instead, they are particular linear combinations of an entire distribution of degree or shared partner statistics. These terms appear very effective at overcoming the problems of degeneracy pointed out for the Markov network models mentioned in Section 4.4. A full discussion of the merits of these terms is beyond the scope of this article. For information on their purpose, see Snijders et al. (2006) and Robins et al. (2007b); for case studies that use them, see Goodreau (2007), Hunter et al. (2008), and Goodreau et al. (2008b); and for a tutorial introduction to their use, see Section 6 of Goodreau et al. (2008a). Here, we focus solely on the technical difficulties accompanying their use in ERGMs.

If ϕ_s in Equation 7 and ϕ_t in Equation 8 are fixed and known, then u(y; ϕ_s) and v(y; ϕ_t) present no special difficulties; one or both may easily be included as components of g(y). However, if ϕ_s or ϕ_t is an unknown parameter to be estimated via maximum likelihood, then the terms introduce some formidable technical and computational challenges. In this case, the model resulting from including u(y; ϕ_s) or v(y; ϕ_t) in g(y) is not of the standard ERGM form (1). However, it may be shown (Hunter and Handcock 2006) that this model is in fact an example of a curved exponential-family model in the sense of Efron (1975, 1978).

As an example, we fit two different models to the faux.mesa.high dataset, each involving the edges term, a uniform homophily effect of grade (i.e., an effect of two students being in the same grade), and a GWESP term. In model4, the ϕ_t parameter of Equation 8 is assumed to be fixed at a value of 0.5; this model is therefore a true ERGM of the form (1). The second model, model4a, is a curved exponential family model in which the ϕ_t parameter is to be estimated (the value 0.5 is used only as an initial value in the numerical estimation procedure). Note the difference in output for the two models, the key being that one holds the ϕ_t parameter fixed at 0.5 and the other estimates it along with the other coefficients. The second model, model4a, may take a few minutes to run.

R> model4 <- ergm(faux.mesa.high ~ edges + nodematch(“Grade”) ++ gwesp(0.5, fixed = TRUE), verbose = TRUE, seed = 789)R> summary(model4)...

Monte Carlo MLE Results:
Estimate Std.	Error MCMC	s.e.	p-value
edges	−6.1369	0.2518	0.038	<1e-04	***
nodematch.Grade	1.8993	0.4140	0.061	<1e-04	***
gwesp.fixed.0.5	1.2277	0.1837	0.020	<1e-04	***

...

To fit model4a, in which verbose = TRUE, we will use verbose = FALSE (the default setting) because verbose = TRUE generates a lot of output in the case of a curved exponential family like this one. However, interested readers may wish to see what happens with verbose=TRUE.

R> model4a <- ergm(faux.mesa.high ~ edges + nodematch(“Grade”) ++ gwesp(0.5, fixed=FALSE), verbose=FALSE, seed=789)R> summary(model4a)...

Monte Carlo MLE Results:
Estimate Std.	Error MCMC	s.e.	p-value
edges	−6.3478	0.4467	0.076	< 1e-04	***
nodematch.Grade	2.0886	0.4845	0.145	< 1e-04	***
gwesp	1.3703	0.3603	0.061	0.000143	***
gwesp.alpha	0.2257	0.2044	0.057	0.269438

...

Note: If check.degeneracy is set to TRUE (the default if FALSE), the degeneracy diagnostic suggests that both model4 and model4a may be degenerate models. These models are given here only to illustrate the difference between fixed = TRUE and fixed = FALSE, not to suggest that they fit these data well.

5. Statistical inference for ERGMs

5.1. Approximating an MLE

From Equation 1, we obtain the loglikelihood function

$$\ell \left(\theta \right)={\theta }^{\mathsf{T}}\mathbf{g}\left({\mathbf{y}}_{\mathrm{obs}}\right)-\log \kappa (\theta ,\mathcal{Y}),$$ (9)

where y_obs denotes the observed network. It is possible to redefine the g(y) vector by subtracting from it the constant vector g(y_obs), thus simplifying expression (9) without changing the model at all. Indeed, this simplification is used by the ergm function. However, we will use expression (9) throughout this article.

Rather than maximize $\ell \left(\theta \right)$ directly, we will consider instead the log-ratio of likelihood values

$$\ell \left(\theta \right)-\ell \left({\theta }_0\right)={(\theta -{\theta }_0)}^{\mathsf{T}}\mathbf{g}\left({\mathbf{y}}_{\mathrm{obs}}\right)-\log \left[\frac{k(\theta ,\mathcal{Y})}{\kappa ({\theta }_0,\mathcal{Y})}\right],$$ (10)

where θ₀ is an arbitrarily chosen parameter vector. [Note: Previously in this article, we have tended to use the term “coefficient” in situations in which either “coefficient” or “parameter” would technically be correct. To be precise, a coefficient in this context is a specific kind of parameter, namely, one that is multiplied by a statistic as in this case or in the case of regression generally. In this section, we may use the terms “parameter” and “coefficient” interchangeably.]

The approximation of ratios of normalizing constants such as the one in expression (10) is a difficult but well-studied problem (Meng and Wong 1996; Gelman and Meng 1998). The main idea we exploit in the ergm function is due to Geyer and Thompson (1992) and may be described as follows: Starting from Equations 1 and 2, a bit of algebra reveals that

$$\frac{\kappa (\theta ,\mathcal{Y})}{\kappa ({\theta }_0,\mathcal{Y})}={\mathsf{E}}_{{\theta }_0}\exp \left\{{(\theta -{\theta }_0)}^{\mathsf{T}}\mathbf{g}\left(\mathbf{Y}\right)\right\},$$

where E_θ0 denotes the expectation assuming that Y has distribution given by P_θ0,Y. Therefore, we may exploit the law of large numbers and approximate the log-ratio by

$$\ell \left(\theta \right)-\ell \left({\theta }_0\right)\approx {(\theta -{\theta }_0)}^{\mathsf{T}}\mathbf{g}\left({\mathbf{y}}_{\mathrm{obs}}\right)-\log \left[\frac{1}{m}\sum _{i=1}^m\exp \left\{{(\theta -{\theta }_0)}^{\mathsf{T}}\mathbf{g}\left({\mathbf{Y}}_i\right)\right\}\right],$$ (11)

where Y₁, . . . , Y_m is a random sample from the distribution defined by P_θ0,Y, simulated using an MCMC routine as described in Section 6.

The stochastic estimation technique described above requires one to select a parameter value θ₀. While the approximation of Equation 11 may in theory be made arbitrarily precise by choosing the MCMC sample size m to be large enough, in practice it is extremely difficult to use this approximation technique unless the value θ₀ is chosen carefully—namely, θ₀ should be “close enough” to the true maximum likelihood estimator $\widehat{\theta }$ or Equation 11 will fail.

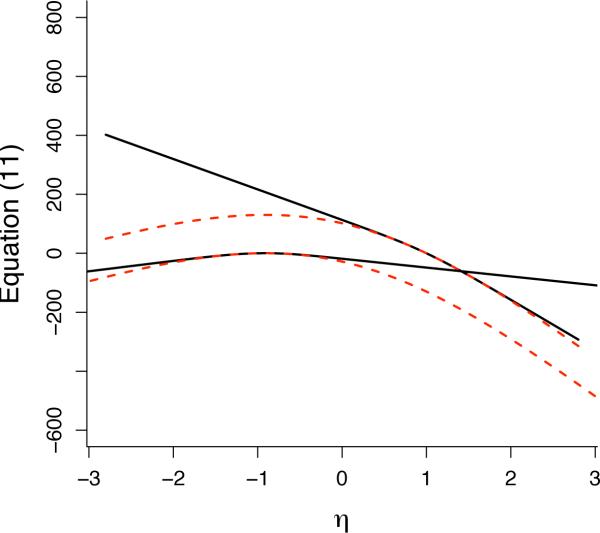
To see why this is so in a simple example, consider model1 from earlier, in which g(y) is just the number of edges in y and for the samplike dataset we found $\widehat{\theta }=-0.9072$. Suppose that we wanted to use the approximation (11) for $\ell \left(\theta \right)-\ell \left({\theta }_0\right)$, where in this case we take θ₀ = 1 for purposes of illustration. [Note: both g(y) and θare scalars in this example, so we do not use bold type to write them.] Since θ₀ = 1 corresponds to a network in which each of the 18 × 17 = 306 possible edges occurs independently with probability exp{1}/(1 + exp{1}) = 0.731, we may easily obtain a random sample g(Y₁), . . . , g(Y_m) by simulating m draws from a binomial distribution with parameters (306, .731). In this simulation, the probability of obtaining a network with g(Y) < g(y_obs) = 88 is extremely small, roughly 2.3 × 10⁻⁵⁹. For all practical purposes, such an event will never happen in a simulation even for very large m. Yet a simple derivation shows that the right side of Equation 11 cannot have a maximizer if there is no Y_i with g(Y_i) < g(y_obs), a fact that also follows from standard exponential-family theory (Barndor-Nielsen 1978). Therefore, we conclude that the stochastic algorithm for approximating the MLE will fail if we select θ₀ = 1 since g(Y_i) < g(y_obs) is an extraordinarily rare event in this case. On the other hand, with θ₀ = −1, it is straightforward to obtain an approximate MLE through simulation. These two cases are illustrated by Figure 2.

Figure 2.

For a simplistic model with g(y) equal to the number of edges, the dotted curves show $\ell \left(\theta \right)-\ell \left({\theta }_0\right)$ for two different values of θ₀, namely θ₀ = 1 (upper curve) and θ₀ = −1 (lower curve). The solid curves are the corresponding approximations using Equation 11. The true MLE, $\widehat{\theta }=-0.9072$, is easily derived in this case. Note that θ₀ = −1 appears to give a good approximation to the loglikelihood near $\widehat{\theta }$, whereas θ₀ = 1 gives an approximation that cannot even be maximized.

5.2. Pseudolikelihood

The default method used by ergm to choose θ₀ is pseudolikelihood estimation, originally motivated by, and developed for, spatial models (Besag 1974). The idea is to use an alternative local approximation to the likelihood function referred to as the pseudolikelihood. The pseudolikelihood for model (1) is identical to the likelihood for a logistic regression model in which the (binary) response data consist of the off-diagonal elements of y_obs and the predictor vectors are given by the change statistics δ_g(y_obs)_ij of Equation 3. Indeed, this is exactly the likelihood that is obtained if one starts with Equation 3 and then assumes in addition that the Y_ij are mutually independent, so that

$${\mathsf{P}}_{\theta ,\mathcal{Y}}(Y_{ij}=1\mid {\mathbf{Y}}_{ij}^c={\mathbf{y}}_{ij}^c)={\mathsf{P}}_{\theta ,\mathcal{Y}}(Y_{ij}=1).$$

The maximum pseudolikelihood estimator (MPLE) for an ERGM, the maximizer of the pseudolikelihood, may thus easily be found (at least in principle) by using logistic regression as a computational device. As the discussion in Section 4.3 shows, when the ERGM is a dyadic independence model not containing the mutual or asymmetric terms, the true likelihood and the pseudolikelihood are the same, which is to say that the true maximum likelihood estimator may be found via an MPLE computation.

When the ERGM in question is not a dyadic independence model, the statistical properties of pseudolikelihood estimators for social networks are not well understood. Recent work (van Duijn, Gile, and Handcock 2007) recommends strongly against their use as estimators. Nonetheless, it is sometimes helpful to be able to check the value of an MPLE. The ergm function may be used to return an MPLE by setting MPLEonly = TRUE. For instance, we may check that the MLE for the dyadic independence ERGM called model3 fitted earlier coincides with its MPLE by verifying that the difference in their coefficient estimates equals the zero vector:

R> model3a <- ergm(faux.mesa.high ~ edges + nodematch(“Grade”, diff = TRUE) ++ nodefactor(“Sex”), MPLEonly = TRUE)R> model3$coef - model3a$coef

edges	nodematch.Grade.7	nodematch.Grade.8
0	0	0
nodematch.Grade.9	nodematch.Grade.10	nodematch.Grade.11
0	0	0
nodematch.Grade.12	nodefactor.Sex.2
0	0

5.3. Profile likelihood computations

It may sometimes be desirable to fix the values of certain parameters in the model at known constants and then maximize the likelihood as a function of the remaining parameters. The resulting maximized value of the likelihood is called the profile likelihood and it is a function of only the parameters that were fixed. In this way, for instance, it is possible to examine a profile likelihood surface for one of more of the parameters. Note that maximizing the profile likelihood function for a subset of the parameters yields the overall MLE.

To achieve this type of profiling using statnet, use offset in an ergm formula. For example, suppose we wish to modify model3, seen previously in this section, so that the edges coefficient is fixed at −6.0 instead of its unconstrained MLE value of −6.248. Then, we would like to maximize the likelihood (i.e., estimate the other coefficients) subject to this constraint. Even though model3 is a dyadic independence model, to carry out this constrained maximization would require a specially modified logistic regression routine that is part of neither ergm nor R; therefore, we will force the ergm function to generate an approximate maximum likelihood estimate using an MCMC algorithm, as follows. The idea is to start with the maximum likelihood found earlier (model3$coef), modify only the “edges” coefficient, and then hold that coefficient constant at −6.0:

R> theta0 <- model3$coefR> theta0[1] <- −6.0R> model3b <- ergm(faux.mesa.high ~ offset(edges) ++ nodematch(“Grade”, diff = TRUE) + nodefactor(“Sex”),+ theta0 = theta0, control = control.ergm(force.mcmc = TRUE),+ seed = 456, verbose = TRUE)R> model3b$coef

edges	nodematch.Grade.7	nodematch.Grade.8
−6.0000000	3.0389517	3.2183996
nodematch.Grade.9	nodematch.Grade.10	nodematch.Grade.11
2.6489700	2.8761216	3.5878954
nodematch.Grade.12	nodefactor.Sex.M
3.8633896	−0.2854673

Note that we had to explicitly state a starting θ₀ value, theta0, for the entire parameter vector (not merely the edges term). Also, the force.mcmc = TRUE option to the control.ergm function is used to force ergm to use a stochastic approximation algorithm to find the MLE, even in the case of a dyadic independence model.

6. Simulating random networks from an ERGM

The form of model (1) allows networks to be generated from it using Markov Chain Monte Carlo (MCMC) algorithms. MCMC algorithms have been much studied and are a natural way to simulate social networks (Gilks, Richardson, and Spiegelhalter 1996; Newman and Barkema 1999). The goal is to construct a Markov Chain on Y with P_θ0,Y(Y = y) as the equilibrium distribution. This is operationalized by starting from a network in y and then making a large number of appropriately sampled Markov transitions until approximate convergence to P_θ0,Y(Y = y) is reached. Subsequent transitions are sampled and form a (sequentially dependent) sample from the desired model. For details on the general MCMC approach, see the extensive literature cited in the above books.

Many chains of networks are possible for a given ERGM, with vastly different mixing properties. However, convergence is ensured under fairly mild conditions (irreducibility and aperiodicity) on the Markov Chain in the limit as the number of transitions approaches infinity. For the social network representation (1), this process has been studied by Crouch, Wasserman, and Trachtenberg (1998), Corander, Dahmström, and Dahmström (1998), and Snijders (2002).

6.1. Different types of Markov chains

A full-conditional MCMC method has a simple form: At each iteration, for some choice of (i, j), Y_ij is set to zero or one according to the conditional probabilities ${\mathsf{P}}_{{\theta }_0,\mathcal{Y}}(Y_{ij}=1\mid {\mathbf{Y}}_{ij}^c={\mathbf{y}}_{ij}^c)$ and ${\mathsf{P}}_{{\theta }_0,\mathcal{Y}}(Y_{ij}=0\mid {\mathbf{Y}}_{ij}^c={\mathbf{y}}_{ij}^c)$ implied by Equation 3. This so-called “Gibbs sampling” or “heat bath” algorithm chooses the pairs (i, j) uniformly at random, sequentially, or using some mixture of the two. Each update requires the change statistics δ_g(y)_ij of Equation 3 to be determined. The speed of the calculation of δ_g(y)_ij (or δ_g(y,X)_ij if covariates are involved) is an important factor in the computational quality of the algorithm (i.e., speed of convergence to equilibrium).

As an alternative to Gibbs sampling, Metropolis algorithms propose transitions from y_current to y_proposed, where at each step of the chain, the algorithm makes a random choice of whether to remain at y_current for an additional step or change to y_proposed, the latter choice occurring with probability

$$\min \left\{1,\frac{{\mathsf{P}}_{{\theta }_0,\mathcal{Y}}(\mathbf{Y}={\mathbf{y}}_{\text{proposed}})}{{\mathsf{P}}_{{\theta }_0,\mathcal{Y}}(\mathbf{Y}={\mathbf{y}}_{\text{current}})}\right\}.$$ (12)

Still more general, Metropolis-Hastings algorithms choose y_proposed from an auxiliary distribution dependent on y_current and are aimed at either focusing the transitions or spreading them more broadly throughout Y. Thus, if q(y₁,y₂) denotes the probability that Y_proposed = y₁ given that Y_current = y₂ under this auxiliary distribution, then the probability (12) is replaced by

$$\min \left\{1,\frac{{\mathsf{P}}_{{\theta }_0,\mathcal{Y}}(\mathbf{Y}={\mathbf{y}}_{\text{proposed}})}{{\mathsf{P}}_{{\theta }_0,\mathcal{Y}}(\mathbf{Y}={\mathbf{y}}_{\text{current}})}\frac{q({\mathbf{y}}_{\text{current}},{\mathbf{y}}_{\text{proposed}})}{q({\mathbf{y}}_{\text{proposed}},{\mathbf{y}}_{\text{current}})}\right\}.$$ (13)

Thus, the Metropolis algorithm of Equation 12 may be viewed as a special case in which the auxiliary distribution is symmetric in the sense that q(y₁,y₂) = q(y₂,y₁).

What makes Metropolis and Metropolis-Hastings algorithms (which include Gibbs sampling as a special case) so appealing is that the normalizing constants (2) disappear from the ratio of ERGM probabilities seen in Expressions (12) and (13); indeed, this ratio is simply

$$\frac{{\mathsf{P}}_{{\theta }_0,\mathcal{Y}}(\mathbf{Y}={\mathbf{y}}_{\text{proposed}})}{{\mathsf{P}}_{{\theta }_0,\mathcal{Y}}(\mathbf{Y}={\mathbf{y}}_{\text{current}})}=\exp \left\{{\theta }_0[\mathbf{g}\left({\mathbf{y}}_{\text{proposed}}\right)-\mathbf{g}\left({\mathbf{y}}_{\text{current}}\right)]\right\}.$$ (14)

In fact, if y_proposed differs from y_current by exactly a single edge toggle, replacing y_ij by 1 − y_ij, then g(y_proposed) − g(y_current) is just ± δ_g(y)_ij. On the other hand, if y_proposed differs substantially from y_current for a particular type of Metropolis-Hastings proposal, then the ratio of Equation 14 can be calculated by considering a sequence of networks, each with one dyad different from the last, starting from the current network and ending at the proposed network. At each step, the ratio is a simple function of the change statistic vector.

6.2. Modifying the Metropolis-Hastings algorithm

Metropolis-Hastings algorithms can converge more efficiently than Gibbs sampling to the target distribution when the proposal density q(·, ·) is well-chosen. The behavior of MCMC algorithms is also very dependent on the choice of statistics g(y). Snijders (2002) reports on some odd convergence properties of the MCMC algorithms described here for particular choices of an ERGM and a parameter vector. In some cases, the sequences of realizations transition quickly between very different networks after periods of minor variation that can be extremely long. Other studies using MCMC algorithms to simulate social network models have reported difficulties in obtaining convergence to realistic distributions (Crouch et al. 1998; Corander et al. 1998). A typical occurrence in such cases is for the algorithm to produce networks that are complete, empty, or otherwise extreme in some way. Such behavior is a byproduct of the models themselves, rather than the MCMC algorithms used to simulate from them (Handcock 2003a,b).

Corander et al. (1998) considered algorithms that hold the number of edges in the network fixed, which avoids the problem of full or empty graphs. However, in most circumstances the density of the network is a product of the social process that produced it and cannot be assumed to be known in advance. Nonetheless, the ergm package supports many different Metropolis-Hastings constraints that hold various network statistics, such as the overall density, the degree distribution, or the degree of each node, constant. These constraints amount to restricting the class Y of networks that are considered to be possible under model (1). The possible constraints available in the ergm package, along with a couple examples of their use, are described in Section 3 of Morris et al. (2008). Possible modifications to the q(y₁,y₂) proposal distribution are discussed in Section 4 of Morris et al. (2008).

6.3. Example: Simulating a network using MCMC

Recall that model2 of Section 4.2, based on a simplified version of Equation 5, stipulates that for an 18-node directed network Y,

$$\mathsf{P}(\mathbf{Y}=\mathbf{y})\propto \exp \{-2.51\times \text{edges}\left(\mathbf{y}\right)+\cdots +3.68\times \text{mutual edges}\left(\mathbf{y}\right)\}.$$

Suppose we wish to use an MCMC idea such as the one described above to simulate a random network according to this model. Here are two equivalent ways to do this using the simulate command:

R> net1 <- simulate(model2, verbose = TRUE, seed = 678)R> net1 <- simulate(samplike ~ edges + sender + receiver + mutual,+ theta0 = model2$coef, verbose = TRUE, seed = 678)

Note that the second of these commands, using a formula along with the theta0 argument, gives quite a bit of flexibility. For instance, one might wish to fit model2 and then examine the effects of small changes to one of the parameters in the fitted model. To do this, one could make a copy of these fitted coefficients — say, by typing the command mycopy <-model2$coef — then make the small changes to this copy and use the altered copy as the parameter values by substituting theta0 = mycopy into the above expression.

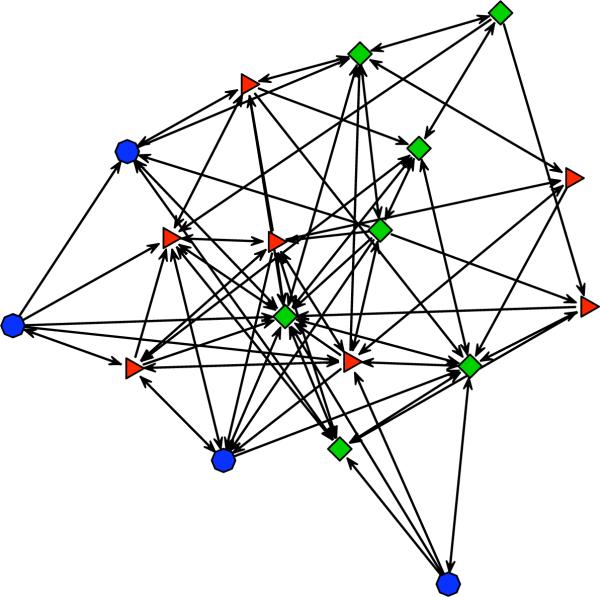
After simulating net1, we may plot it using a command similar to the one used to produce Figure 1, but with net1 in place of samplike; see Appendix A for details. The result of one such experiment is depicted in Figure 3.

Figure 3.

A randomly generated network according to the ERGM with mutuality and edges terms, fitted to the samplike dataset.

Note in particular that the clustering of nodes by (colored) group is no longer evident. This is due to the fact that the ERGM used to generate this simulated network has no terms that represent the effects of the nodal “group” covariate. Since group membership was an endogenous property of the original network, rather than an exogenously defined measure, the inclusion of such terms would raise some interesting theoretical issues that lie outside the scope of this paper. While we cannot use this model to try to reproduce the group membership of specific nodes, we can use it to try to reproduce a network that is isomorphic with respect to the aggregate pattern of clustering. This structural isomorphism is closely related to the concept of “regular equivalence” in the social network literature (Borgatti and Everett 1992).

For a quantitative comparison of the structural similarities in the randomly generated network and the original samplike dataset, we may use the summary.formula capability of ergm, which provides summary statistics for a network. For example:

R> rbind(summary(samplike ~ edges + mutual + idegree(0:3) + triangle),+ summary(net1 ~ edges + mutual + idegree(0:3) + triangle))

edges	mutual	idegree0	idegree1	idegree2	idegree3	triangle
[1,]	88	28	0	0	3	5	193
[2,]	63	20	1	3	2	5	73

The idegree term above refers to in-degree, and in an ergm formula, idegree(0:3) adds four statistics to the g(y) vector: The number of nodes with 0, 1, 2, and 3 in-edges in y, respectively. Morris et al. (2008) give a list of the various graph statistics that may be used in an ergm or summary statement. Furthermore, both Goodreau et al. (2008a) and Morris et al. (2008) contain additional examples of the simulate function applied to networks.

7. Goodness of fit

Recent work on the quality of certain ERGMs, in particular work on degeneracy in ERGMs (Handcock 2003a,b) underscores the following fact: A maximum likelihood estimator $\widehat{\theta }$, while providing in some sense the best possible model from the particular class of models defined by Equation 1 for a particular choice of g(y), does not necessarily result in a particularly good model in a practical sense. It is possible that the model class itself is simply incapable of producing a probability distribution on Y such that there is a reasonable probability of obtaining networks that resemble the data y_obs. Yet we must specify what is meant by “resemble” in this context.

One way in which one network may “resemble” another, particularly in the context of an ERGM with a particular vector g(y), is that their g(y) vectors may be close together. We know from the theory of exponential family models (Brown 1986) that a particular ERGM (1), with θ set equal to the maximum likelihood estimator $\widehat{\theta }$, has the property that

$${\mathsf{E}}_{\widehat{\theta }}\mathbf{g}\left(\mathbf{Y}\right)=\mathbf{g}\left({\mathbf{y}}_{\mathrm{obs}}\right),$$ (15)

so that at least we may be assured that the probability mass of the ERGM is centered at g(y_obs). Yet this is not su cient to imply that a random Y generated from the ERGM will “resemble” y_obs. It is in fact quite possible that Equation 15 could be achieved essentially because the MLE model places nearly all of the probability mass on nearly-empty or nearly-full networks, such that the mean, somewhere in between, is exactly g(y_obs). A striking example of this phenomenon is given in Section 3 of Handcock et al. (2008) in this volume; see also Handcock (2003a).

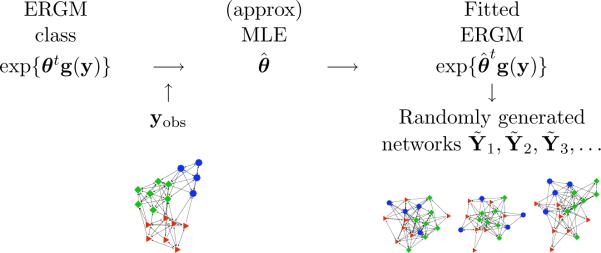
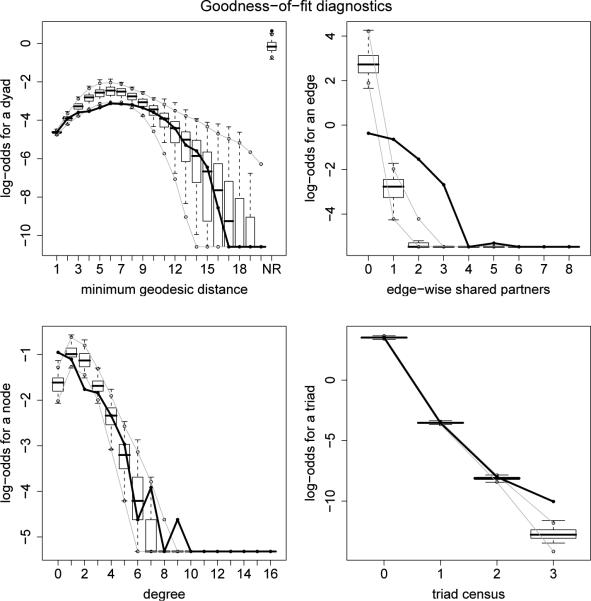
The intuition of the gof function in the ergm package, illustrated by the cartoon of Figure 4, is to compare the observed y_obs with a set of simulated networks Ỹ₁, Ỹ₂, . . . based on certain network statistics — which may or may not overlap those of g(y) itself. For instance, the code below uses four different sets of statistics, specified by the GOF argument, as a basis for comparison between the faux.mesa.high dataset and a series of 100 randomly generated networks obtained from the fitted model3. The interval = 5e+4 argument specifies the number of MCMC steps (50,000 in scientific notation) between sampled networks. Because of the large amount of simulation and compilation of network statistics necessary, the gof function may take several minutes to run.

R> m3gof <- gof(model3, GOF = ~distance + espartners + degree + triadcensus,+ verbose = TRUE, interval = 5e+4, seed = 111)

Figure 4.

The gof function compares features of the observed network, represented at the left, with the same features of a set of networks simulated according to the MLE model.

The four sets of statistics used for the comparison are as follows:

• The geodesic distance distribution: The proportion of pairs of nodes whose shortest connecting path is of length k, for k = 1,2, . . .. Also, pairs of nodes that are not connected are classified as k = ∞.

• The edgewise shared partner distribution: The statistics EP₀,EP₁, . . . of Equation 8, divided by the total number of edges.

• The degree distribution: The statistics D₀, D₁, . . . of Equation 6, divided by n.

• The triad census distribution: The proportion of 3-node sets having 0, 1, 2, or 3 edges among them. Note: For a directed network, the triad census has 16 categories instead of 4; see the triadcensus term in Section 2.5 of Morris et al. (2008).

The par and plot functions below produce the plot shown in Figure 5.

R> par(mfrow = c(2,2))R> plot(m3gof, cex.lab=1.6, cex.axis=1.6, plotlogodds = TRUE)

Figure 5.

The solid line in each plot represents the observes statistics for the faux.mesa.high network, and the boxplots summarize the statistics for the simulated networks resulting from the MLE.

The upper-right plot of Figure 5 reveals that the ERGM with only an edges term, a differential homophily term for grade and a main effect for sex does a poor job of capturing the edgewise shared partner distribution. But considering that model3 is so simplistic, it does a remarkably good job of producing networks that reflect the degree distribution, the pairwise geodesic distance distribution, and the triad census of the original faux.mesa.high dataset. A better model for the faux.mesa.high dataset would include homophily terms and main effects for grade, sex, and race as well as a GWESP term to capture transitivity. Further details on such models may be found in Hunter et al. (2008), where they are fit to real data similar to faux.mesa.high.

8. Discussion

There are many features of the ergm package that it is impossible to document here due to space limitations, but we hope that this article, together with its companion articles in this volume, serves as a useful introduction to the capabilities of the package as well as some of the theory behind it. Of course, questions will inevitably arise that are not answered here or in the package documentation. For this reason, we have established a statnet mailing list at statnet_help@u.washington.edu. To subscribe go to https://mailman.u.washington.edu/mailman/listinfo/statnet_help. Further details are available on the statnet project web page at http://statnetproject.org.

The statnet packages are far from finished. For instance, future versions of the ergm package will address the question of how to fit ERGMs to network data that evolve in time. In addition, while the numerical fitting algorithm has come a very long way—and we are nearly at the stage where a reasonable model can be expected to converge “out of the box”—improving the algorithm is still a topic of active research.

A. R code for network plots

Here we give code to produce the plots in Figures 1(a) and 1(b). The code for Figure 1(a) may also be applied to the net1 simulated dataset to obtain a plot similar to Figure 3. Though not explicit in the code below, the function being called upon to produce the plot is called plot.network and a user may learn about its numerous control options by typing help(plot.network). (For those not familiar with the intricacies of the R programming environment, the plot.network function—called a “method” for the generic function plot—is automatically invoked below because plot is applied to an object, samplike, of class “network”.) Because the default method used by plot.network to position the nodes has a random aspect, we include a set.seed statement to produce exactly the same plot as in Figure 1(a).

R> data(“sampson”)R> gp <- samplike %v% “group”R> gp <- match(gp, unique(gp))R> set.seed(321)R> plot(samplike, vertex.cex = 4, vertex.col = gp+1,R+ vertex.sides = c(3,4,8)[gp], main = “(a)”, cex.main = 3)

The samplike %v% “group” command extracts the nodel covariate called “group” from the samplike object. In the plot command, the vertex.cex, vertex.col, and vertex.sides arguments, respectively, make the nodes larger, color them by group, and use triangles, squares, and octagons to represent them. The main and cex.main arguments add a title and enlarge it for viewing.

In fact, the code above was actually used to produce a .pdf file for use in this article. This was achieved by enclosing the code above between the following two lines, which open a .pdf file for output and then close it, respectively:

R> pdf(“fig1a.pdf”,height = 10,width = 10)...R> dev.off()

Similarly, the following code was used for Figure 1(b):

R> data(“faux.mesa.high”)R> grd <- faux.mesa.high %v% “Grade”R> sx <- faux.mesa.high %v% “Sex”R> vs <- c(4, 12)[match(sx, c(“M”, “F”))]R> col <- c(6, 5, 3, 7, 4, 2)R> set.seed(654)R> plot(faux.mesa.high, vertex.sides = vs, vertex.rot = 45, vertex.cex = 2.5,R+ vertex.col = col[grd - 6], edge.lwd = 2, main = “(b)”, cex.main = 3,R+ displayisolates = FALSE)R> legend(“topright”, legend = 7:12, fill = col, cex = 2.2)

The only new arguments here to the plot command are vertex.rot, which rotates the nodes 45 degrees so that the squares are not oriented as diamonds, edge.lwd, which makes wider-than-normal edge lines for viewing, and displayisolates, which leaves out all nodes without any edges. Finally, the legend command creates a legend showing the grades and their corresponding colors. For more on the capabilities of plot.network and the network package in general, see Butts (2008).