Abstract
Highly active antiretroviral therapy (HAART) can control HIV-1 replication1,2, but suboptimal treatment allows evolution of resistance and rebound viremia3–8. A comparative measure of antiviral activity under clinically relevant conditions would guide drug development and the selection of regimens that maximally suppress replication. Here we show that current measures of antiviral activity including IC50 and inhibitory quotient (IQ) neglect a critical dimension, dose-response curve slope. Using infectivity assays with wide dynamic range, we show that slope has dramatic effects on antiviral activity. Strikingly, slope values are class-specific for antiviral drugs and define intrinsic limitations on antiviral activity for some classes. Nucleoside reverse transcriptase inhibitors (NRTIs) and integrase inhibitors have slopes of ~1, characteristic of non-cooperative reactions, while nonnucleoside reverse transcriptase inhibitors (NNRTIs), protease inhibitors (PIs), and fusion inhibitors unexpectedly show slopes >1. Instantaneous inhibitory potential (IIP), the log reduction in single round infectivity at clinical drug concentrations, is strongly influenced by slope and varies by >8 logs for anti-HIV drugs. IIP provides a more accurate measure of antiviral activity and in general correlates with clinical outcomes. Only agents with slopes >1 achieve high level inhibition of single round infectivity, a finding with profound implications for drug and vaccine development.
A classic description of dose-response relationships is the median effect model based on mass action9,10 (equations 1 and 2, Fig. 1):
| (1) |
| (2) |
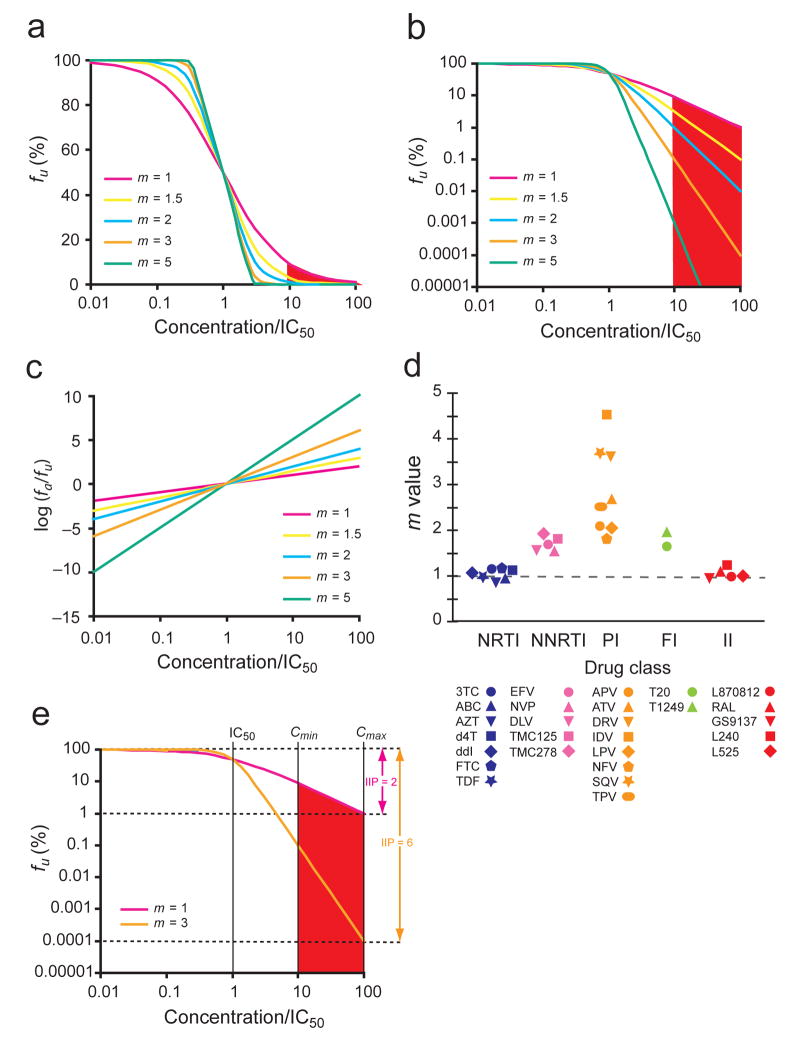
Figure 1.
Effect of slope (m) on dose-response curves of antiretroviral drugs. (a) Hypothetical linear-log plot of the fraction of viruses unaffected (fu) by a drug vs. drug concentration based on the median-effect model for drugs with different m values. Concentrations are normalized by IC50. A typical clinical concentration range 10–100 fold above the IC50 is shaded. (b) A log-log plot of the same curves emphasizing the strong impact of slope on the suppression of infectivity. (c) A median effect plot [log (fa/fu) vs. log drug concentration] (equation 1) of the same curves. The m value is the slope of the line. (d) Each class of anti-HIV-1 drugs has a characteristic slope. The m value for each drug was calculated by linear regression analysis using the median effect model. Each point is the average of more than three experiments. See Supplementary Table online for the mean values and standard deviations (s.d.). (e) Comparison of the antiviral activity of two hypothetical drugs with different m values. Instantaneous inhibitory potential (IIP) is the number of logs of suppression of single round infectivity at a clinically relevant drug concentration. At Cmax, the IIP of a drug with m = 3 is 10,000 fold greater than that of a drug with m = 1.
For inhibition of HIV-1 infection, fa and fu (equals to 1− fa) are the fractions of viruses affected and unaffected by the drug, D is drug concentration, IC50 is the drug concentration that causes 50% of the maximum inhibitory effect, and m is a slope parameter mathematically analogous to the Hill coefficient11, a measure of cooperativity in the binding of multiple ligands to linked binding sites. In this model, drug activity is determined by three parameters: IC50, D, and m. However, the widely used measures IC50 and IQ (the ratio of plasma drug concentrations to IC50)12,13 both ignore slope. In traditional semi-log plots, dose-response curves with different slopes appear similar, approaching 100% inhibition at high drug concentrations (Fig. 1a). However, clinical outcome may depend on whether 99% vs. 99.99% inhibition is achieved14. Displaying the same data on a log-log plot reveals that drugs with the same IC50 or IQ values but higher slopes achieve much greater inhibition at clinically relevant concentrations (Fig. 1b). We therefore hypothesized that slope might have a dramatic effect on antiviral activity.
To test this hypothesis, we obtained dose-response curves for anti-HIV-1 drugs using a single-round infectivity assay with sensitivity to detect infection of individual cells15,16. CXCR4-pseudotyped wild-type viruses carrying green fluorescence protein (GFP) in the env gene were used to infect primary CD4+ T lymphoblasts, the principal target cells for HIV-1 in vivo. Infectivity was quantified by flow cytometry, and fu was calculated as the %GFP+ cells in the presence of drug normalized by the %GFP+ cells without drug. Using the median effect model (equation 1), dose-response curves can be linearized (Fig. 1c), and IC50 and slope can be determined (Supplementary Table online). We chose a single round assay because it is not complicated by virus growth and evolution over a prolonged culture period, reflects the degree of instantaneous inhibition caused by the drugs, and correlates more closely with mechanisms of drug action17.
Analysis of dose-response curves for anti-HIV-1 drugs gave a striking result. Each drug class had a characteristic slope (Fig. 1d, Supplementary Table online). The slopes of all NRTIs were ~1, characteristic of non-cooperative reactions. Five structurally diverse integrase inhibitors also showed slopes close to 1. In contrast, the slopes for NNRTIs and fusion inhibitors were ~1.7, while the slopes for PIs ranged from 1.8 to 4.5. Thus, antiretroviral drugs acting through different mechanisms showed distinct slope values.
To include the influence of slope in a quantitative measure of antiviral activity, we developed a new index termed instantaneous inhibitory potential (IIP), which equals the log reduction in single round infectivity at clinically relevant concentrations (Fig. 1e). IIP is equivalent to log(1/fu) and can be calculated from equations (3)–(5).
| (3) |
| (4) |
| (5) |
Here Cmin, Cave, and Cmax represent steady state minimum, average (AUCτ/dose interval), and maximum plasma drug concentrations for the commonly recommended dose of each drug18. IIP incorporates all three parameters in the median effect model - IC50, D, and m - into a single value with intuitive meaning, the log reduction in infectivity.
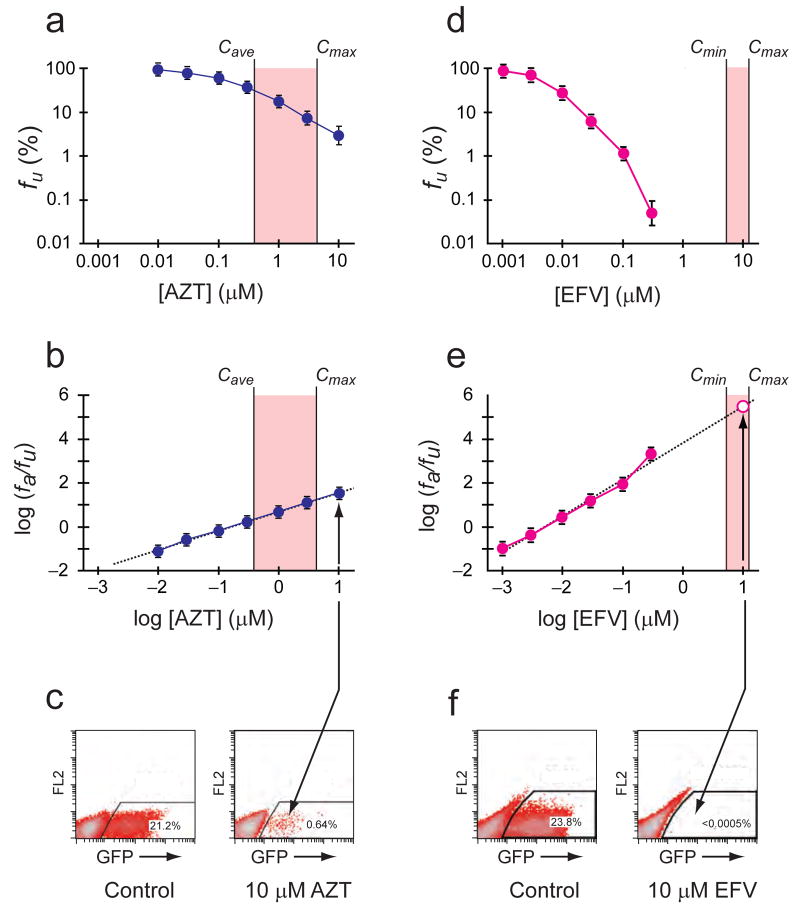
Initial studies showed that the IIP of different drugs varied dramatically (>8 logs) due to the influence of slope (Fig. 1e). For NRTIs, IIP values were ≤3.5 and within the dynamic range of the standard assay (Fig. 2a–c). For NNRTIs and PIs, the IIP values ranged from 2–10. IIP values beyond the dynamic range were determined by extrapolation (Fig. 2d–f). To verify the extrapolated values, we carried out larger scale assays with >106 infected cells. Our results confirm that drugs like efavirenz (EFV) at clinically relevant concentrations can decrease single round infection by >5 logs, as evidenced by the striking absence of GFP+ cells (Fig. 2f).
Figure 2.
Measurement of IC50, m, and IIP. (a,d) Log-log dose-response curves for zinovudine (AZT) and efavirenz (EFV). 50% human serum and 10% fetal calf serum were included in the culture medium to account for protein binding of the drugs. Each point represents the mean±s.d. from more than three experiments. The clinical concentration range for each drug is shaded. Because of the short plasma half-life of the AZT prodrug, the range between Cave and Cmax is shown. Clinical concentrations of AZT produce inhibition that is readily measured by collecting ~50,000 events (live cells). In contrast, clinical concentrations of EFV produce inhibition that can only be measured with assays having a dynamic range of >5 logs. (b,e) Linearized dose-response curves for AZT and EFV based on median effect model. IIP at Cmin, Cave or Cmax was calculated using equations (3)–(5). For EFV, this is graphically equivalent to extrapolation of the median effect plot to higher concentrations (dashed line). To verify values obtained by extrapolation, large scale infections were carried out (open symbol, see below). (c,f) Verifying the IIP of EFV in large scale infections (~2 × 106 events). In cultures with 10 μM AZT, infection events (GFP+ cells) were readily detectable. In cultures with 10μM EFV, less than three GFP+ cells were detected. This represents >5 logs of inhibition, consistent with the values predicted by extrapolation.
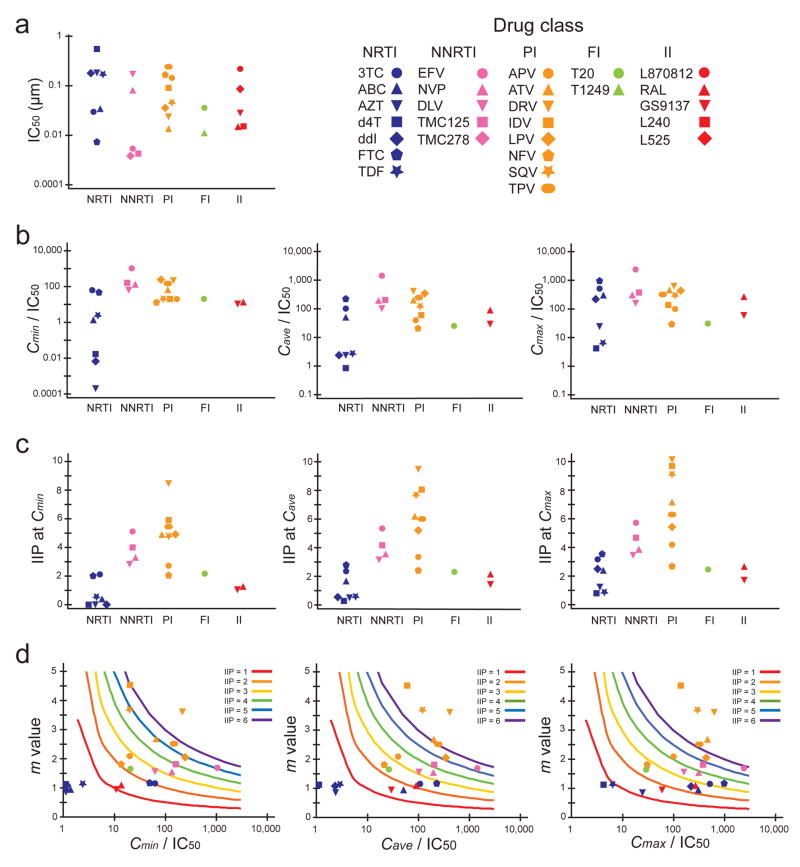
We next compared three indices of antiviral activity, IC50, IQ, and IIP, for different classes of anti-HIV-1 drugs (Fig. 3). There was no general difference in the range of IC50 values for different classes (Fig. 3a). For IQ, the NNRTI EFV had the highest value, but the IQ values for the PI and NRTI classes overlapped (Fig. 3b). However, when IIP was used for comparison, NNRTIs and most PIs gave much higher values than NRTIs (Fig. 3c). This finding partially explains why the most effective initial HAART regimens include an NNRTI or PI14. Particularly striking was the finding that EFV and a subset of PIs produced >5 logs of inhibition at Cave, which is substantially greater than inhibition produced by NRTIs, fusion inhibitors, or integrase inhibitors. Most impressively, the PIs darunavir (DRV), indinavir and saquinavir, produced >9 logs of inhibition at Cmax (Fig. 3c). These drugs had slopes >3.5 (Fig. 1d). The steepness of the dose-response curve, as captured in the m value, is an important factor leading to high IIP, as illustrated in contour plots of IIP as a function of m and IQ (Fig. 3d). Thus the slope parameter is a critical missing dimension in the analysis of antiviral activity.
Figure 3.
Comparison of indices used to describe antiviral activity for five classes of anti-HIV-1 drugs. (a) IC50 determined in the single round infectivity assay. IC50 was determined by least squares regression analysis of median effect plots. (b) IQ values (concentration/IC50) at Cmin, Cave, and Cmax. (c) IIP values at Cmin, Cave, and Cmax. IIP values were determined using equations (3)–(5) from measured IC50 and m values as described in Fig. 2. (d) Contour plots of m vs. IQ. Colored lines are theoretical IIP values representing 1–6 logs of inhibition of a single round of infection based on the median effect model. Note in Fig. 3c that 4 PIs produce >6 logs inhibition at Cmax, largely as a result of high m values. All the data points are the average of more than three experiments. Mean values and s.d. are shown in Supplementary Table online. NRTI data points with IQ values below the scale range were placed at the left edge of x axis in Fig. 3d.
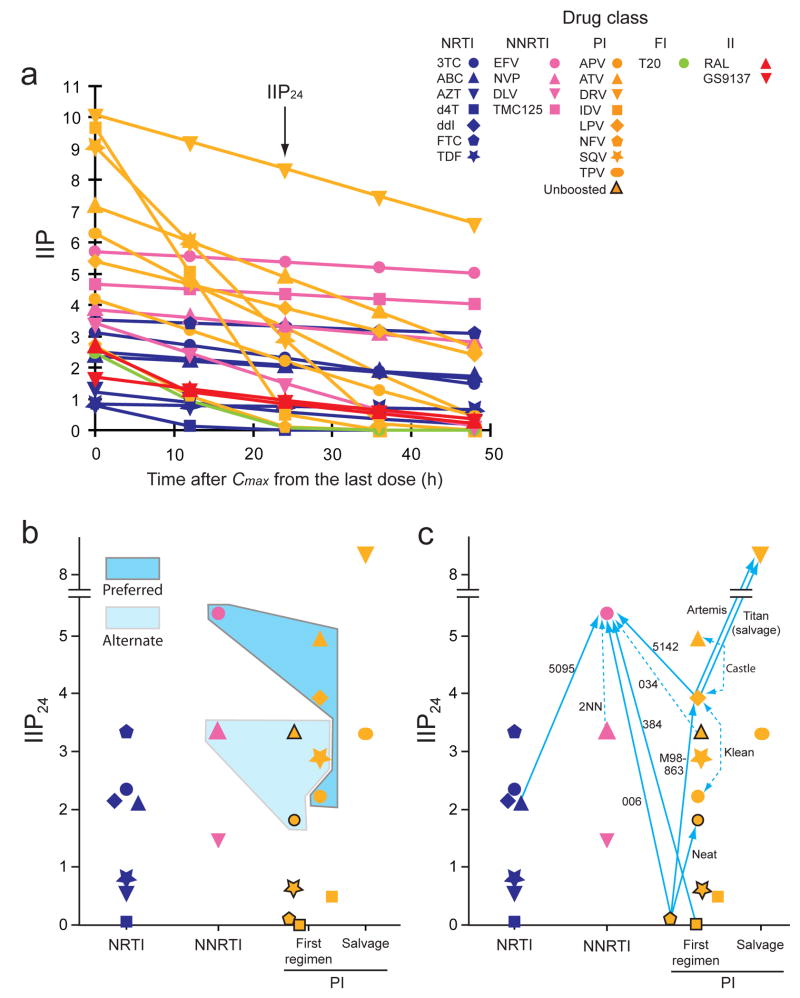
Although high slope endows a drug with high IIP, it also indicates extreme sensitivity to the changes in plasma drug concentration. For drugs with a high slope and short half-life (t1/2), IIP drops quickly during the dosing interval and with missed doses (Fig. 4a and Supplementary Notes online). This result, together with issues of bioavailability, toxicity, and convenience, may explain why indinavir and saquinavir are used less commonly despite their high IIP values. The two drugs that maintain IIP values at 24 hrs after the last dose (IIP24) above 5 logs, EFV and DRV (Fig. 4a), consistently excel in clinical trials14,19–22.
Figure 4.
Correlation of IIP with clinical outcome. (a) Predicted decay of IIP if subsequent doses are missed. IIP is plotted as a function of time after Cmax from the last dose. We calculated IIP using measured m and IC50 values (Supplementary Table online) and published t1/2 values. For NRTIs, we used t1/2 values for the active intracellular triphosphate forms18. Drug levels are assumed to decay exponentially. The initial IIP decay rate is proportional to m/t1/2 (Supplementary Notes online). For drugs with high m values and short t1/2 such as indinavir and saquinavir, IIP drops dramatically if one or two doses are missed, whereas for drugs with long t1/2 such as EFV and DRV, IIP is maintained at a high level even if doses are missed. (b) Relationship between IIP24 values and recommended “Column A” drugs. Recommended initial HAART regimens consist of two NRTIs plus one highly active “Column A” drug. The IIP24 values for the preferred “Column A drugs” (dark shading) tend to be higher than those of the alternate “Column A” drugs (light shading) or non-“Column A” drugs. Data from unboosted PIs are indicated by symbols with a black border. (c) Relationship between IIP24 values and virologic outcomes in major clinical trials (Supplementary Notes online) cited in the treatment guidelines14,19, with trial titles given beside each arrow. Solid arrows point towards drugs with superior virologic activity in head-to-head comparisons with the same background regimens. Broken arrows indicate a trend towards superiority not reaching statistical significance. Double-headed arrows indicate equivalent virologic outcomes.
Since antiviral activity is likely to be a major determinant of clinical outcome, we compared IIP values with clinical trial results (Fig. 4b, c). We used IIP24 as a measure of sustained antiviral activity and the HIV-1 treatment guidelines as a source of clinical outcomes14,19. The analysis showed that drugs with high sustained IIP were favored for initial treatment (Fig. 4b) and tended to demonstrate superiority over drugs with lower IIP in high quality randomized clinical trials (Fig. 4c, Supplementary Notes online). Furthermore, our results indicate that DRV is superior to all available antiretroviral drugs based on IIP, suggesting that DRV-based initial HAART regimens may be uniquely effective. Preliminary results from the Artemis trial in treatment-naïve patients confirm this prediction22.
Our results demonstrate that IIP provides a more accurate in vitro pharmacodynamic measure of antiviral activity than the traditional measures because it takes into account the slope parameter. Nevertheless, IIP is only one factor in clinical outcome. It cannot be directly related to the initial decay rate of viremia, which depends on where in the life cycle drugs act23, or the magnitude and durability of viral load suppression, which are influenced by multiple factors including pharmacokinetics, distribution, toxicity, adherence, drug interactions, and barriers to resistance (Supplementary Notes online). While no in vitro assay can predict clinical outcomes, our results suggest that IIP may identify drugs with high antiviral activity in vivo.
Our data show that slope is characteristic of drug class. A mechanistic explanation can be found by reconsidering the concept of cooperativity in drug action. Although m >1 classically represents positive cooperativity between ligand binding sites on a multivalent receptor11, multiple equilibria models based on mass action24 and statistical models incorporating heterogeneity25 can be applied to antiviral drugs and predict steep dose-response curves without the need to postulate interactions between binding sites (L.S. and R.F.S., unpublished). For all forms of cooperativity leading to steep dose-response curves, the critical requirement is participation of multiple copies of a drug target in the relevant step in the life cycle. Drugs like NRTIs and integrase inhibitors with m =1 (no cooperativity) target reactions in which a single molecular complex of enzyme with viral nucleic acid mediates a critical step - nucleotide addition leading to chain termination or strand transfer26–28. Other RT or integrase molecules present are irrelevant. In contrast, NNRTIs and PIs target the enzymes themselves. Multiple copies of RT and protease participate in the processes of reverse transcription and virion maturation, respectively, allowing for a form of intermolecular cooperativity within the preintegration complex or the maturing virion. The lack of this form of cooperativity for NRTIs and integrase inhibitors results in m values of 1, thus imposing intrinsic limitations on IIP.
Although there may be different mechanistic explanations for high slope values, our demonstration that the slope is a crucial determinant of drug activity is a general result that is an inevitable consequence of the dose-response relationship. This result may apply to all viral infections, as evidenced in the role of slope in the effectiveness of IFNα treatment of HCV infection29. Importantly, these principles apply not only to antiviral drugs, but also to vaccine-induced effector mechanisms including neutralizing antibodies, and any other drugs that target exponential processes, such as the growth of microorganisms or cancer cells.
Methods
Drug preparation
We obtained raltegravir, L870812, L240, L525, GS9137, TMC125, TMC278 from Merck Inc. We obtained all other anti-HIV-1 drugs through the AIDS Research and Reference Reagent Program, Division of AIDS, National Institute of Allergy and Infections Diseases, US National Institutes of Health. AZT, 3TC, ABC, ddI, EFV, NVP, ATV, LPV, NFV, TPV, DRV, SQV, APV, T1249, L240, L525, GS9137, TMC125 and TMC278 were solved in DMSO at 50 mM, aliquoted, and stored at −20 °C. Raltegravir and L-870812 were solved in DMSO at 6 mM, aliquoted, and stored at −20 °C. TDF, FTC, d4T, and IDV were solved in ddH2O at 50 mM, aliquoted, and stored at −20 °C. T20 (Roche) was solved in 0.1 M NaHCO3 at 1 mM, aliquoted, and stored at −80 °C. Drugs were diluted serially in their corresponding solvents and final solvent concentration in cell culture was kept constant at 0.5%.
Virus stocks
We generated pseudotyped virus capable of single round infection as described previously15. Briefly, we transfected HEK293T cells with a GFP-tagged, envelope defective HIV-1 vector (pNL43-ΔE-EGFP) along with a HIV-1 CXCR4 envelope expression vector using lipofectamine 2000 (Invitrogen) according to the manufacture’s protocol. For experiments testing PIs, medium was replaced by RPMI1640 (Invitrogen) supplemented with 50% human serum (Germini) and 10% fetal bovine serum (FBS) (Germini) 6–7 h after transfection and drugs were added at this step. We chose to use 50% human serum to account for the protein binding of the drugs without compromising cell viability. At 48 h after transfection, virus-containing supernatants were spun at 335 × g for 10 min, filtered through a 0.22 μm membrane to remove cell debris, and used for infection or stored at −80 °C. For experiments testing other drugs, medium was replaced by RPMI1640 supplemented with 10% FBS only. At 48 h after transfection, cell debris was cleared as described above, and virus particles were harvested by ultracentrifugation at 100,000 × g at 4 °C for 2 h, aliquoted, and stored at −80 °C. We standardized the amount of virus used for each experiment by p24 using an enzyme-linked immunosorbent assay (Perkin-Elmer).
Single round infectivity assay
We used a modified single round infectivity assay to evaluate anti-HIV-1 drug activity15,16. Briefly, PBMCs were obtained from healthy blood donors by Hypaque-Ficoll gradient centrifugation and activated using phytohemaglutinin (0.5 μg/ml) and interleukin-2 (100 units/ml) for 3 d. CD4+ T cells were selected by magnetic beads (Miltenyi) and were seeded in 96-well plate at 1 × 105/well in RPMI1640 supplemented with 50% human serum, 10% FBS, interleukin-2 (100 units/ml) and cytokine-rich supernatant. Drugs other than protease inhibitors were added at this step and maintained throughout the culture. Standardized amounts of virus were added 16–18 h after the addition of drugs. This period was shown to be sufficient to allow optimal intracellular phosphorylation of NRTIs. We carried out infection by spinnocculation at 1,200 × g, 30 °C for 2 h. Infected cells were incubated at 37 °C for 3 d. Cells were then washed and fixed with 2% formaldehyde. We quantified infectivity as the percentage of GFP+ cells through fluorescence activated cell sorter analysis (BD Bioscience). We did all the experiments in triplicate with cells from at least three different donors. All healthy blood donors gave their informed consent, and the study was approved by the Institutional Review Board of Johns Hopkins University.
Analysis of dose-response curves
We obtained dose-response curves by normalizing the percentage of GFP+ cells without drug treatment to 100%. We obtained the IC50 and the slope (m value) from each dose-response curve by fitting data to the median effect model (equation 1) through least square regression analysis. We calculated IIP using equations (3)–(5). The consistency of slope was checked and was considered constant with r2 > 0.96. For some PIs such as lopinavir, the slopes of dose-response curves increase at higher concentration (Supplementary Fig. 1 online). In this case we used the lowest slope for estimation of IIP. For raltegravir and L240, a low level GFP expression from a small number of cells with unintegrated virus was apparent at high concentrations of the drug. To correct for this effect, we fitted the data to the following equation to obtain mact and x:
| (6) |
where fu obs is the observed fu, fu act, IC50 act, mact are the actual fu, IC50, m values, and x is the percentage of GFP expression from unintegrated virus. We assumed that IC50 act is approximately equal to IC50 obs calculated from fu obs since x is very small. The resulting estimate for x was less than 1.5% in all experiments, and the m values reported for raltegravir and L240 were the adjusted m values (mact) (Supplementary Fig. 2 online).
Supplementary Material
Acknowledgments
We thank healthy blood donors for their participation. We thank the AIDS Research and Reference Reagent Program of the US National Institutes of Health and Merck Inc for providing anti-HIV-1 drugs. We thank Drs. C. Flexner, A. Mildvan, J. Gallant, G. Lucas, J. Cofrancesco, J. Bartlett, D. Hazuda, and R. Moore for helpful discussions and critical review of the manuscript. This work was supported by the US National Institutes of Health grants AI43222 and AI51178, by the Doris Duke Charitable Foundation, and by the Howard Hughes Medical Institute.
Footnotes
Author contributions:
L.S. and R.F.S. designed the experiments. L.S. conducted the experiments. S.P., M.A.M., M.C., H.Z., Y.Z., and E.P. contributed to the development of the single round infectivity assay. L.S., A.R.S., and R.F.S. conducted the data analysis. E.P.A. provided pharmacokinetic data used in the analysis. K.S.A. provided reagents used in the experiments. All of the authors contributed to the manuscript preparation. R.F.S. supervised the project.
References
- 1.Gulick RM, et al. Treatment with indinavir, zidovudine, and lamivudine in adults with human immunodeficiency virus infection and prior antiretroviral therapy. N Engl J Med. 1997;337:734–739. doi: 10.1056/NEJM199709113371102. [DOI] [PubMed] [Google Scholar]
- 2.Hammer SM, et al. A controlled trial of two nucleoside analogues plus indinavir in persons with human immunodeficiency virus infection and CD4 cell counts of 200 per cubic millimeter or less. AIDS Clinical Trials Group 320 Study Team. N Engl J Med. 1997;337:725–733. doi: 10.1056/NEJM199709113371101. [DOI] [PubMed] [Google Scholar]
- 3.Ho DD, et al. Rapid turnover of plasma virions and CD4 lymphocytes in HIV-1 infection. Nature. 1995;373:123–126. doi: 10.1038/373123a0. [DOI] [PubMed] [Google Scholar]
- 4.Wei X, et al. Viral dynamics in human immunodeficiency virus type 1 infection. Nature. 1995;373:117–122. doi: 10.1038/373117a0. [DOI] [PubMed] [Google Scholar]
- 5.Preston BD, Poiesz BJ, Loeb LA. Fidelity of HIV-1 reverse transcriptase. Science. 1988;242:1168–1171. doi: 10.1126/science.2460924. [DOI] [PubMed] [Google Scholar]
- 6.Roberts JD, Bebenek K, Kunkel TA. The accuracy of reverse transcriptase from HIV-1. Science. 1988;242:1171–1173. doi: 10.1126/science.2460925. [DOI] [PubMed] [Google Scholar]
- 7.Larder BA, Darby G, Richman DD. HIV with reduced sensitivity to zidovudine (AZT) isolated during prolonged therapy. Science. 1989;243:1731–1734. doi: 10.1126/science.2467383. [DOI] [PubMed] [Google Scholar]
- 8.Coffin JM. HIV population dynamics in vivo: implications for genetic variation, pathogenesis, and therapy. Science. 1995;267:483–489. doi: 10.1126/science.7824947. [DOI] [PubMed] [Google Scholar]
- 9.Chou TC. Derivation and properties of Michaelis-Menten type and Hill type equations for reference ligands. J Theor Biol. 1976;59:253–276. doi: 10.1016/0022-5193(76)90169-7. [DOI] [PubMed] [Google Scholar]
- 10.Chou TC, Talalay P. Quantitative analysis of dose-effect relationships: the combined effects of multiple drugs or enzyme inhibitors. Adv Enzyme Regul. 1984;22:27–55. doi: 10.1016/0065-2571(84)90007-4. [DOI] [PubMed] [Google Scholar]
- 11.Hill AV. The possible effects of the aggregation of the molecules of haemoglobin on its dissociation curves. J Physiol. 1910;40:iv–vii. [Google Scholar]
- 12.Hoefnagel JG, Koopmans PP, Burger DM, Schuurman R, Galama JM. Role of the inhibitory quotient in HIV therapy. Antivir Ther. 2005;10:879–892. [PubMed] [Google Scholar]
- 13.Morse GD, Catanzaro LM, Acosta EP. Clinical pharmacodynamics of HIV-1 protease inhibitors: use of inhibitory quotients to optimise pharmacotherapy. Lancet Infect Dis. 2006;6:215–225. doi: 10.1016/S1473-3099(06)70436-4. [DOI] [PubMed] [Google Scholar]
- 14.Panel on Antiretroviral Guidelines for Adult and Adolescents. Guidelines for the use of antiretroviral agents in HIV-1-infected adults and adolescents. DHHS. 2008 Jan;:1–128. [Google Scholar]
- 15.Zhang H, et al. Novel single-cell-level phenotypic assay for residual drug susceptibility and reduced replication capacity of drug-resistant human immunodeficiency virus type 1. J Virol. 2004;78:1718–1729. doi: 10.1128/JVI.78.4.1718-1729.2004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.McMahon MA, et al. The HBV drug entecavir - effects on HIV-1 replication and resistance. N Engl J Med. 2007;356:2614–2621. doi: 10.1056/NEJMoa067710. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Ferguson NM, Fraser C, Anderson RM. Viral dynamics and anti-viral pharmacodynamics: rethinking in vitro measures of drug potency. Trends Pharmacol Sci. 2001;22:97–100. doi: 10.1016/s0165-6147(00)01615-1. [DOI] [PubMed] [Google Scholar]
- 18.Acosta EP, Gerber JG, Kuritzkes DR. In: Antiretroviral Pharmacokinetics, Resistance Testing and Therapeutic Drug Monitoring. Libman H, Makadon HJ, editors. American College of Physicians (ACP) Therapy Series: HIV; 2006. [Google Scholar]
- 19.Bartlett JG, Gallant JE. 2007 Medical Management of HIV Infection. Johns Hopkins Medicine Health Publishing Business Group; 2007. p. 510. [Google Scholar]
- 20.Madruga JV, et al. Efficacy and safety of darunavir-ritonavir compared with that of lopinavir-ritonavir at 48 weeks in treatment-experienced, HIV-infected patients in TITAN: a randomised controlled phase III trial. Lancet. 2007;370:49–58. doi: 10.1016/S0140-6736(07)61049-6. [DOI] [PubMed] [Google Scholar]
- 21.Clotet B, et al. Efficacy and safety of darunavir-ritonavir at week 48 in treatment-experienced patients with HIV-1 infection in POWER 1 and 2: a pooled subgroup analysis of data from two randomised trials. Lancet. 2007;369:1169–1178. doi: 10.1016/S0140-6736(07)60497-8. [DOI] [PubMed] [Google Scholar]
- 22.Ortiz R, et al. Efficacy and safety of once-daily darunavir/ritonavir versus lopinavir/ritonavir in treatment-naïve HIV-1-infected patients at week 48. AIDS. doi: 10.1097/QAD.0b013e32830285fb. (in press) [DOI] [PubMed] [Google Scholar]
- 23.Sedaghat AR, Dinoso JB, Shen L, Wilke CO, Siliciano RF. Decay dynamics of HIV-1 depend on the inhibited stages of the viral life cycle. Proc Natl Acad Sci U S A. 2008;105:4832–4837. doi: 10.1073/pnas.0711372105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Weiss JN. The Hill equation revisited: uses and misuses. FASEB J. 1997;11:835–841. [PubMed] [Google Scholar]
- 25.Hoffman A, Goldberg A. The relationship between receptor-effector unit heterogeneity and the shape of the concentration-effect profile: pharmacodynamic implications. J Pharmacokinet Biopharm. 1994;22:449–468. doi: 10.1007/BF02353789. [DOI] [PubMed] [Google Scholar]
- 26.Ambrose Z, Julias JG, Boyer PL, Kewalramani VN, Hughes SH. The level of reverse transcriptase (RT) in human immunodeficiency virus type 1 particles affects susceptibility to nonnucleoside RT inhibitors but not to lamivudine. J Virol. 2006;80:2578–2581. doi: 10.1128/JVI.80.5.2578-2581.2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Pommier Y, Johnson AA, Marchand C. Integrase inhibitors to treat HIV/AIDS. Nat Rev Drug Discov. 2005;4:236–248. doi: 10.1038/nrd1660. [DOI] [PubMed] [Google Scholar]
- 28.Pandey KK, et al. Inhibition of human immunodeficiency virus type 1 concerted integration by strand transfer inhibitors which recognize a transient structural intermediate. J Virol. 2007;81:12189–12199. doi: 10.1128/JVI.02863-06. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Talal AH, et al. Pharmacodynamics of PEG-IFN alpha differentiate HIV/HCV coinfected sustained virological responders from nonresponders. Hepatology. 2006;43:943–953. doi: 10.1002/hep.21136. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.