Summary
Membrane compartments of manifold shapes are found in cells, often sculpted by cellular proteins. In particular, proteins of the BAR domain superfamily participate in membrane sculpting processes in vivo and reshape also in vitro low-curvature membrane liposomes into high-curvature tubes and vesicles. Here we show by means of computer simulations totaling over 1 millisecond, how lattices involving parallel rows of amphiphysin N-BAR domains sculpt flat membranes into tubes. A highly detailed, dynamic picture of the 100-microsecond formation of membrane tubes by lattices of N-BAR domains is obtained. Lattice types inducing a wide range of membrane curvatures, with radii approximately 15 to 100 nm, are explored. The results suggest that multiple lattice types are viable for efficient membrane bending.
Introduction
Proteins from the BAR domain superfamily (Takei et al., 1999; Zimmerberg and McLaughlin, 2004; Ren et al., 2006), ubiquitous in many organisms and cell types, are implicated in cellular processes involving membrane remodeling, including endocytosis, apoptosis and cell-cell fusion (McMahon and Gallop, 2005; Zimmerberg and Kozlov, 2006; Ren et al., 2006). Structurally, BAR domains are α-helical bundles (Peter et al., 2004; Weissenhorn, 2005; Millard et al., 2005; Masuda et al., 2006; Gallop et al., 2006; Henne et al., 2007; Mattila et al., 2007; Shimada et al., 2007), capable of forming homodimers. The dimer surface is curved, with a high density of positively charged residues (Fig. 1A), which is suitable for binding to negatively charged membranes and for bending them (Peter et al., 2004; Weissenhorn, 2005; Millard et al., 2005; Masuda et al., 2006; Gallop et al., 2006; Henne et al., 2007; Mattila et al., 2007; Shimada et al., 2007; Frost et al., 2008; Arkhipov et al., 2008). In addition, the N-terminal amphipathic helices of BAR domains have been implicated in generating membrane curvature (Gallop and McMahon, 2005). In vitro, BAR domains sculpt membrane tubes and vesicles (Takei et al., 1999; Peter et al., 2004; Frost et al., 2008). Cryo-EM micrographs of BAR domain-induced tubes (Takei et al., 1999; Peter et al., 2004; Shimada et al., 2007; Frost et al., 2008) show striations on the tube surface, suggesting a regular arrangement of the proteins. Recent cryo-EM reconstructions (Frost et al., 2008) have revealed in astonishing detail for BAR domains called F-BARs how the proteins on the surface of a membrane tube are arranged in a lattice of spiraling rows, implying a concerted action of multiple BAR domains in membrane tubulation and vesiculation. However, despite these successes, the actual dynamics of membrane sculpting by BAR domains remains unresolved since it is difficult to capture short-lived intermediate structures. Many other questions also remain unanswered, such as what kinds of lattices can be formed by a specific BAR domain, how they are related to the degree of induced curvature, how they are formed and maintained, and how much disorder is viable.
Figure 1.

Effect of different N-BAR domain lattices on membrane curvatures. A, Comparison of all-atom and SBCG models for an N-BAR domain dimer and for a lipid membrane. The colors of beads in the SBCG protein model reflect the bead charge, on the scale from -2.4|e| (red) to +2.4|e| (blue), |e| being the elementary charge. Neutral heads are in cyan, and negative ones in pink. B, Membrane curvatures produced by various lattices of N-BAR domains. Variations in the number of N-BAR domain dimers are denoted as “6BARs”, “12BARs”, etc. Shown are distance S between rows, spiraling angle θ (between rows and the x-axis), and the contact between N-BAR domains within one row (“end-to-end”, “end-to-shoulder”, etc.). For each lattice, five independent simulations were performed; corresponding radii of membrane curvature are plotted versus time in five different colors. For each lattice, the top view of the initial configuration and the side view at t = 1.5 μs, taken from one of the five simulations, are depicted; RC is the current curvature radius for the simulation shown. The R-values are the curvature radii at t = 1.5 μs, averaged over five corresponding simulations, and shown with their respective standard deviations.
To elucidate some of the issues mentioned above, we have performed molecular dynamics (MD) simulations of multiple amphiphysin N-BAR domains (the name “N-BAR” refers to the fact that the structure we consider includes N-terminal helices), the best-studied member of the superfamily (Peter et al., 2004; Arkhipov et al., 2008), arranged into lattices on planar membranes (Fig. 1). Conventional all-atom MD simulations provide a highly resolved description of functioning molecular systems, but are currently limited to a system size of a few million atoms. In the case of N-BAR domains, one needs to simulate multi-million atom systems, due to the large size of individual proteins and the necessity to describe a whole lattice of proteins. Thus, we resort to a coarse-grained (CG) model (Smit et al., 1990; Shelley et al., 2001; Marrink et al., 2005; Shillcock and Lipowsky, 2005; Kasson et al., 2006; Harmandaris and Deserno, 2006; Shih et al., 2006; Bond et al., 2007; Shih et al., 2007b,a; Marrink et al., 2007; Reynwar et al., 2007; Marrink et al., 2008), namely, a shape-based CG model (SBCG) (Arkhipov et al., 2006b,a; Freddolino et al., 2008), that has recently been introduced for membrane bending by N-BAR domains (Arkhipov et al., 2008) (see details in EXPERIMENTAL PROCEDURES). We also perform an all-atom simulation of a system with multiple N-BAR domains consisting of 2.3 million atoms.
In the SBCG approach, a protein is represented by a number of CG beads (50 beads for an N-BAR domain dimer, or ∼150 atoms per CG bead; see Fig. 1A and EXPERIMENTAL PROCEDURES). The beads are connected by harmonic springs to maintain protein shape. Each leaflet of the membrane is represented by two layers of CG beads, one for the lipid heads and one for the tails, a head-tail bead pair representing 2.2 lipid molecules on average (see Fig. 1A and EXPERIMENTAL PROCEDURES). The membranes in both all-atom and CG cases are composed of neutral DOPC lipids with a randomized mixture of 30% negatively charged DOPS lipids (Fig. 1A). The SBCG model (Arkhipov et al., 2008) is solvent-free, the effect of the solvent being represented through effective interactions between CG beads (parameterized based on atomistic simulations and experimental data) and through viscosity of the medium. All-atom simulations employ an explicit representation of water molecules.
The SBCG approach permits one to reach systems sizes of 100 nm and time scales of 100 μs; at the same time, the approach resolves individual protein shapes, thus providing a relatively high-resolution description of simulated processes. Using the SBCG approach, we systematically investigate how lattice characteristics, i.e., density, orientation, and contacts between N-BAR domains, determine the induced membrane curvature. We find that several different lattices produce high curvature corresponding to radii of 15-20 nm. The lattices producing high curvature share similar properties with each other, in particular, an N-BAR domain density of around 10-20 dimers per 1000 nm2. An all-atom simulation successfully tested the SBCG simulations and sheds light on the atomic-level interactions involved in N-BAR domain lattices and membrane bending. The SBCG simulations reveal how N-BAR domain lattices bend flat membranes into complete tubes on the time scale of hundreds of microseconds. Thus, the simulations offer a molecular-level, dynamic picture of collective membrane bending by proteins, which covers several orders of magnitude of resolution in time and space.
Results and Discussion
The simulations performed are listed in Table 1.
Table 1.
Simulations performed. Nrun is the number of independent simulation runs. “Time” is the simulated time for a single simulation in the series. NBAR is the number of N-BAR domain dimers in the simulated system, and Nbead is the total number of particles. “BAR lattices” refers to the series of simulations where various N-BAR domain lattices were investigated on a membrane patch (∼1,000 nm2 in area), as shown in Fig. 1B. “8BARs-AA” refers to one of the N-BAR domain lattices simulated in the all-atom representation; “8BARs-CG” is the corresponding SBCG simulation. Simulations “membrane-tube” and “membrane-half-tube” were started from the point where N-BAR domains were removed from the system in 43BARs-3, half-way during the simulation 43BARs-3 for “membrane-half-tube”, and after tubulation was completed for “membrane-tube” (Fig. S1). Membrane-1, 2, and 3 are control simulations of a flat membrane without BAR domains (see Supplementary Materials, Fig. S2).
| Name | Method | Nrun | NBAR | Nparticle | Membrane dimensions | Time (μs) |
|---|---|---|---|---|---|---|
| BAR-lattices | SBCG | 5×24 | 6-35 | 3,258-4,696 | 64×16 nm2 | 1.5-5 |
| 8BARs-AA | All-atom | 1 | 8 | 2,304,973 | 64×8 nm2 | 0.2 |
| 8BARs-CG | SBCG | 5 | 8 | 1,883 | 64×8 nm2 | 5 |
| 43BARs-1 | SBCG | 1 | 43 | 11,024 | 190×16 nm2 | 40 |
| 43BARs-2 | SBCG | 1 | 43 | 11,024 | 190×16 nm2 | 40 |
| 43BARs-3 | SBCG | 1 | 43 | 11,024 | 190×16 nm2 | 43 |
| 43BARs-4 | SBCG | 1 | 43 | 11,024 | 190×16 nm2 | 59 |
| 24BARs-1 | SBCG | 1 | 24 | 10,881 | 200×16 nm2 | 55 |
| 24BARs-2 | SBCG | 1 | 24 | 10,881 | 200×16 nm2 | 102 |
| 24BARs-3 | SBCG | 1 | 24 | 10,881 | 200×16 nm2 | 200 |
| 24BARs-4 | SBCG | 1 | 24 | 10,881 | 200×16 nm2 | 200 |
| Membrane-tube | SBCG | 1 | 0 | 8,913 | 190×16 nm2 | 10 |
| Membrane-half-tube | SBCG | 1 | 0 | 8,913 | 190×16 nm2 | 10 |
| Membrane-1, 2, 3 | SBCG | 3 | 0 | 9,704 | 200×16 nm2 | 60 |
In order to understand the connection between N-BAR domain lattice types and membrane curvature, we carry out a series of simulations for several lattices. Since many simulations are needed, we consider relatively small patches of membrane (64×16 nm2 ≈1000 nm2), with parallel rows of N-BAR domains (simulations BAR-lattices in Table 1, see Fig. 1B), mimicking parallel rows of BAR domains that appear on the surface of membrane tubes formed in vitro and observed with cryo-EM (Takei et al., 1999; Peter et al., 2004). Simulations of the described scale can be mastered presently only through the SBCG approach. However, in one case, we have carried out also a 200 ns all-atom simulation to test the SBCG model (simulation 8BARs-AA). To ensure computational feasibility, a smaller system is chosen for this purpose, namely, 8 N-BAR domains on top of a 64×8 nm2 patch, an analogous SBCG simulation being carried out as well (8BARs-CG).
The SBCG simulations above are extended to larger systems that permit complete membrane tubulation, namely, ones involving 24 and 43 amphiphysin N-BAR dimers (systems referred to as “24BARs” and “43BARs”) placed on top of a ∼200×16 nm2 patch. Four simulations are performed for each of the two systems, denoted 43BARs-i and 24BARs-i, with i = 1, 2, 3, 4 being the number of the simulation.
Additional simulations of the 200×16 nm2 membrane patch without N-BAR domains were performed as a control (simulations “Membrane-tube”, “Membrane-half-tube”, and “Membrane-1”, 2, and 3 in Table 1; see Supplementary Materials). These simulations show that if N-BAR domains are removed from the membrane after a complete tube is formed, the tube remains stable (Fig. S1). For the case when a compete tube has not formed yet, i.e., when the membrane is bent, but its edges have not yet fused, the membrane relaxes to a less curved conformation if N-BAR domains are removed (Fig. S1). An initially flat membrane without N-BAR domains remains flat, except for relatively small random fluctuations (Fig. S2).
Effect of different N-BAR domain lattices on membrane curvatures
The simulations “BAR-lattices” listed in Table 1 sample N-BAR densities from 6 to 35 dimers per 1,000 nm2, distances S between rows from 1.9 to 8 nm, spiraling angles θ from 0 to 25°, and connections between N-BAR domains within one row from “no contact” to “center-to-center” contact (see Fig. 1B; additional lattices are shown in Supplementary Materials, where the calculation of S and θ is also described). The values of S and θ in Fig. 1 are given for the initial state, as characteristics of the pre-assembled lattices. During simulations, these parameters deviate slightly from the initial values due to membrane bending and N-BAR domain displacement, deviations being within 5° for θ and 0.5 nm (rarely up to 1 nm) for S.
The highest membrane curvatures observed in all simulations correspond to radii of R=13-20 nm, while the curvature radius of the protein itself is 11 nm. Such strongly bent membranes are produced by lattices with approximately 10-20 dimers per 1,000 nm2, S=3-6 nm, and (9=0-5° (although one lattice with (θ=20° produced high curvature as well, see left panel in the middle row in Fig. 1B). These observations are in qualitative agreement with cryo-EM imaging of membrane tubes sculpted by amphiphysin N-BAR domains (Takei et al., 1999; Peter et al., 2004), showing striations with S ∼ 5 – 10 nm. High-resolution cryo-EM reconstructions for F-BAR domains (Frost et al., 2008), which are larger and feature shallower intrinsic curvature, demonstrate S ∼ 6 – 8 nm and θ ∼ 10 – 15°.
Fig. 2 illustrates simulations of one N-BAR lattice in both SBCG and all-atom representations (simulations 8BARs-AA and 8BARs-CG; see also Supplementary Movies 1 and 2). The N-BAR lattice in these simulations is the closest to the 16 BARs lattice probed in SBCG simulations of the 64×16 nm2 membrane patch (Fig. 1B). Similar to SBCG simulations (Fig. 2A), the all-atom simulation shows that the assumed N-BAR lattice remains stable and induces global membrane curvature (Fig. 2B). The global curvature continues to develop throughout the 200 ns simulation. The membrane beneath seven out of eight N-BAR domains establishes a close contact with the concave surface of the N-BAR domains. The eighth N-BAR domain does not establsih yet a close contact to the membrane surface. Differences in membrane contacts between different N-BAR domains within the lattice are also seen in the SBCG simulations. Membrane bending in the all-atom simulation develops slower than that in SBCG simulations: at 200 ns, the radius of curvature is R = 65 nm, while for the SBCG simulation of the same lattice this value of R is reached within 50 ns, and at 200 ns one finds in the SBCG case R = 25±3 nm (averaged over all five simulations 8BARs-CG). A likely reason for the speed discrepancy is that the all-atom representation contains many more degrees of freedom than the SBCG model, which results in stronger friction that is manifested through slower bending. Another reason is that at the beginning of the all-atom simulation more time than in the SBCG simulation is required for the N-BAR domains to form proper contacts with the membrane and with each other. Despite the difference in bending speed, the N-BAR domain lattices generate global membrane curvature in a similar fashion.
Figure 2.
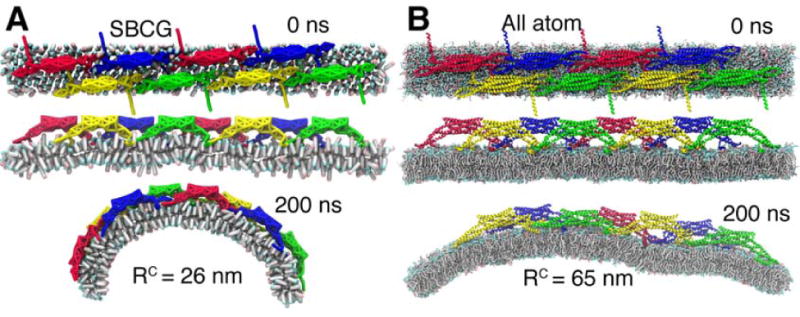
All-atom and SBCG simulations of an N-BAR domain lattice. A, B, Snapshots of the simulations in SBCG and all-atom representations, respectively.
Complete membrane tubulation by lattices of N-BAR domains
In simulations 43BARs-i and 24BARs-i, i = 1,2, 3, 4 (see Table 1), we consider a relatively broad (200 nm) membrane patch. These simulations are aimed at obtaining complete tubulation from an initially flat membrane, as shown in Fig. 3. All simulations i = 1, 2, 3, 4 are independent, start from the same initial structure, but use different initial velocities, which are randomly generated for each simulation according to a Maxwell distribution at T = 310K. Another source of difference between trajectories i = 1, 2, 3, 4 are random forces acting on each CG bead at each time step, the forces being introduced through the Langevin thermostat (as reported in Arkhipov et al. (2008); Phillips et al. (2005)) to maintain constant temperature.
Figure 3.
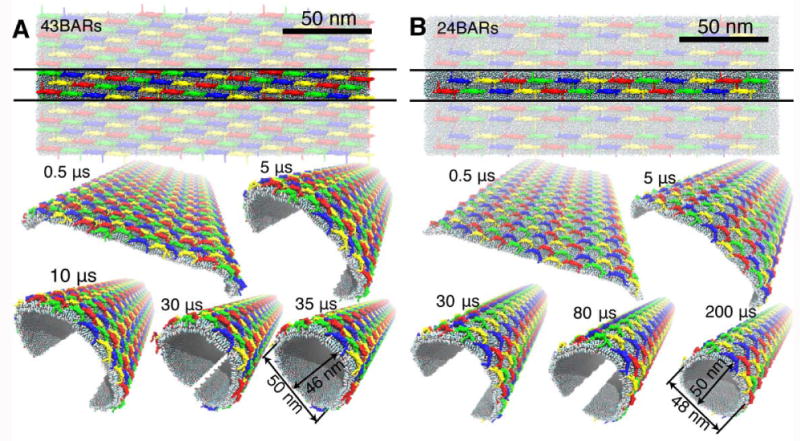
Membrane tubulation by lattices of N-BAR domains. A, B, Tubulations of planar membranes by lattices containing 43 and 24 N-BAR domain dimers per unit cell, respectively. N-BAR domain dimers are colored in blue, yellow, green, and red. For each of the two simulations, the top view of the initial arrangement is provided; one unit cell is highlighted. Snapshots during the simulated tubulation processes are shown, with several periodic images included to demonstrate formation of a tube.
As shown in Fig. 3A, B (see also Supplementary Movies), membrane bending is initiated at the edges of the membrane within a few hundred nanoseconds. The bending propagates then towards the center, rounding the entire membrane on a time scale of 30-200 μs. Eventually, the membrane is driven into a near-tubular state, in which the edges can come into contact and fuse, producing a complete, stable tube. Fig. 3A, B shows snapshots from two simulations in which tubulation is completed within 35 and 200 μs (simulations 43BARs-3 and 24BARs-3, see Fig. 4).
Figure 4.
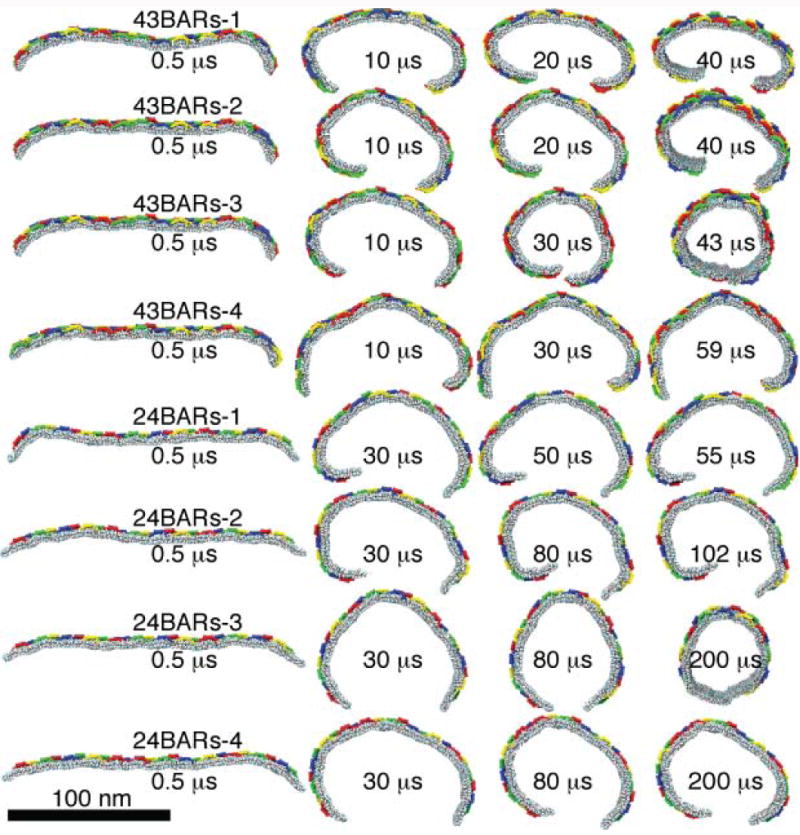
Stochastic differences in tubulation dynamics. Initial conformations are identical for simulations 43BARs (top four rows), and for simulations 24BARs (bottom four rows).
The radii of the tubes formed by either 43 or 24 N-BAR domains are approximately the same, i.e., ∼25 nm. These radii are mainly determined by the original length of the membrane, which was chosen to allow for a formation of a tube with a size that is typically observed in experiments for amphiphysin N-BAR domains in vitro (15-25 nm, Peter et al. (2004)). However, experimentally, tubes with a wide range of radii form, from 15 up to 80 nm, as observed in cryo-EM images obtained by Takei et al. (1999) and Peter et al. (2004). Our simulations with various lattice types (simulations BAR-lattices in Table 1) show that indeed many different radii are viable, depending on the lattice (Fig. 1B). The lattice corresponding to 24BARs (c.f. Fig. 1B, first panel from the left in the top row) is found to bend the membrane to the curvature radius of R = 34±5 nm, while that corresponding to 43BARs (c.f. Fig. 1B, second panel from the left in the top row) results in R = 17 ± 4 nm, i.e., R = 25 nm is in the middle of the range of radii produced by these two lattices. The lattice in 43BARs simulations favors a smaller radius. Due to the stronger bending, the 43BARs lattice (Fig. 3A) completes the tubulation ∼6 times faster than the 24BARs lattice (Fig. 3B).
One also finds significant differences between the individual trajectories among the 43BARs or 24BARs series. Trajectories of simulations starting from the same conformation are shown in Fig. 4. Two of the simulations, 43BARs-3 and 24BARs-3, resulted in the formation of a complete tube. The time when the membrane edges touched each other in these simulations was 32.6 μs and 180 μs, respectively. For others, before the membrane edges approached each other, the system was caught in a metastable state that it could not escape from over the available simulation time. For yet others (such as 24BARs-1 and 2), one of the edges bent significantly stronger than the other edge, resulting in a spiral-like structure. These differences are due to stochastic factors (random initial velocities and fluctuations due to Langevin thermostat), and demonstrate that even with a dense lattice of N-BAR domains, the membrane remains a highly disordered and randomly fluctuating material. Nevertheless, in all simulations the membrane was bent to a tubular or near-tubular state, manifesting the membrane bending fidelity achieved when N-BAR domains are arranged in an appropriate lattice. Formation of a stable tube by itself is a matter of chance and long enough sampling time. In experiments, BAR domain lattices actually pull tubes from low-curvature liposomes (Peter et al., 2004; Frost et al., 2008), where the problem of bringing the two membrane edges together does not exist. However, the question of how much curvature a given lattice of BAR domains can induce applies to such experiments and to our simulations. Therefore, the extent to which the lattices of BAR domains bend membranes and the bending fidelity versus trajectory disorder are results from our 43BARs and 24BARs simulations that should hold in actual scenarios of in vitro membrane tubulation.
N-BAR domain density and the induced membrane curvature
Our observations show that the most efficient membrane bending is achieved by the N-BAR domain lattices with a density of about 10-20 dimers per 1,000 nm2, i.e., an intermediate density among those sampled in all our simulations. It is intuitively clear that lattices with low densities of N-BAR domains produce low curvature, since the bending force is not high enough, and this is indeed what we find in our simulations (see Fig. 1B). But we observe that for densities higher than approximately 20 dimers per 1,000 nm2, the induced membrane curvature becomes low too, which is puzzling. Analysis of the interactions between the concave surface of N-BAR domains and the membrane (see Supplementary Results, Fig. S5) shows that for dense lattices, these interactions are occluded by the N-terminal helices and tips from neighboring N-BAR domains. As a result, scaffolding of the membrane by the N-BAR domain cannot proceed, and the membrane bending is inefficient.
To characterize membrane sculpting further, we estimate the elastic bending energy of the membrane Ebend per one N-BAR domain dimer for each simulated lattice using the Helfrich elastic membrane theory (Helfrich, 1973) (see Supplementary Results and Fig. S6). For all lattices that produce significant curvature (R < 30 nm), values of Ebend are 1-3 kBT, while for lattices with shallow curvature holds Ebend < 0.5 kBT. From the previously reported all-atom and CG simulations of single N-BAR domains (Blood and Voth, 2006; Blood et al., 2008; Arkhipov et al., 2008), we estimate (see Supplementary Results) that a single N-BAR domain can impose a bending energy imprint of 0.6 to 15 kBT, which constitutes a rather broad range of possible values. The actual value in each case depends on how well the contact between the protein and the membrane is established. Thus, the strong membrane bending that we observe in the SBCG simulations for the case of “optimal” lattices requires only a moderate bending energy input from each N-BAR domain, namely Ebend = 1−3 kBT, and does not necessarily involve an “optimal” interaction between the membrane and every single protein of the lattice.
Raising N-BAR domain concentration in experiments leads to the formation of vesicles rather than tubes. Vesiculation is not observed in the simulations for several reasons. First, vesiculation requires membrane breaking not only in the x (as done here), but also in the y-direction (see Fig. 1B), while in our simulations the initial systems consist of a long and narrow (16 nm) membrane patch, replicated periodically along the narrow y-dimension and permitting only tube formation. Second, both vesiculation and tubulation experimentally occur on time scales of minutes to hours, rather than 100 μs. In simulations, N-BAR domains were initially aligned primarily with the membrane's long dimension, pre-arranged in a lattice on the membrane surface. As a result, the modeled system is prepared for forming a segment of a cylinder, permitting full or partial tubulation easily. Thus, the initial state favors fast tubulation (100 μs), while vesiculation would require a rearrangement of the N-BAR domain lattice, making the time scales necessary for observation of the vesiculation much longer (at least minutes to hours, as in experiments). Third, even experimentally, once a BAR domain lattice forms, a significant lattice rearrangement may not happen. Indeed, high-resolution cryo-EM images of tubes formed by F-BARs (Frost et al., 2008) show that tubes of different radii are sculpted by different F-BAR lattices. The fact that experimentally tubes and vesicles with different radii remain stable once they have formed (for F-BAR as well as other BAR domains) suggests that lattices do not rearrange, due to strong interactions between BAR domains within the lattices. Therefore, for pre-formed lattices that favor tubulation, as in our simulations, it is very unlikely that BAR domains would rearrange into a different formation and sculpt the membrane into vesicles, even on experimental time scales.
In in vitro experiments, sculpting of membrane tubes or vesicles proceeds simultaneously with the formation of BAR domain lattices (see Fig. 2A in Frost et al. (2008)), since initially BAR domains are distributed relatively uniformly in bulk solution, rather than being arranged in a lattice on the membrane surface, as in simulations. However, simulating a realistic scenario where BAR domains are distributed in solution and allowed to form lattices spontaneously would require covering minutes to hours in simulations, about seven orders of magnitude beyond the longest simulations one is able to perform. Due to the time and size limitations, to gain the detailed dynamic view of membrane sculpting one has to employ pre-arranged lattices and periodic boundary conditions, which permits presently one to study tubulation, but not vesiculation.
The mechanism of membrane sculpting
The analysis of the dependence of membrane sculpting on the density of N-BAR domains (see above and Supplementary Results, Figs. S5 and S6) shows that the sculpting is mediated by electrostatic interactions between the positively charged concave surface of N-BARs with the negatively charged membrane, and that membrane bending is inefficient when these interactions are occluded. Thus, the membrane sculpting in our simulations arises due to scaffolding of the membrane by the concave surface of N-BAR domains (see also Fig. S3). This conclusion is confirmed by observing the membrane curvature formation in simulations illustrated in Fig. 1B: for low- or intermediate-density lattices, the membrane matches the concave surface of the proteins well, while for the dense lattices, one finds many gaps between membrane and the protein's concave surface. Interestingly, poor scaffolding is observed also for those lattices with intermediate densities that do not bend membranes efficiently, such as those with center-to-center contacts (Fig. 1B). For such lattices, one finds shallower membrane curvature and lower values of energy of interaction between the membrane and concave surface of N-BAR domain (Fig. S5A) than for their counterparts with end-to-shoulder or end-to-end contacts, which bend membranes better.
Besides scaffolding, another mechanism for membrane sculpting by N-BAR domains has been proposed (Gallop and McMahon, 2005), in which N-terminal helices inserted into the membrane lead to a mismatch between the areas of the two membrane leaflets, inducing the curvature (Zimmerberg and Kozlov, 2006). The scaffolding mechanism has been observed in a simulation (Blood and Voth, 2006; Arkhipov et al., 2008) for amphiphysin N-BARs, and experimentally for F-BARs (Frost et al., 2008). Recent MD simulations (Blood et al., 2008) have shown that the embedded N-terminal helices alone can induce membrane curvature, but a very high concentration of helices is required, namely, twice as high as that in our simulations where significant membrane curvature was induced, such as in the case of simulations 12BARs or 16BARs shown in Fig. 1B. In all our simulations where significant bending developed, including the all-atom one, the concentration of N-terminal helices is not high enough to induce bending through the N-helices alone (Zimmerberg and Kozlov, 2006; Blood et al., 2008), and N-BAR domains clearly behave according to the scaffolding mechanism. On the other hand, some of our simulated lattices are very dense so that the number of N-terminal helices could be high enough to generate curvature, but the actual membrane curvature remains very low due to the interdigitation of the N-terminal helices and N-BAR tips, which prevents proper scaffolding.
However, it still remains unclear whether the scaffolding or the N-helix-mediated mechanism promotes membrane sculpting and curvature sensing in reality, especially under cellular conditions (Campelo et al., 2008). In recent experimental-computational work by Löw et al. (2008), the N-terminal helix was found to be flexible and partially disordered. Similarly, the N-helix, modeled as four CG beads on a string, is quite flexible in our CG simulations (see Fig. S5); partial refolding of the helix was observed in all-atom simulations of one N-BAR domain on a membrane (Arkhipov et al., 2008). In the all-atom simulation 8BARs-AA, 11 out of 16 N-helices underwent at least partial refolding during the simulation, although mostly they remained helical and embedded into the membrane. For three of the N-helices we observed a relatively strong local unfolding of the helical motif that was correlated with their transient detachment from the membrane. These experimental and computational observations highlight the dynamic nature of the N-helix. However, the dynamic structure of the N-helix seems to intervene neither with the N-helix embedding into the membrane nor with its anchoring and membrane bending function. While further studies are necessary to clarify the relative contributions of the N-BAR concave surface and of the N-helix to membrane remodeling, it appears that both areas of the protein play important roles, and, perhaps, both mechanisms take place simultaneously.
Contacts between N-BAR domain dimers within lattices
Our simulations show that the arrangement of dimers within one row is decisive for the induced curvature. End-to-end contacts within the rows of the protein lattice were suggested initially (Shimada et al., 2007) for F-BAR domains based on crystal packing, but recently it was found (Frost et al., 2008) that end-to-center contacts form instead. Due to the high intrinsic curvature of amphiphysin BAR domains, end-to-center contacts cannot be formed unless the dimers are tilted with respect to each other and the membrane is already strongly bent. Since our simulations all started from a planar membrane, it was impossible to prepare a system with amphiphysin N-BAR domains arranged end-to-center. However, a lattice similar to one with the end-to-center contacts can be formed on a flat membrane if one uses center-to-center contacts instead (Figs. 1B and 5A; compare Fig. 5A with Fig. 4 in Frost et al. (2008)), but such arrangement was found to produce relatively low curvature, with radii R = 30 to 100 nm (see Fig. 1B and Supplementary Material). The highest curvature, R = 15 – 20 nm, was observed when amphiphysin N-BAR domains are arranged “end-to-end” or “end-to-shoulder” (if the density is also in the appropriate range, 10-20 dimers per 1,000 nm2; see Fig. 1B), the “shoulder” being the place where the main body of the dimer connects to the N-terminal helix (Fig. 5A), which was modeled as sticking out perpendicular to the main body of the dimer (Gallop et al., 2006; Arkhipov et al., 2008).
Figure 5.
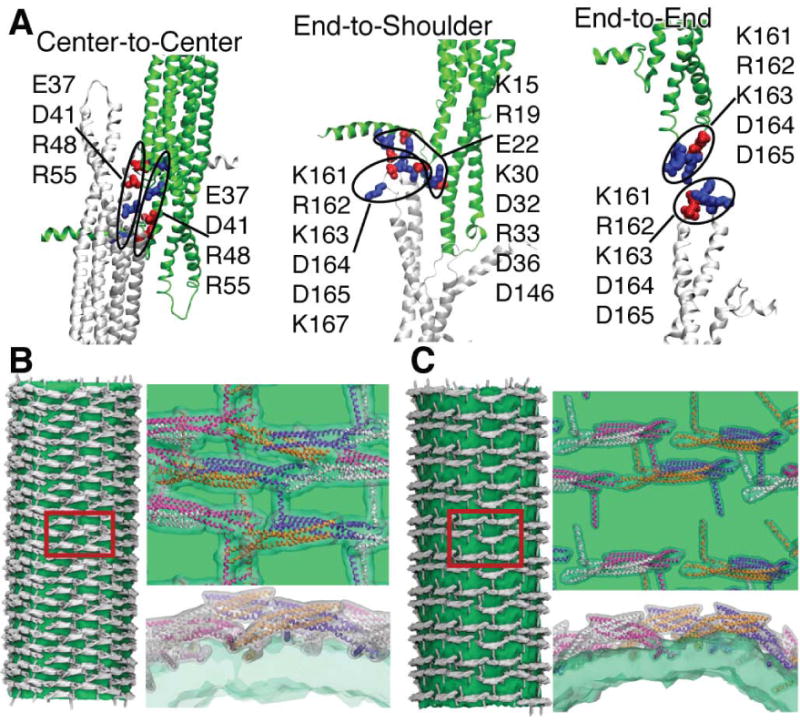
Contacts between N-BAR domains. A, Connections between N-BAR domain dimers within various lattices probed in our simulations (see Fig. 1B). One dimer is shown in white, and the neighboring one in green. Amino acids that are involved in the formation of connections are highlighted in blue (positive charge) and red (negative charge). The left and right panels are schematics of connections “center-to-center” and “end-to-end” (Fig. 1B). The middle panel is the “end-to-shoulder” contact probed in the all-atom simulation 8BARs-AA, CG simulation 8BARs-CG, and several other CG simulations (Fig. 1B). B, C, Reconstructions of tubes formed by the lattices of N-BAR domains (see Fig. 3) for 43BARs (B) and 24BARs (C). Several periodic images are combined to show each tube. The density for lipids is shown in green; all-atom structures of N-BAR domains are fitted to the conformations of each CG N-BAR domain, and the respective density is shown in white. Parts of the tube surfaces (red rectangles) are enlarged and shown on the right, viewed from the top and from the side. All-atom structures of BAR domain monomers are drawn in white, magenta, orange, and violet.
All contacts in the SBCG simulations are stabilized by electrostatic interactions between CG beads, which at the atomic level correspond to interactions between charged residues. In the all-atom simulation, “8BAR-AA”, which has the “end-to-shoulder” arrangement, the contact area can be discerned at atomic detail (middle panel in Fig. 5A). The “end-to-shoulder” arrangement appears particularly favorable due to a high concentration of charged residues at the contact point, e.g. Lys161, Arg162, Lys163, Asp164, Asp165, Lys167 at the tip of the N-BAR domain and Lys15, Arg19, Glu22, Lys30, Asp32, Arg33, Asp36, and Asp146 at the “shoulder” (Fig. 5A), most of which are highly conserved (Peter et al., 2004). In experiments (Peter et al., 2004), mutations of Lys161 and Lys163 into glutamates were found to inhibit tubulation, although the mutations interfered also with the protein binding to the charged membrane.
Crystal packing of amphiphysin BAR domains (Peter et al., 2004) involves extensive contacts, primarily between residues 87 to 116 of a given monomer and residues 161 to 185 of its neighbor, i.e., spanning from the BAR domain center to its tip. Neighboring BAR domains in the crystal are tilted with respect to each other, so that if one monomer is viewed from the top, as in Fig. 1B, the neighboring monomer is seen lying on its side (rotated by ∼90° around its long axis with respect to the first monomer). The crystal contacts seen in Peter et al. (2004) do not arise in lattices for which high membrane curvature develops in simulations. Only the center-to-center contacts in Fig. 1B are remotely similar to those seen in crystal packing, but such lattices do not bend membranes efficiently. Thus, the crystal packing appears to feature an arrangement of N-BARs that does not lead to membrane tubulation, similarly to the previously mentioned case of F-BARs, for which end-to-end contacts are found in crystals (Shimada et al., 2007), but end-to-center contacts are observed in lattices leading to tubulation (Frost et al., 2008).
In Fig. 5 we align all-atom structures of N-BAR domains with the CG BAR domains on the surface of a fully formed tube for “43BARs” (Fig. 5B) and for “24BARs” (Fig. 5C). N-BAR domains mostly maintain their initial contacts within the lattices, which are end-to-end for 24BARs and end-to-shoulder for 43BARs, although one also finds significant local rearrangements. A key feature of the observed lattices (Fig. 5B, C) is their irregularity (although the initial lattice is regular, c.f. Fig. 3A, B). The only available experimental high-resolution images of F-BAR domain-induced tubes (Frost et al., 2008), visualizing highly ordered lattices, were obtained using repeated annealing. Without the annealing, tubes form, but the arrangement of BAR domains is too irregular to permit high-resolution cryo-EM reconstruction (Frost et al., 2008). The N-BAR domain lattice in our simulations features some order, but locally is irregular; no two dimers have exactly the same orientation (except for the repetition due to periodic conditions). Most likely, naturally occurring, i.e., not annealed, BAR domain lattices resemble the simulated ones. We found that tips of the dimers and their N-terminal helices, which are involved in the formation of inter-dimer contacts in the end-to-end and end-to-shoulder lattices, are quite flexible (see Supplementary Material) and maintain a well-connected lattice even if proteins shift significantly. Clearly, these properties allow BAR domain lattices to function efficiently even under conditions of thermal noise and disorder, which are characteristic for living cells. Lattice disorder and nature of contacts can be potentially probed in experiments using FRET (see, e.g., Roy et al. (2008)) and cryo-EM reconstructions (Frost et al., 2008).
Conclusion
We performed multiple simulations, reaching 200 μs, providing a detailed picture of bending planar membranes into tubes by N-BAR domain lattices. Formation of stable tubes with radii similar to those found experimentally was observed. Membrane bending by many different lattices was studied, and a range of curvatures was seen to form, depending on lattice type. An all-atom simulation for one of the N-BAR lattices has been performed and was found to agree with the SBCG simulations, although the comparison suggests that the SBCG results overestimate the speed of membrane bending. General trends of membrane bending and of interactions of N-BAR domain with the membrane and with each other were the same in all-atom and CG simulations.
We find that N-BAR lattices resulting in the highest curvature (with the radii starting at R = 13 nm, which is close to the intrinsic curvature of the amphiphysin N-BAR domain dimer) feature densities of 10-20 dimers per 1000 nm2, a distance between lattice rows of S=3-6 nm, tilting angles of θ=0-5°, and end-to-shoulder or end-to-end contacts between dimers. Thus, membrane tubulation by amphiphysin N-BAR domains is significantly different from that by F-BAR domains (Shimada et al., 2007; Frost et al., 2008), which are larger, induce shallower curvature, and prefer end-to-center contacts (Frost et al., 2008). Since experimentally amphiphysin N-BAR domains produce tubes with a wide range of curvatures, and since all arrangements sampled in our simulations (including “center-to-center”, but excluding “no contact”) result in strong membrane bending when the protein density is appropriate, it is likely that N-BAR domains engage in a number of different connection types to induce tubulation, taking advantage of charged residues scattered on their surface.
It has been suggested that the mechanism of curvature-mediated interactions (Reynwar et al., 2007) plays a role in membrane bending. However, such mechanism can not be discerned in our study because BAR domains are pre-arranged into regular lattices in which they interact with each other strongly, the timescales of self-assembly of BAR domains into lattices being too long for simulations on currently available computers. In the cases where significant global membrane bending is observed in our simulations, N-BAR domains interact directly through a large number of electrostatic charge-charge “bridges”. In experiments with F-BARs (Frost et al., 2008), the membrane-mediated attraction was not obviously present either.
Our results are most relevant for a comparison with tubulation experiments in vitro, for which protein rows on membrane tubes are clearly observed through cryo-EM (Takei et al., 1999; Peter et al., 2004). It remains less clear how amphiphysin N-BAR domains act in cells, where concentration of the protein may be too low for dimers to form and where a dense lattice may not arise. Under cellular conditions, the N-terminal helices may be more important in bending membranes (Campelo et al., 2008) than the protein's concave surface.
N-BAR domain densities that lead to the highest curvature in our simulations (e.g., such as in the 16 N-BAR domains lattice) may in reality produce membrane vesicles rather than tubes. Such vesiculation is a possible reason why tubes with striations corresponding to S < 5 nm have not been, to our knowledge, observed experimentally. Also, the resolution of existing cryo-EM images of tubes produced by amphiphysin BAR domains is too low to make conclusive statements about the values of S or θ. Drawing from the existing images (Takei et al., 1999; Peter et al., 2004), one can conclude nevertheless that lattices such as “12BARs” in Fig. 1B, featuring S=5-6 nm and θ=0-5°, are representative of the arrangement that sculpts high-curvature tubes.
Experimental Procedures
At atomic resolution, a study of complete membrane tubulation by an N-BAR domain lattice involves simulations of 60 million atoms over 100 μs and beyond, either currently impossible. Therefore, we resort to coarse-grained simulations, employing an SBCG approach (Arkhipov et al., 2006b,a,2008; Freddolino et al., 2008) (see Fig. 6), which was developed to simulate proteins and their assemblies (Arkhipov et al., 2006b,a). The SBCG tools are available as a VMD (Humphrey et al., 1996) plugin, i.e., they are available for all researchers along with our simulation program NAMD (Phillips et al., 2005).
Figure 6.
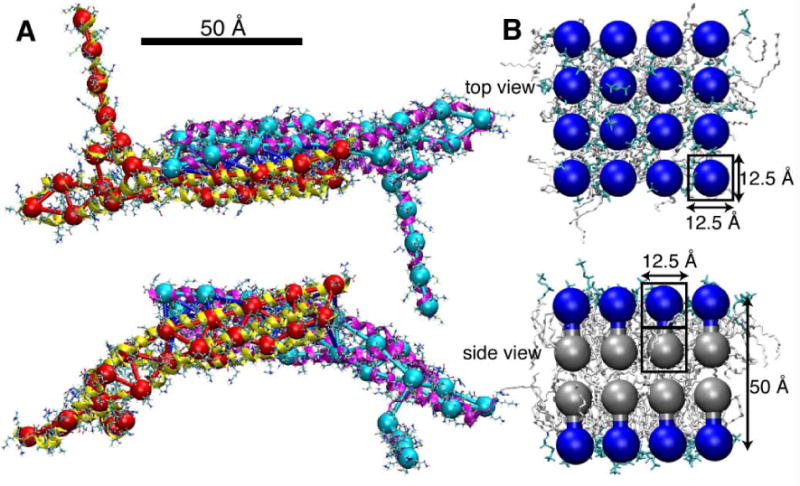
SBCG models of N-BAR domains and lipids. A, N-BAR domain viewed from top and side, the SBCG model (shown in red and cyan) overlapping with the all-atom structure (in both line and cartoon representations). The N-BAR domain dimer is represented by 50 SBCG beads, with ∼150 atoms per CG bead. In the SBCG model, the two monomers are connected by bonds (blue) to preserve the integrity of the dimer. B, A patch of neutral lipid bilayer is shown from the top and from the side, in SBCG as well as in all-atom representations. The “head” and “tail” halves of the all-atom lipids are shown in cyan and white, respectively. Each SBCG “molecule” represents ∼2.2 lipids; the “head” SBCG beads are shown in blue, and the “tail” beads in gray.
For studying membrane bending by BAR domains, the SBCG model has been described and tested extensively (Arkhipov et al., 2008). We have shown that the results of SBCG simulations of N-BAR domain-membrane systems agree well with data available from experiments and from all-atom simulations (Blood and Voth, 2006; Arkhipov et al., 2008). An all-atom simulation of a lattice of 8 N-BAR domains reported here agrees with the results from SBCG simulations. In Arkhipov et al. (2008) we also showed that the SBCG model of a membrane without BAR domains reproduces major properties of a biological membrane, such as its thickness, bending rigidity, and area per lipid. For example, the bending rigidity, kc, has been estimated from SBCG simulations to be kc ≈ (20±10) kBT, whereas experimentally for a biological membrane one finds kc = 10 − 20 kBT. Lipid self-assembly properties have been qualitatively reproduced as well, in that correct phases, such as micellar, lamellar, and inverted hexagonal, form in SBCG simulations starting from random mixtures of lipids, demonstrating that our model captures lipid hydrophobic interactions well. Below, we summarize the main features of the all-atom simulation and of the SBCG model. More details are provided in Supplementary Material
All-atom simulation
The system considered in the all-atom simulation, 8BARs-AA, consists of 8 N-BAR domains arranged in a lattice on a patch of DOPC/DOPS membrane (Fig. 2). This simulation setup has the dimensions of 80×8×36 nm3, and includes 2,304,973 atoms. The system was pre-equilibrated as described in Supplementary Methods, and then simulated for 200 ns. The simulation was performed with NAMD (Phillips et al., 2005) using the CHARMM force field (MacKerell et al., 1998; Feller, 2000).
SBCG protein model
In the framework of the SBCG model (Arkhipov et al., 2006b,a), a protein is represented by a number of CG beads, with the number of beads specified by the user. Positions of CG beads are assigned by a topology conserving algorithm (Ritter et al., 1992) according to the protein's structure. This is done such that the bead distribution reproduces the shape of the protein in a topologically correct way (see Fig. 6A). The beads are connected by harmonic bonds to maintain the protein shape, i.e., in the SBCG model proteins cannot refold or change shape significantly. Each SBCG bead describes a “domain” of atoms in the molecule (the bead's Voronoi cell). The mass of all atoms in the domain and their total charge are assigned to the bead. In the present study, we used 50 beads for each N-BAR domain dimer, which corresponds to ∼150 atoms per bead.
The SBCG model of the N-BAR domain was built (Arkhipov et al., 2008) starting from the atomic coordinates of Drosophila melanogaster amphiphysin BAR domain (PDB code 1URU (Peter et al., 2004)). 35 residues missing at the N-terminus were modeled as a short helix and a flexible link (Arkhipov et al., 2008). The N-BAR domain is a homodimer; CG beads were connected by harmonic bonds within one monomer or between the two monomers if the distance between the beads was below 18 Å.
The motion of CG beads is described by classical mechanics, assuming, however, Langevin equations of motion (described earlier in Arkhipov et al. (2008)). Interactions between beads are described by a CHARMM-like force-field (MacKerell et al., 1998), i.e., bonded interactions are represented by harmonic bond and angle potentials (but no dihedral potentials), and the non-bonded potentials include 6-12 Lennard-Jones (LJ) and Coulomb terms. The choice of parameters for bonded and LJ interactions has been described earlier (Arkhipov et al., 2008) (see Supplementary Material); the parameters are tuned to match the flexibility of the protein as observed in respective all-atom simulations, and to reproduce the hydrophobic/hydrophilic properties of the residues on the protein surface. The solvent is modeled implicitly, through Langevin terms (fluctuating and frictional forces) that represent water viscosity. Based on experimental diffusion constant values, we chose the Langevin equation damping constant to be γ = 2 ps−1 for all beads (Arkhipov et al. (2008)).
Coulomb interactions are modeled using a dielectric constant ε = 1. This choice is based on prior SBCG simulations of a single N-BAR domain interacting with a membrane patch, described in Arkhipov et al. (2008). Simulations performed with ε = 1, 2, 5, 10, 20, 40 showed that ε = 1 furnished the best agreement with all-atom simulations, in terms of membrane curvature and bending speed. The low ε value results because membrane bending is due to short-range electrostatic interactions between the charged N-BAR domain surface and charged lipid heads that are not screened. Furthermore, one should note that the diameter of SBCG beads is ∼ 15 Å. If the distance between two beads is, e.g., 15 Å, the charged residues on the surfaces of the corresponding domains are in direct contact with each other, and the strength of electrostatic interaction actually can be underestimated in this case even when using ε = 1, because the charged beads interact as if there is a distance of 15 Å between the charges, while the real, all-atom charges, may be much closer, just a few Ångströms apart.
The agreement between CG and all-atom simulations reported here (simulations 8BARs-AA and 8BARs-CG, Fig. 2A,B) further supports the choice of ε = 1 for the SBCG model.
SBCG membrane model
The lipid bilayer was modeled, as described earlier (Arkhipov et al., 2008), by two layers of CG beads for each leaflet: one for the lipid heads and one for the lipid tails, a head and a tail bead pair representing several lipid molecules (Fig. 6B). The two beads within a head-tail pair are connected by a harmonic bond. Since the leaflet thickness is ∼25 Å, each bead accounts for the part of the leaflet that is 12.5 Å in height, or for a volume of 12.5×12.5× 12.5 Å3. Thus, a two-bead CG “molecule” accounts for the area 12.5×12.5 Å2 and occupies the volume of 12.5×12.5×25 Å3. With the DOPC area per lipid being ∼70 Å2, each two-bead DOPC “molecule” represents 2.2 DOPC lipids on average, or ∼300 atoms. The LJ and bond parameters for lipid beads are chosen, in general, to reproduce the area per lipid, bilayer thickness, and hydrophobic/hydrophilic properties (Arkhipov et al., 2008). The only differences between DOPC and DOPS lipids in the SBCG model are in the charge and mass of the head bead. Each bead in the DOPC model has zero charge, while for DOPS lipids, a charge of -2.2|e| is assigned to the head bead. The masses are 864.75 amu for the DOPC head and DOPC/DOPS tail beads, and 866.76 amu for the DOPS head bead. To match the charge of the DOPS beads, we introduced “ions”, each with the charge of ±2.2|e| and mass of 1000 amu, roughly corresponding to 8 ions of mixed nature (such as both Na+ and Cl−) with their hydration shells. For the initial conditions in our simulations, “ions” (either positive or negative) were distributed uniformly in the simulated volume (excluding the areas occupied by lipids and proteins).
Due to the very coarse level of the model, one should not actually perceive the CG membrane as consisting of specifically DOPC and DOPS lipids. Rather, one should imagine a general membrane with a certain fraction of negatively charged lipids (30% in our case), with properties such as the area per lipid and membrane thickness tuned to correspond approximately to a DOPC/DOPS membrane.
Supplementary Material
Acknowledgments
We thank Wonhwa Cho, Nitin Bhardwaj, and Hui Lu at the University of Illinois at Chicago. This work was supported through National Institutes of Health grants R0-GM067887 and P41-RR05969; A. A. was supported by the L. S. Edelheit fellowship. The authors acknowledge supercomputer time provided by NSF (Large Resources Allocation Committee grant MCA93S028) and through the University of Illinois. This research also used resources of the Argonne Leadership Computing Facility at Argonne National Laboratory, which is supported by the Office of Science of the U.S. Department of Energy under contract DE-AC02-06CH11357.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- Arkhipov A, Freddolino PL, Imada K, Namba K, Schulten K. Coarse-grained molecular dynamics simulations of a rotating bacterial flagellum. Biophys J. 2006a;91:4589–4597. doi: 10.1529/biophysj.106.093443. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Arkhipov A, Freddolino PL, Schulten K. Stability and dynamics of virus capsids described by coarse-grained modeling. Structure. 2006b;14:1767–1777. doi: 10.1016/j.str.2006.10.003. [DOI] [PubMed] [Google Scholar]
- Arkhipov A, Yin Y, Schulten K. Four-scale description of membrane sculpting by BAR domains. Biophys J. 2008;95:2806–2821. doi: 10.1529/biophysj.108.132563. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Blood PD, Swenson RD, Voth GA. Factors influencing local membrane curvature induction by N-BAR domains as revealed by molecular dynamics simulations. Biophys J. 2008;95:1866–1876. doi: 10.1529/biophysj.107.121160. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Blood PD, Voth GA. Direct observation of Bin/amphiphysin/Rvs (BAR) domain-induced membrane curvature by means of molecular dynamics simulations. Proc Natl Acad Sci USA. 2006;103:15068–15072. doi: 10.1073/pnas.0603917103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bond PJ, Holyoake J, Ivetac A, Khalid S, Sansom M. Coarse-grained molecular dynamics simulations of membrane proteins and peptides. J Struct Biol. 2007;157:593–605. doi: 10.1016/j.jsb.2006.10.004. [DOI] [PubMed] [Google Scholar]
- Campelo F, McMahon HT, Kozlov MM. The hydrophobic insertion mechanism of membrane curvature generation by proteins. Biophys J. 2008;95:2325–2339. doi: 10.1529/biophysj.108.133173. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Feller SE. Molecular dynamics simulations of lipid bilayers. Curr Opin Coll & Interf Sci. 2000;5:217–223. [Google Scholar]
- Freddolino PL, Arkhipov A, Shih AY, Yin Y, Chen Z, Schulten K. Application of residue-based and shape-based coarse graining to biomolecular simulations. In: Voth GA, editor. Coarse-Graining of Condensed Phase and Biomolecular Systems. Chapman and Hall/CRC Press, Taylor and Francis Group; 2008. pp. 299–315. chapter 20. [Google Scholar]
- Frost A, Perera R, Roux A, Spasov K, Destaing O, Egelman EH, De Camilli P, Unger VM. Structural basis of membrane invagination by F-BAR domains. Cell. 2008;132:807–817. doi: 10.1016/j.cell.2007.12.041. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gallop JL, Jao CC, Kent HM, Butler PJ, Evans PR, Langen R, McMahon HT. Mechanism of endophilin N-BAR domain-mediated membrane curvature. EMBO J. 2006;25:2898–2910. doi: 10.1038/sj.emboj.7601174. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gallop JL, McMahon HT. Bar domains and membrane curvature: bringing your curves to the BAR. Biochem Soc Symp. 2005;72:223–231. doi: 10.1042/bss0720223. [DOI] [PubMed] [Google Scholar]
- Harmandaris VA, Deserno M. A novel method for measuring the bending rigidity of model lipid membranes by simulating tethers. J Chem Phys. 2006;125:204905. doi: 10.1063/1.2372761. [DOI] [PubMed] [Google Scholar]
- Helfrich W. Elastic properties of lipid bilayers: theory and possible experiments. Z Naturforsch. 1973;28:693–703. doi: 10.1515/znc-1973-11-1209. [DOI] [PubMed] [Google Scholar]
- Henne WM, Kent HM, Ford MGJ, Hegde BG, Daumke O, Butler PJG, Mittal R, Langen R, Evans PR, McMahon HT. Structure and Analysis of FCHo2 F-BAR Domain: A Dimerizing and Membrane Recruitment Module that Effects Membrane Curvature. Structure. 2007;15:1–14. doi: 10.1016/j.str.2007.05.002. [DOI] [PubMed] [Google Scholar]
- Humphrey W, Dalke A, Schulten K. VMD – Visual Molecular Dynamics. J Mol Graphics. 1996;14:33–38. doi: 10.1016/0263-7855(96)00018-5. [DOI] [PubMed] [Google Scholar]
- Kasson PM, Kelley NW, Singha N, Vrljic M, Brunger AT, Pande VS. Ensemble molecular dynamics yields submillisecond kinetics and intermediates of membrane fusion. Proc Natl Acad Sci USA. 2006;103:11916–11921. doi: 10.1073/pnas.0601597103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Löw C, Weininger U, Lee H, Schweimer K, Neundorf I, Beck-Sickinger AG, Pastor RW, Balbach J. Structure and dynamics of helix-0 of the N-BAR domain in lipid micelles and bilayers. Biophys J. 2008;95:4315–4323. doi: 10.1529/biophysj.108.134155. [DOI] [PMC free article] [PubMed] [Google Scholar]
- MacKerell A, Jr, Bashford D, Bellott M, Dunbrack RL, Jr, Evanseck J, Field MJ, Fischer S, Gao J, Guo H, Ha S, et al. All-atom empirical potential for molecular modeling and dynamics studies of proteins. J Phys Chem B. 1998;102:3586–3616. doi: 10.1021/jp973084f. [DOI] [PubMed] [Google Scholar]
- Marrink SJ, de Vries AH, Harroun TA, Katsaras J, Wassall SR. Cholesterol shows preference for the interior of polyunsaturated lipid membranes. J Am Chem Soc. 2008;130:10–11. doi: 10.1021/ja076641c. [DOI] [PubMed] [Google Scholar]
- Marrink SJ, Risselada HJ, Yefimov S, Tieleman DP, de Vries AH. The martini forcefield: coarse grained model for biomolecular simulations. J Phys Chem B. 2007;111:7812–7824. doi: 10.1021/jp071097f. [DOI] [PubMed] [Google Scholar]
- Marrink SJ, Risselada J, Mark AE. Simulation of gel phase formation and melting in lipid bilayers using a coarse grained model. Chem Phys of Lipids. 2005;135:223–244. doi: 10.1016/j.chemphyslip.2005.03.001. [DOI] [PubMed] [Google Scholar]
- Masuda M, Takeda S, Sone M, Ohki T, Mori H, Kamioka Y, Mochizuki N. Endophilin BAR domain drives membrane curvature by two newly identified structure-based mechanisms. EMBO J. 2006;25:2889–2897. doi: 10.1038/sj.emboj.7601176. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mattila PK, Pykäläinen A, Saarikangas J, Paavilainen VO, Vihinen H, Jokitalo E, Lappalainen P. Missing-in-metastasis and IRSp53 deform PI(4,5)P2-rich membranes by an inverse BAR domain-like mechanism. J Cell Biol. 2007;176:953–964. doi: 10.1083/jcb.200609176. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McMahon HT, Gallop JL. Membrane curvature and mechanisms of dynamic cell membrane remodeling. Nature. 2005;438:590–596. doi: 10.1038/nature04396. [DOI] [PubMed] [Google Scholar]
- Millard TH, Bompard G, Heung MY, Dafforn TR, Scott DJ, Machesky LM, Futterer KT. Structural basis of filopodia formation induced by the IRSp53/MIM homology domain of human IRSp53. EMBO J. 2005;24:240–250. doi: 10.1038/sj.emboj.7600535. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Peter BJ, Kent HM, Mills IG, Vallis Y, Butler PJG, Evans PR, McMahon HT. BAR domains as sensors of membrane curvature: The amphiphysin BAR structure. Science. 2004;303:495–499. doi: 10.1126/science.1092586. [DOI] [PubMed] [Google Scholar]
- Phillips JC, Braun R, Wang W, Gumbart J, Tajkhorshid E, Villa E, Chipot C, Skeel RD, Kale L, Schulten K. Scalable molecular dynamics with NAMD. J Comp Chem. 2005;26:1781–1802. doi: 10.1002/jcc.20289. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ren G, Vajjhala P, Lee JS, Winsor B, Munn AL. The BAR domain proteins: Molding membranes in fission, fusion, and phagy. Microbiology and molecular biology reviews. 2006;70:37–120. doi: 10.1128/MMBR.70.1.37-120.2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Reynwar BJ, Illya G, Harmandaris VA, Müller MM, Kremer K, Deserno M. Aggregation and vesiculation of membrane proteins by curvature-mediated interactions. Nature. 2007;447:461–464. doi: 10.1038/nature05840. [DOI] [PubMed] [Google Scholar]
- Ritter H, Martinetz T, Schulten K. Textbook: Neural Computation and Self-Organizing Maps: An Introduction. revised English Addison-Wesley; New York: 1992. [Google Scholar]
- Roy R, Hohng S, Ha T. A practical guide to single-molecule FRET. Nat Methods. 2008;5:507–516. doi: 10.1038/nmeth.1208. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shelley JC, Shelley MY, Reeder RC, Bandyopadhyay S, Moore PB, Klein ML. Simulations of phospholipids using a coarse grain model. J Phys Chem B. 2001;105:9785–9792. [Google Scholar]
- Shih AY, Arkhipov A, Freddolino PL, Schulten K. Coarse grained protein-lipid model with application to lipoprotein particles. J Phys Chem B. 2006;110:3674–3684. doi: 10.1021/jp0550816. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shih AY, Arkhipov A, Freddolino PL, Sligar SG, Schulten K. Assembly of lipids and proteins into lipoprotein particles. J Phys Chem B. 2007a;111:11095–11104. doi: 10.1021/jp072320b. [DOI] [PubMed] [Google Scholar]
- Shih AY, Freddolino PL, Arkhipov A, Schulten K. Assembly of lipoprotein particles revealed by coarse-grained molecular dynamics simulations. J Struct Biol. 2007b;157:579–592. doi: 10.1016/j.jsb.2006.08.006. [DOI] [PubMed] [Google Scholar]
- Shillcock JC, Lipowsky R. Tension-induced fusion of bilayer membranes and vesicles. Nat Mater. 2005;4:225–228. doi: 10.1038/nmat1333. [DOI] [PubMed] [Google Scholar]
- Shimada A, Niwa H, Tsujita K, Suetsugu S, Nitta K, Hanawa-Suetsugu K, Akasaka R, Nishino Y, Toyama M, Chen L, et al. Curved EFC/F-BAR-domain dimers are joined end to end into a filament for membrane invagination in endocytosis. Cell. 2007;129:761–772. doi: 10.1016/j.cell.2007.03.040. [DOI] [PubMed] [Google Scholar]
- Smit B, Hilbers PAJ, Esselink K, Rupert LAM, van Os NM, Schlijper AG. Computer simulations of a water/oil interface in the presence of micelles. Nature. 1990;348:624. [Google Scholar]
- Takei K, Slepnev VI, Haucke V, De Camilli P. Functional partnership between amphiphysin and dynamin in clathrin-mediated endocytosis. Nat Cell Biol. 1999;1:33–39. doi: 10.1038/9004. [DOI] [PubMed] [Google Scholar]
- Weissenhorn W. Crystal structure of the endophilin-A1 BAR domain. J Mol Biol. 2005;351:653–661. doi: 10.1016/j.jmb.2005.06.013. [DOI] [PubMed] [Google Scholar]
- Zimmerberg J, Kozlov MM. How proteins produce cellular membrane curvature. Nat Rev Mol Cell Biol. 2006;7:9–19. doi: 10.1038/nrm1784. [DOI] [PubMed] [Google Scholar]
- Zimmerberg J, McLaughlin S. Membrane curvature: How BAR domains bend bilayers. Curr Biol. 2004;14:R250–R252. doi: 10.1016/j.cub.2004.02.060. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


