Optimal Experimental Design for Model Discrimination

Abstract

Models of a psychological process can be difficult to discriminate experimentally because it is not easy to determine the values of the critical design variables (e.g., presentation schedule, stimulus structure) that will be most informative in differentiating them. Recent developments in sampling-based search methods in statistics make it possible to determine these values, and thereby identify an optimal experimental design. After describing the method, it is demonstrated in two content areas in cognitive psychology in which models are highly competitive: retention (i.e., forgetting) and categorization. The optimal design is compared with the quality of designs used in the literature. The findings demonstrate that design optimization has the potential to increase the informativeness of the experimental method.

Introduction

Experimentation is fundamental to the advancement of psychological science. When conducting experiments, scientists often have to simplify the situation in which the phenomenon of interest has been observed so that a degree of association between hypothesized causal or correlational variables and human behavior can be established. Tools, most notably computers, assist in this process by providing the control and precision necessary at the many stages of experimentation (e.g., from stimulus selection or creation, to stimulus delivery and behavioral measurement) that are required to infer a causal link between the hypothesized variable and its effect on behavior.

Despite the sophisticated methods and technologies that have been developed and adapted in the service of understanding behavior, key aspects of experimentation depend on the knowledge, experience, and creativity of the scientist. Foremost among these, and the focus of this paper, is experimental design. The choices made in designing an experiment can be critical in determining the experiments’ contribution to the field. Decisions must be made about which variables should be manipulated, which stimuli should be used, presentation schedule, and choice of behavioral measure. Some choices can seem arbitrary (number of stimuli) and others are influenced by pragmatic considerations, such as the time required to complete the experiment. In well-established fields, decisions are usually guided by prior research. But even here, the ramifications of these decisions can be difficult to evaluate, so much so that sometimes they are the focus of investigations in their own right (e.g., Balota & Chumbley, 1984).

For example, decisions about how to manipulate an independent variable are particularly crucial because they are most directly tied to the theoretical question of interest. Participants must be sensitive to different levels of the variable to observe its effect on behavior. Although piloting is one means of ensuring appropriate levels are chosen, without extensive piloting, it can be difficult for the researcher to get a sense of whether the choices will be as informative as possible. Furthermore, the informativeness of these choices will likely be influenced by other factors, such as those noted above (e.g., number of stimuli). An optimal design can be elusive, requiring simultaneous consideration of many variables. To determine the suitability of an experiment for addressing a theoretical question of interest, it would be ideal if one could perform a power analysis on the experimental design itself, and thereby improve statistical inference. In this paper, we introduce a method that is a step toward this goal.

The extent to which an optimal experimental design is necessary for distinguishing contrasting predictions depends on the granularity of the comparison being made. If models are being compared that predict qualitatively different patterns of data on the dependent measure, it is not as crucial to use an optimal design. A case in point is a theory-driven experimental method known as the systems factorial technology, developed for determining the architecture underlying perceptual information processing (Townsend & Wenger, 2004). The method predicts unique inequality patterns of response times for competing architectures. As long as participants clearly produce one such pattern, the magnitude of the pattern is less important. The architecture that does not conform to the prediction is inadequate.

Concerns about design optimality are more critical when models make predictions that differ quantitatively. Such precision is found in formal mathematical models in psychology. In this circumstance, two models may predict the same qualitative data pattern, but the actual quantitative values predicted by the two are not identical. The use of what might be seem like a reasonable design might not be sufficient to yield results that clearly favor one model over the other. If the optimal design is able to do so, its use could generate much more theoretically impactful results.

Precisely because mathematical models are quantitative, it is possible to define an optimal experimental design as an objective utility function to be maximized, in the sense that the design sought has the greatest likelihood of differentiating the models under consideration. In this paper, we introduce such a method, specifically one that can identify an experimental design that is optimal for discriminating among models. Its application is demonstrated in the context of models of retention and models of categorization.

Design Optimization: A Formal Framework

The optimization of an experimental design has been considered at length in the statistics community (e.g., Atkinson & Donev, 1992; Chaloner & Verdinelli, 1995; Kiefer, 1959; Box & Hill, 1967) as well as in other science and engineering disciplines (e.g., El-Gamal & Palfrey, 1996; Bardsley, Wood & Melikhova, 1996; Allen, Yu, & Schmitz, 2003; Kueck, de Freitas & Doucet, 2006). Among a variety of questions about design optimization (DO) that can be addressed, the one that has received the most attention is that of identifying an experimental design that makes the variances of a model’s parameter estimates as small as possible, thereby allowing the model to make the most accurate predictions. This goal is achieved by what is known as the D-optimum criterion, under which the design that maximizes the determinant of the variance-covariance matrix is to be chosen, formally speaking.

Implicit in the D-optimum criterion is the assumption that the model is correct in that it generated the data. Because this is impossible in most real-world problems, a more realistic goal of optimization is to discriminate among several models of the same psychological process. That is, the focus shifts to designs that maximally discriminate between two or more models. This change in focus led to the so called T-optimum criterion (Atkinson & Donev, 1992, ch. 20; Ponce de Leon & Atkinson, 1991; Ucinski & Bogacka, 2005), which is described below. Readers who prefer to skip the technicalities of the criterion, and instead concentrate on its application to models in cognitive psychology, should skip to the next section.

Suppose that we have two models, A and B, that we wish to discriminate experimentally. Identification of the optimal design for this purpose requires evaluating the relative performance of the models over the ranges of their parameters. This is done by fitting each model to data generated by the other. A good design for discriminating between models is one that maximizes the degree of model dissimilarity (i.e., distinguishability) in an appropriately defined sense, operationalized as a badness-of-fit measure between models. Regardless of how it is conceptualized, the task is nontrivial because of the large number of comparisons involved. It also means that the optimal design depends on the parameterization of each model and, even more importantly, on the utility function to be optimized. These issues are formalized below.

The problem of experimental design in model discrimination can be thought of as finding a design d* that maximizes some utility function U(d) that quantifies the quality of the design d. Let us assume that for this design d, the experimental outcome (i.e., data) y_A = (y_A1,..., y_AN) are generated from model A with its parameter vector θ_A, and further, that model M_B is fitted to the data by minimizing the sum of squares errors

$$u(d,{\theta }_A,y_A)=\sum _{i=1}^N{(y_{Ai}-{\mathit{prd}}_{Bi}({\theta }_B^{\ast },d))}^2$$ (1)

where u_A(·) denotes the minimized sum of squares error and ${\mathit{prd}}_{Bi}({\theta }_B^{\ast },d)$ is the prediction by model B at its best-fitting parameter vector θ*_B given the design d. In designing an experiment, we have yet to observe an outcome and we do not know the parameter vector θ_A from which the outcome will be generated. Therefore, the quality of a given design d is assessed by the expectation (i.e., mean) of u(d, θ_A, y_A) in the above equation with respect to the sampling distribution p(y_A|θ_A ,d) and the prior distribution p(θ_A|d) given as follows

$$\int \int u(d,{\theta }_A,y_A)p(y_A\mid {\theta }_A,d)p({\theta }_A\mid d)d{y}_{A}d{\theta }_A$$ (2)

This equation gives an expression of the expected badness-of-fit of model B conditional on the data from model A. Similarly, a corresponding expression can be obtained for the expectation of u(d,θ_B,y_B) by switching the roles of the two models and fitting model A to the data generated from model B. Since we don’t know which of the two models A and B will generate an experimental outcome, we combine the resulting two equations to obtain the desired utility function U(d) to be maximized as

$$\begin{array}{cc}\hfill U\left(d\right)=& p\left(A\right)\int \int u(d,{\theta }_A,y_A)p(y_A\mid {\theta }_A,d)p({\theta }_A\mid d)d{y}_{A}d{\theta }_A\hfill \\ \hfill & +p\left(B\right)\int \int u(d,{\theta }_B,y_B)p(y_B\mid {\theta }_B,d)p({\theta }_B\mid d)d{y}_{B}d{\theta }_B\hfill \end{array}$$ (3)

where p(A) and p(B) are model priors (p(A) + p(B) =1). The resulting utility function U(d) can be interpreted as a measure of model dissimilarity or distinguishability between two models: The larger the value of U(d), the less similar the two models are to each other. It is straightforward to modify the expression in the above equation to accommodate the situation in which more than two models are to be discriminated. In the remainder of this paper, to avoid a possible confusion between the two utility functions, U(d) will be called the global utility function and u(d, θ, y) the local utility function, whenever the context demands it.

As should be clear from equation (3), finding a design d* that maximizes U(d) is a nontrivial undertaking because of the requirement of high dimensional integration and optimization. To appreciate this, note that it is generally not possible to obtain an analytic form solution of the multiple integral, so the integration must be evaluated numerically for a given choice of d. This itself is a formidable challenge given the fact that the integration is defined over the data space and parameter space. The resulting estimate of U(d) must then be maximized over the design variable d, which is often a multi-dimensional vector. Given these multiple computational challenges, the use of standard optimization algorithms, such as the Newton-Raphson method and the Levenverg-Marquardt method, in identifying an optimal design are inadequate. A solution to the design optimization problem in general settings was not possible until recently. Because of this, work focused on problems that were sufficiently simple (e.g., linear models with normal errors) that analytically tractable solutions could be found.

A promising and fully general new approach has been proposed in statistics (Muller, 1999; Muller, Sanso & De Iorio, 2004; Amzal, Bois, Parent & Robert, 2006). It is a Bayesian simulation-based approach that includes a computational trick, which allows one to find the optimal design without having to evaluate the integration and optimization directly. Under the approach, the design optimization problem is recast as a problem of probability density simulation in which the optimal design corresponds to the mode of a density. The density is simulated by Markov chain Monte Carlo (MCMC; Gilks, Richardson & Spiegelhalter, 1996) and the mode is sought by gradually “sharpening up” the density under a simulated annealing procedure (Kirkpatrick, Gelatt & Vecchi, 1983). In the present study, we adopted and implemented this simulation-based approach, with minor modifications, to solve the design optimization problem for model discrimination in equation (3).

The basic idea of this simulation-based approach is to treat d as a random variable and view U(d) as a marginal distribution of an artificial distribution defined over the joint space of (d, y_A, θ_A, y_B, θ_B) as follows

$$h(d,y_A,{\theta }_A,y_B,{\theta }_B)=\alpha [p\left(A\right)u(d,{\theta }_A,y_A)+p\left(B\right)u(d,{\theta }_B,y_B)]\cdot p(y_A,{\theta }_A,y_B,{\theta }_B\mid d)$$ (4)

where α (>0) is the normalizing constant of the artificial distribution and p(y_A,θ_A, y_B,θ_B|d) = p(y_A | θ_A, d) p(θ_A) p(y_B | θ_B, d) p(θ_B). Note that defining the distribution h(·) as above requires the assumption that both u(d, θ_A, y_A) and u(d, θ_B, y_B) are non-negative and bounded. It can then be shown that marginalizing h(·) over (y_A, θ_A, y_B, θ_B ) yields $\int h(d,y_A,{\theta }_A,y_B,{\theta }_B)d{y}_{A}d{\theta }_{A}d{y}_{A}d{\theta }_A=\alpha U\left(d\right)$. This relationship provides a key link between design optimization and density simulation that can be exploited to find an optimal design through the following steps (A more thorough description of the algorithm is provided in Appendix A):

• Step 1: Generate a sample of draws (d, y_A, θ_A, y_B, θ_B)’s from the artificial distribution h(·) using a suitable MCMC chain;

• Step 2: From the sample of draws, empirically estimate the marginal distribution Û(d), up to a constant proportionality, by collecting all d’s but disregarding y_A’s, θ_A’s, y_B’s, and θ_B’s;

• Step 3: Identify the mode of Û(d) as an approximate solution to the design optimization problem.

There may be many locally optimal designs. To overcome the local optimum problem so as to find the globally optimal solution, the artificial distribution h(·) is augmented in the following form

$$h_J(\cdot )={\alpha }_J\prod _{j=1}^J[p\left(A\right)u(d,{\theta }_{Aj},y_{Aj})+p\left(B\right)u(d,{\theta }_{Bj},y_{Bj})]\cdot p(y_{Aj},{\theta }_{Aj},y_{Bj},{\theta }_{Bj}\mid d)$$ (5)

for a positive integer J and α_J > 0. The marginal distribution of h_J(·) obtained after integrating out the outcome variable and model parameters yields α_JU(d)^J. Note that the higher the J value, the more highly peaked the distribution U(d)^J will be around its (global) mode, and therefore the easier the mode can be identified. This is illustrated in the left three panels of Figure 1for a hypothetical marginal distribution U(d)^J defined over a one-dimensional design variable d.

Figure 1.

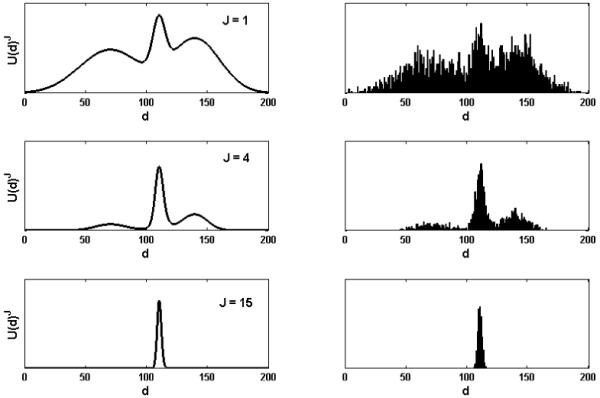
Illustration of the DO algorithm in estimating marginal distributions. The distributions on the left show three marginal distributions U(d)^J with different J values. Shown on the right are their respective empirical estimates obtained by applying the algorithm.

Along with the augmented distribution h_J(·), the earlier three-step procedure for finding an optimal design is modified to include a simulated annealing step such that a sequence of marginal distributions U(d)^J_n are approximated by gradually increasing the value of J_n, or equivalently, by lowering the annealing “temperature” defined as T_n =1/ J_n. Ideally, under a carefully designed annealing schedule, simulated samples of d’s from U(d)^J_n for large J_n will be tightly concentrated around the global optimal design d*. This is illustrated in the right panels of Figure 1. Each of these panels represents an empirical estimate Û(d)^J of the target marginal distribution Û(d)^J shown on the respective left panel, obtained through a simulated annealing based MCMC sampling scheme.

Following Amzal et al (2006), we employed a sequential Monte Carlo (SMC) method, also known as a particle filter, to simulate the artificial distribution h_J. SMC, which is a sequential analog of MCMC, consists of a population of “parallel-running and interacting” Markov chains, called particles, that are eliminated or multiplied according to an evolutionary process. The implementation of SMC does not require one to know the values of the normalizing constants α and α_J.

SMC has been applied to nonlinear dynamical system modeling problems in engineering and computing fields such as signal processing, navigation, automatic control, computer vision, and target tracking (Doucet, de Freitas & Gordon, 2001; Del Moral, Doucet & Jasra, 2006; SMC homepage at http://www-sigproc.eng.cam.ac.uk/smc/). The specific version of SMC we implemented in all of the applications discussed in this paper, including the illustrative examples that begin the next section, is the Resampling-Markov Algorithm (Amzal et al, 2006, p. 776).

Optimal Designs for Discriminating Retention Models

For over one hundred years, psychologists have been interested in how long information is retained in memory after a brief study period (Ebbinghaus, 1885). This question about memory is somewhat unique in that not only is there a large empirical literature on the topic (Rubin Wenzel, 1996; Wickens, 1998) but a fair number of models have been proposed to describe the form of the retention function (see Navarro, Pitt, & Myung, 2004; Wixted & Ebbesen, 1991). Most models do a good job of capturing the basic pattern in the experimental data, of memory worsening as the time interval between study and test increases, but they differ in the exact form of the function and the factors that are thought to influence it.

Design optimization is highly desirable in a situation like this, where there is a crowded field of models that differ primarily in the precision with which they fit empirical data. Model mimicry is widespread, making it difficult to identify a design that has the potential to differentiate the models. In this circumstance, one must identify a design that can exploit what in all likelihood are small differences between models. In the following simulations, we demonstrate the ability of design optimization to do this.

Illustrations of Design Optimization

Before delving into the details of the main demonstrations, we begin with an easy-to-understand example to illustrate what is being optimized when discriminating retention models. Two retention models that have been of interest (e.g., Wixted & Ebbesen, 1991; Rubin & Wenzel, 1996) are the power model (POW) and the exponential model (EXP), both of which are defined in Table 1. Their functions look like those in Figure 2 when their parameters are restricted to a very narrow range. The thin lighter line represents a set of power curves that are generated by varying independently each parameter’s values over 0.95 < a < 1 and 1.00 < b < 1.01. The thick darker line represents the set of exponential curves that are generated by varying each parameter’s values over 0.95 < a < 1 and 0.16 < b < 0.17. Both models predict that memory decays monotonically as the time interval between the study phase and the test phase increases, but as seen in Figure 2 forgetting is predicted to occur much more quickly immediately after the study phase in the power model than the exponential model.

Table 1.

The model equations of the six retention models. In each equation, the symbol p (0 < p < 1) denotes the predicted probability of correct recall as a function of time interval t with model parameters a, b and c. Note that for the power model (POW), the decay factor is defined as (t+1) so that the probability remains between 0 and 1 for all positive t values

Model	Equation
Power (POW)	p = a(t+1)-b
Exponential (EXP)	p = ae-bt
Hyperbolic (HYP)	p = a/(a+tb)
Power with asymptote (POWA)	p = a(t+1)-b+ c
Exponential with asymptote (EXPA)	p = ae-bt+ c
Exponential with exponent (EXPE)	p = ae-btc

Figure 2.

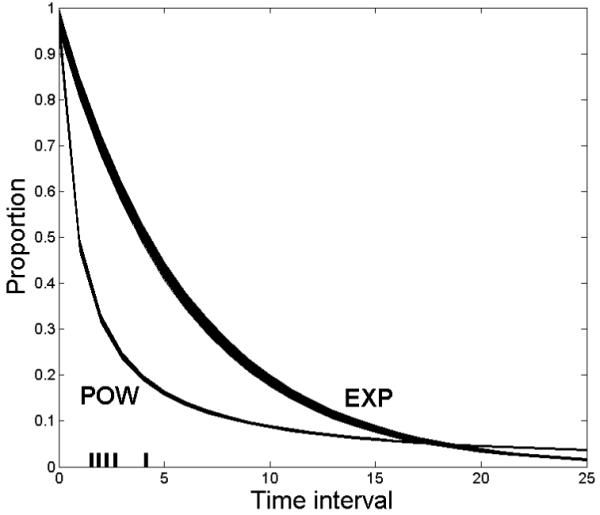
Sets of power and exponential functions when their parameters are restricted to a vary narrow range (see text). The five time intervals that optimally discriminate the two models are indicated by short vertical lines shown on the far left of the horizontal axis.

If a researcher conducts an experiment to compare the predictions of these models, and decides to probe memory at five time intervals between the range of 0 and 25 seconds¹ after study, then the goal of design optimization is to identify those time intervals that yield the most differentiating predictions of the two models. Visual inspection of Figure 2 suggests the values should fall between 1 and 5, where the functions are separated the most. In this region, the power model predicts performance will be much lower than the exponential model.

We applied design optimization to the two models in Figure 2 using the local utility function defined in equation (1). In a retention experiment, the outcome variable y_i (= 0,1,...,n) in the utility equation represents the number of correct responses observed out of n independent test trials or items, and accordingly is binomially distributed with probability p_i and binomial sample size n, formally, y_i ∼ Bin(n, p_i), i = 1,...,N, where p_i denotes a model’s predicted probability of a correct response on each trial at a given time interval t_i. Note that N denotes the number of time intervals employed in an experiment and n denotes the number of binary responses (correct or incorrect) collected at each time interval. We ran the DO algorithm seeking five (N=5) time intervals, (t₁, t₂, ...,t₅), for the same sample size of $n = 10$ for each time interval under the noninformative Jeffreys (1961) priors for both p(θ_A) and p(θ_B) and under equal model priors (i.e., p(A) = p(B) = 0.5) in equation (3), where A = POW and B = EXP. Jeffreys’ priors and equal model priors are employed for all simulations reported in this paper. Justifications for the choice of Jeffreys’ priors are discussed in the General Discussion.

The five points that constitute an optimal design, shown by vertical bars on the x axis in Figure 2, all fall squarely between 1 and 5, confirming intuitions. When the very narrow parameter ranges of the models used in this example are expanded to more typical ranges, it is no longer possible to eyeball optimal time intervals by examining plots as in Figure 2, which is why the design optimization algorithm is necessary.

In addition to identifying an optimal design, one might be interested in the quality of other experimental designs. Are there designs that are similarly good? What set of time values yield a bad design? For example, comparison of the two functions in Figure 2 suggests that selection of five time intervals between 15 and 20 would probably result in a very poor design.

The models in Figure 2 are not suitable to illustrate how design optimization can be used to evaluate design quality, and thereby answer the preceding questions. We therefore made slight changes to these two models and the design to create an appropriate example. The parameter ranges of both models were expanded to those typically used (0 < a <1 and 0 < b < 3). In addition, three time intervals (N = 3) were used instead of five, and the time scale was discretized into increments of 0.5 in the range of 0.5 < t₁ < t₂ < t₃ < 15. These changes created an optimization problem in which the total number of designs (4060) was manageable for study. The global utility values of all designs were calculated individually by a brute force method without using the design optimization (DO) algorithm, and the relative frequency distribution of these utilities (transformed into log utility values) is shown in Figure 3.

Figure 3.

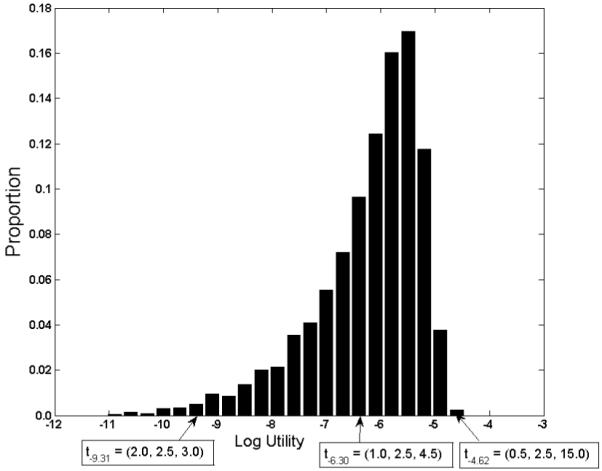
Relative frequency distribution of log global utility values for all possible 3-interval designs T = (t₁, t₂, t₃) created with an increment of 0.5 across the range 0.5 ≤ t₁ ≤ t₂ ≤ t₃ ≤ 15. Shown on the vertical axis is the proportion of 4,060 designs that fall in each interval of the log utility value.

The frequency distribution provides information about the relative potential of the designs (i.e., choice of three time intervals) to discriminate between the two models. This negatively skewed distribution shows that a large number of designs are fairly comparable in their ability to distinguish between the models. An example of one of these “average” designs is shown in the middle box below the graph. The frequency distribution also shows that there are only a small number of very bad and very good designs. An example of each is provided as well. Comparison of the time intervals across the three examples reveals what affects design quality. Although all models share the middle time interval (2.5), they differ in the spacing of the adjacent intervals. For the worst designs, t₁ and t₃ are immediately adjacent to t₂. Design quality improves as t₁ and t₃ move away from t₂, toward their boundary values, to the point where the best designs take advantage of the full range of time values (0.5 and 15).

The three example designs in Figure 3 are not idiosyncratic, but reflect properties that define design quality in this comparison of the power and exponential models. Shown in Figure 4 are the time intervals for the ten worst and ten best designs. As in Figure 3, a bad design is one in which the time intervals are clustered together in the upper half of the time scale. The best designs include intervals at the endpoints plus a middle value near 3.0.

Figure 4.

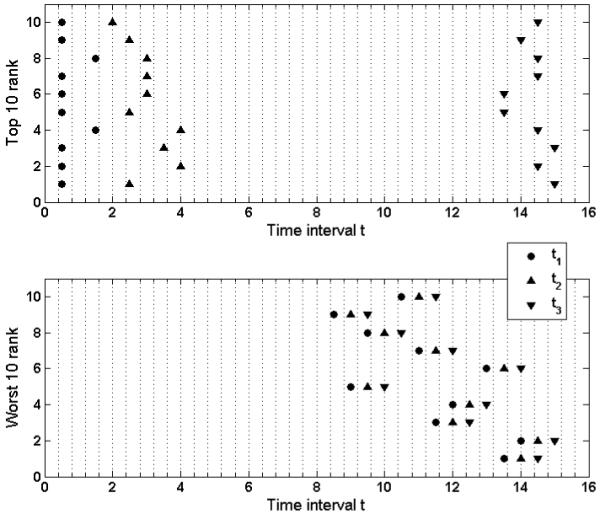
Time intervals of the ten best and worst designs from the distribution in Figure 3.

The fact that there are so many similarly good designs should make it clear that while an optimal design can be identified, it is probably most useful to think of a region in the space of experimental designs that contains sets of time intervals that are close to optimal. In this regard, the goal of design optimization is to identify those regions in which models are most distinguishable. With more complex designs (and models), there could be more than one region.

Discriminating Retention Models

In this section, we apply the DO algorithm to identify optimal experimental designs for discriminating the retention models in Table 1. To do so properly, it was necessary to replace the sum-of-squared- errors local utility function in equation (1), which was used in the preceding examples to simplify presentation of design optimization. In practice, sum-of-squared errors, like any other goodness of fit measure (e.g., maximum likelihood, percent variance accounted for), is a poor choice because it is biased toward the more complex model, which will generally overfit the data (Myung & Pitt, 1997; Pitt, Myung & Zhang, 2002; Pitt & Myung, 2002).

To counter this bias, a model selection method must be used that controls for model complexity, which refers to the ability of a model to fit diverse patterns of data. Various model selection criteria that incorporate complexity have been proposed in the literature, and the interested reader is directed to two special issues of the Journal of Mathematical Psychology for discussion of model selection criteria and their example applications (Myung, Forster & Browne, 2000; Wagenmakers & Waldorp, 2006). In the current study we employed the Fisher Information Approximation (FIA: Grunwald, 2000; Myung, Navarro & Pitt, 2006) as a model selection criterion, the application of which to cognitive modeling has been well demonstrated (e.g., Lee, 2001; Pitt, Myung & Zhang, 2002; Navarro & Lee, 2004; Grunwald, Myung & Pitt, 2005; Lee & Pope, 2006). FIA is an implementation of the minimum description length principle (Rissanen, 1996, 2001) and is defined as

$$\mathit{FIA}=-\ln f(y\mid {\theta }^{\ast })+\frac{k}{2}\ln \frac{n}{2\pi }+\ln \int \sqrt{\mid I\left(\theta \right)\mid }d\theta$$ (6)

where ln f(y|θ*) is the natural logarithm of the maximum likelihood, k is the number of parameters, n is the sample size, and I(θ) is the Fisher information matrix of sample size 1.² The Fisher information matrix quantifies the amount of information contained in the data about the parameters, measured by the relative precision of parameter estimates. A smaller value of the FIA criterion indicates better generalization, and thus, the model that minimizes the criterion should be selected. FIA was chosen because its complexity measure, represented by the second and third terms of the criterion equation, is sensitive to the ‘functional form’ dimension of complexity through I(θ) (Pitt, Myung & Zhang, 2002), as well as to the number of parameters and sample size. As such, the criterion will be particularly useful for the present problem of discriminating among the six retention models, some of which assume the same number of parameters but differ in functional form (e.g., POW and EXP). The local utility function can now be expressed as a measure of model recovery using FIA, with u(d, θ_A, y_A) = 1 if FIA_A < FIA_B and 0 otherwise, and similarly for u(d, θ_B, y_B). With this change of local utility function implemented, we applied the DO algorithm and sought designs that optimally discriminate retention models.

To reiterate, throughout this paper, optimal designs are defined as the ones that maximize the proportion of times in which the true, data-generating model is selected under FIA-based model selection. Obviously, design optimality can also be defined with respect to other methods of model selection such as the Akaike Information Criterion (AIC: Akaike, 1973) and the Bayes factor (Kass & Raftery, 1995). We return to this issue in the General Discussion.

Two important decisions that must be made when designing a retention experiment are the number of time intervals (N) at which memory will be tested and the choice of those time points (T = (t₁, ..., t_N)). In the retention literature, N has varied greatly, from a low of three (Slamecka & McElree, 1983) to a high of 15 (Squire, 1989). Although some studies have used linearly spaced time intervals (Waugh & Norman, 1965; Wickelgren, 1968), most have used geometrically spaced intervals such as T = (1, 2, 4, 8, 16), or ones that are close to or include a geometric progression.

Our investigation explored the impact that choices of N and T have on the ability of a design to discriminate the power and exponential models of retention. We began by comparing the two models using the simplest possible design, N = 3. Because POW and EXP have two parameters, at least three time intervals are needed to make the models identifiable. This comparison is then extended to N = 5, and the tradeoffs in N and T are examined. N is then increased to 25 to test a conjecture that a long geometric progression of time intervals can discriminate the two models. Finally, design optimization is demonstrated with six retention models.

Before discussing the design optimization results, we describe briefly implementation details of the DO algorithm. Unless noted otherwise, we ran all computational simulations implementing the algorithm for the binomial sample size of n = 100 with the time intervals restricted to the range 0 < t_i < 1000, (i = 1,...,N).³ Once a simulation was determined to have reached an asymptote, usually around 300 - 500 iterations for 50 interacting particles, an optimal design solution was recovered as an arithmetic mean of individual designs, each associated with a particle. The global utility (i.e., model recovery rate) of the optimal design was then estimated outside of the algorithm based on a separate sample of 5000 quartets, (θ_A, y_A, θ_B, y_B)’s generated using the design according to equation (3).

For a given N, the quality of an optimal design was evaluated by comparing its model recovery rate with that of two typical designs, one in which the time intervals were spaced linearly and the other in which they were spaced geometrically. For N = 3, model recovery estimates for all three designs are shown in the top half of Table 2. For both linear and geometric spacing, the recovery rate hovers near 60%, with a slight edge for geometric spacings. The similarity of the recovery rates is not surprising given that two of the three time intervals are identical and the third is very similar. The recovery rate for the optimal design T = (9.53, 26.9, 252) is vastly superior (86.3%), and the design solution is quite different. In contrast to the linear and geometric progressions, and many studies in the literature, memory is not probed multiple times during the first 4 - 5 seconds after the study phase. Rather t₁ occurs almost 10 seconds after study. t₂ and t₃ are also spread out, with t₃ occurring over four minutes after study.

Table 2.

Model recovery percentages for discriminating between POW and EXP across designs differing in the number of time intervals (N) and the design (T). W & E(1991) refers to the Wixted and Ebbesen (1991) study

N	Type	T (design)	% Recovery
3	Linear	(1, 2, 3)	58.3
	Geometric	(1, 2, 4)	61.9
	Optimal	(9.53, 26.9, 252)	86.3
5	Linear	(1, 2, 3, 4, 5)	65.3
	Geometric	(1, 2, 4, 8, 16)	76.2
	Optimal	(2.79, 9.07, 24.1, 58.6, 309)	91.5
	W & E (1991)	(2.5, 5, 10, 20, 40)	79.4

When N is increased from 3 to 5 (bottom half of Table 2), model recovery changes predictably. The addition of two more time intervals increases the recovery rate for all designs, but much more so for the geometric than linear spacing (65.3% vs. 76.2%). The optimal design remains substantially superior, with a recovery rate of 91.5%. Inspection of the time intervals again shows that the optimal design contains widely spaced intervals. Although their spacing is not geometric, it is not fixed either. Each successive interval is greater than the preceding one by a factor of between 2.5 and 5.

Identification of an optimal design makes it possible to evaluate the quality of designs used in past studies. Wixted and Ebbesen (1991) compared the exponential and power models, along with others, using a design with N = 5. The model recovery rate for this design, along with its time intervals, is listed in the last row of Table2. Although Wixted and Ebbesen also used a geometric progression, their recovery rate is about 3% higher than the other geometric design. The reason for the improvement must be the wider range of intervals in the Wixted and Ebbesen design. The difference between the ranges is greater than two-fold (15 vs. 37.5). The fact that the optimal design also spans a wide range suggests that the range of time intervals is an important property of a good design.

Additional evidence that widely spaced time intervals are critical for discriminating power and exponential models is that the recovery rate for the optimal design when N = 3 is higher than for three of the four designs when N = 5. The optimal placement of a few time intervals over a wide range can yield a design that is better than one with more intervals that span a shorter range, even when this shorter range might appear to be satisfactory.

These observations about the effect of interval spacing and range on model discriminability raise the question of whether a geometric progression that spans a large enough range (e.g., extend the Wixted and Ebbesen design to ten intervals) could yield a design that is close to optimal. We tested this idea by first identifying the optimal design for N = 25. The simulation details were the same as those used for the comparisons in Table 2. The optimal design yielded a model recovery rate of 97.3%. The time intervals for this design are graphed in Figure 5 as a function of the rank order of the interval (x axis) and the interval’s logarithmic value (y axis). On an logarithmic scale, a geometric progression forms a straight line. The points are close to this. How close is indicated by the dashed line, which is the best-fitting linear exponential function to these points. When the corresponding time intervals on this line are used to discriminate the power model from the exponential model, the recovery rate is virtually as good as that for the optimal design (96.4% vs. 97.3%).

Figure 5.

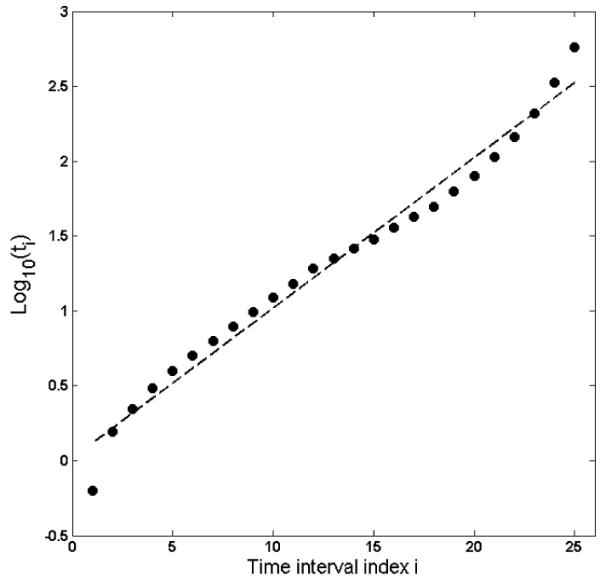
Plot of the optimal 25-point design (circles) for discriminating between the power and exponential models. The dashed line represents the best-fitting geometric design, log₁₀(t_i) = 0.014 + (0.100)i, or equivalently, t_i = 1.26t_i-1 with t₀ =1.03, i = 1,..., 25.

Analysis of an optimal design in the context of poorer designs can reveal what makes a design optimal. With enough time intervals that are geometrically spaced, the design is likely to be close to optimal for discriminating the power and exponential models. Information like this can be used as a heuristic in testing these models, not just in the context of forgetting, but also in other fields were human or animal performance exhibit a similarly shaped function (e.g., practice effects; Anderson, Fincham & Douglass, 1999).

The recovery rates in Table 2 are for a binomial sample size of n = 100. Because model discriminability can vary with sample size, it is useful to know how the results change at smaller and larger sample sizes. Model recovery tests were therefore performed for all four designs when the number of time intervals is five (N = 5) at sample sizes ranging from n = 10 to n = 1000 for each time interval. The results are shown in Figure 6, with sample size on the x axis and recovery rate on the y axis. Note that each data point in the figure was estimated outside of the DO algorithm based on a sample of 5000 quartets, (θ_A, y_A, θ_B, y_B) generated under the given design according to equation (3). Because variability decreases as sample size increases, model recovery rate will increase with any design, so it is not surprising that this trend is present.

Figure 6.

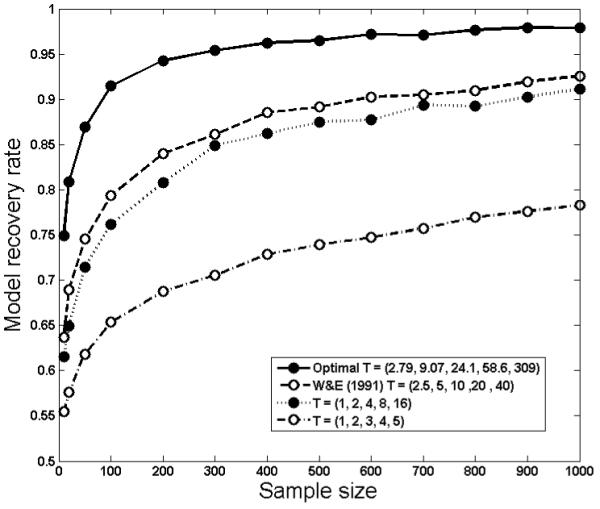
Estimated model recovery rates as a function of sample size for the four five-point designs in Table 2, for discriminating between POW and EXP.

Of more interest are the differences across designs. Even with small samples (20, 50), the optimal design has a sizable recovery advantage over the others, with this advantage being maintained across sample sizes. To show how profitable the optimal design can be over the others, suppose that an experimenter wishes to design an experiment with the goal of achieving a 90\% overall model recovery rate. If the optimal design of T = (2.79, 9.07, 24.1, 58.6, 309) is used, the desired recovery rate can be achieved with about 100 independent Bernouilli trials (i.e., sample size n = 100 presentations at each time point) of stimulus presentation in the experiment. In contrast, use of the Wixted and Ebbesen (1991) design of T = (2.5, 5, 10, 20, 40) or the geometric design of T = (1, 2, 4, 8, 16) would require six or nine times more trials, respectively, to achieve the same recovery performance. These results clearly demonstrate the significant and tangible advantages that design optimization can bring about in model discrimination experiments.

In our last demonstration of design optimization with retention models, we expanded the comparison to all six models in Table 1. The four additional models were chosen because they are strong contenders (hyperbolic) or include the power and exponential models as special cases, making the task of discriminating among them particularly arduous. How good is the optimal design in this situation?

With six models, the global utility function U(d) in equation (3) consisted of six additive terms, instead of two, and involves a total of 36 model fitting exercises. Specifically, for a given design, we generated data from one of the six models, then fitted each of the six models, including the data generating model, to the data, calculated six FIA values, and identified the model with the smallest MDL value. If that model happened to be the data generating model, the local utility u(d, θ, y) was set to 1 and otherwise to 0. This was repeated for the remaining five models.

The optimal design for the six-model comparison was T = (1.23, 6.50, 24.9, 124,556). The analyses that yielded the results in Figure 6 were repeated for the six models: Model recovery rates for the same three fixed designs were compared with the optimal design across sample sizes. The results are graphed in Figure 7. The most noticeable changes when six models were compared are that model recovery rate is significantly worse overall and the poorer designs are less differentiated. In contrast to the two-model comparison, differences in design quality do not begin to emerge until sample size reaches 100, and even at this value the differences are small. One reason for this is that with so many highly competitive models, the sample size necessary to distinguish them must be considerably larger than with two models. The optimal design takes advantage of the benefits of a larger sample (e.g., smaller variance), leading to dramatic improvements in recovery as sample size increases. In contrast, the three other designs do so less well, and thus show much more modest improvements in recovery at larger sample sizes. The net result is that the optimal design is considerably superior to the others when six than two models are compared.

Figure 7.

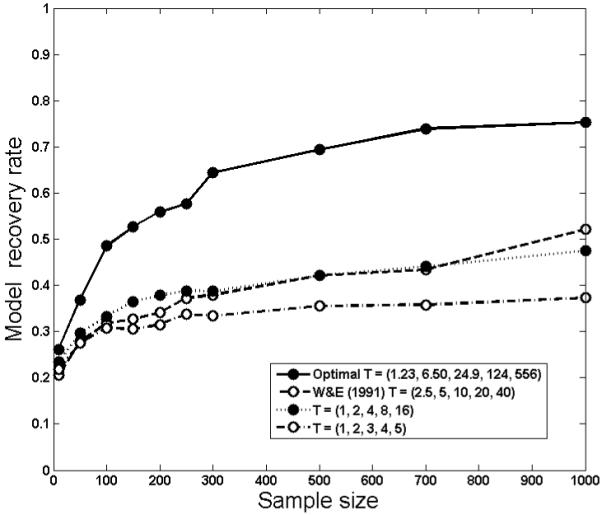
Estimated model recovery rates as a function of sample size for four designs in discriminating among the six retention models in Table 1. The optimal design was found by the DO algorithm as the one that maximally discriminates the six retention models, and the other three designs are from Table 2.

The data in Figure 7 clearly show the difficulty of designing an experiment that can differentiate highly competitive retention models. Even the best design at a large (and unrealistic) sample size has a success rate of no greater than 0.75, although it is still significantly higher than the base-rate of choosing among six models (i.e., 1/6 = 0.1667). A design might be optimal, but this does not necessarily make it satisfactory. If models cannot be discriminated with even an optimal design, then they are quantitatively indistinguishable. Not until they are modified or expanded (e.g., adding new parameters) will they be distinguishable. The results in Figure 7 suggest that retention models may exhibit this characteristic of virtual indistinguishability. Even with a sample size of 100, an optimal design will distinguish between them with a probability of only 0.49.

Optimal Designs for Discriminating Categorization Models

Identification of optimal designs for discriminating retention models involves optimization over a design variable that is a continuous dimension, such as time. The DO algorithm can be applied to discrete variables (e.g., dichotomous stimulus properties) as well, making it quite versatile in terms of what can be optimized. We demonstrate this in the context of categorization models.

Categorization, or category learning, is one of the most fundamental behaviors humans and animals perform, and often serves as a starting point for studying higher-level cognitive phenomena such as reasoning, language, problem solving, and decision making. There are currently two dominant theoretical explanations of how we learn to categorize objects into psychologically equivalent classes. They are the prototype and exemplar theories. According to the prototype account of category learning, we extract a prototypic representation for each category from the instances of that category, storing only a summary of the information in memory, against which new stimuli are compared during categorization (Reed, 1972). In contrast, exemplar theories prescribe that we encode and store in memory all information about every encountered instance (Medin & Schaffer, 1978).

The question of which of these two theories better accounts for human categorization performance has been intensely debated to this day, with the empirical findings often being mixed (e.g., Smith & Minda, 2000; Nosofsky & Zaki, 2002; Vanpaemel & Storms, 2008). One reason for the inconclusive results is that the experimental designs might not have been the most effective for distinguishing models from the two theoretical perspectives. We applied the DO algorithm to find an optimal design for discriminating two well-studied categorization models, and then compared the optimal design to the designs that were used in Smith and Minda (1998).

Multiple prototype and exemplar models have been proposed. We compared the multiplicative prototype model (PRT; Smith & Minda, 1998) with the generalized context (exemplar) model (GCM; Nosofsky, 1986). Given two categories, A and B, both models assume that the number of category A decisions out of n Bernoulli trials given the presentation of an input stimulus S_i follows a binomial distribution with probability P(A|S_i) and sample size n, and, further, that the probability P(A|S_i) is proportional to the similarity between stimulus S_i and category A. The two models differ in how similarity is calculated. In PRT, category similarity is obtained by calculating a similarity measure between stimulus S_i and a category prototype S_A. In GCM, the similarity is calculated by summing across individual similarities. The similarity measure s_ij between the i-th and j-th stimuli is assumed to follow an exponentially decaying function of the city-block distance between the two

$$S_{ij}=\exp \left[-c\left(\sum _{m=1}^M{w}_m\mid x_{im}-x_{jm}\mid \right)\right].$$ (7)

In this equation, x_im is the feature value of stimulus S_i along dimension m, c (> 0) is the specificity parameter representing the steepness of the exponential decay, and w_m (0 < w_m < 1) is the attention parameter applied to the m-th feature dimension satisfying ${\sum }_{m=1}^M{w}_m=1$. In terms of the above similarity measure, the two models define the categorization probability as

$$\mathrm{PRT}:P(A\mid S_i)=\frac{S_{iA}}{\sum _C{S}_{iC}}$$ (8)

$$\mathrm{GCM}:P(A\mid S_i)=\frac{\sum _{j\in A}{S}_{ij}}{\sum _C\sum _{k\in C}{S}_{ik}}$$ (9)

where C = {A, B}. Note from the above equation that both models assume M parameters consisting of θ = (w₁,...,w_M-1, c).

A goal of Smith and Minda (1998) was to determine whether PRT or GCM better reproduces participants’ categorization performance. In the experiment, participants learned to categorize nonsense words into one of two categories, with category feedback provided. There were a total of 14 stimuli to learn, each of which was represented by a six-dimensional (i.e., M = 6) binary vector, with seven belonging to category A and the other seven belonging to category B. Each stimulus was presented four times (i.e., n = 4) in each block of 56 trials.

One feature of the experimental design of Smith and Minda (1998) that can be exploited to improve model discrimination is category structure. There are 64 (= 2⁶) different stimuli that can be constructed by combining the six binary features. The number of possible partitions of 64 stimuli into two categories, each with seven stimuli, is so daunting (₆₄ C₇·₅₇ C₇ ≈ 1.64 × 10¹⁷) that it is difficult to know how good one’s choice will be for discriminating models. Shown in the top half of Table 3 are the category structures that were used in Experiments 1 and 2 of Smith and Minda (1998). Although these two designs might be intuitively appealing and might even have certain theoretical justification, it is difficult to know how effective the designs are for discriminating between PRT and GCM. We used the DO algorithm to identify an optimal design that maximizes model recovery rate.

Table 3.

The top row contains the category structures used in Smith and Minda (1998, Experiments 1 and 2). The bottom row contains the category structures of a simple design and the optimal design found by the DO algorithm. The number above each design is the estimated model recovery rate obtained using the 64 stimulus vectors shown in Appendix B. The numbers in parentheses are the means and standard deviations of recovery rates based on 10 independently and randomly generated replications of the set of stimulus vectors

Smith & Minda (1998) experiments
Linearly separable design 72.9% (71.7 ± 1.4%)		Nonlinearly separable design 88.8% (89.4 ± 0.6%)
Category A	Category B	Category A	Category B
0 0 0 0 0 0	1 1 1 1 1 1	0 0 0 0 0 0	1 1 1 1 1 1
0 1 0 0 0 0	1 1 1 1 0 1	1 0 0 0 0 0	0 1 1 1 1 1
1 0 0 0 0 0	1 1 0 1 1 1	0 1 0 0 0 0	1 0 1 1 1 1
0 0 0 1 0 1	1 0 1 1 1 0	0 0 1 0 0 0	1 0 1 1 1 1
1 0 0 0 0 1	0 1 1 1 1 0	0 0 0 0 1 0	1 1 1 0 1 1
0 0 1 0 1 0	1 0 1 0 1 1	0 0 0 0 0 1	1 1 1 1 1 0
0 1 1 0 0 0	0 1 0 1 1 1	1 1 1 1 0 1	0 0 0 1 0 0

Simple design 53.1% (53.9 ± 1.0%)		Optimal design 96.3% (93.8 ± 3.5%)
Category A	Category B	Category A	Category B
0 0 0 0 0 0	1 1 1 1 1 1	0 0 1 1 1 0	0 0 0 0 1 0
0 0 0 0 0 1	1 1 1 1 1 0	0 1 0 0 0 1	0 1 0 1 0 0
0 0 0 0 1 0	1 1 1 1 0 1	0 1 0 1 1 0	0 1 1 1 0 1
0 0 0 1 0 0	1 1 1 0 1 1	0 1 1 0 1 0	1 0 0 0 1 0
0 0 1 0 0 0	1 1 0 1 1 1	0 1 1 1 0 0	1 1 0 0 1 0
0 1 0 0 0 0	1 0 1 1 1 1	1 0 0 0 0 1	1 1 0 1 0 1
1 0 0 0 0 0	0 1 1 1 1 1	1 1 0 1 1 1	1 1 1 0 1 0

The application of design optimization to this problem involves searching through the discrete space of literally billions of different designs. It turns out that for most of these, PRT is unidentifiable. That is, the model is not sufficiently constrained to yield a unique set of parameter values given observed data. Identifiability is required for maximum likelihood estimation and model selection, and therefore for the application of the DO algorithm.

This problem necessitated a modification to PRT. A quick examination of 500 randomly selected designs revealed that PRT was unidentifiable for 98% of them.⁴ To make PRT identifiable, we modified the model in such a way that its binary feature values were replaced by continuous ones. Specifically, we substituted each 0 in the 64 six-dimensional binary vectors by a random number generated on a uniform distribution between 0.0 and 0.1 and similarly, each 1 by a random number generated on a uniform distribution between 0.9 and 1.0. Appendix B lists all 64 stimulus vectors created in this way and subsequently used in all simulations. With this change, the model is now interpreted in terms of low (0.0 - 0.1) or high (0.9 - 1.0) probability of the presence of a specific feature instead of the absence (0) or presence (1) of that feature. The modification made PRT identifiable in 97% of a random sample of 500 designs.

We applied design optimization to the two categorization models using the binary local utility function expressed as model recovery decisions in equation (6). The specificity parameter of both models was restricted to that typically found (0 < c < 20). The quality of the optimal design was evaluated by comparing its model recovery rate with that of three comparison designs, two from Smith and Minda (1998) and a third one labeled ‘simple design,’ in which the feature values that defined each category are dominated by zeros (category A) or ones (category B). This third design and the optimal design found by the DO algorithm are shown in the lower half of Table 3.

The percentages above all four designs (top value) are the estimated model recovery rates. The optimal design is superior to the three comparison designs (96.3% vs 53.1% - 88.8%).⁵ It looks more complex, with items within and between categories never displaying a predictable pattern. Differences in the quality of the two Smith and Minda designs are also evident, with the nonlinearly separable design being quite good and significantly better than the linearly separable design. The quality of the simple design is somewhat surprising. One might think that it would have made a good design given its simplicity, but it turns out to be worst of all, barely above the chance level (53.1%). One lesson we can learn from this investigation is that what might be an intuitively appealing design might not be the most discriminating design, which can defy easy description. It is in exactly this situation where design optimization is most helpful.

Recall that the quality of the optimal design, and also the three comparison designs, was evaluated conditional upon the particular choice of stimulus vectors shown in Appendix B. It is of interest to examine whether the quality of the four designs depends on the choice of stimulus vectors. To this end, we generated ten replications of each set of stimulus vectors. Each set was generated using the same rules used to generate the original set of 64 vectors in the appendix. The mean and standard deviation of model recovery rates for each design are shown in parentheses in Table 3. For all four designs, the recovery rates obtained with the original stimulus set are well within the ranges obtained for different choices of stimulus vectors.⁶ These results demonstrate that the conclusions obtained under the particular set of stimulus vectors are robust and generalizable to other choices of stimulus vectors.

General Discussion

A well-designed experiment has qualities of a good work of art: It is creative and elegant. These qualities come through in the idea motivating the experiment and the choice and manipulation of variables that test it. Good designs can also be simple, and no matter the outcome, yield data that are highly informative about the topic under investigation.

But good designs rarely come easy. One reason for this is that the consequences of some design decisions (e.g., stimulus selection in categorization experiments) are difficult to evaluate. Design optimization can assist in some of the decision making. We demonstrated its potential in two areas of cognitive modeling, retention and categorization. In its application to retention models, the DO algorithm found designs that were far superior to several comparison designs, including one used in a well-known study in the literature. We also demonstrated the generality of the method by showing that it scales up well when six rather than two retention models are compared, and by applying it to a very different type of design problem, defining the stimulus structure of two categories that will optimally discriminate between two categorization models. Not only did the algorithm find a superior design, but as in the case of the retention models, the method can provide information about the quality of past designs.

In the following paragraphs, we discuss the relationship of design optimization to extant methods of model discrimination, address some practical issues in interpreting design optimization results, and finally, discuss extensions of the methodology.

Relationship of Design Optimization to Landscaping

Design optimization is related to landscaping, a method of assessing model discriminability given a fixed experimental design (Navarro et al, 2004; Wagenmakers, Ratcliff, Gomez, & Iverson, 2004). Landscaping has its roots in the field of model selection. A landscape graph consists of two frequency distributions of the relative fits of two models. Specifically, to obtain a landscape, we first generate simulated data sets from one model and then fit both models to all data sets by computing their log maximum likelihood (LML) values. The resulting LML differences between the two models are then plotted to yield a frequency distribution. Similarly, the distribution of the relative fits to data sets generated by the other model is created. The extent to which the two distributions overlap indicates how easily one model can be discriminated from the other based on their relative fits: The greater the separation, the easier it is to discriminate between the models.⁷

Design optimization can be thought of as a tool that identifies the experimental design that maximizes the distance between the distributions. A landscape of the power and exponential models for the comparison design T = (1, 2, 3, 4, 5) in Table 2 is shown in the upper panel of Figure 8. The solid curve represents the distribution of the relative fits of the models to data generated by the power model, and the dotted curve represents the relative fits of the two models to data generated by the exponential model. Note how significantly the two distributions overlap; the model recovery rate of the two models under FIA is equal to 65.3%. The landscape for the same two models using the optimal design T = (2.79, 9.07, 24.1, 58.6, 309) is shown in the lower panel of Figure 8. The separation of the distributions provides visual confirmation of the superiority of the optimal design. Comparison across graphs shows the extent to which the optimal design is better.

Figure 8.

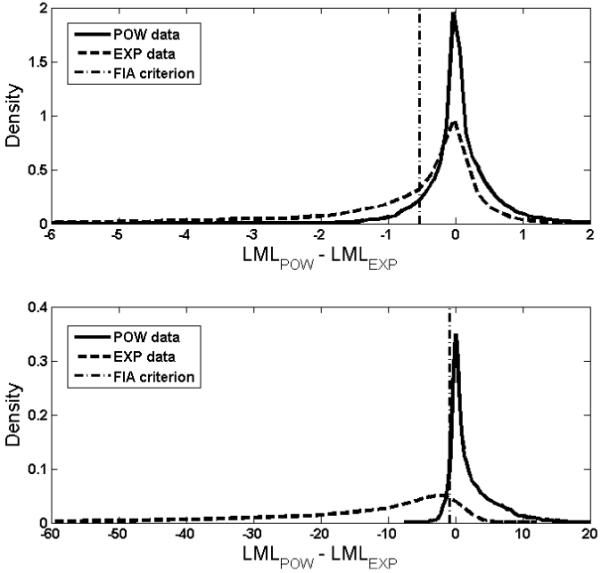
The inherent discriminability of the power and exponential models under two different designs. Graphed are the differences in log maximum likelihood (LML) of the models. The top panel shows the distributions obtained using the design T = (1, 2, 3, 4, 5). The bottom panel shows the distributions obtained using the optimal design solution T = (2.79, 9.07, 24.1, 58.6, 309). See text for details of the simulations.

The connection between design optimization and landscaping suggests an easy-to-apply, but crude, method of identifying an optimal design: Landscape the models across multiple designs and use the one that discriminates the models most. If the design space is small, this method might succeed in identifying an optimal design. Even with a large design space, one could hit upon an optimal design from trial and error (or by automating landscaping), especially if constraints could be placed on the design. Minimally, the use of landscaping will aid in understanding the effects of different designs on model discriminability.

DO can also aid in interpreting landscaping analyses. For example, Navarro et al (2004) used landscaping to compare highly competitive models of retention using data sets from a large number of studies. In one analysis, sample size (N) and the number of time intervals (T) were examined independently and together to determine their contributions to model discriminability. Surprisingly, both were found to be weak predictors of model discriminability. The results in Table 2 suggest that what is most important is the spacing of the points in time at which memory is probed, something Navarro et al did not examine.

Practical Issues in Implementing the DO Algorithm

There are practical issues that the researcher needs to be cognizant of when implementing the design optimization algorithm and interpreting the ensuing results. Before discussing these, it is useful to recount the computational steps in the algorithm. The first step in applying design optimization is to specify the form of the sampling distribution p(y|θ, d) that describes the probability of observing an outcome y given a parameter θ and a design d for a given model, and also the form of the prior distribution p(y|d) of the parameter θ in equation (3). The next step is the specification of the form of the real-valued local utility function u(d, θ, y) that describes the quality of a design d. Since y, θ and the model are all unknown prior to experimentation, the function that is actually optimized is the global utility function U(d) in equation (3) that takes the form of the expected local utility function, averaged over outcomes, parameters, and models weighted by the respective priors. Finally, the DO algorithm is applied to find numerically the optimal design d* that maximizes U(d).

One of the limitations of the above formulation is that it is applicable only to quantitative models with parameterized families of sampling distributions expressed in analytic form. Until a more generalized form of DO is developed, it will be inapplicable to models without explicit sampling distributions, such as connectionist models and other simulation-based models (Anderson & Lebiere, 1998; Busemeyer & Townsend, 1991; Shiffrin & Steyvers, 1997).

Another limitation is the assumption that the set of models under consideration includes the model that actually generated the data (i.e., the “true” model). This assumption, obviously, is likely to be violated in reality because our understanding of the topic being modeled is sufficiently incomplete to make any model only a first-order approximation of the true model. Ideally, one would like to optimize a design for an infinite set of models representing all conceivable realities. To our knowledge, no implementable statistical methodology is currently available to solve a problem of this scope.

The technique is also limited in the range of design variables to which it can be applied. The design variable $d$ to be optimized can be discrete or continuous and even a vector or matrix, but what is required is that the effects of the design variable on the sampling distribution, the prior, or the local utility function must be expressed in explicit functional, or at least computational, forms so that equation (3) can be evaluated on computer within the DO algorithm. Optimization is not possible on design variables that cannot be quantified in this way. Examples include the types of stimuli presented across different retention and categorization studies (e.g., words, nonsense strings, stick figures), the modality of presentation, and type of task (recall or recognition). To the extent that these features of the experiment can be quantified in the model so that they could affect the sampling distribution, the prior, or local utility function, they could be optimized. In general, the more detailed the models (e.g., more parameters linked to mental process) the more ways in which an experiment can be optimized.

It is important for users of the DO algorithm to give some thought to the choice of the local utility function u(d, θ, y). One can think of a number of candidate forms to choose from, each as a measure of model dissimilarity and with its own theoretical justifications. They include the sum of squares error, model recovery rate under a given model selection method (e.g., FIA, AIC, Bayes factor), an information theoretic measure such as the Kullback-Leibler distance (Box & Hill, 1967), and the Hellinger distance (Bingham & Chapman, 2002), to name a few. The specific choice among such measures would be dependent upon the goals and preference of the experimenter, its computational feasibility, and interpretability considerations.

Design optimization as formulated in equation (3) requires the specification of the prior distribution p(θ), from which parameters are to be sampled. We used Jeffreys prior (Jeffreys, 1961) for two reasons: non-informativeness and reparameterization invariance. Jeffreys prior is non-informative in the sense that it assumes no prior information about the parameter (Robert, 2001, pp. 127-141). Reparameterization invariance means that the statistical properties of a model such as its data-fitting ability and model complexity are independent of how the model is parameterized, as they should be.

To illustrate, the exponential model of retention can be expressed as two different functional forms, p = ae^-bt and p = ac^t, which are related through the reparameterization of c = e^-b. With Jeffreys prior, which is reparameterization-invariant, the solutions to the design optimization problem remain unchanged under different, but statistically equivalent, formulations of the model. Unfortunately, the uniform prior defined as p(θ)= c_o for a fixed constant c_o, which is also non-informative, is not reparameterization invariant. As such, one would obtain different optimal designs under the uniform prior depending on the specific parameterizations of the model. This situation is obviously troublesome and hard to justify.

One last point to make regarding priors is that one could, of course, use an informative prior, provided that the prior is either readily available or can be constructed from data sets of previously published studies using Bayes rule. To elaborate, given observed data, we first identify and write down the likelihood function (e.g., binomial or normal), expressed as a function of a model’s parameter, that specifies the likelihood of the parameter given the data. Next, assuming a non-informative prior (e.g., Jeffreys) for the parameter, the posterior distribution is sought by applying Bayes rule. This is done either algebraically, if possible, or numerically using Markov chain Monte Carlo. The resulting posterior distribution is then used as the prior distribution within the DO algorithm.

The fact that the design optimization problem in equation (3) is being solved numerically using the DO algorithm has two important implications that the researcher should be mindful of when implementing the algorithm and interpreting its outputs. First, the algorithm belongs to a class of MCMC methods developed in statistics for sampling from an arbitrary (target) distribution (Gilks, Richardson & Spiegelhalter, 1996). Briefly, on each iteration of an MCMC chain, one first draws a candidate sample from an easy-to-sample-from distribution known as the proposal distribution (e.g., normal or uniform distribution) and then accepts or rejects the sample according to a prescribed transition rule, such as Metropolis-Hastings sampling, using information about the target and proposal distributions. This is repeated over a series of iterations until the chain becomes stationary, from which point on the collection of all accepted samples in subsequent iterations follows the target distribution according to the theory of Markov chain. The target distribution is then estimated based on a large number (e.g., 5000) of accepted samples after convergence is achieved. Given that the sample is finite, the resulting estimate represents a numerical approximation to the target distribution. If the samples are collected prematurely before the chain has converged, then the estimated distribution would be biased. In practice, it is often difficult to assess chain convergence, and further, fully general and easily applicable standards for convergence diagnostics have yet to be developed. In our implementation of the algorithm, we assessed convergence behavior by the combination of visual inspection of the chain and multiple runs of the algorithm, as recommended by practicing statisticians (e.g., Robert & Casella, 2004, chap. 12).

The second implication to consider when using the DO algorithm is that it requires adjusting what are known as tuning parameters (Gilks, Richardson & Spiegelhalter, 1996; Robert & Casella, 2004). They include the initial design to begin with on the first iteration of the algorithm, the shape and variance parameters of the proposal distribution, and the annealing schedule for increasing J in equation (5). Theoretically, the chain is supposed to converge to the target distribution independently of the values of the tuning parameters, but this holds only if the chain is run indefinitely. In practice, the chain has to be terminated after running it over a finite number of iterations. Consequently, the solution obtained at the end of a finite run of the algorithm can be suboptimal, reflecting the residual effects of the particular choices of tuning parameters. It is therefore plausible that the optimal designs we found using the algorithm for the retention and categorization models could turn out to be suboptimal despite steps we took to address the issue (e.g., adjusting tuning parameters and performing sensitivity analyses). What is comforting, however, is that although these designs might not be globally optimal, they are likely close to it, and all are superior to those used in the literature.

Finally, one obvious limitation in the application of DO to model discrimination in psychology is the technical sophistication necessary to use the methodology. In particular, knowledge of density simulation using MCMC is required, which is foreign to many modelers let alone non-modelers. The additional details on the DO algorithm in Appendix A are a modest attempt to bridge this gap. Those with some background in statistics and probability theory should be able to understand the skeleton of the algorithm. Even if this additional information proves inadequate for the interested reader, we expect the gap to be temporary. New generations of the algorithm will likely not only be more powerful, being faster and readily applicable to more complex designs, but they may also overcome many of the technical and implementational details that must be considered with the current algorithm. Such advances will make DO more widely accessible.

Multiplicity of Design Solutions

Our experience with the DO algorithm suggests that there are multiple, close-to-optimal designs for retention models. To give a concrete example, for the five-point optimal designs T_opt = (2.79, 9.07, 24.1, 58.6, 309) in Table 2 with its estimated recovery rate of 91.5%, we identified two additional designs, T₁ = (2.44, 7.73, 20.0, 46.0, 239) and T₂ = (3.38, 10.1, 33.4, 93.3, 381), with their estimated recovery rates being virtually identical to that of T_opt within sampling error, that is, 89.9% and 90.9%, respectively. Clearly, one could find many more designs with recovery performance being close to or nearly identical to that of the optimal design. This multiplicity of optimal solutions is also evident in the top panel of Figure 4, which shows the ten best designs and their associated log utility values, which are extremely close to one another.

What is the reason for the multiplicity of solutions? An explanation can be found by examining the model equations in Table 1. Consider the two-parameter exponential model (EXP) which predicts the probability of correct recall as p_i = ae^-bt_i for a given design T = (t₁, t₂, ..., t_N) and a parameter vector θ = (a, b). A simple algebraic manipulation proves that there exists another design defined as T_α = (αt₁, αt₂, ...,αt_N)$ for any α > 0 that makes exactly the same probability predictions as the above but with a different parameter θ = (a,b/α). How many such designs are there? There are an infinite number of them since the equivalence holds for any choice of a positive value of α.

A similar equivalence can be shown to hold for three other models of retention: HYP, EXPA and EXPE. For POW and POWA, it turns out that an equivalence does not hold exactly, but instead, hold semi-exactly for large time intervals. More generally, for two designs, d₁ and d₂, that make the same model prediction with different parameter values, θ₁ and θ₂, respectively, by definition, the local utility function will be the same for them as well, u(d₁, θ₁, y) = u(d₂, θ₂, y). Importantly however, the two designs do not necessarily yield the same value as the global utility function (i.e., U(d₁) ≠ U(d₂)). This is because U(d) in equation (3) is obtained by integrating the local utility function weighted by the prior p(θ), the value of which depends upon the parameter. Therefore, multiple designs that are equivalent at the level of model prediction do not necessarily translate into equivalent design solutions at the level of U(d).

It is still, however, possible to observe nearly equivalent design solutions, especially if the prior is mostly flat or varies slowly over the parameter space. This is apparently the case with the retention models. What it means is that if we were to plot the global utility function U(d) over the entire design space, we would not see a lone peak at some d*, but instead, we would see many peaks that together form a high ridge resembling something like the Rocky Mountains Range. Given these observations, one should interpret the retention results from this perspective.

Extensions of Design Optimization

The design optimization framework introduced in this paper is sufficiently general to permit extensions to more complex optimization problems and other ways of achieving optimization. Many experiments require numerous decisions be made about the design. An obvious extension of the current method is to optimize designs with respect to multiple design variables simultaneously. For instance, in our study of retention models, the choice of time intervals T = (t₁, .., t_N) was the sole design variable to be optimized, with the number of time intervals (N) and the number of binomial samples (n) collected at each time interval both being held constant. Naturally, one would like to optimize designs with respect to all three variables, with this super design variable being defined as d_super = (N, n₁, n₂, ..., n_N, t₁, t₂, ..., t_N). Preliminary investigation of this possibility has not yet been successful because the problem is computationally challenging. The super design variable consists of a combination of discrete (n_i) and continuous (t_i) variables, and the dimension (N) of the design space itself is a variable being optimized. The current DO algorithm is not up to this more complex task, and a new, more powerful algorithm will have to be developed to handle the challenges presented by simultaneous, multi-variable optimization.

Another way to extend the current design optimization framework is to apply it iteratively over repetitions of an experiment, usually with a minimal number of observations in each repetition, rather than only once. One takes advantage of the information gained in one experiment to improve optimization in the next. Experimental designs are adaptively updated over a series of multiple stages in which design optimization and experimentation are performed repeatedly in succession. Sequential design optimization is generally more efficient (i.e., requiring fewer observations to discriminate models) than non-sequential design optimization, but can be computationally much more challenging to implement. This is because in sequential design optimization an optimal design is being sought based on the outcome at the current stage but also by taking into account the potential for future stages. Despite this challenge, sequential design optimization, in particular from a Bayesian D-optimum design perspective, has recently been explored and applied to adaptive parameter estimation problems that arise in psychophysics (Kujala & Lukka, 2006; Lesmes, Jeon, Lu & Dosher, 2006), neurophysiological experiments (Lewi, Butera & Paninski, in press), clinical trials (Muller, Berry, Grieve, Smith & Krams, 2007), astrophysics (Loredo, 2004), and educational games (Kujala, Richardson & Lyytinen, in press).

Sequential design optimization can be implemented within the current (non-sequential) design optimization framework with minor modifications. The process would proceed as follows. Given initial model and parameter priors, we would seek an optimal design using the DO algorithm. Using this optimal design, we would conduct an experiment. The data would then be used to update the model and parameter priors using Bayes rule. With the resulting model and parameter posteriors, the DO algorithm would again be run to seek another optimal design. This procedure would be repeated over a series of stages until an appropriate stopping criterion is met. We are currently exploring the promise of sequential design optimization.

Conclusion

Perusal of the literatures in which models of a cognitive process are compared shows that it is no easy task to design an experiment that discriminates between them. One reason for this is uncertainty about the quality of the experimental design in achieving its goal. The design optimization algorithm can assist in overcoming this problem, and thereby improve the likelihood of model discrimination. It can also provide information on the quality of past designs, possibly shedding light on why they did or did not succeed. Its application in psychology should lead to more informative studies that advance understanding of the psychological process under investigation as well as the models developed to explain them.

Appendix A

This appendix describes in greater detail the design optimization algorithm. The example makes use of the two retention models, POW and EXP, under Jeffreys’ priors, discussed in the General Discussion sectionof the paper. The reader is advised to read it prior to reading this appendix. An optimal design is defined as the one that maximizes the model recovery rate of the data-generating model using FIA-based model selection.

First, the global utility function U(d) in equation (3) is defined in terms of the design variable d, the likelihood function and the prior, which are given by

$$d=(t_1,t_2,...,t_N)(e.g.,N=3)$$

$$p(y\mid \theta ,d)=\prod _{i=1}^N\frac{n!}{(n-y_i)!y_i!}{p}_i{(\theta ,t_i)}^{y_i}{(1-p_i(\theta ,t_i))}^{n-y_i}$$

$$I_d{\left(\theta \right)}_{ij}=-\frac{1}{n}E\left[\frac{{\partial }^2\ln f(y\mid \theta )}{\partial {\theta }_i\partial {\theta }_j}\right](i,j=1,2)$$

$$p(\theta \mid d)=\frac{\sqrt{\mid I_d\left(\theta \right)\mid }}{\int \sqrt{\mid I_d\left(\theta \right)\mid }d\theta }$$

where y = (y₁, y₂,..., y_N) with y_i = {0, 1, 2,..., n} and θ = (a,b). The binomial probability parameter p_i(θ, t_i) in the above equation takes the form of p_i(θ, t_i) = a(t_i+1)^-b for POW and p_i(θ,t_i = ae^-bt_i for EXP. It is worth noting that the Fisher information matrix generally depends upon the design as well as the parameters. This is indicated by the subscript d in I(θ).

In order to find an optimal design d* that maximizes U(d), one should be able to sample (y_A1,..., y_AJ, θ_A1,..., θ_AJ, y_B1,..., y_BJ, θ_B1,..., θ_BJ) from the artificial distribution h_J(·) in equation (5), where each y_.. is a N-dimensional vector and each θ_.. is a 2-dimensional vector. In what follows, we describe how this is performed using a combination of three statistical computing techniques: maximum likelihood estimation, numerical integration, and density simulation using Markov chain Monte Carlo.

The simulation results discussed in the present article were obtained by implementing the Resampling-Markov (R-M) algorithm that employs multiple interacting Markov chains, as described in Amzal, Bois, Parent and Robert (2006, p. 776). In this appendix, however, for the purpose of illustration, we describe Muller’s algorithm (Muller, Sanso, De Iorio, 2004, Algorithm 1, pp. 789-790) instead. This algorithm employs a single Markov chain and therefore is easier to implement and conceptually simpler to understand. The price to pay for easier implementation is a loss in efficiency (i.e., slower convergence), although in theory both algorithms should find an optimal design if run long enough. The steps of the Muller algorithm are as follows:Muller Algorithm:

1. Initialize iteration t = 1, J(t) and d(t) (e.g., J(1) = 10, d(1) = (4,5,6) for N = 3).

2. Given d(t), obtain the complexity penalty measures for POW and EXP by numerically integrating the third term of FIA in equation (6) and combining the resulting value with that of the second term.

3. for j = 1: J(t){

   • (3.1) Sample θ_Aj(t) from p(θ_A|d(t)) (e.g., by constructing another separate Markov chain);
   • (3.2) Sample y_Aj(t) from p(y_A|θ_Aj(t), d(t));
   • (3.3) Fit both models, POW and EXP, to data y_Aj(t), find the maximum likelihood values (e.g., using the Newton optimization algorithm) and combine them with the complexity penalty measures according to equation (6) to obtain FIA_A and FIA_B;
   • (3.4) Set u(d(t), θ_Aj(t), y_Aj(t)) to 1 if FIA_A < FIA_B and to 0 otherwise;
   • (3.5) Sample θ_Bj(t) from p(θ_B|d(t)) (e.g., by constructing another separate Markov chain);
   • (3.6) Sample y_Bj(t) from p(y_B|θ_Bj(t), d(t));
   • (3.7) Fit both models, POW and EXP, to data y_Bj(t), find the maximum likelihood values (e.g., using the Newton optimization algorithm) and combine them with the complexity penalty measures according to equation (6) to obtain FIA_A and FIA_B;
   • (3.8) Set u(d(t), θ_Bj(t), y_Bj(t)) to 1 if FIA_A > FIA_B and to 0 otherwise;

   }end.

4. Evaluate $w\left(t\right)={\sum }_{j=1}^{J\left(t\right)}\ln [p\left(A\right)u(d\left(t\right),{\theta }_{Aj}\left(t\right),y_{Aj}\left(t\right))+p\left(B\right)u(d\left(t\right),{\theta }_{Bj}\left(t\right),y_{Bj}\left(t\right))]$ (e.g., set p(A) = p(B) = 0.5).

5. Propose a new, candidate design d^c from a symmetric proposal distribution q(d|d(t)) such that q(d₁|d₂) = q(d₂|d₁) for all d₁ and d₂ (e.g., q(d|d(t)) ∼ N(d(t), σ²I)).

6. Given d^c, obtain the complexity penalty measures for POW and EXP by numerically integrating the third term of FIA and combining the resulting value with that of the second term.

7. for j = 1: J(t){

   • (7.1) Sample θ_Aj,c from p(θ_A|d^c) (e.g., by constructing another separate Markov chain);
   • (7.2) Sample y_Aj,c from p(y_A|θ_Aj,c,d^c);
   • (7.3) Fit both models, POW and EXP, to data y_Aj,c, find the maximum likelihood values (e.g., using the Newton optimization algorithm) and combine them with the complexity penalty measures according to equation (6) to obtain FIA_A and FIA_B;
   • (7.4) Set u(d^c, θ_Aj,c, y_Aj,c) to 1 if FIA_A < FIA_B and to 0 otherwise;
   • (7.5) Sample θ_Bj.c from p(θ_B|d^c) (e.g., by constructing another separate Markov chain);
   • (7.6) Sample y_Bj,c from p(y_B|θ_Bj,c, d^c);
   • (7.7) Fit both models, POW and EXP, to data y_Bj,c, find the maximum likelihood values (e.g., using the Newton optimization algorithm) and combine them with the complexity penalty measures according to equation (6) to obtain FIA_A and FIA_B;
   • (7.8) Set u(d^c, θ_Bj,c, y_Bj,c) to 1 if FIA_A > FIA_B and to 0 otherwise;

   }end.

8. Evaluate $w^c={\sum }_{j=1}^{J\left(t\right)}\ln [p\left(A\right)u(d^c,{\theta }_{Aj,c}\left(t\right),y_{Aj,c}\left(t\right))+p\left(B\right)u(d^c,{\theta }_{Bj,c}\left(t\right),y_{Bj,c}\left(t\right))]$.

9. Evaluate the acceptance probability defined as

   $$\mathit{AP}=\min \{1,\exp (w^c-w\left(t\right))\}$$

   • (9.1) Generate a uniform random number r between 0 and 1;
   • (9.2) If r < AP, accept the candidate design d^c and set d_next = d^c. Otherwise, leave d^c unchanged so set d_next = d(t).

10. Set t = t+1 and d(t) = d_next. Increase J such that J(t) ≥ J(t-1) following an annealing schedule (e.g., increase J by 1 every five iterations).

11. Repeat Steps 2-10 until the chain converges. All accepted d(t) ’s thereafter should represent an optimal design solution. In practice, one can estimate the optimal solution as the mean of m such d(t) ’s (e.g., m = 50)

    $${\widehat{d}}^{\ast }=\frac{1}{m}\sum _{t=t_c+1}^{t_c+m}d\left(t\right)$$

    where t_c denotes the iteration number at which the chain is judged to have converged.

Appendix B

Appendix B.

The tables below shows 64 stimulus vectors created from the corresponding 64 six-dimensional binary vectors by substituting a random number between 0.0 and 0.1 for each “0” and another random number between 0.9 and 1.0 for each “1”, and subsequently used in design optimization for the two categorization models

Stimulus	Feature element
Number	1	2	3	4	5	6
1	0.0223	0.0254	0.0226	0.0342	0.0723	0.0036
2	0.0240	0.0498	0.0615	0.0898	0.0452	0.9643
3	0.0626	0.0312	0.0874	0.0600	0.9810	0.0999
4	0.0343	0.0067	0.0527	0.0306	0.9385	0.9658
5	0.0053	0.0397	0.0742	0.9615	0.0632	0.0987
6	0.0361	0.0036	0.0385	0.9633	0.0993	0.9974
7	0.0107	0.0339	0.0811	0.9053	0.9250	0.0634
8	0.0355	0.0932	0.0917	0.9591	0.9284	0.9240
9	0.0232	0.0561	0.9736	0.0947	0.0655	0.0908
10	0.0840	0.0267	0.9317	0.0765	0.0041	0.9049
11	0.0577	0.0133	0.9567	0.0066	0.9340	0.0682
12	0.0340	0.0608	0.9955	0.0918	0.9943	0.9804
13	0.0578	0.0359	0.9726	0.9094	0.0420	0.0241
14	0.0254	0.0189	0.9417	0.9140	0.0868	0.9543
15	0.0232	0.0168	0.9339	0.9455	0.9808	0.0021
16	0.0713	0.0227	0.9438	0.9084	0.9045	0.9858
17	0.0485	0.9996	0.0116	0.0872	0.0674	0.0763
18	0.0235	0.9190	0.0127	0.0478	0.0329	0.9682
19	0.0099	0.9835	0.0641	0.0714	0.9057	0.0165
20	0.0190	0.9262	0.0784	0.0068	0.9516	0.9709
21	0.0299	0.9836	0.0858	0.9550	0.0289	0.0209
22	0.0936	0.9256	0.0450	0.9809	0.0529	0.9564
23	0.0218	0.9585	0.0673	0.9635	0.9641	0.0804
24	0.0261	0.9040	0.0969	0.9812	0.9077	0.9347
25	0.0918	0.9603	0.9682	0.0225	0.0293	0.0470
26	0.0579	0.9074	0.9738	0.0803	0.0097	0.9801
27	0.0134	0.9016	0.9875	0.0340	0.9155	0.0924
28	0.0557	0.9978	0.9978	0.0453	0.9645	0.9825
29	0.0405	0.9124	0.9151	0.9380	0.0742	0.0592
30	0.0682	0.9275	0.9400	0.9505	0.0043	0.9860
31	0.0394	0.9081	0.9820	0.9334	0.9800	0.0386
32	0.0921	0.9613	0.9728	0.9866	0.9277	0.9655
33	0.9615	0.0256	0.0957	0.0653	0.0729	0.0091
34	0.9610	0.0227	0.0763	0.0055	0.0910	0.9057
35	0.9800	0.0604	0.0407	0.0249	0.9113	0.0061
36	0.9230	0.0075	0.0832	0.0354	0.9392	0.9177
37	0.9442	0.0694	0.0115	0.9934	0.0127	0.0140
38	0.9495	0.0427	0.0857	0.9302	0.0989	0.9070
39	0.9158	0.0449	0.0838	0.9978	0.9196	0.0947
40	0.9990	0.0398	0.0211	0.9889	0.9486	0.9459
41	0.9592	0.0594	0.9590	0.0225	0.0039	0.0668
42	0.9022	0.0311	0.9522	0.0502	0.0503	0.9069
43	0.9551	0.0203	0.9287	0.0756	0.9041	0.0237
44	0.9703	0.0903	0.9139	0.0335	0.9539	0.9843
45	0.9163	0.0408	0.9444	0.9542	0.0135	0.0819
46	0.9458	0.0784	0.9596	0.9869	0.0724	0.9205
47	0.9680	0.0405	0.9994	0.9427	0.9523	0.0864
48	0.9255	0.0740	0.9801	0.9763	0.9749	0.9381
49	0.9037	0.9061	0.0795	0.0148	0.0642	0.0054
50	0.9101	0.9570	0.0471	0.0737	0.0963	0.9766
51	0.9073	0.9713	0.0827	0.0049	0.9770	0.0881
52	0.9582	0.9942	0.0909	0.0227	0.9721	0.9899
53	0.9440	0.9099	0.0704	0.9422	0.0656	0.0750
54	0.9484	0.9234	0.0422	0.9046	0.0643	0.9654
55	0.9388	0.9241	0.0455	0.9321	0.9503	0.0658
56	0.9792	0.9265	0.0798	0.9841	0.9365	0.9178
57	0.9154	0.9208	0.9505	0.0944	0.0148	0.0118
58	0.9024	0.9288	0.9828	0.0704	0.0270	0.9164
59	0.9517	0.9641	0.9645	0.0200	0.9251	0.0809
60	0.9513	0.9108	0.9376	0.0763	0.9966	0.9169
61	0.9018	0.9055	0.9452	0.9271	0.0697	0.0259
62	0.9654	0.9328	0.9404	0.9581	0.0068	0.9714
63	0.9058	0.9031	0.9671	0.9913	0.9373	0.0277
64	0.9422	0.9951	0.9118	0.9047	0.9427	0.9384