The attentional blink provides episodic distinctiveness

Abstract

The attentional blink (Raymond et al 1992) refers to an apparent gap in perception that can be elicited when a second target follows a first at a temporal lag of several hundred milliseconds. . Theoretical and computational work have provided a variety of explanations for early sets of blink data, but more recent data have challenged these accounts by showing that the blink is attenuated when subjects encode entire strings of stimuli (Nieuwenstein & Potter, 2006, Olivers et al 2007, Kawahara et al 2007), are distracted (Olivers & Nieuwenhuis 2005) or are provided with irrelevant motion cues (Arend, Johnston, & Shapiro 2006) while viewing the RSVP stream. In this paper, we describe the Episodic Simultaneous Type Serial Token model (eSTST), a computational account of encoding visual stimuli into working memory which suggests that the attentional blink is a cognitive strategy rather than a resource limitation. This model is composed of neurobiologically plausible neural elements and simulates the attentional blink with a competitive attentional mechanism facilitates the formation of episodically distinct representations within working memory. In addition to the blink, the model addresses the phenomena of repetition blindness and whole report superiority, producing predictions which are supported by experimental work.

Introduction

Encoding information into working memory is a fundamental part of our ability to interact effectively with the world. By temporarily buffering information in a working memory store, cognitive processes can continue to utilize stimuli that are no longer available in the environment. However, there are limitations to the rate at which we can sample visual stimuli for representation in working memory. One key limitation of this encoding process may be the rate at which discrete stimuli can be encoded into discrete representations. When two visual displays are presented within less than 100 ms of each other, behavioral evidence suggests a a failure to encode the two stimuli as separate events (Shallice 1964; Allport 1968; c.f. VanRullen & Koch 2003). However, at temporal separations of 100 to 400 ms, a different limitation is revealed; observers will often fail to report the second stimulus, an effect known as the attentional blink (AB; Raymond, Shapiro & Arnell, 1992).

According to a recently proposed computational model called the Simultaneous Type, Serial Token account (STST; Bowman & Wyble 2007), the attentional blink is a reflection of a mechanism intended to divide working memory representations into discrete tokens - i.e., episodic memory representations. In this view, forming a token for a first target suppresses the selection of new target stimuli so as to prevent the latter targets from being integrated with the first target’s working memory representation. Crucially, however, several recent studies have provided evidence that challenges this view by showing that observers can accurately report the identities of several target items presented in direct succession, without suffering an attentional blink (Olivers, Van Der Stigchel & Hulleman 2007; Kawahara, Kumada & Di Lollo 2006; Nieuwenstein & Potter 2006).

These results suggest that attention must use a more flexible mechanism for mediating attentional deployment than that described by STST. To accommodate these new findings, we propose the Episodic Simultaneous Type/Serial Token (or eSTST) model. In the present study, we show that this revised model of temporal attention and working memory is capable of explaining the recent findings that challenged STST, addressing both the attentional blink and prolonged sparing within the same model. In addition, the model provides new predictions which suggest that the ability to report the identities of several consecutive target items should come at a cost to episodic distinctiveness. The results from three experiments reported here show that this cost can be measured in increased repetition blindness, order errors and temporal conjunctions. Finally, we take advantage of the neurally inspired implementation of eSTST to predict neural activity which can be verified at the single neuron level in primate working memory experiments.

Empirical Background

Rapid Serial Visual Presentation (RSVP) has been used extensively to study the temporal properties of visual perception; Chun & Potter, 1995; Kanwisher, 1987; Potter 1976; Raymond, Shapiro & Arnell, 1992; Reeves & Sperling 1986; Weichselgartner & Sperling 1987). In this paradigm, subjects view a sequence of rapidly presented (e.g. 10/sec) stimuli, generally at the center of a display, with each item masking the one that came before it. Because each item is rapidly masked, incoming information has to be encoded rapidly or it will be lost. The attentional blink arises in such presentation when observers have to detect or identify two target items embedded in an RSVP sequence of distractor items (e.g., Broadbent & Broadbent 1987; Raymond et al., 1992). A common version of such a dual-target paradigm is shown in Figure 1a. In this task, the observer has to report the identities of two letters embedded in an RSVP sequence of digits. The results from this type of task typically show that T2 performance is largely unimpaired if presented at lag-1 (i.e. when T2 immediately follows T1), but is sharply impaired at lag 2 (i.e. with one intervening distractor) and recovers over the next several hundred milliseconds.

Figure 1.

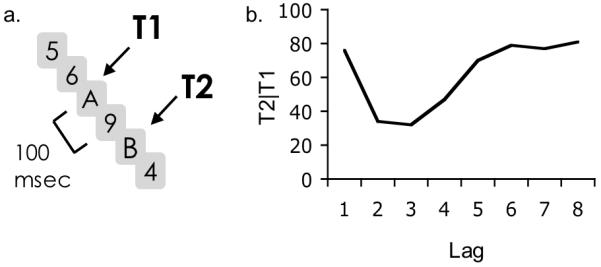
a. The letters-in-digits paradigm. Time is represented from top to bottom in this diagram. The lag between T1 and T2 is varied from 1 (no intervening distractors) to 8 (7 distractors). Lag 2 is depicted here. b. Detection of T2s on trials in which T1 was perceived exhibits an attentional blink.

The STST Model

The Simultaneous Type/ Serial Token model is a neural network which describes the process of extracting and then encoding specific targets from a temporal stream of stimuli in a way that preserves their temporal order.

Types and Tokens

STST is based on the premise that visual working memory uses both types and tokens (e.g. Kanwisher 1987, Mozer 1989) operating in two stages (Chun & Potter 1995, Chun 1997a). Token based memory systems provide an episodic context that allows encoding of temporal order and repetitions, neither of which are easily realized in simpler buffer maintenance accounts (Deco, Rolls & Horwitz 2004; see Bowman & Wyble 2007 for a more extensive discussion).

Types constitute a semantically organized representational workspace within which visual input is analyzed to extract features, objects and concepts. However, types cannot represent instance specific (episodic) memories. In fact, types are not directly stored in working memory at all; these nodes are only active during encoding and retrieval. This facet of the model is critical in permitting repetitions of an already stored item to be processed.

Tokens store episodic working memory representations. A single stored token contains a pointer to a type, which can later be used to retrieve the content of the memory by reactivating the type node. This system inherently represents temporal order; any type bound to token 1 is considered to be encoded before a type bound to token 2.

Temporal Attention

According to the STST model (Bowman & Wyble, 2007), lag-1 sparing and enhanced processing of the T1 +1 item (Chua, Goh & Han, 2001) indexes a temporal window of attentional enhancement that is triggered upon detection of T1. This window of attentional enhancement is considered to reflect a similar mechanism as that involved in transient attention (Nakayama & Mackeben, 1989; Muller & Rabbitt 1989; Yeshurun & Carrasco 1999; see also Nieuwenhuis, Gilzenrat, Holmes & Cohen 2005, Shih 2007). The brief episode of attentional enhancement is reflected in the finding that detection and identification of a masked visual target is substantially improved when the target appears within about 50-150 ms of the onset of a highly salient stimulus. Consistent with this interpretation of sparing, Wyble, Bowman & Potter (submitted) showed that identification of a categorically defined target that appears in a dynamic display of distractor items is improved if the target appears within a window of 200 ms or less from a preceding target. Further support for this theory is suggested by the finding that sparing occurs even when a distractor item is presented between two RSVP targets, provided that the targets appear at an SOA of about 100 ms or less (Bowman & Wyble 2007; Potter, Staub & O’Connor 2002; Nieuwenhuis et al 2005). Thus, sparing appears to reflect a spatio-temporally constrained window of attentional enhancement that is deployed in response to detection of a potentially relevant stimulus.

The transition from sparing to the attentional blink results from the end of the initial transient attentional episode and the suppression of further attention until the T1 has been encoded. In particular, STST assumes that working memory encoding suppresses transient attention to new information in order to protect the ongoing processing of T1. Thus, transient attention elicited by T1 allows both T1 and any shortly following T2 (e.g. lag-1) to be selected and encoded into short-term memory. However, once working memory encoding of T1 is underway, the allocation of attention to new inputs is suppressed, giving rise to the attentional blink.

A Shift in the Empirical Landscape

Although STST explained many of the hallmark effects observed in studies of the attentional blink, recent work has provided several new findings that seem problematic for the model. In particular, these studies identified a number of manipulations that attenuate the blink in ways not foreseen by STST, or most of the competing AB accounts. The common denominator of these manipulations is that encoding a target presented during the attentional blink window is in fact easy as long as that target is directly preceded by an item that can assist it in triggering attention or allows the attentional response triggered by T1 to be sustained. Thus, a T2 presented during the attentional blink can be reported without much difficulty if it is preceded by an item that captures attention because it matches the target template (Nieuwenstein 2006; Nieuwenstein, Chun, Hooge & Van der Lubbe 2005; Olivers et al. 2007). Similarly, there are findings indicating that sustained attention can alleviate the attentional blink. In particular, Nieuwenstein & Potter (2006) reported that a string of six consecutive items can be encoded without an obvious blink. When the same stimulus string was viewed in partial report condition (i.e. only reporting targets of a particular color), the standard blink effect was observed even though subjects were then asked to encode only two of the six targets. Subsequent work demonstrated that this effect generalizes to any uninterrupted series of targets, even if presented amongst distractors (Figure 2). This phenomenon has been called spreading the sparing, for the way in which lag-1 sparing seems to be extended across an arbitrarily long sequence of targets (Olivers, Van der Stigchel & Hulleman, 2007; Kawahara, Kamada & DiLollo 2006).

Figure 2.

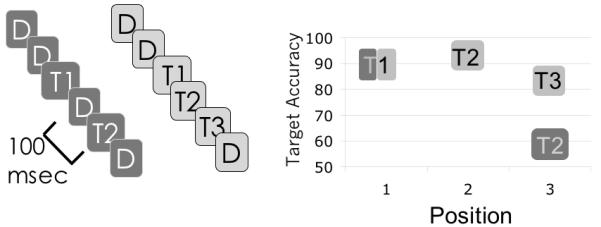
In the data of Olivers et al (2007), the attentional blink is observed for a second target that is separated from the first target by a distractor (i.e. the dark grey condition). However if that intervening distractor is replaced by a target, subjects exhibit sparing of the last target (i.e. the light grey condition).

Thus, it cannot be the case that the AB is the result of limited ability to encode multiple targets if observers can encode three targets in the same time as they would otherwise fail to encode two. Accounts which describe the blink as a competition between T1 and T2 (Dehaene, Sergent, & Changeux 2003) or describe more general notions of limited cognitive resources (Kranczioch, Debener, Maye & Engel 2007) are difficult to reconcile with findings of spreading of sparing and whole report superiority. Furthermore, in the experiments described above, the subject does not know which type of trial (i.e. TTT or TDT) was about to occur. Consequently, explanations involving a pre-trial allocation of attention (e.g. the over investment hypothesis described by Olivers & Nieuwenhuis 2006) cannot be used to explain spreading of sparing because trials were presented in a mixed block.The critical question posed by these data is this: If subjects can encode sequences of successive targets without suffering an attentional blink, why does the blink occur when they attempt to encode two temporally discrete targets separated by distractors? The eSTST model proposes that our visual system is designed to flexibly mediate the allocation of attention; an uninterrupted sequence of targets can be encoded, but if there is a gap in the targets, attention is briefly switched off in order to divide the encoding process into two sequential episodes. This behavior emerges dynamically through a regulatory circuit that we describe in this work.

What’s new in eSTST?

The model we describe is structurally similar to STST, consisting of types, tokens and a temporal attention mechanism. However these three elements now interact to produce a competitive regulation of attention. The deployment of attention at any point in time is controlled by competing inhibitory and excitatory connections from WM encoding and target input, respectively (Figure 3). This implementation allows each target in a string of consecutive targets to sustain a recurrent excitation of attention However, if no new target arrives at the input layer during a period of 200 or more ms after the onset of the preceding target, the ongoing consolidation of preceding target information succeeds in suppressing attention. When this occurs, a subsequent target receives no amplification and is less able to reactivate attention. As a result, targets following a gap in a target string are frequently missed (Figure 4).

Figure 3.

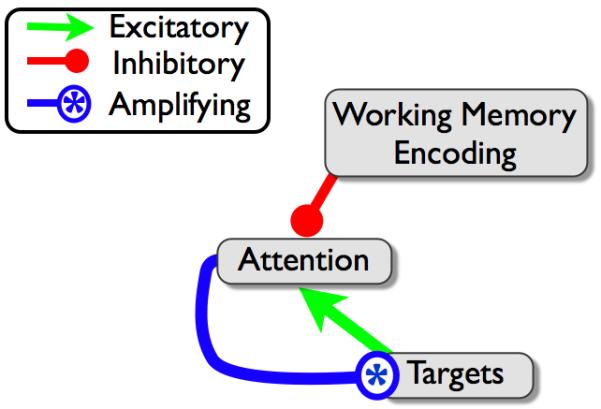
Competitive regulation of attention; bottom up target input attempts to trigger attention while encoding processes attempt to shut off attention.

Figure 4.

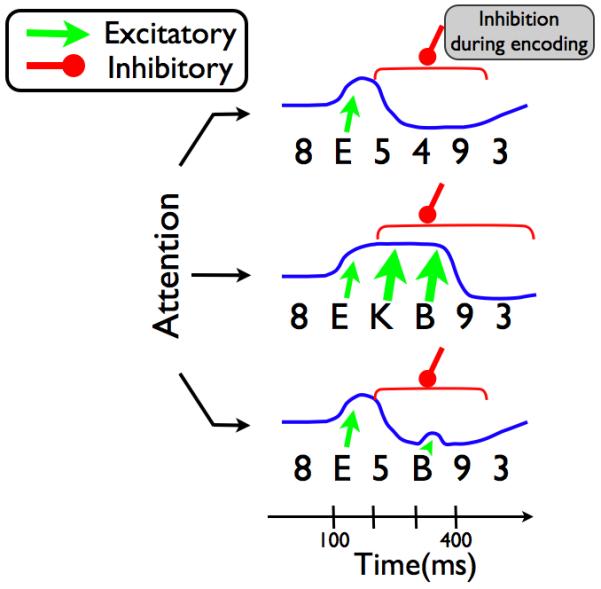
Schematic demonstration of the competitive regulation of attention for a single letter target among a series of distractors, (top), three targets in a row (middle) and two targets separated by a distractor (bottom). The height of the blue line corresponds to the amount of attention deployed at a particular moment. Attention begins at a baseline level and can be shifted upwards or downwards depending on whether excitation from targets or suppression from ongoing encoding is dominating the competition. For three targets in a row, the suppression elicited from the first target onwards is counteracted by the amplified excitation from T2 and T3. However an intervening distractor provides sufficient time for attention to be suppressed, producing an attentional blink for the following target.

A second important modification concerns the allocation of tokens. In STST, it was assumed that token binding is initiated in sequence, such that a second token can only begin after the first had completed. This mechanism attempted to allocate one type per token. However two targets could bind to a single token in the particular case of lag-1 presentation, with the consequent sacrifice of temporal order information about which came first. Extending this implementation to sparing of four consecutive targets predicts that no order information is preserved among them and this is not the case, as we will see below.

In eSTST, tokens are more strictly defined; each token can bind to one target only, as described by the original definitions of a visual token (Mozer 1989, Kanwisher 1991). If multiple targets arrive at the input nodes more rapidly than they can be encoded, the system allows multiple tokens to be bound in a staged fashion, with token 1 completing first, token 2 second and so on. Thus, in eSTST, the tokens are serial in the order that their encoding is completed.

Modelling methods

The model has five major components, as shown in figure 5: input nodes in which input is presented, type nodes which represent the identities of targets as they are being encoded into working memory, binding pool and tokens which store episodic representations of targets in working memory, and finally the blaster, a node which mediates the deployment of attention. The description given here is simplified; all of these elements are formally described in the appendix. All nodes in the model are simple linear accumulators, with activity that decays to zero over time according to equation 1.

$$a_{\left(t\right)}={a_{(t-1)}}^{\ast }\text{decay}+{\text{input}}_{\left(t\right)}$$ (1)

Figure 5.

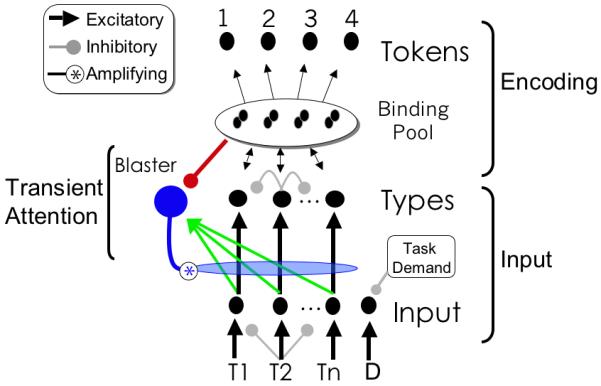
Schematics of the full eSTST model. Input from early visual areas excites input nodes and feedforward inhibition simulates backward masking. Task demand represents the influence of task instructions in specifying the category of targets, and acts by inhibiting distractor nodes, preventing them from entering working memory and triggering attention. Inhibition between type nodes simulates weak interference between coactive type representations.

In equation 1, a_(t) represents the activation of a node at a particular time, which is the sum of its previous activation a_(t-1) multiplied by a decay rate, and a combination of excitatory and inhibitory input. Some nodes excite themselves and can sustain their own activation, which allows information to be stored in working memory.

Connections between nodes are excitatory or inhibitory, with the exception of the blaster’s attentional amplification. All connections in the model are nonmodifiable; only the activation level of nodes can change. A trial is simulated in time steps. Each step corresponds to 10 mlliseconds. There are no random factors or noise; given the same parameters, every simulation produces the same output.

Input: A Sequence of Targets and Distractors

Targets or distractors are presented at each time step by activating one of the input nodes (for simplicity, all distractors are represented by a single node). Target inputs vary systematically in strength over a range of values, reflecting variation in the relative effectiveness of different combinations of targets and masks. It is this variance in strength that explains why some T2s are able to survive the blink, and why some T1’s are missed.

When a given item is presented to the model, the corresponding input node is clamped to a designated value. At the end of the stimulus, this input node rapidly decays back to zero due to masking from the following item in the RSVP stream. Items followed by a blank in the stream decay more slowly during the blank interval, representing persistence in iconic memory in the absence of a backwards mask. Figure 6 illustrates the activation traces of target input nodes for different conditions.

Figure 6.

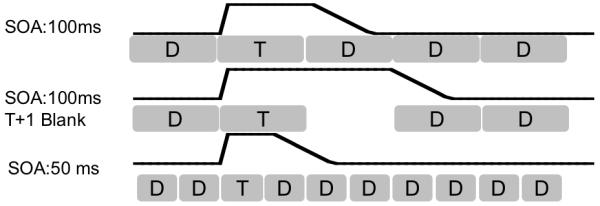
The profile of input nodes for different configurations used in simulations, including a target presented at 100ms SOA, a target with the same SOA followed by a blank, and a target presented at 50ms SOA.

Task Demand

In eSTST, a task demand mechanism specifies the set of targets by inhibiting distractor nodes, preventing them from activating type nodes. In this way, distractors provide masking of targets, but do not enter the encoding stage. This aspect of the model has important implications that will be brought out in the discussion.

Output: Identity and Temporal Order of Targets

The output of the eSTST model is measured at the end of a simulation to retrieve both the identity and order of items that are stored in working memory. For each token that has been encoded into working memory, the type node which is bound to that token is retrieved. If two tokens are bound to the same type, the model is considered to have encoded a repetition of that type. The order of reported items is determined by the order of the tokens that represent them. Token 1 is reported first; token 2 reported second and so on.

Temporal Attention: The Blaster

The model is predicated on the idea of a rapid and transient deployment of attention in response to a target. This attentional resource is nonspecific, meaning that when active, it amplifies all input in a manner similar to neuromodulation (e.g. by norepinephrine as modeled by Nieuwenhuis, et al. 2005). This is implemented by the so-called blaster; a single node, which receives excitatory input from all of the target input nodes and, in turn, provides attention to all input nodes. In addition, the blaster receives inhibitory input from the token layer, and it is the competition between excitatory and inhibitory inputs which determines whether a target triggers the blaster.

Working Memory Encoding

The goal of encoding, on each trial, is to encode all targets into working memory in the order in which they occur, including repetitions. Encoding occurs by binding types to tokens. These bindings are stored by holding an attractor state in self-excitatory nodes. Such attractors have the advantage that they can store information without hebbian synaptic modification, which has not been found to occur rapidly enough to support encoding and subsequent retrieval in tasks such as this. Storing information in attractors is a common approach in working memory models (e.g., Deco, et al. 2004; Hasselmo & Stern, 2006) and is consistent with findings of sustained neural activity in monkeys performing working memory tasks (Miller, Erickson & Desimone 1996)

Binding a Type to a Token

To encode the occurrence of an item into working memory, such as the letter ‘J’ in an RSVP stream of digits, the activated type node corresponding to ‘J’ is bound to Token 1. This binding represents the fact that ‘J’ was seen, and that it was the first target encountered in the stream.

This encoding requires storing a link from a type to a token. In the model, a population of nodes, referred to as the binding pool (Bowman & Wyble 2007), stores these links by selectively activating nodes that correspond to specific combinations of type and token. For example, in figure 7, the binding unit labeled J/1 stores a binding between type ‘J’ and token 1.¹ At the beginning of a trial, both tokens are available, but the system selectively binds the first target to token 1.

Figure 7.

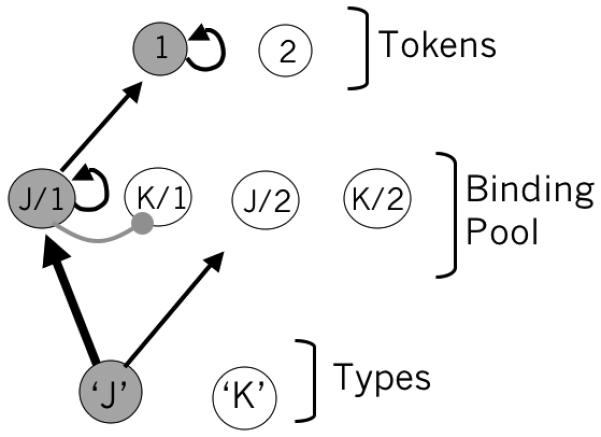
The binding pool contains nodes selective for conjunctions of types and tokens. In this example, the type ‘J’ is being bound to token 1. When encoding is complete, self excitatory connections will sustain the activation in the binding pool and token 1.

Binding occurs when a type node is sufficiently active to excite corresponding nodes in the binding pool (J/1 and J/2 in this example), which race to threshold. The encoding system is configured such that input to J/1 has a slight advantage over input to J/2 and this ensures that binding units corresponding to token 1 will reach threshold before those corresponding to token 2. When any of these binding units reaches threshold, three things happen: (a) the binding unit enters a self excitatory attractor, sustaining its own activation until retrieval, (b) it excites its corresponding token, serving as a pointer that an item is stored in working memory and (c) it inhibits other binding pool nodes corresponding to the same token, thereby preventing other items from binding to the same token for the duration of the entire trial. As a result, the system will have bound the first target to the first token.

Binding Multiple Types

Multiple types can be in the binding process simultaneously, but one of the binding units will reach threshold first, encoding the winning type into token 1. The remaining type(s) will continue binding to remaining tokens, with token 2 completing next. However, this race model of encoding is prone to order errors; a strongly activated T2 can beat a weaker T1 if they are presented closely in time. This confounding of activation strength with perceived target order in RSVP is similar to that proposed by Reeves & Sperling (1986). If the system is to infallibly encode the order of two stimuli, it is necessary that the second target begins encoding only after the first target is finished processing. We argue that the inhibition of the blaster (and therefore the attentional blink itself) exists precisely to impose this temporal segregation of target encoding.

There is weak lateral inhibition between type nodes, which reflects the interference of processing multiple items at the same time. This inhibition is not involved in the attentional dynamics that result in the blink; however, this interference is important for simulating costs of encoding multiple items within the same attentional episode, such as the T1 impairment at lag-1 which we discuss below.

Sustaining types during encoding

During encoding, the model sets up a temporary recurrent circuit between the binding pool and type nodes until encoding is completed. To implement this recurrence, we add gate nodes to the binding pool units. Thus, each binding unit is actually a gate/trace pair of nodes, as shown in Figure 8a (denoted G and T respectively). During encoding, the gate node is active, passing activation from the type node to the trace node, but also provides recurrent activation back to the type node, producing a temporary attractor state.

Figure 8.

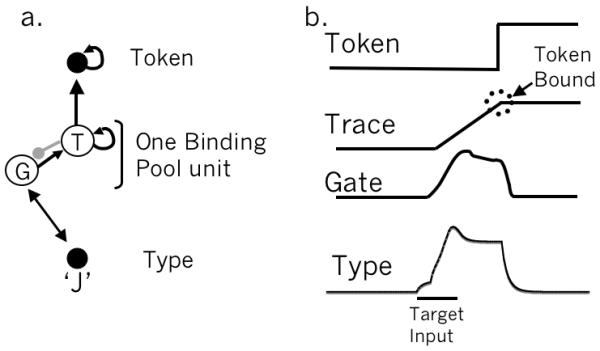
a. Encoding involves a temporary recurrent circuit between a type node and a gate node in the binding pool. b. The temporal dynamics of binding for a single target. The elevated portion of activation for the type and gate nodes reflects the recurrent attractor state between them that is cut off abruptly when the token is bound (see appendix for more detail).

The temporal dynamics of encoding a single target are shown in Figure 8b. The type node is initially excited by target input with the help of the blaster. The gate node is excited by the type node and recurrent excitation between gate and type establishes a temporary attractor state. The goal of encoding, however, is to store the item without committing the type node. Therefore, the trace node slowly accrues activation until it crosses threshold, at which point it inhibits the gate, shutting off the attractor. When this occurs, the type is no longer required, and without feedback from the gate mode, the type node’s activation rapidly decays back to baseline. This is a point of departure from the STST account of Bowman & Wyble (2007) which used a different mechanism to sustain type nodes during for encoding.

Types and repetitions

A type node can only be used to process one instance of a target at a time. If a repetition of a target occurs while a prior instance of the same target is still being encoded, the new input simply enhances the activation of the already active type node. This facilitates encoding of the previous instance of the target, but does not initiate encoding of a new token. Only if the previous encoding had been completed when the repetition arrives can the system encode a new instance of the target. This property of the binding process gives rise to repetition blindness during RSVP.

Delay of attentional deployment

All but one parameter were fixed for all of the simulations described below. The onset of the blaster is subject to a delay parameter corresponding to the difficulty of target detection. For targets defined by category, such as letters in a digit stream, this delay is set to 40 ms. For whole report, which requires no target discrimination, the delay is set to 10 ms.

Data Addressed

The eSTST model is validated against a spectrum of data from different experiments. All of the following phenomena are replicated with the same model and parameter settings, except in the case of whole report, which has unique task instructions.

The Attentional Blink

T2 accuracy is impaired for 200-400ms following accurate report of a T1 with strong sparing of T2 at lag-1 (Raymond et al 1992; Chun & Potter 1995).

The role of post-target blanks

The blink is attenuated by blanks after either T1 (Chun & Potter 1995, Seiffert & Di Lollo 1997) or T2 (Giesbrecht & DiLollo 1998).

The Cost of lag-1 sparing

T1 accuracy is impaired at lag-1 and swaps of temporal order are frequent at lag-1 (Chun & Potter 1995).

Lag-2 Sparing at 20 item/sec

Sparing is a function of the temporal separation between one item and the next. For RSVP at about 50 ms/item, sparing of T2 is evident at lag-2 (Bowman & Wyble 2007).

Spreading of sparing

When a string of three or four consecutive targets are presented, the entire sequence is spared, eliminating the blink and producing best performance for the second target presented (Olivers et al. 2007, Kawahara et al. 2007).

Cueing

During the blink, if two targets are presented in rapid succession, the second one has improved accuracy (Nieuwenstein 2006; Olivers et al. 2007).

Whole Report

When there are no distractors in the RSVP stream there is a first target advantage, as opposed to a second target advantage found in spreading of sparing (Nieuwenstein & Potter 2006).

Simulation results and discussion

Encoding a target into working memory

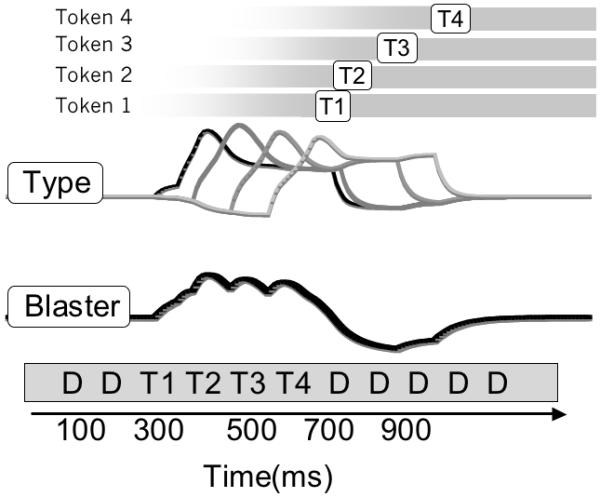
When a type node is activated by bottom-up input, it is encoded into working memory through the allocation of a token. The dynamics of this process can be seen in Figure 9, in which a single target is presented for 100 ms, amidst a stream of distractors, producing the following sequence of events. (a) The input node excites the type node and the blaster. The blaster is rapidly triggered, which strongly amplifies further input to the type node, (b) the type node initiates token allocation, entering a temporary attractor state with the token. This attractor state sustains its activation while token activation increases over the following 200-400 ms. During encoding, suppression of the blaster can be observed as a negative shift in its activation. (c) When one of the trace nodes crosses a self-sustaining threshold, the attractor state is terminated, and the type node decays back to baseline. For the remainder of the trial, the token stays allocated and the target is successfully encoded into working memory as token 1.

Figure 9.

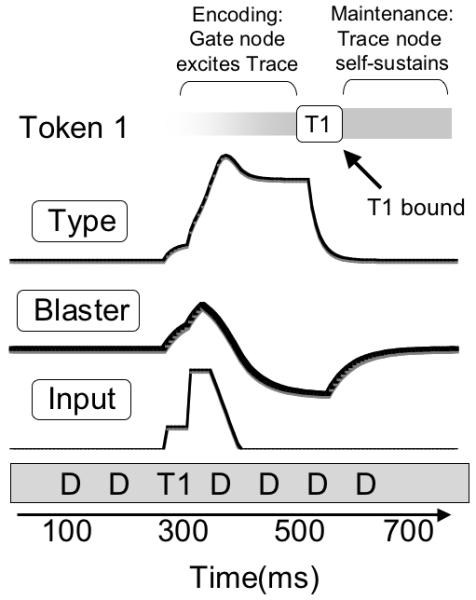
Schematic of encoding a single target from an RSVP stream. From bottom to top: the input layer is first activated, triggering the blaster, which amplifies the input (visible as a stepwise increase in input strength). The type node is initially excited by bottom up input and is sustained during encoding, represented abstractly with a grey bar at the top of the figure. Note that the blaster is strongly suppressed by ongoing encoding and then recovers to baseline.

Encoding Multiple Targets

For tasks require report of two targets in an RSVP sequence, the dynamics of the model’s function fall into one of three regimes depending on the elapsed time between T1 and T2, measured in 100 ms “lags”: sparing (lag-1), blinking (lags-2-4), and post-blink (lags-5-8). Figure 10 illustrates the dynamics of the network at lags 5, 3 and 1 for example trials at particular target strengths.

Figure 10.

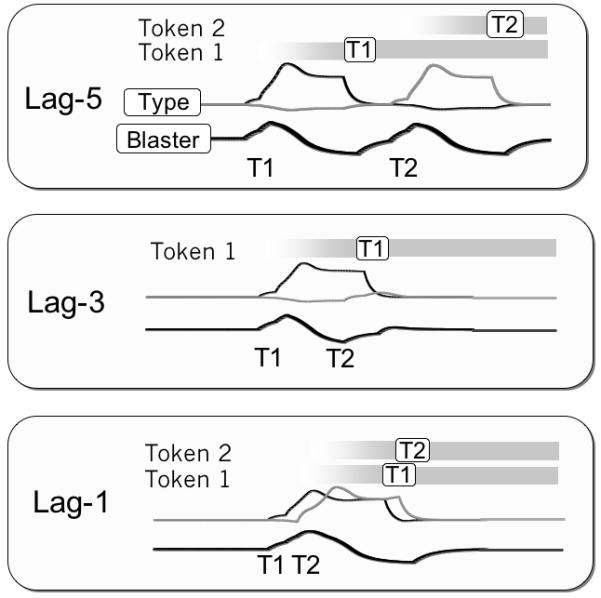
Schematic depiction of the eSTST model processing two targets at lags of 1, 3 and 5. Both targets are encoded at lag 1 and 5, but T2 is missed at lag 3.

Post Blink

Presentation of the T2 at lags 5-8 is sufficiently late that T1 encoding is complete. Therefore, the blaster is no longer suppressed and can respond rapidly when T2 is presented. In this case, the two targets are bound sequentially and are thus free of mutual interference as well as the possibility of order confusion.

Blink

At lags 2-4, the T2 arrives while T1 encoding is ongoing. Top down suppression of the blaster makes it difficult for T2 to trigger attention, and thus the T2 type node is only weakly activated. On a minority of trials (not shown in Figure 10), the T2 is strong enough that it breaks through the blink.

Sparing

T2s that arrive 100 ms after T1 (i.e. lag-1) are able to benefit from the attention deployed to the T1. An attended T2 sustains the activation of the blaster, despite the top down suppression, and strongly activates its type node. T1 and T2 are bound in parallel with order determined by their relative strength. In this example trial, the targets are bound in the correct order.

By iterating simulations over many different values of T1 and T2 strength, the model simulates the attentional blink. Figure 11 displays the output of the model alongside matching human data for the basic blink condition, as well as the different aspects of performance described immediately below. The data are from Chun & Potter (1995), Experiments 1 and 3, and Giesbrecht & DiLollo (1998), Experiment 1.

Figure 11.

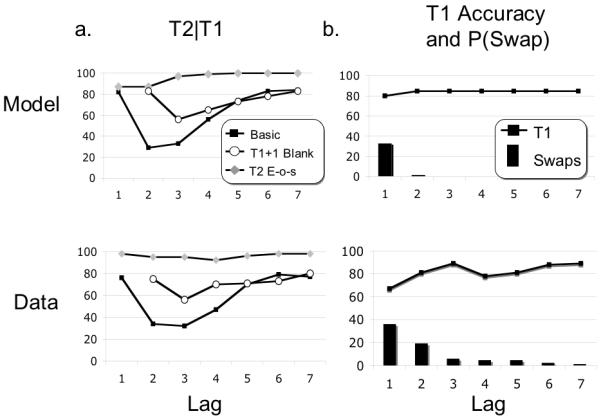
Simulation results alongside empirical counterparts from subjects. Shown are accuracy of T2 conditional on T1 and accuracy of T1 and the probability of reversing temporal order (i.e. P(swap)). The model demonstrates a basic blink that is attenuated by blanks either at T1+1 or by placing T2 at the end of the stream (a). It also demonstrates a reduction in T1 performance that is exclusive to lag 1, as well as a large increase in swap errors (b). All human data are taken from Chun and Potter (1995) except for the T2 end-of-stream data, which are from Giesbrecht and DiLollo (1998).

Post-target Blanks

The attentional blink is sensitive to blanks placed after either T1 or T2; either manipulation will attenuate it. Modeling the blink-attenuating effect of T1+1 blanks is a particularly challenging aspect of this data, because, as the T1 becomes more salient, the T2 is easier to report (Bowman, Wyble, Chennu & Craston In Press)

The eSTST model, like the STST account (Bowman & Wyble 2007), demonstrates a reduced blink when blanks are inserted into the stream after T1 or T2. Such blanks reduce backward masking of the target. For a T2, unmasking increases the length of the T2 trace in iconic memory (e.g. at the input layer), giving the T2 more opportunity to outlive the blink and be encoded. A T1+1 blank increases the duration of the T1 trace in the input layer, thereby increasing the excitation of the T1 type node. With more strength, the encoding process is more rapid. Thus, on a T1+1 blank trial, the blink is so brief that a T2 has a better chance of outliving the blink and being encoded. However, our model argues that a muted blink should still be present in these cases, an issue we return to in the general discussion.

The Costs of Lag-1 Sparing

In eSTST, T2 can be spared by binding T1 and T2 in parallel, but this form of encoding has detrimental effects, two of which are revealed when T2 is presented one lag after T1. In this case, T1 accuracy is impaired because of competition with T2. Also, the order of the targets is often encoded incorrectly, because items being processed in parallel are in a race to complete the available token. When T2 occurs at lag-1, T2 begins the race 100 ms after the T1, but if T2 is exceptionally strong (i.e. due to the inherent variation in target input strength), it may beat T1 in the race and be bound to Token 1, leaving the T1 to be bound to Token 2. Note that this is a significant departure from the STST model (Bowman & Wyble 2007), in which sparing was the result of binding T1 and T2 to the same token. In eSTST, only one stimulus can ever be bound to one token. Figure 12 demonstrates how a strong T2 can beat a weak T1 in the race to complete binding to token 1, forcing the T1 into token 2. The result from this trial would be that both T1 and T2 would be reported, but in the wrong order (i.e. a swap).

Figure 12.

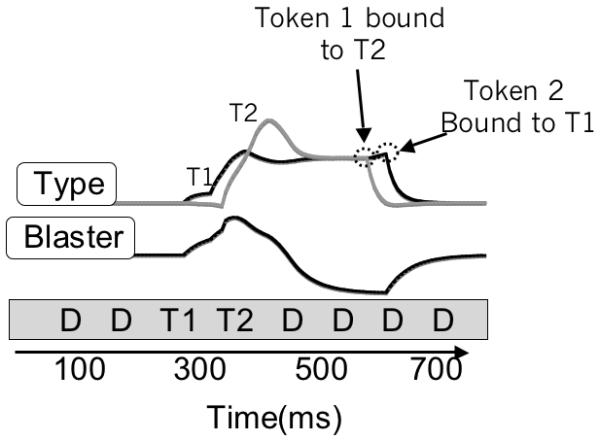
For T1 and T2 presented at lag-1, the encoding system can make a temporal order error, which occurs in this example. T2 input is sufficiently stronger than T1 that the T2 type node wins the race for token 1 and forces T1 to be encoded to token 2.

Sparing and Blinking are Temporally Delineated

In Bowman & Wyble (2007), experimental work demonstrates that if the presentation rate is doubled to 20 items/sec (50 ms SOA), sparing is obtained at lag-2. A similar point is observed in the data of Potter, Staub & O’Conner (2002), Experiment 1. This finding suggests that there is a temporal window of sparing following the first target.

These data also suggest that the blink is a function of temporal lag. When a T2 is presented 200 ms after the T1, it is most vulnerable to being blinked, whether it is the fourth item at 50 ms SOA or the second item at 100 ms SOA. The eSTST model demonstrates the same pattern, as shown in Figure 13.

Figure 13.

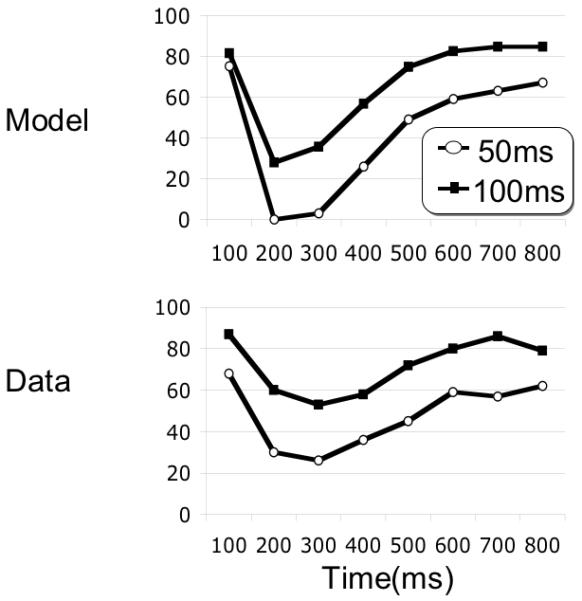
Model simulation and human data for 94ms and 54ms SOA presentation rates, simulating the data published in Bowman & Wyble (2007). For the 54 ms presentation rate, lags were 2-4-6-8-10-12-14-16, producing target onset asynchronies (TOA) similar to lags 1-8 for 94 ms SOA. Critically, sparing is obtained for the lag-2 position (108 ms) in the 54ms SOA data, and the blink has the same time course. The simulation used SOA’s of 50 and 100ms in the two conditions.

Spreading the Sparing

During RSVP, with input of the form DTDTD (T1 and T2 targets separated by a distractor at an SOA of 100ms, and embedded in a sequence of distractors), report of the second target will be impaired. This is the attentional blink. However when the sequence presented is DTTTD (T1, T2 and T3 presented in succession at 100 ms SOA), all three targets are usually reported, a finding referred to as spreading the sparing (Olivers et al 2007).

The eSTST model suggests that spreading the sparing is the result of a sustained deployment of attention in response to a series of targets. Each target boosts the activation of the blaster, which allows the following target to be seen. This allows a sequence of two, three or four consecutive targets to sustain the activation of the blaster, effectively holding the attentional gate open (figure 14). The model simulates the results of Olivers et al (2007) Experiment 1, as shown in figure 15.

Figure 14.

Simulated spreading the sparing for four targets presented in sequence. The blaster stays active despite top down inhibition, being sustained by continued target input.

Figure 15.

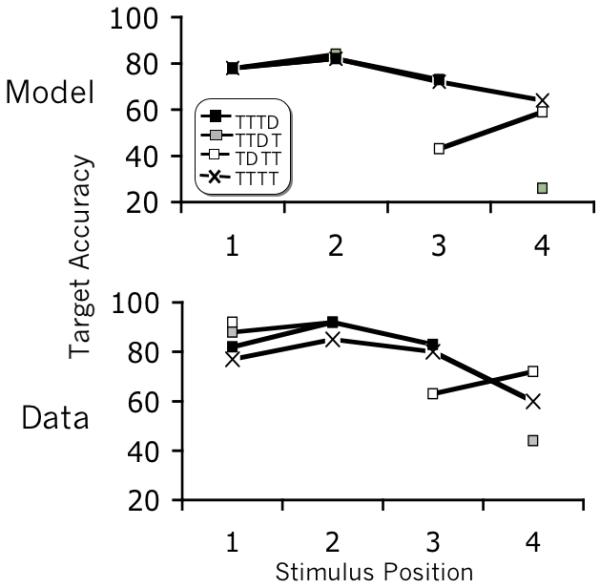
Simulated results and human data from Experiment 1 of Olivers, Hulleman & Van Der Stigchel (2007) for the main experimental conditions with three or four targets. These results simulate spreading the sparing (TTTT), the onset of the blink after a distractor (TTDT), and cueing produced by two targets during the blink (TDTT).

Cueing

The interaction between top down suppression and bottom up input reproduces another critical feature of the dynamics of rapid visual encoding: cueing. Nieuwenstein et al (2005; see also Nieuwenstein, 2006) demonstrated that a target presented during the blink can be seen more readily if it is preceded by another item containing a target specifying feature (e.g. color). What these results suggest is that suppression of the blaster during the blink is not absolute. A target (or a stimulus resembling a target) can excite attention enough that a following target can benefit from the cueing effect. A similar finding arises in Olivers et al (2007) and Kawahara et al (2007), who show that the string TDTT results in impaired accuracy for the second target, but improved accuracy for the third target (i.e. compared to a target presented at the same relative time in the configuration TDDT).

Figure 15 illustrates how the model reproduces the data from conditions TDTT and TTDT of Olivers et al (2007). In the case of TDTT, the second target boosts the activation of the blaster, aiding the following target in triggering attention more rapidly, and improving its accuracy compared to a target preceded by a distractor.

Whole Report vs Sparing

Nieuwenstein & Potter (2006) demonstrated that subjects fail to exhibit an attentional blink during whole report, a paradigm requiring subjects to report a string of consecutive items. Whole report is similar to the case of spreading the sparing, in that a string of consecutive targets is to be encoded. Neither paradigm produces an attentional blink, suggesting that a similar encoding process occurs whether the targets have to be selected from distractors, or are presented in isolation.

There is a subtle but important difference between the relative strength of the first two targets between whole report and target strings, as illustrated in Figure 16. When targets need to be identified amongst distractors, there is a delay in the deployment of attention that gives the second target an advantage over the first. When no target identification has to be made, attention is deployed more rapidly, giving the first target an advantage over the second.

Figure 16.

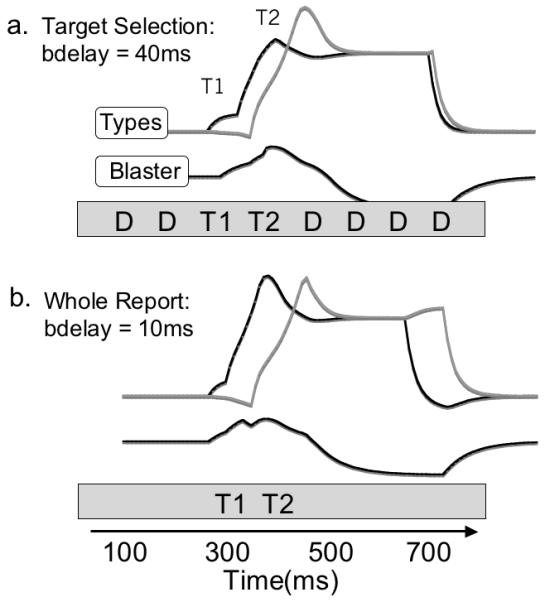
The difference between selective report (a) and whole report (b) is simulated in the model by changing the delay between the triggering of the blaster, and the onset of the attentional effect from 40ms to 10 ms. The result is a relative shift from a second target advantage to a first target advantage.

Figure 17 shows a replication of the accuracy data for the first four targets in the whole report condition of Experiment 1 in Nieuwenstein & Potter (2006) (SOA of 107ms) and the four target condition of Experiment 1 in Olivers et al (2007) (SOA of 100 ms). For items presented in a whole report paradigm, the first target is better perceived than the second. For a string of targets presented in a stream of distractors, the second target is better perceived than the first. Potter, Staub & O’Connor (2002) also describes the second target advantage for targets in a distractor stream at short SOAs. The model reproduces this same difference. Thus, eSTST suggests that the second target advantage in selective report RSVP paradigms can be explained as a processing delay in the deployment of attention.

Figure 17.

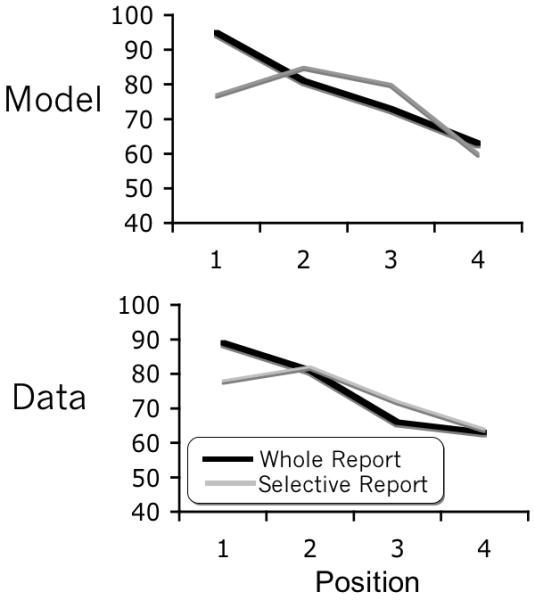
Simulated results and human data (from Nieuwenstein & Potter 2006, and Olivers et al 2007) for selective report and whole report. The critical difference between the two is the relative advantage of the first and second targets.

Behavioral Predictions: Identifying the Cost of Sparing

Having demonstrated the versatility of the eSTST model in reproducing a spectrum of data from different experiments with a single set of parameters, we now turn to the critical question; why is the visual system designed to exhibit an attentional blink if it is capable of sparing a sequence of targets? Some of the aforementioned data suggest that sparing comes with a cost. For example, in the classic letter-digit attentional blink paradigm, lag-1 sparing of T2 produces a reduction in T1 report, as well as temporal order errors when both targets are reported. The eSTST model suggests that we can find more evidence of the cost of sparing by looking at repetition blindness, order errors within strings of three or four targets, and an increase in conjunction errors between parts of complex items.

Prediction I: Repetition Blindness gets worse during sparing

Repetition Blindness (RB) is a well known phenomenon in visual working memory paradigms. When observers are asked to encode two instances of the same item within a very short period of time (often less than 500 ms), often only one of the two instances will be perceived. Generally it is thought that RB involves a loss of the second item, although it is possible to demonstrate a loss of the first instance (Neill, Neely, Hutchison, Kahan & VerWys 2002). Previous work has suggested that repetition blindness is attenuated if the second instance is made episodically distinct from the first (Chun 1997a) by changing its color. The eSTST model suggests that we can also affect the episodic relationship of the two instances with the presence or absence of targets between the repeated items.

The full spectrum of theoretical and empirical work related to RB is beyond the scope of this article, but the eSTST model simulates the phenomenon. Within our model, if a second instance of a type is presented while the system is still encoding the first instance, the second instance is incapable of forming a separate tokenized representation. Tokenization failure as a cause of RB has been described previously (Kanwisher 1987, Anderson & Neill 2002).

In our model, if the encoding stage is loaded with multiple targets in parallel (i.e. spreading the sparing or whole report), interference between three or four simultaneously active types prolongs the encoding of those targets (see figure 14 for an example of encoding four targets), and thus extends the temporal window of repetition blindness. Specifically, if the sequence T_iT_jT_kT_i is shown to a subject, the second instance of item T_i will be strongly impaired, compared to the fourth item in the sequence T_iT_jT_kT_m. In contrast, the sequence T_iD_jD_kT_i allows more rapid encoding of the first instance of T_i due to the lack of competition from simultaneous targets, thus freeing up the i type node to process the repetition arriving 300 ms later. As we show below, the model is almost completely blind to repetitions in the TTTT case but not the TDDT case.

It is notable that whole report (similar to the TTTT condition simulated here) is generally used in repetition blindness experiments. Park & Kanwisher (1994) explored the role of non targets between repeated items and found an attenuation of RB just as predicted here. However in their experiment, the two instances of the repeated letter were in different cases. To properly evaluate the model’s prediction that RB can be nearly complete for same case repetitions, we tested the ability of subjects to encode a repetition during RSVP of all uppercase stimuli.

Methods

Participants

The fifteen participants were volunteers from the MIT community of age 18-35 who were paid to participate in the experiment, which took approximately 30 minutes. All reported corrected or normal vision.

Apparatus and stimuli

The experiment was programmed using Matlab 5.2.1 and the Psychological Toolbox extension (Brainard, 1997), and was run on a PowerMac G3. The Apple 17” monitor was set to a 1024 × 768 resolution with a 75 Hz refresh rate. An RSVP stream was presented centrally at the location of a fixation cross. SOA between items was 93 ms with no ISI.

Black digits in 70 point Arial were used as distractors. The letters I, M, O, Q, S, T, W, X, Y and Z, as well as digits 1 and 0 were excluded. Stimuli were approximately 1.3 by 2.1 degrees in angle at a viewing distance of 50 cm.

Procedure

Trial types occurred in a 2 × 3 design which defined what sequence of target items (letters) appeared amidst the long sequence of distractors (digits). The first factor defined whether the middle two positions of the four critical items were targets or distractors. The second factor defined whether the stimulus in the final position was a new target, a repetition of the first target, or a distractor to create a catch trial. Catch trials were included to avoid giving subjects the expectation of either two or four targets per trial. Thus, the six conditions specified the following sequences of four items in equal proportion: TDDT, TDDD, TDDR, TTTT, TTTD, TTTR, in which T represents a random target chosen without repetition, D represents a random distractor chosen without repetition and R represents a repetition of the first target. These target sequences were positioned randomly within a stream of randomly chosen distractors with the first target’s position chosen randomly from [18 to 33] and the last item was followed by at least 5 distractors with a total RSVP stream length of at least 30 items.

Instructions presented at the beginning of a trial told subjects to report all of the letters they could. Participants were warned that there might be repetitions and to report a letter twice if it was seen twice.

After each trial, participants were asked to “Enter all of the letters you saw, including repetitions”. Subjects were allowed to correct their input string with backspace while entering it, and were not given feedback. Trials were considered correct if subjects reported the correct identity, without regard to correct order.

Results and Discussion

Results of both simulation and experimental data are presented in figure 18, showing conditional accuracy for the final target presented in the four critical experimental conditions; blinking unrepeated (TDDT), blinking repeated (TDDR), sparing unrepeated (TTTT) and sparing repeated (TTTR). Accuracy values in the unrepeated conditions indicate the probability of reporting the final target given report of the first target. In the repeated conditions, accuracy indicates the probability of reporting two instances of the repeated item, as a percentage of the number of trials in which at least one instance of the repeated item was reported. Neither measure considers report order. In both sparing (TTTT vs TTTR; paired t = 9.9, p < .001, d = 3.5) and blinking (TDDT vs TDDR; paired t = 4.48, p < .001, d = 1.38) cases, significant RB was observed.

Figure 18.

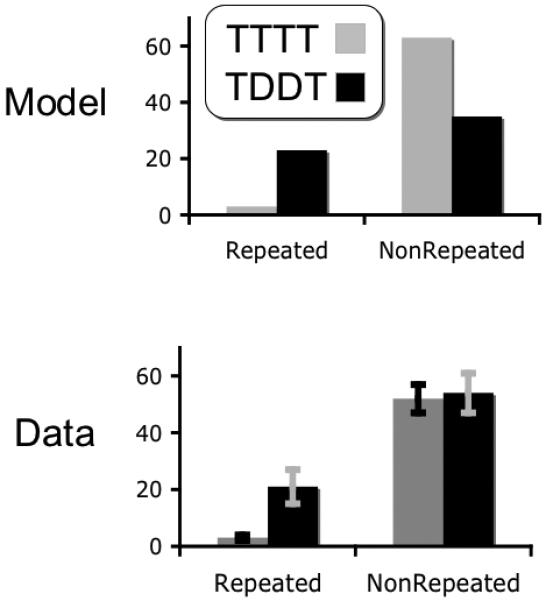
Simulated results and human data for a repetition blindness experiment. Shown, the conditional probabilities of reporting the final target of the sequence given correct report of the first target. Both the model and human subjects were almost completely blind to repetitions occurring in the TTTT case.

Critically, the model predicts that encoding a repetition in the sparing condition is nearly impossible while repetitions are successfully encoded for some of the blinking trials. The data shows a very similar pattern, with lower ability to report the repeated item in the sparing than blinked trials (paired t = 3.43, p < .004, d = 1.13).

Prediction II: Order Report for Sparing Multiple Targets

AB data from Chun & Potter (1995) demonstrates that sparing of a single target is accompanied by a marked reduction in reporting the correct order of the two targets. Our model predicts that sparing of more targets is accompanied by even greater loss of temporal order accuracy.

Report order was examined for the set of trials in which the model successfully encoded four targets in simulated whole report as described previously (i.e. the blaster delay is set at 10 ms, and SOA at 110 ms to simulate the 107ms SOA). These data were plotted as the frequency of reporting a given item in each of four possible report positions in figure 19a. The encoded order is the result of variation in target strength from trial to trial. If a T2 is particularly weak, the T3 may outpace it in the race to bind to Token 2, forcing T2 into Token 3 or possibly even Token 4. All four items are most often reported at their correct positions, but order accuracy is especially low for targets in the middle two positions, producing a pronounced U-shape to the accuracy curve.

Figure 19.

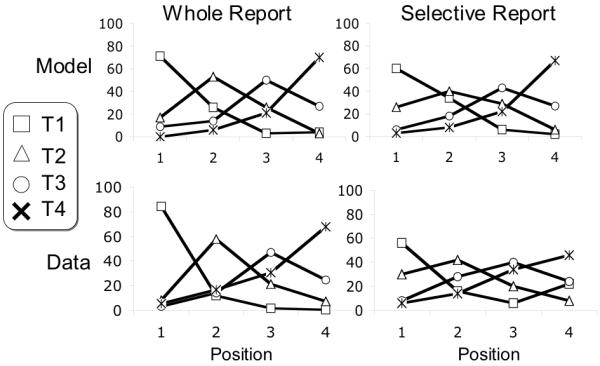
Simulated and actual temporal order information for four reported targets. Whole report data (a) are from a reanalysis of the data of Nieuwenstein & Potter (2006) while selective report data are from the RB experiment reported above. In each graph are shown four lines, illustrating the frequency of reporting each target in each of the four possible positions.

To test this prediction, data from Nieuwenstein & Potter (2006) were analyzed for report order, considering all trials in which subjects reported at least the first four of the six items. This criterion selected 321 trials from the 16 subjects. Reports sometimes contained more than 4 items. For clarity, reports of any of the first four items in position 5 and 6 were collapsed together with position 4.

The whole report data above are consistent with the model (Figure 19a), particularly with respect to the U shape, favoring correct order report of the first and last target items. However, in this experiment, subjects were reporting items from a six item sequence, which may have affected the order accuracy of the last item, particularly after having collapsed report positions 4, 5 and 6 into position 4.

To address this issue, the data from the repetition blindness experiment, which had three and four target trials (i. e. the TTTD and TTTT conditions), were analyzed and compared with the model’s prediction for the same conditions. In these simulations of four targets in a target selection paradigm, the blaster delay was set to 40 ms, the SOA to 90 ms, and order accuracy was examined for conditions of four successfully retrieved targets.

The resultant simulated order data are shown in figure 19b for four targets. Note that the predicted pattern is similar in character to the whole report data; the same U shaped trend is found with T1 and T4 most often in their correct positions, and poorly ordered report of T2 and T3. The change in the blaster delay to 40 ms produces a second target advantage, which also increases the probability that T2 is reported as the first item. Thus order report is worse for the first target than with the whole report data.

The human data provide a good qualitative match to the pattern observed in simulated order report, showing the same characteristic U shape. Order accuracy is worse than in whole report, particularly for the first target. The four target data are derived from 50 trials of a possible 600 trials in which the 15 subjects reported all four of the targets.

We also examined order accuracy for the trials in which three targets were presented and reported by subjects. In this condition, again both the model and the human data show a U shape. T1 T2 and T3 are reported in the correct position 61, 44 and 65 percent of the time in simulation and 58, 43 and 56 percent of the time in the human data. The order data are derived from 196 trials in which subjects reported all three targets correctly.

Prediction 3: Temporal Mispairings during Sparing

A final qualitative prediction proposes that, during sparing, encoding is prone to making temporal errors between components of multi-feature objects, similar to the notion of illusory conjunctions (Treisman & Schmidt 1982). There is already evidence that temporal binding errors interact with the blink (Chun 1997b, Popple & Levi 2007) and that the blink produces a delay in temporal binding (Nieuwenstein et al. 2005, Vul, Nieuwenstein & Kanwisher, In Press). Here we suggest that during sparing, a different pattern of temporal binding error emerges; We propose that the blink helps to reduce the occurrence of these temporal misbindings, but that during sparing, migration of individual elements between T1 and T2 targets occur frequently.

To evaluate this hypothesis, we reanalyze a set of data originally presented in Bowman & Wyble (2007) with the aim of testing the hypothesis that temporal migrations between individual elements of complex targets co-occurred with lag-1 sparing. This experiment used an RSVP stream of digit distractors containing two letter pairs, occurring at 110ms intervals (Figure 20a). In this experiment, subjects were prompted to report the two letter pairs they saw. They were not forced to guess, and were given two prompts, one for the T1 pair and the other for the T2 pair. This paradigm allows us to examine the frequency of mispairings of letters as the temporal interval between them is varied from lag 1 to lag 8.

Figure 20.

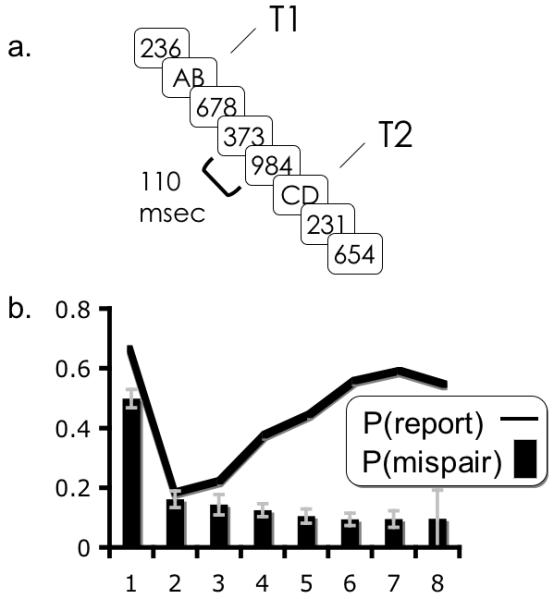
a. The paradigm used in the experiment reported in Bowman & Wyble (2007). b. Accuracy at lags 1-8. Bars indicate the percentage of temporal mispairings at different lags in the letter pair experiment described in Bowman & Wyble (2007). The line indicates probability of T2 report at different lags.

In the new analysis, T2 accuracy was scored as the average probability of reporting either letter (i.e. left or right) of the target pair, revealing a classic attentional blink, including prominent lag-1 sparing (Figure 20b). To assess the chance of mispairing parts of T1 and T2, we considered the set of trials for which subjects encoded at least two of the four presented letters. Each such trial was scored as a mispairing if two letters from one letter pair were reported as coming from separate pairs; if two letters from different pairs were reported together as a single pair; or if both pairs were reported but with their halves miscombined. As can be seen in figure 20b, accurate pairing of two or more letters at lag-1 was not appreciably different from chance (i.e. 50%) but fell abruptly at lag 2 and remained at a nearly constant baseline level for the remaining lags. An ANOVA over the percentage of mispairings with lag as the single factor was significant, (F(7,70) = 33.85, p <.0001 η_p² = .77). When lag-1 was excluded from the analysis, an ANOVA showed no main effect of lag, F(6,60) = 2.11, p > .06 η_p² = .173), suggesting that there was no difference between the number of mispairings at lags greater than 1. Neurophysiological correlates of tokenized target encoding

A particular strength of a temporally explicit model such as eSTST is that the timing of simulated processes can be directly compared with their putative analogs in human subjects using MEG and EEG recordings. Furthermore, the simulated neuronal dynamics provide insight for the interpretation of single cell recordings in monkeys performing working memory tasks.

Electrophysiological correlates of the time course of encoding

In human EEG recordings, the P3 component, is thought to reflect the deployment of processing resources responsible for encoding the item into working memory (Vogel, Luck & Shapiro 1998, Kranczioch, Debener, & Engel, 2003; Martens, Elmallah, London, & Johnson, 2006) and can last for several hundred milliseconds after a target is presented in RSVP. We suggest that this prolonged period of post-target processing reflects the activation of binding pool gate nodes and type nodes within both the STST (Bowman & Wyble 2007) and eSTST models (but see Nieuwenhuis Aston-Jones & Cohen 2005 for an alternative account). Accordingly, it is possible to generate “virtual” ERP components from the activation dynamics of these models to test them against recorded ERP components, as shown in Craston, Wyble, Chennu & Bowman (In press). Virtual P3’s generated from eSTST, particularly their timing and duration, are similar to those produced by STST, since both models simulate the attentional blink as a reflection of working memory encoding. The similarity between these electrophysiological data and the activation dynamics of the model provide corroborative support for our theoretical positions that (a) registering a target as a reportable percept in working memory takes several hundred milliseconds beyond the stimulus presence, and (b) that the attentional blink reflects this process (see also McArthur, Budd & Michie 1999).

Predicted Binding mechanisms in prefrontal cortex

The STST and eSTST models predict putative activation profiles of single neurons in brain areas involved with encoding the temporal order of multiple stimuli. Such predictions are speculative, but nonetheless provide theoretical inroads into large data sets produced by neurophysiology experiments that record from hundreds of neurons.

The substrate of working memory storage within the model, corresponding to tokens and the binding pool, may reside in frontal areas of the brain. These areas are thought to play a role in the memory of temporal order and frequency of multiple stimuli in humans (Milner, Petrides & Smith 1985). The importance of frontal areas in temporal ordering tasks has also been demonstrated in monkeys, in which lesions of the mid-dorsal part of lateral prefrontal cortex (DLPFC) produce severe and permanent deficits in working memory for the order of three objects, despite preserved ability to remember or recognize single items (Petrides 1995). A neural substrate for this capacity is suggested in recordings from monkey lateral prefrontal areas, where neurons with sustained delay activity were highly sensitive to the specific orderings of three stimuli (Ninokura, Mushiake & Tanji 2003) and the integration of stimulus and order information Ninokura, Mushiake & Tanji 2004).

Assuming that these areas of the dorsolateral PFC represent the equivalent of token and binding pool activation, we can delineate classes of neural firing patterns that may be found in tasks involving multiple objects that are to be remembered in sequence. These predictions are particularly important for experimental paradigms that allow stimuli to be repeated within a trial because repetitions make it possible to contrast stimulus selectivity with temporal order representations. The following discussion refers to the simulated activation dynamics of tokens and binding pool nodes as described above, and as depicted in figures 7 and 8.

Binding Pool

We predict that neurons allocated to representing an item in the binding pool will be most selective for one instance of an object in a sequence but not further instances. Some such neurons will be primarily active during encoding (gate nodes), and some will be primarily active during maintenance (trace nodes). In this framework, a further class of neurons function as gate shutoff nodes (see Appendix A.1) to prevent spurious encoding of repetitions. Such neurons would be activated at the end of encoding, firing strongly until the end of a stimulus sequence, but would not persist during the delay. We can also predict that neurons associated with encoding will outnumber those associated with maintenance, as several gate nodes in the binding pool are activated by a target, but only a single trace node sustains activation.

Tokens

Neurons corresponding to token representations will be devoid of stimulus specific firing, but should respond primarily to the position of a stimulus in the encoding sequence (e.g. first, second, etc). Some such neurons will be active selectively during encoding (token gate nodes) and others during maintenance (token trace nodes). See Bowman & Wyble (2007) for further discussion of the dynamics of tokenized representations.

Warden & Miller (2007)

Warden & Miller (2007) recorded neurons in frontal areas of monkeys which exhibit changing patterns of selectively as first one, then a second object is added to working memory. This experiment is ideal for testing our predictions in that the stored sequence contains repetitions, and the task requires encoding the temporal order of the two stimuli. The investigators describe an example neuron that responds strongly for several hundred milliseconds after the first presentation of its preferred stimulus, but is less active during presentation of the second stimulus. This profile is similar to the activation of a binding pool gate neuron; it participates in encoding a first instance of a preferred item, but is then suppressed by a trace node, which renders it unavailable during further encoding. Warden & Miller also describe a regression analysis of firing patterns during the delay period after the second stimulus is encoded and find that while the population of neurons as a whole loses its selectivity for the first stimulus, some neurons remain positively correlated with the first stimulus and others become anticorrelated. Our model suggests that selectivity is not lost; rather, some of the recorded neurons may be trace nodes (the positively correlated neurons), and others gate nodes (the negatively correlated neurons) and the majority of stimulus selective neurons are not activated strongly enough to participate in the sustained working memory representation.

General Discussion

In the present study, we described the episodic Simultaneous Type / Serial Token (eSTST) model of the attentional blink. This model concerns a modification of the Simultaneous Type / Serial Token model (STST) previously proposed by Bowman and Wyble (2007). The new model was borne out of a need to accommodate recent findings that posed a fundamental challenge to STST, most notably the fact that observers can encode sequences of successive target items without suffering an attentional blink. The key modification of STST that allows eSTST to accommodate this result is the notion that attention allocation is governed by competing inhibitory and excitatory inputs from working memory processing and newly encountered targets, respectively. This makes the model more flexible, as it allows for attention to be sustained, or retriggered while a first target is being encoded into working memory.

The model also suggests that this state of affairs comes at a cost: Although sustained attention may allow for accurate report of the identities of several successive target items, the resulting memory representations lack episodic distinctiveness. Observers can thus report the identities of successive target items, but they have difficulty recalling them in the correct order, different features of successive multi-part objects tend to be mispaired, and the ability to encode repetitions is impaired.

The episodic distinctiveness hypothesis

One implication of the model is that visual encoding is designed to enhance the episodic structure of information encoded into working memory; stimuli that are presented in an uninterrupted sequence are encoded in parallel; stimuli that are interrupted by gaps are segregated into temporally isolated representations. Thus, we argue that the attentional blink is not a malfunction or limitation of attentional control (as is assumed by the interference account of Shapiro, Raymond & Arnell, 1994; the refractory account of Nieuwenhuis et al. 2005; and the Temporary Loss of Control theory described by Di Lollo, Kawahara, Ghorashi & Enns 2005). Rather, the blink reflects a cognitive strategy of enforcing the episodic distinction between separately presented targets.

Functionally, this is the result of a temporary inhibition of attention, which attempts to delay new targets from entering the encoding stage if there has been a gap in the target sequence. However, presenting targets without interruption reveals the flexibility of this mechanism in the form of sparing. We propose that when sparing occurs, multiple targets enter the encoding stage at the same time. The system can encode all of them, but without ensuring that they are episodically distinct.

Sparing represents a tradeoff between the benefit of encoding multiple items in parallel, and the detriment in maintaining their episodic distinctiveness. This cost is manifest in a variety of deficits, including interference between items (i.e. loss of T1 at lag 1), loss of temporal order, conjunctions between parts of complex items, and increased repetition blindness.

The Limited Role of Distractors In Producing the Blink

A point of serious theoretical contention between competing accounts of the blink is the role of distractors in an RSVP stream. Many theoretical accounts describe a direct role for distractors in causing the blink. In the case of the Di Lollo et al. (2005) TLC account, the T1+1 distractor forces a reset of input filters to the distractor category, such that a following T2 fails to be encoded as a target. In interference theory, the T1+1 distractor enters working memory with T1 and produces interference. Another theory is described by Raymond et al. (1992), which proposes that an attentional gate is shut-and-locked in response to the T1+1 distractor. A variant of this idea proposes that an inhibitory process is initiated reactively by a distractor that immediately follows a target (Olivers 2007).

The eSTST model proposes something quite different; the blink is caused entirely by target processing. Mechanistically, the inhibitory connection from the binding pool to the blaster causes the blink during encoding of a target. Distractors are inhibited at the type layer and are incapable of directly affecting the binding process. Their effect on the AB is indirect in that they mask the targets and thus lengthen the duration of encoding T1 and reduce the reportability of T2.

One line of evidence supporting this idea stems from the following studies, which point to the fact that it is primarily the masking properties of distractors which defines their role in the attentional blink. Maki, et al (2003) demonstrate that the pixel density of distractors is more important than their conceptual familiarity to subjects. Their work, as well as the experiments of Olivers et al (2007), show that false fonts are similarly effective distractors as familiar characters, such as digits. For word targets, Maki, Couture, Frigen & Lien (1997) found that word and nonword distractors produce similar blink effects. Along similar lines, McAuliffe & Knowlton (2000) demonstrate that manipulating the conceptual difference between T1 (a letter) and its mask (‘V’ vs inverted ‘V’) had no effect on the blink magnitude. Grandison, Ghiradelli & Egeth (1997) also published a series of studies that replaced the T1+1 item with simple stimuli, including a white square, a white screen flash, and a metacontrast box and found blinks in each case.

A more direct prediction of the idea that target processing causes the blink is that the effect should be observable in the absence of post T1 distractors. Experiments by Visser (2007) and Ouimet & Jolicouer (2006) have found exactly this result. In some of the reported experiments, the interval between T1 and T2 is a blank display, and yet prominent blinks are reported for difficult T1 tasks. Nieuwenstein, Potter & Theeuwes (In Press) demonstrate that even for relatively easy T1 tasks (e.g. an unmasked letter at 100 ms SOA), a prominent blink can be observed if the T2 task is sufficiently difficult. These findings are difficult to reconcile with the idea that the blink is induced by distractors, as described by Olivers (2007), but they fit well with the theory of competitive regulation of attention as described here.

Conclusion

In the present study, we proposed a computational model of the attentional blink which explains this effect in terms of the interactions between working memory encoding and mechanisms of attention allocation. Central to this account is the notion that working memory encoding of a first target event suppresses the allocation of attention to new perceptual inputs so as to prevent these inputs from being integrated with the episodic memory of the first target. To accommodate the fact that observers can encode sequences of successive targets without suffering an attentional blink, the model assumes that that this suppressive effect is counteracted by the excitation of attention by newly presented targets. Consequently, the deployment of attention may be prolonged across several successive target items, resulting in accurate report of the target identities. Crucially, however, this ability to attend and encode successive targets occurs at the expense of episodic information; items are often recalled in an incorrect order, the ability to detect repetitions is markedly reduced, and there is an increase in binding errors for multi-part objects.

This model suggests that the attentional blink reflects a self imposed limitation on the encoding of visual information. In particular, it proposes an antagonistic relationship between engagement of working memory encoding, and the deployment of attention. We suggest further that there could be a link between the attentional blink and paradigms which measure an impairment in the report of stimuli that are present for considerable periods of time. For example, inattentional blindness is observed when subjects are cognitively engaged; they fail to notice the onset or arrival of novel or otherwise arresting stimuli (Simons & Chabris 1992, Fougnie & Marois 2007). In such tasks, engagement of central mechanisms may maintain a sustained suppression of the reflexive deployment of attention by the visual system.

One implication of this idea is that there should be a connection between the attentional blink, and cognitive load, although more data is necessary before a computationally explicit account of cognitive load can be described. Specifically, it is necessary to investigate how the strength of the suppression which causes the blink is affected by cognitive load. Preliminary efforts in this direction (Olivers & Nieuwenhuis 2005) suggest that this suppression is relaxed by distracting subjects with an additional task, resulting in an attenuated blink effect. Likewise, the attentional blink may also be be attenuated by engaging motion processing mechanisms, as suggested by the results of Arend, Johnston & Shapiro (2006). Further experimental work along these lines are needed to understand the link between the attentional blink, and cognitive load effects which produce phenomena such as inattentional blindness. Such results will allow models of the blink to be refined and thereby applied to cognitively demanding tasks that people face in more natural settings.

Appendix

Appendix A.1: Modeling Methods

Input

Each accuracy curve is created by running the model repeatedly as target input strengths are iterated over specified ranges. The range of values used for T1 and T2 were [.31, 1.39] in steps of .09. Encoding of T1 and T2 identity and the probability of reporting the wrong order (i.e. P(swap)) are evaluated at each of the 8 lags for each pairwise combination of the 13 T1 and T2 values (i.e. 169 trials). In three or four target sequences, targets are iterated over the same range in nine steps of .135, resulting in 3^9 or 4^9 simulated trials in three or four target conditions.

Time steps correspond to 10 ms. Target presentation times are scheduled to occur at appropriate times for each condition to simulate the chosen pattern of targets and distractors depending on the SOA. Input node activation continues for a very brief period after the end of presentation of a target, reflecting rapidly decaying information in early sensory areas. Thus, during input of a target, input_j(t) is held at the corresponding value chosen from the range above for 12 timesteps for 100 ms SOA stimuli, 7 steps for 50ms and 13 steps for 110ms, followed by a linear decline to 0.0 in increments of .12 per time step if that item is followed by another item (i.e. it is masked), or .01 during a blank interval. This enhanced decay of targets followed by other items reflects the effect of backward masking.

Type Activation

Activation of type nodes has the following dynamics

$$\begin{array}{cc}\hfill {\text{type}}_{i\left(t\right)}=({\text{type}}_{i(t-1)}\ast \text{decay})+({\text{input}}_{i\left(t\right)}\ast (1+\text{typeamp}\ast {\left\{{\text{blaster}}_{(t-\text{bdelay})}\right\}}_{\text{bthresh}}))& -{\mathit{inhib}}_{\left(t\right)}+{{\text{gatefeedback}}_i}_{\left(t\right)}\hfill \\ \hfill & {\left\{x\right\}}_a=1.0\text{if}x>=a\hfill \\ \hfill & 0.0\text{if}x<a\hfill \end{array}$$ (2)

In this activation equation, type_i(t) is the activation of type i at time t, input_i(t) is the input to that type, decay is the decay rate (.7). At each time step the input to a type is amplified if the blaster was above threshold (bthresh = 1.7) bdelay time steps prior to time t. The amplification has value typeamp, set at 2.5. The parameter bdelay is 4 for partial report (a 40 ms delay) and 1 for whole report simulation. The term inhib_(t) is the weak interference between co-active targets and is computed as the bounded sum of type activation in equation 2.

$$\begin{array}{cc}\hfill {\text{inhib}}_{\left(t\right)}=\sum _{j=1:4}{\left[{\text{type}}_{j\left(t\right)}\right]}_0^{\infty }\ast \text{irate}& \hfill \\ \hfill & {\left[x\right]}_a^b=b,\text{if}x>=b\hfill \\ \hfill & x,\text{if}x>=a\&x<b\hfill \\ \hfill & a,\text{if}x<a\hfill \end{array}$$ (3)

The term irate is a constant, set at .045. The term gatefeedback_i(t) is the recurrent excitation from gates j = 1:4 in the binding pool to type i which can sustain that type during binding.

$${\text{gatefeedback}}_{i\left(t\right)}={\left[\underset{j=1:4}{\mathit{MAX}}\left({\text{gate}}_{ij\left(t\right)}\right)\right]}_0^8\ast \text{feedbackrate}$$ (4)

The parameter feedbackrate is set at .42. MAX represents a function which takes the maximum value over the gate nodes (see Yu, Giese & Poggio (2002) for discussion of the utility and biological plausibility of max functions in neural networks).

The Binding Pool

The binding pool is an arrangement of nodes that allows the model to store a link between a type and a token by holding an attractor state in a self-excitatory node. The pool is populated by binding units, one per combination of type i = [1, 4] and token j =[1, 4]. Each binding unit consists of one gate and one trace node. Gate nodes are excited by type nodes and receive an ordered pattern of bias so that binding units for token 1 are bound more rapidly than units for token 2 and so on.

$${\text{gate}}_{ij\left(t\right)}=({\text{gate}}_{ij(t-1)}\ast \text{gdecay})+({[{\text{type}}_{i\left(t\right)}-\text{typethresh}]}_0^{\infty }\ast \text{typeweight}+{\text{binderbias}}_j)-({[{\text{gateshutoff}}_{i\left(t\right)}-\text{gsthresh}]}_0^1+\sum _{i=1:4}{[{\text{trace}}_{ij\left(t\right)}-\text{tracethresh}]}_0^1)\ast \text{gateinhib}$$ (5)

Parameter typeweight is set to 0.25, typethresh to 2.0, gdecay is 0.93 and binderbias_j is [-.005,-.01, -.015, -.02] for tokens j = [1,2,3,4]. Variable gateshutoff_i(t) represents the activation of a node, defined below in equation 7. When above threshold gsthresh (value 1.2), this node temporarily inactivates the gates for type i after it has been bound, and keeps them inactive until type i is inactive. This mechanism prevents the system from encoding spurious repetitions of a single, uninterrupted presentation of a stimulus. The final term inhibits all gate nodes for token j once it has been bound (i.e. a trace node crosses threshold tracethresh of value 10.0) to prevent that token from binding a second time. Parameter gateinhib is set at any arbitrarily large number to ensure that gate_ij(t) is rendered inactive by any suprathreshold activity from gateshutoff or trace nodes that inhibit it.

Trace nodes accumulate input from gate nodes without decay.

$${\text{trace}}_{ij\left(t\right)}={\left[{\text{trace}}_{ij(t-1)}\right]}_0^{100}+({\left[{\text{gate}}_{ij}\left(t\right)\right]}_0^{\infty }\ast \text{gateweight})+({[{\text{trace}}_{ij(t-1)}-\text{tracethresh}]}_0^{001}\ast \text{traceself})$$ (6)

When a trace node trace_ij crosses threshold tracethresh, it becomes strongly self excitatory (e.g. traceself is set at 10,000) and thus is self sustained at a ceiling value of 100. Restricting the value of the difference trace_ij(t)-tracethresh to the range [0 - .001] and then multiplying by a large value implements an all-or-none attractor dynamic, which is necessary due to the coarse time-step. Parameter gateweight is 0.014.

When any trace node j has entered its attractor state, the corresponding token j is then considered bound to type i (it is not necessary to simulate tokens explicitly in this abstract representation). Because the time steps of our simulation are coarse we implement hard winner take all behavior between the trace nodes for a single token, rather than simulating it through lateral inhibition. Thus, as soon as trace_ij(t) crosses threshold, all other trace nodes for the token j are immediately suppressed on that time step.

To ensure that a single type presentation is bound to only a single token, all gates for type i are suppressed until that type node becomes nearly inactive. This is implemented through a set of self excitatory nodes controlled by the following activation equation.

$${\text{gateshutoff}}_{i\left(t\right)}=({\text{gateshutoff}}_{i(t-1)}\ast \text{gsleak})+({[{\text{gateshutoff}}_{i(t-1)}-\text{gsthresh}]}_0^{001}\ast \text{gsweight})+{\text{tbound}}_{i\left(t\right)}+({[{\text{type}}_{i\left(t\right)}-\text{gstypethresh}]}_0^{0.01}\ast \text{gssustain})$$ (7)

When a token j is bound to type i (i.e. trace_ij exceeds tracethreshold), the gateshutoff node for type i receives a brief pulse of input to push it into an attractor state (tbound_i(t) = 1.0 for one step). This gateshutoff node suppresses gates for type i. As long as the type node i remains above gstypethresh, gateshutoff_i(t) receives sufficient input (both from itself, and the type node) to stay in an attractor. Parameter gssustain is set at 30. As soon as the type node dips below gstypethresh = 4 the attractor state collapses and the system becomes ready to encode a second instance of type i. This circuit ensures that the system generally behaves sensibly during RSVP with respect to repetitions; an unbroken presentation of a target produces only a single tokenized representation of that item. The visual input driving the type node has to switch off at the input layer if the system is to encode a second tokenized representation of the same item. Parameter gsleak is .7, gsthresh is 1.2 and gsweight is 100.

The complete connectivity of nodes within the binding pool is shown in figure 21, separated into two parts for clarity. Figure 21a depicts the interconnectivity for binding units for two types and one token. Figure 21b depicts binding units for one type and two tokens.

Figure 21.

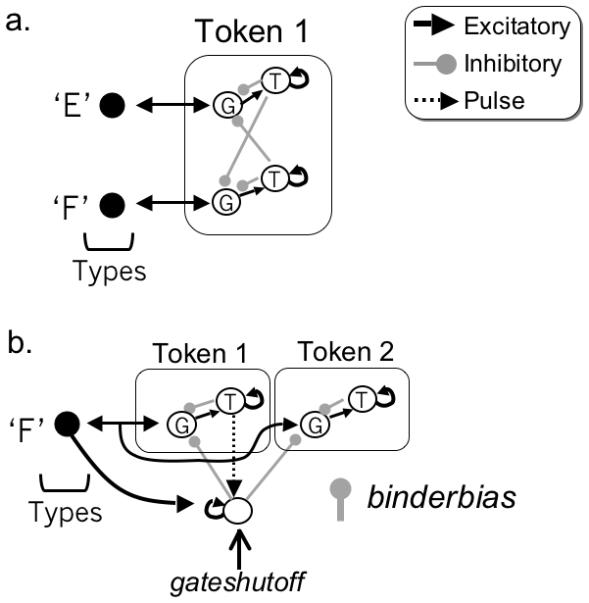
The complete connectivity of the binding pool, illustrating how two types compete for a single token (a) and how a type that has been encoded is prevented from being encoded a second time until it has ceased to be active (b). Also shown in the lower figure is the pattern of bias inputs to the token gates that force token 1 to complete binding prior to token 2, provided that token 1 has not already been bound. The node at the bottom of (b) implements this behavior, triggered by successful completion of token 1, it becomes active and stays so until the type node ‘F’ is no longer active. While active, it prevents gate nodes from becoming active so that ‘F’ cannot be spuriously encoded twice from a single presentation. This mechanism comes with a cost of repetition blindness. It is not shown here, but this same inhibitory node acts across the entire set of four tokens.

Tokens

In this implementation, trace nodes in the binding pool effectively represent tokens, because only a single feature (i.e. letter identity) is bound to a token. For more complex implementations (e.g. requiring a conjunction of features bound to a single token), an explicit implementation of tokens would be required. Blaster

The Blaster is a single thresholded node that amplifies input when above threshold.

$${\text{blaster}}_{\left(t\right)}=({\text{blaster}}_{(t-1)}\ast \text{bleak})+(\sum _i{\text{input}}_{i\left(t\right)}\ast (1+\text{blasteramp}\ast {\left\{{\text{blaster}}_{(t-\text{bdelay})}\right\}}_{\text{bthresh}}))-{\text{binhib}}_{\left(t\right)}$$ (8)

The term bleak is .85. Crucial to the competitive regulation of attention, the blaster amplifies its own input when above threshold (see equation 2) The term blasteramp is 0.75.

The term binhib_(t) represents the top down inhibition from active gate nodes. To compute this term, the activation of all gates is summed, multiplied by slope = .04, and divided by the same value +1, to scale the values to the range [0, 1].

$${\text{binhib}}_{\left(t\right)}=\frac{\sum _{ij}{\left[{\text{gate}}_{ij\left(t\right)}\right]}_0^{\infty }\ast \text{slope}}{\sum _{ij}{\left[{\text{gate}}_{ij\left(t\right)}\right]}_0^{\infty }\ast \text{slope}+1}\ast \text{binhibweight}$$ (9)

Parameter binhibweight is 1.5.

Retrieval

Performance is evaluated at the end of each trial by taking inventory of the tokens which are bound (i.e. active trace nodes in the binding pool). Each instance of a token corresponds to one report of the type to which it is bound. Order is determined by the order of the tokens.

Critical Parameters

There are several critical parameters that were used to tune the model to fit the data set. (1) The strength of target input is specified by two parameters defining upper and lower bounds on a uniform distribution which determines baseline accuracy of single target report. (2) The rate of encoding is determined by the magnitude of the gate->trace weight: gateweight. This parameter determines the length (and to some degree depth; length and depth are not independent) of the blink. (3) The strength of the inhibitory projection to the blaster from gates: binhibweight determines, primarily, the depth of the blink. (4) The weak inhibition between type nodes: irate determines the degree to which T1 performance suffers during lag-1 sparing. (5) The delay of attentional deployment: bdelay is varied to fit the magnitude of lag-1 sparing, with a longer delay leading to higher sparing. These parameters were varied to fit the T1 and T2|T1 accuracy data in the attentional blink (Figure 11). Once these parameters are set, other simulation outputs, such as the propensity to produce swap errors, to be blind to repetition, or to successfully encode a string of targets, are emergent properties of the SOA and sequence of targets.

Appendix A.2 The Binding Pool and the Binding Problem

The type/token binding pool that we have implemented here requires MxN nodes where M is the number of types and N is the number of tokens. The size of this pool is an important issue that requires discussion of two points.

MxN is not the Combinatorial Explosion

The MxN factor is not the same as the combinatorial explosion commonly referred to in discussion of the binding problem. In that context, binding any of M types to any other type using conjunctive representations requires M² nodes (e.g. binding red to square requires having a red-square node). Binding 3 types into one object (e.g. a red and green colored square requires three types) requires M³ nodes to represent each possible instance of an item. In comparison, the binding pool uses MxN nodes to encode N representations in working memory (i.e. usually five or fewer) of items of arbitrary complexity (i.e. any combination of the M types can be combined into each representation).

Distributed Representation

This MxN solution described here is exhaustive and inefficient in the sense that each combination of type and token is uniquely represented by a conjunctive node. This implementation is intended as a simplification of what can be implemented as a distributed representation (O’Reilly, Busby & Soto 2003). Preliminary modeling work has demonstrated that a binding pool with distributed representations can be quite compact. Initial exploration of this issue, described in Wyble & Bowman (2006), prescribes a distributed implementation of the binding pool containing just 500 nodes that can store distinct bindings between three tokens and three arbitrary types from a population of 5000 type nodes without significant interference. Thus, the binding pool of 500 nodes stores arbitrary bindings between three tokens and three of 5000 types. Therefore, the distributed solution to this problem scales well to large scale representational implementations, and the binding pool can be much smaller than the population of type nodes it indexes. With such an asymmetry between the size of binding pool and type nodes, a compact population of binding neurons in frontal areas could store information from a much larger area of cortex (e.g. posterior sensory areas of the brain).