A population-coding model of attention's influence on contrast response: estimating neural effects from psychophysical data

Abstract

Human psychophysics and monkey physiology studies have shown that attention modulates early vision – contrast sensitivity and processing. But how can we bridge the effects of attention on perceptual performance to their neural underpinnings? Here we implement a population-coding model that estimates attentional effects on population contrast response given psychophysical data. Model results show that whereas endogenous (sustained, voluntary) attention changes population contrast-response via contrast gain, exogenous (transient, involuntary) attention changes population contrast-response via response gain.

Introduction

Covert attention allows us to selectively process information at a given location in our visual field, in the absence of eye movements (Posner, 1980). Numerous psychophysical and neurophysiological studies indicate that covert attention influences one of the earliest stages of visual analysis, contrast processing (Carrasco, 2006; Reynolds & Chelazzi, 2004). But how can we relate changes in neural activity to behavior? The fundamental problem of linking neural response to behavior has been approached from a number of angles. One popular approach has been to predict the behavior of a monkey based on the activity of individual cells, using models such as choice-probability (e.g. Britten, Shadlen, Newsome & Movshon, 1992; Parker & Newsome, 1998; Zohary, Shadlen & Newsome, 1994). However, this approach is limited by the heterogeneity of single-unit responses: whereas the expected performance computed from some neurons match behavior well, other neurons fail to predict behavior (Britten et al., 1992; Shadlen, Britten, Newsome & Movshon, 1996). Indeed, single-unit studies of covert attention have found similar variability in predicted performance (Reynolds, Pasternak & Desimone, 2000). This approach is further limited by the fact that attentional gain mechanisms have been shown to be fairly diverse, differing widely from neuron to neuron. Whereas some neurons exhibit response gain modulation with attention, others show contrast gain, and yet others show a mixed effect (Williford & Maunsell, 2006).

Population-coding could be another way to linking neural response with behavior. Due to the inherently noisy nature of individual neurons, it is likely that our brain analyzes neural responses by recruiting activity across large cell populations to guide perception and behavior, rather than only relying on the activity of few cells (Abbott & Dayan, 1999; Pouget, Dayan & Zemel, 2000, 2003). Assuming that ensembles of neural activity drive behavioral effects, we investigate how attention might affect the contrast response as coded by a neural population, that is, the pooled neural response in a given brain area to a stimulus as contributed by neurons that are optimally and not optimally tuned to the stimulus. Jazayeri and Movshon (2006) proposed a population-coding model of optimal representation of sensory information in motion-direction discrimination, which estimates the likelihood of a stimulus given the pooled neuronal response by calculating the weighted sum of individual sensory-neurons responses. We extend this model to orientation discrimination, and modulate the model response as function of stimulus contrast and attentional state to estimate how attention changes the population contrast-response, given known psychophysical attentional effects with humans.

The present model infers the expected change in contrast response for a population of neurons, given human performance in psychophysical tasks similar to those used in monkey neurophysiology (Martinez-Trujillo & Treue, 2002; McAdams & Maunsell, 1999; Reynolds et al., 2000; Williford & Maunsell, 2006). Two-alternative forced-choice orientation-discrimination tasks have been used extensively in human psychophysics to address the effects of attention on contrast sensitivity (Cameron, Tai & Carrasco, 2002; Carrasco, Penpeci-Talgar & Eckstein, 2000; Ling & Carrasco, 2006a, 2006b; Lu & Dosher, 1998; Lu & Dosher, 2000; Lu, Lesmes & Dosher, 2002; Pestilli & Carrasco, 2005; Pestilli et al., 2007), as performance in this task is monotonically contingent on contrast (Nachmias, 1967). Thus, orientation discrimination is an ideal candidate for direct comparisons of psychophysical and neurophysiological results. The model derives orientation discrimination performance (d′) by determining how likely it is that each possible stimulus alternative was presented, given the population response. To do so, the likelihood of each stimulus is computed as the sum of individual neurons' responses, weighted by the log of their own tuning function. This weighting biases the input such that responses are tuned away from the discrimination boundary (vertical in our case). Theoretically, this is the optimal strategy for decoding orientation from a population response (Jazayeri & Movshon, 2006). Empirically, there is behavioral evidence in support of this notion, showing that we tend to overestimate fine orientation differences, i.e. we misperceive these differences as being broader than they really are (Jazayeri & Movshon, 2007).

The overall population response to the stimulus is scaled as function of contrast, with the contrast response characterized by a compressive nonlinearity, as shown in single-cell responses (Albrecht & Hamilton, 1982; Albrecht, Thorell & Hamilton, 1981; Naka & Rushton, 1966). To model the effect of attention, the population contrast response is modulated by two possible gain mechanisms, contrast- and response-gain, found in single-unit studies (Figure 1a and 1c; Martinez-Trujillo & Treue, 2002; Reynolds & Chelazzi, 2004; Reynolds et al., 2000; Williford & Maunsell, 2006). Whereas contrast gain predicts the maximal attentional modulation at the dynamic range of the contrast response function (Figure 1b), response gain predicts that attentional modulation increases monotonically as a function of contrast (Figure 1d). Incorporating this compressive nonlinearity allows us to visualize and make quantitative predictions regarding how the population contrast response function (pCRF) is altered by attention.

Figure 1. Gain mechanisms of attention in single-cell responses to contrast.

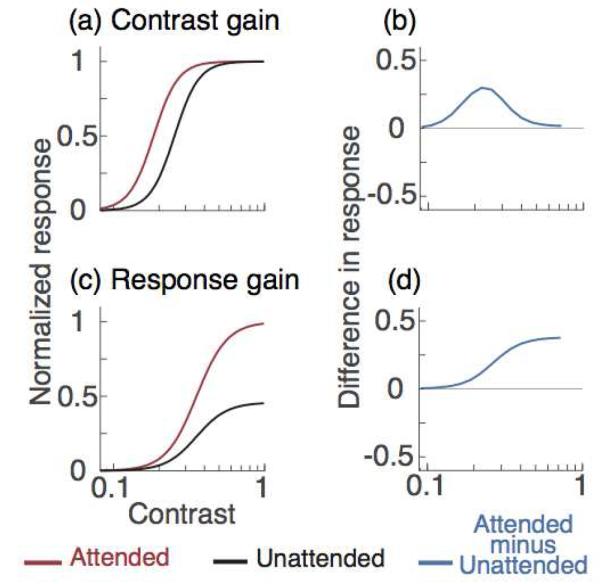
The black and red curves represent the contrast response functions of a hypothetical neuron when attention is directed away from and towards a stimulus, respectively. (a) Contrast gain, attention shifts the neuron's contrast response function toward lower contrast. (b) The effect is greater near the middle of the contrast response function than at low and high contrasts. (c) Response gain, attention multiplies neuron response by a constant factor; (d) the attentional effect increases with contrast.

Behaviorally, using a cue to direct observers' covert spatial attention enhances performance and contrast sensitivity at the attended location and impairs it at unattended locations (Ling & Carrasco, 2006a, 2006b; Lu & Dosher, 2000; Pestilli & Carrasco, 2005; Pestilli, Viera & Carrasco; 2007). The magnitude of the attentional modulation depends on the type of attention deployed, and the stimulus contrast. Whereas endogenous (voluntary, sustained) attention alters performance only for stimuli at intermediate contrast levels, reminiscent of a contrast-gain mechanism (Ling & Carrasco, 2006a), the effects of exogenous (involuntary, transient) attention primarily increase with contrast, reminiscent of a response-gain mechanism (Ling & Carrasco, 2006a, Pestilli & Carrasco, 2005, Pestilli et al., 2007).

Model

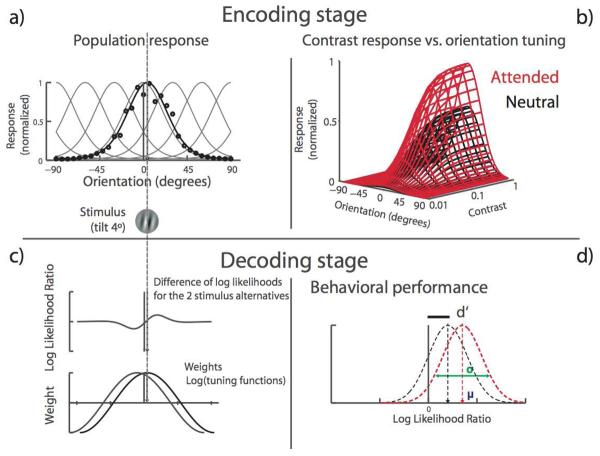
The model comprises an encoding and a decoding stage; Figure 2 represents the model structure in a schematic form.

Figure 2. Population-coding model for orientation discrimination with contrast-dependent responses.

The model is composed of an encoding front stage and a decoding back stage. It predicts the likelihood that a stimulus gives rise to the neural population response by computing the weighted sum of individual neurons' responses. The encoding stage is a bank of orientation-tuned neurons, modeled as circular normal (a, equation 2). To generate a population response (black line), the response of each neuron (black dots), given by the individual tuning curves (gray lines) is scaled by the population's sensitivity to contrast, as described by a Naka-Rushton function (b, equation 4). The decoding stage computes the likelihood of each stimulus alternative and uses their log-likelihood ratio to choose the most likely one. Each neuron's contribution to the decision is determined by the product of its firing rate (resulting from its orientation-tuning and contrast-response properties) and the log of its tuning curve (equation 5). Neurons' responses are signal-correlated, such that response correlation varies as a function of tuning similarity (c, equation 3). Sensitivity (d′) is computed by estimating the most likely stimulus alternative. The model reaches a decision by computing the mean likelihood-ratio of the two possible alternatives (+4° and −4°) and the variance around this mean (d, equations 7-10).

Encoding stage

The model consists of a population of N self-similar neurons uniformly tuned for orientation. Here we assume a population of 300 detectors. Each neuron's tuning function is approximated by a circular normal, described by the von Mises function, f_i (θ) :

$$f_i\left(\theta \right)=e^{k[2\cos (\theta -{\theta }_i)-1]},$$ [1]

where κ is the concentration parameter (bandwidth), θ is the stimulus orientation (the studies we fit to used 4° and 2.5°), and θ_i is the preferred orientation of the i^th neuron.

We assume that when a stimulus is presented, the probability that each neuron fires a certain number of spikes in an interval of t seconds is well described by a Poisson process:

$$p(n_i\mid \theta )=\frac{{\left({\mathit{Rtf}}_i\left(\theta \right)\right)}^{n_i}}{n_i!}{e}^{-\mathit{Rtf}\left(\theta \right)},$$ [2]

where n_i is the spike count for the i^th neuron, t is the stimulus duration (in seconds), and R is the contrast-dependent response (in impulses per second). Note that although it is established that the Poisson-like characteristics of spike variability break down with brief stimulation durations (Müller, Metha, Krauskopf & Lennie, 2001), for computational simplicity, we assumed that the responses to short stimuli are Poisson distributed, and that deviations in the statistical nature of the modeled neural noise would only lead to slight quantitative differences, rather than qualitative ones.

The relation between contrast and neural response (R) is well-described by a compressive nonlinearity, the Naka-Rushton function (Albrecht & Hamilton, 1982, Albrecht et al., 1981, Naka & Rushton, 1966):

$$R=M+\frac{a_1{R}_{\max }{C}^{\beta }}{C^{\beta }+a_2{C}_{50}^{\beta }},$$ [3]

where M is the baseline population response, C is the contrast of the stimulus, R_max is the maximum firing rate of the population, β is the slope of the contrast response function, and C₅₀ is the half-point between baseline and asymptote (threshold). Of key importance are the parameters a₁and a₂, which are the attentional parameters for response- and contrast-gain mechanisms respectively. a₁ represents response gain modulation, increasing the response multiplicatively such that higher contrast levels lead to greater attention modulation. a₂ represents contrast gain modulation, re-centering the contrast response function by changing the contrast level at which 50% of the maximum response is reached.

The model assumes that neurons' responses are signal-correlated, such that response correlation varies as a function of tuning similarity (Averbeck, Latham & Pouget, 2006). Thus, responses of similarly-tuned neurons are facilitated, while the responses of neurons tuned differently are suppressed. This pair-wise correlation in response is represented as:

$${\rho }_{\mathit{ij}}={\rho }_{\max }{e}^{\delta [2\cos ({\theta }_i-{\theta }_j)-]},$$ [4]

where ρ_max is the maximum correlation, δ is the concentration parameter, and θ_i and θ_j are the preferred orientations of the i^th and j^th neuron.

Decoding stage

Given that we now have an estimate of the response and variance across detectors, we can derive the Likelihood function used to decode the most likely stimulus presented, given the observed population response. We assume that for fine discriminations, observers are not actually basing their decoding primarily on the response of the detector tuned for the stimulus, but rather adopt the optimal strategy (Jazayeri & Movshon, 2006), which is to rely on the response of more broadly tuned detectors. This idea that observers bias their response towards flanker detectors for fine discrimination is buttressed by a recently demonstrated illusion showing that observers tend to exaggerate the direction of fine global-orientation motion (Jazayeri & Movshon, 2007). Thus, we represent this pooling as the product of each neuron's tuning function, weighted by its natural log, which in this case is the optimal weighting function. This weighed pooling is represented as:

$$\mathit{LogL}\left(\theta \right)=\kappa \underset{i=1}{\overset{N}{}}{n}_i\cos \left[2(\theta -{\theta }_i)\right],$$ [5]

We assume that observers make a comparison of the probability that the response could have arisen from the two stimulus alternatives, which we can represent as a likelihood ratio. The likelihood ratio for the case of two stimulus alternatives, θ₁ and θ₂ (symmetrical around the vertical), can be derived as the difference between each stimulus' respective log likelihood:

$$\mathit{LogLR}=2\kappa \sin \left(2\Delta \theta \right)\underset{i=1}{\overset{N}{}}{n}_i\sin \left[2({\theta }_i-{\theta }_m)\right],$$ [6]

where Δθ is the difference in orientation between the two stimulus alternatives, and θ_m is their mean orientation, or discrimination boundary (0° for a ±4° orientation discrimination task).

The first and second moment of the log likelihood ratio define the mean, μ_LR, and variance, ${\sigma }_{\mathit{LR}}^2$ of the log likelihood ratio:

$${\mu }_{\mathit{LR}}=2\kappa R\sin \left(2\Delta \theta \right)t\underset{i=1}{\overset{N}{}}{f}_i\left({\theta }_i\right)\sin \left[2({\theta }_i-{\theta }_m)\right];$$ [7]

$${\sigma }_{\mathit{LR}}^2={\left[2\kappa \sin \left(2\Delta \theta \right)\right]}^2\mathit{Rt}\underset{i=1}{\overset{N}{}}\underset{j=1}{\overset{N}{}}{\rho }_{\mathit{ij}}\sqrt{f_i\left({\theta }_1\right)f_j\left({\theta }_1\right)}\sin \left[2({\theta }_i-{\theta }_m)\right]\sin 2({\theta }_j-{\theta }_m)].$$ [8]

Based on the derived mean (μ_LR) and variance $\left({\sigma }_{\mathit{LR}}^2\right)$ of the log likelihood ratio, we can predict performance in an orientation discrimination task. Accuracy in the task is defined as:

$$P_{\mathit{correct}}=\frac{1}{\sqrt{2\pi {\sigma }_{\mathit{LR}}^2}}\underset{0}{\overset{\infty }{}}{e}^{\frac{-{(x-{\mu }_{\mathit{LR}})}^2}{2{\sigma }_{\mathit{LR}}^2}\mathit{dx}}$$ [9]

Finally, accuracy (P_correct) is transformed to d ′ by the following equation:

$$d^{\prime }=\sqrt{2}\mathit{Zscore}\left(P_{\mathit{correct}}\right).$$ [10]

The d ′ value predicted by the model is then compared to observers' performance in two-alternative forced-choice orientation-discrimination task, as function of contrast (Nachmias, 1967).

Experimental methods

We fit the model to data from two psychophysical studies, Ling and Carrasco (2006) and Pestilli et al. (2007), both measuring the influence on attention on contrast psychometric functions.

Ling and Carrasco (2006) assessed the effect of both endogenous and exogenous attention on contrast sensitivity. Observers were asked to report the orientation (right or left) of a Gabor that appeared alone at 1 of 8 possible isoeccentric locations. In a given trial, target Gabors were preceded by one of three types of precues: an endogenous cue, an exogenous cue, and a neutral cue. The endogenous cue was a line at fixation that pointed towards the upcoming target location, directing observers to willfully deploy their endogenous attention to that location. The exogenous cue was a transient dot that flashed adjacent to the upcoming target location, reflexively grabbing exogenous attention to that location. The neutral cue was a dot that appeared at fixation, providing no information as to the location of the upcoming target, serving as a baseline condition. The three cues conveyed the same information with regard to the temporal onset of the target. Psychometric functions were measured via the method of constant stimuli, with the Gabor contrasts ranging from .09 to .62 in 14 log steps.

Pestilli et al. (2007) assessed the effect of exogenous attention at both the attended and the unattended locations on contrast sensitivity. To do so, we presented two Gabors simultaneously, one at each side of the fixation point. In each trial, one of the Gabors was preceded by one of two types of precues: exogenous cue and neutral cue (both as described above). Following stimulus presentation, observers were asked to report the orientation (right or left) of the Gabor indicated by a subsequent response cue. The cue was considered Valid when the location of the precue and the response cue matched (50% of the time), and Invalid when they did not match (50% of the time). Thus, the cue was uninformative and observers were explicitly told so. Psychometric functions were measured via the method of constant stimuli, with the Gabor contrasts ranging from .01 to .8 in 8 steps.

Results

The model comprises a set of parameters that define a population of neurons. For the present results we used parameters based on those found in V1 (Albrecht & Hamilton, 1982, Kohn & Smith, 2005). Table 1 shows the actual parameter values used to fit the data. Models were fit to the accuracy data using non-linear regression, and then transformed to d′. Note that although the value of the parameters changes the population of interest and the raw quantitative output of the model, their choice would not have any qualitative influence on potential differential attentional effects on the pCRF.

Table 1. Model parameters.

The first two columns show the values of the parameters used to construct the neural population. The third column explains the parameters of the contrast response function. The fixed parameter values are based on previous neurophysiological findings.

κ: Concentration parameter of the tuning function (π/4.5).	N : Number of neurons in the population (300).	M : baseline neural response (spikes/s).
R : Contrast response (defined by equation [3]).	f(θi): ith neuron's tuning function.	Rmax : Maximum neural response (spike/s).
θt: Preferred orientation of ith neuron (4° or 2.5°).	θm : Mean difference in orientation between the two stimulus alternatives (0).	C : Stimulus contrast. C50 : Stimulus contrast at half maximum response.
t : Stimulus duration (0.1 and 0.03 s for each respective study).	ρij : Correlation in response between the ith and jth neuron (ρmax : .2; δ: .1).	β: Slope of the contrast response function.
Δθ: Half difference in orientation between the two stimulus alternatives (4° or 2.5°).		Attentional gain parameters: a1 (Response gain), a2 (Contrast gain)

The model was fit with only three free parameters for the neutral condition (R_max, β, C₅₀) and one (a₁or a₂) or two (a₁ and a₂) free parameters for the attentional conditions (attended-endogenous or attended-exogenous and unattended-exogenous). Data from the neutral attention condition was fit first by fixing all the parameters of the model except the three that define the contrast response function (Eq. 3; R_max, C₅₀, β). For the neutral condition data sets, both attentional parameters a₁ (response gain) and a₂ (contrast gain) were fixed at 1, designating no attentional gain modulation. After estimating the three pCRF parameters for the neutral condition data, we treated these estimates as fixed parameters when fitting the attentional data, now only allowing the attentional gain parameters to vary: a₁ (response gain), a₂ (contrast gain) or both of them (mixed model).

We fit the model with data from two studies that have investigated effects of endogenous and exogenous attention at both attended and unattended locations. Data from Ling and Carrasco (2006) were used to estimate the change in neural contrast response underlying the behavioral improvement brought about by endogenous and exogenous attention. Data with exogenous attention from Pestilli, Viera and Carrasco (2007) were used to estimate changes in contrast response that underlie the enhancement in sensitivity at attended locations, and the impairment at unattended locations.

Endogenous attention: Ling & Carrasco (2006)

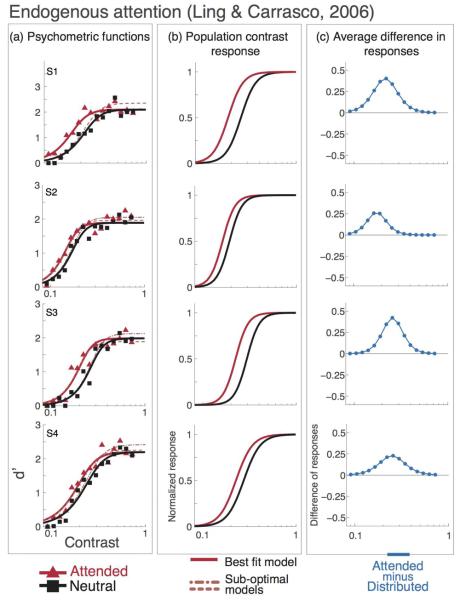
Figure 3a shows the model fits to the endogenous attention experiment in Ling and Carrasco (2006). For each observer, an increase in pure contrast gain (a₂) led to superior fits over a pure response gain model (a₁). Figure 4 shows the r² values for each model (contrast gain, response gain and the mixed model), observer and attentional condition.

Figure 3. Endogenous attention psychometric functions, data and model predictions from Ling & Carrasco (2006).

Individual observer data, model fits and attentional effect. Black lines and squares represent the neutral-attention condition, red lines and triangles represent the endogenous attention condition. Short-dash lines show the best fit for the mixed model (contrast gain plus response gain), long-dash lines show the best fit for the response gain model. a) Data and psychometric functions estimated by the model. b) Estimated contrast response functions. c) Difference in response between neutral- and endogenous-attention conditions. The best model for endogenous attention is contrast gain; attention shifts the pCRF horizontally towards lower contrast (b) and the difference in population response is highest within the middle of the pCRF (c).

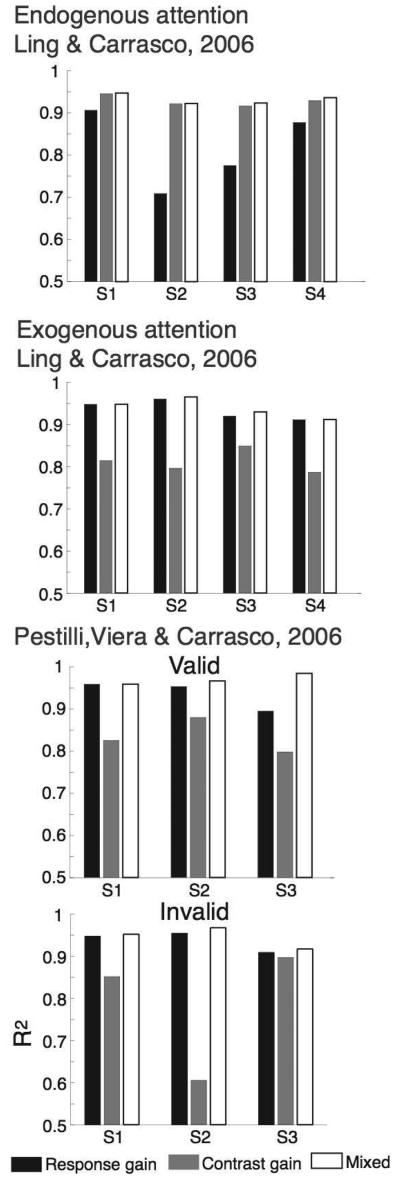
Figure 4. Quality of fit for each gain model.

Each graph reports r² values for each model –contrast gain, response gain and the mixed model– observer and attentional condition). r² values are higher for contrast gain than for response gain with endogenous attention (top panel) and higher for response gain than for contrast gain with exogenous attention (middle and two bottom panels). The mixed model has one more parameters and overall show higher r² values; we performed a nested hypothesis test to show when the increase in r² due to the additional parameter is significant (see text and Table 2).

To determine which model best accounted for the data, an F-test was performed comparing the r² obtained by the model with two parameters (mixed model: a₁ and a₂) to the one obtained with only one of the two parameters (a₁ or a₂). F was computed as:

$$F({\mathit{df}}_1,{\mathit{df}}_2)=\frac{(r_{\mathit{full}}^2-r_{a_i}^2)}{{\mathit{df}}_1}/\frac{(1-r_{\mathit{full}}^2)}{{\mathit{df}}_2},$$ [11]

where df₁ = k_full − k_ai and df₂ = c_num − k_full − 1. k_full is the number of parameters of the full model (i.e., 2; a₁ and a₂), k_ai is the number of parameters of the attentional model (i.e., 1; a₁ or a₂) and c_num is the number of contrasts (i.e., 8 for Pestilli, Viera & Carrasco, 2007, 14 for Ling & Carrasco, 2006).

With endogenous attention, the contrast gain model did the best job of accounting for the data. For all observers, the contrast gain model provided a better fit than the response gain model (Figure 3a; Table 2), and a nested hypothesis test (F-test; (Lu & Dosher, 1998) revealed that the mixed model was not statistically superior to the contrast gain model (p-values reported in Table 2).

Table 2. Probability values for the F-test.

A) Pestilli, Viera & Carrasco (2007) the results for exogenous attention in this study are well explained by a response-gain model (green-shaded areas; contrast-gain wins over the mixed, two-parameters, model). Except for the valid-cue condition in observer S3, where the mixed model (two parameters model) is needed. B) Ling & Carrasco (2006) the results for endogenous attention (Endo) in every observer are well described by a contrast-gain model (green-shaded are cell; contrast-gain wins over the mixed, two-parameters, model), but not by a response-gain model (orange-shaded cells; the mixed, two-parameters model, wins over response-gain). The results for exogenous attention (Exo) in every observer are well described by a response-gain model (green-shaded cells; response-gain wins over the mixed, two-parameters, model), but not by a contrast-gain model (orange-shaded cells; the mixed, two-parameters model, wins over contrast-gain).

A) Pestilli, Viera & Carrasco (2007)
	S1		S2		S3
	Valid	Invalid	Valid	Invalid	Valid	Invalid
RG vs. Mixed	1	0.4	0.1	0.1	0	0.4
CG v.s Mixed	0	0	0	0	0	0.18
B) Ling & Carrasco (2006)
	S1		S2		S3		S4
	Endo	Exo	Endo	Exo	Endo	Exo	Endo	Exo
RG vs. Mixed	0	1	0	0.13	0	0.13	0	1
CG v.s Mixed	0.5	0	1	0	0.21	0	0.17	0

One parameter model wins over mixed model

Mixed model wins over one parameter model

Figure 3b shows the estimated pCRF underlying the behavioral performance in the endogenous attention experiment (Ling & Carrasco, 2006). All observers exhibit a leftward shift in the estimated pCRF with endogenous attention, indicative of contrast gain modulation. Figure 3c depicts the attentional modulation as the difference between the neutral and the attended pCRF's. As predicted for contrast gain, the maximal attentional modulation is clearly within the dynamic range of the pCRF.

Exogenous attention: Ling & Carrasco (2006) and Pestilli et al. (2007)

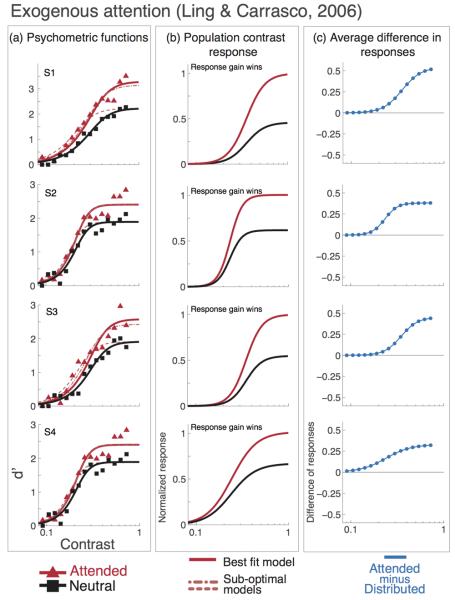
With exogenous attention, the response gain model did the best job of accounting for the data for both Ling & Carrasco (2006) and Pestilli et al. (2007). For all observers, the response gain model provided a better fit than the contrast gain model (Figure 4 shows the r² values for each model –contrast gain, response gain and the mixed model– observer and attentional condition), and a nested hypothesis test revealed that the mixed model was not statistically superior to the response gain model (Figure 5 and 6; p-values reported in Table 2). When exogenous attention was drawn towards a stimulus, model results from both studies suggest that the behavioral findings were brought about by an increase in the response gain of the underlying pCRF. When exogenous attention was drawn away from a stimulus (Pestilli et al., 2007), consistent with a response gain mechanism, the response gain of the underlying pCRF was attenuated.

Figure 5. Exogenous attention. Psychometric functions, data and model predictions from Ling & Carrasco (2006).

Individual observer data, model fits and attentional effect. Black lines and squares represent the neutral-attention condition, red lines and triangles represent the exogenous attention condition. Short-dash lines show the best fit for the mixed model (contrast gain plus response gain), long-dash lines show the best fit for the response gain model. a) Data and psychometric functions estimated by the model. b) Estimated contrast response functions. c) Difference in response between neutral- and exogenous-attention conditions. The best model for exogenous attention is response gain; the effect of attention on the pCRF increases with contrast (b) and the difference in population response is highest at high contrast (c).

Average results

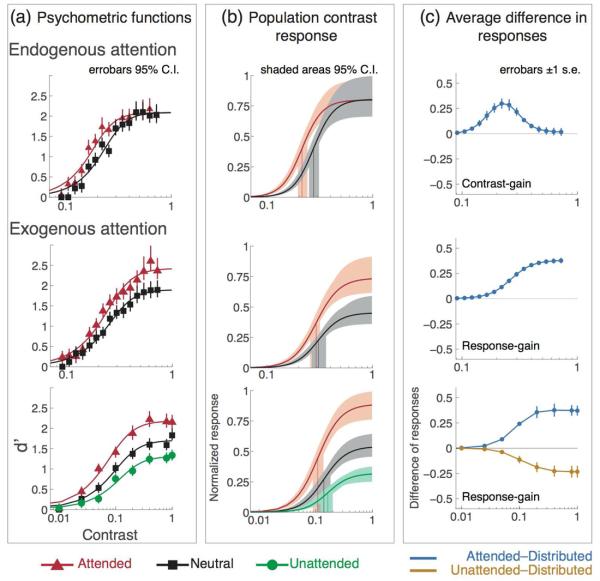
Figure 7 shows the average results. Endogenous attention affects the pCRF strictly via contrast gain, increasing contrast response solely within the dynamic range of the contrast response function (top row). Exogenous attention affects the pCRF strictly via response gain, increasing contrast response progressively across the whole contrast response function at attended locations (middle and bottom rows) and decreasing it at unattended locations (bottom row).

Figure 7. Average data & model fits.

(a) Model fits and averaged psychometric data for attended (red), neutral condition attention (black) and unattended (green) conditions. (b) Normalized population contrast response functions (pCRF) for contrast and response gain. The best model for endogenous attention is contrast gain; attention shifts the pCRF horizontally towards lower contrast. The best model for exogenous attention is response gain; attention increases pCRF incrementally from low to high contrast (middle and bottom panels); attention decreases pCRF at unattended locations (bottom panel). (c) Average difference in responses (from column b): neutral-minus-attended (blue) and neutral-minus-unattended (gold), across all observers in each study. Errorbars in (a) are 95% confidence intervals (C.I.), obtained by non-parametric bootstrap. Shaded areas in (b) show model parameters' (c50 and Rmax) variability obtained by fitting the model to each one of the bootstrapped samples within the 95% C.I. in (a).

To determine which parameters of the pCRF were affected on average by attention we used a bootstrap analysis (Efron & Tibshirani, 1993). For each study, data were combined across observer, attentional condition and contrast level. The analysis shows the variability of the estimated model parameters given the variability in the data. We estimated the variability of the psychometric data at each contrast level in each attentional condition by sampling with replacement 10,000 times from the combined data set, and fitted the model to each one of these 10,000 samples (by fixing all the model parameters but allowing both R_max and C₅₀ to vary). We then defined the 95% confidence intervals (C.I.) on the bootstrapped-data and estimated parameter distributions. Figure 7a, shows the estimated variability around each individual data point (vertical error bars, 95% C.I.), and column Figure 7b shows the estimated variability of the model parameters fitted to the bootstrapped data. The shaded areas for each individual pCRF envelope the 95% C.I. of the obtained parameters distributions (for R_max and C₅₀). Results for endogenous attention show that whereas the 95% C.I. for the R_max parameter overlap (shaded areas around each function's asymptote) the 95% C.I. for the C₅₀ do not overlap (shaded areas around the drop-down vertical lines marking the average C₅₀ value). Results for exogenous attention show that the 95% C.I. for the C₅₀ parameter overlap, but that the 95% C.I. for the R_max do not overlap. These results indicate that whereas endogenous attention changes contrast-gain without affecting asymptotic response, exogenous attention changes response-gain without affecting the threshold.

Discussion

We implemented a population-coding model based on Poisson dynamics, which predicts changes in the contrast response properties of a neural population given psychophysical performance. We assumed the tuning bandwidth and the correlation parameter values reported for V1 data (Albrecht & Hamilton, 1982; Kohn & Smith, 2005; see Table 1). With these few biologically-plausible assumptions, the model properly describes human psychophysical performance and estimates changes in contrast response in a neural population with only two free parameters: threshold and asymptote of the contrast response function. Whereas endogenous attention shifts the pCRF towards lower contrast via contrast-gain (Figure 3, top row and Figure 4), exogenous attention increases population response multiplicatively with stimulus contrast at attended locations and decreases it at unattended locations via response-gain (Figure 3, middle and bottom rows and Figure 5 and 6).

Figure 6. Exogenous attention. Psychometric functions, data and model predictions from Pestilli, Viera, & Carrasco (2007).

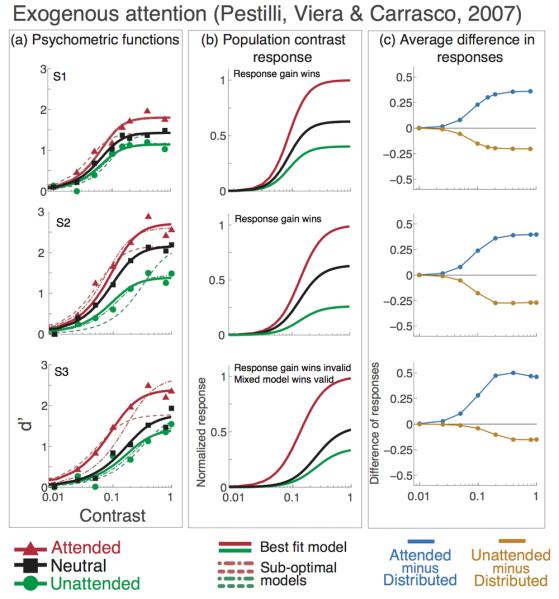
Individual observer data, model fits and attentional effect. Black lines and squares represent the neutral-attention condition, red lines and triangles represent the valid-cue exogenous attention condition. Green lines and circles represent the invalid-cue exogenous attention condition. Short-dash lines show the best fit for the mixed model (contrast gain plus response gain), long-dash lines show the best fit for the response gain model. a) Data and psychometric functions estimated by the model. b) Estimated contrast response functions. c) Difference in response between neutral- and valid-cues (light blue) and neutral- and invalid-cues (gold) conditions. A positive or negative value means that there is an increase or decrease in response, respectively, when attention is directed to a stimulus, as compared to the neutral cue condition in which attention is directed to both locations. The best model for exogenous attention is response gain; the effect of attention on the pCRF increases with contrast (b), response is higher for attended and lower for unattended stimuli) and the difference in population response is highest at high contrast for attended stimuli and lowest at high contrast for unattended stimuli (c).

For endogenous attention, psychophysical studies have shown effects consistent with contrast gain (Ling & Carrasco, 2006a), response gain (Morrone, Denti & Spinelli, 2002, 2004) or a hybrid model in which attention first undergoes contrast gain, and at a later stage, response gain (Huang & Dobkins, 2005). What could explain these discrepant results? There are several differences in the way attention was manipulated in these studies. Studies supporting a response gain mechanism (Morrone, Denti & Spinelli, 2002, Morrone, Denti & Spinelli, 2004) used a concurrent task paradigm in which observers either performed a demanding rapid serial visual presentation (RSVP) task at fixation along with a peripheral task, or they viewed the RSVP passively, allowing more attention to be allocated to the peripheral task. Huang and Dobkins (2005) attribute the difference between their results and those of Morrone et al. to experimental parameters. They claim that the contrasts they tested capture the entire response functions and that the dual task used by Morrone et al. was not demanding enough. Ling and Carrasco (2006) differ from those studies in how attention was deployed and the task performed. Whereas concurrent tasks draw resources away from the processing of stimuli (e.g. Lee, Itti, Koch & Braun, 1999), Ling and Carrasco (2006) directed observers' endogenous attention towards a location in the visual field via spatial cueing. Both the endogenous spatial-cueing manipulation and the orientation-discrimination task used by Ling and Carrasco (2006) are most similar to the tasks performed in the relevant monkey neurophysiology studies. Monkeys are trained to attend to one of several possible stimulus locations and have to detect an orientation change (target) among a series of vertically oriented distracters (Reynolds et al., 2000; Williford & Maunsell, 2006; McAdams & Maunsell, 1999) or a change in global motion direction (Treue & Martinez-Trujillo, 1999).

For exogenous attention, there is scarce psychophysical data, and no neurophysiological data regarding gain mechanisms. Ling and Carrasco (2006) reported that a mixed model accounted for the data better than response gain or contrast gain alone. The analysis reported here supports response gain. The discrepancy is due to the fact that they fitted contrast response functions to accuracy data. Hence, the expansion of the contrast response function at high contrast was limited and compressed, and a change in threshold parameter was required to account for the data. In contrast, our model was fit to d′, which has no theoretical upper bound.

Investigating the interaction between the effects of exogenous attention and contrast adaptation, Pestilli, Viera and Carrasco (2007) measured changes in sensitivity and in performance for orientation discrimination at attended and unattended locations across the psychometric function. They reported that the effect of attention increased with stimulus contrast and also that contrast threshold decreased. However, in that study threshold was defined as the stimulus contrast necessary to attain 70% accuracy, and such measure does not imply a change in the C₅₀ parameter of the contrast response function, as modeled in the present study.

How might attention affect the gain of population contrast response? One proposed mechanism is firing synchrony (Fries et al., 2001). Indeed, attention-enhanced synchronization could result in a response gain modulation on the population contrast response (Kim et al., 2007). Although our model cannot test neural synchronization, both behavioral results and model fits show contrast gain to be mediating the effects of endogenous attention. Further investigation is necessary to clarify why different stimulus and task parameters affect the way endogenous attention change neural gain at the population level and the contrast response behaviorally. Another possibility put forth is that attention multiplicatively scales the inputs to the normalization circuit (Reynolds & Chelazzi, 2004). This can in turn result in either a multiplicative scaling of firing rate (McAdams & Maunsell, 1999; Treue & Martinez-Trujillo, 1999) or a change in contrast gain (Reynolds, Pasternak & Desimone, 1999), depending on task and sensory conditions.

Why would different types of attention lead to different gain signatures? Furthermore, why would different tasks and stimuli lead to different gain signatures? Understanding the mechanism that underlies neuronal gain changes may offer some insight. Chance, Abbott and Reyes (2002) showed that response gain modulation is driven by changes in the firing rate of balanced background synaptic input, where decreasing the amount of background input leads to increases in response gain, and vice versa. Importantly, they posit that this background noise modulation can originate from local or distal sources, and that the influence of background inputs from local cortical connections can have a stronger influence than more distal cortical inputs. Based on this framework, they speculate that the contrast-gain-like signature some have observed with endogenous attention (e.g., Reynolds et al., 2000) may arise because the locus of attentional modulation, where the background input is being attenuated, is distant from the recording site. A high-contrast stimulus evokes high amounts of local background input, which wash out the influence of the distal attention-modulated background input. Perhaps by assessing the gain signature, one can gauge the proximity between a cortical site being probed, and the true locus of the attentional modulation; the more local the attentional modulation is relative to the site of interest, the more the modulation signature should resemble response gain. This framework may shed light on a number of issues.

First, in relation to the present study, we assume that our orientation-discrimination task was carried out in an early cortical visual area, V1. For endogenous attention we observed contrast-gain modulation, whereas for exogenous attention we observed response-gain modulation. The former could be due to attentional modulation from a more distal source, as endogenous attention is more ‘top-down’ in nature than exogenous attention, and requires feedback from higher-level cortical areas. Correspondingly, one could conclude that the source of attentional modulation that leads to a response-gain-like signature with exogenous attention is the result of local modulation. This would be in line with the notion that exogenous attention is more bottom-up in nature, and that the source of exogenous attention's modulation is closer to V1. Indeed, there is evidence that increases in the gain of the local feedforward cholinergic system produce a response gain-like change in the response of downstream visual neurons (Disney, Aoki & Hawken, 2007). In addition, the contrast response of thalamic inputs to visual cortex is modulated by the alertness state of an animal in a way that is consistent with response gain (Cano, Bezdudnaya, Swadlow and Alonso, 2006). In a way, it could be hypothesized that exogenous attention has an effect relatively more independent from the task and stimulus nature than endogenous attention, which can improve performance by adapting to the task at hand (Yeshurun, Montagna & Carrasco, 2008).

Second, this framework could shed light on the mixed-bag of previous findings for gain mechanisms of individual neurons and attention, and offers a potential explanation for why different task types and different stimuli would lead to different attentional gain signatures. Some have reported that the attention effect is manifested by contrast gain (Reynolds et al., 2000; Martinez-Trujillo & Treue, 2002), others have reported that the effect is mediated by response gain (McAdams & Maunsell, 1999), and yet others have reported that some cells are modulated by contrast gain, some by response gain, and some by increased baseline firing (Williford & Maunsell, 2006).

Williford and Maunsell (2006) found that a response gain model provided a marginally better fit to their data than did a contrast gain model, but both models provided excellent fits to the data in terms of the percent of variance explained. By examining the key subset of neurons that had both an attention-modulation and a saturating contrast response functions in the unattended condition (their Figure 6G, also 6H, 6I) they found a diminished effect of attention from ∼80% increase in firing rate at low contrast to ∼20% at high contrast (see their Figure 6G). This is consistent with the conclusion reached in the present study regarding endogenous attention, the gain factor diminishes at high contrast.

The tasks and stimuli used in the experiments varied from study-to-study, and as a consequence the cortical subpopulation s recruited to suit the particular tasks or stimuli probably differ. Perhaps these disparate results could also be explained within the local/distal connection framework. It is conceivable that this difference could lead to changes in the cortical distance between the original source of attentional modulation, and the area being recruited for the task or stimuli. For instance, it could be possible that the cells that showed response-gain modulation were from V4 layers that had fewer synaptic steps from the source of attentional modulation, thus allowing the background input from the attentional source to influence the response of that cell even at high contrasts. Correspondingly, perhaps cells exhibiting contrast-gain-like modulation resided in V4 layers that had more synaptic steps from the source of attentional modulation. Further experiments and modeling could elucidate whether this local/distal framework for gain modulation applies to attentional modulation.

Conclusion

Whereas individual neurons are variable, the population response needs to be univocal to reliably guide behavior. Multi-unit recording and neuroimaging techniques (e.g., EEG, fMRI and Optical Imaging) have potential to measure larger-scale responses, but capturing the vast scale of population responses remains a methodological challenge, and how attention affects neural populations remains empirically untested. Psychophysical data (Ling & Carrasco, 2006; Pestilli et al., 2007) and the estimated parameters of the population-coding model presented here support the idea that attention acts on population contrast response via different mechanisms: contrast gain for endogenous attention and response gain for exogenous attention.