Predictive Modeling of Defibrillation utilizing Hexahedral and Tetrahedral Finite Element Models: Recent Advances

Abstract

ICD implants may be complicated by body size and anatomy. One approach to this problem has been the adoption of creative, extracardiac implant strategies using standard ICD components. Because data on safety or efficacy of such ad hoc implant strategies is lacking, we have developed image-based finite element models (FEMs) to compare electric fields and expected defibrillation thresholds (DFTs) using standard and novel electrode locations. In this paper, we review recently published studies by our group using such models, and progress in meshing strategies to improve efficiency and visualization. Our preliminary observations predict that they may be large changes in DFTs with clinically relevant variations of electrode placement. Extracardiac ICDs of various lead configurations are predicted to be effective in both children and adults. This approach may aid both ICD development and patient-specific optimization of electrode placement, but the simplified nature of current models dictates further development and validation prior to clinical or industrial utilization.

Introduction

ICD implant is the standard of care for patients at risk of fatal cardiac arrhythmias [Bokhari 2004; Buxton 1999]. Although ICDs are usually implanted transvenously, this is not possible for patients of small children or for those with intracardiac shunts or anatomical obstruction to lead placement. To address these anatomical constraints, a variety of innovative, ad hoc implant approaches have been used, placing electrodes singly or in combination in a variety of extracardiac subcutaneous, epicardial and caval locations, and locating generator pockets in the abdomen or elsewhere [Berul 2001; Stephenson 2006]. Fully subcutaneous ICDs are also in development, to increase the simplicity of implant and therefore its accessibility as indications for ICD use continue to expand [Grace 2005]. Common to all these approaches has been the adaptation of existing ICD components to complex and often unique anatomical problems, with the goal to achieve a workable implant solution with acceptable DFTs.

Prior research has elucidated predictive relationships between distribution of myocardial voltage gradient and both defibrillation efficacy and myocardial injury. However, the effects of interactions between variations in body size, habitus and novel ICD geometries on these fields are largely unstudied. Efficacy estimates for novel ICD implants are based on post-implant DFT testing, extrapolation of data from the use of subcutaneous arrays in adults and limited animal research [Berul 2001]. Our current research models the effects defibrillating electrical fields on anatomically derived myocardial and torso models using finite element techniques. Finite element modeling (FEM) of conductivity models of the adult torso has been shown to correlate well with clinically observed DFTs [Aguel 1999, DeJongh 1999, Jorgenson 1995, Mocanu 2004]. We extended the FEM approach to allow modeling of different electrode orientations, within variable body sizes and habitus, and under anatomically variable conditions. We have found that anatomical choices made in virtual ICD electrode placement, which reflect realistic variations in surgical practice, result in clinically significant changes in predicted myocardial fields. Here we review the application development, initial results and alternative meshing strategies for predictive, image-based modeling of clinical defibrillation, recently reported in Heart Rhythm [Jolley 2008]. We discuss the limitations of this methodology, parametric sensitivity analysis and plans for further development of this technique.

Methods

Image Acquisition, Segmentation and Electrode Placement

Torso models were constructed from 64-detector CT scans (1.25mm slices) of normal subjects obtained from a radiology database with IRB approval. Scans were selected for good tissue contrast, minimal cardiac motion artifact and diversity of body size and habitus. Scans were segmented by tissue type using thresholding, connected component and level set techniques with the open-source software 3D Slicer (Surgical Planning Library, www.slicer.org). Segments were hierarchically combined and imported into SCIRun, an open-source package for scientific visualization and computation, for electrode placement and solution of the bioelectric field (Scientific Computing and Imaging Insitute [SCI], www.sci.utah.edu). A custom software module was developed for the SCIRun package the allowed anatomically precise, interactive placement of virtual coil and can electrodes within the models. This interface allowed placement of electrodes in clinically realistic positions, as judged by comparison of resulting models with AP and lateral X-rays of lead positions in exemplary patients.

Meshing and Finite Element Calculation

The segmented models and user-placed electrodes were combined into an FEM. Initially these were composed of hexahedral, which have the advantage of algorithmic simplicity. However, more recently we have investigated development of tetrahedral meshes, a more efficient approach to modeling complex geometry. These meshes reduce the computational burden of solving the mesh, as well as providing a more anatomical realistic representation of the volume data. Using a lookup table of conductivity values based on literature-derived values for muscle, fat, bone, lung, blood, and myocardium and other tissues [Geddes 1967; Aguel 1999; DeJongh 1999; Jorgenson 1995; Mocanu 2004], a conductivity map of the torso was formed and projected onto the computational mesh by sampling. Boundary conditions were assigned: electrode surface elements had constant potential and there was no current flow across the torso surface. A linear, isotropic volume conductor and conditions of constant voltage and current were assumed, and the FEM was solved as a volume conductor problem. The Galerkin finite element formulation with tri-linear interpolation was applied. The following figure demonstrates modeled solutions.

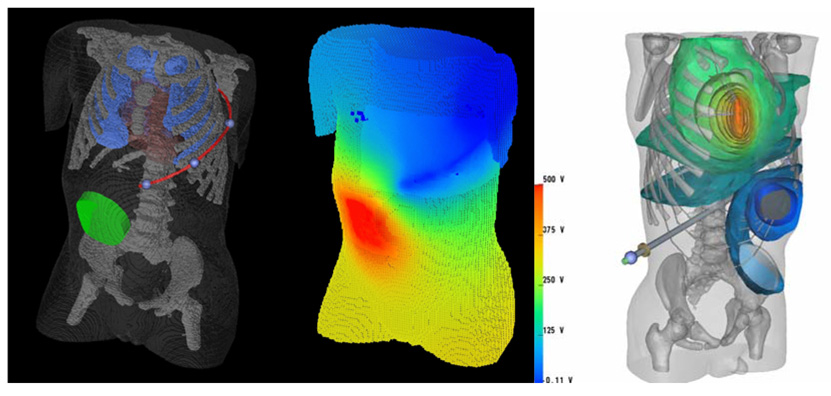
Figure 1.

Left: Hexahedral mesh finite element model of a 2-year old torso, which has been segmented from a CT scan. The heart, lungs, skeleton and body surface are visible, as are an abdominally placed ICD generator and a long subcutaneous ICD lead tracking in the left infra-axillary area. Center: Body surface voltage potentials predicted by FEM for this configuration. Right: A computation of defibrillation fields in an improved torso model consisting of 2 million tetrahedral elements. The ICD can is located in the abdomen and the electrode over the sternum.

Solution Calculation, Defibrillation Metrics, and Data Analysis

The critical mass hypothesis was used to define a metric of defibrillation “success” [Zipes 1975]. This proposes that an applied electrical field will result in defibrillation if it produces a threshold voltage gradient over some “large” fraction of the myocardial mass. This hypothesis is simplistic but empirically useful for the experimental prediction of DFT. The criterion used in this study as a predictor of successful defibrillation was a voltage gradient of 5 V/cm generated over 95% of the myocardium. The DFT was calculated by the energy relation DFT = ½ CV², where C is the estimated generator capacitance, and V the voltage needed to meet the critical mass criterion.

Results

Using a reference model was a standard transvenous implant (left pectoral can to SVC and RV) in the 75 kg torso, our predicted DFTs in this model were similar to those recorded in clinical use [Jolley 2008]. A variety of transvenous, epicardial, and subcutaneous coil configurations all predicted feasible defibrillation within the range of energies currently provided by ICD discharge. Transvenous orientations typically resulted in the lowest DFTs, but subcutaneous arrays and epicardial placements were also clinically feasible, and could be optimized by manipulation of electrode and can position. Larger body size was correlated with higher DFTs. Can placement opposite a subcutaneous electrode resulted in lower DFTs than orientations where the can and electrode are placed on the same side of the body. Predicted DFTs of clinically reported electrode configurations varied by as much as 10 fold in a single subject.

Myocardial voltage gradient distribution was also dependent on electrode size and location. Subcutaneous electrodes tended to create a relatively homogeneous distribution of myocardial voltage gradient, while transvenous and epicardial placement resulted in a broader distribution of voltage gradient, with significant volumes of the myocardium in close proximity to the electrode exposed to voltage gradients > 30V/cm. This effect was accentuated for low efficiency orientations due to the need for higher energy to meet the threshold for defibrillation.

The mesh resolution was chosen to minimize differences (<1%) from a maximally dense of 250×250×250 elements, and locally refined around electrodes to enable accurate calculation of increased field gradients in these areas [Stinstra 2007], resulting in FEMs of 1–1.5 million elements. Application of a strategy of local mesh refinement in regions of high field gradient reduces the model size (or computational cost) by >85% without compromising the geometric detail or accuracy. Recent work in tetrahedral meshing strategies promises to increase computational efficiency further and improve quality of anatomical visualization.

Discussion

Utilization of ICDs in pediatric and congenital heart populations has risen, as indications for defibrillator therapy have broadened and apparent risks decreased. We have explored trends and compared electrode performance using computational models of standard and unconventional ICD orientations in torsos of various sizes. Initial data demonstrate the feasibility of this approach and show the clinically significant magnitude of these trends across a wide variety of ICD implant strategies. Our principle finding was that surgical decisions made prior to and during ICD implant in a given patient have the potential to result in large variations of the predicted efficiency of the system. This suggests that prediction of efficient defibrillation strategies using interactive, image-based models may be used to optimize ICD electrode placement in specific patients, to develop alternatives to standard implant techniques, and to test innovative ideas for device design.

Our model may serve as a useful basis for intra-subject comparisons, or for making general observations regarding principles of shock vector anatomy in relation to the induced myocardial electrical field, but fails to model the known phenomena of defibrillation completely. It lacks a mechanistic model of defibrillation and does not incorporate several factors (particularly myocardial) known to affect the outcome of defibrillation shocks. We have assumed no temporal, spatial or patient-specific variability in tissue conductivity. The possible passive electrical effects of anisotropy of myocardial cellular tissue structure are not considered, nor are the electrode/tissue interface, complex capacitance in time-varying electrical signals, the complexities of fibrillation wavefront behavior, and the effects of shock polarity and biphasic waveforms on the induction of virtual electrodes within the myocardium. Countering these important methodological limitations, these models are intended, not to provide unbiased DFT estimation, but to explore the relative effects of variation in cardiothoracic and electrode geometry.

In this preliminary approach, the simplifications used allow for algorithmic and computational efficiency, as computational efficiency would otherwise limit the ability to generate useful models in a practical time frame. One approach increasing computational efficiency is to reduce the number of nodes specified in the finite element model. The best approach to this is dependent in part on the detailed anatomy of the tissue being modeled, as highly dispersed and branching structures may need to be accurately modeled to preserve electrical connectivity relevant to the model results. As mentioned, our initial efforts in that area have been focused on adaptive hexahedral meshes, which can be used to provide higher resolution in areas of high field gradient (especially in the areas of the model in close proximity to electrode tissue interfaces). Further refinement is likely to occur with the development of robust algorithms for generation of tetrahedral meshes from volume images [Baghdadi 2005]. The strengths and weakness of hexahedral and tetrahedral FEMs for functional anatomical modeling have been explored in other biomedical applications (e.g., orthopedic stresses [Ramos 2006, Ulrich 1998]), and it is fair to say that the optimum approach is likely to be highly application-specific. In our problem, minimizing the number of nodes is critical to achieving computational efficiency, and visualization quality is enhanced using tetrahedral as opposed to hexahedral meshing techniques. We anticipate that development of maximally efficient models will ultimately allow incorporation of capacitance, tissue anisotropy, a mechanistic model of cardiac defibrillation and local variations in metabolism and refractoriness.