Maximum Likelihood Inference for the Cox Regression Model with Applications to Missing Covariates

Abstract

In this paper, we carry out an in-depth theoretical investigation for existence of maximum likelihood estimates for the Cox model (Cox, 1972, 1975) both in the full data setting as well as in the presence of missing covariate data. The main motivation for this work arises from missing data problems, where models can easily become difficult to estimate with certain missing data configurations or large missing data fractions. We establish necessary and sufficient conditions for existence of the maximum partial likelihood estimate (MPLE) for completely observed data (i.e., no missing data) settings as well as sufficient conditions for existence of the maximum likelihood estimate (MLE) for survival data with missing covariates via a profile likelihood method. Several theorems are given to establish these conditions. A real dataset from a cancer clinical trial is presented to further illustrate the proposed methodology.

1 Introduction

There is a vast literature on parameter estimation in the Cox model in presence of missing covariates, including Schluchter and Jackson (1989), Lin and Ying (1993), Lipsitz and Ibrahim (1996, 1998, 2000), Paik (1997), Paik and Tsai (1997), Chen and Little (1999), Herring and Ibrahim (2001), Leong, Lipsitz, and Ibrahim (2001), Chen (2002), Pons (2002), Herring, Ibrahim, and Lipsitz (2002, 2004), and Chen, Ibrahim, and Shao (2006). However, there is very little literature addressing specific theoretical conditions for the existence of MLE’s of the Cox model in either the full data case or in the presence of missing covariate data. We are not aware of specific literature that establishes specific theoretical results for existence of such estimates. This is what we set out to do in this paper. Specifically, we provide necessary and sufficient conditions for existence of the Maximum Partial Likelihood Estimate (MPLE) with no missing data as well as sufficient conditions for existence of the Maximum Likelihood Estimate (MLE) with Missing at Random (MAR) covariate data via the profile likelihood method. The methodology proposed here is quite new and will shed light on the characterizations of existence of the MPLE or MLE for the Cox model with complete data as well as with missing covariate data. The profile likelihood method for obtaining the MLE in the presence of MAR covariates is quite different from the other parametric and semiparametric approaches seen in the literature. The profile likelihood method is genuinely non-parametric in estimating the cumulative baseline hazard and does not require a semi-parametric estimate of the baseline hazard as is required in Lipsitz and Ibrahim (1998) and Herring and Ibrahim (2001).

We mention that Jacobsen (1989) establishes a necessary and sufficient condition for existence of the MPLE for the Cox model without missing covariate data, Chen, Ibrahim, and Shao (2004) consider issues in posterior propriety and characterize conditions for existence of the MLE in generalized linear models with MAR covariate data, and Huang, Chen, and Ibrahim (2005) carry out a detailed investigation of posterior propriety in generalized linear models with nonignorably missing covariate data. The methods and models considered in those papers are quite different from the Cox model setting. In the Cox model, i) we no longer have independence between the observations in the construction of the partial likelihood, that is, the complete data log-likelihood is not a sum of n independent observations, ii) the Cox regression model, and in particular, Cox’s partial likelihood, is an inherently semiparametric model, and thus a profile likelihood method considered here is quite different than the fully parametric models considered in Chen, Ibrahim, and Shao (2004) and Huang, Chen, and Ibrahim (2005), and iii) right censoring and tied observations require new theory not developed in Chen, Ibrahim, and Shao (2004) and Huang, Chen, and Ibrahim (2005). Thus, i) – iii) will require new theory for characterizing conditions for existence of the MPLE and MLE of the regression coefficients in the Cox model allowing for tied observations.

The significance of this work thus has two aspects. First, the proposed methodology will allow the data analyst to determine, for a given dataset, whether the MPLE or MLE exists before carrying out the analysis. Such a methodology is critical since it is not always clear from the computer output in an analysis whether the MPLE or MLE exists or not. Second, such conditions will be useful for determining suitable starting values for EM-type algorithms when fitting these models. Thus, the practical consequences of the proposed methodology is that we provide valuable tools for checking existence of the MPLE or MLE as well as inferential and computational tools for maximum likelihood based inference for the Cox model with or without MAR covariates.

The rest of this article is organized as follows. Section 2 presents several motivating examples. We give necessary and sufficient conditions for the existence of the MPLE with no missing data in Section 3 and give sufficient conditions for existence of the MLE in the presence of MAR covariate data in Section 4. The computational development involving the Monte Carlo EM (MCEM) algorithm is given in Section 5. Section 6 presents a detailed analysis of a lung cancer dataset to further illustrate the proposed methodology. Proofs of all theorems are given in the Appendix.

2 Motivating Examples

To fix ideas, let y_i denote the minimum of the censoring time C_i and the survival time T_i, and let x_i = (x_i1,…,x_ip)′ be the p × 1 vector of covariates associated with y_i for the i^th subject. Denote by β = (β_1,…, β_p)′ the p × 1 vector of regression coefficients. Also, δ_i = 1{T_i = y_i} is the indicator for the event for i = 1, 2, …, n, where n is the total number of observations and ℛ(t) = {i : y_i ≥ t} is the set of subjects at risk at time t. Then, the partial likelihood of Cox (1975) is given by

$$L_p(\mathit{\beta }\mid D_{\mathit{obs}})=\prod _{i=1}^n{\left[\frac{exp({\mathit{x}}_i^{\prime }\mathit{\beta })}{{\sum }_{j\in \mathcal{R}(y_i)}exp({\mathit{x}}_j^{\prime }\mathit{\beta })}\right]}^{{\delta }_i},$$ (2.1)

where D_obs = {(y_i, δ_i, x_i) : i = 1, 2, …, n} is the observed univariate right censored survival data. As usual, we assume throughout that x_i does not include an intercept, since the interceptis not estimable in the Cox partial likelihood, and that given x_i, T_i and C_i are independent. For the completely observed data D_obs, the maximum partial likelihood estimate (MPLE) is defined as β̂ = arg max L_p(β|D_obs). The asymptotic properties of β̂ have been well studied in the literature, and in fact, the MPLE can be computed via standard statistical software, such as the SAS procedure, PROC PHREG. However, it remains unclear when the MPLE exists and when it does not for a given dataset. To motivate the proposed methodology, we consider the following two examples.

Example 1: A Simple Illustration

Suppose n = 3, y₁ and y₂ are two failure times, y₃ is a right censored survival time, and we have one binary covariate x. Let x₁, x₂, and x₃ denote the three observed values of x. Assuming y₁ < y₂ < y₃, the partial likelihood of Cox (1975) is then given by

$$L_p({\beta }_1\mid D_{\mathit{obs}})=\frac{exp(x_1{\beta }_1)}{exp(x_1{\beta }_1)+exp(x_2{\beta }_1)+exp(x_3{\beta }_1)}\times \frac{exp(x_2{\beta }_1)}{exp(x_2{\beta }_1)+exp(x_3{\beta }_1)},$$

where D_obs = {(y_i, x_i), i = 1, 2, 3}. We consider two special cases.

Case 1

x₁ = x₂ = 0 and x₃ = 1. In this case, we have $L_p({\beta }_1\mid D)=\frac{1}{2+exp({\beta }_1)}\times \frac{1}{2+exp({\beta }_1)}$. Then, we can see that the maximum value of L_p(β₁|D) is attained at β₁ = −∞. Thus, the MPLE does not exist.

Case 2

x₁ = 0, x₂ = 1, and x₃ = 0. In this case, we have $L_p({\beta }_1\mid D_{\mathit{obs}})=\frac{1}{2+exp({\beta }_1)}\times \frac{exp({\beta }_1)}{exp({\beta }_1)+1}$. Then, the MPLE does exist. In fact, the MPLE of β₁ is $\frac{1}{2}log(2)$.

In Example 1, the partial likelihood function behaves quite differently by simply switching two observed values of the covariate: one leads to the existence of the MPLE and the other does not. Thus, a natural question is what are general if and only if conditions for the existence of the MPLE in the Cox model? From this illustrative example, we can see that this is not an easy problem to solve, as it requires an in-depth theoretical investigation to find such conditions.

Example 2: Prostate Cancer Data

We consider data, which consist of n = 550 men who were treated with radiation therapy following with six months of with short-course androgen suppression therapy for localized prostate cancer with at least one adverse risk factor (prostate-specific antigen [PSA] > 10 ng/mL, biopsy Gleason score 7 to 10, or 2002 American Joint Commission on Cancer (AJCC) clinical tumor category T2b or T2c) between 1989 and 2002. The outcome variable (y_i) in years was time to prostate cancer death, which is continuous and subject to right censoring, and δ_i = pfail denotes the censoring indicator which equals 1 if the i^th subject died due to prostate cancer, and 0 otherwise. The goal of this study was to determine whether the number of risk factors present was associated with time to prostate cancer death (Tsai et al., 2006).

Define A = I {PSA > 10}, B = I {Gleason ≥ 7}, and C = I {T2b or T2c}. We consider five covariates: AB, AC, BC, ABC, and age. There are no missing values in this data set. A Cox proportional hazards model was fitted to this data set. The following outputs were produced by SAS Procedure PHREG:

Variable	DF	Parameter Estimate	Standard Error	Chi-Square	Pr > ChiSq
AB	1	0.39759	1.23355	0.1039	0.7472
AC	1	−14.30314	2107	0.0000	0.9946
BC	1	0.59060	1.22714	0.2316	0.6303
ABC	1	2.22155	0.80450	7.6253	0.0058
age	1	0.02262	0.04821	0.2201	0.6390

From the above results, we see that although SAS Procedure PHREG does produce the estimates for all five covariates, clearly there is some identifiability problem with the covariate, AC, as it has a large value of the estimate along with a huge standard error compared to all other covariates. Now, the question is: are the MPLEs are really existent in this Cox model?

Example 3: Small Cell Lung Cancer Data

We consider data from a phase III advanced non-small-cell lung cancer (SCLC) clinical trial conducted by the University of North Carolina at Chapel Hill (LCCC 9719). The results of this study have been published in Socinski et al. (2002). The goal of this trial was to compare a defined duration of therapy (A) to continuous therapy followed by second line therapy (B) in order to determine optimal duration of therapy in SCLC patients. LCCC 9719 had n = 230 patients. We consider here five prognostic factors: x₁ = treatment (2 arms: A and B, coded as 1 and 0), x₂ = gender (female and male, coded as 0 and 1), x₃ = age in years, x₄ = highest grade toxicity (recorded by cycle) (2 levels: 0 versus > 0, coded as 0 and 1), and x₅ = quality of life (QOL) FACTG score. For these five prognostic factors, x₄ and x₅ had missing information and x₁, x₂, and x₃ were completely observed for all cases. In this dataset, there is a total missing covariate data fraction of 52.74% on these two covariates. The outcome variable (y_i in months) is time to progression, which is continuous and subject to right censoring, and δ_i denotes the censoring indicator which equals 1 if the i^th subject had disease progression, and 0 otherwise. The median follow up time is 3.94 months and the range of the follow up time is (0.10, 12.26) months. There are d = 102 distinct progression times and ties are present in the dataset. A summary of the dataset is given in Table 1. In the presence of missing covariates, a joint probability distribution must be specified for the progression time and the missing covariates, and a profile likelihood method is hence proposed for obtaining the MLE in Section 4, as a partial likelihood approach in this context may not be as desirable.

Table 1.

Summary of LCCC 9719 Data

completely observed variables
x1	A	114
(frequency)	B	116
x2	Male	144
(frequency)	Female	86
x3	mean	62.24
(years)	std dev	10.17
y	censored	83
(frequency)	relapsed	147
missing covariates
x4	0	155
(frequency)	1	10
	missing	65
x5	mean	78.14
(QOL score)	std dev	15.31
	missing	81
both x4 and x5	missing	27
one of x4 or x5	missing	119

3 Existence of the MPLE With No Missing Data

In this section, we characterize very general conditions for the existence of the MPLE of β for a given dataset D_obs under the Cox model with no missing covariate data. Define X^* to be

$$X^{\ast }=({\delta }_i({\mathit{x}}_j-{\mathit{x}}_i),j\in \mathcal{R}(y_i),1\le i\le n{)}^{\prime }.$$ (3.1)

Let k_i denote the number of subjects in ℛ(y_i) for i = 1, 2,…, n. Also let $K={\sum }_{i=1}^n{k}_i$. Then, X^* is a K × p matrix. Using X^*, we are led to the following theorem.

Theorem 3.1

The MPLE of β in (2.1) exists if the following conditions are satisfied:

• (C1) X^* is of full rank p; and

• (C2) There exists a positive vector v, i.e., each component of v is positive, such that

$$X^{{\ast }^{\prime }}\mathit{v}=0.$$ (3.2)

In addition, if (C1) is satisfied, then (C2) is a necessary condition for the existence of MPLE for β.

The proof of Theorem 3.1 is given in the Appendix.

Remark 3.1

In X^* defined by (3.1), the rows corresponding to δ_i = 0 or x_j = x_i can be excluded. Thus, the effective numbers of rows in X^* can be reduced substantially. Specifically, let $k_i^{\ast }={\sum }_{j\in \mathcal{R}(y_i)}1\{{\mathit{x}}_j\ne {\mathit{x}}_i\}$, where the indicator function 1{x_j ≠ x_i} = 1 if x_j ≠ x_i and 0 otherwise. Then, the effective numbers of rows in X^* is given by $K^{\ast }={\sum }_{i=1}^n{\delta }_i{k}_i^{\ast }$.

Remark 3.2

When ties are present, as discussed in Klein and Moeschberger (2003, Chapter 8), the partial likelihood may be defined as

$$L_{pt}(\mathit{\beta }\mid D_{\mathit{obs}})=\prod _{i=1}^d\frac{exp({\mathit{z}}_i^{\prime }\mathit{\beta })}{{\left[{\sum }_{j\in \mathcal{R}(y_i)}exp({\mathit{x}}_j^{\prime }\mathit{\beta })\right]}^{d_i}},$$ (3.3)

where $d={\sum }_{i=1}^n{\delta }_i$, z_i = Σ_j∈i x_j, d_i = the number of events at y_i, and _i is the set of all individuals who have the event at time y_i. We can thus rewrite (3.3) as

$$L_{pt}(\mathit{\beta }\mid D_{\mathit{obs}})=\prod _{i=1}^n\frac{exp({\delta }_i{\mathit{x}}_i^{\prime }\mathit{\beta })}{{\left[{\sum }_{j\in \mathcal{R}(y_i)}exp({\mathit{x}}_j^{\prime }\mathit{\beta })\right]}^{{\delta }_i}},$$

and Theorem 3.1 can be easily extended to the cases when ties are present. Note that the partial likelihood given by (3.3) is the likelihood of Breslow (1974), and the Breslow likelihood is the default choice in SAS to handle ties in the failure times.

Remark 3.3

Suppose y₁ ≤ y₂ ≤ ··· ≤ y_n. Then, from condition (C2), it is easy to observe that if there exists a j such that x_1j ≤ x_2j ≤ ··· x_nj, the MPLE of β does not exist. Also, when one of the components of x_i, say, x_ij, is binary and the x_ij’s take the same value for δ_i = 1 or the the x_ij’s take the same value for δ_i = 0, then the MPLE of β does not exist.

Remark 3.4

When conditions (C1) and (C2) are satisfied for a subset of the data, the MPLE still does exist. To see this, we assume that the subset consists of the first n^* observations. Then we have

$$L_p(\mathit{\beta }\mid D_{\mathit{obs}})\le \prod _{i=1}^{n^{\ast }}{\left[\frac{exp({\mathit{x}}_i^{\prime }\mathit{\beta })}{{\sum }_{j\in \mathcal{R}(y_i),j\le n^{\ast }}exp({\mathit{x}}_j^{\prime }\mathit{\beta })}\right]}^{{\delta }_i}.$$

The existence of the MPLE can obtain by simply applying Theorem 3.1 to the above upper bound. These subset conditions are only sufficient but not necessary. However, this result is particularly useful for large datasets, for which checking conditions (C1) and (C2) may not be computationally feasible.

Remark 3.5

Jacobsen (1989) also characterizes a necessary and sufficient condition for the existence of the MPLE. His condition can be stated as follows: there is no a ∈ R^p such that a′δ_i(x_j − x_i) ≥ 0 for j ∈ ℛ(y_i) and 1 ≤ i ≤ n. According to Lemma A.1, we can see that Jacobsen’s condition implies (C2). Thus, (C2) is necessary for existence and for uniqueness. We note that the conditions stated in Theorem 3.1 are sufficient. However, compared to Jacobsen’s condition, the conditions (C1) and (C2) given in Theorem 3.1 are easier to check. First, it is straightforward to check condition (C1) that X^*has full column rank. As discussed in Appendix A of Roy and Hobert (2007), condition (C2) can be checked with a simple linear program using the ‘simplex’ function from the ‘boot’ library in the R programming language.

Example 1: A Simple Illustration (revisited)

Recall that in Example 1, we have n = 3, y₁ < y₂ < y₃, δ₁ = δ₂ = 1, and δ₃ = 0. For Case 1 in which x₁ = x₂ = 0 and x₃ = 1, we have k₁ = 3, k₂ = 2, k₃ = 1, and K = 6. Thus, using (3.1), (X^*) = (0, 0, 1, 0, 1, 0)′, which is a 6 × 1 matrix. After excluding the rows corresponding to δ_i = 0 or x_j = x_i, the effective number of rows in X^* is K^* = 2. It is easy to see that X^* is of full rank, which is 1. Also, for any v = (v₁, v₂, v₃, v₄, v₅, v₆)′ such that v_i > 0, (X^*)′v = v₃ + v₅ > 0. Thus, by Theorem 3.1, the MPLE does not exist.

For Case 2, where x₁ = 0, x₂ = 1, and x₃ = 0, using (3.1), we have (X^*)′ = (0, 1, 0, 0, −1, 0). Let v = (v₁, v₂, v₃, v₄, v₂, v₅)′ for v_j > 0, j = 1, 2, …, 5, (X^*)′v ≡ 0. Obviously, X^* is of full rank. Thus, the MPLE does exist by Theorem 3.1.

In general, we have X^* = (0, x₂ − x₁, x₃ − x₁, 0, x₃ − x₂, 0)′ and (3.2) reduces to

$$\begin{array}{l}(0,x_2-x_1,x_3-x_1,0,x_3-x_2,0)(v_1,v_2,v_3,v_4,v_5,v_6{)}^{\prime }\\ =v_2(x_2-x_1)+v_3(x_3-x_1)+v_5(x_3-x_2)=0.\end{array}$$ (3.4)

Condition (C1) requires that at least two of x₁, x₂, and x₃ are different. If x₁ = x₂ and condition (C1) holds, then there is no positive solution v to (3.4) regardless of the value of x₃. Thus, the MPLE always does not exist when x₁ = x₂. However, if x₁ < x₂, then the MPLE exists if x₃ < x₂ and does not exist if x₃ ≥ x₂. Similarly, if x₂ < x₁, the MPLE exists if x₃ > x₂ and does not exist if x₃ ≤ x₂. One interesting observation is that even if x₃ < x₁ < x₂, the MPLE still exists although x₃, for which δ₃ = 0, is distinct from {x₁, x₂} in the sense that δ₁ = δ₂ = 1. Thus, the condition for existence of the MPLE cannot be characterized by the value of δ_i alone by fitting, for example, a binary regression model to δ_i while treating (1, x_i)′ as a vector of covariates.

Example 2: Prostate Cancer Data (revisited)

After we further examined the data, we found that

Variable	δ= 0	δ= 1	Total
Only one of A, B, C	253	2	255
Only AB not C	116	1	117
Only AC not B	35	0	35
Only BC not A	64	1	65
ABC	71	7	78
Total	539	11	550

From the above table, “only AC not B” is the only group, in which there are no events. This explains why we obtained the unusual estimate and standard error for the regression coefficient corresponding to AC. From Remark 3.3, it becomes apparent that the MPLEs do not exist for this dataset if we fit the five covariates in the Cox model. One way to fix this problem is to combine AB, AC, and BC as one variable, which was called the two-factors only variable in Tsai et al. (2006).

4 Profile Maximum Likelihood Estimation in the Presence of Missing Covariates

When there are missing covariates, we assume that the distribution of the censoring time C_i does not depend on the missing covariates and the missingness is MAR. In this case, we cannot directly use the Cox partial likelihood since we need to model the failure time and the covariates jointly. Thus, instead of the partial likelihood approach, we use a profile likelihood approach when we have MAR covariates.

For notational simplicity, we assume that all failure times are distinct and let y₁, y₂, …, y_d be d distinct failure times. Let h₀(y) ≥ 0 denote the baseline hazard function and also let $H_0(y)={\int }_0^y{h}_0(u)du$ denote the baseline cumulative hazard function. Let ${\mathit{x}}_i=({\mathit{x}}_{i,\mathit{mis}}^{\prime },{\mathit{x}}_{i,\mathit{obs}}^{\prime }{)}^{\prime }$ and D_obs = (y_i, δ_i, x_i,obs, i = 1,2, …, n). Also let D = (y_i, δ_i, x_i,obs, x_i,mis, i = 1, 2,…, n) denote the complete data. In addition, let r_i = (r_i1, r_i2, …, r_ip)′ to be the vector of the p missing covariate indicators such that r_il = 0 when x_il is missing and r_il = 1 when x_il is observed for i = 1, 2, ···, n and l = 1, 2, ···, p. Since we assume ignorable missingness in the covariates (i.e., MAR covariates and the parameters of the missing data mechanism are distinct from the sampling model), we do not need to model r_i. Also, we assume that the parameters of the distributions for the censoring times C_i’s are distinct from the sampling model. Thus, for ignorably missing covariates, ignoring the parts adhering to censoring and the missing data mechanism, the observed data likelihood function based on the Cox model (Cox, 1972) is given by

$$\begin{array}{l}L(\mathit{\beta },h_0,\mathit{\alpha }\mid D_{\mathit{obs}})\\ =\int \left[\prod _{i=1}^d{h}_0(y_i)exp({\mathit{x}}_i^{\prime }\mathit{\beta })\right]exp\{-\sum _{j=1}^n{H}_0(y_j)exp({\mathit{x}}_j^{\prime }\mathit{\beta })\}\left[\prod _{i=1}^{n}f({\mathit{x}}_{i,\mathit{mis}},{\mathit{x}}_{i,\mathit{obs}}\mid \mathit{\alpha })\right]d{\mathit{x}}_{\mathit{mis}},\end{array}$$ (4.1)

where x_mis = (x_i,mis, i = 1, 2, …, n), f(x_i,mis, x_i,obs|α) denotes the joint distribution of x_i, and α is the vector of parameters for the covariate distribution.

It is well known that the partial likelihood can be expressed as a profile likelihood (Johansen, 1983) by substituting a nonparametric maximum likelihood estimator for the cumulative baseline hazard function H₀(y), which is a function of the fixed coefficients β, and that this nonparametric maximum likelihood estimator is necessarily a pure-jump estimator with jumps precisely at the observed event times. Following the profile likelihood approach (see, for example, Klein and Moeschberger (2003, Chapter 8)), we have

$$\begin{array}{l}\underset{h_0}{sup}L(\mathit{\beta },h_0,\mathit{\alpha }\mid D_{\mathit{obs}})\\ \le \int \underset{h_0}{sup}\left[\prod _{i=1}^d{h}_0(y_i)exp({\mathit{x}}_i^{\prime }\mathit{\beta })\right]exp\{-\sum _{j=1}^n{H}_0(y_j)exp({\mathit{x}}_j^{\prime }\mathit{\beta })\}\left[\prod _{i=1}^{n}f({\mathit{x}}_{i,\mathit{mis}},{\mathit{x}}_{i,\mathit{obs}}\mid \mathit{\alpha })\right]d{\mathit{x}}_{\mathit{mis}}\\ =\int \underset{h_0}{sup}\left[\prod _{i=1}^d{h}_0(y_i)exp({\mathit{x}}_i^{\prime }\mathit{\beta })\right]exp\{-\sum _{j=1}^n(\sum _{y_k\le y_j}{h}_0(y_k))exp({\mathit{x}}_j^{\prime }\mathit{\beta })\}\left[\prod _{i=1}^{n}f({\mathit{x}}_{i,\mathit{mis}},{\mathit{x}}_{i,\mathit{obs}}\mid \mathit{\alpha })\right]d{\mathit{x}}_{\mathit{mis}}\\ =\int \underset{h_0}{sup}\prod _{i=1}^d\left[h_0(y_i)exp({\mathit{x}}_i^{\prime }\mathit{\beta })exp\{-h_0(y_i)\sum _{j\in \mathcal{R}(y_i)}exp({\mathit{x}}_j^{\prime }\mathit{\beta })\}\right]\left[\prod _{i=1}^{n}f({\mathit{x}}_{i,\mathit{mis}},{\mathit{x}}_{i,\mathit{obs}}\mid \mathit{\alpha })\right]d{\mathit{x}}_{\mathit{mis}}\\ =\int \left\{\prod _{i=1}^{d}exp({\mathit{x}}_i^{\prime }\mathit{\beta }){\left[\sum _{j\in \mathcal{R}(y_i)}exp({\mathit{x}}_j^{\prime }\mathit{\beta })\right]}^{-1}\right\}\left[\prod _{i=1}^{n}f({\mathit{x}}_{i,\mathit{mis}},{\mathit{x}}_{i,\mathit{obs}}\mid \mathit{\alpha })\right]d{\mathit{x}}_{\mathit{mis}}.\end{array}$$ (4.2)

We note that in (4.2), the function

$$\left[\prod _{i=1}^d{h}_0(y_i)exp({\mathit{x}}_i^{\prime }\mathit{\beta })\right]exp\{-\sum _{j=1}^n{H}_0(y_j)exp({\mathit{x}}_j^{\prime }\mathit{\beta })\}$$

is maximized when h₀(y_j) = 0 except for the times at which events occur. Thus, the MLE of(β,α) exists if the upper bound in the right-hand side of (4.2) goes to zero when $\parallel \mathit{\beta }\parallel +\parallel \mathit{\alpha }\parallel =\sqrt{{\mathit{\beta }}^{\prime }\mathit{\beta }}+\sqrt{{\mathit{\alpha }}^{\prime }\mathit{\alpha }}\to \infty$. Write

$$L(\mathit{\alpha }\mid D_{\mathit{obs}})=\int \prod _{i=1}^{n}f({\mathit{x}}_{i,\mathit{mis}},{\mathit{x}}_{i,\mathit{obs}}\mid \mathit{\alpha })d{\mathit{x}}_{\mathit{mis}}.$$ (4.3)

The following theorem characterizes the conditions for existence of the MLE of (β, h₀, α) when the x_ij’s are bounded.

Theorem 4.1

If the x_ij’s are bounded, i.e., a_i ≤ x_ij ≤ b_i, define X^** to be $X^{\ast \ast }=({\delta }_i({\mathit{x}}_j^{\ast }-{\mathit{x}}_i^{\ast })$, j ∈ℛ(y_i), δ_j = 0, 1 ≤ i ≤ n)′, where $x_i^{\ast }=(({\mathit{x}}_{i,\mathit{mis}}^R{)}^{\prime },{\mathit{x}}_{i,\mathit{obs}}^{\prime }{)}^{\prime }$ and each component of ${\mathit{x}}_{i,\mathit{mis}}^R$ is equal to either $a_i^{\ast }={\delta }_i{a}_i+(1-{\delta }_i)b_i$ or $b_i^{\ast }=(1-{\delta }_i)a_i+{\delta }_i{b}_i$ for all i. Then, the MLE of (β, h₀, α) in (4.1) exists if the following conditions are satisfied: (C1^*) lim_||α||→∞ L(α|D_obs) = 0; (C2^*) X^** is of full rank; and (C3^*) there exists a positive vector v such that X^**′v = 0.

The proof of Theorem 4.1 is given in the Appendix. The main intuition behind Theorem 4.1 is that when the MLE exists under conditions (C2^*) and (C3^*) for the most extreme possible values of the missing covariates, then the MLE also exists for any intermediate values of the missing covariates, and averaging over the missing values will not affect the existence of the MLE. In Theorem 4.1, the elements of the matrix X^* corresponding to the missing covariates are “filled-in” by either $a_i^{\ast }={\delta }_i{a}_i+(1-{\delta }_i)b_i$ or $b_i^{\ast }=(1-{\delta }_i)a_i+{\delta }_i{b}_i$, where $a_i^{\ast }$ and $b_i^{\ast }$ are in fact the two possible extreme values of the missing covariates when the x_ij’s are bounded.

The next theorem gives the sufficient conditions for existence of the MLE of (β, h₀, α) when the x_ij’s unbounded.

Theorem 4.2

If the x_ij’s are unbounded, the MLE of (β, h₀, α) in (4.1) exists if condition (C1^*) in Theorem 4.1 and conditions (C1) and (C2) in Theorem 3.1 are satisfied for the completely observed cases.

The proof of Theorem 4.2 is given in the Appendix. Theorem 4.2 is practically useful as the conditions stated in this theorem are easy to check than those given in Theorem 4.1. We note that in Theorem 4.2, we are not doing a complete case analysis. Instead, we use a subset of the data with the completely observed cases to establish the sufficient conditions for the existence of the MLE when the missing covariates are unbounded.

Remark 4.1

Assume that the maximum number of missing components of x_i, i = 1, …, n, is p_i. Then, to verify the conditions given in Theorem 4.1, we need to check only the conditions (C2^*) and (C3^*) for at most 2^p_i possible X ^**’s.

Remark 4.2

When there are no missing covariates, it is easy to observe that the profile maximum likelihood estimate of β reduces to the MPLE, while the profile maximum likelihood estimate of α is the MLE.

Remark 4.3

Ibrahim, Lipsitz and Chen (1999) and Chen and Ibrahim (2001) provide a comprehensive set of guidelines for specifying the joint distribution of the covariate vector x_i through a series of one dimensional conditional distributions. Condition (C1^*) stated in Theorem 4.1 holds for many covariate distributions considered in Ibrahim, Lipsitz and Chen (1999) and Chen and Ibrahim (2001).

Remark 4.4

When there are ties in the event times, similar to Remark 3.2, the upper bound given in (4.2) can be modified as

$$K\int \left\{\prod _{i=1}^{d}exp({\mathit{z}}_i^{\prime }\mathit{\beta }){\left[\sum _{j\in \mathcal{R}(y_i)}exp({\mathit{x}}_j^{\prime }\mathit{\beta })\right]}^{-d_i}\right\}\left[\prod _{i=1}^{n}f({\mathit{x}}_{i,\mathit{mis}},{\mathit{x}}_{i,\mathit{obs}}\mid \mathit{\alpha })\right]d{\mathit{x}}_{\mathit{mis}},$$

where K > 0 is independent of β, α, and x_i, and z_i and d_i are defined in (3.3). Thus, all the theory developed in this subsection is still valid in the presence of ties.

Next, we consider an interesting special case where each missing component of x_i is discrete and bounded.

Corollary 4.1

Assume that each missing component of x_i is discrete and bounded. Then condition (C3^*) given in Theorem 4.1 is also necessary for the existence of the MLE for (β, h₀) if condition (C2^*) is satisfied.

The proof of Corollary 4.1 directly follows from the fact that when each missing component of x_i is discrete and bounded, we have

$$\begin{array}{l}\underset{h_0}{sup}L(\mathit{\beta },h_0,\mathit{\alpha }\mid D_{\mathit{obs}})=\sum _{{\mathit{x}}_{\mathit{mis}}}\underset{h_0}{sup}\left[\prod _{i=1}^d{h}_0(y_i)exp({\mathit{x}}_i^{\prime }\mathit{\beta })\right]exp\{-\sum _{j=1}^n{H}_0(y_j)exp({\mathit{x}}_j^{\prime }\mathit{\beta })\}\\ \times \left[\prod _{i=1}^{n}f({\mathit{x}}_{i,\mathit{mis}},{\mathit{x}}_{i,\mathit{obs}}\mid \mathit{\alpha })\right].\end{array}$$

Thus, details of the proof are omitted for brevity.

5 Computational Development

When there are no missing covariates, computing the MPLE of β is straightforward and, in fact, the MPLE can be computed via standard statistical software, such as the SAS procedure, PROC PHREG. In the presence of missing covariates, the EM algorithm is required. Martinussen (1999) proposes an efficient EM algorithm for computing the MLE and its standard error in the presence of discrete missing covariates. When x_i,mis is continuous or mixed continuous and categorical, we need to develop a Monte Carlo EM (MCEM) algorithm, which is an extension of Martinussen’s algorithm for computing the MLE’s of β, h₀, and α as well as their standard errors.

To implement the MCEM algorithm, let γ = (β, h₀, α). Let γ^(t) denote the parameter estimate of γ at the t^th EM iteration. In the E-step, we take an MCMC sample of size $m_i^{(t)},{\mathit{x}}_{i,\mathit{mis}}^{(t1)},{\mathit{x}}_{i,\mathit{mis}}^{(t2)},\dots ,{\mathit{x}}_{i,\mathit{mis}}^{(t{m}_i^{(t)})}$, from

$$f(x_{i,\mathit{mis}}\mid x_{i,\mathit{obs}},y_i,{\mathit{\gamma }}^{(t)})\propto exp({\delta }_i{\mathit{x}}_i^{\prime }{\mathit{\beta }}^{(t)})exp\{-H_0^{(t)}(y_i)exp({\mathit{x}}_i^{\prime }{\mathit{\beta }}^{(t)})\}f({\mathit{x}}_{i,\mathit{mis}},{\mathit{x}}_{i,\mathit{obs}}\mid {\mathit{\alpha }}^{(t)})$$

for i = 1, 2, …, n. Note that this conditional distribution is log-concave as long as f(x_i,mis, x_i,obs |α^(t)) is log-concave in each component of x_i,mis. We then compute

$$\begin{array}{l}Q(\mathit{\gamma }\mid {\mathit{\gamma }}^{(t)})=\sum _{i=1}^d\left[log{h}_0(y_i)+\frac{1}{m_i^{(t)}}\sum _{k=1}^{m_i^{(t)}}{\mathit{x}}_i^{(tk{)}^{\prime }}\mathit{\beta }\right]-\sum _{j=1}^n{H}_0(y_j)\left[\frac{1}{m_i^{(t)}}\sum _{k=1}^{m_j^{(t)}}exp({\mathit{x}}_j^{(tk{)}^{\prime }}\mathit{\beta })\right]\\ +\sum _{i=1}^n\frac{1}{m_i^{(t)}}\sum _{k=1}^{m_i^{(t)}}logf({\mathit{x}}_{i,\mathit{mis}}^{(tk)},{\mathit{x}}_{i,\mathit{obs}}\mid \mathit{\alpha }),\end{array}$$ (5.1)

where ${\mathit{x}}_i^{(tk)}=({\mathit{x}}_{i,\mathit{mis}}^{(tk{)}^{\prime }},{\mathit{x}}_{i,\mathit{obs}}^{\prime }{)}^{\prime }$ and H₀(y_j) = Σ_{yl≤yj,δl=1} h₀(yl). In the M-step, we compute

$${\mathit{\beta }}^{(t+1)}=\underset{\mathit{\beta }}{argmax}\sum _{i=1}^d\left\{\left[\frac{1}{m_i^{(t)}}\sum _{k=1}^{m_i^{(t)}}{\mathit{x}}_i^{(tk{)}^{\prime }}\mathit{\beta }\right]-log\left[\sum _{j\in \mathcal{R}(y_i)}\frac{1}{m_j^{(t)}}\sum _{k=1}^{m_j^{(t)}}exp({\mathit{x}}_j^{(tk{)}^{\prime }}\mathit{\beta })\right]\right\},$$ (5.2)

$$h_0^{(t+1)}(y_i)={\left[\sum _{j\in \mathcal{R}(y_i)}\frac{1}{m_j^{(t)}}\sum _{k=1}^{m_j^{(t)}}exp({\mathit{x}}_j^{(tk{)}^{\prime }}{\mathit{\beta }}^{(t+1)})\right]}^{-1},H_0^{(t+1)}(y_i)=\sum _{y_j\le y_i,{\delta }_j=1}{h}_0^{(t+1)}(y_j),$$ (5.3)

and

$${\mathit{\alpha }}^{(t+1)}=\underset{\mathit{\alpha }}{argmax}\sum _{i=1}^n\frac{1}{m_i^{(t)}}\sum _{k=1}^{m_i^{(t)}}logf({\mathit{x}}_{i,\mathit{mis}}^{(tk)},{\mathit{x}}_{i,\mathit{obs}}\mid \mathit{\alpha }).$$

Following Booth and Hobert (1999), in the MCEM algorithm, we take m^(t+1) = m^(t) + Δm, where Δm > 0. With this dynamic MCMC sample size m^(t), the MCEM algorithm requires much less computational time. Also a large m^(t) is not needed in early iterations of the algorithm since γ^(t) is still far from the MLE γ̂ and the algorithm is not near convergence. As t increases m^(t) increases, and a more computationally accurate estimate of Q(γ|γ ^(t)) is obtained in the E-step.

When x_i,mis is categorical, the E-step at the (t + 1)^st iteration reduces to the EM by the Method of Weights (Ibrahim, 1990). With the EM by the Method of Weights, a similar M-step can be developed. We refer to Ibrahim (1990) and Martinussen (1999) for the detailed development of the EM algorithm in this case. It is easy to see from (5.2) that when there are no missing covariates, β^(t+1) is the MPLE of β, which is consistent with Remark 4.2.

Let γ̂ denote the estimate of γ at EM convergence. Using Louis’s method (Louis, 1982), the estimated observed information matrix of γ based on the observed data is not difficult to compute. Note that the complete-data likelihood function can be written as

$$L(\mathit{\beta },h_0,\mathit{\alpha }\mid D)=\prod _{i=1}^n\left[{(h_0(y_i)exp({\mathit{x}}_i^{\prime }\mathit{\beta }))}^{{\delta }_i}exp\{-H_0(y_i)exp({\mathit{x}}_i^{\prime }\mathit{\beta })\}f({\mathit{x}}_i\mid \mathit{\alpha })\right].$$ (5.4)

Thus, the log-likelihood function for the i^th observation is given by

$$l(\mathit{\gamma }\mid {\mathit{x}}_i,y_i,{\delta }_i)={\delta }_i[log{h}_0(y_i)+{\mathit{x}}_i^{\prime }\mathit{\beta }]-H_0(y_i)exp({\mathit{x}}_i^{\prime }\mathit{\beta })+log(f({\mathit{x}}_i\mid \mathit{\alpha })).$$ (5.5)

Write the gradient vector of Q(γ|γ^(t)) as

$$\stackrel{.}{Q}=(\mathit{\gamma }\mid {\mathit{\gamma }}^{(t)})=\sum _{i=1}^n{\stackrel{.}{Q}}_i(\mathit{\gamma }\mid {\mathit{\gamma }}^{(t)})=\sum _{i=1}^n\frac{1}{m_i^{(t)}}\sum _{k=1}^{m_i^{(t)}}\frac{\partial l(\mathit{\gamma }\mid {\mathit{x}}_i^{(tk)},y_i,{\delta }_i)}{\partial \mathit{\gamma }},$$

and write the matrix of second derivatives of Q(γ|γ^(t)) as

$$\ddot{Q}=(\mathit{\gamma }\mid {\mathit{\gamma }}^{(t)})=\sum _{i=1}^n\frac{1}{m_i^{(t)}}\sum _{k=1}^{m_i^{(t)}}\frac{{\partial }^{2}l(\mathit{\gamma }\mid {\mathit{x}}_i^{(tk)},y_i,{\delta }_i)}{\partial \mathit{\gamma }\partial {\mathit{\gamma }}^{\prime }}.$$

In addition, write the complete data score vector as

$$S(\mathit{\gamma }\mid D)=\sum _{i=1}^n{S}_i(\mathit{\gamma }\mid {\mathit{x}}_i,y_i,{\delta }_i)=\sum _{i=1}^n\frac{\partial l(\mathit{\gamma }\mid {\mathit{x}}_i,y_i,{\delta }_i)}{\partial \mathit{\gamma }}.$$

Then, the estimated observed information matrix of γ̂ is given by

$$\mathcal{I}(\widehat{\mathit{\gamma }})=-\ddot{Q}(\widehat{\mathit{\gamma }}\mid \widehat{\mathit{\gamma }})-\left\{\left[\sum _{i=1}^n\frac{1}{m_i^{(t)}}\sum _{k=1}^{m_i^{(t)}}{S}_i(\widehat{\mathit{\gamma }}\mid {\mathit{x}}_i^{(k)},y_i)S_i(\widehat{\mathit{\gamma }}\mid {\mathit{x}}_i^{(k)},y_i{)}^{\prime }\right]-\sum _{i=1}^n{\stackrel{.}{Q}}_i(\widehat{\mathit{\gamma }}\mid \widehat{\mathit{\gamma }}){\stackrel{.}{Q}}_i(\widehat{\mathit{\gamma }}\mid \widehat{\mathit{\gamma }}{)}^{\prime }\right\},$$ (5.6)

where ${\mathit{x}}_{i,\mathit{mis}}^{(1)},{\mathit{x}}_{i,\mathit{mis}}^{(2)},\dots ,{\mathit{x}}_{i,\mathit{mis}}^{(m_i^{(t)})}$ is an MCMC sample of size $m_i^{(t)}$, from f(x_i,mis|x_i,obs, γ̂), and ${\mathit{x}}_i^{(k)}=({\mathit{x}}_{i,\mathit{mis}}^{(k{)}^{\prime }},{\mathit{x}}_{i,\mathit{obs}}^{\prime }{)}^{\prime }$. Thus, the estimate of the asymptotic covariance matrix of γ̂ is [ℐ(γ̂)]⁻¹.

Finally, we note that when there are ties in the failure times, (5.7), (5.2), and (5.3) can be modified as

$$\begin{array}{l}Q(\mathit{\gamma }\mid {\mathit{\gamma }}^{(t)})=\sum _{i=1}^d\left[d_{i}log{h}_0(y_i)+\frac{1}{m_i^{(t)}}\sum _{k=1}^{m_i^{(t)}}{\mathit{z}}_i^{(tk{)}^{\prime }}\mathit{\beta }\right]-\sum _{i=1}^d{h}_0(y_i)\sum _{j\in \mathcal{R}(y_i)}\left[\frac{1}{m_j^{(t)}}\sum _{k=1}^{m_j^{(t)}}exp({\mathit{x}}_j^{(tk{)}^{\prime }}\mathit{\beta })\right]\\ +\sum _{i=1}^n\frac{1}{m_i^{(t)}}\sum _{k=1}^{m_i^{(t)}}logf({\mathit{x}}_{i,\mathit{mis}}^{(tk)},{\mathit{x}}_{i,\mathit{obs}}\mid \mathit{\alpha }),\end{array}$$ (5.7)

where ${\mathit{z}}_i^{(tk)}={\sum }_{j\in {\mathcal{D}}_i}({\mathit{x}}_{j,\mathit{mis}}^{(tk{)}^{\prime }},{\mathit{x}}_{j,\mathit{obs}}^{\prime }{)}^{\prime }$,

$${\mathit{\beta }}^{(t+1)}=\underset{\mathit{\beta }}{argmax}\sum _{i=1}^d\left\{\left[\frac{1}{m_i^{(t)}}\sum _{k=1}^{m_i^{(t)}}{\mathit{z}}_i^{(tk{)}^{\prime }}\mathit{\beta }\right]-d_{i}log\left[\sum _{j\in \mathcal{R}(y_i)}\frac{1}{m_j^{(t)}}\sum _{k=1}^{m_j^{(t)}}exp({\mathit{x}}_j^{(tk{)}^{\prime }}\mathit{\beta })\right]\right\},$$ (5.8)

and

$$h_0^{(t+1)}(y_i)=d_i{\left[\sum _{j\in \mathcal{R}(y_i)}\frac{1}{m_j^{(t)}}\sum _{k=1}^{m_j^{(t)}}exp({\mathit{x}}_j^{(tk{)}^{\prime }}{\mathit{\beta }}^{(t+1)})\right]}^{-1},H_0^{(t+1)}(y_i)=\sum _{y_j\le y_i,{\delta }_j=1}{h}_0^{(t+1)}(y_j).$$ (5.9)

The calculation of ℐ(γ̂) needs to be modified accordingly in the presence of ties. Again, the above formulation can be easily extended to the case where x_i,mis is categorical.

6 Analysis of Small Cell Lung Cancer Data

For the LCCC 9719 data discussed in Section 2, we use the proposed methods to estimate the regression coeffients assuming the missing covariates are MAR. We consider a Cox regression model for [y_i |x_i, β, h₀] allowing for right censoring. Thus, we have

$$f(y_i\mid {\delta }_i,{\mathit{x}}_i,\mathit{\beta },h_0)={\left[h_0(y_i)exp\{{\mathit{x}}_i^{\prime }\mathit{\beta })\}\right]}^{{\delta }_i}exp\{-H_0(y_i)exp({\mathit{x}}_i^{\prime }\mathit{\beta })\},$$

where x_i = (x_i1,…, x_i5)′ is a 5 × 1 vector of covariates, i = 1, 2, …, n, β = (β₁,…,β₅)′ is the vector of the corresponding regression coeffcients, h₀(y_i) and H₀(y_i) denote the baseline hazard function and the cumulative baseline hazard function, respectively. Since x_i1, x_i2, and x_i3 are always observed, they do not need to be modeled. Thus, we only need to model two missing covariates (x₄, x₅) conditioning on the completely observed covariates throughout. We consider two models: [x₄|x₁, x₂, x₃][x₅|x₁, x₂, x₃, x₄] and [x₄|x₁, x₂, x₃, x₅][x₅|x₁, x₂, x₃] for (x₄, x₅). We use a logistic regression model for x_i4 and a normal linear regression model for x_i5. Specifically, for example, for [x₄|x₁, x₂, x₃][x₅|x₁, x₂, x₃, x₄], we have

$$f(x_{i4}\mid x_{i1},x_{i2},x_{i3},{\mathit{\alpha }}_4)=\frac{exp\{x_{i4}({\alpha }_{40}+{\alpha }_{41}{x}_{i1}+{\alpha }_{42}{x}_{i2}+{\alpha }_{43}{x}_{i3})\}}{1+exp({\alpha }_{40}+{\alpha }_{41}{x}_{i1}+{\alpha }_{42}{x}_{i2}+{\alpha }_{43}{x}_{i3})},$$

where α₄ = (α₄₀, α₄₁, α₄₂, α₄₃)′, and

$$f(x_{i5}\mid x_{i1},x_{i2},x_{i3},x_{i4},{\mathit{\alpha }}_5)=\frac{1}{\sqrt{2\pi {\alpha }_{55}}}exp\{-{[x_{i5}-({\alpha }_{50}+{\alpha }_{51}{x}_{i1}+\cdots +{\alpha }_{54}{x}_{i4})]}^2/(2{\alpha }_{55})\},$$

where α₅ = (α₅₀, α₅₁, …, α₅₅)′.

To illustrate how to apply the Theorems presented in Sections 2 and 3, we consider a subset of the LCCC 9719 data, which is given in Table 2. Since all of the covariates are observed in this subset, using (3.1) after excluding the rows corresponding to δ_i = 0 or x_j = x_i, X^* is a 35× 5 matrix. The first 8 rows are given by ${\mathit{x}}_i^{\prime }-{\mathit{x}}_1^{\prime }$ for i = 1, 2, …, 8, and the last row is given by ${\mathit{x}}_9^{\prime }-{\mathit{x}}_7^{\prime }$. Using Maple (Version 8) linsolve, with Maple code “linsolve(X^*, v);”, after loading a linalg package, we obtain a closed form solution for X^*′v = 0 and find that there indeed exists a positive vector v > 0 satisfying X^*′v = 0. Also, |X^*′X^*| = 9.2344 × 10¹⁰ > 0. Thus, conditions (C1) and (C2) given in Theorem 3.1 are met for this subset. As discussed in Remark 3.4, when the conditions (C1) and (C2) are satisfied for a subset of the data, these two conditions hold for the entire set of completely observed cases. In addition, we can show that lim_||α||→∞ L(α|D_obs) = 0, where L(α|D_obs) is defined by (4.3), using the results established in Chen and Shao (2001) and hence, details are omitted here for brevity. Thus, based on Theorem 4.1, the MLE does exist for the entire dataset.

Table 2.

A Subset of LCCC 9719 Data

Obs (i)	yi	δi	xi1	xi2	xi3	xi4	xi5
1	0.394	1	1	0	68	0	54
2	1.083	1	0	0	81	0	79
3	1.116	1	1	1	82	0	64
4	1.149	1	0	1	58	1	86
5	1.313	1	1	1	52	1	54
6	3.973	1	1	0	69	1	92
7	6.665	1	0	0	54	1	83
8	9.521	0	1	0	62	0	67
9	14.380	0	0	1	81	0	80

Since the MPLE of β and the MLE of (β, h₀, α) exist for this dataset, we can compute various estimates of β and α₄ and α₅. We standardized age and QOL score in order to make the numerical computations more stable. We used the SAS procedure PHREG to obtain the MPLE of β for the complete case (CC) analysis (i.e, an analysis deleting all of the missing values). The MCEM algorithm discussed in Section 5 was implemented using FORTRAN 77 with IMSL, the estimated observed information matrix ℐ(γ̂) given by (5.6) is of dimension (102+15)×(102+15), and its inverse was computed via the IMSL subroutine DLINDS. The Gibbs sampling algorithm was used to generate the Monte Carlo sample with 500 “burn-in” iterations at each MCEM iteration. In the MCEM, we took m⁽⁰⁾ = 500 and Δm = 50. The convergence criterion for the MCEM algorithm for obtaining the MLE was that the squared distance between the t^th and (t + 20)^th iterations was less than 10⁻³. The MCEM algorithm for obtaining the MLE of (β, h₀, α) required only 25 iterations using m(t) = 1750 at convergence.

The resulting MPLEs and MLEs are shown in Tables 3, 4, and 5 for the complete case (CC) analysis as well as analyses incorporating all of the cases with two different models for (x₄, x₅). In the tables, standard errors (SEs), Z-statistics, p-values, and 95% confidence intervals for β are also reported. We can see some differences between the estimates in Tables 3 and 4. In the CC analysis, the 95% confidence interval for β₁ is (−0.024, 0.967) while the 95% confidence interval is (0.133, 0.820) in the analysis incorporating all of the cases, which indicates that the regression coefficient for treatment is not significant at the 0.05 level in the CC analysis, but significant in the analysis incorporating all of the cases. This indicates that continuous therapy followed by second line therapy may have a strong effect (i.e., more beneficial) compared to defined duration of therapy with respect to time to progression. Also, the SEs from the analysis incorporating all of the cases are consistently smaller than those from the CC analysis for all of the β_j’s. This is expected since more information is used in the all case analysis.

Table 3.

Maximum Partial Likelihood Estimates of β for Complete Case Analysis

Parameter	MPLE	SE	Z-statistic	p-value	95% CI
β1	0.471	0.253	1.864	0.062	(−0.024, 0.967)
β2	0.068	0.243	0.280	0.780	(−0.409, 0.545)
β3	−0.020	0.130	−0.154	0.878	(−0.275, 0.235)
β4	0.878	0.411	2.140	0.032	(0.074, 1.684)
β5	−0.138	0.119	−1.158	0.247	(−0.372, 0.096)

Table 4.

Maximum Likelihood Estimates of β Based On All Observed Data and Model [x₄|x₁, x₂, x₃][x₅|x₁, x₂, x₃, x₄] for Missing Covariates

Parameter	MLE	SE	Z-statistic	p-value	95% CI
β1	0.477	0.175	2.723	0.006	(0.133, 0.820)
β2	0.174	0.180	0.966	0.334	(−0.179, 0.528)
β3	−0.021	0.090	−0.238	0.812	(−0.198, 0.155)
β4	0.914	0.381	2.400	0.016	(0.168, 1.661)
β5	−0.052	0.105	−0.490	0.624	(−0.258, 0.155)

Table 5.

Maximum Likelihood Estimates of β Based On All Observed Data and Model [x₄|x₁, x₂, x₃, x₅][x₅|x₁, x₂, x₃] for Missing Covariates

Parameter	MLE	SE	Z-statistic	p-value	95% CI
β1	0.477	0.175	2.722	0.006	(0.133, 0.820)
β2	0.173	0.180	0.959	0.338	(−0.181, 0.527)
β3	−0.021	0.090	−0.233	0.816	(−0.197, 0.155)
β4	0.914	0.388	2.356	0.018	(0.154, 1.674)
β5	−0.053	0.106	−0.501	0.616	(−0.261, 0.155)

The reason why we considered two models for (x₄, x₅) is that there are two possibilities in modeling the joint covariate distribution as a sequence of one dimensional conditional distributions. As Ibrahim, Lipsitz, and Chen (1999) point out, it is important to conduct a sensitivity analysis to examine whether inference about the parameters of primary interest, which are the β_j’s in this case, is robust with respect to the order of conditioning in the covariate distributions. From Tables 4 and 5, both estimates and SEs for all the β_j’s are very close for these two joint covariate distributions. Thus, inference about β is quite robust with respect to these two different orders of conditioning.

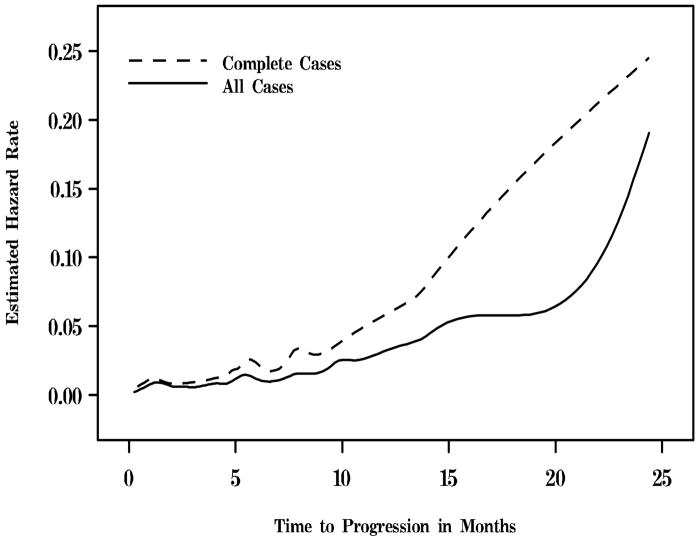
Finally, the estimated baseline hazard functions h₀(y) are plotted in Figure 1 for the complete case analysis as well as the analysis incorporating all of the cases, labeled Complete Cases and All Cases, respectively. In the all case analysis, the model [x₄|x₁, x₂, x₃][x₅|x₁, x₂, x₃, x₄] for (x₄, x₅) was used since an almost identical estimated baseline hazard function was obtained under the model [x₄|x₁, x₂, x₃, x₅][x₅|x₁, x₂, x₃]. Strikingly, the CC analysis resulted in a much different (larger) estimate of the baseline hazard than the all case analysis, which further demonstrates the importance of incorporating all of the cases into the analysis.

Figure 1.

Estimated baseline hazard function (h₀(y)) for CC and all cases analyses.

Appendix: Proofs of Theorems

We first establish a useful result, which is formally stated in the following lemma.

Lamma A.1

Let X^* be an n^* × p matrix (p < n^*). Also let R^n* denote the n^*-dimensional Euclidean space. If there is no positive vector v = (v₁, v₂, …, v_n^*)′ ∈ R^n* (denoted by v > 0, i.e., v_i > 0 for i = 1, 2, …, n^*) such that

$$X^{{\ast }^{\prime }}\mathit{v}=0,$$ (A.1)

then there exists a non-zero vector b ∈R^p such that

$${\mathit{b}}^{\prime }{\mathit{x}}_i^{\ast }\le 0,$$ (A.2)

where ${\mathit{x}}_i^{\ast }$ is the i^th row of X^*.

Proof

Let 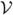= {X^*′ v: v > 0, v ∈ R^n*}. Then is a convex cone in R^p (see Theorem 2.6 in Rockafellar (1970)). Since (A.1) does not hold, by Corollary 11.7.3 of Rockafellar (1970), there exists some non-zero vector b such that ∀ v > 0, b′X^*′v ≤ 0 and hence ∀ v ≥ 0, b′X^*′v ≤ 0. In particular, (A.2) holds.

Proof of Theorem 3.1

Observe that for δ = 0 or 1 and x > −1

$${\left(\frac{1}{1+x}\right)}^{\delta }={\int }_0^{\infty }{e}^{-t(1+\delta x)}dt.$$ (A.3)

Without loss of generality (WLOG), assume y₁ ≤ y₂ ≤ … ≤ y_n. Then

$$\begin{array}{l}{L}_p(\mathit{\beta }\mid D_{\mathit{obs}})=\prod _{i=1}^n{\left(\frac{exp({\mathit{x}}_i^{\prime }\mathit{\beta })}{{\sum }_{j\in \mathcal{R}(y_i)}exp({\mathit{x}}_j^{\prime }\mathit{\beta })}\right)}^{{\delta }_i}=\prod _{i=1}^n{\left(\frac{1}{1+{\sum }_{j>i}exp(({\mathit{x}}_j-{\mathit{x}}_i{)}^{\prime }\mathit{\beta })}\right)}^{{\delta }_i}\\ =\prod _{i=1}^n{\int }_0^{\infty }exp\left(-t_i(1+{\delta }_i\sum _{j>t}exp(({\mathit{x}}_j-{\mathit{x}}_i{)}^{\prime }\mathit{\beta }))\right)d{t}_i\\ ={\int }_{R^{+n}}exp(-\sum _{i=1}^n{t}_i)\prod _{1\le i\le n,j>i}{\left(exp\left(-exp(-({\mathit{x}}_i-{\mathit{x}}_j{)}^{\prime }\mathit{\beta }\right)\right)}^{t_i{\delta }_i}d\mathit{t}\\ ={\int }_{R^{+n}}exp(-\sum _{i=1}^n{t}_i)\prod _{1\le i\le n,j>i}F{(({\mathit{x}}_i-{\mathit{x}}_j{)}^{\prime }\mathit{\beta })}^{t_i{\delta }_i}d\mathit{t},\end{array}$$ (A.4)

where t = (t₁, t₂, …, t_n)′, R⁺ⁿ = R⁺ ×…×R⁺ with R⁺ = (0, ∞), and F (u) = exp(−exp(−u)).

Sufficiency

WLOG, we assume that L_p(β|D_obs) ≢ 0. Then, there exists a β₀ such that L_p(β₀|D_obs) > 0. Let M > 1 such that

$$\frac{1}{1-logF(-M)}<L_p({\mathit{\beta }}_0\mid D_{\mathit{obs}}).$$

For β satisfying max_{1≤i≤n,j>i} δ_i(x_j − x_i)′β > M, there exist i₀ and j₀ achieving the maximum such that δ_i0(x_i0−x_j0)′β < −M. Since F is a nondecreasing distribution function, we have

$$\begin{array}{l}{L}_p(\mathit{\beta }\mid D_{\mathit{obs}})\le {\int }_{R^{+n}}exp(-\sum _{i=1}^n{t}_i)F{({\delta }_{i_0}({\mathit{x}}_{i_0}-{\mathit{x}}_{j_0}{)}^{\prime }\mathit{\beta })}^{t_{i_0}}d\mathit{t}\le {\int }_{R^{+n}}exp(-\sum _{i=1}^n{t}_i)F{(-M)}^{t_{i_0}}d\mathit{t}\\ ={\int }_0^{\infty }exp\{-[1-logF(-M)]t_{i_0}\}d{t}_{i_0}=\frac{1}{1-logF(-M)}\le L_p({\mathit{\beta }}_0\mid D_{\mathit{obs}}).\end{array}$$ (A.5)

When max_{1≤i≤n,j>i} δ_i(x_j−x_i)′β ≤ M, following Lemma 4.1 in Chen and Shao (2001), conditions (C1) and (C2) imply that

$$\parallel \mathit{\beta }\parallel =\sqrt{{\mathit{\beta }}^{\prime }\mathit{\beta }}\le D\text{for}\text{some}0<D<\infty .$$ (A.6)

Combining (A.5) and (A.6) leads to sup_β L_p(β|D_obs) = sup_{β: ||β||≤D} L_p(β|D_obs). Since L_p(β|D_obs) is a continuous and bounded function, there exists a β̂ such that

$$L_p(\widehat{\mathit{\beta }}\mid D_{\mathit{obs}})=\underset{\mathit{\beta }:\parallel \mathit{\beta }\parallel \le D}{sup}{L}_p(\mathit{\beta }\mid D_{\mathit{obs}})$$

and hence the MPLE exists.

Necessity

Assume that the MPLE of β exists. Then, there is a β^* such that

$$L_p({\mathit{\beta }}^{\ast }\mid D_{\mathit{obs}})=\underset{\mathit{\beta }}{sup}{L}_p(\mathit{\beta }\mid D_{\mathit{obs}})\text{and}\parallel {\mathit{\beta }}^{\ast }\parallel <\infty .$$

Assume that condition (C2) does not hold. Then, by Lemma A.1, there exists a non-zero vector b such that δ_i(x_j − x_i)′b ≤ 0 for all 1 ≤ i ≤ n and j > i. Thus,

$$\begin{array}{l}{L}_p({\mathit{\beta }}^{\ast }+s\mathit{b}\mid D_{\mathit{obs}})={\int }_{R^{+n}}exp(-\sum _{i=1}^n{t}_i)\prod _{1\le i\le n,j>i}F{({\delta }_i({\mathit{x}}_i-{\mathit{x}}_j{)}^{\prime }{\mathit{\beta }}^{\ast }+{\delta }_{i}s({\mathit{x}}_i-{\mathit{x}}_j{)}^{\prime }\mathit{b})}^{t_i{\delta }_i}d\mathit{t}\\ ={\int }_{R^{+n}}exp(-\sum _{i=1}^n{t}_i)\prod _{1\le i\le n,j>i}F{({\delta }_i({\mathit{x}}_i-{\mathit{x}}_j{)}^{\prime }{\mathit{\beta }}^{\ast }-s{\delta }_i({\mathit{x}}_j-{\mathit{x}}_i{)}^{\prime }\mathit{b})}^{t_i{\delta }_i}d\mathit{t}\end{array}$$

which is an increasing function of s when condition (C1) holds. This is a contradiction. This shows that condition (C2) is necessary for the existence of the MPLE for β if condition (C1) is satisfied.

Proof of Theorem 4.1

Write

$$L^{\ast }(\mathit{\beta },\mathit{\alpha }\mid D_{\mathit{obs}})=\int \left\{\prod _{i=1}^{d}exp({\mathit{x}}_i^{\prime }\mathit{\beta }){\left[\sum _{j\in \mathcal{R}(y_i)}exp({\mathit{x}}_j^{\prime }\mathit{\beta })\right]}^{-1}\right\}\left[\prod _{i=1}^{n}f({\mathit{x}}_{i,\mathit{mis}},{\mathit{x}}_{i,\mathit{obs}}\mid \mathit{\alpha })\right]d{\mathit{x}}_{\mathit{mis}}$$ (A.7)

It is sufficient to prove that

$$\underset{\parallel \mathit{\beta }\parallel +\parallel \mathit{\alpha }\parallel \to \infty }{lim}{L}^{\ast }(\mathit{\beta },\mathit{\alpha }\mid D_{\mathit{obs}})=0.$$ (A.8)

Observe that

$$L_p(\mathit{\beta }\mid D)=\prod _{i=1}^{d}exp({\mathit{x}}_i^{\prime }\mathit{\beta }){\left[\sum _{j\in \mathcal{R}(y_i)}exp({\mathit{x}}_j^{\prime }\mathit{\beta })\right]}^{-1}$$

is an increasing function in ${\mathit{x}}_j^{\prime }\mathit{\beta }$ for δ_j = 1 and a decreasing function in ${\mathit{x}}_j^{\prime }\mathit{\beta }$ for δ_j = 0. For 1 ≤ l ≤ p, let $x_{il}^R=b_i^{\ast }={\delta }_i{a}_i+(1-{\delta }_i)b_i$ if β_l ≥ 0 and $x_{il}^R=a_i^{\ast }=(1-{\delta }_i)a_i+{\delta }_i{b}_i$ if β_l < 0. Write $x_i^{\ast }=(({\mathit{x}}_{i,\mathit{mis}}^R{)}^{\prime },{\mathit{x}}_{i,\mathit{obs}}^{\prime }{)}^{\prime }$ and ${\mathit{x}}_{i,\mathit{mis}}^R=(x_{il}^R,r_{il}=0,1\le l\le p{)}^{\prime }$. Let ℛ_i = ℛ(y_i) − {i}. Then we have

$$L_p(\mathit{\beta }\mid D)\le L_p^{\ast }(\mathit{\beta }\mid D)\equiv \prod _{i=1}^{d}exp(({\mathit{x}}_i^{\ast }{)}^{\prime }\mathit{\beta }){\left[exp(({\mathit{x}}_i^{\ast }{)}^{\prime }\mathit{\beta })+\sum _{{\delta }_j=0,j\in {\mathcal{R}}_i}exp(({\mathit{x}}_j^{\ast }{)}^{\prime }\mathit{\beta })\right]}^{-1}.$$ (A.9)

It directly follows from (A.7), (A.9) and (4.3) that

$$L^{\ast }(\mathit{\beta },\mathit{\alpha }\mid D_{\mathit{obs}})\le L_p^{\ast }(\mathit{\beta }\mid D)L(\mathit{\alpha }\mid D_{\mathit{obs}}).$$

Following the proof of Theorem 3.1, ${lim}_{\parallel \mathit{\beta }\parallel \to \infty }{L}_p^{\ast }(\mathit{\beta }\mid D)=0$ if conditions (C2^*) and (C3^*) are satisfied. Consequently, we obtain (A.8) under condition (C1^*).

Proof of Theorem 4.2

Let 1 = (1, 1, …, 1)′. Then we have

$$L_p(\mathit{\beta }\mid D)\le \prod _{{\mathit{r}}_i=\mathbf{1},1\le i\le d}exp({\mathit{x}}_i^{\prime }\mathit{\beta }){\left[exp({\mathit{x}}_i^{\prime }\mathit{\beta })+\sum _{{\delta }_j=0,{\mathit{r}}_j=\mathbf{1},j\in {\mathcal{R}}_i}exp({\mathit{x}}_j^{\prime }\mathit{\beta })\right]}^{-1}.$$

Therefore, the above inequality, condition (C1^*) in Theorem 4.1, and conditions (C1) and (C2) stated in Theorem 3.1 directly yield the existence of the MLE of (β, h₀, α).