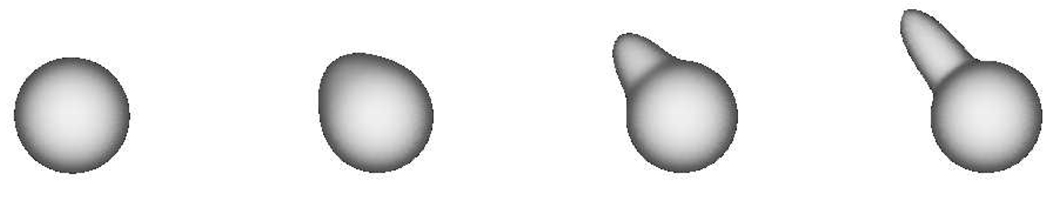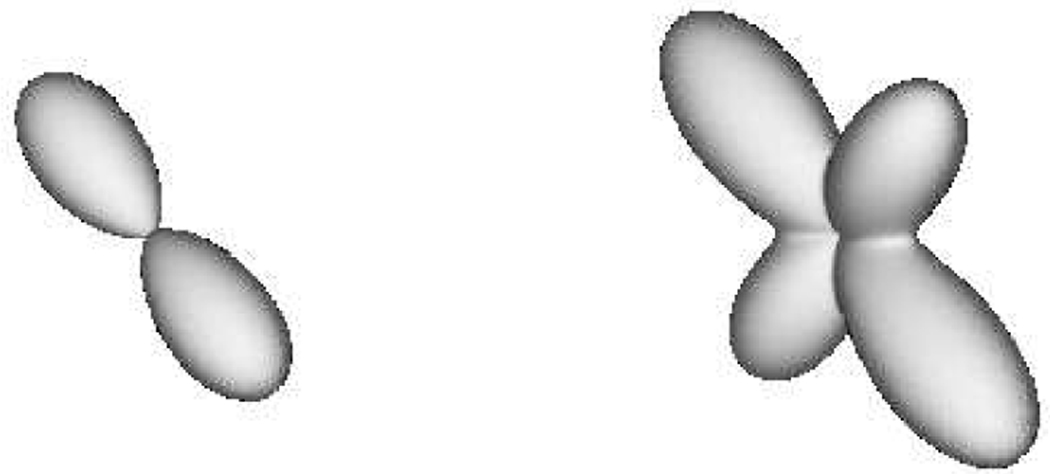VON MISES-FISHER MIXTURE MODEL OF THE DIFFUSION ODF

Abstract

High angular resolution diffusion imaging (HARDI) permits the computation of water molecule displacement probabilities over the sphere. This probability is often referred to as the orientation distribution function (ODF). In this paper we present a novel model for representing this diffusion ODF namely, a mixture of von Mises-Fisher (vMF) distributions. Our model is compact in that it requires very few parameters to represent complicated ODF geometries which occur specifically in the presence of heterogeneous nerve fiber orientations. We present a Riemannian geometric framework for computing intrinsic distances (in closed-form) and for performing interpolation between ODFs represented by vMF mixtures. We also present closed-form equations for entropy and variance based anisotropy measures that are then computed and illustrated for real HARDI data from a rat brain.

1. INTRODUCTION

Diffusion tensor models have been used in the past to explain the local geometry of the diffusivity function characterizing the tissue being imaged. A diffusion tensor model assumes a single dominant direction of diffusion and hence is well suited for modeling tissue that exhibits unidirectional diffusivity behavior. However, more general mathematical models are needed to represent the diffusivity function in regions of crossing fibers. The DTI model is well known for its deficiency in coping with such complex local geometries and high angular resolution diffusion weighted imaging is one way to overcome this problem. There are several methods, in literature, for processing HARDI data sets. For example, Tuch [1, 2] developed the HARDI acquisition and processing and later Frank [3] used the spherical harmonics expansion of the HARDI data to characterize the local geometry of the diffusivity function.

In order to design efficient algorithms, we seek a continuous parametric model for the ODF with a small number of parameters, which is capable of describing diffusion in the presence of intravoxel orientational heterogeneity (IVOH). To put our proposed model in perspective we will first review some of the models for diffusion used in published literature.

1.0.1. Gaussian Mixture Model

Gaussian mixture models (GMMs) are commonly used to model multimodal distributions. The GMM is a convex combination of Gaussian density functions. Each Gaussian component is characterized by a 3 × 3 covariance matrix which has 6 independent elements. For diffusion data, all components have a mean = 0.

We are primarily concerned with the directional characteristics of diffusion, which can be characterized by the marginal distribution, P(θ, ϕ) obtained by integrating over the radial component of the displacement probability P(x). This will allow us to use a simpler model for the ODF. Additionally, with the GMM, we must be careful to impose the positive-definiteness constraint on the covariance matrix of each component. Previously Fletcher and Joshi [4] have described geodesic analysis on the space of diffusion tensors. The analysis includes an algorithm for computing the intrinsic mean of diffusion tensors. Later in this paper we will present a similar analysis for our proposed model.

1.0.2. Spherical Harmonics

The spherical harmonic (SH) expansion is a useful representation for complex-valued functions on the sphere. One can represent the diffusivity function by the expansion $d(\theta ,\varphi )={\displaystyle {\sum }_{l=0}^L{\displaystyle {\sum }_{m=-l}^l{a}_{l,m}{Y}_{l,m}(}}\theta ,\varphi )$, where Y_l,m are the spherical harmonic basis functions. Frank [5] presented a truncated expansion of the diffusivity function, at order L = 4 (or higher) to account for diffusion in the presence of complicated fiber geometries. An L = 4 expansion requires at least 15 complex-valued coefficients per voxel. In general, an order L expansion can describe diffusion with L/2 fiber directions. Many others [6, 7] have pursued this route of representing the diffusivity function in a spherical harmonic basis. The peaks in the spherical harmonic representation of the diffusivity function, however, do not correspond to the fiber directions. Instead, one needs to find the peaks of the orientation diffusion probability functions to determine the fiber orientations.

1.0.3. Generalized Tensors

The diffusion tensor imaging model described earlier represents diffusion using a rank-2 tensor. Diffusion has been described more generally by Özarslan et al. [8] by considering Cartesian tensors of higher rank. A Cartesian tensor of rank n will, in general, have 3ⁿ elements. However, due to symmetry, the number of distinct components in a high rank diffusion tensor will be much smaller. Ozarslan et al., [9] generalized the concept of the trace of a matrix, to quantify the anisotropy of diffusion described by tensors of arbitrary rank. Since tensors of odd rank imply negative diffusion coefficients, only even rank tensors are appropriate for describing diffusion. For diffusion tensors of rank 4, 6, and 8, the number of distinct components are 15, 28, and 45 respectively. It is, however, not clear how to extract fiber directions from these higher rank tensor representations.

2. THE VON MISES-FISHER MIXTURE MODEL

Since we are dealing with multivariate data over the sphere, S², we wish to express the data using distributions over this domain. Numerous distributions over spherical domains are discussed in detail by Mardia and Jupp [10]. We propose a model for the ODF in terms of the von Mises-Fisher distributions. This model has fewer variables than the previously discussed models, allows the fiber directions to be extracted easily, involves constraints which are simpler to satisfy, and leads to a closed-form expressions for several useful measures.

The von Mises distribution over the circle can be generalized to the sphere in arbitrary dimension (S^p−1) by keeping the log of the distribution linear in the random variable x as in

$$M_p(\mathrm{x}|\mu ,\kappa )={\left(\frac{\kappa }{2}\right)}^{p/2-1}\frac{1}{2\pi \mathrm{\Gamma }(p/2)I_{p/2-1}(\kappa )}\text{exp}(\kappa {\mu }^T\mathrm{x})$$ (1)

where the hypersphere is embedded in ℜ^p, |x| = 1 and |μ| = 1, and I_k denotes the modified Bessel function of the first kind, order k. The concentration parameter, κ, quantifies how tightly the function is distributed around the mean direction μ. For κ = 0 the distribution is uniform over the sphere. The distributions are unimodal and rotationally symmetric around the direction μ.

For p = 3 the distribution is called the von Mises-Fisher (vMF) distribution, and can be written

$$M_3(\mathrm{x}|\mu ,\kappa )=\frac{\kappa }{4\pi \text{sinh}(\kappa )}\text{exp}(\kappa {\mu }^T\mathrm{x}).$$ (2)

A useful characteristic of the vMF distribution is that the product of two vMFs can also be written as an unnormalized vMF. Since

$$\text{exp}({\kappa }_i{\mu }_i^T\mathrm{x})\text{exp}({\kappa }_j{\mu }_j^T\mathrm{x})=\text{exp}({({\kappa }_i{\mu }_i+{\kappa }_j{\mu }_j)}^T\mathrm{x})$$ (3)

we have

$$\begin{array}{c}\hfill M_3(\mathrm{x}|{\mu }_i,{\kappa }_i)M_3(\mathrm{x}|{\mu }_j,{\kappa }_j)\propto M_3(\mathrm{x}|{\tau }_{ij},{\rho }_{ij}),\\ \hfill \text{where}{\rho }_{ij}=\sqrt{{\kappa }_i^2+{\kappa }_j^2+2{\kappa }_i{\kappa }_j({\mu }_i·{\mu }_j)},\\ \hfill \text{and}{\tau }_{ij}=\frac{{\kappa }_i{\mu }_i+{\kappa }_j{\mu }_j}{{\rho }_{ij}}.\end{array}$$ (4)

We will use this fact in the next section.

Since the vMF distribution is unimodal, we will choose a convex combination of these distributions to model the ODF. Also, as the ODF is antipodally symmetric, we will need a mixture to describe diffusion in even a single fiber region, but since the antipodal pairs have μ₁ = −μ₂, we can specify a mixture with just 3 variables per component: the two spherical coordinate angles describing μ; and the real, positive parameter κ. The vMF mixture model for the ODF has the form

$$P(\mathrm{x})={\displaystyle \sum _{i=1}^m{\omega }_i{M}_3(\mathrm{x}|{\mu }_i,{\kappa }_i)\text{with}{\displaystyle \sum _{i=1}^m{\omega }_i=1,\text{and}{\omega }_i\ge 0}}$$ (5)

where m is the number of components in the mixture. The convexity constraint on {ω} ensures that the mixture still has nonnegative probabilities, and will integrate to 1. Since vMF distributions obey the property (3), the product of two von Mises-Fisher mixture models is also proportional to a vMF mixture model.

2.1. Fitting the vMF Mixture

The diffusion orientation transform (DOT) presented by Özarslan [11] can be used in two ways : parametrically and nonparametrically. The first way yields a spherical harmonic expansion for the ODF. The second technique, which we employ, permits the rapid sampling of the ODF over a set of arbitrary directions. Following the learning algorithm in [12], we apply the Expectation-Maximization (EM) algorithm to compute the parameters of the vMF mixture.

It is likely that most voxels can be described by a mixture of 4 vMF distributions quite well. In this case the model requires only 15 real-valued parameters to completely describe it. Once we have fit the vMF mixture to the ODF, we can directly extract the fiber directions, {μ_i}.

2.2. Entropy of the vMF mixture

We seek closed-form equations for several measures, since this will eliminate the need for time consuming, and possibly inaccurate, numerical integration. The entropy of the mixture model, which can be used as measure of anisotropy, can take several analytical forms. Although the Shannon entropy of these distributions cannot be written in closed-form, some of the Renyi entropies [13] may. The Renyi entropy is defined as $H_{\alpha }(X)=\frac{1}{1-\alpha }\text{log}({\sum }_{x}P{(x)}^{\alpha })$. In particular, the Renyi entropies of integer orders α > 1 can be written in closed-form. Since the expression will have m^α terms, we will concentrate on the case α = 2.

$$\begin{array}{cc}{H}_2(X)\hfill & =-\text{log}\left({\displaystyle {\int }_0^{2\pi }{\displaystyle {\int }_0^{\pi }P{(x)}^2\text{sin}\theta d\theta d\varphi }}\right)\hfill \\ \hfill & =-\text{log}\left({\displaystyle \sum _{i=1}^m{\displaystyle \sum _{j=1}^m\frac{{\omega }_i{\omega }_j{\kappa }_i{\kappa }_j}{4\pi \text{sinh}{\kappa }_i\text{sinh}{\kappa }_j}\frac{\text{sinh}{\rho }_{ij}}{{\rho }_{ij}}}}\right)\hfill \end{array}$$ (6)

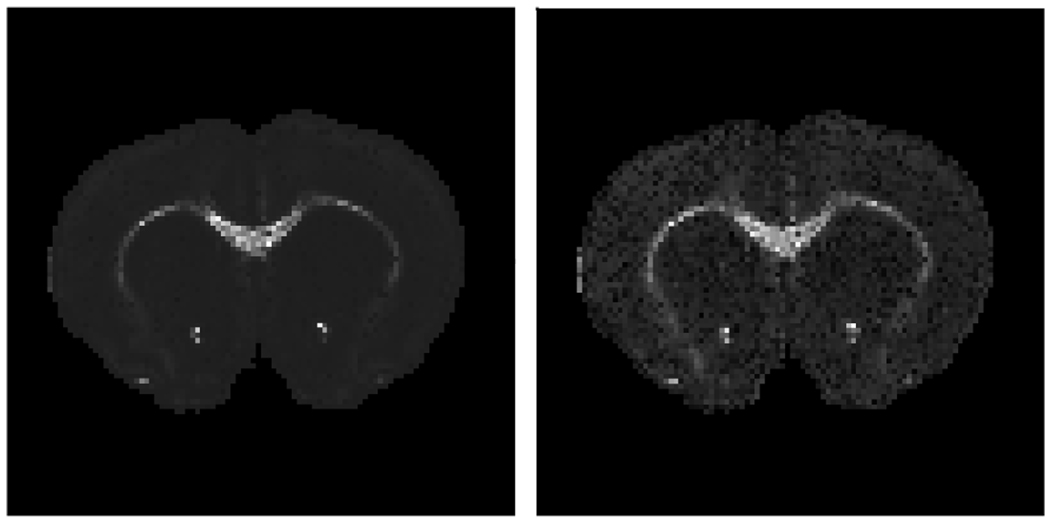
Closed-form expressions for L₂ distance, cosine similarity, and relative Renyi entropies can also be derived. Anisotropy maps computed from a rat brain data set are shown in Figure 3. The left image shows H₂ computed from the vMF field. The right image shows the weighted concentration parameter $({\displaystyle {\sum }_i^m{\omega }_i{\kappa }_i)}$ at each voxel. As evident, both images show high intensity in known areas of white matter in the brain, however the H₂ image is less noisy.

Fig. 3.

H₂ and mean κ anisotropy computed for rat brain data.

3. THE SPACE OF VMF DISTRIBUIONS

The von Mises-Fisher distribution is parameterized by two variables: the concentration parameter κ ∈ ℜ⁺ and μ ∈ S². For each point in ℜ⁺ × S² there is a corresponding vMF distribution. The curved geometry of this space of vMF distributions will influence how we compute distances, geodesics, interpolation functions and means. A general treatment of the geometry of the spaces formed by parametric distributions is given by Amari [14].

3.1. Riemannian Geometry

The space of vMF distributions forms a differentiable manifold, which can be considered to be embedded in a higher dimensional space. The embedding space induces a metric on the manifold that allows for an intrinsic way to measure distances on the manifold. A Riemannian manifold is a smooth manifold supplied with a Riemannian metric. This metric takes the form of an inner product, 〈υ, ω〉_p defined on the tangent space, T_pM, for each point, p, on the manifold, M. The Riemannian metric allows us to measure the length of a curve between two points, p, q on M. The notions of metric, distance, geodesics, interpolation and mean are all related. The mean can be defined as the point, μ, which satisfies

$$\underset{\mu \in M}{\text{min}}{\displaystyle \sum _{i=1}^N{d}^2(\mu ,x_i)}$$ (7)

where d(p, q) is the distance between points p and q. Interpolation can be defined in terms of a weighted mean, so we can interpolate between the distributions p, q by minimizing

$$\underset{\mu \in M}{\text{min}}t{d}^2(\mu ,p)+(1-t)d^2(\mu ,q)$$ (8)

Computing the mean (or ”center”) of a group of distributions has several applications: interpolation, atlas construction, segmentation, and others. Previously, the intrinsic mean problem has been solved with a gradient descent algorithm [15, 16, 17] by writing the gradient of the energy function in Equation (7) in terms of the Log map.

3.2. Riemannian Exp and Log Maps

Let M be a manifold, and T_pM be the tangent space at p ∈ M. Consider all geodesies going through the point, p, on M. Given a tangent vector, υ ∈ T_pM, it is known that there is a unique geodesic, γ, such that γ(0) = p, and γ′(0) = υ. If the manifold is geodesically complete, as it is in our case, the Riemannian exponential map, Exp_p : T_pM → M, can be defined as

$${\text{Exp}}_p(\upsilon )=\gamma (1)$$ (9)

The Riemannian log map is the inverse of the exponential map, Log_p : Exp_p(υ) → T_pM. If the log map, Log_p exists at q, we can write the Riemannian distance between p and q as d(p, q) = ‖Log_p(q)‖. We have used the fact that the direct product of symmetric spaces is also a symmetric space to deduce that the space of vMF distributions is symmetric. Now we will use this fact to compute the Exp map for vMFs. For spaces which are expressed as direct products, we can write the exponential map as the direct product of the exponential maps for the constituent spaces. For a single vMF, let p = (κ, μ) represent the distribution M₃(x|κ, μ), and υ = (a, u) ∈ T_pM be the tangent vector. Then

$${\text{Exp}}_p(\upsilon )=(\kappa \text{exp}(a),Q\left[\begin{array}{c}\hfill u_x\frac{\text{sin}\Vert u\Vert }{\Vert u\Vert }\hfill \\ \hfill u_y\frac{\text{sin}\Vert u\Vert }{\Vert u\Vert }\hfill \\ \hfill \text{cos}\Vert u\Vert \hfill \end{array}\right])$$ (10)

where Q is the orthogonal matrix which transforms μ to [0, 0, 1]^T. The distance between vMFs can be written using the Log maps as

$$d(({\kappa }_{i,}{\mu }_i),({\kappa }_j,{\mu }_j))=\sqrt{\text{log}{(\frac{{\kappa }_j}{{\kappa }_i})}^2+{({\text{cos}}^{-1}({\mu }_i·{\mu }_j))}^2}.$$ (11)

An example of interpolation between two vMF distributions using this formulation is shown in Figure 4.

Fig. 4.

Interpolation between two vMF distributions.

4. THE SPACE OF VMF MIXTURES

It may seem that we can simply extend the results of the previous section, and consider the vMF mixtures to come from the space (ℜ⁺ × ℜ⁺ × S²)^m. However, considering the set of weights as a point in (ℜ⁺)^m ignores the convexity constraint on the weights. The space (ℜ⁺)^m includes linear combinations of vMFs whose weights do not sum to 1.

Instead, we consider the square roots of the weights, $\{\sqrt{{\omega }_1}\dots \sqrt{{\omega }_m}\}$. The convexity constraint now becomes: ${\sum }_{i=1}^m{\sqrt{{\omega }_i}}^2=1,{\omega }_i>=0$ So, we can consider the space of the square roots of the weights to be a hypersphere, S^m−1. Then, the space of mixtures with m components is S^m−1 × (ℜ⁺ × S²)^m.

4.1. Riemannian Exp and Log Maps

For the vMF mixture, the exponential map is the direct product of the exponential maps for each vMF, and the exponential map for S^m−1. Since we are quite unlikely to have more than 4 fiber orientations present within a single voxel, we will consider further the case of mixtures having 4 components (m = 4). In this case, the space of the square roots of {ω_i} is the unit hypersphere S³. Fortunately, the space S³ is well studied, since this is equivalent to the space of unit quaternions. In fact, S³ forms a Lie group with respect to the quaternion multiplication operator.

The exponential and log maps for S³ are

$$\begin{array}{cc}{\text{Exp}}_p(\upsilon )\hfill & ={\left[\frac{\text{sin}(\frac{1}{2}\Vert \upsilon \Vert )}{\Vert \upsilon \Vert }\upsilon ,\text{cos}(\frac{1}{2}\Vert \upsilon \Vert )\right]}^T,\hfill \\ {\text{Log}}_p(q)\hfill & =\frac{2{\text{cos}}^{-1}(q_{\omega })}{|q_{\upsilon ec}|}{q}_{\upsilon ec}\hfill \end{array}$$ (12)

where q_υec and q_ω are the vector and scalar parts respectively of the quaternion q.

We may now simply extend the results of the previous section to formulate the distance between mixtures. An example of interpolation between mixtures is shown in Figure 5.

Fig. 5.

Interpolation between two vMF mixtures.

5. CONCLUSION

We have introduced a novel model for representing the orientational distribution probability function with mixtures of von Mises-Fisher distributions. This model was shown to lead to closed-form expressions for distances and anisotropy measures. A geodesic framework for working with this model was also presented.

Future work will focus on exploiting the properties of this model to devise efficient model-based segmentation and atlas construction algorithms.

Fig. 1.

Example vMF distributions (κ = 1, 5, 15, 25) with same mean direction, μ.

Fig. 2.

Example vMF mixtures for voxels with one and two fibers.