Viscoelastic Characterization of Peripapillary Sclera: Material Properties by Quadrant in Rabbit and Monkey Eyes

Abstract

In this report we characterize the viscoelastic material properties of peripapillary sclera from the four quadrants surrounding the optic nerve head in both rabbit and monkey eyes. Scleral tensile specimens harvested from each quadrant were subjected to uniaxial stress relaxation and tensile ramp to failure tests. Linear viscoelastic theory, coupled with a spectral reduced relaxation function, was employed to characterize the viscoelastic properties of the tissues. We detected no differences in the stress-strain curves of specimens from the four quadrants surrounding the optic nerve head (ONH) below a strain of 4 percent in either the rabbit or monkey. While the peripapillary sclera from monkey eyes is significantly stiffer (both instantaneously and in equilibrium) and relaxes more slowly than that from rabbits, we detected no differences in the viscoelastic material properties (tested at strains of 0–1 percent) of sclera from the four quadrants surrounding the ONH within either species group.

Glaucomatous optic neuropathy is one of the three leading causes of blindness in the US [1,2] and is the result of damage to the neural tissues of the optic nerve head (ONH). Its clinical hallmarks are posterior cupping (bowing back) of the surface of the ONH, and a characteristic pattern of visual field loss.

While IOP-lowering is central to the treatment of the disease [2,3], there is wide disagreement over the role of IOP in the development and progression of glaucoma [3–5]. Much of the confusion over the role of IOP in glaucoma stems from two groups of patients: those exhibiting ocular hypertension (elevated IOP) that never develop the disease, and those that develop glaucoma with no measurable increase in IOP (normal tension glaucoma).

The sclera is the principal load-bearing tissue of the eye and consists primarily of collagen. The primary function of the sclera is to resist intraocular pressure, provide attachment sites for the ocular musculature and support the retina in the spheroid shape necessary for focused vision. The thickness and predominant collagen fibril orientation of this tissue are dependent on location in the globe [6–9]. However, whether the fibril orientation has a large effect on scleral material properties remains controversial [6,10–13].

The scleral shell is pierced by the scleral canal, an elliptical hole (1–2.5 mm in diameter) in the posterior portion of the globe, through which the retinal ganglion cell axons pass on their path to form the orbital optic nerve (Fig. 1). The scleral canal is spanned by a series of thin, fenestrated connective tissue sheets known as the lamina cribrosa (Fig. 1B, 1C). The lamina cribrosa provides structural and nutritional support to the retinal ganglion cell axons as they pass through the scleral canal. The tissues within the scleral canal are collectively known as the papilla or optic nerve head (ONH).

Fig. 1.

(A) Diagram of the anatomy of the eye, showing the location of the scleral canal and ONH; (B) histologic sagittal section through the scleral canal and ONH showing the peripapillary sclera, lamina cribrosa, and retinal ganglion cell axons, and (C) histologic transverse section through the scleral canal and ONH showing the connective tissue structure of the scleral canal, lamina cribrosa, and central retinal vessels.

IOP-related stress in the tissues of the ONH and sclera is considerable even at normal levels of intraocular pressure (10–20 mm Hg) [2], and the deformations resulting from those stresses may be affected by factors such as scleral canal geometry, lamina cribrosa tissue density and geometry, extracellular matrix composition, and other factors that vary significantly among individuals [14–17]. This biologic variability may explain a particular patient's vulnerability to normal levels of IOP or their immunity to relatively high levels of pressure.

Although attempts to study the properties of sclera have been made by several researchers [10–13,18,19], little work has been done to quantify these data in a form consistent with linear viscoelastic theory. All studies to date report a nonlinear stress-strain relationship, as well as creep or stress relaxation behavior. No studies have used strain rate controlled testing, which is important to maintain consistency in the application of the testing regime. To our knowledge, viscoelastic material properties of the sclera in monkeys have not been previously reported.

To begin the investigation into the material properties of load-bearing ocular tissues, we performed uniaxial stress relaxation and tensile ramp to failure tests on strips of peripapillary sclera (sclera within 4 mm of the scleral canal) harvested from the eyes of New Zealand white rabbits and rhesus and cynomolgous monkeys. Nonhuman primates are generally used to study damage to the ONH due to elevated IOP, as they exhibit an IOP-related optic neuropathy that is indistinguishable from human glaucoma [20].

This study was designed to test two principal hypotheses. First, that the material properties of rabbit sclera are not significantly different from those of monkeys, and therefore the rabbit can serve as an easily accessible animal model for the study of scleral responses to IOP. Second, that peripapillary scleral material properties do not differ in scleral specimens (Fig. 2A) from the superior, inferior, nasal, and temporal quadrants surrounding the ONH in either species.

Fig. 2.

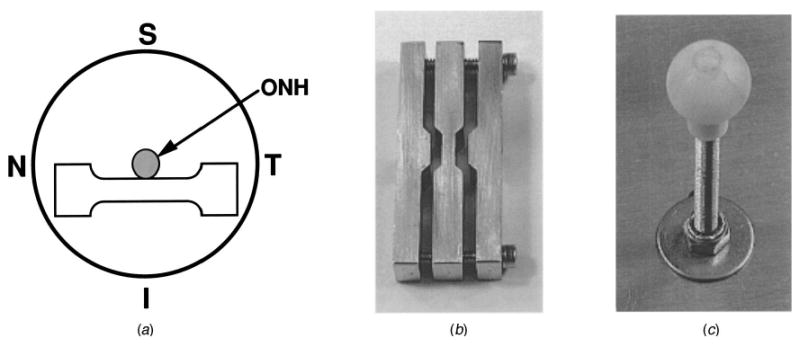
(A) Diagram of the posterior view of a scleral shell showing the orientation of a scleral tensile specimen from the inferior quadrant (similar specimens were generated in the superior, nasal, and temporal quadrants); (B) photograph of the tensile specimen cutting die, and (C) photograph of the scleral shell holding ball.

Material and Methods

Specimen Generation

A single scleral tensile specimen (Fig. 2A) was generated from each eye of mature New Zealand white rabbits (3–4 kg) and rhesus and cynomolgous monkeys (4.3–7.5 kg; 3–7 yrs old) as follows. Each animal was anesthetized with an intramuscular injection of ketamine/xylazine, and sacrificed with an intravenous sodium pentobarbital injection. Immediately following sacrifice, each eye was enucleated then cleaned of all extraorbital tissues, and the anterior chamber and vitreous were removed. Two anterior-to-posterior cuts from the limbus to the equator were made in the scleral shell on opposite sides of the globe. These cuts facilitated the shell being placed on a polyethylene ball corresponding to the size of the scleral shell (Fig. 2C).

The ONH was removed from the surrounding sclera with a 6-mm-diameter trephine (surgical hole punch) for use in another study, with care taken to include as little of the peripapillary sclera in the testing quadrant as possible (typically ≤1 mm). After trephination, the retina and choroid were separated from the scleral shell. A tensile specimen-cutting die (Fig. 2B), consisting of 3 mating stainless steel parts that compressed flexible razor blades into a precise dog-boned shape, was rotated over the surface of the scleral shell in a single, steady motion. Care was taken to orient the specimen cutter such that the gage length was centered on the optic nerve head and as close to the scleral canal as possible (Fig. 2A). This operation generated a precise tensile specimen of peripapillary sclera with a gage length of 8 mm, a gage width of 3 mm, and grip-end widths of 7 mm. Scleral thickness in the gage section of several specimens was measured immediately post-mortem under a microscope fitted with a micrometer scale. For the measured specimens, scleral thickness averaged approximately 750 μm in rabbits and 400 μm in monkeys, and that value was used to calculate cross sectional area for all specimens in the study. The specimens were kept wet with phosphate-buffered saline (PBS) for the 30 to 90 minutes that lapsed between the time of sacrifice and the start of the testing.

Specimen Mounting

Each scleral tensile specimen was inserted into custom soft tissue grips, which were developed to allow tensile testing of thin soft tissues without specimen slippage or failure at the grip interface (Fig. 3B). The grips were mounted in a specialized fixture, which maintained a grip-to-grip length of 20 mm and assured that each tensile specimen was inserted perpendicularly to the grip faces. Following loading of the specimen, the grips were secured to the test frame within a testing environment chamber (Fig. 3A), with the lower grip fixed and the upper grip pinned to a loading rod. A low-friction u-joint was integrated into the loading rod (Fig. 3A) to assure that only axial forces were transmitted to the specimen during loading. Care was taken to avoid applying any force to the specimen during the grip mounting process.

Fig. 3.

(A) Photograph of the testing environment chamber, and (B) a close-up photograph (inside the testing environment chamber) showing a dummy specimen mounted in the grips and in contact with the extensometer arms.

Testing Apparatus and General Methodology

All testing was performed in a custom testing environment chamber (Fig. 3A), which immersed the specimen in a fog of 37°C, isotonic, pH 7.4 PBS for the duration of each testing sequence. This chamber was mounted on a MTS Bionix 858 servo-hydraulic test frame (MTS, Inc.; Eden Prairie, MN), fitted with an integrated MTS Teststar II computer-based test controller and digital data acquisition system. A contact force extensometer (Fig. 3B) (MTS Model 632.32F) and a 250 N load cell (MTS Model 661.11A, in the 10 percent range) were used to measure strain and load, respectively. After a preload of approximately 0.08 N was applied, the extensometer was brought into contact with the central 5 mm of the gage length of the specimen with an approximate contact force of 3 g per arm, which was maintained for the duration of the test. No observable increase in the axial preload resulted from the mounting of the extensometer. Use of an extensometer allowed us to test in strain rate control, and assured that we obtained accurate measures of strain in the gage section of the specimen.

We chose to implement a stress relaxation-based protocol, which enabled us to measure strain directly from the specimen and pursue strain-rate controlled testing that would not be possible utilizing a displacement-based test. This is especially important given the highly viscous nature of scleral tissue, which makes calculating strain from displacement difficult. Also, strain-rate controlled testing assures that the testing protocol is applied identically for each specimen, which eliminates a potential source of error in the reported parameters.

Testing of Peripapillary Rabbit Sclera in Tension

For each of the two testing protocols (stress relaxation and tensile ramp to failure), peripapillary scleral tensile specimens were generated from the superior, inferior, nasal, and temporal quadrants of individual eyes as previously described. A total of 32 specimens (n = 8 per quadrant) were used in each test. Within each testing protocol group, testing quadrant was randomly assigned to the animals and eyes, as was the eye enucleation and testing order.

The material properties of rabbit sclera have been shown to be largely insensitive to strain rate (tested at 0.1, 1, and 10 percent/s) at low values of strain (below 4 percent) [21]. A strain rate of 1 percent/s was chosen for all testing, which has been shown to be fast enough to minimize viscous effects during the various tensile ramps, yet slow enough to minimize the difficulties inherent in strain-rate-controlled testing [21]. The tensile load and gage strain were recorded at 0.01 s intervals.

Preconditioning

After loading and mounting, each specimen was preconditioned with 10 cycles of 0–150 μm of grip-to-grip displacement at a rate of 150 μm/s in displacement control. This cyclic displacement yielded approximately 1 percent total strain amplitude.

Stress relaxation testing

After preconditioning, the specimens were subjected to a stress relaxation test consisting of a tensile ramp in strain rate control at a strain rate of 1 percent/s to 1 percent strain, with the ramp-ending displacement held for 1000 s.

Tensile ramp to failure testing

After preconditioning, the specimens were subjected to a tensile ramp to failure (or to a maximum of 20 percent strain) in strain rate control at a strain rate of 1 percent/s.

In the rabbits, the stress relaxation and tensile ramp to failure tests were performed in different groups of eyes, which allowed for the refinement of each testing protocol independently.

Testing of Peripapillary Monkey Sclera in Tension

In the testing of scleral specimens from monkey eyes, we combined these refined testing protocols into a 3-stage tensile test, which consisted of a two-phase preconditioning stage, followed by stress relaxation and tensile ramp to failure stages (Fig. 4), with each stage separated by a 360 second recovery period at zero displacement.

Fig. 4.

Diagram of the time course of the three-stage uniaxial tensile testing protocol applied to the monkey scleral specimens.

Sixteen monkeys were sacrificed as previously described and peripapillary scleral tensile specimens from the superior, inferior, nasal, and temporal quadrants (n = 6 specimens per quadrant) were tested as follows. After applying a 0.08 N tensile preload and mounting the extensometer, each specimen was subjected to the first phase of preconditioning, which consisted of 10 cycles of 0–150 μm of grip-to-grip displacement at a rate of 150 μm/s in displacement control, followed by a 360 s recovery period at zero displacement. The specimen was then subjected to a second preconditioning phase consisting of 10 cycles of 50–350 μm displacement at 175 μm/s, and rested again for 360 s. The second phase of preconditioning generated strain amplitudes of approximately 1 percent, and was performed to provide a cyclic loading regime that could be used for validation of future computational models of scleral tensile specimens. The specimen was then subjected to a stress relaxation test consisting of a tensile ramp in strain rate control at a strain rate of 1 percent/s to 1 percent strain, with the ramp-ending displacement held for 1000 s. Following a third 360 s recovery period at zero displacement, each specimen was subjected to a tensile ramp to failure (or a maximum of 20 percent strain) at a strain rate of 1 percent/s (Fig. 4). Data for tensile load and gage strain were recorded at 0.01 s intervals.

Analytical Methods

Linear viscoelastic theory incorporating a reduced relaxation function [22] was employed to characterize the quadrant-dependent viscoelastic properties of peripapillary sclera. Briefly, a viscoelastic material, when subjected to a step strain input, ε₀, exhibits a stress relaxation response that can be expressed as follows.

$$\sigma ({\epsilon }_0,t)=G(t){\sigma }^e({\epsilon }_0).$$ (1)

In this formulation, σ^e(ε₀) is the equilibrium elastic stress at t = ∞, which, in the present study, was assumed to obey Hooke's law of σ^e=E_∞ε₀, where E_∞ is Young's modulus at equilibrium (i.e., equilibrium modulus). G(t) is the time-dependent, reduced relaxation function, which satisfies G(∞) = 1.

The relaxation function most frequently used in soft tissue biomechanics is the continuous spectrum function, which was originally developed by Neubert [23] and popularized by Fung [22], and is:

$$G(t)=1+c\left[E_1\left(\frac{t}{{\tau }_L}\right)-E_1\left(\frac{t}{{\tau }_S}\right)\right],$$ (2)

where c is the spectral magnitude, τ_S and τ_L are the short-term and long-term relaxation time constants, respectively, and E₁ is the exponential integral function [24]. For the sake of computational efficiency, we employed the following discrete spectral function;

$$G(t)=1+\text{ln}\left(\frac{{\tau }_L}{{\tau }_S}\right)\frac{c}{n}\text{∑}_{i=1}^n{e}^{-t/{\tau }_i}.$$ (3)

In this discrete spectral relaxation formulation, n is the number of spectral time constants, and

$${\tau }_i={10}^{[\text{log}({\tau }_S)+(i-1)\Delta \tau ]}\text{where}\Delta \tau =\frac{\text{log}({\tau }_L)-\text{log}({\tau }_S)}{(n-1)}$$ (4)

and τ₁ = τ_S and τ_n = τ_L. The discrete spectral function described in Eqs. (3)–(4) converges to the continuous spectral function in Eq. (2) as n approaches infinity [25]. Unlike other discrete relaxation functions [22], the three characteristic parameters (c, τ_S, and τ_L) in the present discrete spectral function (Eq. (3)) can be uniquely defined and become identical to those of Eq. (2) regardless of n, as long as n exceeds the threshold value needed to satisfy convergence. In the present study, the minimum valve of n required for convergence was determined using chi squared (a measure of goodness of fit) in the regression algorithm as described below.

Using the present discrete relaxation function, the viscoelastic behavior of scleral specimens, when subjected to a step strain input, ε₀, will be represented by Eq. (1) as a stress relaxation with σ(0⁺) = [1 + c ln(τ_L/τ_S)]E_∞ε₀ and σ(∞) = E_∞ε₀. This allows us to determine the instantaneous modulus of the tissue, E₀₊ = σ(0⁺)/ε₀ = [1 + c ln(τ_L/τ_S)]E_∞, defined at time t = 0⁺.

Since the stress relaxation tests performed in the present study were conducted using a tensile ramp of 1 second duration at a strain rate of 1 percent/s instead of a step strain input [26], the stress response at time t will be expressed as

$$\sigma (t)={\int }_0^{t}G(t-\xi )\frac{\partial {\sigma }^e(\epsilon )}{\partial \epsilon }\frac{\partial \epsilon }{\partial \xi }d\xi$$ (5)

where

$$\epsilon (t)=\{\begin{array}{ll}\dot{\epsilon }t& \text{for}0\le t\le t_0\\ {\epsilon }_0& \text{for}{t}_0\le t\end{array}$$ (6)

and ε̇ = dε/dt = 0.01/s, t₀ =1 s, and ε₀ = 0.01. Hence, for a linear increase in strain at a finite rate, ε̇, beginning at t=0 and ending at t = t₀, the stress, according to Eqs. (5)–(6), becomes

$$\sigma (t)=\dot{\epsilon }{E}_{\infty }\left\{\text{ln}\left(\frac{{\tau }_L}{{\tau }_S}\right)\frac{c}{n}\text{∑}_{i=1}^n{\tau }_i(1-e^{-t/{\tau }_i})+t\right\}\text{for}0\le t\le t_{\text{0}}$$ (7)

$$\sigma (t)=\dot{\epsilon }{E}_{\infty }\left\{\text{ln}\left(\frac{{\tau }_L}{{\tau }_S}\right)\frac{c}{n}\text{∑}_{i=1}^n{\tau }_i(e^{t_0/{\tau }_i}-1)e^{-t/{\tau }_i}+t_0\right\}\text{for}{t}_{\text{0}}\le t$$ (8)

Equations (7) and (8) were fit simultaneously to the two stages of the experimental stress relaxation data (the tensile ramp and the relaxation phase) using the Levenberg-Marquardt nonlinear, least-squares algorithm [26,27], which yields unique estimates of c, τ_S, τ_L and E_∞ for a given value of n. In this regression analysis, chi squared was used as an objective function to determine the minimum n required for the parameters to converge to their unique, terminal values. The minimum value of n required to assure convergence varied from 2 to 4 for the rabbit specimens and 3 to 7 for the monkey specimens. No significant change in the estimated parameters resulted from increasing n beyond that required to minimize chi squared.

Statistical Analysis

An analysis of variance (ANOVA) was employed to compare the stress values obtained at the integer percentage values of strain (1,2,…,10 percent) for the 4 quadrants within each species group. A second ANOVA was used to determine the effects of testing quadrant on the dependent variables E₀₊, E_∞, τ_S and τ_L within each species. Confidence intervals were calculated using the standard error, which employs the pooled variance of all values analyzed within each ANOVA.

Results

Mean stress-strain curves for tensile ramps at a strain rate of 1 percent/s are plotted by peripapillary quadrant for rabbit and monkey sclera in Figs. 5 and 6, respectively (95 percent confidence bars). In rabbit sclera, we could not detect differences in these curves by quadrant at strains below 4 percent. However, at strains of 4 percent and above the stress-strain curves diverge, indicating that the stiffness of specimens from the inferior quadrant is greater than those from the other three quadrants at high levels of strain. In the monkey, we could detect no differences in the stress-strain curves from 0–10 percent strain by quadrant. The monkey sclera exhibited a bilinear stress-strain response, with a change in slope occurring in all quadrants at approximately 2 percent strain. This occurred to a lesser degree in rabbit sclera from the superior, nasal, and temporal quadrants surrounding the ONH, but was not observed in specimens from the inferior quadrant.

Fig. 5.

Mean stress-strain curves for peripapillary rabbit sclera from the superior, inferior, nasal, and temporal quadrants tested in uniaxial tension at a strain rate of 1 percent/s (95 percent confidence bars).

Fig. 6.

Mean stress-strain curves for peripapillary monkey sclera from the superior, inferior, nasal, and temporal quadrants tested in uniaxial tension at a strain rate of 1 percent/s (95 percent confidence bars).

The material properties (with 95 percent confidence intervals) of rabbit and monkey sclera are listed by quadrant, and overall in Tables 1 and 2, respectively. By ANOVA, none of the material property parameters were significantly different by quadrant within either species group. Sclera from monkey eyes exhibited a long-term relaxation time constant and instantaneous and equilibrium moduli that were significantly higher than those from rabbit eyes (P < 0.0001).

Table 1. Material Properties of Rabbit Sclera by Quadrant and Overall (95 percent confidence intervals).

	Quadrant
Parameter	Superior	Inferior	Nasal	Temporal	95 percent C.I.	Overall	95 percent C.I.
Instantaneous Modulus†, E0+ (MPa)	9.6	13.3	10.3	13.1	±2.4	11.6	± 1.1
Short-term Time Constant, τS (s)	0.567	0.695	0.447	0.461	±0.222	0.542	±0.144
Long-term Time Constant, τL (s)	70.3	61.3	47.6	52.5	±13.6	57.9	±6.3
Equilibrium Modulus, E∞ (MPa)	0.548	0.893	0.914	0.789	±0.323	0.786	±0.140

^†E₀₊ = [1 + c ln(τ_L/τ_S)]E_∞

Table 2. Material Properties of Monkey Sclera by Quadrant and Overall (95 percent confidence intervals).

	Quadrant
Parameter	Superior	Inferior	Nasal	Temporal	95 percent C.I.	Overall	95 percent C.I.
Instantaneous Modulus†, E0+ (MPa)	34.3	33.4	29.9	25.3	±5.8	30.7	±2.6
Short-term Time Constant, τS (s)	0.636	0.415	0.416	0.813	±0.540	0.571	±0.213
Long-term Time Constant, τ L (s)	209	156	126	222	±82	178	±35
Equilibrium Modulus, E∞ (MPa)	5.51	4.37	3.62	2.91	±2.36	4.10	±0.97

^†E₀₊ = [1 + c ln(τ_L/τ_S)]E_∞

The average stress relaxation response curves for each species are plotted in Fig. 7. These curves were generated using overall mean values for c, τ_S, τ_L, and E_∞ (Tables 1 and 2), coupled with the maximum number of spectral time constants observed within each species group (n = 5 for rabbit specimens and n = 7 for monkey specimens). Note the high degree of stress relaxation over the short duration of the test in both species, and the significantly higher instantaneous modulus, equilibrium modulus, and long-term relaxation time constant exhibited in monkey sclera when compared to the rabbit tissue.

Fig. 7.

Mean stress relaxation responses of rabbit and monkey peripapillary sclera (all quadrants combined). For a statistical comparison of the parameters used to generate these curves, see overall data in Tables 1 and 2.

Discussion and Conclusions

In this report, we employed experimental and analytical techniques to determine the viscoelastic material properties of peripapillary sclera from rabbit and monkey eyes. There are three primary results of this work. First, we detected no differences in the stress-strain curves of specimens from the four quadrants surrounding the ONH below strains of 4 percent in the rabbit and 10 percent in the monkey. From 4–10 percent strain, specimens from the inferior quadrant in the rabbit exhibited a significantly different stress-strain relationship than those from the other quadrants, with the inferior quadrant specimens being significantly stiffer than those from other quadrants. Second, we could detect no differences in the viscoelastic properties (tested at strains of 0–1 percent) of peripapillary sclera from the superior, inferior, nasal, and temporal quadrants surrounding the optic nerve head in either rabbit or monkey (P > 0.05), which supports our hypothesis that peripapillary scleral material properties are homogeneous. Finally, peripapillary sclera from monkey eyes exhibited a significantly higher instantaneous modulus, equilibrium modulus, and long-term relaxation time constant compared with rabbit eyes (P < 0.0001), which indicates that the rabbit sclera is not suitable as a model for the IOP-related behavior of monkey sclera.

In the rabbit, sclera from the inferior quadrant exhibits greater stiffness and absorbs more energy than that from the other three quadrants at strain levels above 4 percent (Fig. 5). In the rabbit, the posterior ciliary arteries (PCAs) that feed the choroid (the vascular layer immediately beneath the retina) and ONH pierce the sclera along the nasal-temporal axis just inferior to the scleral canal. This anatomical configuration places the majority of these arterial penetrations within the gage section of the inferior quadrant scleral tensile specimens. We hypothesize that in order to maintain sufficient arterial blood flow through these vessels, the sclera in this region must be relatively resistant to IOP-induced deformation. This may explain the relatively stiff and tough nature of the inferior peripapillary sclera at high strains when compared to that of other quadrants. In monkey and human eyes, on the other hand, the PCAs usually pierce the sclera nasal and temporal to the ONH but are not clustered in the inferior quadrant as observed in the rabbit [28,29], which may partially explain the lack of material property differences by quadrant at high strains in the monkey.

Sclera from both species exhibits quick stress relaxation and does not maintain a high equilibrium stress (Fig. 7). The average equilibrium stress observed at the termination of the stress relaxation test (t = 1000 s) is equivalent to IOPs of approximately 26 and 12 mm Hg in the monkey and rabbit, respectively [30]. Sclera is constantly under a pressure load and must have properties that allow the tissues to maintain that stress in equilibrium, and this finding is consistent with the other studies on the properties of rabbit sclera [31,32].

All previously reported testing of sclera, as well as that in this study, has been performed in vitro where the sclera was not supported by the surrounding extraocular tissues. There is evidence to suggest that extraorbital pressure in the rabbit is substantial (about 20 percent of IOP) and follows fluctuations in intraocular pressure [33]. The pressure gradient across the posterior scleral shell (within the orbit) is therefore lower than what IOP alone suggests. There is also the possibility that the extraorbital tissues provide a physical backstop against IOP-related, creep-driven expansion of the globe. This is likely a complex system, and further work is necessary to quantify the relationship between IOP, stress relaxation, creep, and the intraocular-to-extraocular pressure gradient in both species.

The load-bearing behavior of sclera from rabbits is significantly different from that of monkeys, with monkey sclera being much stiffer (both instantaneously and in equilibrium) and stress relaxing more slowly than sclera in the rabbit (Tables 1, 2). The noted material property differences may be due to interspecies differences in the extracellular matrix of the sclera. As a result, rabbit sclera is not suitable as a mechanical model of monkey sclera.

The results of this study are subject to the following limitations. First, for the purposes of calculating stress, we assumed scleral thicknesses of 750 μm and 400 μm in the rabbit and monkey, respectively, based on the measurement of a sample of the specimens. The sclera is composed of two layers, sclera and episclera. The episclera is a layer of loose connective tissues similar in appearance to the dense, load-bearing sclera. Our histologic studies have shown that separation of these two layers via dissection is extremely difficult, especially in fresh tissues [8,9]. With no methodology in place to distinguish between the load-bearing and loose connective tissue layers, accurate measurement of scleral thickness in fresh tissue is difficult. The estimates of scleral thickness we employed match well with the histologic measurements we report in perfusion-fixed monkey eyes [8,9]. We have no histomorphometric data for scleral thickness in the rabbit and are therefore forced to rely on the measurement of fresh tissues. This is a potential source of error, although comparisons between quadrants should be valid.

Second, the preload necessary to assure consistent mounting of the extensometer arms generated scleral stresses that are relatively high compared to normal levels of IOP. According to thin-walled pressure vessel theory [30], a uniaxial 0.08 N tensile preload is equivalent to IOPs of approximately 50 mm Hg in the rabbit and 40 mm Hg in the monkey. This is higher than the intraocular pressures of 8–18 mm Hg we measured in resting, anesthetized animals. Intraocular pressures of this magnitude are not without precedent, however. Coleman and Trokel [34] recorded an IOP of 110 mm Hg in a human subject during squint (hard, forced blink). Ku and Greene [31] reported that an eye rub induced an in vivo IOP of 150 mm Hg in a rabbit. Intraocular pressures over 40 mm Hg are not uncommon in monkey eyes with experimentally induced glaucoma [8,35].

Beginning our test with a preload may move the measured response out of the nonlinear, low modulus region of the stress-strain curve, which typically occurs at low values of stress [9,31]. This is evident in the linear nature of the stress strain curves seen in the tensile ramp to failure tests at low strains (Figs. 5, 6). This may also explain the fact that the instantaneous elastic modulus we report for rabbit sclera (Table 1) is higher than the elastic modulus reported previously [32,36]. However, this may also be due to the fact that we calculate the true instantaneous modulus, and all previously reported values likely underestimate the true modulus due to stress relaxation that occurs during any finite loading ramp. Our data support this notion, especially in light of the extremely fast relaxation of scleral tissue (Fig. 7).

Third, we utilized uniaxial tensile testing to ascertain the material properties of an anisotropic tissue, which has a predominant collagen and elastin fibril orientation based on location [6,37]. Our assumption of homogeneous properties is based on previous work on fibril orientation in the peripapillary region, where the fibrils follow a circular path ringing the scleral canal [6,37]. Therefore if tensile specimens are obtained from the peripapillary region, with the axial direction of their gage section oriented tangent to the scleral canal, one could argue that the fibrils are oriented axially in the central 5 mm gage section of each specimen, irrespective of quadrant. Hence, uniaxial testing of tensile specimens from the peripapillary region should give valid estimates of the material properties of sclera in the direction of predominant fibril orientation. Also, the stiffness of sclera in other directions (not parallel to the predominant fibril orientation) will likely be lower than that reported here. Uniaxial testing does not allow for characterization of the anisotropic aspects of scleral properties, but the included material property estimates will serve as a basis for future biaxial testing.

This work was performed, in part, to develop the experimental and analytical methodologies necessary to perform subsequent studies on the peripapillary scleral material properties in humans. In addition to reporting the material properties of rabbit and monkey sclera in the physiologic strain range, we have gained insights into the quadrant-dependent behavior of peripapillary sclera at physiologic and pathophysiologic levels of strain. The estimates of the material properties listed in Tables 1 and 2 will provide a foundation upon which to base future studies on the mechanical behavior of the sclera. In addition, these viscoelastic material property estimates will be incorporated into finite element models of the posterior scleral shell and ONH in monkeys, which are being constructed [38] to further investigate the role of IOP in glaucoma.