SDU: A Semidefinite Programming-Based Underestimation Method for Stochastic Global Optimization in Protein Docking

Abstract

This paper introduces a new stochastic global optimization method targeting protein-protein docking problems, an important class of problems in computational structural biology. The method is based on finding general convex quadratic underestimators to the binding energy function that is funnel-like. Finding the optimum underestimator requires solving a semidefinite programming problem, hence the name semidefinite programming-based underestimation (SDU). The underestimator is used to bias sampling in the search region. It is established that under appropriate conditions SDU locates the global energy minimum with probability approaching one as the sample size grows. A detailed comparison of SDU with a related method of convex global underestimator (CGU), and computational results for protein-protein docking problems are provided.

I. INTRODUCTION

This work is motivated by a fundamental and challenging problem in computational structural biology. Proteins interact with each other and with other chemical entities in the cell to form complexes consisting of two (or more) macromolecules. Protein-protein interactions play a central role in metabolic control, signal transduction, and gene regulation. Proteins also interact with a large number of small molecules that serve as substrates, inhibitors, or cofactors in metabolic reactions, as well as with external compounds acting as drugs in modulating biological behavior. Determining the three-dimensional (3-D) structure of a complex from the atomic coordinates of two or more interacting molecules is known as the molecular docking problem. Experimental techniques -x-ray crystallography or nuclear magnetic resonance (NMR)– can provide such 3-D structures but are time-consuming, expensive, and not universally applicable as many molecular complexes are short-lived and exist only under well defined cellular conditions. As a result, solving these problems computationally is critical and has attracted a lot of attention.

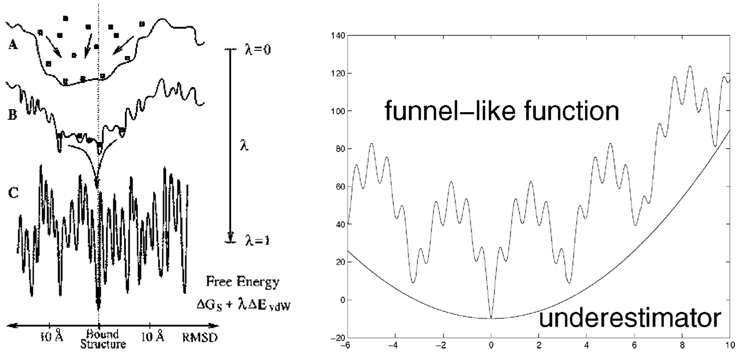
Docking two proteins can be seen as a control problem as one has to control one of them as it approaches and docks with the other; this has parallels with problems arising in robot arm manipulation [1], [2]. From a static point of view, thermodynamic principles imply that proteins bind in a way that minimizes the Gibbs free energy of the complex. These energy functions have multiple deep funnels and a huge number of local minima of less depth that are spread over the domain of the function (see Fig. 1). This “complexity” of the energy landscape is perhaps best articulated in the Levinthal paradox [3]: The probability that nature could find the native 3-D structures (or “conformations”) by random search seems uncomfortably close to zero. More recently though, it was recognized that the funnel-like shape of the energy function may explain why proteins bind with other molecules very fast and in so doing they may follow multiple pathways on the energy surface (see [4]). In this paper, we introduce a new optimization method for solving docking problems. It is exactly this funnel-like shape of the energy function we set out to exploit.

Fig. 1.

(Left) Protein docking funnels and the operation of the docking method SmoothDock [8]. (Right) A funnel-like shaped function and a quadratic function underestimating the surface spanned by the local minima.

In general, the energy functions include forces that act in different space-scales, resulting in multi-frequency behavior, and leading to a huge number of local minima caused by high-frequency terms. Even though some global optimization methods (see [5]) have been useful in the related problem of protein folding, it appears that only simulated annealing has been consistently used in docking. Specifically, Baker et al. [6] employ simulated annealing on a progressively improving approximation of the energy function. This has been fairly effective but it is computationally expensive and, thus, applicable to relatively small problem instances. A number of other recent approaches have attempted, with some success, to use the funnel-like shape to guide the global search to the vicinity of the global minimum [e.g., the semiglobal simplex (SGS) by Dennis and Vajda [7], and SmoothDock by Camacho and Vajda [8]]. Of most, relevance to this paper is the convex global underestimator (CGU) method of Phillips et al. [9] where convex canonical quadratic underestimators are used to approximate the envelope spanned by the local minima of the energy function. It has been shown that CGU does not perform well in some cases and that its performance deteriorates as the dimension of the search space increases [7]. We contend that a critical reason for this poor performance is the restricted class of underestimators used in CGU. This restriction amounts to a lack of flexibility in capturing the overall shape of the funnels and hence an inability to locate promising regions.

We use the same strategy of using quadratic convex functions to underestimate the envelope spanned by the local minima of the energy function. However, we consider the class of general convex quadratic functions for underestimation. In this case, given a finite set of local minima, finding the optimal underestimator amounts to solving a semidefinite programming (SDP) problem, hence the term SDU. The dual to this problem involves linear matrix inequalities (LMIs) which have found ubiquitous use in control theory lately. Another key contribution of the new method we introduce is the use of a biased exploration strategy that is guided by the underestimator. We show, theoretically as well as experimentally, that SDU outperforms CGU, often significantly. Moreover, we show that SDU will indeed (probabilistically) converge to the global minimum when applied to a general class of funnel-shaped functions as the number of local minima used for underestimating the energy function grows. This suggests that SDU has the potential to be useful in solving molecular docking problems. A number of numerical results, some involving real instances of the protein-protein docking problem, reinforce this conclusion.

The rest of this paper is organized as follows. Section II presents background material on docking and surveys various approaches. Section III presents the SDU method. Comparisons with CGU are in Section IV. SDU’s convergence properties are discussed in Section V. Numerical results for a set of test functions are in Section VI. Some results on docking proteins are discussed in Section VII. We end with conclusions in Section VIII.

Notational Conventions

Throughout this paper, all vectors are assumed to be column vectors. We use lower case boldface letters to denote vectors and for economy of space we write x = (x₁,…,x_n) for the column vector x.x′ denotes the transpose of x, 0 the matrix (or vector) of all zeroes, e the vector of all ones, I the identity matrix, and e_i the ith unit vector. For any vector x we write ‖x‖₁ for the L1 norm, i.e., ${\Vert \mathbf{x}\Vert }_1={\displaystyle {\sum }_{i=1}^n\left|x_i\right|}$, and ‖x‖ for the Euclidean norm. We use upper case boldface letters to denote matrices and write $\mathbf{A}={(A_{i,j})}_{i,j=1}^n$ for the matrix A with (i, j)th element equal to A_i,j. We denote by diag(x) the diagonal matrix with elements x₁,…,x_n in the main diagonal and zeroes elsewhere. We also denote by diag(A, B) the block diagonal matrix with matrices A and B in the main diagonal and zeroes elsewhere. We define

$$\mathbf{F}•\mathbf{Y}\triangleq {\displaystyle \sum _{i=1}^n{\displaystyle \sum _{j=1}^n{F}_{i,j}{Y}_{i,j}}}$$ (1)

which is the Frobenius inner product of matrices. Finally, for any event 𝒮, 1 {𝒮} denotes its indicator function.

II. PRELIMINARIES AND BACKGROUND

In this section, we provide some biological background on the docking problem in order to establish the appropriate context for the optimization methodology we introduce.

State-of-the-art protein-protein docking approaches start by identifying conformations with good surface/chemical complementarity where the two interacting proteins are considered rigid bodies. Accordingly, the problem of forming a complex by docking one protein—the ligand—to the other—the receptor—has parallels with problems arising in rigid body motion and robot arm manipulation (see, e.g., Murray et al. [1], Gwak et al. [2]). In particular, one has to control the ligand as it approaches and docks with the receptor. The ligand’s relative position lies in the Euclidean group of rigid-body motion, SE(3), which is the semidirect product of ℝ³ (translations) and the rotation group SO(3). The dynamics of the ligand’s approach to the receptor play an important role in nature but are hard to model (and computationally prohibitive to simulate) in the time-scale they evolve. The problem is further complicated by the fact that proteins are not rigid bodies and experience conformational changes as they bind (mostly the side-chains on the interface). The protein-protein docking literature (e.g., [8] and the references therein) is predominantly treating the docking problem as a static problem and this is the view we will initially adopt for this problem.

Protein-protein docking approaches initially screen conformations by various measures of surface complementarity which can be efficiently computed using fast Fourier correlation techniques (FFTs). However, when docking unbound conformations these methods yield many “false positives” (i.e., conformations that have good score but are far from the native one). An effective approach used by Comeau et al. [10] is to cluster the conformations obtained by the FFT filtering based on how close they are. (A common metric of distance between conformations is the root mean square deviation (RMSD) of their atomic coordinates). Clustering identifies low free energy regions (funnels) one needs to further explore. We will be referring to the problem of exploring a funnel as the medium-range problem. The proposed SDU method aims at solving this problem by exploring the funnel shape of the energy function. Next we review key properties of the free energy functions.

A. Free Energy and its Mathematical Properties

Free Energy Models

At fixed temperature and pressure, a complex of two molecules adopts the conformation that corresponds to the lowest Gibbs free energy of the system that includes the component molecules and the solvent—usually water—surrounding them. Thus, in docking calculations the natural target function to minimize is an approximation of the Gibbs free energy, G^RL, of the receptor-ligand complex, or that of the binding free energy, ΔG. In particular, ΔG = G^RL − G^R − G^L, where G^R and G^L are the free energies of the receptor and ligand, respectively, and both G^R and G^L are independent of the conformation of the complex; thus, minimizing G^RL reduces to minimizing ΔG.

We use free energy evaluation models that combine molecular mechanics with continuum electrostatics and empirical solvation terms [11]. For protein docking applications, the binding free energy can be approximated as

$$\mathrm{\Delta }G=\mathrm{\Delta }{E}_{\mathit{\text{elec}}}+\mathrm{\Delta }{G}_{\mathit{\text{des}}}^{*}-T\mathrm{\Delta }{S}_{\mathit{\text{sc}}}+\mathrm{\Delta }{E}_{\text{vdw}}$$ (2)

where ΔE_elec is the change in electrostatic energy upon binding, ΔE_vdw is the change in van der Waals energy, and $\mathrm{\Delta }{G}_{\mathit{\text{des}}}^{*}$—the desolvation free energy—is associated with the removal of the solvent from the interacting surfaces of the protein and ligand, where the * denotes that it includes the change in the solute-solvent van der Waals energy. The entropy term, −TΔS_sc, accounts for the decrease in entropy experienced by the interface side chains upon binding.

Multifrequency Behavior

The free energy function can be regarded as the sum of three components with different frequencies. First, the following “smooth” component

$$\mathrm{\Delta }{G}_s=\mathrm{\Delta }{E}_{\text{elec}}+\mathrm{\Delta }{G}_{\mathit{\text{des}}}-T\mathrm{\Delta }{S}_{\mathit{\text{sc}}}$$ (3)

changes relatively slowly along any reaction path, where the desolvation free energy ΔG_des does not include the solute-solvent van der Waals term. The full contribution of the desolvation forces is estimated by the atomic contact potential (ACP) [12], where the ACP potential includes the self-energy change on desolvating charge or polar atom groups and the side chain entropy loss, i.e., ΔG_ACP = ΔG_des − TΔS_sc. ΔG_ACP is much less sensitive to structural perturbations than ΔE_vdw and ΔE_elec. The electrostatic energy ΔE_elec changes with an intermediate frequency, and the frequency of change is very high for ΔG_vdw. Thus, the van der Waals component is essentially a high frequency noise, because on its own it carries very little information about the distance from the native state.

Funnel-Like Shape

As discussed in Section I, the concept of the funnel-shaped energy landscapes (see Fig. 1) has had a significant impact on understanding protein folding and docking. This behavior has a physical explanation. Due to the term ΔE_vdw, the free energy function defined by (2) exhibits high sensitivity to structural perturbations. In addition, in any conformation without steric overlaps the van der Waals energy term is favorable, resulting in a number of local minima. Since most random perturbations yield overlaps, the local minima are separated by high energy barriers. In the conformations without overlaps, the solute-solute and solute-solvent interfaces are equally well packed, and thus the intermolecular van der Waals interactions in the bound state are largely balanced by solute-solvent interactions in the free state. Therefore, restricting consideration to such conformations, both ΔE_vdw and the van der Waals contributions to the desolvation free energy can be removed, and the binding free energy is reduced to the smooth components described by (3). Thus, in local minima in which the internal and van der Waals terms are close to zero, the free energy surface is essentially determined by the “smooth” free energy component ΔG_s.

B. Implications for Global Optimization and Our Method

Summarizing the discussion thus far it is evident that the free energy function in (2) has a huge number of local minima caused by high-frequency terms; primarily the van der Waals term. Even if one ignores changes in the interface side-chains, local minimization in SE(3)[2] enhanced with multistart would have to be quite lucky to approach a global minimum in some reasonable time. Generic global optimization approaches (e.g., those supported by GAMS [13]) typically require some regularity conditions (e.g., twice continuously differentiable functions) and are not designed for minimizing complex free energy functions having a huge number of local minima. A deterministic branch-and-bound global optimization method, the αBB method (see [5]), has been a part of a successful protein-folding approach [14] but it can be costly since it systematically explores all of the search region. The same will be true for other deterministic approaches. In fact, this is part of the motivation of the hybrid approach by Klepeis et al. [15] that combine αBB with a randomized search approach using ideas from genetic algorithms. To the best of our knowledge, the only systematic optimization method consistently applied in protein-protein docking is simulated annealing [6]. The CGU method [9], which motivated our work, has also been used in protein folding.

Fortunately, the funnel-like shape of the energy function can provide some guidance. Suppose we have identified (by FFT filtering and clustering) a number of conformations in the native energy funnel and we seek to determine the native conformation. The low-frequency energy terms [cf. (3)] form a smooth function which can often be well approximated by a convex quadratic. To exploit this structure we work on the envelope surface spanned by the set of local minima. This surface inherits the smooth behavior of the low-frequency energy terms. More specifically, we generate a large number of local minima and construct a convex quadratic function that forms the tightest underestimator of all of them. This quadratic function suggests the location of the deep energy valley containing the native structure. We use this information to iteratively refine our search. We note that this approach does not need access to individual energy terms; it only requires access to a program evaluating ΔG.

III. SDU: SEMIDEFINITE UNDERESTIMATOR METHOD

SDU consists of two key components: i) underestimating the surface spanned by the local minima [see Fig. 1 (right)], and ii) using the underestimator to guide further exploration.

A. Constructing an Underestimator

Let us denote by f : ℝⁿ → ℝ the free energy function we seek to minimize and assume we have obtained a set of K local minima ϕ¹,…,ϕ^K of f(·). We are interested in constructing a convex quadratic function U(ϕ) that underestimates f(·) at all local minima ϕⁱ, i = 1,…,K. Let

$$U(\mathit{\varphi })\triangleq \mathit{\varphi \prime }\mathbf{Q}\mathit{\varphi }+\mathbf{b\prime }\mathit{\varphi }+c$$

where Q ∈ ℝ^n×n is positive semidefinite (hence, U(·) is convex), b ∈ ℝⁿ, and c is a scalar.

Using an L1 norm as a distance metric the problem of finding the tightest possible such underestimator U(·) can be formulated as follows:

$$\begin{array}{cc}\text{min}\hfill & {\displaystyle \sum _{j=1}^K(f({\mathit{\varphi }}^j)-c-{\mathit{\varphi }}^{\mathit{j\prime }}\mathbf{Q}{\mathit{\varphi }}^j-\mathbf{b\prime }{\mathit{\varphi }}^j)}\hfill \\ \hfill & \text{s.t.}f({\mathit{\varphi }}^j)\ge c+{\mathit{\varphi }}^{\mathit{j\prime }}\mathbf{Q}{\mathit{\varphi }}^j+\mathbf{b\prime }{\mathit{\varphi }}^j,j=1,\dots ,K,\mathbf{Q}⪰0\hfill \end{array}$$ (4)

where the decision variables are Q, b, and c, and “⪰ 0” denotes positive semidefiniteness.

Let now introduce vectors b⁺, b⁻ ≥ 0, scalars c⁺,c⁻ ≥ 0 satisfying b = b⁺ − b⁻ and c = c⁺ − c⁻, and slack variables s = (s₁,…,s_K). Define the block diagonal matrix

$$\mathbf{Y}\triangleq \text{diag}(\mathbf{Q},\text{diag}({\mathbf{b}}^{+}),\text{diag}({\mathbf{b}}^{-}),c^{+},c^{-},\text{diag}(\mathbf{s})).$$ (5)

Define F₀ ≜ diag(diag(0), −diag(e)), F_j ≜ diag(ϕ^j ϕ^j′, diag(ϕ^j), −diag(ϕ^j), 1, −1, diag(e_j)), for all j = 1,…,K, where 0 is the (3n + 2)-dimensional zero vector, e is the K-dimensional vector of ones, and e_j is the jth unit vector. Let also E_i,j denote the (3n+K+2)×(3n+K+2) matrix with all elements equal to zero except the (i,j)th element which is equal to 1. Then, (4) can be written:

$$\begin{array}{c}(\mathbf{\text{SDP}}-\mathbf{P})\text{max}{\mathbf{F}}_0•\mathbf{Y}\hfill \\ \text{s.t.}{\mathbf{F}}_j•\mathbf{Y}=f({\mathit{\varphi }}^j),j=1,\dots ,K\hfill \\ {\mathbf{E}}_{i,j}•\mathbf{Y}=0,i=n+1,\dots ,3n+K+2,j=1,\dots ,i-1\hfill \\ \mathbf{Y}⪰0\hfill \end{array}$$ (6)

where the decision variable is the matrix Y. Problem (SDP-P) in (6) is a semidefinite programming (SDP) problem (see [16] or [17]). SDP problems can be solved efficiently using interior-point methods [16]. General purpose solvers for SDP problems are readily available (e.g., [18]).

The dual to (SDP-P) in (6) is the problem

$$\begin{array}{cc}(\mathbf{\text{LMI}}-\mathbf{D})\hfill & \text{min}{\displaystyle \sum _{j=1}^K{x}_{j}f({\mathit{\varphi }}^j)}\hfill \\ \hfill \text{s.t.}& \mathbf{Z}={\displaystyle \sum _{j=1}^K{x}_j{\mathbf{F}}_j+{\displaystyle \sum _{i=n+1}^{3n+K+2}{\displaystyle \sum _{j=1}^{i-1}{w}_{i,j}{\mathbf{E}}_{i,j}-{\mathbf{F}}_0}}}\hfill \\ \hfill & \mathbf{Z}⪰0\hfill \end{array}$$ (7)

where the decision variables are the x_j’s and w_i,j’s. Problem (LMI-D) can be seen as the problem of minimizing a linear function subject to a linear matrix inequality (LMI). The following theorem summarizes the construction of the underestimator.

Theorem III.1

Consider a function f : ℝⁿ → ℝ and a set of local minima ϕ¹,…,ϕ^K of f(·). Let (Q,b⁺,b⁻,c⁺,c⁻,s) form an optimal solution Y of Problem (SDP-P) in (6), where Y is defined as in (5). Let U(ϕ) ≜ ϕ′Qϕ+(b⁺ − b⁻)′ϕ + (c⁺ − c⁻). Then U(·) satisfies f(ϕ^j) ≥ U(ϕ^j) for all j = 1,…,K, while minimizing ‖(f(ϕ¹),…,f(ϕ^K)) − (U(ϕ¹),…,U(ϕ^K))‖₁. Moreover, the dual to Problem (SDP-P) is the LMI problem (LMI-D) in (7).

Hereafter, we will say that a function U(·) satisfying the statement of Theorem III.1 underestimates f(·) at points ϕ¹,…,ϕ^K. Fig. 1 (Right) illustrates such an underestimator.

B. Sampling

Suppose we are seeking the native conformation in some region ℬ. Using a set of local minima ϕ¹,…,ϕ^K ∈ ℬ of f(·) we construct an underestimator U(·) as described in Section III-A. Depending on the samples we used, and assuming that the constructed underestimator reflects the general structure of f(·), the global minimum of U(·), say ϕ^P, is in the vicinity of the global minimum of f(·). We will be referring to ϕ^P as the predictive to conformation.

Clearly, the distance of the predictive conformation from the native one depends on whether the underestimator is constructed using a sufficiently rich set of local minima. However, even if that is the case, locating the global minimum is difficult since van der Waals interactions create a large enough number of local minima around the native conformation. Our strategy is to sample in the area around ϕ^P such that conformations close to ϕ^P are more likely to be selected. In addition, conformations with high enough energy can safely be ignored. This can be achieved by using the following probability density function (pdf) in ℬ:

$$g(\mathit{\varphi })=\frac{U(\mathit{\varphi })-U_{\text{max}}}{{\int }_{\mathcal{B}}(U(\mathit{\varphi })-U_{\text{max}})d\mathit{\varphi }}\triangleq \frac{U(\mathit{\varphi })-U_{\text{max}}}{A},\mathit{\varphi }\in \mathcal{B}$$

where U_max = max_ℬ U(ϕ) and A denotes the integral in the denominator.

To generate random samples in ℬ using the above pdf we will use the so called acceptance/rejection method. Let h(ϕ) = 1/V be the uniform pdf in ℬ where V = ∫_ℬ dϕ. Notice that

$$g(\mathit{\varphi })\le \frac{V(U({\mathit{\varphi }}^P)-U_{\text{max}})}{A}h(\varphi ),\forall \mathit{\varphi }\in \mathcal{B}$$

and set R(ϕ) equal to the ratio of the left hand side over the right-hand side of the above, i.e.,

$$R(\mathit{\varphi })\triangleq \frac{U(\mathit{\varphi })-U_{\text{max}}}{U({\mathit{\varphi }}^P)-U_{\text{max}}}.$$

In order to discard high energy conformations we are interested in sampling points in ℬ with associated probability density in some interval [ζ,1], where ζ ∈ [0,1). The algorithm in Fig. 2 outputs such a sample point. To see that notice that in Step 1 we generate uniformly distributed samples in the set {(x,y) | x ∈ ℬ,y ∈ [ζ,1]}. The rule of Step 2 accepts uniformly distributed samples in {(x,y) | x ∈ ℬ,ζ ≤ y ≤ g(x)}. Thus, the output ϕ of the algorithm is distributed in ℬ according to g(·).

Fig. 2.

Algorithm generating a sample in ℬ drawn from g(·) with associated density in [ζ,1].

We finally note that the algorithm in Fig. 2 requires knowing U_max. In many cases, this is straightforward to obtain. Consider for instance the case where ℬ is a polyhedron; one special case of practical interest is when ℬ is a box set of the type {x | l_i ≤ x_i ≤ υ_i, i = 1,…,n}. Then, since U(·) is convex it achieves its maximum at an extreme point of ℬ. Alternatively, one can use an estimate of U_max, e.g., max_i U(ϕ_i).

C. The SDU Algorithm

We now have all the ingredients to present our SDU algorithm. The algorithm seeks a global minimum of f(·) in some region ℬ of the conformational space; it is presented in Fig. 3. Throughout the algorithm, we maintain a set ℒ of interesting local minima obtained so far including the best such local minimum denoted by ϕ^G. The evolution SDU depends on the parameters K,ζ ∈ [0,1], m and ϵ, and on the way we define the neighborhood 𝒩(ϕ^P) in Step 5. These will be appropriately tuned in every problem instance.

Fig. 3.

SDU algorithm.

A couple of remarks on the proposed SDU algorithm are in order. The algorithm combines exploration with focalization in energy favorable regions of the conformational space (energy funnels). The exploration is in fact biased towards these energy favorable funnels. This is intended to avoid computationally expensive exploration in areas of the conformational space that are not likely to contain the native structure.

We should point out that we make no claims that SDU converges to the global minimum of f(·). In fact, it is straight-forward to see that it will not find the global minimum if we do not use enough local minima to determine the underestimator or when f(·) is arbitrary and does not have a funnel-like shape. However, later in the paper we will provide arguments that (probabilistically) guarantee convergence for funnel-like functions under a suitable set of conditions.

IV. THE IMPORTANCE OF THE UNDERESTIMATOR’S STRUCTURE

Next, we review some earlier work, study its limitations, and assess the relationships with SDU. Let us consider the SDU algorithm under the following key modifications.

1. Underestimation: In deriving U(·) impose the constraint that Q is a diagonal positive semidefinite matrix. Then the semidefinite constraint can be replaced by a non-negativity constraint for all diagonal entries. It follows that Problem (SDP-P) can be reformulated as a linear programming problem (LP) which can be easily solved.

2. Sampling: Replace our biased sampling with random (uniform) sampling in the neighborhood of 𝒩(ϕ^P) of ϕ^P.

The resulting method is the so called convex global underestimator (CGU) method by Phillips et al. [9] for minimizing funnel-like free energy functions in molecular modeling problems. We will argue that these two differences with our proposed SDU drastically affect the performance of the corresponding optimization method. In particular, limiting the underestimator search to the class of canonical parabolas substantially reduces the efficiency and accuracy of CGU for general problems where the surface spanned by the local minima is not typically aligned with the canonical coordinates defining the underestimating parabola. Dennis and Vajda [7] report many such cases where CGU performs poorly. Some attempts in addressing this limitation have been made by Rosen and Marcia [19] but again handling special cases.

A. Comparing the CGU and SDU Underestimating Approaches

As we discussed in Section III, a quadratic underestimator will not be informative if either i) f(·) is not funnel-shaped and the envelope of local minima can not be well approximated by a convex quadratic, or ii) if we do not use a rich enough set of local minima in constructing U(·). In the following we wish to remove these two potential sources of poor performance in order to better assess the underestimating power of CGU and SDU. More specifically, we consider the “ideal” case of underestimating a convex quadratic given by $f(\mathbf{t})=\mathbf{t\prime }\overline{\mathbf{Q}}\mathbf{t}+\overline{\mathbf{b}}\prime \mathbf{t}+\overline{c},\text{where}\overline{\mathbf{Q}}⪰0$. We assume that i) an infinite number of sample points of f(·) in some compact sampling region ℬ is at our disposal when we construct the underestimator, and ii) f(·) is continuous on ℬ. The construction of the underestimator based on utilizing all sample points in ℬ can be formulated as the following (infinite-dimensional) optimization problem:

$$\text{min}{\displaystyle {\int }_{\mathrm{t}\in \mathcal{B}}(f(\mathbf{t})-U(\mathbf{t}))d\mathbf{t}\text{s.t.}f(\mathbf{t})\ge U(\mathbf{t}),\mathbf{t}\in \mathcal{B}}$$ (8)

where the decision variables are the (yet unspecified) parameters defining U(t).

Suppose first that we use the SDU underestimating approach and seek to construct a function U(t) = t′Qt + b′t + c, where Q ⪰ 0. Consider the problem in (8) for such a U(t). The next proposition is immediate.

Proposition IV.1

SDU can underestimate f(·) exactly, in particular, $(\mathbf{Q},\mathbf{b},c)=(\overline{\mathbf{Q}},\overline{\mathbf{b}},\overline{c})$ is an optimal solution of (8).

We next consider the CGU underestimation approach. Specifically, we seek to construct a function U(t) = t′Dt + b′t + c, where D = diag(d₁,…,d_n) and d_i ≥ 0 for i = 1,…,n. Consider the problem in (8) for such a U(t). For simplicity of exposition let us assume that the search region ℬ is the hypercube defined as ℬ = ℬ₁ × … × ℬ_n where ℬ_i = [l_i, u_i] and u_i − l_i = T for all i = 1,…n. We denote $\mathbf{a}(\mathbf{t})=(t_1^2,\dots ,t_n^2,t_1,\dots ,t_n,1)$,

$$\begin{array}{c}\mathbf{h}=({\displaystyle {\int }_{t_1\in {\mathcal{B}}_1}\frac{t_1^{2}d{t}_1}{T}},\dots ,{\displaystyle {\int }_{t_n\in {\mathcal{B}}_n}\frac{t_n^{2}d{t}_n}{T}},{\displaystyle {\int }_{t_1\in {\mathcal{B}}_1}\frac{t_{1}d{t}_1}{T}},\hfill \\ \hfill \dots ,{\displaystyle {\int }_{t_n\in {\mathcal{B}}_n}\frac{t_{n}d{t}_n}{T}},1)\end{array}$$

and z = (d₁,…,d_n,b₁,…,b_n,c). Then, after some algebra, (8) becomes equivalent to

$$(\mathbf{\text{LSIP}}-\mathbf{P})\text{max}\mathbf{h\prime }\mathbf{z}\text{s.t.}\mathbf{a\prime }(\mathbf{t})\mathbf{z}\le f(\mathbf{t}),\mathbf{t}\in \mathcal{B}$$ (9)

where z is the decision vector. Note that (LSIP-P) involves an infinite number of constraints. A problem with such a structure is known as the linear semi-infinite programming (LSIP) problem (see [20]). Its dual can be formulated in measure space as follows:

$$\begin{array}{c}(\mathbf{\text{LSIP}}-\mathbf{D})\text{min}{\displaystyle {\int }_{\mathcal{B}}f(\mathbf{t})d\mu (\mathbf{t})}\hfill \\ \hfill \text{s.t.}{\displaystyle {\int }_{\mathcal{B}}\mathbf{a}(\mathbf{t})d\mu (\mathbf{t})=\mathbf{h},\mu \in M^{+}(\mathcal{B})}\end{array}$$ (10)

where M⁺(ℬ) denotes the set of non-negative regular Borel measures on ℬ.

1) Approximate Problem Converges to LSIP

Next we explore the relationship of the underestimator obtained by solving (LSIP-P) in (9) to the underestimator obtained as in Section III, namely, by using the function values f(t¹),…,f(t^K) at a set of samples t¹,…,t^K from ℬ.

We introduce some additional terminology and notation. Let M_2n+1 be the cone generated by a(t) for t ∈ ℬ, i.e., M_2n+1 = {w | w = ∫_ℬ a(t)dμ(t), μ ∈ M⁺(ℬ)}. We denote by int(M_2n+1) the interior of M_2n+1. We also denote by $L_{\ge }^P(\mathbf{h},\theta )$ the level sets of the (primal) problem (LSIP-P), in particular, $L_{\ge }^P(\mathbf{h},\theta )=\{\mathbf{z}|\mathbf{a\prime }(\mathbf{t})\mathbf{z}\le f(\mathbf{t}),\forall \mathbf{t}\in \mathcal{B};\mathbf{h\prime }\mathbf{z}\ge \theta \}$. We will say that the primal (LSIP-P) is consistent if it has a feasible solution. We will say that (LSIP-P) is superconsistent if the interior of the feasible set is non-empty, that is, if there exist z* such that a′ (t)z* < f(t) for all t ∈ ℬ (this is Slater’s condition). Similarly, we will say that the dual (LSIP-D) is consistent if h ∈ M_2n+1; the dual will be termed superconsistent if h ∈ int(M_2n+1).

Lemma IV.2

Assume that (LSIP-P) is consistent. Then, (LSIP-D) is superconsistent and all primal level sets $L_{\ge }^P(\mathbf{h},\theta )$ are bounded.

Proof

Recall that we have assumed ℬ to be compact and f(·) continuous on ℬ. We will first show that (LSIP-D) is superconsistent. To that end, note that the uniform measure in ℬ is a feasible solution of (LSIP-D), which implies that h ∈ M_2n+1. Furthermore, the boundary of M_2n+1 consists of vectors a(t*) for some t* ∈ ℬ. Observe that h is not on the boundary, i.e., h ∈ int(M_2n+1) which establishes the superconsistency of (LSIP-D). Using a result from [20, Th. 6.11] the boundedness of all primal level sets follows.

Next consider an approximate finite problem constructed from (LSIP-P) by only enforcing a finite number of constraints, say for t¹,…,t^K ∈ ℬ. More generally, let $\overline{\mathcal{B}}\subset \mathcal{B}$ be a finite subset of ℬ and form the LP

$$(\mathbf{\text{LP}}-\mathbf{P})\text{max}\mathbf{h\prime }\mathbf{z}\text{s.t.}\mathbf{a\prime }(\mathbf{t})\mathbf{z}\le f(\mathbf{t}),\mathbf{t}\in \overline{\mathcal{B}}$$ (11)

which can be seen as a finite approximation of (LSIP-P). Define $d(\overline{\mathcal{B}})={\text{max}}_{\mathbf{t}\in \mathcal{B}}{\text{min}}_{\overline{\mathbf{t}}\in \overline{\mathcal{B}}}\Vert \mathbf{t}-\overline{\mathbf{t}}\Vert$ as a metric of density of $\overline{\mathcal{B}}$ in ℬ. Then, the boundedness of all (LSIP-P) level sets suffices to guarantee the convergence of the (LP-P) solutions to the (LSIP-P) solutions. The result, which is from [20], is provided in the following theorem.

Theorem IV.3

For every ϵ > 0 there exists δ_ϵ > 0 such that for all $\overline{\mathcal{B}}\subset \mathcal{B}\text{with}d(\overline{\mathcal{B}})<{\delta }_{ϵ}$ it is the case that (LP-P) is solvable, and for every solution $\overline{\mathbf{z}}$ of (LP-P) there exists a solution z* of (LSIP-P) such that $\Vert \overline{\mathbf{z}}-{\mathbf{z}}^{*}\Vert <ϵ$.

The result is insightful because it suggests that when we use enough samples the quality of the CGU underestimator does not depend on sample selection but rather on the fundamental structure of the underestimator function.

2) Limitations of the CGU Underestimator

We now have the necessary machinery to analyze the CGU underestimator. In particular, we consider a class of functions to be underestimated and demonstrate how the CGU underestimator fails.

Suppose we wish to underestimate $f(\mathbf{t})=\mathbf{t\prime }\overline{\mathbf{Q}}\mathbf{t}+\overline{\mathbf{b}}\prime \mathbf{t}$, where

$$\overline{\mathbf{Q}}=\text{diag}\left(\left[\begin{array}{cc}{\alpha }_1& \beta \\ \beta & {\alpha }_2\end{array}\right],{\alpha }_3,\dots ,{\alpha }_n\right)$$ (12)

n ≥ 2, α_i > 0 for all i, β < 0, and α₁α₂ − β² ≥ 0 to guarantee $\overline{\mathbf{Q}}⪰0$. This choice of $\overline{\mathbf{Q}}$ can be seen as the simplest $\overline{\mathbf{Q}}$ with off-diagonal elements; the argument we present next can be generalized to more general cases as well. Let the underestimator be given by U(t) = t′Dt + b′t + c, where D = diag(d₁,…,d_n) ⪰ 0, b = (b₁,…,b_n) and c ∈ ℝ. The CGU underestimator is informative if it manages to locate the minimum of f(t). In particular, we would like the minimizer of U(t) to coincide with the minimizer of f(t). We will show by contradiction that this is not possible in general.

Consider an instance of the underestimation problem at hand where ℬ is the hypercube defined as ℬ = ℬ₁ × … × ℬ_n where all ℬ_i’s are identical and given by ℬ_i ≜ [−2T/3,T/3] for all i = 1,…,n and T > 1. (LSIP-D) takes the form

$$\begin{array}{c}(\mathbf{\text{LSIP}}-\mathbf{D})\text{min}{\displaystyle \sum _{i=1}^n{\alpha }_i{\mathit{I}}_2+{\displaystyle \sum _{i=1}^n{\mathit{I}}_1{b}_i+2\beta {\mathbf{E}}_{\mu }[t_1{t}_2]}}\hfill \\ \hfill \text{s.t.}{\displaystyle {\int }_{\mathcal{B}}\mathbf{a}(\mathbf{t})d\mu (\mathbf{t})=\mathbf{h},\mu \in M^{+}(\mathcal{B})}\end{array}$$ (13)

where E_μ[·] denotes expectation with respect to μ, I₂ = (1/T) ∫_ℬ1 t²dt = T²/9, and I₁ = (1/T) ∫_ℬ1 tdt = −T/6. Since β < 0 the dual problem is equivalent to the problem of selecting a measure μ in order to maximize E_μ[t₁t₂] subject to the constraint that the first and second moments of the marginal distributions under μ match those of the uniform distribution (cf. definition of h in Section IV-A). However, for any measure μ ∈ M⁺(ℬ) the expectation E_μ[(t₁ − t₂)²] is nonnegative, hence

$$2{\mathbf{E}}_{\mu }[t_1{t}_2]\le {\mathbf{E}}_{\mu }[t_1^2]+{\mathbf{E}}_{\mu }[t_2^2]=2{\mathit{I}}_2.$$

It follows that at optimality the above inequality holds with equality, that is, t₁ and t₂ are colinear.

Next, let V_(LSIP-P) and V_(LSIP-D) denote the optimal values of (LSIP-P) and (LSIP-D), respectively. We have already shown (cf. Lemma IV.2) that (LISP-D) is superconsistent. Moreover, the argument in the previous paragraph suggests that V_(LSIP-D) is finite. Consequently, (LSIP-D) has an optimal solution and V_(LSIP-D) = V_(LSIP-D) (cf. [20, Th. 6.9]). In the terminology of [20] we have perfect duality. The necessary and sufficient conditions for optimality of a primal-dual pair are primal feasibility, dual feasibility, and perfect duality.

Let (ẑ, μ̂) be an optimal primal-dual pair, where $\widehat{\mathbf{z}}=({\widehat{d}}_1,\dots ,{\widehat{d}}_n,{\widehat{b}}_1,\dots ,{\widehat{b}}_n,ĉ)$, and μ̂ is a measure in M⁺(ℬ) with the properties identified previously. The optimality conditions are

$${\displaystyle \sum _{i=1}^n{t}_i^2{\widehat{d}}_i+{\displaystyle \sum _{i=1}^n{t}_i{\widehat{b}}_i+ĉ\le {\displaystyle \sum _{i=1}^n{t}_i^2{\alpha }_i+2\beta t_1{t}_2+{\displaystyle \sum _{i=1}^n{t}_i}{\overline{b}}_i,\forall \mathbf{t}\in \mathcal{B}}}}$$ (14)

$${\displaystyle {\int }_{\mathcal{B}}\mathbf{a}(\mathbf{t})d\widehat{\mu }(\mathbf{t})=\mathbf{h},\widehat{\mu }\in M^{+}(\mathcal{B})}$$ (15)

$${\displaystyle \sum _{i=1}^n{\mathit{I}}_2{\widehat{d}}_i+{\displaystyle \sum _{i=1}^n{\mathit{I}}_1{\widehat{b}}_i+ĉ={\displaystyle \sum _{i=1}^n{\alpha }_i{\mathit{I}}_2+{\displaystyle \sum _{i=1}^n{\mathit{I}}_1{\overline{b}}_i+2\beta {\mathit{I}}_2.}}}}$$ (16)

Consider now the primal feasibility condition (14) at t = 0 and at t = −2Te/3. These two inequalities along with (16) imply ĉ = 0. Furthermore, (14) at t = −Te/3 and at t = Te/3 along with (16) yield

$${\displaystyle \sum _{i=1}^n({\widehat{b}}_i-{\overline{b}}_i)=0.}$$ (17)

Next, fix some j ∈ {3,…,n} and some k > 3/T and apply (14) at t such that t_j = −1/k, t_l = 1/k for all l ≠ j and at t such that t_j = 1/k, t_l = −1/k for all l ≠ j. These, along with (17), ĉ = 0, and (16), imply

$${\widehat{b}}_1+{\widehat{b}}_2={\overline{b}}_1+{\overline{b}}_2{\widehat{b}}_j={\overline{b}}_j,j=3,\dots ,n.$$ (18)

Now, for any j ∈ {3,…,n} and some k > 3/T apply (14) at t such that $t_j=\sqrt{2}/k,t_l=1/k$ for all l ≠ j and at t such that t_j = 0, t_l = 1/k for all l ≠ j. These inequalities, along with (17), ĉ = 0, and (16), lead to

$${\widehat{d}}_1+{\widehat{d}}_2={\alpha }_1+{\alpha }_2+2\beta {\widehat{d}}_j={\alpha }_j,j=3,\dots ,n.$$ (19)

To proceed consider ẑ with ĉ = 0 satisfying (18) and (19). Let $x={\widehat{d}}_1-{\alpha }_1-\beta \text{and}y={\widehat{b}}_1-{\overline{b}}_1$. We will show that (x,y) = (0,0). Assume otherwise. Using (18) and (19) the primal feasibility condition (14) reduces to

$$(t_1-t_2)[\beta (t_1-t_2)+x(t_1+t_2)+y]\le 0,\forall t_1,t_2\in {\mathcal{B}}_1.$$ (20)

Let 0 < δ < T/3 and apply the above at (t₁,t₂) = (δ, −δ) and (t₁,t₂) = (−δ, δ). It follows

$$2\beta \delta \le y\le -2\beta \delta .$$

If y ≠ 0, by selecting δ close enough to zero we can violate primal feasibility. Therefore, y = 0. Further, let 1 < k < T and apply (20) at (t₁,t₂) = (k/3,1/3) and (t₁,t₂) = (1/3,k/3). It follows:

$$\beta \frac{k-1}{k+1}\le x\le \beta \frac{1-k}{k+1}.$$

If x ≠ 0, by selecting k close enough to one we can violate primal feasibility. Therefore, x = 0. In summary, we have

$$\begin{array}{cc}{\widehat{d}}_i={\alpha }_i+\beta ,i=1,2\hfill & {\widehat{d}}_j={\alpha }_j,j=3,\dots ,n\hfill \\ {\widehat{b}}_j={\overline{b}}_j,j=1,\dots ,n\hfill & ĉ=0.\hfill \end{array}$$ (21)

The minimum of the CGU underestimator, say t̂, is given by t̂ = −(1/2)D̂⁻¹b̂ which due to (Section IV-A.II) yields

$$\begin{array}{cc}{\widehat{t}}_i=-\frac{{\overline{b}}_i}{2({\alpha }_i+\beta )},i=1,2\hfill & {\widehat{t}}_j=-\frac{{\overline{b}}_j}{2{\alpha }_j},j=3,\dots ,n.\hfill \end{array}$$

However, the minimum of f(·), say t*, is given by

$$\begin{array}{c}{t}_1^{*}=-\frac{1}{2({\alpha }_1{\alpha }_2-{\beta }^2)}({\alpha }_2{\overline{b}}_1-\beta {\overline{b}}_2)\hfill \\ t_2^{*}=-\frac{1}{2({\alpha }_1{\alpha }_2-{\beta }^2)}({\alpha }_1{\overline{b}}_2-\beta {\overline{b}}_1),t_j^{*}=-\frac{{\overline{b}}_j}{2{\alpha }_j},j=3,\dots ,n.\hfill \end{array}$$

Clearly, t̂ is different from t̂ in general and the CGU underestimator can not locate the minimum of f(·). We summarize the result of this subsection in the following theorem.

Theorem IV.4

Let $f(\mathbf{t})=\mathbf{t\prime }\overline{\mathbf{Q}}\mathbf{t}+\overline{\mathbf{b}}\prime \mathbf{t}$, where $\overline{\mathbf{Q}}⪰0$ is given in (12). Further, let Û(t) = t′D̂t + b̂′t + ĉ be the function formed from the optimal solution to (LSIP-P), i.e., the optimal CGU underestimator to f(t). Then, in general, the minimizer of the underestimator is different from the minimizer of f(t).

The result of Thm. IV.4 is significant since it establishes that the CGU underestimator cannot locate the minimum of f(·) even if it uses an infinite number of samples. In contrast, according to Proposition IV.1 and Theorem IV.3, SDU will find the minimum of f(·) as the number of samples grows to infinity.

V. On SDU’s Convergence

In this section, we provide a rough analysis of the SDU algorithm and show that under appropriate conditions it converges to the global minimum of f(·). Since the free energy functions we seek to minimize are funnel-like, for the remainder of this section we will impose a set of structural assumptions on f(·) and the search region ℬ that reflect this structure. We denote by epi(f) the epigraph of f(·) which is defined as epi(f) = {(ϕ,w) | ϕ ∈ ℬ, f (ϕ) ≤ w}. We also denote by conv(𝒮) the convex hull of any set 𝒮.

Assumption A

Assume that f(ϕ) satisfies the following set of conditions: i) it is continuously differentiable; ii) f(·) has a unique global minimum in ℬ; iii) ℬ is compact; iv) for all local minima ϕ of f(·) there exists an open set such that ϕ is the unique minimizer of f(·) within this set; (iv) the extreme points of conv(epi(f)) lie on a quadratic function Ũ(ϕ) = ϕ′Q̃ϕ + b′ϕ+c̃; v) Ũ(ϕ) has a unique global minimum which is identical with the global minimum of f(·) in ℬ.

For functions that satisfy Assumption A we will say that they have a funnel-like shape [see Fig. 1 (Right)]. The next proposition provides a sufficient condition for exactly determining the quadratic function Ũ(·) which tightly underestimates all local minima of f(·).

Proposition V.1

Let Assumption A prevail. Consider the SDU algorithm of Fig. 3 and suppose that in Step 1 we obtain at least K = ((n+1)(n+2))/2 distinct local minima ϕ¹,…,ϕ^K of f(·) which are extreme points of conv(epi(f)). Then, the underestimator U(·) obtained in Step 2 is identical to Ũ(·).

Proof

Constructing the underestimator U(·) is equivalent to solving problem (4). Clearly, (Q, b, c) = (Q̃, b̃, c̃) is an optimal solution because it is feasible and achieves a zero cost. At local minima ϕ^j we have U(ϕ^j) = f(ϕ^j) for all j = 1,…,K which form a linear system of equations. This linear system has (n² + n)/2 unknown elements of Q plus n unknown elements of b plus the unknown value of c. It follows that for K ≥ ((n + 1)(n + 2))/2 we obtain the exact quadratic function which passes from all extreme points of conv(epi(f)).

The following theorem establishes that given sufficient sampling of the search region ℬ the SDU underestimation procedure can locate the global minimum of f(·) which we denote by ϕ*.

Theorem V.2

Let Assumption A prevail. Consider the SDU algorithm of Fig. 3 and assume that ℬ contains at least ((n + 1)(n + 2))/2 distinct local minima of f(·) which are extreme points of conv(epi(f)). Suppose that in Step 1 of the algorithm we obtain K local minima ϕ¹,…,ϕ^K of f(·) starting from uniformly distributed starting points in ℬ. Then, the global minimum ϕ^P of the underestimator U(·) obtained in Step 2 of the algorithm converges in probability to the global minimum ϕ* of f(·) as K → ∞, namely, lim_K→∞ P[ϕ^P = ϕ*] = 1.

Proof

Due to Assumption A function f(·) satisfies all the conditions of the capture theorem [21, Prop. 1.2.5]. In particular, for every local minimum ϕ^j of f(·) which is an extreme point of conv(epi(f)) there exists an open set 𝒮_j = {ϕ | ‖ϕ − ϕ^j‖ < ϵ^j} such that any convergent local minimization algorithm initialized with any point in 𝒮_j converges to ϕ^j.¹ We assumed that ℬ contains at least M = ((n + 1)(n + 2))/2 distinct local minima of f(·) which are extreme points of conv(epi(f)). Without loss of generality let ϕ¹,…,ϕ^M ∈ ℬ and set ρ_j = (∫_{ϕ∈𝒮j∩ℬ} dϕ)/(∫_ϕ∈ℬ dϕ), for j = 1,…,M. Note that there exists an ϵ > 0 such that ρ_j > ϵ for all j. By virtue of Proposition V.1 we need at least M = ((n + 1)(n + 2))/2 distinct local minima of f(·) which are extreme points of conv(epi(f)) in order to exactly construct Ũ(ϕ); this suffices to yield ϕ*. Let P [success] the probability that we do indeed obtain M distinct local minima of f(·) which are extreme points of conv(epi(f)) by randomly sampling K points in ℬ and performing local minimization starting from every sample. Let also 𝒜_j the event that such random sampling yields ϕ^j, j = 1,…,M, at least once. For any event 𝒜 we denote by 𝒜̅ its complement. We have

$$\begin{array}{cc}\mathbf{P}[\text{success}]\hfill & \ge \mathbf{P}[{\mathcal{A}}_1\cap \cdots \cap {\mathcal{A}}_M]=1-\mathbf{P}[\overline{{\mathcal{A}}_1}\cup \cdots \cup \overline{{\mathcal{A}}_M}]\hfill \\ & \ge 1-{\displaystyle \sum _{j=1}^M\mathbf{P}[\overline{{\mathcal{A}}_j}]=1-{\displaystyle \sum _{j=1}^M{(1-{\rho }_j)}^K.}}\hfill \end{array}$$ (22)

The first inequality shown previously is due to the fact that on the right-hand side we consider only local minima ϕ¹,…,ϕ^M; ℬ may contain additional local minima which are extreme points of conv(epi(f)). The second inequality above uses the union bound. Next observe that since the ρ_j are bounded away from zero the right hand side of (22) converges to one as K → ∞.

We can think of Theorem V.2 as a simple sanity check of the SDU underestimation approach. It implies that given an appropriate funnel-like structure, SDU can locate the global minimum of the free energy function with probability approaching one as the number of random samples in ℬ increases. Actual free energy functions are expected to deviate from the structure put forth in Assumption A. In particular, the local minima of f(·) may not be tightly underestimated by a quadratic function and/or the global minimum of a quadratic underestimator may not coincide with ϕ*. These factors have motivated the form of the SDU given in Fig. 3.

VI. NUMERICAL RESULTS FOR A SET OF TEST FUNCTIONS

In this section, we apply SDU to test functions that were selected to resemble free energy functions. Throughout we compare SDU with CGU.² Here, and for all numerical results reported in this paper, we have used the SDPA [18] semidefinite programming solver.

The test functions we use are from [7] and are given by

$$\begin{array}{c}f(\mathit{\varphi })=f_1(\mathit{\varphi })+f_2(\mathit{\varphi })+f_3(\mathit{\varphi })\hfill \\ f_1(\mathit{\varphi })={\displaystyle \sum _{i=1}^{n/2}(a{\varphi }_{2i-1}^2+b{\varphi }_{2i}^2),f_3(\mathit{\varphi })={\displaystyle \sum _{i=1}^{n}A|\text{sin}(\gamma {\varphi }_{2i})|}}\hfill \\ f_2(\mathit{\varphi })={\displaystyle \sum _{i=1}^{n/2}\left[-c\text{cos}(\alpha {\varphi }_{2i-1})-d\text{cos}(\beta {\varphi }_{2i})\right]}\hfill \end{array}$$ (23)

where ϕ = (ϕ₁,…,ϕ_n), a = 1, b = 2, c = 3, d = 4, α = 3π, β = 4π, and γ = 3.3π. Note that the origin is the global minimum of f(·). The parameter A determines the amplitude of the high frequency term f₃(·), thus, the larger A the more “noisy” and harder to optimize we expect f(·) to be.

First, and to illustrate once again the flexibility that a general quadratic underestimator adds, we consider a version of the test function in (23) for n = 2 and rotate the coordinate system with respect to the two axis by 45°.³ Fig. 4 (top) depicts the underestimators (along a certain vertical hyperplane) obtained by CGU and SDU, denoted by U_CGU(·) and U_SDU(·) respectively, intheir first iteration based on 20 (= 8n + 4 for n = 2 as required by CGU) uniformly sampled local minima. U_CGU(ϕ) has the global minimum at (0.5225, −0.7238) and U_SDU(ϕ) at (0.2669, 0.4581), which is closer to the true global minimum (0, 0). The bottom figure in Fig. 4 depicts the contours of the two underestimators illustrating that they predict rather different global minima.

Fig. 4.

SDU derives tighter underestimators.

Our next example, concerns the six-dimensional version of the test function in (23). This is in fact the appropriate space for rigid docking problems (translation and rotation). We applied both CGU and SDU and report various indicators of their performance. For both cases the search region ℬ was selected as the box {ϕ | −100 ≤ ϕ_i ≤ 10,i = 1…,n} so that the global minimum at the origin is not at the center of ℬ. We used 8n + 4 initial samples in ℬ as required by CGU (which is more than what Proposition V.1 suggests for SDU when n = 6). We use the following notation: i) ${\mathit{\varphi }}_0^P$ denotes the initial predictive conformation, that is, the minimum of the initial underestimator we obtain (Step 2 of SDU); ii) ${\widehat{\mathit{\varphi }}}_0^P$ denotes the local minimum of f(·) obtained by starting the local minimization at ${\mathit{\varphi }}_0^P$; iii)ϕ^G denotes the best local minimum of f(·) found throughout the evolution of the algorithm; iv) D(ϕ) denotes the (Euclidean) distance of a conformation ϕ from the known optimal conformation which is at the origin, i.e., $D(\mathit{\varphi })={\left({\displaystyle {\sum }_{i=1}^n{\varphi }_i^2}\right)}^{1/2}$; v) η denotes a metric of success of the corresponding algorithm adjusted to the difficulty of the optimization problem, more specifically, η = 1{D(ϕ^G) < 1} for the case A = 10, η = 1 {D(ϕ^G) < 1.2}, for the case A = 20, and η = 1{D(ϕ^G) < 1.5} for the case A = 30; and, finally, vi) n_f denotes the number of times the corresponding algorithm evaluates the function f(·) during its course.

Table I reports results for the function in (23) and Table II (left) reports results for the function in (23) when we rotate the coordinate system by 60° with respect to all six axes. In each of these tables we considered three problem instances for A equal to 10, 20, and 30, respectively. For each case, we performed 100 independent runs of both CGU and SDU.⁴ The various values we report are the means of the corresponding quantities over the 100 independent runs. We also report the corresponding standard deviations; σ_X denotes the standard deviation of X.

Table I.

CGU AND SDU APPLIED TO THE TEST FUNCTION IN (23) WHEN n = 6

Method		CGU	SDU	CGU	SDU	CGU	SDU
A		10		20		30
${\varphi }_0^P$	$D({\varphi }_0^P)$	0.701	0.448	1.343	0.772	1.468	0.983
	${\sigma }_{{\varphi }_0^P}$	0.291	0.164	1.185	0.295	0.659	0.429
${\widehat{\varphi }}_0^P$	$D({\widehat{\varphi }}_0^P)$	0.864	0.654	1.558	1.155	1.713	1.466
	${\sigma }_{{\widehat{\varphi }}_0^P}$	0.527	0.558	1.281	0.802	0.921	0.930
	$f({\widehat{\varphi }}_0^P)$	18.260	13.151	56.159	48.955	92.472	76.981
	${\sigma }_{f({\widehat{\varphi }}_0^P)}$	13.532	12.435	35.353	21.347	28.816	29.100
ϕG	D(ϕG)	0.752	0.435	1.400	0.897	1.723	1.067
	σϕG	0.578	0.304	0.695	0.631	0.729	0.566
	f(ϕG)	−3.424	4.659	15.247	28.911	26.321	49.757
	σf(ϕG)	6.425	9.435	7.304	13.810	9.298	20.167
η(%)		69	95	46	88	41	83
nf		157.30	91.67	153.66	91.48	169.52	92.38

Table II.

LEFT: CGU AND SDU APPLIED TO THE TEST FUNCTION IN (23) WHEN n = 6 AND THE COORDINATE SYSTEM IS ROTATED BY 60° WITH RESPECT TO ALL SIX AXES. RIGHT: SDU APPLIED TO THE 1BRS (TOP) AND 1MLC (BOTTOM)

Method		ASA	CGU	SDU	ASA	CGU	SDU	ASA	CGU	SDU
A		10			20			30
${\varphi }_0^P$	$D({\varphi }_0^P)$		3.506	0.456		11.528	0.731		11.727	1.035
	${\sigma }_{{\varphi }_0^P}$		2.548	0.184		25.15	0.302		20.629	0.400
${\widehat{\varphi }}_0^P$	$D({\widehat{\varphi }}_0^P)$		3.306	0.659		4.722	0.829		8.614	1.259
	${\sigma }_{{\widehat{\varphi }}_0^P}$		1.736	0.639		2.991	0.440		13.424	0.661
	$f({\widehat{\varphi }}_0^P)$		50.769	25.649		109.156	66.150		415.843	95.0605
	${\sigma }_{f({\widehat{\varphi }}_0^P)}$		27.153	12.260		82.185	23.013		1669.64	29.169
ϕG	D(ϕG)	2.66	1.837	0.490	3.53	2.539	0.799	4.16	3.013	1.128
	σϕG	0.92	0.672	0.322	1.04	0.952	0.509	1.13	1.117	0.698
	f(ϕG)	−0.87	8.108	17.006	9.01	26.319	49.985	19.53	42.614	75.172
	σf(ϕG)	7.48	5.19	10.46	10.5	9.45	17.01	12.28	12.18	22.28
η(%)		0	7	93	0	3	86	0	4	84
nf		86106	230.36	91.89	81500	229.84	85.95	82273	246.74	89.77

i	${\varphi }_1^G$	${\varphi }_2^G$	${\varphi }_3^G$	f(ϕG)	D(ϕG)
1	−0.195	−2.716	0.702	−65.58	2.82
2	−0.403	0.282	−0.197	−102.25	0.53

i	${\varphi }_1^G$	${\varphi }_2^G$	${\varphi }_3^G$	f(ϕG)	D(ϕG)
1	−0.831	−0.935	1.428	−24.30	1.90
2	−0.831	−0.935	1.428	−24.30	1.90
3	0.056	−0.444	−0.550	−64.57	0.70
4	0.056	−0.444	−0.550	−64.57	0.70
5	−0.144	0.764	0.059	−69.29	0.78
6	−0.144	0.764	0.059	−69.29	0.78
7	−0.033	0.549	0.287	−71.19	0.62

We should note that the most important performance metric is the closeness of the conformation found to the best one (measured by D(ϕ^G) and η). There are a number of reasons for this preference, including that i) the 3-D structure of the bound complex determines its function, ii) molecular simulation may be used to discover the native conformation starting from a conformation close to it, and iii) the energy evaluation models used by molecular docking algorithms are approximations of the actual free energy function. As a result, a conformation closer to the native one (like the ones SDU discovers) is more useful than some deep local minima further away (like the ones CGU may discover).

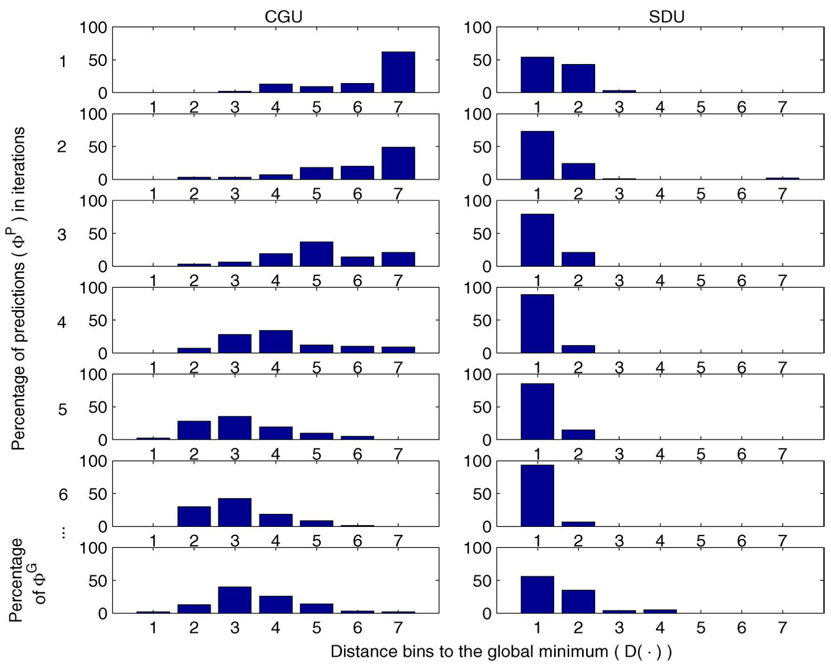
For the cases where the test function is not rotated, CGU, not surprisingly, performs reasonably well. SDU produces conformations with somewhat higher energy but closer to the native one. The performance difference between SDU and CGU is more dramatic in the cases where the test function has been rotated. In the three cases considered CGU fails to discover a conformation close enough to the native one while SDU largely succeeds (observe the differences in η). The key reason, we believe, is that SDU can better capture the structure of the native funnel, which is used to bias sampling in that area. This latter point is perhaps more clearly illustrated in Fig. 5. We draw histograms of the distance of the predictive conformation during the evolution of both algorithms. Histograms k = 1,…,6 appearing from top to bottom correspond to ${\mathit{\varphi }}_k^P$ obtained at the kth iteration. The horizontal axis plots the values of $D({\mathit{\varphi }}_k^P)(D({\mathit{\varphi }}^G)$ for the bottom graph) and the vertical axis plots the percentage of problem instances (out of the 100 runs). It can be seen that SDU starts with a much better initial predictive conformation than CGU and maintains its predictive conformation within 2 units of the native one at all subsequent iterations. The best local minimum found by SDU is not always within 1 unit, but in 84% of the cases it was within 1.5 unit (versus 4% with CGU).

Fig. 5.

Histograms of predictions and final solutions reported by CGU and SDU for the case corresponding to 𝒜 = 30 in Table II (left).

We also compared SDU and CGU to a commonly used simulated annealing algorithm, the ASA algorithm in [22] (see Table II). Even though ASA reaches some deep local minima it ends up converging far away from the global minimum.

In terms of computational efficiency and running time, CGU and ASA take on the order of a few seconds in a top-of-the-line PC and SDU takes on the order of 5 minutes without particular effort at optimizing the code. The key reason is that SDU solves a number of (relatively large) SDP problems. However, SDU performs much fewer function evaluations (by a factor of 3 compared to CGU and by a factor of 1000 compared to ASA as it is evident by the n_f values in Table II). For the test functions we considered in this section the function evaluation time is negligible using (23). Yet, in docking actual proteins function evaluations (e.g., using CHARMM [23] or other complex potentials) dominate all other tasks; for instance, in the results we report in the next section function evaluations take more than 90% of the running time.

VII. APPLICATIONS IN RIGID-BODY PROTEIN DOCKING

In this section, we report results from applying SDU to a number of protein-to-protein docking instances. We assume that both proteins are rigid bodies. This is certainly true for their backbones and, as we will see, we will allow some flexibility in determining the conformation of the side chains in the interface between the two proteins. We consider 3-D problems where one protein is held fixed, both proteins are oriented based on information we obtain from the known bound structure, and we seek to determine the position of the second protein in the bound structure with respect to the first one. We constrain these three translational variables to be in a 10Å cube centered around the origin of the coordinate system, which corresponds to the native position of the ligand. That is, we have already identified the dominant funnel of the energy function and seek to solve the medium-range energy minimization problem within this funnel.

The (free) energy functional we minimize includes van der Waals interactions (ΔE_vdw), the desolvation energy (ΔE_des) and the electrostatic energy (ΔE_elec). We use the software package CHARMM [23] to evaluate the free energy and to perform local minimization. We allow side-chains to be flexible during the local minimization phase; this is critical as side-chains in the interface between the two proteins can not be considered rigid and they are packed in a way that minimizes the overall free energy of the bound complex.

In Table II (right) and Table III we report results for the complexes 1BRS (barnase/barstar), 1MLC (a monoclonal antibody and lyzozyme complex), and 2PTC (a trypsin-inhibitor complex). The bound structure for each case has the ligand centered at the origin, that is, the optimal solution is (0, 0, 0). The initial search region ℬ is a 10Å cube. In each iteration (indexed by i in the tables), we report the best structure found so far, ϕ^G, the corresponding energy f(ϕ^G) (in kcal/mol), and the RMSD distance D(ϕ^G) from the native structure (inÅ). As discussed earlier, the key measure of success is the proximity of D(ϕ^G) to zero.

Table III.

SDU APPLIED TO 2PTC

i	${\varphi }_1^G$	${\varphi }_2^G$	${\varphi }_3^G$	f(ϕG)	D(ϕG)
1	1.001	−2.555	1.395	−25.98	3.08
2	1.307	−2.369	1.363	−28.77	3.03
3	1.088	−1.610	1.310	−33.47	2.34
4	1.083	−2.612	−0.120	−34.46	2.82
5	1.617	−1.750	0.919	−36.42	2.56
6	0.888	−1.297	0.083	−46.37	1.58
7	−0.182	−0.587	0.529	−49.98	0.81
8	0.170	−0.669	−0.387	−53.93	0.82

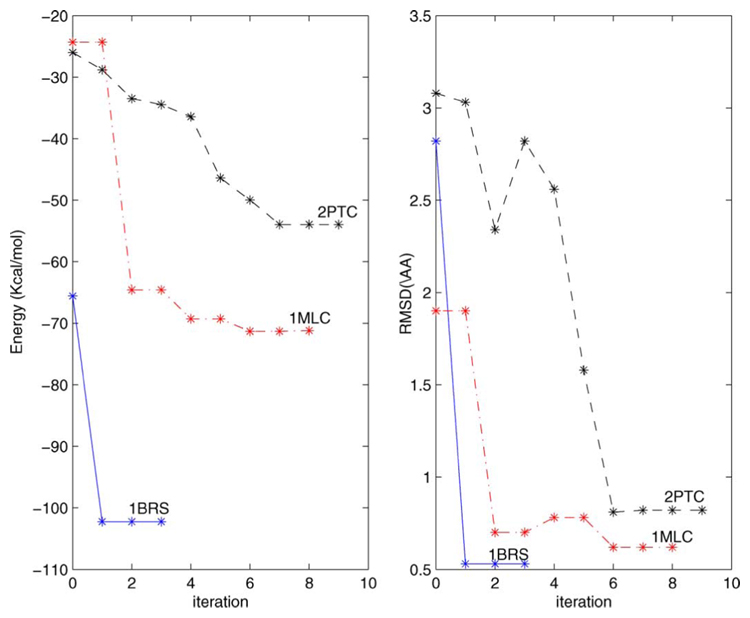
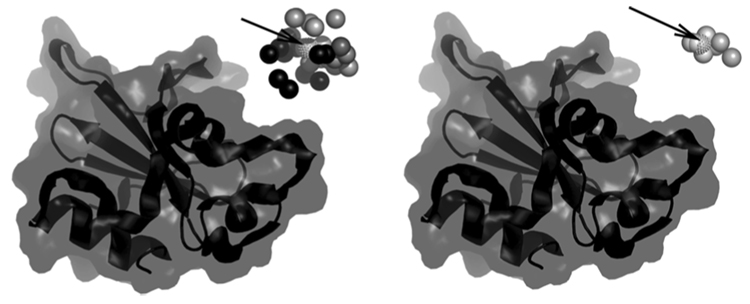
The evolution of SDU in all three complexes considered is depicted in Fig. 6. A better illustration is given in Fig. 7 for the 1BRS complex. In both figures we plot the fixed receptor. We generated 28 random positions of the ligand in the initial search region and in the left figure we plot a sphere at the center of the ligand for each one if these 28 ligand positions. Spheres in lighter shades of gray correspond to lower energy conformations. The position of the native ligand is shown as a dotted sphere and pointed by an arrow. After performing the first iteration of SDU we sample a new set of ligand positions using the procedure in SDU’s Step 5 (b) (cf. Fig. 3). The centers of these ligands are depicted in the right figure. The corresponding structures are both very close to the native one and have low energies.

Fig. 6.

Evolution of SDU for the 1BRS, 1MLC, and 2PTC complexes.

Fig. 7.

Illustration of the 1BRS docking procedure.

We conclude by noting that the starting point for our medium-range optimization is the cluster of best conformations produced by the techniques in [10]. As seen in Fig. 6, these produce conformations within 3–5 Å from the native one. Our method is able to reduce this distance to less than 1 Å in all three complexes considered. In most cases this is considered a very successful identification of the native conformation as the (approximate) energy models used do not provide a much greater degree of accuracy.

VIII. CONCLUSION

We introduced a new method for minimizing free-energy functions appearing in molecular docking and other important problems in computational structural biology. These energy functions are notoriously hard to minimize as they consist of terms acting in disparate space-scales and have a huge number of local minima. Yet, in certain areas they exhibit a funnel-like shape which we use to our advantage.

Our method works on the surface spanned by local minima. We developed a technique based on semidefinite programming to form a general convex underestimator of the energy function. The underestimator guides random, yet biased, exploration of the energy landscape. We established, theoretically as well as numerically, that our method performs better than an alternative (CGU) method. Finally, we applied our algorithm to some protein-protein docking problems and showed that the resulting conformation is extremely close to the native one (within 1 Å RMSD). This improves upon the 3–5 Å RMSD that current state-of-the-art methods produce.

Biographies

Ioannis Ch. Paschalidis (M’96–SM’06) received the Diploma in electrical and computer engineering from the National Technical University of Athens, Athens, Greece, in 1991, and the S.M. and Ph.D. degrees in electrical engineering and computer schience from the Massachusetts Institute of Technology, Cambridge, in 1993 and 1996, respectively.

He joined Boston University, Boston, MA, in 1996, where he is currently an Associate Professor of Manufacturing Engineering, Electrical and Computer Engineering, and the Co-Director of the Center for Information and Systems Engineering. His current research interests lie in the fields of systems and control, optimization, networking, operations research, and computational biology.

Dr. Paschalidis is an Associate Editor of Operations Research Letters and the IEEE TRANSACTIONS ON AUTOMATIC CONTROL.

Yang Shen (S’06) received the B.E. degree in automatic control from the University of Science and Technology of China (USTC), Hefei, China, in 2002. He is currently working toward the Ph.D. degree in systems engineering at Boston University, Boston, MA, and is affiliated with the Center for Information and Systems Engineering (CISE) and the Structural Bioinformatics Laboratory.

His research interests include modeling, simulation, and optimization of complex systems, especially biological systems of protein–protein or protein–ligand interactions.

Pirooz Vakili received the Ph.D. degree in mathematics from Harvard University, Cambridge, MA, in 1989.

He is currently an Associate Professor in the Department of Manufacturing Engineering at Boston University, Boston, MA. His current research interests include efficient Monte Carlo simulation, optimization, computational finance, and bioinformatics.

Sandor Vajda (M’86) received the Diploma in electrical engineering from the Gubkin Institute, Russia, in 1972, the Diploma in applied mathematics from the Eotvos Lorand University, Hungary, in 1980, and the Ph.D. degree in chemistry from the Hungarian Academy of Science in 1983.

In 1990, he joined Boston University, Boston, MA, where he is a Professor of Biomedical Engineering and the Co-Director of the Biomolecular Engineering Research Center. His current research interests are in method development for modeling of biological macromolecules, with emphasis on molecular interactions. In 2004, he and his students founded SolMap Pharmaceuticals, Cambridge, MA, a start-up company focusing on fragment-based drug design.