Comparison of Maximum Entropy and Filtered Back-Projection Methods to Reconstruct Rapid-Scan EPR Images

Abstract

Reconstruction of two-dimensional images by filtered back-projection (FBP) and by the maximum entropy method (MEM) was compared for spectral-spatial EPR images with differing signal-to-noise ratios. Experimental projections were recorded using direct-detected rapid scans in the presence of a series of magnetic field gradients. The slow-scan absorption lineshapes were calculated by Fourier deconvolution. A Hamming filter was used in conjunction with FBP, but not for MEM. Imperfections in real experimental data, as well as random noise, contribute to discrepancies between the reconstructed image and experimental projections, which may make it impossible to achieve the customary MEM criterion for convergence. The Cambridge MEM algorithm, with allowance for imperfections in experimental data, produced images with more linear intensity scales and more accurate linewidths for weak signals than was obtained with other MEM methods. The more effective elimination of noise in baseline regions by MEM made it possible to detect weak trityl ¹³C trityl hyperfine lines that could not be distinguished from noise in images reconstructed by FBP. Another advantage of MEM is that projections do not need to be equally spaced. FBP has the advantages that computational time is less, the amplitude scale is linear, and there is less noise superimposed on peaks in images. It is useful to reconstruct images by both methods and compare results. Our observations indicate that FBP works well when the number of projections is large enough that the star effect is negligible. When there is a smaller number of projections, projections are unequally spaced, and/or signal-to-noise is lower MEM is advantageous.

1. Introduction

Reconstruction of most real-world images is based on finite data sets with superimposed noise. Some information about the object always is lost in the data acquisition, which limits the accuracy of the reconstructed image. The challenge is to find the “best” image with the least noise and fewest artifacts.

Filtered backprojection (FBP) was initially used in X-ray tomography to create images from projections. Now it is widely used in other imaging modalities where the data are integrated values for some parameter along lines through the object to be characterized [1]. In EPR imaging spectra measured in the presence of a magnetic field gradient are mathematically homologous to X-ray projections collected with parallel beams for each viewing angle. FBP is computationally fast, accurate, easily implemented [2], and widely used in commercial instrumentation. However, there are inherent limitations to FBP. Projections must be collected with equal angle increments to encompass 180°. If too few projections are used to construct an image, ridges radiate out from sharp features in the image, which is called the “star” or “streaking” effect. Reconstruction of an image from a data set that does not include projections over a full 180° range (a missing angle data set) results in ridges at angles that correspond to the edges of the angular range that would have been sampled by the missing projections. These ridges can be partially mitigated by iterative reconstruction and estimates of the missing projections [3, 4]. For many physical observables it is known that the quantities must be positive, so a non-negativity constraint can be used to decrease some artifacts.

In practice there are time and/or instrumental constraints that limit the signal-to-noise and/or number of projections that can be acquired, so it is important that a reconstruction algorithm work well with a limited number of projections and limited signal-to-noise. Since the signal is broadened by the magnetic field gradient, the signal-to-noise is poorer at the higher magnetic field gradients that are needed to enhance spatial resolution [5]. It has also been pointed out that, depending upon the characteristics of the object to be imaged, some projections may be more informative than others [6, 7] and there may be cases in which the smallest number of projections required to adequately define an object could be achieved with unequally spaced projections. These factors all indicate the need to compare FBP with other reconstruction algorithms.

An alternative to FBP is the maximum entropy method (MEM). From a very large set of possible images that are consistent with experimental data, the one with the maximum entropy can be identified as the “best” [8, 9]. MEM has been applied to a variety of problems in mathematics, astronomy, physics, technology, biology, etc. (see, for example [8–14]). In magnetic resonance, its applications have been primarily in spectroscopy to suppress baseline noise and simultaneously improve resolution [15, 16]. Many successful applications of MEM are in multidimensional NMR spectroscopy, where useful signals occupy only a small fraction of the area of the image which is therefore called a ‘nearly black’ image. By contrast, a typical EPR image is unlikely to be nearly black. One concern is that the relative intensities and line widths of signals in images generated by MEM may be altered, which complicates signal quantitation. Non-linear distortions can, however, be accurately calibrated by adding to the experimental data synthetic signals with known properties. Non-linear distortion of these signals can be used to correct intensities of experimental peaks [10].

There have been a small number of conflicting reports on the utility of MEM for magnetic resonance (MR) image reconstruction. Although Constable and Henkelman [17] concluded that MEM “does not work” for MR image reconstruction, Smith et al. [18] and Johnson et al. [19] demonstrated that when MEM was applied to a 2D EPR image, baseline noise was suppressed and images could be reconstructed from smaller numbers of projections without interference from the “star” effect. An important distinction between the images examined in the two studies was that the MRI data were acquired in the time domain, which creates an array of evenly-spaced points in k-space that can be Fourier transformed to generate an image. In contrast, the EPR projections were acquired as equally spaced points in the signal domain, which corresponds in the frequency domain to a set of radial rays through a central point.

In the present study we seek to determine the advantages and disadvantages of the FBP and MEM methods for reconstruction of rapid-scan spectral-spatial EPR images. These images display the EPR spectrum as a function of position in the sample [5]. Accurate spectral lineshapes are important for interpretation of information in the image. It was therefore of interest to compare images reconstructed with the two techniques from data that contained varying amounts of noise.

1.1 Implementations of MEM

MEM has been implemented in ways that differ in the expression for entropy and in the mathematical procedure that is used to maximize the criterion, Q(f) [14, 20–22].

$$\text{Q}(\text{f})=\text{S}(\text{f})-\lambda \text{C}(\text{f}),$$ (1)

where S(f) is the entropy, λ is the Lagrange multiplier, C(f) is a measure of the discrepancy between a reconstructed image and the experimental data, and f is the 1-D array of N points in the reconstructed image.

$$\text{C}(\text{f})={\chi }^2=\sum _{\text{k}=1}^{\text{M}}{({\text{R}}_{\text{k}}(\text{f})-{\text{D}}_{\text{k}})}^2/{\sigma }_{\text{k}}^2.$$ (2)

where M is the number of experimental data points, σ_k is the standard deviation of the noise that can be defined as the variance for an individual point or the width of the Gaussian distribution for baseline points, D_k is the experimental data, and R is the operator appropriate for the experiment. For an EPR image, R is the Radon transformation and for NMR data collected in the time-domain, R is the Fourier transform.

The Lagrange multiplier λ in Eq.(1) determines the relative weights of S(f) and C(f). For each value of λ, solution of Eq.(1) gives a different image f_λ. In the limit of large λ, the role of entropy is reduced and the reconstructed image contains noise, experimental artifacts and other information that is not strongly supported by the data. Decreasing λ results in poorer agreement between the image and the experimental data, but the information contained in the image is considered to be more reliable. In the limit of λ=0, maximization of Q(f) = S(f) gives an image with no information derived from the experimental data. It is commonly accepted that one should select λ such that C(f) = M. In this case the reconstructed image fits the data to within the limitations of the noise. Some MEM algorithms vary λ iteratively until C(f) = M [23, 24]. Since probability is inherently positive, non-negativity is an inherent property of the method.

The entropy, S(f), can be defined in different ways that originate from the Shannon formula [25, 26]

$$\text{S}(\text{f})=-\sum _{\text{i}=1}^{\text{N}}{\text{f}}_{\text{i}}log({\text{f}}_{\text{i}}),$$ (3)

Since the f_i values are interpreted as probabilities, ${\displaystyle \sum _{\text{i}}^{\text{N}}}{\text{f}}_{\text{i}}=1$, which provides an additional constraint on the algorithm.

Alternatively, entropy can be defined as [27]:

$$\text{S}(\text{f})=-\sum _{\text{i}}^{\text{N}}{\text{f}}_{\text{i}}[log({\text{f}}_{\text{i}}/{\text{f}}_{0\text{i}})-1],$$ (4)

where f₀ is a ‘default’ image, to which f_λ will tend if the parameter λ in Eq.(1) is very small. In most MEM applications f₀ is chosen to be flat. If some a priori information about the image to be reconstructed is available it can be helpful to incorporate this information into the ‘default’ image (see, for example, [28]).

In the unique maximum entropy image the gradients ∇S and ∇C are parallel. The non-parallelism between these two vectors is estimated by the equation:

$$\text{TEST}=\frac{1}{2}\mid \frac{\nabla \text{S}}{\mid \nabla \text{S}\mid }-\frac{\nabla \text{C}}{\mid \nabla \text{C}\mid }\mid .$$ (5)

The ideal situation with TEST=0 is often difficult to reach and more modest criteria have to be used. It is suggested [27] that the iteration process can be terminated when value C(f) = Aim is reached provided TEST<0.1. Aim usually is equal to M. In this case, the reconstructed image can be considered as the unique maximum entropy image.

In this study the Cambridge algorithm for MEM [27] is compared with the algorithm used by Smith and Stevens [18]. Instead of treating λ as an input parameter that must be optimized [18], the focus of the Cambridge algorithm [27] is on minimizing C(f) while maximizing S(f). While in other algorithms the next approximation of the image is searched along a single direction, the Cambridge algorithm uses a more efficient multidimensional (normally three) method, based on vectors constructed from the first and second derivatives of the functions C(f) and S(f).

1.2 Specific Considerations for Spectral-spatial EPR Imaging

From a mathematical point of view, the difference between most NMR applications and EPRI is in the use of different operators R (see Eq. (2)). For most NMR applications R is Fourier transformation. By applying inverse Fourier transformation to experimental data one can always find an image that fits the experimental data exactly, f_exact = R⁻¹D. However, this is not what people usually want. Any distortions in the data, such as noise, are incorporated into the resulting image so the exact image may not be the ‘best’ representation of the object. MEM algorithms may help to obtain an image that does not fit the data as well as f_exact does but MEM outputs can be considered as more reliable. If Radon transformation is used as in the case of EPRI, consistency of all the projections becomes important. Any inconsistency in the data such as random noise and signal distortion by hardware and data acquisition imperfections make it impossible to find an exact image. In other words no image can be found that exactly fits the data, so R(f_exact) ≠D and C(f)>0.

For in vivo or rapid-scan EPR imaging experiments, in addition to random noise there are distortions such as instability of baseline and of resonator frequency. Shifts in resonator frequency cause shifts of the EPR spectra and may be accompanied by phase shifts that cause dispersion signal admixture. Small frequency shifts cause broadening of peaks in the reconstructed image and larger shifts could result in spurious peaks. The discrepancy between the experimental projection and the ideal projection caused by a frequency shift may be larger than random noise in the regions with high signal intensities and may vanish where intensities are close to baseline.

In the papers that applied MEM to reconstruction in EPRI [18, 19] Eq.(2) was applied assuming constant σ_k = σ, which implies that there is a normal distribution of misfit errors with standard deviation σ:

$$\mid R_k(f)-D_k\mid \le {\sigma }_{\text{k}}$$ (6)

However, as noted above distortions caused by hardware imperfections may be much larger in some regions of the dataset than noise level. In this case all distortions that exceed noise level are introduced into the final reconstructed image. On the other hand, the use of a larger constant σ that is high enough to take all distortions into consideration is not suitable for the regions where random noise dominates. It is equivalent to noise level overestimation. In this situation the constraint C(f) = M may not be reachable at all and is no longer useful. The standard deviation σ_k in Eq. (2) could be substituted by an effective σ_k^eff that takes both distortions and random noise into consideration. In this case the algorithm can search for the image with maximum entropy provided that C(f) = M is fulfilled. In the present paper two ways to adjust σ_k are compared.

2. Experimental Section

2.1 Sample Preparation

Lithium phthalocyanine (LiPc) prepared electrochemically following procedures in the literature [29, 30] was provided by Prof. Swartz, Dartmouth University. Well-shaped needles were selected, placed in a 4 mm OD (3 mm ID) quartz tube, evacuated overnight on a high vacuum line, and then the tube was flame sealed. A solution (0.5 mM) of Nycomed trityl-CD₃ (methyl-tris(8-carboxy-2,2,6,6-tetramethyl(d₃)-benzo[1,2-d:4,5-d′]bis(1,3)dithiol-4-yl)tri-potassium salt) in water was placed in a 10 mm OD (9 mm ID) tube, degassed by bubbling with N₂ and then flame sealed. The distance between the centers of the two tubes was 11 mm.

2.2 Magnets, gradient coils, resonator

Rapid scan signals at 250 MHz were obtained on a locally designed and built spectrometer [31]. A 4-coil air-core magnet with a pair of Z-gradient (Maxwell) coils to produce the gradients [32] was used. The Hall probe was located in an auxiliary magnet coil system connected in series with the main magnet [33]. To allow setting of the dc magnetic field with 10 times greater resolution than is available in the Bruker software at the low magnetic fields required for these experiments, the auxiliary magnet system had a coil constant 10 times greater than the magnet that was used for the experiments, but otherwise is similar to that described in [33].

The resonator was constructed from 6 equally spaced turns of no. 20 copper wire [31]. It has an internal diameter of 25 mm and height of 50 mm. The spacing between the turns is 10 mm. The turns were series capacitively coupled using Voltronics 25 series non-magnetic porcelain chip capacitors. The resonator frequency was tuned using a combination of 10 and 3.7 pF capacitors. With the sample in the resonator, the resonant frequency was 246.73 MHz. The measured Q of the empty resonator was 155 ± 5. The resonator efficiency (B₁/√P) was determined to be 0.35 ± 0.05 G/√Watt [31]. The resonator and the scan coil assembly were shielded using a non-magnetic aluminum stock pot that is 33 cm in diameter and 26 cm high. Electrical contact between the pot and its cover was achieved with finger stock. Having the shield outside the scan coils helps to eliminate field inhomogeneities produced by the eddy currents that are observed when the shield is between the scan coils and the resonator. Calibration of the scan widths gave a field constant of 10.8 ± 0.2 G/A.

2.3 Spectroscopy

The imaging experiments were performed with 60 experimental projections (4 missing projections) using the missing angle data acquisition algorithms for 2D spectral-spatial imaging [34, 35]. Projections were equally spaced between −82.97° and +82.97°. Rapid scan signals were recorded using triangular scans with modulation frequencies in the range of 1 to 8 kHz and scan widths in the range of 0.85 to 6.93 G. The RF power was 0.44 mW. A 4^th order hardware Butterworth filter (Krohn-Hite model 3955) was used with a cutoff frequency of 1 MHz and input and output gain of 20 dB. To test the sensitivity of the reconstruction algorithms to experimental noise, two data sets were recorded for each projection. One data set was taken by averaging 5,000 scans, for which many projections have relatively low signal-to-noise (S/N), and the second data set was averaged for 50,000 scans, which gives significantly improved S/N. The slow-scan lineshapes were recovered from the rapid-scan spectra using Fourier deconvolution [31]. Typical projections at low and high gradient are shown in Fig. 1. Comparison spectra that are denoted as “slow scan” were recorded in rapid-scan mode using a scan frequency (700 Hz) and scan width (0.6 G) for which the scan rate is low enough that a slow-scan absorption signal was obtained, or as conventional slow-scan spectra.

Figure 1.

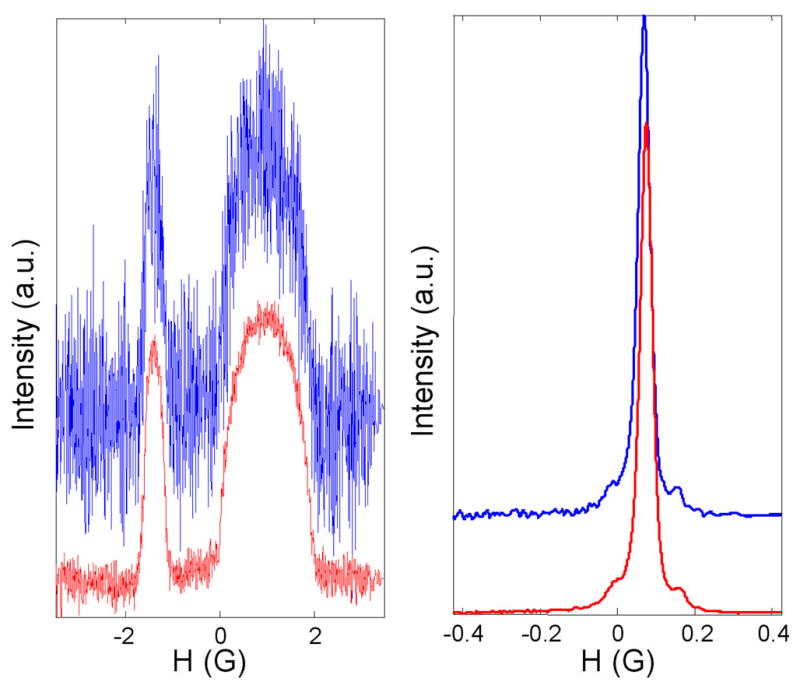
Rapid scan projections in the presence of magnetic field gradients, after Fourier deconvolution to recover the slow-scan lineshapes. a) Gradient = 2.2 G/cm. b) Gradient = 0.01 G/cm. For each pair of scans the upper and lower traces were obtained by averaging 5,000 or 50,000 scans, respectively.

To test the impact of the number of projections on the image reconstruction algorithms a set of 30 projections (assuming 2 missing projections) was calculated from each of the sets of 60 projections. Interpolation was used to generate projections at equally spaced intervals between −81.56° and 81.56° as required for reconstruction of a spectral-spatial image.

2.4 Algorithm Details

Images were reconstructed on grids of 200×200 pixels using 287 data points per projection. Since our aim was to compare MEM and FBP algorithms, the same sets of 30 or 60 projections were used for both cases. MEM does not require projections to be collected with equal angle increments so there is no need to estimate “missing” projections as in FBP.

2.4.1 FBP

The missing angle algorithm for FBP [35] was implemented in MatLab 7.0. A Hamming filter was applied to the experimental projections. To permit the same matrix formats for the FBP and MEM algorithms Radon transformation matrixes were built with sizes 40000×17220 (40000×8610) for 60 (30) projections, instead of using the intrinsic MatLab Radon transformation routines. Fortunately, these huge matrices are sparse, and defining them as the sparse type in MatLab allows use of only 50 (25) Mb of memory. Otherwise, these matrices would require several gigabytes of RAM. The other advantage of doing Radon transformation by matrix multiplication on the image in vector form is that it is about twice as fast as the Matlab intrinsic routines.

2.4.2 Cambridge MEM algorithm [27, 36]

As noted in the introduction, imperfections in experimental data may make it impossible to achieve C(f) = M using the definition of C(f) given in eq. (2). Therefore an alternate definition of C(f) that still permits use of the efficiencies of the Cambridge algorithm is proposed.

$$\text{C}(\text{f})=\sum _{\text{k}=1}^{\text{M}}{({\text{R}}_{\text{k}}(\text{f})-{\text{D}}_{\text{k}})}^2/{\sigma }_{\text{k}}^{{\text{eff}}^2}$$ (7)

Two approaches to selecting ${\sigma }_k^{\mathit{eff}}$, defined in eq. (8) and (10), were examined. In both cases a different σ_k was calculated for each projection.

$${\sigma }_{\text{k}}^{\text{eff}}={\sigma }_{\text{k}}+\mid \text{smoothed}({\epsilon }_{\text{k}})\mid ,\text{k}=1,2,\dots ,\text{M}.$$ (8)

$$\text{Where}{\epsilon }_{\text{k}}={\text{R}}_{\text{k}}({\text{f}}_{min})-{\text{D}}_{\text{k}},\text{k}=1,2,\dots ,\text{M}.$$ (9)

Practical implementation of this idea shows that better results are obtained when ε is smoothed to eliminate high-frequency noise.

$${\sigma }^{\text{eff}}=\kappa \sigma$$ (10)

The parameter κ was adjusted so that the C(f) = M constraint was fulfilled.

The algorithm was implemented as described in ref. [27]. Program code was generated in Matlab using built-in matrix operations. This approach required the image matrix and dataset to be aligned column-wise. The images were represented by vectors of 40000 elements, while 60 (30) projections were given by the vector 287*60=17220 (287*30=8610) elements. The image f_min was obtain by minimization of the function C(f) (Eq.(7) ) using an iterative procedure in which the next f⁽ⁿ⁺¹⁾ approximation of the reconstructed image was found as follows

$${\text{f}}^{(\text{n}+1)}={\text{f}}^{(\text{n})}+\alpha \nabla \text{C}({\text{f}}^{(\text{n})}),$$ (11)

where parameter α is calculated to reduce C(f) along the direction given by the gradient ∇C:

$$\alpha =-\frac{{\displaystyle \sum _{\text{k}=1}^{\text{M}}}{\text{A}}_{\text{i}}{\text{B}}_{\text{i}}}{{\displaystyle \sum _{\text{k}=1}^{\text{M}}}{\text{B}}_{\text{i}}^2},\text{A}={\text{Rf}}^{(\text{n})}-\text{D};\text{B}=\text{R}\nabla \text{C}({\text{f}}^{(\text{n})}).$$ (12)

where R is the Radon transform operator and D is experimental data.

With f obtained by means of Eqs. (11,12) σ_eff is calculated according to Eq.(8) or Eq.(10). Iterations started from a flat guess image and nearly flat ‘default’ image. The guess image f and ‘default’ image f₀ cannot be identical. In this case ∇S=0, would result in a divide by zero error (see, for example, Eq.5)

1. After 10 iterations have been completed, the ‘default’ image f₀ is replaced by the current image f divided by 10, i.e. f_0i = f_i/10.

2. After another 10 iterations, f₀ is replaced similarly.

3. Step 2 is repeated until C(f) = M is reached. The process is complete, provided that TEST < 0.1.

Similar final images were obtained by different methods of scaling f to generate f₀.

2.4.3 Smith and Stevens MEM algorithm [18]

The iteration process starts with a guess image. Elements of the image are updated iteratively according to the equation:

$${\text{f}}_{\text{i}}\to {\text{f}}_{\text{i}}\mid 1+\alpha \frac{\partial \text{S}/\partial {\text{f}}_{\text{i}}}{\mid \partial \text{S}/\partial \text{f}\mid }-\alpha \frac{\partial \text{C}/\partial {\text{f}}_{\text{i}}}{\mid \partial \text{C}/\partial \text{f}\mid }\mid ,$$ (13)

where α is a parameter that defines the length of the step in the direction of ascending S and descending C. Iterations are interrupted when convergence stops or its rate becomes too slow to give improvement in the image in a reasonable time. In the ref. [18] it was suggested that the algorithm should start from flat guess images that have maximum entropy, which ensures that the resulting images satisfy the global extremum criteria TEST < 0.1. In our study an extensively smoothed version of the image generated by FBP also was used as a starting image for this algorithm.

3. Results

3.1 Data Acquisition

Rapid-scan EPR projections were recorded for a sample containing tubes of LiPc and of trityl-CD₃. Examples at high and low gradients are shown in Fig. 1a and 1b, respectively. Note that this direct-detection method gives the EPR absorption signal [37]. The S/N in the projections was calculated as the ratio of the amplitude at the peak of the signal to the root-mean-square noise in the baseline at the left of the scan. When 5,000 scans were averaged the S/N was 228 at very low gradient and 10 at a gradient of 2.2 G/cm, which is a much smaller degradation than occurs when first-derivative spectra are recorded [31]. When 50,000 scans were averaged the S/N improved to 727 at very low gradient and 29 at a gradient of 2.2 G/cm. The improvement in S/N with increasing number of scans is approximately proportional to the square root of the number of scans, as expected if noise is stochastic. The intensities of the signals from the LiPc and trityl-CD₃ samples were selected to make the amplitudes of features in the image similar. Since the spatial extent of the trityl-CD₃ sample is substantially greater than for the LiPc sample, the amplitude of the trityl-CD₃ signal in the absence of a gradient is much greater than for the LiPc sample. Thus, the projections at low gradient that are shown in Fig. 1b are dominated by the trityl-CD₃ signal, which can be recognized by the characteristic ¹³C hyperfine lines that are separated by 0.166 G.

The quality of the data and of individual projections can be examined. The image f_min that fits experimental data as well as possible is found by minimization of the function C(f). The C_min=C(f_min) is a characteristic of data inconsistency. The lower C_min the better the projections match the image. The projections obtained from this ‘best’ image can be compared with experimental projections to estimate mismatch error for every single point in the dataset (Eq. (9)). In Eq. (9) ε is represented as a 1-D vector including all projections. However, it proved to be very helpful to write the ε-matrix as a two-dimensional array, where projections are columns. This figure clearly shows ‘bad’ projections, which have greater mismatch between an experimental projection and the reconstructed image. If ε is large for a particular column, it is likely that something went wrong when this projection was measured. If it is a frequency shift, the image can be improved by correcting this faulty projection.

3.2 Reconstruction and Comparison of Images

Images were reconstructed from four datasets: (1) 60 spectra each averaged 5,000 times; (2) 60 spectra, each averaged 50,000 times; (3) 30 spectra, each averaged 5,000 times; and (4) 30 spectra, each averaged 50,000 times. Images for each dataset were reconstructed by four methods which are denoted as follows:

FBP – filtered back projection.

CMEM – Cambridge algorithm with σ^eff calculated using Eq. (8)

CMEM2 – Cambridge algorithm with σ^eff, calculated using Eq.(10)

SMEM – the algorithm, developed by Smith and Stevens

In addition four auxiliary images (AUX) were reconstructed under conditions that correspond to infinitely large λ, and used for comparison with images obtained with different approaches to estimating σ^eff. Quantitative parameters for each of these algorithms are summarized in Tables 1–3 and discussed in the text. In all the images the spacings between the two tubes in the phantom and dimensions of the tubes are in good agreement with measured dimensions. The results shown in the Figures 2 – 7 emphasize FBP and CMEM for data set (1) which has the larger number of projections, but poorer signal-to-noise and data set (4) which has the smaller number of projections and better signal-to-noise. Figures 2–7 show images with their spatial and spectral profiles for these cases.

Table 1.

	CMEM				CMEM2				SMEMd				AUX
Data a	5,000		50,000		5,000		50,000		5,000		50,000		5,000		50,000
	30	60	30	60	30	60	30	60	30	60	30	60	30	60	30	60
C/Cfbp b	0.26	0.76	0.65	1.25	0.4	0.98	0.61	1.27	0.54	1.01	1.61	2.68	0.1	0.3	0.27	0.58
TESTc	0	0	0	0	0	0	0	0	0.1	0.07	0.08	0.05	-	-	-	-

^a30 and 60 are the numbers of projections. 5,000 and 50,000 are the numbers of averages.

^bRatio of the root-mean-square deviation between the experimental data and projections from the reconstructed image C obtained by each of the MEM algorithms compared with C for FBP reconstruction.

^cTEST for convergence to unique maximum entropy image (eq. 5), which should be zero in ideal case.

^dThe starting image was obtained from the FBP image by smoothing it so extensively that it was almost flat.

Table 3.

Linewidths^a (mG) of signals for trityl-CD₃ and LiPc calculated from spectral slices

	Trityl-CD3				LiPc
Datab	5,000		50,000		5,000		50,000
	30	60	30	60	30	60	30	60
FBP c	36	35	36	35	51	56	53	53
CMEM c	35	35	35	34	56	52	54	52
CMEM2 c	36	34	35	34	53	45	53	50
SMEM c	34	34	34	34	51	50	49	50
AUX c	36	34	36	34	53	55	56	53
Direct d	35	35	35	35	54	54	54	54

^aLinewidths are reported as the full width at half height of the absorption signal. There are 200 data points per spectral slice of 0.34 G. By interpolation it was possible to calculate linewidths with an uncertainty of about 1 mG.

^b30 and 60 are the numbers of projections. 5,000 and 50,000 are the numbers of averages.

^cLinewidths calculated from spectral slices taken images reconstructed by the methods defined in the text.

^dMeasured directly from EPR spectra for LiPc and trityl.

Figure 2.

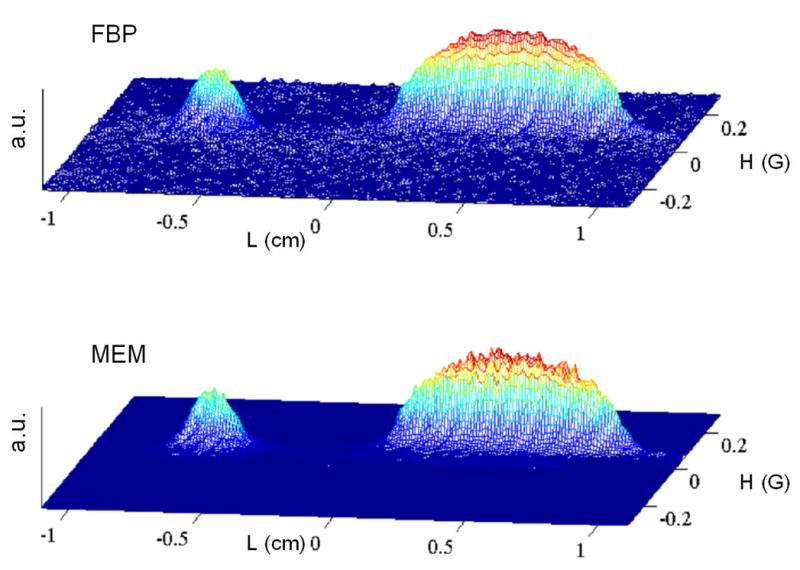
2-D spectral-spatial EPR image of a small tube containing solid LiPc and a larger tube containing an aqueous solution of trityl-CD₃. The centers of tubes were separated by 11 mm. Each of the 60 projection was averaged 5,000 times with scan frequencies of 1 to 8 kHz and a scan rate of 13.9 kG/s. A Hamming filter was used in conjunction with FBP. No filtering was used for reconstruction by CMEM algorithm. Statistics for the images are shown in Tables 1–3.

Figure 7.

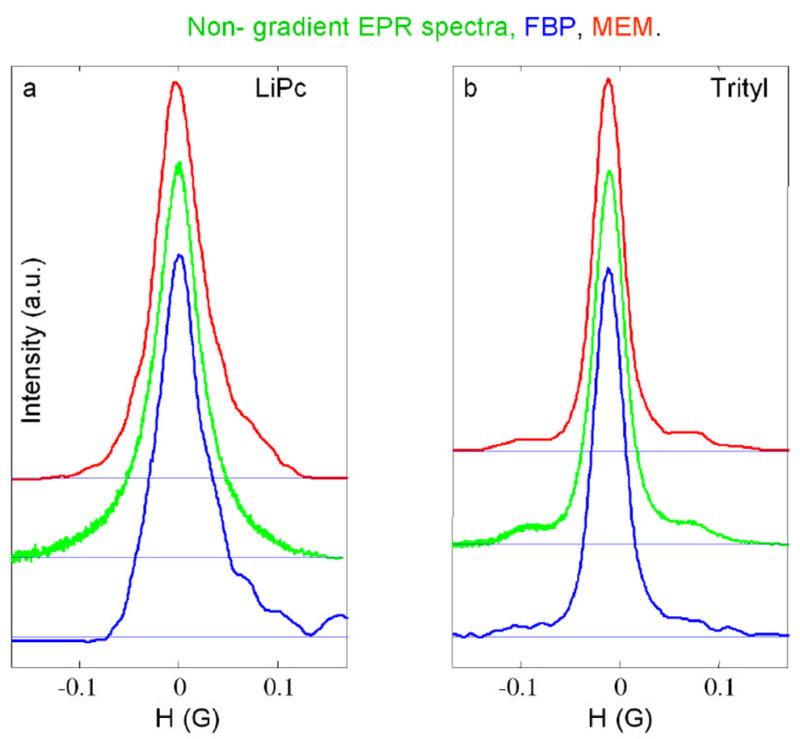
Spatial profiles of the images shown in Fig. 6 obtained by the summation of numerical 2D image matrix along spectral axis. Red lines show MEM profile; blue lines show FBP profile.

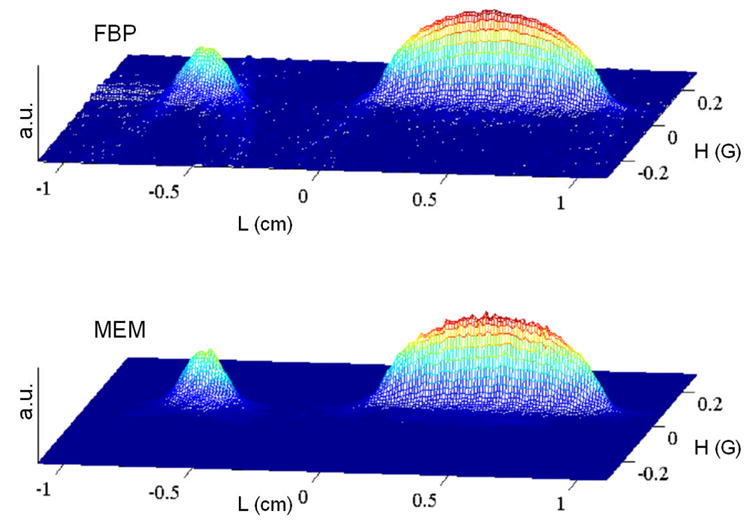
Table 1 summarizes the χ² errors (C) for the reconstructed images and the TEST for global convergence (eq. 5). For each data set C/C_fbp is smallest for the AUX image, although the noise is higher (data not shown). These AUX images, which were reconstructed under conditions that correspond to infinitely large λ (Eq. 1), have the best match with experimental data. The problem with such images is that all imperfections are incorporated into the images. MEM is used to find an image that does not fit the data quite as well but contains less noise and less other imperfections. The ratios C/C_fbp increase in the order AUX < CMEM < CMEM2 < SMEM. Increases in the ratio can mean less noise, but could also result from lost information so the parameter TEST (Eq.5) must be examined. The smaller the value of TEST, the closer the image is to the global extremum, which guarantees the minimum loss of useful information for a given misfit C. The images reconstructed by the CMEM and CMEM2 methods give TEST values less than 0.01. Values of TEST for images generated by SMEM are larger than for the Cambridge algorithm but still are below the tolerable level TEST=0.1. The larger values of TEST imply that entropy is not maximized as effectively by the SMEM method as by the CMEM or CMEM2 methods.

Images reconstructed by CMEM and FBP are compared in Fig. 2 and 5. The lower noise in the baseline regions of the images reconstructed by CMEM than by FBP are evident in the pairs of images. However, in the regions of highest intensity the noise is actually higher in the CMEM images than the FBP images because the Hamming filter reduces the noise superimposed on the FBP image to a greater extent than MEM does. Even so, the ability of the MEM method to reduce noise in baseline regions reveals hyperfine structure of the trityl signal even for cases where it is corrupted by noise in the FBP images (see Fig. 3).

Figure 5.

2-D image of the same object as shown in Fig. 2 with the same experimental parameters, except that each of the 30 projections was averaged 50,000 times which results in better S/N. Statistics for the images are shown in Tables 1–3.

Figure 3.

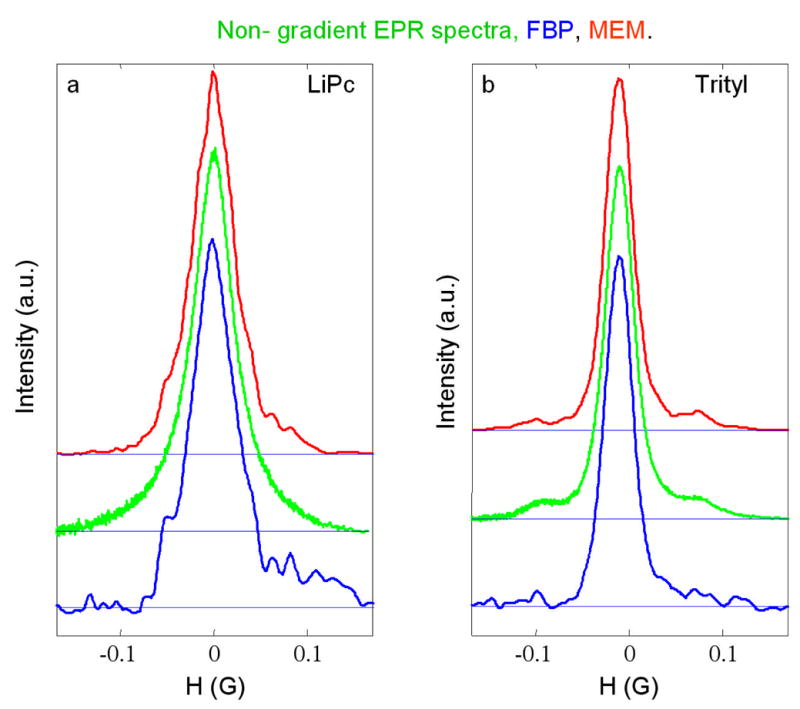
Spectral slices through the 2-D spectral-spatial image in Fig. 2 for (a) the LiPc signal and for (b) the trityl-CD₃ signal at the positions for maximum signal intensity. The red (upper) and blue (lower) lines are from the images reconstructed by CMEM and FBP, respectively, and calculated by summing three slices. The green lines (middle) are the corresponding slow-scan lineshapes obtained by Fourier deconvolution of non-gradient rapid scans recorded with 500 Hz modulation frequency and a 0.6 G sweep width.

It is well-known fact that MEM is a non-linear algorithm that can introduce nonlinearities [38] in the intensities in an image, so it is important to check the images. One measure of the linearity of the intensity scale is the ratio of the amplitude of the more intense trityl peak to the less intense LiPc peak (Table 2), which was calculated in two ways. (a) The spatial slices through the image were summed (as in Figs. 4, 7) and the ratios of the peak heights in these 1D slices are summarized in Table 2, row 1. The expected value of this 1D ratio, estimated by measuring the amplitudes of the LiPc and trityl peaks for the high-gradient projections, is 1.12. This calculation can be done because the EPR signals from two radicals do not overlap. The 1D peak ratios for the FBP images (Table 2) are very close to the expected value. For the data sets obtained with 50,000 averages the 1D peak ratios from the CMEM images are significantly better than from the SMEM images indicating improved linearity. For the data sets with only 5000 averages the greater noise on the peaks contributed to poorer peak ratios. (b) Ratios for the average of six points at the tops of the peaks are summarized in Table 2, row 2, and should be the same for all images. No attempt was made to correct for superimposed noise. The average of the ratios for the two FBP images calculated from the datasets with 50,000 averages is 1.78, which is taken as the comparison value for other images. The values for the corresponding AUX images (1.75) are similar. MEM algorithms represent non-linear distortion which is stronger for noisier datasets. The SMEM algorithm suffers from nonlinearity to a greater extent than CMEM does.

Table 2.

Ratios of Trityl to LiPc Peak Intensities

	FBP				CMEM				SMEM				AUX
Data a	5,000		50,000		5,000		50,000		5,000		50,000		5,000		50,000
	30	60	30	60	30	60	30	60	30	60	30	60	30	60	30	60
1D Spatial b	1.15	1.12	1.1	1.11	1.29	1.32	1.24	1.22	1.39	1.31	1.37	1.32	1.16	1.11	0.98	1.04
2D image c	1.89	1.83	1.78	1.78	2.07	1.87	1.79	1.78	1.9	1.97	1.94	1.91	1.92	1.83	1.74	1.75

^a30 and 60 are the numbers of projections. 5,000 and 50,000 are the numbers of averages.

^bRatio of intensities of trityl and LiPc peaks in 1D profile obtained by summing the spatial slices in the image.

^cRatio of intensities of trityl and LiPc on the tops of the peaks in 2D images.

Figure 4.

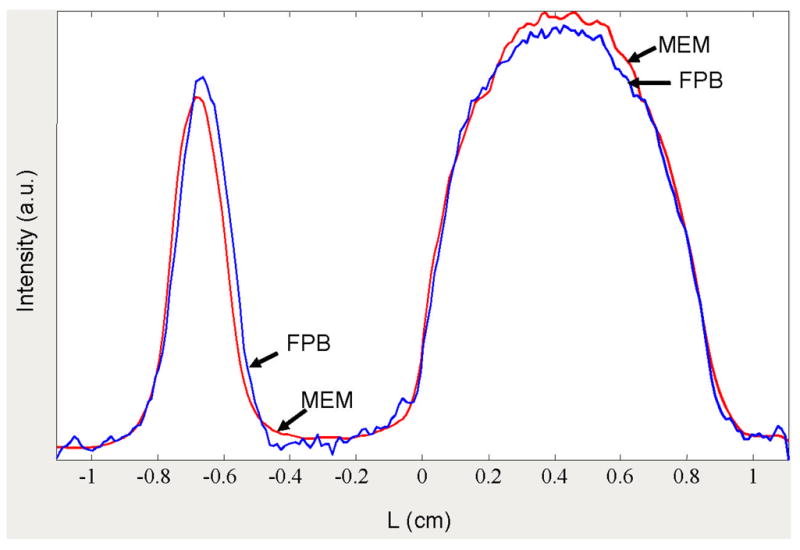
Spatial profiles of the images shown in Fig. 2 obtained by the summation of numerical 2D image matrix along spectral axis. Red lines show MEM profile; blue lines show FBP profile.

Table 3 summarizes important spectral information. Linewidths were determined by fitting Lorentzian lineshapes to the sum of three spectral slices through the peaks of intensities for the LiPc and trityl signals in the images (see Figs. 3, 6). Although the LiPc signal has a simple Lorentzian lineshape, the trityl lineshape is more complicated, including C¹³ sidebands. The regions in the spectra for the ¹³C hyperfine lines were not included in the fitting. The linewidths for the trityl signal in all of the images agreed with directly measured signals within expected accuracy. There was greater scatter in the linewidths for the LiPc signal (Table 3). The discrepancies are greater for the CMEM2 and SMEM methods than for FBP or CMEM. However, in general, the linewidths obtained by fitting the LiPc spectra are quite good. The linewidths of the LiPc signal obtained by SMEM are systematically underestimated (Table 3), which indicates a systematic non-linearity in intensities. The non-linearity in the SMEM images can be decreased by starting iteration from a smoothed FBP image instead of from a flat image (values not tabulated). However, these images can not be considered as ones having maximum entropy because values of TEST are in the range of 0.2–0.3. The ¹³C hyperfine lines are better defined by MEM than by FBP and the relative intensities are in reasonable agreement with slow scan spectra (Fig. 3,6).

Figure 6.

Spectral slices, analogous to those in Fig. 3, through the image in Fig. 5. The red (upper) and blue (lower) lines are from the images reconstructed by CMEM and FBP, respectively, and calculated by summing three slices. The green lines (middle) are the corresponding slow-scan lineshapes obtained by Fourier deconvolution of non-gradient rapid scans recorded with 500 Hz modulation frequency and a 0.6 G sweep width.

It is surprising to see how poor the LiPc lineshapes are in Fig. 3. For example, the LiPc spectra from the FBP image are strongly distorted in comparison with CMEM curve. Although the discrepancies in measured linewidths for the LiPc signal for CMEM (−2mG) and FBP (2mG) methods are equal, the fit of the Lorentzian lineshape to the MEM slices is 2–3 times better than to the FBP slices. It is clear that fitting a known lineshape function to the spectral slices permits relatively accurate lineshape estimation even from imperfect spectral slices. The sources of FBP spectral slice distortions are noise and streak artifacts (see Figs. 2,5). The streaks appear because of imperfections in the data including frequency shifts, the small number of projections, and the missing angle. The streaks caused by the small number of projections disappear in AUX and CMEM images. The streaks from data imperfections (or, perhaps, from ‘missing’ projections) are equally seen in AUX and FBP images, but suppressed in MEM images (see Figs. 2,5). Reduction of these artifacts in CMEM images improves the spatial resolution as shown in Figs. 4 and 7. The MEM curves are narrower and have more symmetrical shape than the FBP profiles. The left-shift of the LiPc peak in the MEM profile relative to the FPB profile (Fig. 4) is the result of the artifacts in FBP. The fact that the tops of the peaks for MEM and FBP 2D images coincide supports this statement.

4. Conclusions

Two different implementations of the Cambridge MEM algorithm [27] (CMEM, CMEM2) and the maximum entropy algorithm developed by Smith and Stevens [18] (SMEM) were compared with the commonly used FBP method. The CMEM method has found to give more accurate results than CMEM2 or SMEM, so the focus is on the comparison between CMEM and FBP.

FBP is a linear method. As mentioned in the introduction, both the advantage and disadvantages of MEM originate from its nonlinear behavior. This study seeks to determine the pros and cons of MEM for reconstruction of spectral-spatial EPR images. Figures 2–7 together with quantitative analysis given in Tables 1–3 reveal important differences between the two algorithms. MEM entirely suppresses noise in the regions with no useful signals (base plane) and shows less noise filtering at the top of peaks in the image, which is a non-linear behavior. On the contrary, the linear FBP method spreads noise from projections evenly over the image. Generally, the FBP images are noisier than MEM images for noisy datasets. From the practical point of view it is important to know how this difference impacts the spectral and spatial information extracted from the image. Spatial profiles were obtained by integration of two-dimensional image along spectral axis. This smoothes random noise and eliminates difference in noisiness on the tops of the MEM and FBP peaks in spatial profiles. If the goal is to determine the linewidth of the signal from a species with known lineshape, non-linear fitting can be applied. In this case accuracy of the entire fitted curve is important and noise is less of a problem than other distortions. Our results show that spectra obtained by both FBP and CMEM show similar accuracy, when compared to directly measured EPR spectra. Thus, the difference in nonlinear noise distribution over the images doesn’t strongly impact the linewidth information. Nonlinearity of the MEM method, however, is significant in spatial profiles. Quantitative analysis of the ratios of trityl and LiPc peak intensities shows stronger nonlinear distortion for MEM images for noisier data. The weaker LiPc peak is underestimated in these profiles. In contrast, the ratio of peaks in FBP-reconstructed images exhibits little variation, which can be attributed to the linearity of the reconstruction procedure. However, this does not make spatial profiles obtained by FBP method more informative. Images show streaks around the peaks, which when integrated along spectral axes contribute to the spatial profile. As a result there is distorted information about distribution of radicals in the sample. A significant advantage of MEM is that weak trityl ¹³C hyperfine lines could be distinguished from noise more readily than by FBP.

In summary, each approach was found to have advantages and disadvantages. For FBP the advantages are: (i) less computation time is required, (ii) the relative intensities of features in the image are more accurate. The disadvantages of FBP are: (i) the “star” effect is observed when the number of projections is small, (ii) projections must be equally spaced, (iii) imperfections in a small number of projections adversely impact the whole image, (iv) both noise and streak-like artifacts in the image distort spin concentration profile along spatial axis; For MEM the advantages are: (i) even with a small number of projections, there is no “star” effect, (ii) less noise in baseline regions of the image permits recognition of weak signals, (iii) nonnegativity is implicit in the algorithm, (iv) projections do not need to be at equally spaced angular increments, (v) more accurate shape of the spatial profile, (vi) better matching with experimental projections. The disadvantages of MEM are: (i) it is computationally intensive, (ii) the amplitude scale is nonlinear and amplitudes of weak peaks are underestimated, and (iii) noise superimposed on peaks is higher than with FBP. The overall pattern is that FBP works well when the number of projections is large enough that the star effect is negligible and signal-to-noise is higher. MEM has advantages when projections are not equally spaced, when there are fewer projections, and/or when signal-to-noise is not as good.