ELUCIDATING THE INHIBITION MECHANISM OF HIV-1 NON-NUCLEOSIDE REVERSE TRANSCRIPTASE INHIBITORS THROUGH MULTI-COPY MOLECULAR DYNAMICS SIMULATIONS

Abstract

HIV-1 reverse transcriptase (RT) inhibition is a major focus of current anti-AIDS drug discovery and development programs, comprising 17 of the 31 FDA-approved compounds. The emergence of the non-nucleoside RT inhibitor (NNRTI) class of compounds provides a highly specific and structurally diverse set of drugs, which act non-competitively to perturb normal RT function. Despite a relatively rich set of crystallographic data of RT in various states, details of the allosteric modulation of RT dynamics by NNRTIs are lacking. Capturing this inhibitory mechanism could fuel the design of more effective inhibitors at the NNRTI site and also drive the identification of novel allosteric sites. To address this, we have performed multi-copy molecular dynamics (MD) simulations of RT in the presence and absence of the NNRTI nevirapine (cumulative total simulation time 360 ns). By comparing the collective motions of both the MD and crystallographic structures, we demonstrate that the chief effect of NNRTIs is to constrain a key rigid-body motion between the “fingers” and “thumb” subdomains of the p66 subunit. We show that the NNRTI binding pocket (NNIBP) is proximal to the hinge points for this essential motion and NNRTIs therefore act as “molecular wedges”, sterically blocking the full range of motion. To explain how this impaired movement might result in the experimentally observed loss of polymerase activity, we show that the motion influences the geometry of key catalytic residues on opposite faces of the NNIBP. From a methodological point of view, our results suggest that the multi-copy MD simulation approach is very useful when studying proteins which perform such large conformational changes.

Introduction

Human Immunodeficiency Virus/Acquired Immunodeficiency Syndrome (HIV/AIDS) currently represents the fourth leading cause of death worldwide and has been projected to become the third leading cause by 2030 ¹. The gravity of this infectious disease has lead to the development and approval of a range of pharmaceutical compounds, which interfere with various stages of the HIV-1 retroviral life cycle ². Due to the drug resistance mechanisms of retroviruses, HIV chemotherapeutic regimens typically administer a combination of these compounds, spanning different classes of drugs and often different targets ³. Currently, the most popular drug target is the HIV-1 reverse transcriptase (RT) enzyme, which is required for the conversion of retroviral RNA into DNA and is thus vital for viral replication ⁴. Existing RT inhibitors can be divided into two classes: nucleoside RT inhibitors (NRTIs), which mimic the endogenous substrates and bind competitively at a catalytic site, and non-nucleoside RT inhibitors (NNRTIs), which bind non-competitively at an allosteric site ^{5, 6}. NNRTIs are attractive by virtue of their high specificity for HIV-1 RT, whereas NRTIs cause severe side effects by also inhibiting human DNA polymerases ⁷. Furthermore, NNRTIs are more amenable to structure-based drug design efforts as they do not require prior metabolic activation and can adopt a more diverse range of structures ⁸. However, NNRTIs are afflicted with the same vulnerability to drug-resistance mutations which affects other retroviral drugs and which is manifested in a highly variant binding site ⁹. To date, four NNRTIs have been approved for clinical use by the Food and Drug Administration (FDA): nevirapine, delavirdine, efavirenz and, most recently, etravirine ^{10, 11}. Etravirine (and rilpivirine, which is currently undergoing Phase III clinical trials) are members of the recent diarylpyrimidine (DAPY) group of NNRTIs, which has generated significant excitement through its tolerance of RT mutations which incapacitate previous NNRTIs ^{12, 13}. Crystallography has shown that the DAPY chemical structure permits the conformational flexibility to bind in multiple “poses” and thus elude mutations which impair the binding of other, more rigid inhibitors ¹⁴.

HIV-1 RT catalyzes the transcription of the single-stranded RNA viral genome into a double-stranded DNA form, which can be integrated into the human genome as the provirus. A wealth of crystallographic studies has been performed on RT, yielding ~60 high-resolution structures of the protein in a variety of states (as reviewed in ¹⁵ and documented in ¹⁶). These include the “apo” form (no substrate and no inhibitor – e.g. PDB code 1DLO ¹⁷ and 1HMV ¹⁸), substrate-bound forms (binary complexes of protein with nucleic acid substrate and the ternary complex of protein with nucleic acid and nucleoside triphosphate – e.g. PDB codes 2HMI ¹⁹ and 1RTD ²⁰) and NNRTI-bound forms (co-crystallized NNRTIs, but no substrate – e.g. PDB codes 1BQM ²¹ and 1EP4 ²²). RT is a 1,000 amino-acid heterodimer of p66 and p51 subunits, which are each composed of “fingers”, “thumb”, “palm” and “connection” subdomains. The spatial arrangement of these subdomains is very different between the two subunits and it is thought that the p51 subunit mainly plays a structural role, with polymerization occurring at the p66 subunit ¹⁵. Together, the fingers, palm and thumb subdomains of p66 resemble a right hand and form a “clamp” which holds the double-stranded template-primer in position. Notably, the palm subdomain contains the “catalytic triad” of three aspartate residues (Asp110, Asp185 and Asp186), which are essential for the addition of nucleotide to the growing primer strand and the so-called “primer grip”, which is though to be required for correct positioning of the 3′ end of the primer ²³. The p66 subunit contains an additional subdomain, known as the RNase H (RNH) domain, which is responsible for the other enzymatic activity of the protein - degradation of the RNA strand during polymerization.

The allosteric NNRTI binding pocket (NNIBP) is located approximately 10 Å away from the p66 polymerase active site and is not present in either the apo or substrate-bound crystal structures. In these cases, the NNIBP is occluded, predominantly by the aromatic sidechains of Tyr181 and Tyr188, which must undergo large torsional rotations in order to swing out of the pocket to accommodate NNRTIs ²⁴. Although the co-crystallized NNRTIs represent diverse structures and show differences in binding modes within the NNIBP, they all elicit similar structural rearrangements with respect to the NNRTI-free forms. The most consistent, and short-range, NNRTI-induced effect is a relative movement of two β-sheets which lie on opposite sides of the NNIBP ^{9, 25, 26}. A more long-range effect is a change in the dimensions of the nucleic acid clamp, formed by the space between the fingers, palm and thumb subdomains. While this cleft is essentially occluded in the apo form, it opens to accommodate nucleic acid in the substrate-bound form and opens even further in the NNRTI-bound form, despite the absence of nucleic acid ^{18, 20}.

Despite these insightful comparative observations of crystallographic “snapshots” of RT, the molecular mechanism by which NNRTIs inhibit reverse transcription is still unknown. However, various models have been postulated, based on structural and biochemical data. Coined “molecular arthritis”, the first scheme suggests that NNRTIs lock the enzyme in an inactive conformation, by immobilizing the thumb subdomain ²⁷. Biochemical evidence has since crucially revealed that NNRTIs do not affect the ability of RT to form a ternary complex with nucleic acid and nucleoside triphosphate, but specifically inhibit the chemical step of nucleotide incorporation into the primer strand ^28,29. This has prompted and supported inhibition models involving observed distortions of residues local to the polymerase active site, namely the primer grip and catalytic triad. The former proposes that the shift of the primer grip causes incorrect placement of the 3′ primer end relative to the catalytic site and consequently a catalytically incompetent constellation of these key protein and nucleic acid atoms ²³. The latter proposes a similar fate, although more directly, through movement of the natural position of the catalytic triad ²⁶. More recently, fluorescence experiments have suggested that NNRTI-induced loosening of the fingers-thumb grip (as seen in the crystal structures) may cause RT to slide away from the 3′ primer end and thus prevent polymerization ³⁰.

In the light of such predictions, various computational methods have been employed to explore aspects of the conformational dynamics of RT which cannot be addressed experimentally. Short timescale molecular dynamics (MD) simulations of RT have given insights to the structural flexibility of the enzyme in various starting conformations and with various ligands. Rapid collapse of the thumb subdomain from an “open” to a “closed” conformation has been presented via 1 nanosecond (ns) implicit solvent simulations ³¹. 1.1 ns explicit solvent MD simulations demonstrated increased RT flexibility in the presence of double-stranded DNA, compared to the apo form ³². A non-equilibrium MD study (involving simulations 3 ns in length and modelling a subset of the protein residues) revealed details of NNRTI binding/unbinding and supported the “molecular arthritis” model of inhibition, together with NNRTI-induced expansion of the nucleic acid clamp ³³. Most recently, 2.5 ns explicit solvent MD simulations of RT in NNRTI-bound and NNRTI-free conformations also supported the “molecular arthritis” model and found that resistance mutations were able to partially reverse this effect ³⁴. A coarse-grained modeling method has been adopted by Bahar and co-workers, who have used elastic networks to model the collective dynamics of RT in different conformations ^{35, 36, 37}. Their findings have indicated the relative flexibility and cooperativity of the RT subdomains and most interestingly revealed hinge regions which may be allosteric inhibitor targets. However, different versions of the network model have yielded conflicting results on the effect of NNRTIs on the motion of the thumb subdomain (the gaussian network model indicated a “severe repression” ³⁵, while the anisotropic network model showed “marginal” effects for the same NNRTI ³⁷). Moreover, NNRTI-induced effects were deduced from radically different structures, probably because the network model is too coarse to detect the effect of a drug on the same structure (a drug molecule is modelled as a single network node).

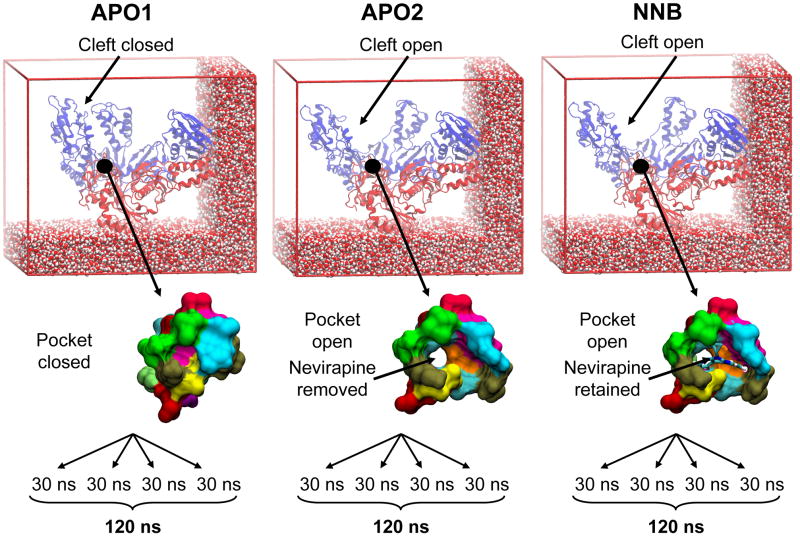
In this work, we present a multi-copy MD simulation study of RT, comparing protein conformational dynamics in the presence and absence of the FDA-approved NNRTI nevirapine. Our chief aim is to detect NNRTI-induced changes in the native dynamics of RT and thus clarify the inhibition mechanism of NNRTIs, in the light of existing experimental and computational findings. Our motivation is that a better understanding of how NNRTIs abolish enzymatic function will enhance future NNRTI drug design and help identify novel allosteric sites near other catalytic regions critical for HIV replication. Three simulation systems have been studied: i) Apo RT with the nucleic acid binding cleft closed (APO1); ii) Apo RT with the nucleic acid binding cleft open (APO2); iii) Nevirapine-bound RT with the nucleic acid binding cleft open (NNRTI-bound, NNB) – see Figure 1 for summary. Principal component analysis (PCA) is used to demonstrate the debilitating effect of nevirapine on a key global motion of RT, through steric block of a hinge region. This motion influences the geometry of key substrate-binding and catalytic residues and thus strongly supports the proposed “primer grip” and “catalytic triad” inhibition models. This study is distinguished from previous RT simulation work through a dramatic increase in simulation time, thanks to continuing advances in computer hardware. A series of four 30 ns trajectories are carried out for each of the three systems (cumulative total of 360 ns) – each an order of magnitude longer than the longest previous trajectory of 3 ns ³³. The combination of significantly longer trajectories and the multi-copy approach ³⁸ allows for a more exhaustive conformational sampling of RT, compared to individual, shorter trajectories. Tackling the issue of incomplete sampling is particularly germane in this study, considering the magnitude of the structural variation observed crystallographically and the large size of the protein.

Figure 1.

Snapshots of the three RT simulation systems under investigation. Differences in the starting conformation of the nucleic acid binding cleft and occupancy of the NNRTI binding pocket are highlighted. Four 30 ns trajectories were generated for each system. RT is shown in cartoon representation, with p66 and p51 subunits colored blue and red, respectively. A subset of water molecules are shown as VDW spheres. The binding pocket residues are shown as a molecular surface, with each residue colored uniquely. Nevirapine is shown in stick representation and colored by atom type.

Results and Discussion

Crystallographic Ensemble

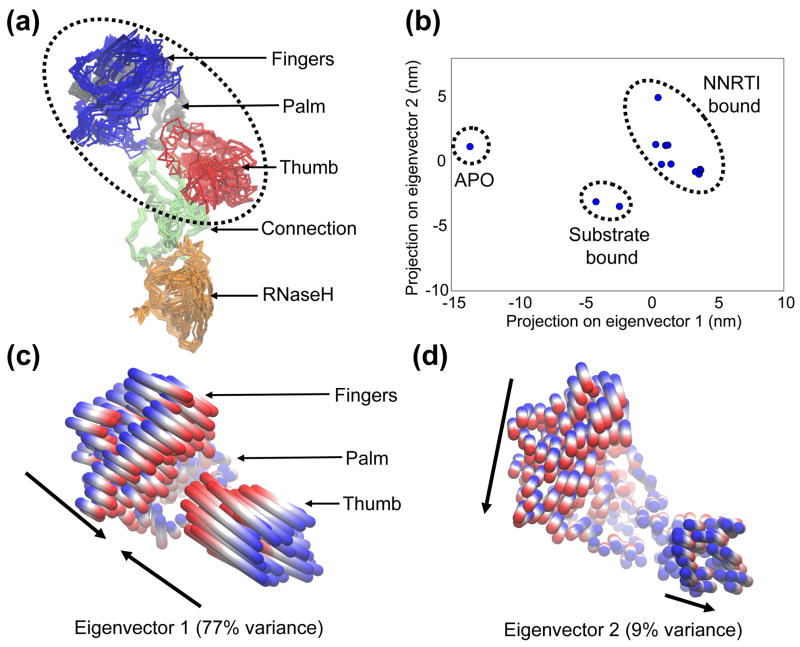
Before investigating the conformational dynamics of RT from the MD simulations, it is important to establish the structural changes which have already been captured via x-ray crystallography, as an experimental reference. To this end, we compiled a set of 13 x-ray structures which represent the different crystal forms (1 × apo, 2 × substrate bound and 10 × NNRTI-bound) and consequently the majority of the conformational variation (see Figure 2 for details). Although there are ~60 crystal structures available, the bulk of these are NNRTI-bound and mutant forms which only contain subtle, local differences from each other and therefore do not significantly affect the global variance of the protein. The “crystallographic ensemble” (Figure 2A) has been subjected to PCA in order to examine the conformational differences, as has been performed previously on other proteins for which substantial crystallographic data exists (e.g. ^{39, 40}). The first two eigenvectors from the PCA capture 86% of the variance of the entire crystallographic ensemble and thus represent large-scale collective motions, with subsequent eigenvectors capturing significantly smaller fluctuations. It is thought that the large displacements seen in the first few eigenvectors of such analyses represent functionally important global movements (the so-called “essential dynamics”), while lower order eigenvectors are smaller, localized fluctuations that do not influence function ⁴¹. Accordingly, PCA studies focus on these dominant motions and Figure 2B shows the projection of each member of the crystallographic ensemble onto the plane defined by the top two eigenvectors. This plot illustrates the relationship between the crystal structures within this 2-dimensional “essential subspace” and one can define clusters which correlate with the ligation state of the protein. As expected, the greatest separation is seen between the apo and ligand-bound forms, which contain closed and open forms of the nucleic acid binding cleft, respectively. A more subtle shift is seen between the substrate-bound and NNRTI-bound clusters, as a result of smaller changes in the fingers and thumb subdomains.

Figure 2.

Conformational changes of the “crystallographic ensemble” of RT x-ray structures, captured with PCA. (a) Superposition of the p66 subunits of each member of the ensemble. Protein is shown in Cα trace representation, with each subdomain colored individually. The region referred to as the “polymerase region” is circled, composed of the fingers, palm and thumb subdomains. (b) 2D projection of each structure onto the plane defined by the top two eigenvectors from PCA of the ensemble. The ligation state of each cluster of structures is indicated, with the PDB codes as follows: APO (1DLO); Substrate bound (1RTD, 2HMI); NNRTI bound (1VRT, 2ZD1, 1HNV, 1BQM, 1VRU, 1FK9, 1EP4, 1DTQ, 1RT4, 1RT1). (c) and (d) Collective motions of the polymerase region captured by eigenvectors 1 and 2. Motions are illustrated as linear interpolations between the extreme projections of the structures onto the eigenvectors. Each cylinder therefore describes the path of each Cα atom between the extremes (on a blue-white-red color scale). Arrows indicate the approximate direction of each subdomain.

To characterize the collective motions represented by these dominant eigenvectors, interpolations between the extreme projections of the crystal structures have been shown in Figures 2C and 2D. The bulk of the displacement is seen in the polymerase region in both cases and eigenvector 1 represents a concerted opening and closing event at the nucleic acid binding cleft (Figure 2C). The anti-correlated, rigid-body motions of the fingers and thumb subdomains modulate the size of the cleft and make dramatic changes in position, representing 77% of the variance in the crystallographic ensemble. The functional significance of this motion probably lies in its role in the clamping and release of the nucleic acid substrate, which happens at multiple stages during reverse transcription. Observing the projections onto this mode along the x-axis in Figure 2B, the apo form represents the most closed state of the cleft, in the absence of nucleic acid (fingers and thumb subdomains contacting each other). Widening of the fingers-thumb distance in the substrate-bound forms represents the accommodation of nucleic acid into the cleft, analogously to the “venus flytrap” models of substrate binding/recognition ⁴². Further expansion is seen in all of the NNRTI-bound structures (through additional movement of the fingers), which may be linked to the inhibition mechanism and stabilizes a “hyper-open” form of the empty cleft. Eigenvector 2 represents a significantly smaller displacement of atoms, representing 9% of the variance of the crystallographic ensemble (Figure 2D). This motion involves orthogonal movements of the fingers and thumb subdomains, with the thumb moving outwards in concert with the fingers moving towards the center of the protein. While the functional significance of this motion is less clear, it is possible that this flexibility is required for the polymerase region to translocate along the growing nucleic acid, after successive nucleotide additions. Indeed, a role for motion of the thumb subdomain has previously been proposed in a model for the translocation mechanism ⁴³.

Simulation Dynamics

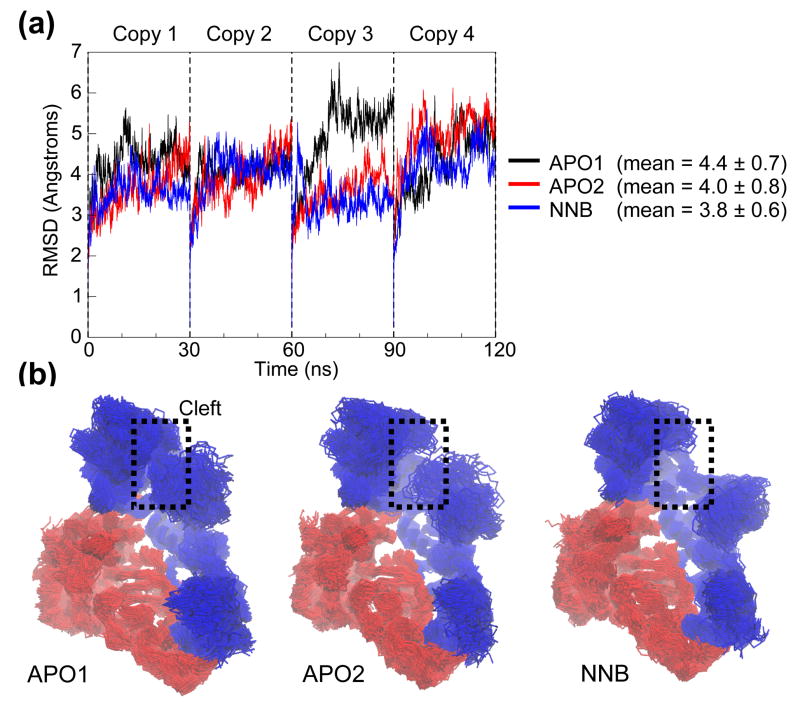
The conformational drift of the RT structure throughout the MD simulations has been measured in terms of the root mean-square deviation (RMSD) with respect to the starting structure (Figure 3). Plotting the RMSD of all Cα atoms as a function of time for the four simulation copies reveals relatively large changes in structure, indicative of significant domain movements (Figure 3A). After an initial sharp rise in each simulation (as the crystal coordinates adjust to simulation conditions), RMSDs vary within a window of between 3 Å – 6.5 Å and in some cases appear to stabilize. However, in most cases the structural drift is continual, the RMSDs not reaching the “plateau” characteristic of less mobile structures. Notably, even the largest RMSDs are contained within an upper-bound set by the RMSD between the two starting structures (7 Å). This suggests that such large drifts are reasonable, given the structural plasticity observed experimentally. Such values have not been attained in previous shorter MD simulations of RT, where structures have typically not exceeded 3.5 Å RMSD from the starting structure and appear to stabilize (e.g. ^{32, 34}). Interestingly, if RMSD analysis from our simulations is restricted to such timescales (i.e. the first 3 ns), the resulting RMSDs are substantially lower and show much softer fluctuations reminiscent of stabilization (data not shown). We therefore propose that the longer timescales attained in this study allow for greater structural changes through enhanced conformational sampling. Another striking feature of the RMSD plots is the difference between individual copies of the same simulation system, which suggests that the multi-copy approach has been successful in generating more conformational variation than a single trajectory. Comparing the structural drift between apo and NNRTI-bound forms across all copies does not yield any significant differences, although the mean RMSD is slightly lower for the NNRTI-bound simulations. This comparison highlights another disadvantage of running single trajectories – if one were to simply analyze the third copy of each system, for example, one might conclude that the APO1 system is substantially less stable than the APO2 and NNB systems. In fact, this difference is diluted when we consider the other three copies and consequently obtain better statistics.

Figure 3.

Conformational drift. (a) RMSD of all Cα atoms from the starting structure, as a function of time. Each 30 ns simulation copy is concatenated into a single 120 ns trajectory for analysis. (b) Superposition of 100 RT snapshots (taken at 1.2 ns intervals) from each simulation system. Protein is shown in Cα trace representation, with p66 and p51 subunits colored blue and red, respectively. Attention is drawn to variations in the dynamics of the nucleic acid binding cleft.

Which RT domains and motions are responsible for the large drifts seen in the RMSD analysis? Figure 3B shows the backbone traces of the three simulation ensembles after least-squares fitting, with notable conformational changes occurring at the nucleic acid binding cleft. Large fluctuations of the fingers and thumb subdomains are seen from both the initial closed conformation in APO1 and the open confirmation in APO2. However, there is a noticeable reduction in the opposing movement of the fingers and thumb in the NNB ensemble, which is clearly identified by the visibility of the palm subdomain (largely occluded in APO2). While there is contact between the tips of the fingers and thumb subdomains in APO2, these regions do not approach each other by the same extent in the NNB ensemble. These qualitative results suggest that modulation of the opening and closing of the nucleic acid binding cleft is deficient with nevirapine bound.

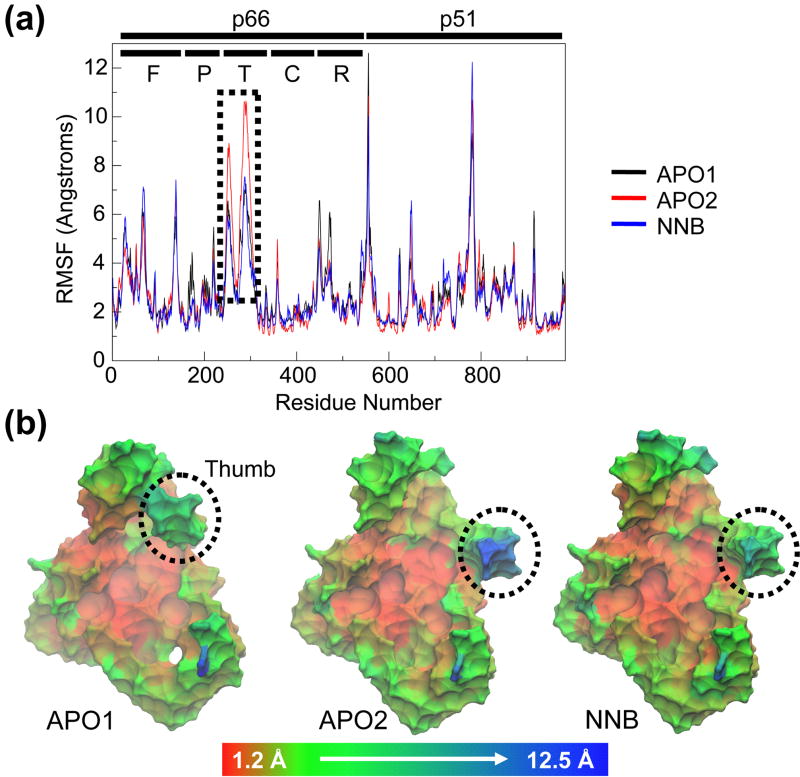
A quantitative analysis of the flexibility of the different subdomains of RT is performed through the root mean-square fluctuation (RMSF) of Cα atoms, with respect to their time-averaged positions (Figure 4). Plotting the RMSF as a function of residue number (Figure 4A) reveals greatest movements from the fingers and thumb subdomains of the p66 subunit, as observed above. A smaller degree of flexibility is seen at the RNH domain, while the p51 subunit generally shows much lower values than p66, consistent with its structural role in the heterodimer. The two sharp peaks in the latter half of the plot belong to the highly mobile C-terminus of p66 and a very flexible solvent-exposed loop in the center of p51. Comparing the RMSFs of the different simulations reveals very similar profiles and we do not observe the ligation state dependent differences seen in previous studies, whereby NNRTI binding reduced RT flexibility across all residues ³⁴. However, a pronounced local effect of NNRTI binding is observed at the tip of the p66 thumb subdomain (indicated by the dotted box in Figure 4A). The APO2 simulations (red) show a marked increase in thumb flexibility compared to the NNB simulations (blue). In contrast, the APO1 simulations show identical p66 thumb flexibility to the NNB simulations, likely reflecting the different starting conformations of the cleft. The RMSF results are visualized in the context of the 3-dimensional starting structure of each system in Figure 4B. These images depict a relatively immobile core at the center of the heterodimer, with all flexibility occurring around the periphery of the structure. Together with the snapshots seen in Figure 3B, it is clear that the outermost region of the p66 thumb domain is more mobile in the absence of nevirapine, specifically making stronger moves towards the fingers.

Figure 4.

Conformational flexibility. (a) RMSF of all Cα atoms from their time-averaged positions. Each subunit is indicated by black lines, along with the subdomains of the p66 subunit (F=fingers, P=palm, T=thumb, C=connection, R=RNH). (b) Starting structures of each system, colored by RMSF on a red-green-blue color scale (scale is non-linear to clarify less mobile regions). Protein is shown in molecular surface representation (Cα atoms only). Thumb subdomain is highlighted.

Essential Dynamics Analysis

The results above suggest that nevirapine may exert a local effect on the flexibility of residues in the polymerase region. However, considering the high dimensionality of proteins, it is particularly difficult to identify which motions are of biological importance. In order to filter out functionally relevant collective motions (the likely targets of an inhibition mechanism) from local “noise”, we have performed PCA to uncover the essential dynamics of each simulation ensemble ⁴¹. This allows us to characterize the essential motions from each simulation and compare them both with each other and with the motions from the crystallographic ensemble (as seen in Figure 2). Such a technique has proved valuable in identifying ligand-induced effects on functional dynamics of the apo-enzyme in other work (e.g. ^{44, 45, 46}).

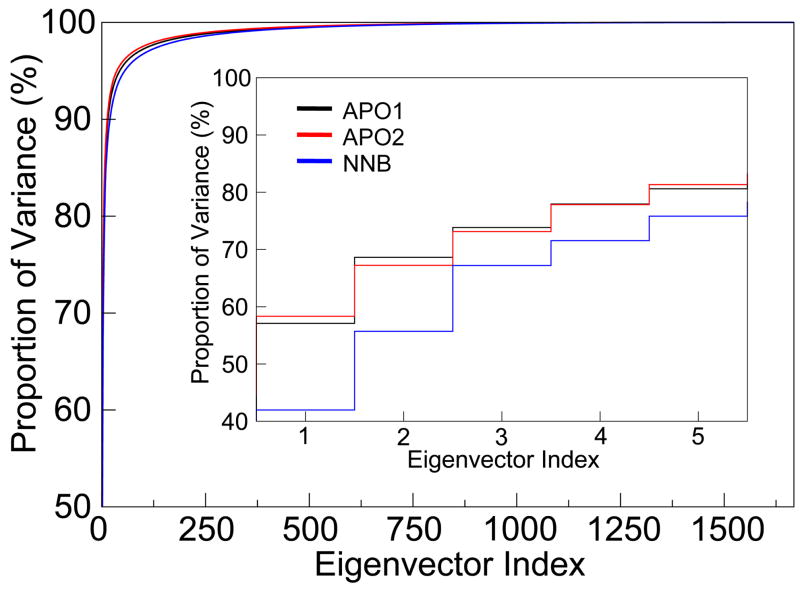
Figure 5 shows the cumulative proportion of the total variance (i.e. total mean-square fluctuation) which is captured by each eigenvector from the PCA of the MD trajectories. This plot clearly illustrates that the bulk of the protein dynamics are described in a relatively small number of eigenvectors, which represent collective movements of atoms. From the inset, the first eigenvector in each system dominates, representing as much as 58% of all fluctuations, while successive degrees of freedom capture significantly smaller modes. While this trend is seen in all systems, it is clear that the total proportion of variance captured by the first few eigenvectors is consistently lower for the NNB system compared to both the APO1 and APO2 systems. This result suggests that nevirapine binding affects the essential dynamics of RT, possibly by dampening key motions (which have stronger displacements in the apo form).

Figure 5.

Essential dynamics analysis. Cumulative proportion of total variance captured by the eigenvectors from PCA of the MD ensembles. Inset shows the values for the top 5 eigenvectors, which encompass the “essential subspace”.

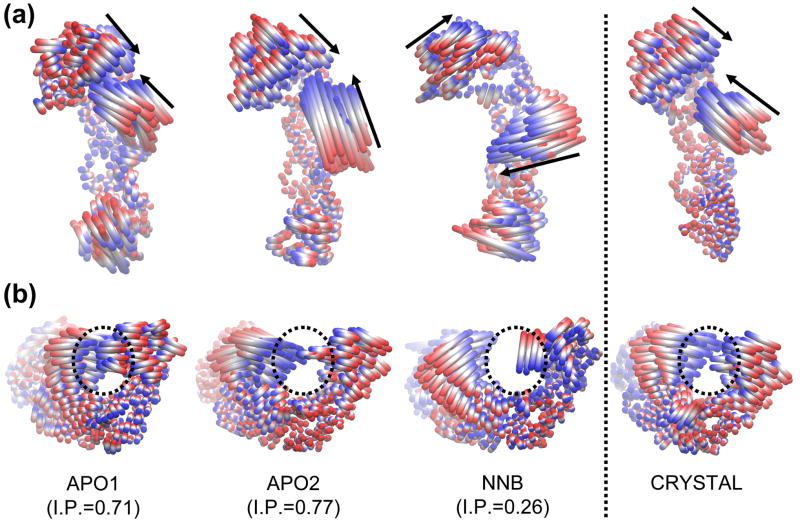
The most significant result of the analysis was obtained when we compared the essential motions captured by the first few eigenvectors, by initially viewing animations of the extreme projections of the trajectories. The motion represented by eigenvector 1 showed dramatic differences around the polymerase region when comparing the apo and NNRTI-bound simulations (Figure 6). In the APO1 and APO2 simulations, eigenvector 1 is characterized by an opening/closing of the fingers and thumb subdomains which is very similar to that seen in the crystallographic ensemble. Views of the motion from both the top and the side of the protein reveal qualitative similarities which are supported by high inner product values of 0.71 and 0.77, respectively. The amplitude of the motion is slightly stronger in the APO2 system, largely due to the greater motion of the thumb subdomain and likely because of the initial open configuration of the cleft. In sharp contrast, eigenvector 1 of the NNB simulations shows a very different motion, with the fingers and thumb subdomains making movements roughly orthogonal to those seen in the apo simulations. As a result, there is no change in the size of the cleft, as no moves are made towards the center of the cleft, and the dissimilarity of the motion is seen in the low inner product value of 0.26. This result explains the different variance of the fingers and thumb subdomains seen in the trajectory snapshots in Figure 3B – i.e. opening and closing of the cleft is not the dominant mode of motion in the NNB system. In fact, eigenvector 1 from the NNB system actually bears resemblance to eigenvector 2 from the crystallographic ensemble (as seen in Figure 2D) and this is reflected in the high inner product value of 0.7 between these two motions. Furthermore, motions more similar to the characteristic opening/closing motion of the cleft are seen in less dominant modes of the NNB system, with eigenvectors 2 and 6 having higher inner products of 0.57 and 0.66, respectively. By definition, these lower order eigenvectors represent significantly less fluctuation than the first eigenvector (combined, eigenvectors 2 and 6 represent 17% of the total variance in the NNB system, compared to 42% for eigenvector 1). Therefore our results show that opening and closing motions of the cleft are attenuated in the presence of nevirapine, such that they are relegated to less dominant modes in the PCA results.

Figure 6.

Comparison of the motion described by eigenvector 1 from the MD and crystallographic ensembles. Motions are illustrated as linear interpolations between the extreme projections of the structures onto the eigenvectors. (a) and (b) Two alternative views of the motion, from above and behind the nucleic acid binding cleft, respectively. Arrows indicate the approximate direction of the fingers and thumb subdomains. Dotted circles highlight the nucleic acid binding cleft. The inner product (I.P.) between the eigenvector from each MD system and the crystallographic ensemble is indicated.

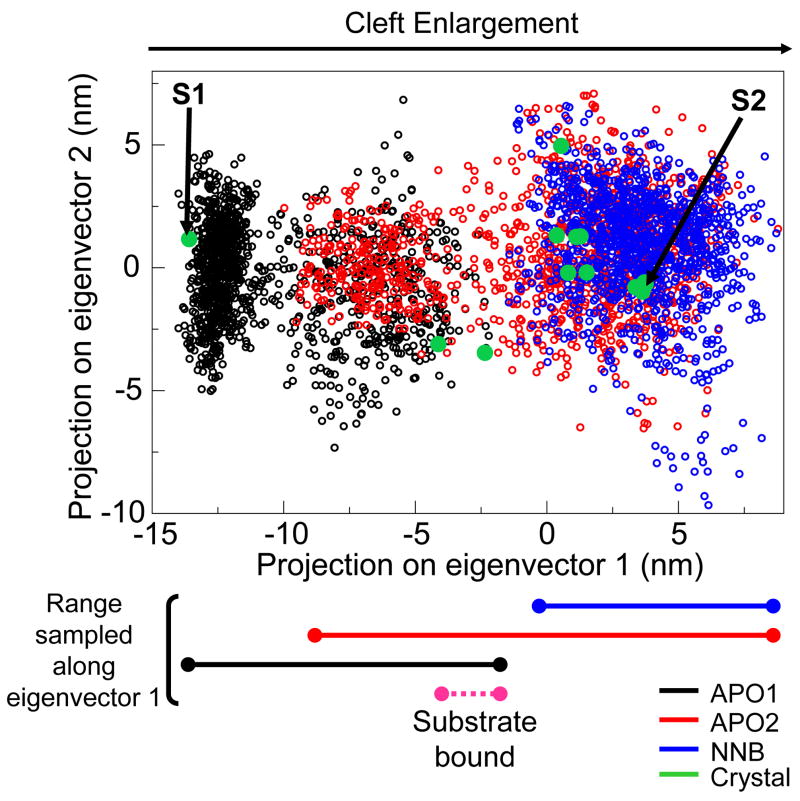
In order to directly compare regions sampled by the essential motions from the trajectories, we have projected the simulation ensembles onto the plane defined by the top two eigenvectors of the crystallographic ensemble (for example, as seen in ⁴⁷). As expected, notable differences are seen in the fluctuation of the systems along eigenvector 1 (Figure 7). The APO1 system largely occupies the closed cleft region, but also contains a cluster of states in a more open conformation, similar to that seen in the substrate-bound crystal forms. Similarly, the APO2 system explores both the open region common to NNRTI bound structures and a second more closed conformation. Interestingly, the APO1 and APO2 systems show considerable overlap in the cluster of conformations which is furthest from their starting structures. This “semi-open” state of the cleft marks the midpoint between the two starting structures and could represent a low energy conformation which initially binds the nucleic acid substrate. In contrast, the NNB system is largely confined to the NNRTI-bound region of the plane, which is a subset of approximately half the region sampled by the APO2 system. Unlike the APO2 system, in the cleft closure events that do occur, none are strong enough to overlap with either the substrate-bound structures or the APO1 structures. For eigenvector 2, we observe similar ranges sampled by all systems, supporting the earlier observation that this motion is unrestricted by nevirapine binding.

Figure 7.

Comparative sampling of essential motions. 2D projection of MD structures onto the plane defined by the top two eigenvectors from PCA of the crystallographic ensemble (as also shown in Figure 2). Unfilled circles represent the projections of structures taken from each MD system. Filled green circles represent projections of the crystal structures. “S1” and “S2” indicate the starting crystal structures used for the APO1 and APO2/NNB systems, respectively. The approximate range of eigenvector 1 sampled by each MD system is indicated below, along with the range sampled by the two substrate bound crystal structures.

Another method which has been used to detect inter-simulation differences is the “combined essential dynamics” approach, whereby PCA is performed on the concatenated MD trajectories ^{45, 48}. The individual trajectories are then projected onto the resulting eigenvectors to identify which regions are sampled. Thus, the reference set of essential dynamics is obtained from MD simulation rather than crystallography. We repeated the 2D projection shown in Figure 7 using this combined approach and produced a plot with striking similarity, suggesting high correlation between the principal components from the crystallographic and combined 360 ns MD ensemble (see Supplementary Info). Indeed, the inner products of the top two eigenvectors from the two different sources of structures are very high at 0.93 and 0.8, respectively. Interestingly, these values are higher for the combined 360 ns MD ensemble than the individual 120 ns sub-ensembles, an effect which has been observed previously when comparing crystallographic and MD principal components of the T4 lysozyme ⁴⁷. We note that the inner products for eigenvectors 3 and greater are considerably smaller; however these motions combined represent only 14% and 25% of the fluctuations of the crystallographic and MD ensembles, respectively. This result serves to validate the MD method in its reproduction of the experimentally observed large-scale motions of RT.

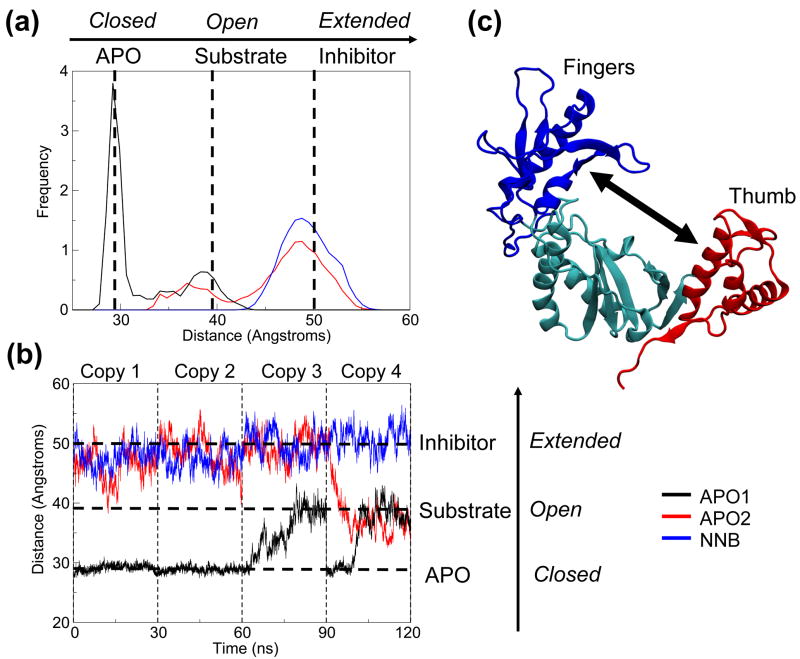
The PCA results suggest that nevirapine binding is associated with a defective opposing motion of the p66 fingers and thumb subdomains, which dominates the crystallographic and apo simulation ensembles. We validated this by measuring the distance between the center-of-mass of the thumb and fingers subdomains as a function of time (Figure 8). The distribution of inter-domain distances correlates very well with the densities of the regions sampled by each system along eigenvector 1 and shows the overlap of the apo systems (Figure 8A). Both apo systems are able to make opening/closing motions, which allows them to attain inter-domain distances similar to those seen in the substrate-bound crystal structures. The cleft of the NNB system is unable to close to the same extent as the APO2 system and thus cannot reach the dimensions of the substrate bound structures. This suggests that incomplete closure of the cleft may preclude the formation of a catalytically active complex with nucleic acid. Analyzing the distances as a function of time, we can clearly see the value of running multi-copy simulations (Figure 8B). For the APO1 simulation, the fingers and thumb retain their initial closed conformation for the first two copies, but open up in the third and fourth copies. In the APO2 simulations, a pronounced closing event occurs in the fourth copy, with fluctuations that attain the cleft size of the substrate-bound crystal structure in the first and second copy. In the NNB simulations, the distance fluctuates around its initial value, never reaching the cleft size of the substrate-bound crystal structure in any copies. These measurements support our observation that nevirapine weakens the inter-domain motion of the fingers and thumb subdomains, locking them in an extended conformation. Furthermore, they show that multi-copy simulations of this timescale are necessary to observe such large conformational changes, which may not be captured otherwise.

Figure 8.

Center-of-mass distance between fingers and thumb subdomains. (a) Normalized histogram of distances calculated for each MD system. (b) Distances as a function of time. Dotted lines indicate the distances for APO (PDB code 1DLO), substrate bound (PDB code 1RTD) and NNRTI bound (PDB code 1VRT) crystal structures, as references. (c) Cartoon representation of the polymerase region, illustrating the distance calculated. Fingers, thumb and palm subdomains are colored blue, red and cyan, respectively.

NNRTIs Act As Molecular Wedges

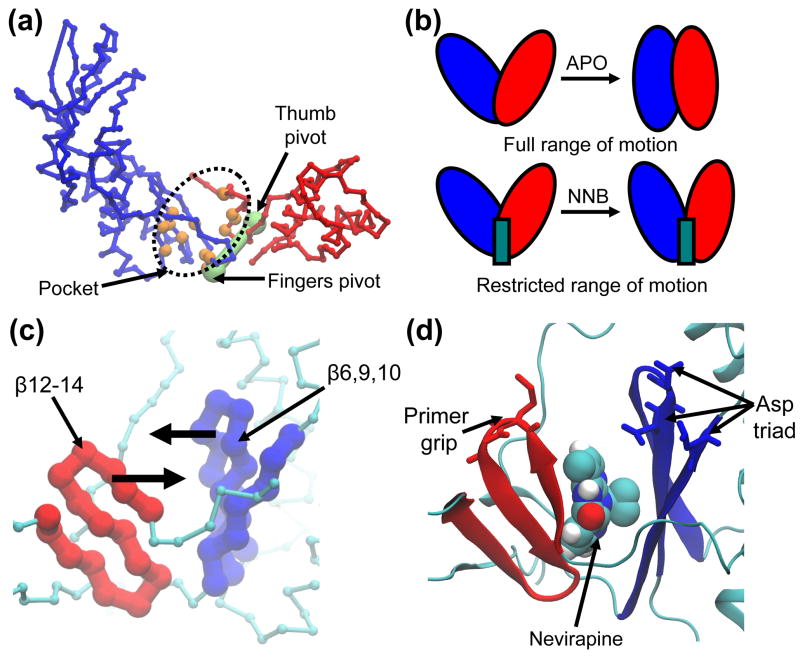
How does nevirapine exert an inhibitory effect on the dominant subdomain motion of the RT polymerase region? Further inspection of this motion was performed using HingeFind ⁴⁹, which allowed us to define the two groups of residues which make opposing rigid body movements along this mode. The first group is composed of the fingers subdomain and neighbouring residues of the palm subdomain (colored blue in Figure 9A), while the second group is composed of the thumb subdomain and neighbouring residues from the palm subdomain (colored red in Figure 9A). By using the extreme projections on this motion, we were able to calculate the hinge axis and pivot-point for the rigid-body motion of each group (green spheres in Figure 9A). Importantly, the pivot for each motion is located adjacent to the NNIBP, and thus NNRTIs bind at the hinge region for both groups. Because full motion along this mode requires the opposing movement of residues which line the NNIBP, the presence of a NNRTI effectively “wedges” this hinge region through steric block, and thus precludes full closure of the two groups (Figure 9B). We therefore propose that NNRTIs block a key hinge region in the polymerase region, which normally permits the full opposing motion of the fingers and thumb subdomains (and associated palm residues). Previous computational studies of RT, using elastic network models, have also implicated the NNIBP region in a hinge-bending function ^{35, 37}. A very similar ligand-induced effect is seen in a previous simulation study of apo and calcium-bound annexin V, whereby calcium dampens a key hinge-bending motion and favors more open hinge conformations ⁴⁴. Interestingly, recent structures of the bacterial RNA polymerase (RNAP) reveal a very similar mechanism of inhibition by antibacterial compounds ⁵⁰. These drugs bind at a hydrophobic site analogous to the NNIBP of RT and are thought to inhibit the enzyme by blocking a hinge that modulates the size of a nucleic acid binding cleft. Therefore, this allosteric hinge blocking mechanism may be universal to related nucleic acid binding proteins and could be a useful target for therapies targeting novel enzymes.

Figure 9.

NNRTIs block a key hinge region in the polymerase region of RT. (a) Proximity of the binding pocket to the pivot points for rigid-body motion of the fingers and thumb subdomains. Residues lining the pocket are colored in orange and pivot points (calculated using HingeFind) are colored in green. Fingers and thumb subdomains (and associated regions of the palm subdomain) are colored in blue and red, respectively. Polymerase region shown in Cα trace representation. (b) Schematic illustration of the hinge-blocking mechanism proposed for NNRTIs. NNRTIs wedge the hinge region and preclude full movement of the hinge (i.e. opening/closing of the cleft). (c) and (d) Closeup view of the hinge region. Two β-sheets line the binding pocket and slide against each other during normal function of the hinge. β-sheets are colored according to the subdomain they move in concert with. These β-sheets house the primer grip (residues Met230, Gly231) and catalytic aspartate triad (residues Asp110, Asp185, Asp186), which are shown in stick representation.

How does the defective hinge bending motion of RT preclude the chemical step of DNA polymerization? In the immediate vicinity of the hinge region are two β-sheet structures of the palm subdomain which lie on either side of the NNIBP and effectively “sandwich” the NNRTI. The first is composed of β-strands 12–14 (associated with the thumb subdomain motion) and the second is composed of β-strands 6, 9 and 10 (associated with the fingers subdomain motion). The hinge-bending motion causes the two sheets to “shear” against each other (Figure 9C), thus bringing the sheets closer together when the hinge closes and further apart when the hinge opens. The upper section of these structures each houses crucial residues for polymerization: the first sheet includes the primer grip and, on the opposite side, the second sheet includes the catalytic triad (Figure 9D). Restriction of the hinge motion by a NNRTI would therefore constrain the constellation of the primer grip, catalytic triad and bound substrate, causing the formation of an unproductive ternary complex. A second possibility is that defective closure of the hinge and cleft reduces the number of contacts between RT and its nucleic acid substrate, causing the 3′ primer end of the substrate to prematurely move away from the polymerase active site. This suggestion is based on recent work by Liu and coworkers, who propose that the loosening of the RT cleft around its nucleic acid substrate is part of the natural cycle of reverse transcription and causes the enzyme to slide away from the 3′ primer end when transcription is complete ³⁰.

Conclusions

In this work, we have performed all-atom MD simulations of the HIV-1 RT enzyme, in both the presence and absence of the NNRTI nevirapine. The principal aim of this study was to identify how the binding of a NNRTI at an allosteric site affects the conformational dynamics of RT such that it inhibits DNA polymerization. We have employed PCA as a tool to extract the essential dynamics from both experimental (crystallographic) and theoretical (MD) ensembles of RT structures, focussing on the catalytic p66 subunit. Comparison of the dominant modes of motion from each source revealed that while NNRTI-free simulations reproduced very similar movements to those of the crystallographic dataset, those of the NNRTI-bound simulations were quite distinct. Most significantly, the NNRTI-bound enzyme is severely constrained in its sampling of the dominant mode of fluctuation, which is characterized by the opening/closing motion of the fingers and thumb subdomains. We have shown that NNRTIs bind close to the hinge region for this motion and “wedge” between the subdomains, thus restricting the range of the hinge-bending mechanism. This result is supported by previous computational studies, which predicted from static structures that the NNIBP lies at an important hinge region and that NNRTI-induced interference is the basis of inhibition ^{35, 37}. We finally sought to link the mechanical obstruction of the hinge region with the resulting impaired catalytic function. We found that the hinge motion influences the geometry of two key regions of the active site, which lie on β-sheets on opposite sides of the NNIBP – the primer grip and the catalytic triad. As the hinge opens and closes, the separation between these groups increases and decreases, respectively. Thus, inhibition is likely to be achieved through constrained relative movements of these residues, the constellation of which is thought to be vital to catalysis ^{19, 26}. We found that the “wedging” effect of nevirapine precludes full closure of the hinge motion and therefore NNRTIs may keep the primer grip and catalytic triad too distant for correct alignment of the ternary complex. Our proposal that a defective hinge distorts the polymerase active site is also supported by kinetic analyses which concluded that nucleotide incorporation is indirectly blocked by NNRTIs through a change in the conformation of the active site, as opposed to direct interference with the chemical reaction ⁵¹. We note that there may be other, longer range effects of the blocked hinge mechanism which may also contribute to inhibition of RT by NNRTIs.

Considering the magnitude of RT structural variation observed

crystallographically, a multi-copy simulation approach was adopted in this study, whereby four independent trajectories were generated for each system. In addition, the timescale of the simulations was extended to an order of magnitude greater than previous MD studies of RT, yielding a cumulative total simulation time of 360 ns. Our aim was to enhance the conformational sampling of such a large protein, on the grounds that extended and multiple trajectories increase the probability of transitions between energy minima ³⁸. Indeed, significant inter-copy differences were observed in the dynamics of RT, which allowed a more complete sampling of the dominant mode of fluctuation compared to shorter and/or independent trajectories. That this motion is central to the key effect of NNRTI binding makes enhanced sampling all the more necessary for our objective. The extremely high correlation between the two most dominant motions extracted from the crystallographic and combined MD ensembles gives confidence that the multi-copy MD simulation approach can reproduce experimental structural variation.

Despite continued advances in computer hardware, conventional all-atom MD simulations of proteins are still restricted to the nanosecond timescale and are liable to becoming trapped in energy minima. Therefore, techniques have been developed to increase transitions across energy barriers and thus enhance conformational sampling, while retaining the granularity of all-atom structures. Such methods include accelerated MD ⁵², replica exchange ⁵³ and conformational flooding ⁵⁴, and represent promising approaches for future computational studies of RT. Another possibility is the essential dynamics sampling method ⁵⁵, whereby sampling is enhanced along a subset of modes extracted from existing simulations using PCA (i.e. the dominant eigenvectors). This would allow us to efficiently study the effect of a range of NNRTIs on the opening/closing motion of the p66 polymerase region, in isolation from other degrees of freedom. In particular, it could be used to predict the potency of NNRTIs and design novel compounds which optimally block the hinge region. We also note the potential of using PCA of MD ensembles for the discovery of new RT hinge regions which may also be susceptible to occlusion. Such a site on the RNH subdomain has previously been proposed ³⁷ and our preliminary results suggest the existence of a viable drug binding site in this vicinity. Work is currently underway to use MD simulation to predict the mechanical impact of compounds which bind in this region, with the aim of debilitating motions necessary for the RNase activity of RT. Finally, MD simulations such as those described here can be combined with virtual docking methods to suggest leads for new drugs ^{56, 57, 58}.

Methods

Simulation Systems

Two different RT crystal structures were used to generate the initial protein coordinates for the MD simulations, as shown in Figure 1. The APO1 system starts from the 2.7 Å unliganded structure of RT, which is characterized by both an occluded nucleic acid binding cleft and NNIBP (PDB code 1DLO ¹⁷). The APO2 and NNB systems start from the 2.2 Å nevirapine bound structure, which has an open nucleic acid binding cleft and an open NNIBP (PDB code 1VRT ⁵⁹). To generate the APO2 system, the nevirapine molecule was removed from the NNIBP (eventually to be replaced by water molecules during the solvation step). It is impossible to generate a nevirapine bound version of the APO1 system as the NNIBP does not exist and therefore there is no way to dock a drug molecule. The APO2 system was designed to assess the effect of NNRTI presence/absence on the same starting structure as the NNB system.

Simulation Setup

Missing heavy atom coordinates in PDB code 1DLO were taken from a substrate-bound structure of RT (PDB code 2HMI) after least-squares superposition and subsequent energy minimization. The same procedure was used to model missing heavy atom coordinates in PDB code 1VRT, this time using PDB code 1DLO as the template. Hydrogen atoms were added using the “pdb2gmx” procedure of the GROMACS package (http://www.gromacs.org). Both “repaired” protein structures contained a total 983 amino acids: residues 1–556 from the p66 subunit and residues 557–983 from the p51 subunit.

Nevirapine was parameterized for the MD force field using the PRODRG2 program, which also adds hydrogen atoms and assigns atomic partial charges ⁶⁰. The assigned partial charges were validated by comparison with those calculated with the RESP module of AMBER ⁶¹, which uses the electrostatic potential produced by the ab initio quantum chemistry package GAUSSIAN ⁶² at the Hartree-Fock level with the 6–31G^* basis set.

Protein structures were centered in a simulation cell of dimension 13.2 nm × 11.2 nm × 11.3 nm and energy minimized (together with nevirapine, when present) to remove unfavorable atomic contacts. The system was then solvated with explicit water molecules, energy minimized and chloride counter-ions were added to preserve electroneutrality. The solvated systems contain approximately 160,000 atoms. Final energy minimization was followed by an equilibration phase of 1 ns, during which all protein (and nevirapine, when present) heavy atoms were position restrained, to allow relaxation of the solvent around the solute. The unrestrained production runs were then simulated for 30 ns each. A total of 12 × 30 ns trajectories were generated (cumulative total simulation time of 360 ns).

All energy minimization was performed using 100 steps of the steepest descents algorithm. Equilibration was performed using harmonic restraints on all heavy atoms (force constant = 1000 kJ mol⁻¹ nm⁻²), a Berendsen thermostat ⁶³, and pressure maintained at 1 bar by a Berendsen barostat ⁶³. Convergence of the potential energy and volume of the system was used to ensure adequate solvent relaxation during equilibration. A separate equilibration (and subsequent production run) was performed for each of the four copies of each system, by using a different randomization seed for the initial atomic velocities ³⁸. For analysis, the four 30 ns trajectories from each system were concatenated into a single 120 ns trajectory. The unrestrained production runs were performed with a Nosé-Hoover thermostat ^{64, 65} and pressure maintained at 1 bar by a Parrinello-Rahman barostat ⁶⁶. Simulations were run in the NPT ensemble and at a temperature of 300 K. Particle mesh Ewald (PME) was used to treat long-range electrostatics ⁶⁷ and the single point charge (SPC) water model ⁶⁸ was used for the solvent (as recommended for the GROMOS force field). Chloride anions were positioned randomly among the solvent to neutralize the net positive charge of the protein. An integration time step of 2 fs was used. The LINCS algorithm was used to restrain all bond lengths ⁶⁹. Simulations were set up, performed and analyzed using the GROMACS v.3.3.1 molecular dynamics simulation package ^{70, 71, 72}. The latest parameter set for the GROMOS force field (53A6) was used ^{73, 74}. All molecular graphics were produced with VMD ⁷⁵.

Principal Component Analysis

In this study, Principal Component Analysis (PCA) has been used to identify and compare the principal modes of motion of the catalytic p66 subunit of RT, using both crystallographic and MD structure ensembles. We focus on p66 as this is the subunit where polymerization and NNRTI binding takes place and is thus the most relevant region for exploring the inhibitory effects of nevirapine. Firstly, the covariance matrix is constructed, based on the 3-dimensional positional fluctuations of Cα atoms from their ensemble average position (after least-squares fitting to remove overall rotational and translational motion). Next, diagonalization of the covariance matrix yields a set of eigenvectors and corresponding eigenvalues, which represent the direction and amplitude of the motion, respectively. The eigenvectors are then ranked by decreasing eigenvalue, such that the first eigenvector represents the largest contribution to the total fluctuation of the system. In order to visualize the motions represented by the eigenvectors, the structures from the ensembles can be projected onto each eigenvector of interest and transformed back into Cartesian coordinates. The two extreme projections along the eigenvector (for example, the most open and most closed states of a “breathing” motion) can then be interpolated to create an animation (illustrated statically in this study by showing all frames simultaneously).

Principal components are compared in this study in two ways. The directions of two eigenvectors generated from different ensembles (e.g. with and without inhibitor bound) can be qualitatively compared from visual observation of the animation. Quantitatively, eigenvector directions can be compared using the inner product of two vectors, with a value of 0 indicating orthogonal directions and 1 indicating identical directions. A second approach is to compare the region sampled along common eigenvectors, by analyzing the range and distribution of ensemble projections along those eigenvectors. For example, this can be used to compare the ability of simulation ensembles to sample a motion which is obtained from an experimental dataset.

Construction and diagonalization of the covariance matrix is performed using the “g_covar” procedure of GROMACS. Projections of structures onto eigenvectors, generation of interpolation animations and calculation of inner products is performed using the “g_anaeig” procedure of GROMACS.

Supplementary Material

01

Figure S1. Combined essential dynamics analysis of 360 ns MD ensemble. (a) 2D projection of MD structures onto the plane defined by the top two eigenvectors from PCA of the 360 ns combined MD ensemble. Unfilled circles represent the projections of structures taken from each MD system. Filled green circles represent projections of the crystal structures. (b) Inner product matrix of the top 5 eigenvectors derived from the 360 ns MD ensemble and the crystallographic ensemble. Values are colored on a scale from white (0) to black (1) to indicate the similarity of the eigenvectors. Values for the top 2 eigenvectors are indicated. (c) Proportion of total variance captured by the top 2 eigenvectors (PC1 and PC2) of the 360 ns MD ensemble and the crystallographic ensemble.