Linear dichroism and circular dichroism in photosynthesis research

Abstract

The efficiency of photosynthetic light energy conversion depends largely on the molecular architecture of the photosynthetic membranes. Linear- and circular-dichroism (LD and CD) studies have contributed significantly to our knowledge of the molecular organization of pigment systems at different levels of complexity, in pigment–protein complexes, supercomplexes, and their macroassemblies, as well as in entire membranes and membrane systems. Many examples show that LD and CD data are in good agreement with structural data; hence, these spectroscopic tools serve as the basis for linking the structure of photosynthetic pigment–protein complexes to steady-state and time-resolved spectroscopy. They are also indispensable for identifying conformations and interactions in native environments, and for monitoring reorganizations during photosynthetic functions, and are important in characterizing reconstituted and artificially constructed systems. This educational review explains, in simple terms, the basic physical principles, and theory and practice of LD and CD spectroscopies and of some related quantities in the areas of differential polarization spectroscopy and microscopy.

Electronic supplementary material

The online version of this article (doi:10.1007/s11120-009-9424-4) contains supplementary material, which is available to authorized users.

Introduction

In order to understand the primary processes of photosynthesis, it is essential to have a detailed and an accurate information about the molecular architecture of the pigment system of the antenna and the reaction center complexes, as well as their (macro-)assemblies.

The non-invasive techniques of linear dichroism (LD) and circular dichroism (CD) have contributed significantly to our knowledge of the molecular organization of different complexes and of the pigment systems in entire membranes from a great variety of photosynthetic organisms. It was suspected already in the mid-1970s and the early 1980s, and confirmed by later systematic LD spectroscopic studies, that the pigment dipoles are aligned under well-defined orientation angles with respect to the main axes of the complexes and/or of the membrane planes, and that the non-random orientation of the pigment molecules is a universal property: this holds true for virtually all the photosynthetic pigments and in all organisms (Clayton 1980; Breton and Verméglio 1982). CD spectroscopy has also been widely used since the early 1970s and 1980s, during which the basic features and the occurrence of excitonic interactions in virtually all pigment–protein complexes have been established (Pearlstein 1991).

In the last two decades, LD and CD spectroscopies have gradually matured to become quantitative tools, which provide important information on different pigment systems and different, often high, levels of complexity, also under physiologically relevant conditions. Two chapters in the earlier books (Van Amerongen and Struve 1995; Garab 1996) have provided a detailed description of LD and CD techniques and the main areas of applications, while the monograph on photosynthetic excitons (Van Amerongen et al. 2000) has provided the theoretical background necessary for the in-depth interpretation of short-range, excitonic interactions between pigment molecules. For more complex, highly organized systems, the CD theory of psi (polymer and salt-induced)-type aggregates should be used (Keller and Bustamante 1986; Tinoco et al. 1987).

The purpose of this educational review is to provide an introduction to LD and CD spectroscopies, as well as to some related differential polarization spectroscopy and microscopy techniques. We explain, in simple terms, the basic physical principles and demonstrate, via a few recent examples, the use of these tools in photosynthesis research. For a deeper understanding, readers are referred to the reviews and monographs cited above, and to articles quoted below in this review. For a basic understanding of the physical principles related to photosynthesis, see Clayton (1980).

Transition dipole moments of photosynthetic pigment molecules

The absorption of light at a given wavelength corresponds to the transition from an electronic ground state to a given excited state of the molecule. The transition dipole moment, μ, which is associated with the electronic transition can be envisaged as a two-headed vector. The transitions for most photosynthetic pigments and most absorbance bands can be assigned to well-defined orientations with respect to the molecular coordinate system (see supplemental Fig. S1). (However, for some absorbance transitions, e.g., for chlorophyll (Chl) a in the Soret region (in the blue part of the spectrum), the transition is more complex because the excitation in this region results in the excitation of two or more absorption transition dipole moments, and the transition moment must thus be described in terms of averages of different transitions (Van Zandvoort et al. 1995).)

The squared length of the transition dipole moment is proportional to the extinction coefficient of the molecule for the given absorbance band. The specific transition dipole moment for the given transition determines not only the strength of the absorption but also the ability of the molecule to interact with polarized light, and sets the conditions for intermolecular interactions as well. For linearly polarized light, the absorbance is proportional to the square of the scalar product of the electric vector (E) of the light and the transition dipole vector (μ), i.e., the absorbance is proportional to E² μ² cos² α, where α is the angle between the two vectors. This is the basis of all LD measurements. In circularly polarized light spectroscopy, i.e., for CD, the interaction between the light and the sample also depends, albeit often in a complex manner, on the orientations of the transition dipole moments of the molecules that compose the structure.

Linearly and circularly polarized light: LD and CD measurements

For linearly polarized light (often called plane-polarized light), the electric vector E (“the light vector”) oscillates sinusoidally in a direction (plane) which is called the polarization direction (plane). For circularly polarized light, the magnitude of E remains constant, but it traces out a helix as a function of time. In accordance with the convention used in CD spectroscopy, in the right and the left circularly polarized light beams, when viewed by an observer looking toward the light source, the end-point of E rotates clockwise and counterclockwise, respectively. (See supplemental Movie 1.)

On using the principle of superposition, it can easily be shown that circularly and linearly polarized light beams can be represented as the sum of two orthogonal linearly polarized beams, in which the amplitudes are equal and the phases are shifted exactly by a quarter or a half of the wavelength, respectively (supplemental movie 1). This principle can be used for producing orthogonal linearly (e.g., vertically and horizontally) or circularly (left- and right-handed) polarized beams. In most commercially available dichrographs and home-built setups, this is done by using a photoelastic modulator (PEM) that operates at high frequency, typically at 50 kHz. In this way, the polarization state of the measuring beam is modulated sinusoidally. In order to measure the dichroism of the sample, the signal of the detector is demodulated by a proper circuit, usually an AC amplifier locked at the frequency and phase of the polarization modulation. This yields a difference, or differential polarization (DP) signal, ΔI. The corresponding, linear- or circular-dichroism signals are calculated from the ratios of ΔI and I, the signal from the average transmitted light intensity; this ratio is proportional to LD (or CD) = A₁ − A₂, the absorbance difference of the two orthogonally polarized beams (ΔA ≈ −2.3 ΔI/I). Hence linear- and circular-dichroism measurements usually can be performed on the same experimental setup. Indeed, most dichrographs, designed for sensitive CD measurements, offer the accessory for LD measurements. In these instruments, the high-frequency modulation and demodulation techniques are very important in warranting high signal to noise ratios, which in turn make very weak signals, 10⁻⁴–10⁻⁵ OD in magnitude, measurable. Unlike CD, LD—for “good” samples, exhibiting strong, 10–20% dichroism—can be measured with the aid of spectrophotometers and passive polarization optical elements. (Care must be taken to avoid possible artefacts due to, e.g., polarization selective monochromators or detectors. A simple test is: LD must reverse sign if rotated by 90º around the direction of propagation of the measuring beam.)

Linear dichroism

In order to obtain a non-zero LD signal in a macroscopic sample, the particles must be aligned because in random samples, the difference between the absorbance with the two orthogonally polarized beams averages to zero, i.e., the LD vanishes even if the samples possess intrinsically anisotropic molecular architectures. Evidently, the magnitude of the LD depends on the efficiency of the alignment of the sample, and ultimately on the selection of the method of orientation.

Methods of orientation of membranes and particles

The first rule is that there is no single good technique; rather, different methods are suited for different samples and purposes.

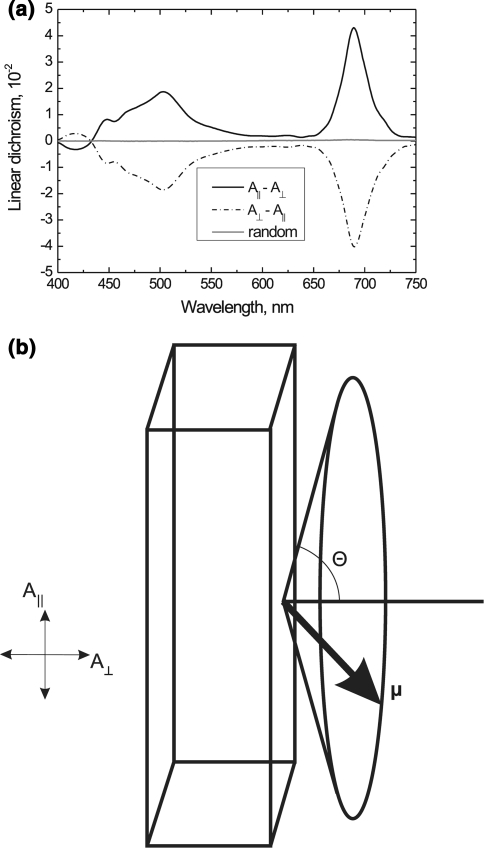
For whole chloroplasts and entire thylakoid membranes, a magnetic field of about 0.5 T (Tesla) provides a very good, nearly saturating degree of alignment. It aligns the membranes with their planes preferentially perpendicular to the field, thus offering convenient edge-aligned position of the membranes (Fig. 1). (With this alignment, A₁ and A₂, respectively, are the absorbances of the polarized light parallel and perpendicular to the membrane plane, i.e., LD = A_‖ − A_⊥; for the face-aligned position, the propagation of the measuring beam being perpendicular to the membrane plane, A₁ = A₂.) Moreover, this technique poses no limitation on the reaction medium; also, the aligned state can readily be trapped at low temperatures (or in gel). Field strengths of 0.5–1 T can readily be obtained between two alloy magnets, and thus the alignment can be performed in the sample compartment. Magnetic alignment can also be used for lamellar aggregates of Light-Harvesting Chl a/Chl b Complex II (LHCII), which may require somewhat higher fields for saturation. These magnetic alignments are based on sizeable diamagnetic anisotropies of the sample, which arise due to ordered arrays of molecules or particles possessing well defined, but individually very small diamagnetisms. Hence, the orientability and the dependence of LD (or an analogous quantity, such as the dichroic ratio (DR = I_‖/I_⊥) of the polarized fluorescence emission) on the magnetic field strength provide information on the long-range microscopic order in the particles (see Barzda et al. 1994 and references therein). (I_‖ and I_⊥ denote the corresponding polarized fluorescence intensities.)

Fig. 1.

a Linear-dichroism spectra of edge-aligned thylakoid membranes oriented in a magnetic field (1 cm optical pathlength, 5 mm cell thickness, 20 μg/ml Chl content; the sample was placed between two permanent magnets producing a homogenous field of about 0.5 T). With edge alignment of the membranes, i.e., with their planes preferentially perpendicular to the magnetic field vector, LD_max is obtained as shown in the scheme in b. When the cell is rotated by 90º around the axis parallel with the measuring beam, the LD inverts sign, but its shape does not change. (M. Szabó, G. Steinbach and G. Garab, unpublished.) Note that for polarized fluorescence emission, when excited with non-polarized light, the orientation of the emission dipoles can be measured with respect to the membrane plane. In this case, the orientation angle can most conveniently be obtained from DR = I_∥/I_⊥ = (tan²θ)/2

The method of orientation in AC electric fields can usually be applied in low ionic strength media; the mechanism relies on the existence of a permanent dipole moment of the particle and/or on induced dipole moments. For whole thylakoids and LHCII, smaller LD values are obtained, since the lamellae are preferentially oriented parallel to the field vector, and thus the electric dichroism, due to the rotation of the membrane planes, is considerably smaller than the LD obtained with magnetic alignment. This technique can also be used for small particles, but because of the inconvenience of using high field strengths and high frequencies, it is less frequently used than, e.g., gel squeezing. Electric dichroism can provide important additional information on the surface electric properties of membranes (Dobrikova et al. 2000).

The most widely used method is the polyacrylamide gel squeezing technique, which permits the alignment of particles of different sizes and shapes, embedded in the gel (Abdourakhmanov et al. 1979). It is interesting to note that in addition to the alignment of disc- and rod-shaped membranes or particles, the squeezing—by deformation—can induce LD in vesicles, e.g., thylakoid blebs and photosystem I (PSI) vesicle, which possess inherent anisotropy due to the non-random orientation of their transition dipoles with respect to the membrane “planes”; however, without squeezing, these vesicles appear isotropic, and thus, their orientation pattern cannot be revealed (Kiss et al. 1985). Usually, no restriction applies for the reaction media, but one must be aware of the fact that upon the addition of acrylamide, the membranes lose their electrical impermeability, and the chirally organized macrodomains of the complexes also gradually disassemble (Osváth et al. 1994), an effect observed for some lamellar aggregates of LHCII as well. Thus, some caution is advised with the use of this technique especially for sensitive, highly organized molecular assemblies.

In order to induce the highest LD for a given magnitude of squeezing for disc-shaped and rod-like particles, the squeezing should be one or two dimensional, respectively. For vesicles, one-dimensional squeezing yields a higher degree of dichroism. In all these cases, the distribution functions of the particles can be calculated, and thus, the LD can be given as a function of squeezing parameter, and thus opening the possibility for the determination, with good precision, of the orientation angles of the transition dipoles (see Garab 1996 and references therein).

Quantitative evaluation of LD data

For idealized cases, e.g., for perfectly aligned and planar membranes, the orientation angle θ of the transition dipole with respect to the membrane normal can readily be calculated: LD = A_∥ − A_⊥ = 3A (1 − 3 cos²θ)/2, where A is the isotropic absorbance and the subscripts _∥ and _⊥, respectively, stand for polarization planes parallel and perpendicular to the idealized membrane plane. It follows that if a transition dipole is oriented at θ = 54.7°, the magic angle, LD will vanish similarly as for random samples or random orientations of the same transition dipole moment. (A similar equation for the rod-shaped particles is LD = A_∥ − A_⊥ = 3A (3 cos²θ − 1)/2, in which the orientation angle is determined with respect to the long axis of the particle, e.g., a pigment–protein complex; this axis is taken as the _∥ direction.) The orientation angle can be obtained from S = LD/3A, which can vary between −0.5 and 1 as a function of θ. Evidently, in real systems, the value of S depends not only on the θ orientation angle of the dipole but also on the distribution of the lamellar plane around their idealized alignment. This distribution function, as mentioned above, is determined by the squeezing parameter (Ganago and Fock 1981; Garab 1996). Additional corrections might be necessary, e.g., for structural factors, such as the membrane curvature.

In order to calculate the orientation angle from the LD spectra, one can also use internal calibration, to a known orientation of a molecule within the complex (Croce et al. 1999; Georgakopoulou et al. 2003), and make additional measurements, such as the polarized fluorescence emission—for the Fenna–Matthews–Olson complex (FMO) (Wendling et al. 2002).

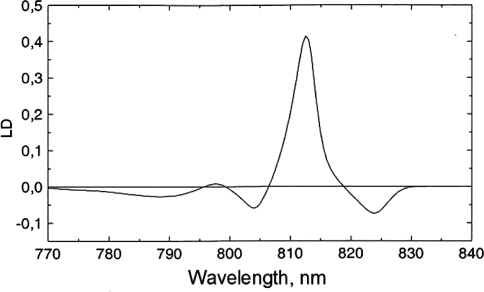
In practice, it is often not possible to speak of the orientation angle θ because a complex may contain many pigments with overlapping absorption bands (for a proper way of dealing with those cases, see, e.g., Van Amerongen et al. 2000). This is illustrated for the FMO complex of Prosthecochloris austuarii in Fig. 2, where the 77K linear-dichroism spectrum is shown together with the corresponding absorption spectrum. The LD spectrum shows a large negative band just above 810 nm, which is due to several overlapping sub-bands. This means that the corresponding transition dipole moments are preferentially oriented along the symmetry axis. The opposite is true for the bands at 805 and 825 nm, which exhibit positive LD. On combining these results with the results of polarized fluorescence spectroscopy, an absolute calibration is possible (Wendling et al. 2002). The size of the LD appears to be in agreement with the orientations of the BChls a in the crystal structure, provided that the Q_y transition dipole moment is parallel to the Y-axis in the BChls a. This finding shows that the red-most transition dipole moment of BChl a indeed closely coincides with the Y-axis of the molecule, this is implicitly assumed in many theoretical simulations of the spectroscopic properties of BChl a containing proteins. The absolute calibration of the LD spectrum allowed Wendling et al. (2002) to quantitatively relate the crystal structure to the LD spectrum, including the precise transition energies (site energies) of all the 7 BChl a pigments (which are influenced by the direct protein environment).

Fig. 2.

LD spectrum of the FMO (Fenna Matthews Olson) complex from Prosthecochloris aestuarii obtained with a squeezed gel. The spectrum is represented upside down, and the peak at 815 nm indicates that the corresponding transition dipole moments are more or less perpendicular to the C₃-symmetry axis of the complex (Vulto et al. 1998a)

The FMO complex of Chlorobium tepidum was analyzed in a similar way. The spectra are grosso modo quite similar to those of Prosthecochloris aestuarii, and the spectral simulations based on the crystal structure agree even better with the experimental results (Vulto et al. 1998a). The linear-dichroism measurements were not sufficient for the complete assignment of the site energies and interaction strengths, but they turned out to be crucial. Additional information was obtained from other (polarized) spectroscopic techniques, including CD. Moreover, the pathways of excitation energy transfer and relaxation were studied with transient absorption experiments and could satisfactorily be extracted from the data, using the results of the steady-state (polarized) experiments (Vulto et al. 1998b, 1999). Graham Fleming and coworkers (Brixner et al. 2005), at the University of California at Berkeley, have been able to visualize the flow of excitation energy in the FMO complex using 2D ultrafast spectroscopy. The results were in rather good agreement with those of Thijs Aartsma and coworkers (Vulto et al. 1998b, 1999). It is important to point out, however, that the assignment of the pigment site energies based, amongst others, on the LD experiments, was also essential for the interpretation of the 2D experiments. In conclusion, LD measurements have been crucial for linking the crystal structures of photosynthetic complexes to their corresponding steady-state and time-resolved spectroscopic properties.

A nice example of how LD measurements can also provide structural information at the molecular level is provided by the study of Croce et al. (1999), in which the LD of LHCII was measured and analyzed. The LD of the carotenoid neoxanthin molecule was compared to that of another carotenoid, a lutein. At that time, the crystal structure of LHCII was available at only 3.4 Å resolution, showing the luteins but not the neoxanthin. The LD results allowed the authors to model both the orientation and position of the neoxanthin rather accurately; the refined crystal structure at 2.72 Å, obtained afterward (Liu et al. 2004), fully confirmed the proposed model. The LD results on LHCII in the Q_y absorption region (between 640 and 690 nm) (Van Amerongen et al. 1994) were subsequently instrumental in modeling steady-state and time-resolved spectroscopic results on LHCII in relation to the crystal structure, which led to a complete picture of the flow of excitation energy throughout the complex after excitation (Novoderezhkin et al. 2004, 2005), like the one done for the FMO complex.

Another example of the usefulness of LD measurements concerns the work of Frese et al. (2000, 2004). These authors demonstrated in an elegant way that the presence of the protein PufX in the photosynthetic membrane of purple bacteria leads to the lining up of the reaction centers and their light-harvesting antenna in a parallel way with respect to each other in the membrane. In the absence of PufX, their mutual orientations appear to be random. This conclusion could be drawn from a subtle but distinctive difference in the LD spectrum for preparations with and without PufX. As far as we know, LD is the only technique to demonstrate this difference so clearly in such an easy way.

The facts that the transition dipole moment μ is a property of the molecule and that this vector can be given in the molecular coordinate system, and LD data can be quantitatively evaluated, justify the notion that “LD is poor man’s crystallography” as is illustrated in the examples above. Indeed, with the knowledge of the position and the binding site of the molecule, and with the known chemical structures involved, “high resolution” structural information can be deduced using LD data. However, LD can or perhaps should rather be considered as biologists’ coarse-scale (or auxiliary) crystallography, because it can readily be applied to the native systems and orientation angles in the membrane. It can also help in comparing natural and reconstituted complexes (Yang et al. 2008) and different gene products (Caffarri et al. 2004). In combination with mutation analysis, LD can also be used to obtain the orientation of the transition dipole moments of the individual chromophores (Simonetto et al. 1999). The knowledge of the orientations of the pigment transition dipoles (and of the molecules) is needed for the interpretation of the electrochromic absorbance changes in the thylakoid membranes (Szabó et al. 2008). It might also be of use in Stark spectroscopy experiments on isolated and non-randomly aligned complexes, e.g., in oriented lamellar aggregates. (Stark spectroscopy deals with the effects of applied electric fields on the absorption or emission spectrum of a molecule (Boxer 1996).) The dependency of the so-called electrochromic absorbance changes on the orientation of the molecules arises from the fact that the field-induced frequency shift of a given absorbance band depends on the relative orientation of the field vector and the transition dipole moment vector of the molecule; in molecules possessing permanent dipole moments, it also depends on the difference between the ground- and excited-state polarizability of the field-indicating pigment molecules (Junge 1977).

The orientations of the transition dipole moments are functionally very important: they strongly influence the rates and the routes of excitation energy transfer in the pigment system, which depends on the mutual orientation of the transition dipoles of the acceptor and donor molecules (Van Grondelle et al. 1994). With regard to the excitation energy distribution, excitonically coupled molecules, which usually give rise to characteristic CD bands (see below), and influence the absorbance and fluorescence properties, are of special interest. Since these also depend on the mutual orientation of the corresponding transition dipoles of the interacting molecules, LD data are also of paramount importance in this respect.

Circular dichroism

Circular dichroism (CD) refers to the phenomenon where the left- and right-handed circularly polarized light are absorbed to a different extent. CD is usually defined as the (wavelength-dependent) difference in absorption of the left- and the right-handed circularly polarized light: CD = A_L − A_R. CD arises from the intra- or intermolecular asymmetry (helicity) of the molecular structure. The helicity (chirality or handedness) of the structure means that it cannot be superimposed on its mirror image. As the handedness of a structure is the same from any direction, CD can be observed in randomly oriented samples. (In fact, the general theories are given for spatially averaged samples.)

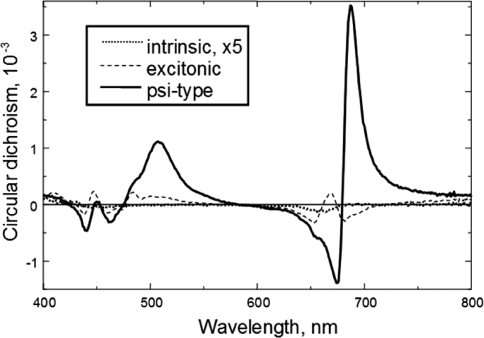
CD signals can originate from different molecular systems of different complexity, and they can give rise to different bands of different physical origins: (i) In the basic case, CD arises from intrinsic asymmetry or the asymmetric perturbation of a molecule (Van Holde et al. 1998). For a single electronic transition, CD has the same band shape as the absorption, and its sign is determined by the handedness of the molecule (often referred to as positive or negative Cotton effect). (ii) In molecular complexes or small aggregates, CD is generally induced by short-range, excitonic coupling between chromophores (Tinoco 1962; DeVoe 1965). Excitonic interactions give rise to a conservative band structure (i.e., the positive and negative bands of the split spectrum, plotted on an energy scale, are present with equal areas). (iii) In chirally organized systems, e.g., in the so-called psi-type aggregates, such as DNA aggregates, condensed chromatins, and viruses, very intense CD signals have been observed, with non-conservative, anomalously shaped bands, which are accompanied by long tails outside the absorbance originating from differential scattering of the sample (Keller and Bustamante 1986; Tinoco et al. 1987). Hierarchically organized systems, such as granal thylakoid membranes, or lamellar aggregates of LHCII (Simidjev et al. 1997), contain all the three different types of signals; they are superimposed on each other (Fig. 3).

Fig. 3.

Circular-dichroism spectra exhibited by the thylakoid pigments at different levels of organization. The pigment concentrations (adjusted to 20 μg Chl(a + b)/ml) are identical in the three samples: the acetonic (80%) extract—yielding intrinsic CD (for easier comparison, the signal is multiplied by a factor 5), pea thylakoid membranes suspended in low salt hypotonic medium (30 mM Tricine pH 7.8, 10 mM KCl, 2 mM EDTA)—dominated by the sum of the excitonic bands, and the same membranes suspended in isotonic medium in the presence of Mg ions (the medium above is supplemented with 330 mM sorbitol and 5 mM MgCl₂). (V. Barzda, M. Szabó and G. Garab, unpublished.)

Intrinsic CD of photosynthetic pigment molecules

In monomeric solutions, chlorophylls and carotenoids exhibit very weak CD signals: for 1 absorbance unit, in the range of some 10⁻⁵ intensities. In general, molecules with planar and rather symmetric structures (such as (B)Chls) and those as rods (such as carotenoids) result in weak rotational strengths (R), which are a measure of the CD intensity (R is proportional to the scalar product of the electric and magnetic dipole moments). In most photosynthetic systems, the contributions from these intrinsic CD signals can safely be ignored or corrected, based on the absorbance band structure and the CD in the pigment solutions (cf. Fig. 3—intrinsic CD, in acetonic solution). It is also possible, however, that the protein environment induces some twisting of, for instance, carotenoids or the open ring tetrapyrrole chromophores (phycobilins) in phycobilisomes of cyanobacteria. This effect can complicate the interpretation of CD spectra, since it is hard to make quantitative estimates of its corresponding spectral shape and size. Fortunately, the conjugated ring systems of (B)Chls are not easily twisted, and for those molecules, both the intrinsic and the induced effects can be ignored. An exception has been found in a Chl a/Chl c antenna, where a strong CD band, having the same band structure as the absorbance, has been detected in a long-wavelength absorbing Chl a molecule (Büchel and Garab 1997). This CD band is most probably induced by distortion of the porphyrin ring by a charged aromatic amino acid residue (cf. Pearlstein 1991).

Excitonic CD signals

When two Chls are excitonically interacting (an excitonic dimer), two new absorption bands (+ and −) appear instead of the two absorption bands of the individual non-interacting Chls (1 and 2). The relative intensities of both the absorption bands (and their dipole strengths D) are given by D_± = ½ (μ²₁ + μ²₂) +− (μ₁ · μ₂) and, in general, they differ from each other (Van Amerongen et al. 2000). The excitonic CD originates from the fact that the polarization of the light changes while passing [through] the excitonically interacting molecules, which have a fixed position and orientation with respect to each other. Since this change is small, the CD is also small when compared to the total absorption. The magnitude of absorption is typically an order of magnitude higher than the intrinsic CD of the same pigment molecules (Fig. 3). The rotational strength depends largely on the mutual orientation of the participating pigment dipoles and the strength of their interaction. The + and − absorption bands of the dimer correspond to a rotational strength of R_± = ∓ πn/2λ (r₁₂ · μ₁ × μ₂), where λ is the wavelength of the light in vacuum, n is the refractive index around the pigments, which is included to correct for the influence of the medium on the wavelength (note that n is often neglected in the literature), and r₁₂ is the vector connecting the center of Chl 1 to that of Chl 2. The CD of each band is related to the rotational strength according to: CD_±/A_iso± = 4R_±/D_±. Note the factor 4 in this relation is due to the historical usage of ellipticity as a unit for circular dichroism. These equations can readily be generalized to systems with more excitonically interacting pigments (Somsen et al. 1996). There are a few important points to notice. For the dimer, it is immediately clear that the absolute size of the positive CD is equal to that of the negative CD, despite the fact that the intensities of the corresponding absorption bands can be very different: the excitonic CD spectrum, when plotted on an energy scale, is conservative.

In the case of more interacting pigments, the CD of the different bands may vary substantially but the sum (or better, the integration) over the different bands should lead to a value of 0 in the case of excitonic CD. In practice, spectra are often non-conservative, for instance, due to contributions from intrinsic CD signals or due to interactions with transition dipole moments outside the measured spectral interval. In the first approximation, these non-conservative contributions show the shape of the absorption spectrum in the region of interest. Therefore, the CD spectrum can be “corrected” for these effects by subtracting the absorption spectrum multiplied by a certain factor, making the resulting spectrum conservative. The simple expressions given above make it tempting to think that the absorption and CD spectral bands have the same shape, and there are numerous examples in the literature where people have fitted absorption and CD spectra with sub-bands that are required to have the same shape in both spectra while the amplitudes were allowed to be different. However, this is not correct because excitonic CD bands are narrower than their counterparts in the absorption spectrum, as discussed by Somsen et al. (1996). In the case of a dimer, there is a very simple way to correct both for the effect of non-conservativeness and the differences in bandwidth in absorption and CD, and we refer to Somsen et al. (1996) for further details.

We emphasize here one more useful point that is often not realized when dealing with CD. The CD spectra will evidently change shape when the transition energy (site energy) of one or both interacting pigments change (for instance, because of a change in the direct environment caused by a mutation in the protein) or when the broadening of the bands changes, for instance, due to a change in temperature. Despite these changes, the first moment of the rotational strength R^[1] remains unchanged. This first moment is defined as the integral of νR(ν) or νCD(ν) in the spectral region of interest, where ν is frequency of the light at a particular wavelength. Instead of the frequency, one can also use the energy corresponding to a particular wavelength. This parameter is the most unambiguous parameter that can be obtained from a CD spectrum and linked to the crystal structure, not only for the dimers but also for larger systems and it can, for instance, be related to the relative orientations and positions of pigments in a photosynthetic complex (Somsen et al. 1996).

Although the CD spectra of pigment–protein complexes contain a wealth of information about the organization of the pigment molecules, there are only a few cases in which the spectra have been satisfactorily interpreted in terms of structure. (We emphasize that in addition to the complexity of the system, and thus of the model calculations, additional factors, as indicated in the above paragraph, influence the CD signals. Conversely, with the use of structural information, the elucidation of this additional information becomes possible.) The best examples are for the antenna complexes: FMO and purple bacterial light-harvesting proteins (Louwe et al. 1997; Vulto et al. 1998a; Georgakopoulou et al. 2002, 2006; Wendling et al. 2002), with known atomic resolution structural models. For LHCII, model calculations by Georgakopoulou et al. (2007) have reproduced the main spectral features of trimeric and monomeric forms, as well as several alterations due to pigment mutations. Remarkable variations have been observed in the CD of the large aggregates of BChls in chlorosomes, and different explanations have been given (Somsen et al. 1996; Prokhorenko et al. 2003). For many other cases even without attempting model calculations, CD spectroscopy remains a sensitive tool, e.g., for fingerprinting isolated native and reconstituted, as well as membrane embedded complexes (Yang et al. 2006, 2008; Lambrev et al. 2007), and for monitoring of the oligomerization state of these complexes (Garab et al. 2002; Büchel 2003) and the effect of single mutations (Morosinotto et al. 2003; Croce et al. 2004; Mozzo et al. 2008).

Polymer and salt-induced (psi)-type CD bands

Psi-type aggregates are three-dimensional macroaggregates containing a high density of interacting chromophores and possessing sizes commensurate with the wavelength of the measuring light and a long-range chiral order of their chromophores. These are of interest because they are contained in many highly organized biological materials. The CD theory of psi-type aggregates (Keller and Bustamante 1986; Kim et al. 1986; Tinoco et al. 1987) is based on the classical theory of coupled oscillators (DeVoe 1965). The theory of H. DeVoe considers that light induces oscillating (transition) dipoles in the polarizable groups of the object, and the induced dipoles interact as static dipoles. In contrast to small aggregates, where it is sufficient to consider the short-range dipole–dipole interactions, with r⁻³ dependence (r is the distance between the dipoles), in psi-type aggregates, the full electrodynamic interaction between the dipoles must be taken into account. At distant points of observation, the oscillating dipole can be regarded as a radiating spherical wave. Thus, the chromophores at large distances can be coupled via radiation and intermediate coupling mechanisms between the dipoles (with r⁻¹ and r⁻² dependencies, respectively). For psi-type aggregates, the radiation and intermediate couplings between the chromophores in the aggregate cannot be neglected, and they play an important role in determining the shape and magnitude of the psi-type CD spectrum. In the suspension of small aggregates, or in large aggregates that possess no long-range order, the relatively weak CD signals, arising from these relatively weak interactions, cancel each other. In contrast, in psi-type aggregates, they can sum up due to the long-range chiral order of the chromophores, explaining that the magnitude of the psi-type CD spectrum is controlled by the size (and chromophore density) of the particle (Kim et al. 1986; Barzda et al. 1994). The shape of the psi-type CD spectrum is determined mostly by the pitch and the handedness of the aggregate. In small aggregates, the entire aggregate at any instant is at the same phase of the wave upon interaction with the light. In contrast, in large aggregates, which are commensurate with the wavelength, this is not true, and retardation effects can play an important role (Kim et al. 1986).

As a result of the long-range chiral order and additional long-distance interactions in psi-type aggregates, these aggregates exhibit unusual CD spectroscopic properties, which have also been identified and studied in granal thylakoid membranes (Fig. 3) and lamellar aggregates of LHCII. They exhibit large, anomalously shaped bands, which are superimposed on the excitonic bands, without interfering with them (Garab et al. 1988a); they also display long tails outside the principal absorbance bands, which originate from differential scattering of left and right circularly polarized beams (Garab et al. 1988b). We stress that the same type of samples such as those of large disordered LHCII aggregates (Simidjev et al. 1997) or thylakoids that are suspended in low ionic strength hypotonic media (Garab et al. 1991) (see also Fig. 3, dashed curve), exhibit no psi-type CD but similarly intense (but not differential) light scattering.

Theory predicts that the magnitude of the psi-type CD signal is controlled by the volume (size), chromophore density, and pitch of the helically organized macrodomain (Kim et al. 1986). For the size dependency, Barzda et al. (1994) have provided clear evidence for it, using lamellar aggregates of LHCII. The intensity of the psi-type CD was gradually decreased by mild detergent treatment, which was accompanied by a gradual decrease of the diamagnetic susceptibility; this latter quantity evidently depends on the size and the order of the components in the aggregates. At the same time, in photosynthesis, large aggregates can serve as the basis for long-distance migration of the excitation energy, which might be important in energy supply for the reaction centers and its down-regulation via non-photochemical quenching.

Psi-type CD has been shown to depend on the macro-organization of the pigment system. LHCII and LHCII-only domains (cf. Dekker and Boekema 2005) have been shown to play significant roles in this organization (Garab and Mustárdy 1999; Holm et al. 2005). Using minor antenna mutants, the role of ordered arrays of LHCII–PSII super-complexes has been demonstrated with the aid of CD measurements on leaves and isolated thylakoid membranes, and electron microscopy on PSII membranes (Kovács et al. 2006). In Arabidopsis mutants, the level of PsbS protein correlated with the amplitude of the psi-type CD, which is consistent with the notion that PsbS regulates the interaction between LHCII and PSII in the grana membranes (Kiss et al. 2008). No systematic study has been conducted in algal cells, but it is clear that the chiral macro-organization features vary from species to species (or perhaps genera to genera). Only relatively weak psi-type CD could be identified in the Chla/Chlb/Chl/c containing alga Mantoniella squamata (Prasinophyceae) (Goss et al. 2000). Whole cells and isolated chloroplasts of the Chl c-containing alga Pleurochloris meiringensis (Xanthophycea) exhibit intense psi-type bands (Büchel and Garab 1997). Whole cells of the diatom Phaeodactylum tricornutum, containing fucoxanthin-Chl a/Chlc proteins as the main light-harvesting antenna complexes, appear to show intense psi-type CD (Szabó et al. 2008). However, the isolated light-harvesting complexes of these species, despite their marked oligomerization, do not appear to assemble into (sufficiently large or sufficiently chirally organized) psi-type aggregates (Büchel and Garab 1997; Lepetit et al. 2007; see also Büchel 2003).

Psi-type aggregates in thylakoids and LHCII lamellae deserve special attention for several reasons. Monitoring the CD allows us to observe highly organized molecular assemblies. Further, LHCII, with its high resolution structure and psi-type CD features, might serve as a suitable model system to establish a more advanced theory for this type of molecular aggregates. Last, but not the least, these structures are highly flexible. Reversible reorganizations have been shown to occur both in thylakoid membranes and LHCII aggregates (Garab et al. 1988c; Barzda et al. 1996; see also Dobrikova et al. 2003 and references therein). Similar reorganizations have been observed in diatoms (Szabó et al. 2008). It appears that the macro-organization level of these hierarchic assemblies react most readily to perturbations; this might be important for adjusting the functions without significantly altering the structure and composition of the constituents.

Special cases, related techniques

In this section, we list some of the special cases and measuring techniques, which are (at least potentially) of interest in photosynthesis research.

Regarding the anisotropic organization of the molecules, it must be pointed out that it manifests itself not only in LD but also in virtually all other transitions that possess fixed orientations with respect to the molecular frames. Most notably, the anisotropic molecular architecture can be characterized via polarized fluorescence emission. The measurement of the dichroic ratio (DR) of the polarized fluorescence on oriented samples, excited with non-polarized light and detected with polarizers transmitting the light parallel and perpendicular to, e.g., the membrane plane gives us the same information about these emission dipoles (Q_Y transitions) as the corresponding LD measurements. Evidently, the sensitivity and selectivity of the two measurements differ, e.g., in thylakoid membranes, at low temperatures, the most intense, long wavelength emission band originates from a small population of molecules, with very weak absorbance (Garab and Breton 1976; Van Amerongen et al. 1991,1994; Barzda et al. 1994).

The same arguments hold true for CD. Circularly polarized luminescence (CPL) provides information, which is analogous but complementary to CD. This is especially valuable for the giant (psi-type) CD. Despite the different possible optical distortions, CPL and CD have provided essentially the same information on the macro-organization of thylakoid membranes (Gussakovsky et al. 2000). A major advantage of the CPL technique is that it can easily be used for in vivo measurements. CPL measurements have shown that the chiral macrodomains are sensitive to drought stress (Gussakovsky et al. 2002); further, changes have been detected in the handedness of the chiral macroaggregates in intact leaves and isolated chloroplasts, induced by illumination of leaves with different colored lights (Gussakovsky et al. 2006, 2007).

An important application of UV-CD is the determination of the secondary structures of proteins, based on semi-empirical theoretical models. The characteristic CD arises by excitonic interactions, which depend in a characteristic way on the arrangement of the amino acid residues (Van Holde et al. 1998). Visible and UV-CD data can provide complementary information. Surprisingly, large differences have been revealed between the sensitivity of the complexes—against detergent and organic solvents, and heat and light treatments—when monitored with CD in the visible and in the far UV regions, i.e., when fingerprinting for the pigment interactions and the secondary structure of the proteins, respectively (Büchel and Garab 1998; Wang et al. 1999).

In scattering materials, dichroism can be measured via, e.g., FDLD (fluorescence detected LD), provided that the fluorescence is proportional to the absorbance (or follows a known dependence on it). FDLD can also be used in laser scanning microscopy, where it offers the convenience of confocal imaging (Steinbach et al. 2008).

In general, laser scanning microscopy (LSM) combined with differential polarization (DP) techniques, similar to the one in dichrographs are suitable to detect microscopic LD or the DR of the emission, or other DP features. Earlier, DP microscopy, using scanning stage and transmission confocality, was used for LD and CD imaging of chloroplasts (Finzi et al. 1989). Recently, a DP-LSM was employed to reveal the strongly inhomogeneous birefringence of magnetically aligned chloroplasts (Garab et al. 2005). DP-LSMs hold the promise to map, in 2D and 3D, the anisotropic features in whole organelles and intact organisms.

Abbreviations

A

Absorbance

BChl

Bacteriochlorophyll

Chl

Chlorophyll

CD

Circular dichroism

CPL

Circularly polarized luminescence

DP-LSM

Differential polarization laser scanning microscopy

DR

Dichroic ratio

FDLD

Fluorescence-detected linear dichroism

FMO

Fenna–Matthews–Olson [complex]

LD

Linear dichroism

LHCII

Light-harvesting chlorophyll-a/b-protein complex of photosystem II

OD

Optical density

PEM

Photoelastic modulator

PSI or II

Photosystem I or II

psi

Polymer and salt induced