Symmetric Inverse Consistent Nonlinear Registration Driven by Mutual Information

Abstract

A nonlinear viscoelastic image registration algorithm based on the demons paradigm and incorporating inverse consistent constraint (ICC) is implemented. An inverse consistent and symmetric cost function using mutual information as a similarity measure is employed. The cost function also includes regularization of transformation and inverse consistent error (ICE). The uncertainties in balancing various terms in the cost function are avoided by alternatively minimizing the similarity measure, the regularization of the transformation, and the ICE terms. The diffeomorphism of registration for preventing folding and/or tearing in the deformation is achieved by the composition scheme. The quality of image registration is first demonstrated by constructing brain atlas from 20 adult brains (age range 30 to 60). It is shown that with this registration technique: 1) the Jacobian determinant is positive for all voxels and 2) the average ICE is around 0.004 voxels with a maximum value below 0.1 voxel. Further, the deformation based segmentation on Internet Brain Segmentation Repository, a publicly available dataset, has yielded high Dice similarity index (DSI) of 94.7% for the cerebellum and 74.7% for the hippocampus, attesting to the quality of our registration method.

1. Introduction

Nonlinear registration techniques are widely used to align magnetic resonance images of brain in longitude scans, monitor and quantify disease progression through morphometry, build group-based digital atlases, and compare brain functional activity in different subjects [1–2]. It is highly desirable that the image registration be inverse consistent to assure that 1) the changes measured from transformations do not depend on the order of mapping [3–4] and 2) handle large deformations by avoiding local minima [5]. Inverse consistency can be realized by forcing the composition of forward and backward transforms to be identity. The norm of difference between the composite and identity transformations can be used as a measure of the inverse consistency error (ICE). In spite of the importance of inverse consistency, most currently used nonlinear registration methods employ asymmetric cost functions that are not inverse consistent. Violating the inverse consistency condition may result in large ICE that can be, on the average, a few voxels [6].

Several studies have recently reported symmetric or inverse consistent registration [3–4, 6–14]. For example Christensen et al [3, 4] have constructed a cost function that is both inverse consistent and symmetric. But this method requires explicit calculations of the inverse of transformation, which is computationally expensive. Calculation of discrete inverse transformation at sub-voxel level accuracy may also be difficult [7]. Also the minimization of different terms in the cost function was based on variational form [3, 4, 6]. Since the inverse consistency is balanced with other terms that need to be minimized in the cost function, the resulting transformation may not be fully inverse consistent [8]. For example, to achieve low ICE, the algorithm may need to sacrifice the registration performance [10]. Thirion [12] has employed the bijective scheme that does not involve explicit calculation of the inverse transformation. But the bijective scheme employed by Thirion [12] is not fully symmetric. In the above methods [3–4, 12], the similarity measure in the cost function is based on sum of square differences (SSD). SSD may not be the most appropriate similarity measure when registering image volumes with significant intensity differences. Other studies have implemented symmetric driving force that is derived from both images [14–16]. While the Jacobian of the transformation is used to combine the driving force from both images, these methods do not enforce the inverse consistency explicitly and sub-voxel ICE cannot be expected [16].

Diffeomorphic mapping between images is required to prevent folding and/or tearing to preserve the image topology. This means that the transformation has to be smooth and the mapping has to be one-to-one. In order to achieve diffeomorphic mapping, the transformation has to be updated through composition scheme that is based on the fact that the composition of homeomorphic transformation is homeomorphic [2, 17].

The main focus of this study is to implement a registration algorithm that is symmetric and inverse consistent and to overcome some of the problems described above. Specifically, our algorithm employs mutual information (MI) as the similarity measure and MI flow [18] as the external force for driving the registration process to deal with the potential intensity variations in the target and source images. The inverse consistent registration was realized by constructing a totally symmetrical cost function that includes MI, regularization of transformation, and ICE terms. In our method, the two transformations were maintained during registration without calculating the inverse transformations. The performance of the proposed registration algorithm was verified by segmentation of publicly available datasets (Internet Brain Segmentation Repository) [19].

2. Methods

Image registration involves finding the transformation, T_IJ: I → J, where I and J are the two image volumes to be registered. T_IJ is the transformation that maps image I to image J, and its displacement field is represented by U (p) for each voxel p of image I, such that T_IJ (p) = p + U(p). U (p) is a vector, which has three components, U_α (p) (α ∈ {x, y, z}) in the x, y, z directions. A voxel, p, with intensity, I(p), in image I corresponds to a point T_IJ(p) with intensity J(p+U(p)) in image J; J(p+U(p)) is denoted by (J ◦ U )(p). The viscoelastic regularization [2] is used to determine the transformation T_IJ, and the corresponding cost function is given by:

$$\begin{array}{l}{E}_{IJ}=E_{\mathit{Sim}}(I,J\circ T_{IJ})+\rho E_{\mathit{reg}}(T_{IJ})\\ =E_{\mathit{Sim}}(I,J\circ U)+\beta R(\nabla u_{\alpha })+\gamma R(\nabla U_{\alpha })\end{array}$$ (1)

In Eq. (1), u_α = ∂U_α/∂t denotes the three components of the correction field u. R(∇u_α) and R(∇U_α) are the viscous regularization on the correction field and the elastic regularization on the displacement field, respectively. The parameters β and γ are regularization parameters and are not explicitly used in our minimization. In this study, recursive Gaussian filtering [20] is used to regularize the correction and the displacement fields. The strength of smoothing in the Gaussian filtering reflects the regularization parameters.

We can also define the transformation, T_JI: J → I (T_JI (p) = p + W(p) and W(p) is the corresponding displacement field) to map from image J to image I by minimizing:

$$\begin{array}{l}{E}_{IJ}=E_{\mathit{Sim}}(J,I\circ T_{JI})+\rho E_{\mathit{reg}}(T_{JI})\\ =E_{\mathit{Sim}}(J,I\circ W)+\beta R(\nabla w_{\alpha })+\gamma R(\nabla W_{\alpha })\end{array}$$ (2)

2.1 Symmetric Consistent Nonlinear Registration

For inverse consistency, inverting the transformation T, obtained by minimizing equation (1), should yield T_JI such that T_JI = T_JI⁻¹. Thus, the measurement based on the deformation field, e.g. Jacobian determinant, should be consistent whether image J is registered to image I or vice versa. The bijectivity solution proposed in demons algorithm [12] is the first method to report inverse consistent nonlinear registration, but the cost function is not fully symmetric. A comprehensive solution to the inverse invariance was proposed by Christensen et al. [4]. However, their algorithm is only asymptotically inverse consistent, depending on the weight of ICC. This algorithm requires explicit calculation of inverse deformation for each iteration, which is computationally expensive and also sub-voxel accuracy is not always guaranteed.

We present an inverse consistent nonlinear registration algorithm, which is computationally efficient by avoiding explicit calculation of the inverse deformation and can achieve sub-voxel ICE without sacrificing the performance of registration. The cost function that is minimized includes E _IJ, E _JI and the inverse consistency term E_inv:

$$E=E_{IJ}+E_{JI}+\lambda E_{\mathit{inv}}$$ (3)

where, $E_{\mathit{inv}}={\displaystyle \sum _p}\mid \mid R_I(p)\mid {\mid }^2+\sum _p\mid \mid R_J(p)\mid {\mid }^2$, R_I (p) = T_IJ (T_JI (p))− p and R_J (p) = T_JI (T_IJ (p)) − p are the residual fields defined on both images I and J, and λ is the regularization parameter. The composition of transformation is performed using tri-linear interpolation. The inverse consistency errors on both images I and J are given by the residual field on both image: ICE_I (p)=||R_I (p)|| and ICE_J (p)=||R_J (p)||. Since T_IJ and T_JI are defined in different image spaces, forcing T_JI = T_IJ⁻¹ is a non-trivial task and numerical errors are unavoidable. In our studies, the symmetry of image registration is achieved by forcing the both composite transformations (T_IJ ◦ T_JI and T_JI ◦ T_IJ) to approach identity. Even though we still denote I as the source and J as the target as in conventional registration, the above formula does not differentiate between the target and source images and the cost function in (3) is totally symmetric.

2.2 Calculating the Dual MI Flow

In the last ten years, information theory-based similarities, such as mutual information (MI), have been developed for image registration [21]. Information-based similarity measures only assume statistical dependence between two images and therefore can be applied to images with intensity differences. In our study, MI was integrated into the symmetric cost function as a similarity measure. We applied Hermosillo’s method [18] to derive the MI flow to find a dense displacement field. The similarity measure was evaluated by constructing continuous probability density function (PDF) through kernel based techniques [18]. We define the MI between image I and image J as:

$$E_{\mathit{Sim}}(I,J\circ T_{IJ})=-{MI}_U^{I,J}=-\underset{R^2}{\int }{p}_U^{I,J}(i,j)log\frac{p_U^{I,J}(i,j)}{P^I(i)P_U^J(j)}$$ (4)

In Eq. (4), by taking negative of MI, the maximization of MI is translated into minimization of the cost function. In the above equation $p_U^{I,J}(i,j)$ is the joint PDF between images I and J with displacement U. P^I (i) is the intensity distribution of image I, and $P_U^J(j)$ is the intensity distribution of image J with displacement U. The correction field on image I can be expressed as:

$$u=\epsilon \left[\psi \ast \left(\frac{1}{p_U^{I,J}(i,j)}\frac{\partial p_U^{I,J}(i,j)}{\partial j}-\frac{1}{p_U^J(j)}\frac{\partial p_U^J(j)}{\partial j}\right)\right](I,J\circ U)\nabla (J\circ U)$$ (5)

Unlike Hermosillo’s MI flow, the correction field in Eq. (5) does not have the regularization term on the displacement field. Instead, the regularization of the transformation was performed separately through Gaussian filtering. In Eq. (5), ψ is a 2D Gaussian filter and ε is the step size for gradient descent. Similarly, the correction field w on image J can also be derived:

$$w=\epsilon \left[\psi \ast \left(\frac{1}{p_W^{J,I}(j,i)}\frac{\partial p_W^{J,I}(j,i)}{\partial i}-\frac{1}{p_W^I(i)}\frac{\partial p_W^I(i)}{\partial i}\right)\right](J,I\circ W)\nabla (I\circ W)$$ (6)

2.3 Minimization of the Symmetric Cost Function

There are two classes of algorithms for minimizing the cost function in intensity-based nonlinear registration [22]. The first one is the standard intensity based (SIB) algorithm in which the same transformation is used to compute the intensity similarity measure and is constrained to remain smooth. The second one is the pair and smooth algorithm (P&S) which updates the transformation field to minimize the similarity measure and then smoothes the updated transformation field. The P&S solutions are more uniform and controllable since the tradeoff is limited only to the geometric quantities [22]. In our studies we applied the P&S algorithm to minimize the cost function in Eq. (3). The regularization parameters β, γ, and λ in the cost function were not explicitly used. The parameters β and γ are reflected in the kernel width of the Gaussian smoothing. The parameter λ reflects the weighting term of the ICE in the total cost function. Adjusting the residual fields more number of times (the number of times ICC applied in a single iteration) corresponds to larger values of λ since the ICC is enforced by adjusting the residual fields to approach zero.

The minimization involves: a) updating the deformation fields defined on both images by minimizing the regular cost functions E_IJ and E_JI that are not guaranteed to be inverse consistent and b) enforcing the inverse consistency by adjusting the deformation fields to force the composition of the transformation fields T_JI and T_IJ to approach identity. The various steps of the proposed ICC algorithm to minimize the symmetric cost function are given below:

1. compute the correction fields u (p) and w (p) defined on the grid points of both images based on gradient descent using Eqs. (5) and (6),

2. apply the viscous regularization by Gaussian filtering of both correction fields u and w,

3. update the displacement fields by the composition strategy: U = U ◦ u and W=W ◦ w,

4. for all grid points p on both images, adjust the displacement field U(p)=U(p)+ (T_JI ◦ T_IJ (p) − p)/2 and W (p)=W (p)+(T_IJ ◦ T_JI (p) − p)/2 to reduce ICE,

5. regularize the displacement field U and W by Gaussian filtering,

6. adjust the displacement field again as in step (4) after displacement field regularization to further enforce ICC.

To enforce the inverse consistency during registration, the displacement fields were adjusted twice based on the composition of forward and backward transformations before and after elastic regularization in steps (4) and (6). The above steps were carried out iteratively until a fixed number of iterations was reached. In order to deal with large deformation and speed up convergence, a coarse-to-fine multi-resolution approach was embedded into the deformation algorithm. This approach uses low-resolution images derived from the original image to begin the iterative processing. After a preset number of iterations (see section 2.4), the displacement field was passed on to the next higher resolution image as the starting solution.

In summary, our registration method falls in the same paradigm as demons algorithm in the sense that the alternative minimization strategy used in demons algorithm is implemented to minimize the cost function. In our method, MI, instead of sum of square intensity differences, was used as the similarity measure to drive the registration. Composition scheme, instead of additive scheme, was implemented in the algorithm for diffeomorphic registration. Our inverse consistency constraint is different from the bijectivity scheme proposed in demons algorithm [12]. The bijectivity solution proposed in demons algorithm is not fully symmetric and the residual is exactly controlled only on the grid points of one image. As a result, the ICE obtained by demons bijectivity tends to be only less than one voxel on average [12]. Our inverse consistency constraint was achieved by forcing the residual fields defined on both images to approach zero and is thus fully symmetric.

2.4 Evaluation of the Registration Algorithm

Evaluating the performance of nonlinear image registration algorithms is difficult due to lack of gold standard and the unavailability of a ground truth [23–24]. In the absence of the ground truth, we used three criteria for evaluating the registration performance. 1) Initially, we visually inspected the registered images with and without ICC. Then the properties of transformations were inspected to ascertain that the transformations are one- to-one mapping (eg. no negative Jacobian determinant) and are inverse consistent (e.g. sub-voxel ICE). 2) We created a brain atlas from the images obtained from the Open Access Series of Imaging Studies (OASIS) [25]. OASIS consists of stripped (stripped of extramenigeal tissues) and intensity corrected MR images with an istropic resolution of 1mm³ of 416 subjects in the age range of 18 to 96 years. We randomly selected 20 adult brains from OASIS dataset to construct an average brain atlas to demonstrate the quality of our image registration algorithm. And we have registered an 89 years old female brain from OASIS to our atlas to demonstrate the performance of our algorithm even when the deformation was relatively large. 3) We used deformation based segmentation and compared with manual segmentation results. Deformation based segmentation is widely used as an objective criterion for evaluating the performance of registration algorithm [23–24]. In the deformation based segmentation, all the images that undergo registration are manually parcellated into different structures or segmented into different tissues by experts. In the absence of ground truth, the manually segmented maps by experts are considered to represent the truth. We compared the similarity between the manually labeled maps with the deformation based results. The images were obtained from Internet Brain Segmentation Repository (IBSR) dataset [19]. This dataset consists of T1-weighted image volumes from 18 brains along with manual tissue segmentation and anatomical structures. The 17 image volumes, IBSR02 to IBSR18, were co-registered with the first image volume, IBSR01 with our registration method. After registration, the manually segmented images and anatomical parcellation maps of these 17 image volumes were deformed to the first image volume. The 17 deformed maps were compared with the manually produced maps (available at the IBSR website) of the first image volume using the Dice similarity index (DSI) [26]. DSI is given by:

$$\mathit{DSI}=\frac{2\#(S_g\cap S_d)}{\#S_g+\#S_d}$$ (7)

where S_g is the segmented target image (with the structure/tissue maps) and S_d is the segmented deformed image. In the above equation # denotes the number of elements in the segmented image set. We compared the performance of our algorithm with the two most popular nonlinear registration algorithms: the demons algorithm [12] and the B-spline based free form deformation (FFD) model [27]. The demons algorithm is freely available as a standard Insight Toolkit (ITK) distribution at http://www.itk.org and the B-spline based FFD is available at http://www.doc.ic.ac.uk/~dr/software/.

For all the results reported in this paper, the σ value of the Gaussian filtering for viscoelastic regularization was set to 1. This value of σ was reported to have the best performance for the demons algorithm [28]. The parameter ε was set to 1/1000; thus the magnitude of the correction field on both images was less than 0.3 to allow for some redundancy and maintain the homogeneous properties of both the correction fields [2]. Our studies showed that σ of 5 to 15 for Gaussian filtering of the joint PDF (ψ in Eqs. (5) and (6) ) worked well for registration of the T1 image pair and therefore we set σ to 10. Multiresolution paradigm in which the images were successively down sampled by factors of 4, 2, and 1(full resolution). The number of iterations for these levels of resolution were set to 1000, 128, and 32, respectively. We also investigated the effect of number of iterations on the convergence of MI. The results showed that in most of the cases the MI approached asymptotic value around 1/3–1/2 of number of iterations indicated above. The parameter setting for ITK demons was same as that was used for our method. Three levels of multiple-resolutions were also used in the B-spline based FFD method with the grid control points spacing of 40mm along each direction. The number of iterations and the number of steps were 10 at each resolution. From coarse to fine, the length of steps were 20mm, 10mm, and 5mm, respectively.

All the computations were performed in C programming language on a Windows based PC with 3 GHz processor and 2 Gb RAM.

3. Results

3.1 Atlas Based on OASIS Data

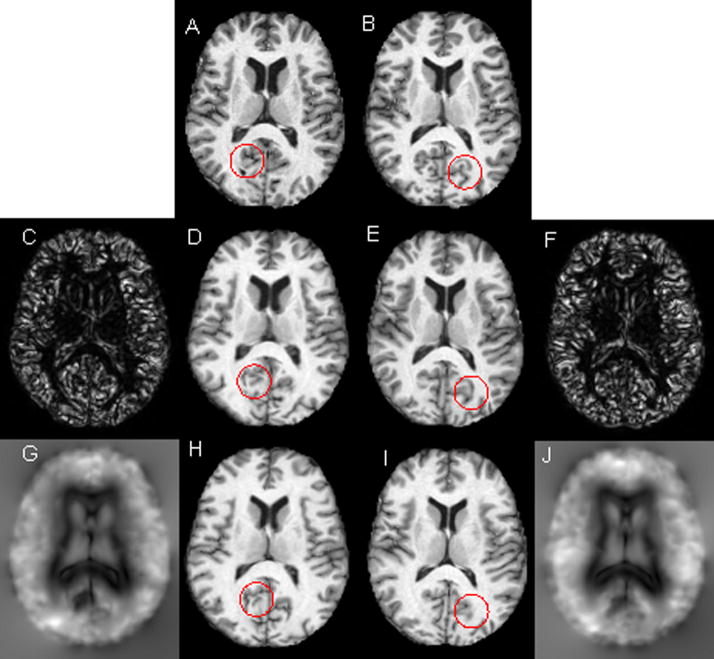
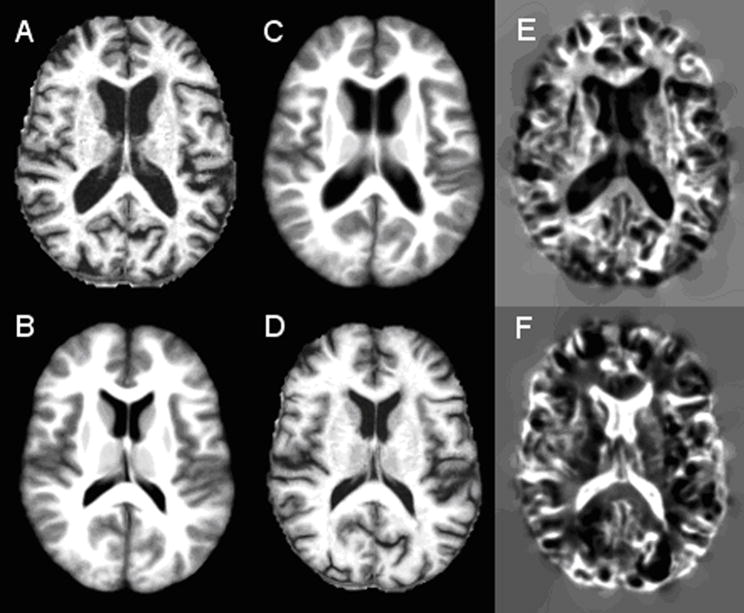
Figure 1 shows, as an example, the registration results obtained on the OASIS data set with and without ICC. The top row shows axial source image (A) and the target image (B) to be registered. The registration results with and without ICC are shown in the second and third rows, respectively. These images/maps clearly demonstrate that inclusion of ICC significantly reduced ICE and improved the registration performance. For example, the deformed image shown in the second row appears to be very similar to the original image (first row). However, the deformed image produced without ICC (third row), especially in the ventricular region and parts circled by red, does not appear to be well registered. More specifically, the ICE produced by the registration method without ICC was observed to be as large 11 voxels, with a mean value around 4 voxels. The maximum ICE produced by the inclusion of ICC was below 0.07 voxels, with a mean value around 0.003 voxels. This shows that inclusion of ICC can dramatically reduce ICE.

Figure 1.

Registration results with and without ICC. First row: axial MR images (A) source and (B) target image to be registered. Second row: registration results with ICC: (C) ICE in the source space and (D) deformed target image, (E) deformed source image and (F) ICE on the target image space. Third row: registration results without ICC: (G) ICE in the source image space, (H) deformed target image, (I) deformed source image and (J) ICE in the target image space. The intensity range of ICE maps in the second row is from 0 to 0.07 and the corresponding intensity range in the third row is from 0 to 11.

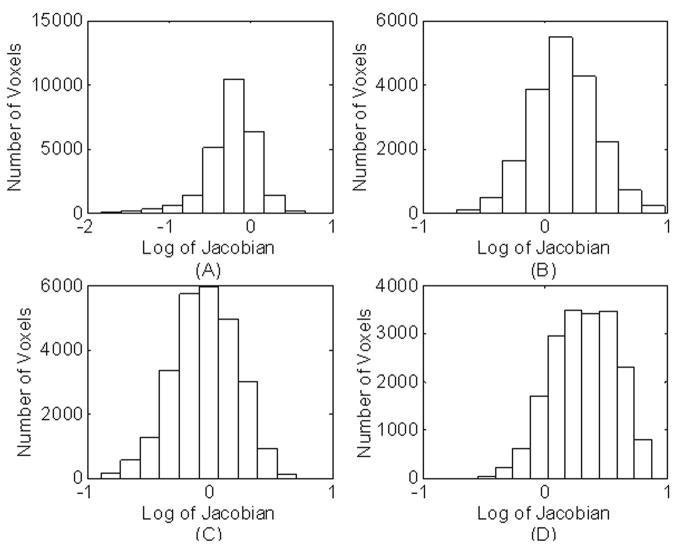
The application of the composition scheme and the parameter selection (σ = 1 for Gaussian smoothing) used in our algorithm have produced positive Jacobian determinant for all voxels with and without ICC. The histograms of the logarithm of Jacobian determinants with and without ICC, were calculated for the ventricles and are shown in Fig. 2. The Jacobian histograms produced by including the ICC resulted in sharper peaks (Figs. 2A and 2B). In contrast, the Jacobian histograms produced without ICC show much broader peaks (Figs. 2C and 2D). The mean values of logarithm of Jacobian shown in Figs. 2A and 2B are nearly inverse to each other. But, this is not the case for the histograms without ICC (Figs. 2C and 2D).

Figure 2.

Histogram of the log Jacobian determinant for the registration with ICC measured in the ventricular area for: (A) source image and (B) target image. The corresponding histograms without ICC are shown in (C) and (D).

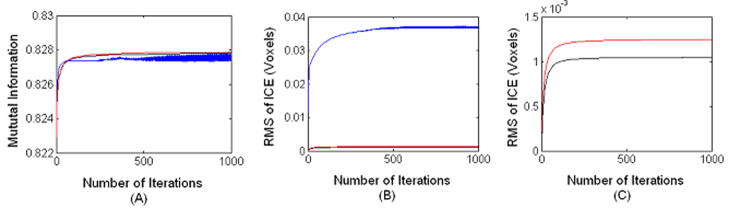
We have compared the performance of the registration algorithms that includes 1) both steps 4 and 6, 2) step 6 alone with our fully symmetric residual method, and 3) demons bijective scheme in step, 6. Since we applied alternative minimization scheme or the pair and smooth algorithm (P&S) [12, 22], the weight parameters are not explicitly used. This makes it difficult to plot the variation of the total cost function with the number of iterations. Therefore, we have plotted only the MI part in the total cost functions and the root mean square (RMS) of ICEs on both images (source and target images) (RMS(ICE)= (Σ||R_I (p)||² +Σ||R_J (p)||² )/2N)^0.5). We plotted RMS since it is closely related to E_inv in the total cost function. Inclusion of steps (4) and (6) produced 30% lower RMS of ICEs relative to that produced by the symmetric residual method with step (6) alone. These results also show that the similarity terms produced with steps (4) and (6) is only 0.1% lower than that produced with step 6 alone. Fig. 3a shows that the demons bijective scheme produced lower similarity measure compared to the other two fully symmetric inverse consistent methods. Also Fig 3b shows that the demons bijecitive scheme produced RMS of ICEs about 0.03 voxels and our fully symmetric ICC method produced RMS of ICEs at around 0.001 voxels. Also, the MI produced by demons bijective scheme shows very significant fluctuations.

Figure 3.

Variation of MI (A), RMS of ICE (B and C) with number of iterations for three different ICC methods: demons bijectivity (blue), proposed ICC method with step 6 alone using symmetric residual fields (red), and the proposed method that includes step(4) and (6) (black). For visual clarity, the RMS of ICEs of the proposed method (black and red) shown in B are depicted with a magnified scale in (C).

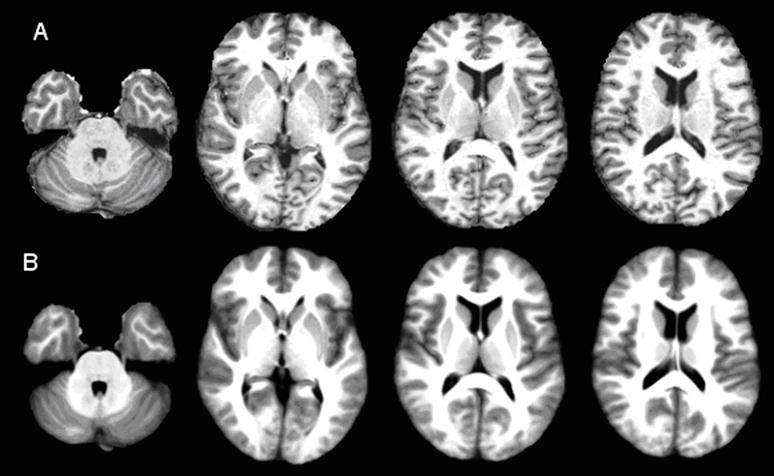
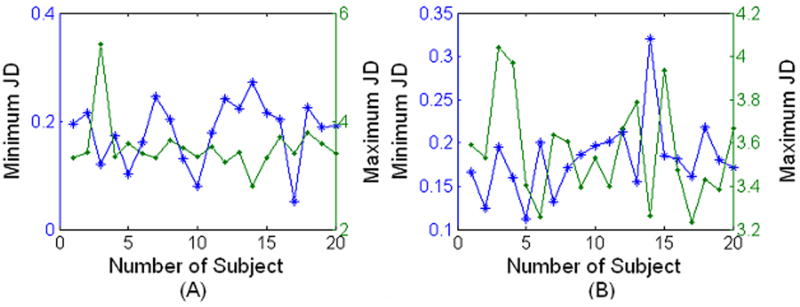
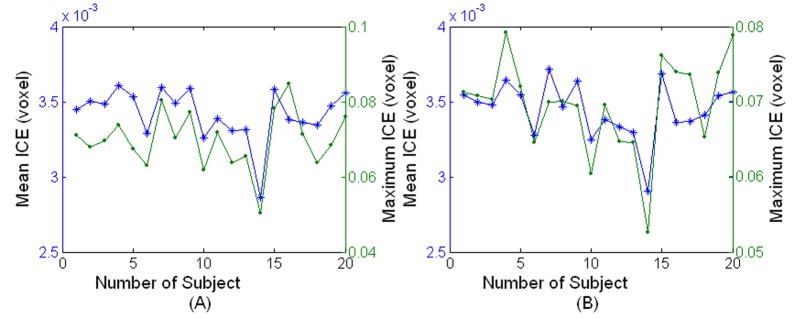
Figure 4 shows the brain atlas produced from 20 brains after registering to one individual brain (template). The 20 brains were randomly selected from the OASIS dataset with the age varying from 30 to 60 years. The created atlas shown in Fig. 4B, at least visually, appears similar to the template image shown in Fig. 4A. The brain atlas is remarkably sharp and some of the fine features can be seen clearly in Fig. 4B. The sharpness of the averaged brain itself does not guarantee the performance of the registration, but at least validates the optimization procedure [9]. Since our proposed method maintains the deformation field along forward and reverse directions, we calculated the Jacobian determinant of the deformation field on the subject and template image spaces separately for the 20 registrations used to create the averaged brain atlas (Fig. 5). The positive Jacobian determinant for all voxels (Fig. 5) demonstrates that our registration scheme provides one-to-one mapping [4]. The ICE measured on both images is shown in Fig. 6 for the 20 registrations. As can be seen in Fig. 6, the maximum ICE is less than 0.1 voxel and the mean ICE is about 0.004 voxel for all the 20 registrations. This demonstrates that our proposed algorithm can produce inverse consistent registration with sub-voxel ICE.

Figure 4.

Axial MR images from two sections: (A) individual template image and (B) corresponding slices from the atlas based on twenty brains.

Figure 5.

Minimum (*) and Maximum (·) Jacobian determinant (JD) measured on (A) subject image and (B) template image from twenty registrations.

Figure 6.

Mean (*) and Maximum (·) ICE measured on (A) template image and (B) subject image for twenty registrations.

As a demonstration that our method can deal with relatively large deformation, we registered an 89 year old brain from the OASIS dataset to the atlas that we created. As can be observed from Figs. 7A-D, our method can potentially handle relatively large deformation. The shrinkage and dilation of ventricles in the Jacobian maps can be clearly seen in Figs. 7E and F, respectively. The values of the Jacobian determinant varied from 0.04 – 4.65 and 0.03 – 7.54 in the maps shown in Figs. 7E and 7F, respectively.

Figure 7.

Results of registration of an elderly female brain and the created atlas: (A) elderly individual brain, (B) section from the atlas, (C) atlas deformed to the space of individual brain, (D) individual brain deformed to the atlas space. The Jacobian determinant maps in the individual image and the atlas spaces are shown in (E) and (F) respectively.

3.2 Deformation Based Segmentation Using IBSR Data

The 17 image volumes in the IBSR database, IBSR02 to IBSR18, were co-registered with the first image volume, IBSR01. After registration, the manually segmented images and anatomical parcellation maps of these 17 image volumes were deformed to the first image volume. The 17 deformed maps were compared with the manually produced maps of the first image volume. The DSI between the 17 deformed segmentation/parcellation maps and the manually generated map of the first image volume was calculated as a measure of the accuracy of the segmentation/parcellation. We have also compared the performance of our algorithm with the two most popularly used nonlinear registration algorithms: the demons algorithm [12] and the B-spline based FFD model [27].

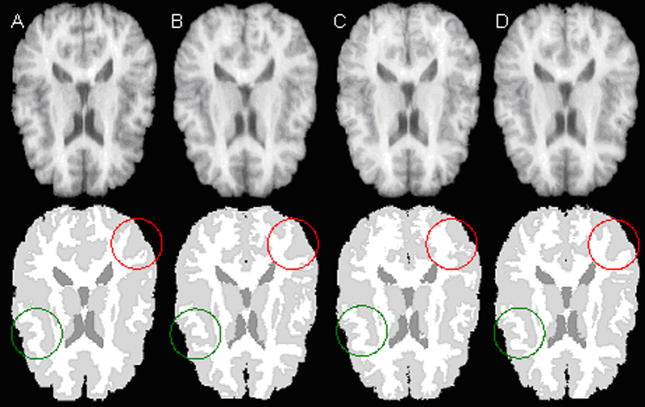
As an example, Fig. 8 shows one slice of the deformed IBSR02 tissue segmentation to IBSR01 image produced by B-spline based FFD (Fig. 8B), ITK Demons (Fig. 8C) and our method (Fig. 8D). For comparison, the corresponding IBSR01 image and the manually segmented tissue map are shown in Fig. 8A. Visual inspection, particularly the areas circled by red and green, shows that the segmentation map produced by our method is superior to that of demons and FFD algorithms. We have also parcellated cerebellum, hippocampus, putamen, caudate, lateral ventricles and thalamus using the three methods and the results are summarized in Table 1. Usually, DSI above 0.6 for smaller structures and 0.8 for larger structures are considered to be good [6]. As can be seen from Table 1, while all the methods produced high DSI, our method yielded superior results for all the six structures. Quantitative analysis based on two tailed paired t-test indicates that our method produced significantly higher similarity measure on five structures except for caudate. For caudate, the DSI produced by our method is only significantly higher than the B-spline based FFD, but not significantly better than demons. Between the two popular registration algorithms, the demons algorithm produced significantly higher DSI than the B-spline based FFD in the caudate region. The differences in the DSI by these two methods for the other five structures are not significant. Our method produced highest DSI of 94.7% in the cerebellar region and achieved DSI of 74.3% even in the hippocampal region.

Figure 8.

Selected slices (top row) and segmented images (bottom row). The segmented images were obtained from (A) manual segmentation of IBSR01 (reference). (B), (C), and (D) are deformed segmented images of IBSR02 using B-spline, ITK demons, and our algorithm, respectively.

Table 1.

Dice similarity index obtained from IBSR datasets on six anatomical structures: cerebellum, hippocampus, putamen, caudate, lateral ventricle, and thalamus using (a) B spline, (b) ITK demons and (c) our method. The P values were obtained by two tailed paired t-test. The P value was obtained by comparing our method with the better of the B spline and ITK demons algorithms.

Anatomic Structures	B spline based FFD	ITK demons	Proposed method	P values
Cerebellum	0.929±0.052	0.900±0.052	0.947±0.010	0.0001
Hippocampus	0.680±0.072	0.676±0.072	0.743±0.032	0.00007
Putamen	0.783±0.027	0.792±0.027	0.828±0.014	0.000001
Caudate	0.717±0.049	0.766±0.049	0.778±0.035	0.06
Lateral Ventricles	0.774±0.067	0.788±0.067	0.827±0.047	0.0037
Thalamus	0.822±0.022	0.840±0.022	0.854±0.019	0.0019

Table 2 summarizes the tissue segmentation result for all the three registration methods. Our method produced DSI of 84.7%, 79.7%, and 78.7% for the GM, WM, and CSF respectively. Based on the paired t-test, among all the three methods, the DSI produced with our method was significantly higher relative to the other two methods. Also the demons algorithm resulted in negative Jacobian for about 1% voxels. For the B-spline based registration, about 0.1% voxels had negative Jacobian. Our method did not produce negative Jacobian determinant for any voxel and resulted in an average ICE of less than 0.0004 voxels.

Table 2.

Dice similarity index based on the IBSR datasets for tissue segmentation using (a) B spline, (b) ITK demons and (c) our method. The P value was obtained by comparing our method with the better of the B spline and ITK demons algorithms.

Tissues	B spline based FFD	ITK Demons	Proposed method	P values
Gray Matter	0.810±0.018	0.821±0.028	0.847±0.018	0.00015
White Matter	0.747±0.024	0.771±0.024	0.797±0.023	0.000023
CSF	0.730±0.057	0.753±0.055	0.787±0.044	0.0022

The total computational time for our registration method with ICC is about 40–45 minutes for registering two image volumes (176 slices).

4. Discussion

In this study, we implemented a nonlinear viscoelastic registration method for inverse consistent registration. Image registration plays a central role in image processing. It is, therefore not surprising that considerable efforts are still ongoing in developing robust and accurate nonlinear registration techniques. There is a growing realization that image registration has to be both inverse consistent and diffeomorphic. Our method differs from the published techniques in a number of ways. Our method employs a mutual information based cost function that is totally symmetric. In our method, the uncertainties in balancing the divergent terms in the cost function were avoided by alternatively minimizing the similarity measure, the regularization of the transformation, and the ICE terms. The diffeomorphism of registration was obtained by composition of the displacement field with homogenous correction field. The inverse consistency was achieved by adjusting the symmetric ICE to approach zero.

The consistent registration method used in our studies is similar to the one proposed by Christensen et al. [4]. However, Christensen’s method, besides being computationally more expensive, needs to strike a balance between the performance of registration and ICC. The performance of registration sometimes needs to be sacrificed in order to achieve low inverse consistency error [15]. In this paper we used the dual residual measures to enforce inverse consistency in both directions. Calculation of residuals is computationally efficient.

The results show that the ICE achieved by our proposed method is at sub-voxel level with maximum ICE of less than 0.1 voxels and average ICE of less than 0.004 voxels. At the same time, the inverse transformation with sub-voxel accuracy was obtained without explicitly calculating the inverse. The performance of the registration was demonstrated by the sharpness of the constructed atlas and the deformation based segmentation/parcellation. The results show that our registration method produced higher Dice Similarity Index than the two most popular used registration methods. Dice Similarity Index applied to the public dataset should provide us more objective criteria to evaluate the performance of the registration algorithm. With ICC, the algorithm will push the displacement to follow inverse consistent path to achieve maximum similarity which should be smoother and closer to the ground truth [13]. When the similarity terms are quite similar, smoother transformation provides more reasonable results. The positive values of Jacobian determinant that we obtained for all voxels validate the diffeomorphism of our registration algorithm. Our results also demonstrate the ability of our method to handle relatively large deformation.

Bricq et al. [29] recently compared the DSI based on 18 subjects in the IBSR dataset using three different tissue segmentation methods: 1) Hidden Markov Chains[29] - (GM - 79.94 ± 5.57%, WM - 86.53 ± 1.73%), 2) Expectation Maximization based Segmentation (EMS) [30] (GM - 78.94 ± 5.68%, WM - 85.87 ± 2.27%), and 3), SPM5 [31] (GM - 78.7 ± 13.9%, WM - 85.27 ± 4.13%). Since we maintain the two deformation fields during registration, we mapped the manual tissue segmentation of IBSR01 onto the 17 images and obtained the deformation based tissue segmentation on 17 image volumes. The Dice similarity indices obtained between the mapped IBSR01 segmentations and the manual tissue segmentation of the remaining 17 images are 84.64 ± 1.32% and 79.66 ± 2.32% for GM and WM, respectively. It is true that tissue segmentation that is completely based on our registration method would not produce better segmentation than the methods indicated above. Nevertheless it is gratifying that the average difference in the DSI between our deformation based segmentation and the segmentation methods evaluated by Bricq et al. [29] is less than 1%. In addition, our method has higher DSI for gray matter and low variance for both gray - and white matter.

5. Conclusions

A nonlinear viscoelastic image registration method that includes inverse consistent constraint (ICC) is presented and evaluated. The cost function used in this algorithm is totally symmetric and includes mutual information as the similarity measure, regularization of transformation and inverse consistent error (ICE). A strategy that alternatively minimizes various terms in the cost function is adapted. The composition scheme is used for achieving diffeomorphism for preventing folding and/or tearing in the deformation. Visual and quantitative evaluation using two freely available datasets (OASIS and IBSR) show that with the proposed registration technique positive Jacobian determinant is obtained for all voxels with low ICE value. Deformation based segmentation of the IBSR dataset yielded high Dice similarity indices for various brain structures, attesting to the quality of the proposed registration method.