Atomic force microscopy analysis of cell volume regulation

Abstract

Cells swell in response a hypoosmotic challenge. By converting osmotic pressure to hydrostatic pressure at the cell membrane via van’t Hoff’s law, and converting that to tension via Laplace’s law one predicts that the cell membrane should stretch and become stiff. We tested this prediction using the atomic force microscopy. During osmotic swelling cells did not become stiff and generally became softer. This result contradicts the assumption of the cell membrane as the constraining element in osmotic stress but is consistent with the cytoskeleton acting as a cross-linked gel. Models of the cells’ response to osmotic stress must include energy terms for three-dimensional stresses.

I. INTRODUCTION

The regulation of cell volume is critical to life. Cells exposed to environments that are different from the cellular interior are subjected to an osmotic stress whether they are in saltwater or freshwater. If a hypoosmotic stress is too great, the cells can break open and die. The animal cells have learned how to regulate their volume over a reasonable range of environmental challenges, but how they do this is still in question. In the case of a hypoosmotic challenge, the homeostatic process that returns a cell to the resting volume is termed by physiologists the regulatory volume decrease (RVD). The control of cell volume of animal cells has traditionally been modeled as water flux driven by solute fluxes created at the cell membrane [1]. The cell interior is assumed to consist of a dilute solution of salts and macromolecules. However, many animal cells can withstand exposure to distilled water [2]. The predicted hydrostatic pressure is calculated from van’t Hoff’s law II=RTc (RT=24.4 Atm/M at 25 °C), where c is the solute concentration that is on the order of 300 mOsm. If the membrane were the only constraint on the osmotic pressure it would have to sustain several atmospheres of hydrostatic pressure, but a lipid bilayer can withstand only ~ 3% area strain before lysing [3]. As a cell swells, the membrane will be stretched [4] and hence should become stiffer [5]. The tension in a uniformly curved piece of membrane can be estimated from Laplace’s law T = Pr/2 where T is tension, P is pressure, and r the radius of curvature. This is a force balance equation and will apply regardless of the constitutive properties of the membrane, whether it is a naked bilayer or reinforced [6].

If we model the cell as a 10 µm diameter vesicle, Laplace’s law predicts it should lyse at an internal pressure of ~0.03 Atm. This corresponds to an osmotic gradient of only ~ 1 mM. Yet, Wan et al. [2] found that molluscan neurons could be exposed to distilled water for >60 min without lysing. How can cells support the osmotic stress from exposure to distilled water that is expected to produce a hydrostatic pressure of ~7 Atm?

One method is to increase the cell volume and area. When a cell swells it dilutes the internal solutes, reducing the pressure gradient and thereby postponing lysis [4,5,7] Cells can increase volume by unfolding membrane pleats and adding new membrane from stores. Groulx et al. [5] found that cells could swell threefold in area and tenfold in volume before lysing in ~10 min. Since II depends linearly on the solute concentration, a tenfold increase in volume will reduce the gradient tenfold assuming no loss of solutes. In Groulx’s case this was not enough to prevent lysis.

There are two other nonexclusive methods to reduce lysis: decrease the radius of curvature or reduce the pressure. Supporting the membrane with a protein lattice reduces the radius of curvature to the order of the lattice spacing [8–10]. If the lattice should fracture [11], hydrostatic pressure will push the lipid bilayer outward forming what is known as a bleb [8]. Cells repair blebs by using contractile proteins attached to the bilayer to pull the membrane back toward the cell interior [2,8].

The other method of protecting the membrane is to reduce the hydrostatic pressure and this is most simply accomplished by lowering the chemical potential of the internal water. This idea is not as arcane as it first appears. In contrast to vesicles, sponges soak up water and swell but they become softer and do not lyse. Sponges absorb water until the elastic stress in the interior walls raises the free energy of the water to match that of the greater entropy of the external water. The degree of swelling is limited by the elastic properties of the matrix.

The cytoskeleton is not a passive sponge but a living sponge. It is metabolically active and capable of changing its crosslink density, stress and elasticity and is thus capable of controlling the chemical potential of intracellular water [2,8,12,13]. The cytoskeleton has been periodically implicated in the ability of cells to regulate their own volume [14] but there has been no accepted mechanistic interpretation. Recent experiments using viscometry [15] and atomic force microscopy (AFM) [16] suggested that cells soften when swollen [17] and this contradicts the traditional view of cell volume regulation as driven solely by water fluxes coupled to solute transport.

With an improved AFM protocol [18] that permitted long term recording, we measured the stiffness of the cell surface under osmotic stress. We conclude that osmotic stress is not confined to the cell surface but is distributed throughout the cell.

II. MATERIALS AND METHODS

The isotonic (340 mOsm) and hypotonic (90 mOsm) solutions had equal ionic strength and we used mannitol to alter the osmolarity [18]. (Note that isotonic, the term commonly used in physiology, is defined as the solution osmolarity that does not cause a cell to change its volume. Tonicity may differ from osmolarity since the cell membrane is selectively permeant to different solutes.)

To alter cytoskeletal and membrane structure cells were treated with a variety of pharmacological agents: 2 µM cytochalasin D (Sigma, St Louis, MO), 25 µM colchicine (Sigma), 7 mM formaldehyde (J.T Baker, Phillipsburg, NJ), and 0.15 mM sodium azide (J.T. Baker). Cells were incubated in cytochalasin D and formaldehyde for at least 30 mins before the experiment. Cells were placed in sodium azide for 1 h and in colchicine at 37°C for 4 h prior to testing. The reagents were present in both isotonic and hypotonic solutions. All solutions contained 1% BSA (Sigma) to minimize adhesion between the probe and the cell [19].

Cells

Primary rat astrocytes were cultured as previously reported [18]. Normal rat kidney (NRK-49F) cells, mouse fibroblasts (3T3), rat phaeochromocytoma (PC-12) cells, and human embryonic kidney (HEK-293) cells were obtained from American Type Culture Collection (ATCC, Manassas, VA) and cultured in DMEM. Cells were plated on 35 mm poly-L-lysine coated glass coverslips and used within 1–2 days after passage (3–5 days for astrocytes).

Atomic force microscopy

The AFM was a modified Que-sant Nomad [20], and unless otherwise noted, the probe was a Veeco Microlever C (k=0.01 N/m) with a 15 µm polystyrene bead glued to the tip [21]. The photodetector (PDT) output was calibrated to z displacement by measuring the detector output with a known displacement of the piezo (PZT) z axis [18].

To stabilize the recording for long term measurements, we developed a differential algorithm that performed force distance measurements alternating between the cell and the adjacent glass cover slip [18]. The probe was positioned over a region of the cell that was not more than 4 µm above the glass so that the height of the swollen cell did not exceed the dynamic z range of the AFM (6 µm). We set the contact force to 100 pN and then controlled the AFM using the software called SAM [18]. SAM generated multiple force-distance (F-z) curves while alternating the cantilever’s horizontal position from above the cell to 10 µm to the side of the cell. Contact with the glass provided a fiducial z reference for the F-z data from the cell and removed instrumental drift (at the expense of time resolution). The cycle was repeated at 0.2 Hz (one F-z curve every 5 s) and the protocol continued throughout the experiment providing hundreds of F-z scans per cell. The noise of the system was negligible as determined by repeated measurements on glass [18].

The experiment measured cell height and stiffness versus time following an osmotic challenge (cell height is monotonically related to cell volume [5]). Since the constitutive properties of the cytoskeleton are nonlinear [22], we minimized the perturbation by using both a soft cantilever (0.01 N/m) and a large tip radius [21]. To reach a dynamic equilibrium we did F-z cycles on the cell for 5 min before acquiring data.

Analysis of F-z data

The Hertz model of a hard sphere indenting an elastic solid surface is commonly applied to the analysis of cell stiffness [21] despite the erroneous assumptions that the cell is a smooth, semi-infinite, isotropic, time-independent, homogeneous elastic solid [23]. While we had reservations about applying the Hertz model to our data, the parameters of interest were the differential effects associated with osmotic perturbation rather than absolute values. The Hertz model predicts that

$$F=4/3*\sqrt{R}{z}^{1.5}E/(1-{\upsilon }^2),$$ (1)

where R is the radius of the indenter, z is the indentation distance relative to the plane surface, E is Young’s modulus, and υ is Poisson’s constant. We assumed υ=0.3 and using a nonlinear optimizer (QFC) fit each trace to the Hertz response with a linear baseline to allow for possible drift in a given F-z curve (parameters a and b):

$$F=az+b+k*{(z-z_0)}^{1.5}H(z-z_0),$$ (2)

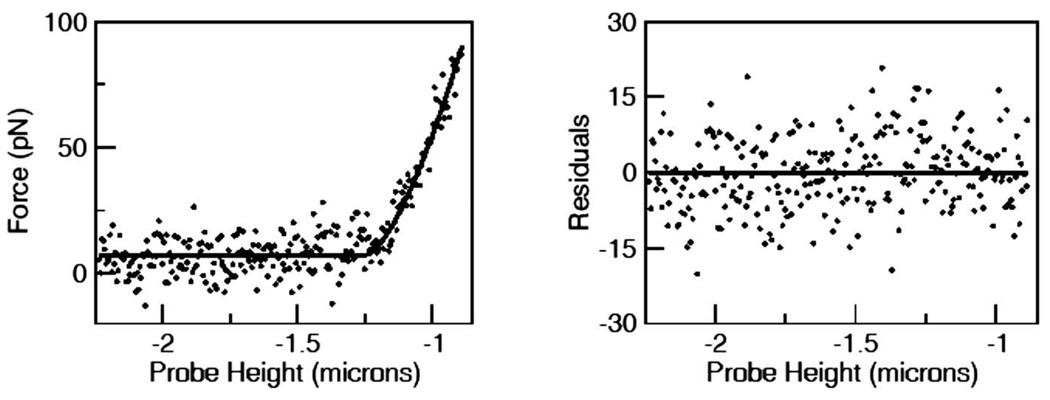
where H is the Heaviside step function $k=4/3*\sqrt{R}E/(1-{\upsilon }^2)$ The optimizer fit all the parameters, including z₀, the cell height. The data were fit well and the residuals were randomly distributed (Fig. 1). Each F-z curve yielded a value for Young’s modulus and the height z₀.

FIG. 1.

Left panel: an example of the F-z fit to the Hertz model of Eq. (1) for an NRK-193 cell. The parameters of the fit to Eq. (1) are a =0 pN/µm, b = 8 pN, k=396 pN/µm^1.5,z₀ = –1.2 µm. These parameters correspond to E=94 Pa. Right panel: the residuals of the fit are randomly scattered and well fit by a Gaussian (not shown) and the runs test has probability of 0.88.

III. RESULTS

Figure 1 shows the F-z curve from a resting NRK-193 cell and the fit to Eq. (2). The residuals plotted in the right panel. Each F-z fit such as that shown in Fig. 1, after correction for drift, provided a single data point in the time series used to characterize the response to osmotic stress. Figure 2 shows the cell height and Young’s modulus of a rat astrocyte in response to a hypotonic challenge. As expected, the cell swelled and after reaching maximum height in about two minutes returned toward baseline, reaching a steady state at about 70% of the peak. The rate of regulation followed the reported time course of volume regulation in astrocytes [24]. Figure 2(b) shows that the Young’s modulus decreased as the cell swelled, and rather than becoming stiff as one might expect of an inflated vesicle, i.e., the cell became softer. Cells are known to increase their production of ATP in response to stress [25,26], and the coupling of ATP to cytoskeletal mechanics has been invoked to explain the effect of ATP on red blood cells [27]. We poisoned our cells with sodium azide to remove the energy supply by blocking ATP hydrolysis [28]. The cells swelled but lost RVD and Young’s modulus did not increase significantly (Fig. 3) implying that active metabolism is not responsible for the softening.

FIG. 2.

The height (a) and stiffness (b) of an astrocyte subjected to a challenge of 250 mOsm 5 min into the record (arrow). The cells swelled and showed a partial RVD but the cell softened after swelling. Each data point represents the parameters obtained from a fit such as that shown in Fig. 1.

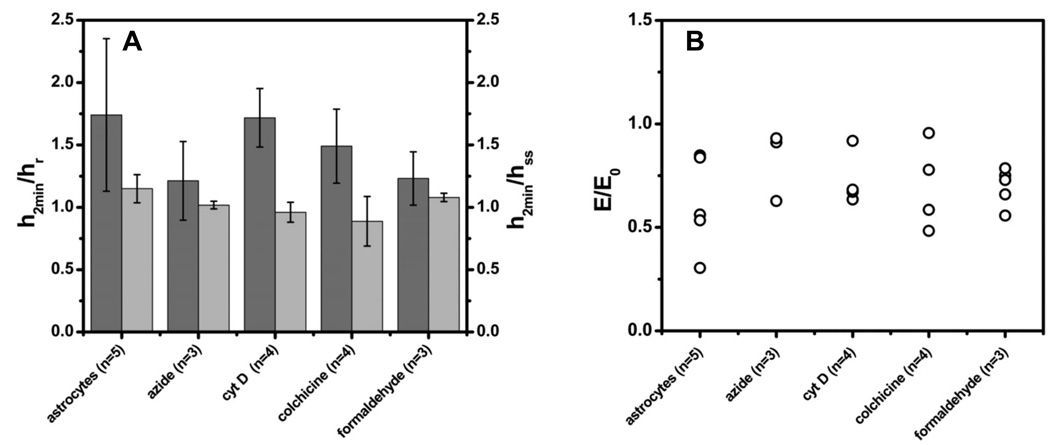
FIG. 3.

The response of astrocytes to a 250 mOsm osmotic challenge under various conditions. (a) Dark grey bars (h_2min, left ordinate) are the peak swelling height at 2 min after solution change normalized by the resting cell height h_r Note that cells swelled under all conditions. The ratio of the peak height h_2min to the steady state height h_ss ~ 15 min from challenge, formed a simple measure of RVD which was mild even in control cells. All the cells shrank with time after the peak. (b) This scatter plot shows that none of the treatments caused swollen cells to become stiffer. The points are the mean value of E at peak swelling and normalized by E₀, the stiffness at rest. Note that the cross-linking fixative, formaldehyde, did not stiffen the cell suggesting that it was naturally cross-linked before fixation.

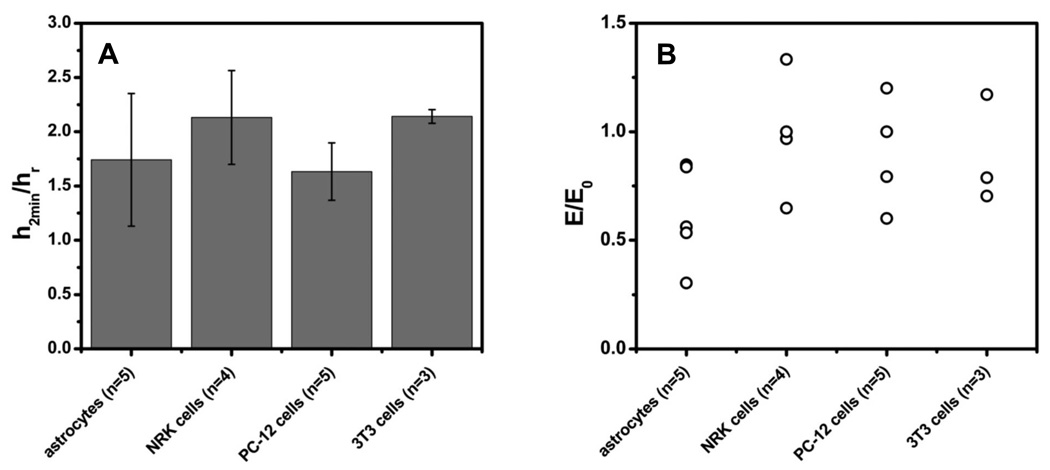
To explore the role of more specific cytoskeletal elements, we treated the cells with colchicine to disrupt microtubules [29] and cytochalasin-D to disrupt actin filaments [30]. Both agents inhibited RVD [31] but in both cases osmotic swelling did not make the membrane stiff. Cytochalasin caused the swollen cell to become even softer (Fig. 3 and this is probably a manifestation of the phenomena that cytochalasin inhibits the contractile activity of actomyosin gels [8]. We attempted to stiffen the cytoskeleton and prevent rearrangement by fixing the cells with 2% formaldehyde [32]. Fixation did not affect swelling and the cells still became softer [Fig. 3(b)]. The fact that fixation did not make the cells significantly stiffer implies that the cytoskeleton was cross-linked prior to fixation. Figure 4 shows that other cell types displayed similar mechanical properties to astrocytes.

FIG. 4.

All cell types tested swelled with a hypoosmotic challenge (a) but none of them became significantly stiffer (b). (a) The mean peak height h_2min normalized by the resting height h_r The scatter plot of (b) shows the Young’s modulus at peak swelling for different cells E normalized by the modulus at rest E₀.

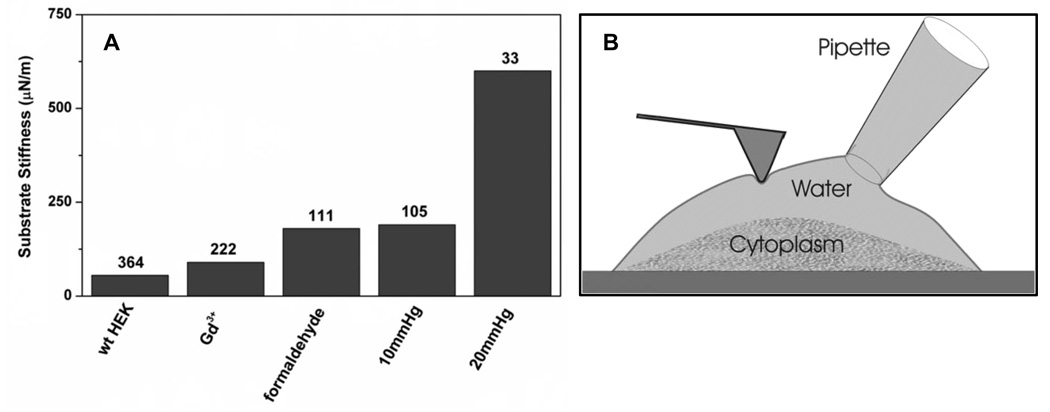
As part of an independent AFM study of ion channels [33], we found that the most effective method to stiffen the cell surface was to inflate the cell with hydrostatic pressure through a patch pipette. Hydrostatic pressure applied intracellularly at the level of the membrane caused it to fracture from the deeper cytoskeleton and form a bleb [34]. As expected from Laplace’s law, this two-dimensional membrane does became stiff [25]. Stiffening required only 0.01–0.03 Atm, orders of magnitude less than the 6 Atm of osmotic pressure estimated to accompany a hypotonic challenge (see Fig. 5).

FIG. 5.

A comparison of different methods used to stiffen HEK293 cells showing that intracellular hydrostatic pressure <0.02 Atm applied through a patch pipette is by far the most effective means to stiffen the membrane. The numbers over the bars are the estimated indentation of the probe (nm) with an applied force of 20 pN. These data were obtained with standard pyramidal point Veeco Microlever B (k=0.02 N/m) probes. Gd⁺³ was applied at 10 µM and formaldehyde at 10%. (b) Cartoon showing how inflation of the cell through the patch pipette can stiffen the membrane if it separates from the cytoskeleton.

IV. DISCUSSION

The fact that cells did not stiffen with osmotic swelling indicates that the key assumption of Laplace’s law, that the mechanics are two dimensional, does not apply to most cells [35,36]. The stresses must be distributed in three dimensions like a gel or a sponge. Studies of the osmotic properties of cross-linked gels such as polyacrylamide [37] have demonstrated that the higher the density of cross-links, the lower the osmotic pressure. The origin of the effect is clear if one realizes that complete cross-linking creates a solid block with no osmotic pressure. The osmotic pressure of flexible polymers is obviously higher than predicted from the molar concentration. For example, in the volume of a bacteriophage, one molecule of DNA can exert an osmotic pressure of 20 Atm [38].

The activity of water in a cross-linked gel is different from bulk water since it includes the strain energy of the lattice. In the simplest terms, when water flows into a gel its free energy increases by PΔV, where P is the local hydrostatic pressure and ΔV is the volume of water. Within the cytoskeletal lattice, P is probably in the range of several negative Atm, but that is not enough to alter the chemical potential of diffusible solutes. The free energy of the water within the lattice depends upon the strain energy of the lattice, changing the elasticity of the lattice will transport water. Since the cytoskeleton is capable of active contraction and relaxation [8,17,39], cells should be able to extrude or imbibe water simply by restructuring the cytoskeleton. The cytoskeleton is a heterogeneous mixture of many cross linked polymers so that when swelling fractures the stiffer filaments, the softer intermediate filaments may pick up the stress. The prediction is that cells can transport water uncoupled from solute transport [40–42].

The crosslink density of the cytoskeleton is modulated by many factors including mechanical stress [43,44], metabolites and second messengers such as Ca⁺² whose concentration can be readily modified by transport across the cell membrane. The membrane has been treated as the key player in cell volume regulation [45–49]. There are many proposals for the existence of membrane based volume sensors such as stretch-activated ion channels, but there are no reliable mechanistic explanations for how cell volume, an extrinsic variable, is controlled by the intrinsic variable of membrane stress [48,50–52]. The data in this paper suggests that there may be no explicit molecular sensor for cell volume, any more than there is a molecular sensor for the volume of a sponge; the volume is set by a force balance.

Are we to disregard the role of the membrane in cell volume regulation? To regulate cell volume there must be a net movement of neutral solutes that may be salts moving through exchangers [49], anion and cation channels in parallel, or the transport of neutral molecules such as taurine [53–56]. Ion channels themselves cannot regulate cell volume since the net movement of charged molecules in amounts that are osmotically relevant would lead to excessive membrane potentials. However, the movement of solutes is coupled to the movement of water and it is the water content of a cell that determines its volume, but the feedback mechanism that determines cell volume does not appear to be located in the membrane.

The gel-like properties of the intracellular cytoskeleton mimic the gel-like properties of the extracellular matrix in tissues [56]. Since the cytoskeleton is mechanically coupled to the extracellular matrix through membrane proteins [43,57], that coupling will lead to a sharing of stress between the inside and the outside of a cell. The degree of sharing needs to be determined. In the extreme case, bacteria possess a rigid extracellular cell wall [58,59] to support osmotic challenges.

The data presented in this paper show that hydrostatic pressure in animal cells is different from osmotic pressure and this arises because van’t Hoff’s law assumes that the chemical potential of the solute is the same on both sides of the membrane. The difference between hydrostatic and osmotic pressure fits with electrophysiological data in which direct mechanical stimulation and osmotic swelling produce different responses [60]. Direct stimulation increases cation permeability while swelling increases anion permeability. Osmotic pressure is commonly applied as a mechanical stressor for cells with the unstated assumption that it is equivalent to hydrostatic pressure. The difference between osmotic and hydrostatic pressure may account for the difficulty in using osmotic pressure to activate mechanically sensitive ion channels.

The dynamically cross-linked cytoplasm of animal cells is essential for the viability and flexibility of animal cells. Since lipid bilayers are permeable to water [61,62], cells will tend to swell when exposed to water. However, freshwater animals live their life in pseudoequilibrium with a ~20 mOsm solution, and regardless of the ingenious details of animal physiology, it is more energy efficient to have cells balance their osmotic pressure with the environment rather than to require a steady state water efflux. If freshwater animals need to extrude solutes in order to extrude water, they would have to obtain new solutes from food and trace salts from the dilute environment in order to extrude more water. By allowing cytoplasmic water to exist under hydrostatic pressure within the cytoplasm, cells can live closer to equilibrium and homeostatic processes need only correct deviations from equilibrium.

The control of cell volume was a critical step in evolution when metabolism began to occur within closed compartments. Bacteria solved the problem by providing a rigid outer wall. The animal cells solved the problem by crosslinking the interior. Future models of animal cell volume regulation need to include the strain energy of the cytoplasm.