The Support Reduction Algorithm for Computing Non-Parametric Function Estimates in Mixture Models

Abstract

In this paper, we study an algorithm (which we call the support reduction algorithm) that can be used to compute non-parametric M-estimators in mixture models. The algorithm is compared with natural competitors in the context of convex regression and the ‘Aspect problem’ in quantum physics.

1. Introduction

During the past decades emphasis in statistics has shifted from the study of parametric models to that of semi- or non-parametric models. An advantage of the latter models is their flexibility and ability to ‘let the data speak for themselves’. However, problems that can usually be solved using standard techniques in the parametric case, can be much more difficult in the semiparametric situation. One of these problems is that of computing an M-estimator, which is defined as the minimizer of a random criterion function over an appropriate parameter set. In parametric models, estimates can often be computed explicitly or approximated using some numerical technique for solving (low dimensional) convex unconstrained optimization problems like steepest descent or Newton. In semi- and non-parametric models, the computational issues often boil down to high dimensional constrained optimization problems. Especially in the context of methods involving resampling or when a profile likelihood is to be computed in a semiparametric model (where estimates often have to be computed many times), the availability of computationally efficient algorithms is crucial.

Within the general theory of optimization, methods can be found to solve optimization problems in the context of these models. For instance, interior point methods (see e.g. Wright, 1994) and active set methods (see e.g. Luenberger, 1973 and, in a statistical context, Dümbgen et al., 2007). Also within the field of statistics, algorithms have been developed that are particularly useful in certain statistical applications. Perhaps the best known example of this type is the Expectation Maximization (EM) algorithm of Dempster et al. (1977), which is designed to compute maximum likelihood (ML) estimates based on incomplete data. Another example is the iterative convex minorant algorithm that is introduced in Groeneboom & Wellner (1992) and further studied in Jongbloed (1998). That algorithm is based on isotonic regression techniques as can be found in Robertson et al. (1988). It is mostly used to compute shape-restricted estimators of distribution functions in semiparametric models. Another class of algorithms developed in the statistics community is the class of vertex direction (VD) algorithms as introduced and studied in Simar (1976), Böhning (1986) and Lesperance & Kalbfleisch (1992).

In this paper, we study what we call a support reduction (SR) algorithm. This algorithm is designed to compute M-estimators in mixture models, using unconstrained optimizations iteratively. Examples will be seen in section 3, but applications of the algorithm can also be found in the literature. Jongbloed et al. (2005) apply the algorithm to compute a non-parametric least squares (LS) estimate of a self-decomposable density, Van Dam et al. (2005) in the context of quantum physics experiments, Langaas et al. (2005) to compute the ML estimate of the distribution of p-values in a multiple testing setting, Birke & Dette (2007) to compute the LS estimator of a convex regression function, Groeneboom et al. (2007) to compute a non-parametric estimator in the current status model with competing risks and Jongbloed & Van der Meulen (2008) to compute the ML- and LS estimator of a concave distribution function based on data corrupted with noise. In Groeneboom et al. (2003), an earlier version of the present paper, the algorithm is used to compute the LS estimate of a convex decreasing density and the ML estimator of the distribution function in the Gaussian deconvolution problem. An R package, called MLEcens, using the support reduction algorithm, has been developed by Maathuis (2007), for computing the ML estimator for bivariate interval censored data. The R package can also be used for univariate censored data (see the dataset ‘cosmesis’, coming with this package) and for interval censored data with competing risks (see the dataset ‘menopause’, also coming with this package).

Within optimization theory, the SR algorithm can be classified as a specific instance of an active set method. Within the field of statistical computing the algorithm fits in the class of vertex direction algorithms. An algorithm, related to our support reduction algorithm, can be found in Meyer (1997) (her ‘hinge algorithm’), which led the first author to the idea of the iterative spline algorithm for convex regression, as described in section 3 of Groeneboom et al. (2001a).

This paper is organized as follows. In section 2, we introduce the basic support reduction algorithm, describe situations where it can be applied and prove convergence under general conditions. In section 3, the algorithm is compared with natural competing algorithms for two interesting examples. The first is LS estimation in convex regression and the second ML estimation in the so-called ‘Aspect problem’ from quantum statistics. In the latter example, we describe in detail the steps of an iterative quadratic minimization method, where the support reduction algorithm is used for the quadratic minimization, and line search is used to go from one quadratic minimization problem to the next one. This is the most common method in applications of the support reduction algorithm, and also used in the R package of Maathuis (2007). We describe the steps in detail, since this example provides a prototype for this method.

2. Description of the basic algorithm and convergence

Let Θ be a parameter set (in applications often finite), and let ℳ₊ be the convex cone of bounded discrete positive (i.e. non-negative) measures with finite support on a σ-algebra on Θ, containing all singletons. So, in particular, ℳ₊ contains all Dirac measures δ_θ.

Consider the following type of optimization problem, assuming it is well defined (this should be verified in a particular model),

$$\text{minimize}\psi (\mu )\text{for}\mu \in {\mathcal{M}}_{+},$$ (1)

where ψ is a convex function on ℳ₊, with values in ℝ ∪ {∞}.

To have a specific example in mind, consider the problem of maximum likelihood estimation in the (standard) Gaussian deconvolution model. In that model, there is a sample Y₁, …, Y_n from a distribution described by an unknown probability measure P₀ on ℝ. Instead of observing this sample, a sample X₁, …, X_n is observed, where each X_i is the sum of Y_i and an independent standard normally distributed random variable. The X_i s are then a sample from a probability density which is a location mixture of the standard normal density with a mixing measure P₀. If φ denotes the standard normal density, the ML estimate of P₀ is found by maximizing

$$\sum _{i=1}^{n}log\int \phi (x_i-\theta )\text{d}P(\theta ),$$

over all probability measures P on Θ= ℝ, for given observed data x₁, …, x_n, generated by the convolution density. We transform this problem to an optimization problem of type (1) on the convex cone ℳ₊ by transforming it to the following optimization problem: minimize

$$\psi (\mu )=-n^{-1}\sum _{i=1}^{n}log\int \phi (x_i-\theta )\text{d}\mu (\theta )+\int \text{d}\mu (\theta )$$

over μ ∈ ℳ₊. The second term of the expression on the right-hand side of the last display corresponds to a Lagrangian term with parameter λ = 1, which ensures that the solution over the cone ℳ₊ will in fact be a probability measure, i.e. will have total mass 1. It can be proved that the solution of this minimization problem exists and does not have a larger number of support points than the size of the sample (the points of support will not belong to the set of observation points, though).

Remark 1

This example illustrates a feature that can often be observed. A complicated optimization problem over a class of probability measures can be restated as optimization problem over the class ℳ₊. For a quite general proof of this in the context of mixture models, see e.g. Lindsay (1983), theorem 3.1, p. 89. For a wide range of other problems, it can be proved on a case-to-case basis.

Let us return to (1). We assume that we can extend the convex function ψ to a convex function on the set ℳ of all bounded (not necessarily positive) measures with finite support on Θ. In order to describe the algorithm, to show that its steps are well defined and that it converges, we need some assumptions. Dirac measure at θ will always be denoted by δ_θ.

The solution of (1) can (under certain conditions) be characterized in terms of a ‘directional derivative function from the right’ D_ν(ψ) ‘in the direction of ν′ defined by

$$[D_{\nu }(\psi )](\mu )=\underset{\epsilon \downarrow 0}{lim}{\epsilon }^{-1}(\psi (\mu +\epsilon \nu )-\psi (\mu )).$$

Note that whenever ψ(μ) < ∞, convexity of ψ guarantees existence of [D_ν(ψ)](μ). We will use the simpler notation D_θ(ψ) instead of D_δθ (ψ). We use the following conditions.

Assumption A1

ψ is a convex function on ℳ₊ such that for each μ, ν ∈ ℳ₊ where ψ is finite,

$$\underset{\epsilon \downarrow 0}{lim}{\epsilon }^{-1}\{\psi (\mu +\epsilon (\nu -\mu ))-\psi (\mu )\}=[D_{\nu }(\psi )](\mu )-[D_{\mu }(\psi )](\mu ).$$

Moreover, [D_ν(ψ)](μ) (and similarly [D_μ(ψ)](μ)) has representation:

$$[D_{\nu }(\psi )](\mu )=\int [D_{\theta }(\psi )](\mu )\text{d}\nu (\theta ).$$ (2)

Assumption A2

If, for μ∈ℳ₊, μ has strictly positive mass at θ and ψ(μ) < ∞, then ψ(μ+ εδ_θ) is finite for ε sufficiently small in absolute value (negative values of ε allowed), and the finite derivative of ψ in the direction of δ_θ exists and is given by

$$[D_{\theta }(\psi )](\mu )=\underset{\epsilon \to 0}{lim}{\epsilon }^{-1}(\psi (\mu +\epsilon {\delta }_{\theta })-\psi (\mu )).$$

Here the point is that ε may approach zero from above and below for those θ with strictly positive μ-measure.

Possibly these conditions are not really necessary, in particular not in their present strong form, but they are satisfied in our examples and make the proofs run smoothly. The lemma below, a proof of which can be found in the Appendix, characterizes the solution of (1) in terms of D_θ(ψ). Intuitively, this lemma states that μ̂ minimizes ψ over ℳ₊ if and only if the directional derivative of the function ψ, evaluated at μ̂, in the direction of the allowable (positive and negative) Dirac measures, is non-negative. This says that letting the measure μ̂ put additional mass at any points in Θ is not profitable in the sense that it will not decrease the function ψ and decreasing its mass at current support points does not lead to a lower value for ψ either.

Lemma 1

Let the assumptions A1 and A2 be satisfied. Suppose that the measure μ̂ ∈ ℳ₊. Then

$$\widehat{\mu }={\text{argmin}}_{\mu \in {\mathcal{M}}_{+}}\psi (\mu )if\mathit{and}\mathit{only}if[D_{\theta }(\psi )](\widehat{\mu })\{\begin{array}{ll}\ge 0\hfill & \mathit{for}\mathit{all}\theta \in \mathrm{\Theta }\hfill \\ =0\hfill & \mathit{for}\mathit{all}\theta \in \text{supp}(\widehat{\mu }).\hfill \end{array}$$ (3)

This characterization of the solution leads to the following basic algorithm.

The support reduction algorithm

• Step 1: initialize k = 0, choose initial θ⁽⁰⁾ ∈ Θ and μ⁽⁰⁾ = cδ_θ⁽⁰⁾ ∈ ℳ₊ such that

  $$0<c={\text{argmin}}_{c\ge 0}\psi (c{\delta }_{{\theta }^{(0)}}),$$

  or do:

• Step 1′: initialize k = 0, choose initial support set $S=\{{\theta }_1^{(0)},{\theta }_2^{(0)},\dots ,{\theta }_{\ell }^{(0)}\}\subset \mathrm{\Theta }$ and weights c₁, …, c_ℓ> 0 such that $\psi ({\sum }_{i=1}^{\ell }{c}_i{\delta }_{{\theta }_i(0)})<\psi (0)$ and use ‘sequential unrestricted minimizations and support reductions’ (to be explained below) to obtain μ⁽⁰⁾, with support $S^{\prime }\subset \{{\theta }_1^{(0)},{\theta }_2^{(0)},\dots ,{\theta }_{\ell }^{(0)}\}$, such that

  $${\mu }^{(0)}={\text{argmin}}_{\{\mu \in {\mathcal{M}}_{+}:\text{supp}(\mu )=S^{\prime }\}}\psi (\mu ).$$

  In this way, we find a subset S′ of S so that on this set unrestricted minimization gives a solution which belongs to ℳ₊.

• Step 2: compute [D_θ(ψ)](μ^(k)) and choose some θ^* ∈ Θ with [D_θ^* (ψ)](μ^(k)) < 0; if such θ^* cannot be found, STOP.

• Step 3: define the ‘extended current support set’ by S = supp(μ^(k)) ∪ {θ^*}.

• Step 4: use ‘sequential unrestricted minimizations and support reductions’ (to be explained below) to obtain μ^{(k + 1)} with support S′ ⊂ S satisfying (in the same sense as in Step 1′)

  $${\mu }^{(k+1)}={\text{argmin}}_{\{\mu \in {\mathcal{M}}_{+}:\text{supp}(\mu )=S^{\prime }\}}\psi (\mu ).$$

• Step 5: k ← k + 1, return to Step 2.

Steps 1′ and 4 in this description need some extra clarification. Step 1 could be called (using a currently popular jargon) a ‘bottom-up’ approach, whereas Step 1′ usually represents a ‘top-down’ approach, where one starts with an overparametrization. Step 1′ plays an important role in situations where the support reduction algorithm is used in an iterative quadratic minimization (e.g. Newton) scheme of a non-quadratic objective function. We will discuss this method in detail for the Aspect experiment example in the next section. In this situation one does not want to start at zero at the beginning of each new quadratic minimization, but instead one wants to use the solution found in the preceding quadratic minimization. In such a case one uses Step 1′ as the start of the new iteration step, where the solution of the preceding quadratic minimization and its support set S is used to start the quadratic minimization with Step 1′.

Given the support set S = {θ₁, …, θ_ℓ}, the following function is minimized over ℝ^ℓ:

$$\phi (a_1,\dots ,a_{\ell })=\psi \left(\sum _{i=1}^{\ell }{a}_i{\delta }_{{\theta }_i}\right).$$ (4)

The solution a = (a₁, …, a_ℓ) of this problem generates a measure $\stackrel{\sim }{\mu }={\sum }_{i=1}^{\ell }{a}_i{\delta }_{{\theta }_i}$, not necessarily belonging to ℳ₊ (because a_i might be negative for some i). If this function happens to belong to ℳ₊, it is the new iterate (μ⁽⁰⁾ in step 1′ or μ^{(k + 1)} in step 4). Otherwise, one travels as far as possible along the line segment connecting the current iterate with this infeasible μ̃. That in step 4 a move of positive length can indeed be made, follows from lemma 2 in the Appendix. For step 1′ it is obvious since c_i > 0 for all i. Having reached the boundary of ℳ₊ in this manner, a new measure, say μ̄ is obtained, for which at least one of the support points is dropped. Using the new thus restricted support S, one can again minimize the function (4) (with smaller ℓ) and obtain a new μ̃. If μ̃ ∈ ℳ₊, μ^{(k + 1)} = μ̃ in step 4 (μ⁽⁰⁾ = μ̃ in step 1′). Otherwise, one moves as far as possible from μ̄ towards μ̃ to obtain the new μ̄, etc. How this works will be demonstrated in detail with the Aspect example in the next section.

In order to prove convergence of the algorithm, we need an extra assumption on ψ, related to its curvature.

Assumption A3

For any specific measure μ⁽⁰⁾ ∈ ℳ₊ with ψ(μ⁽⁰⁾) <∞, there exists an ε̄ ∈ (0, 1] such that for all μ ∈ ℳ₊ with ψ(μ) < ψ(μ⁽⁰⁾) and θ ∈ Θ, the following implication holds:

$$\underset{\epsilon \downarrow 0}{lim}{\epsilon }^{-1}(\psi (\mu +\epsilon ({\delta }_{\theta }-\mu ))-\psi (\mu ))\le -c<0\Rightarrow \psi (\mu +\epsilon ({\delta }_{\theta }-\mu ))-\psi (\mu )\le -\frac{1}{2}\epsilon c\text{for}\text{all}\epsilon \in (0,\overline{\epsilon }].$$

The proof of the convergence theorem below can be found in the Appendix. Note that an additional assumption on the choice of the new support point θ^* is needed in order to get a convergent algorithm.

Theorem 1

Let μ̂ be a minimizer of ψ over ℳ₊. Denote by μ^(k) a sequence generated by the SR algorithm. Also suppose that in each iteration the new support point θ^* is chosen such that

$$[D_{{\theta }^{\ast }}(\psi )]({\mu }^{(k)})\le \frac{1}{2}\underset{\theta \in \mathrm{\Theta }}{inf}[D_{\theta }(\psi )]({\mu }^{(k)}).$$

Then, under the assumptions A1 to A3, ψ(μ^(k)) ↓ ψ (μ̂) as k → ∞.

3. Simulation studies

Convex regression

Given are data ${\{(x_i,y_i)\}}_{i=1}^n$ in ℝ² with 0 < x₁ < x₂ < … < x_n and the problem is to find the LS convex regression of these points. In other words, to find the convex function f̂ minimizing the sum of squares

$$f\mapsto \frac{1}{2}\sum _{i=1}^n{(y_i-f(x_i))}^2$$

over the class of convex functions. Since this objective function only depends on f via its values at the points {x_i: 1 ≤ i ≤ n}, without loss of generality, we can restrict the minimization to piecewise linear convex functions with changes of slopes only possible at these points. This observation puts the problem in the framework of section 2. See also remark 1. We take Θ= {−1, 0, 1,…, n + 1}. The solution of the LS problem can be written as a linear combination of the functions

$$f_j(x)=\{\begin{array}{ll}-1\hfill & \text{for}j=-1\hfill \\ 1\hfill & \text{for}j=0\hfill \\ (x_j-x)1_{[0,x_j]}(x)\hfill & \text{for}1\le j\le n\hfill \\ -f_n(x)\hfill & \text{for}j=n+1.\hfill \end{array}$$

Using the set-up of section 2, we let the convex cone of measures ℳ₊ be the set of non-negative bounded measures μ on Θ. Defining f_μ(x) = f_Θf_θ(x) dμ (θ), the minimization problem boils down to the problem of minimizing

$$\psi (\mu )=\frac{1}{2}\sum _{i=1}^n{(y_i-f_{\mu }(x_i))}^2,$$

over μ ∈ ℳ₊. To ensure uniqueness of the solution, we only allow the solution μ̂ to have strictly positive mass at either −1 or at 0, and likewise either strictly positive mass at n or at n + 1.

The support reduction algorithm can be implemented easily with initialization step 1. The algorithm is a discrete analogue of the iterative spline algorithm, discussed in Groeneboom et al. (2001a) and as such applied in Birke & Dette (2007). It is easily verified that assumptions A1 to A3 are satisfied in this setting. In fact, the function ψ on ℳ₊ can be identified with a convex function φ: ${\mathbb{R}}_{+}^{n+3}\to \mathbb{R}$, defined by

$$\phi (a_{-1},\dots ,a_{n+1})=\frac{1}{2}\sum _{i=1}^n{\left\{y_i-\sum _{j=-1}^{n+1}{a}_j{f}_j(x_i)\right\}}^2,$$

where a_j is the mass of the corresponding μ at θ_j = j. This function is also well defined on ℝⁿ⁺³, is convex, and satisfies clearly the conditions A1 to A3.

An interesting competitor of the support reduction algorithm is the interior point algorithm. We studied two versions of the interior point algorithm: the interior point algorithm with logarithmic barrier and a primal and dual version of the interior point algorithm. In our experience, the interior point algorithm with logarithmic barrier worked best, and we will therefore only report on the results of that algorithm in the present problem.

Defining r ∈ ℝⁿ by r_i = f (x_i), the cone of convex functions can be identified with the cone 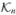⊂ ℝⁿ,

$${\mathcal{K}}_n=\left\{r\in {\mathbb{R}}^n:\frac{r_i-r_{i-1}}{x_i-x_{i-1}}\le \frac{r_{i+1}-r_i}{x_{i+1}-x_i}\text{for}\text{all}i=2,\dots ,n-1\right\}.$$

The objective function for the interior point method with logarithmic barrier is in the present case given by

$${\phi }_{\lambda }(r)=\frac{1}{2}\sum _{i=1}^n{(y_i-r_i)}^2+\lambda \sum _{i=1}^{n-2}log\left(\frac{r_{i+2}-r_{i+1}}{x_{i+2}-x_{i+1}}-\frac{r_{i+1}-r_i}{x_{i+1}-x_i}\right),r=(r_1,\dots ,r_n).$$

The idea is now to start with a value of λ that is not too small, say λ = 1, then to minimize φ_λ(r) as a function of r. This is done in the inner iteration loop by doing steps in Newton directions, but staying inside the allowed set of functions until the Euclidean norm of ∇φ_λ (r) is smaller than a prescribed value, say 10⁻⁸. Then we decrease λ, say to λ/2, starting with the value of r found by the Newton-type algorithm for the case λ = 1, and again doing steps in Newton directions, but staying inside the allowed set of functions until the Euclidean norm of ∇φ_λ(r) is smaller than a prescribed value. This is repeated until λ is smaller than another prescribed value, say λ ≤10⁻⁸. In decreasing λ, the solution will in general move to the boundary of the domain of the set with the original restrictions, but, in contrast with the support reduction algorithm, it will move to the solution from the interior of 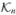, and the solution will at each step involve all generators of the convex cone.

The algorithms were programmed in C, using the Metrowerks Code Warrior compiler, version 5.5, and run on a G4 PowerBook, with a 1.67 GHz PowerPC processor and 1 GB DDR SDRAM memory. Time was clocked with the clock() C procedures, using the C header file time.h.

We used the ran1.c random number generator algorithm of Numerical Recipes in C, starting with a seed equal to −200 and generated with this random samples of 10,000 normally distributed random variables, with expectation 0, and standard deviation 1, 0.1 and 0.01, respectively, and added these to the values of the function y = x², on an equidistant grid of points on [−1, 1], with distance 0.0002 between the points.

As the solution has large ‘blocks’ of equal difference ratios (r_{i + 1} − r_i)/(x_{i + 1} − x_i), and since the interior point method with logarithmic barrier can only accommodate to solutions where all these difference ratios are different, one cannot expect the interior point method to attain the same accuracy as the support reduction algorithm. And indeed we could not push the parameter μ further down than μ= 10⁻⁸ (without getting into numerical difficulties with the inversion of the Hessian band matrix for the parameters r_i), for which value the criterion function is still slightly larger than the one obtained by the support reduction algorithm. How important this is for practical purposes is of course another matter.

The support reduction algorithm was run until the inequality conditions of lemma 1 were satisfied within a tolerance of 10⁻⁸, i.e. the expression on the left side of the inequalities had to be larger than −10⁻⁸. Note that the algorithm is so designed that the equality conditions of lemma 1 will automatically be satisfied. The support reduction algorithm works best if the noise is rather large, whereas the interior point method with logarithmic barrier has a more or less constant behaviour. This is illustrated in Table 1.

Table 1.

Performance of the support reduction algorithm (SR), and the interior point method (IP) with logarithmic barrier for sample size 10,000

	Number of iterations	Time (seconds)	$\frac{1}{2}{\sum }_{i=1}^n{({\widehat{r}}_i-y_i)}^2$	Noise
SR	27	0.24	4950.840019	Normal (0,1)
IP	27	4.53	4950.840168	Normal (0,1)
SR	48	0.36	49.4252297	Normal (0,0.1)
IP	27	4.41	49.4253782	Normal (0,0.1)
SR	143	0.95	0.491968	Normal (0,0.01)
IP	27	4.46	0.492106	Normal (0,0.01)

The number of (outer) iterations for the interior point method is the same for the three examples, but this is just the number of times that the original λ is divided by 2 to get below 10⁻⁸. We had to allow for 100 inner iterations for the interior point method, otherwise the inner minimization problem did not get solved, which makes the algorithm start diverging instead of converging. Therefore the number of (outer) iterations may be a slightly misleading indicator of its performance. For the last example the generators found by the support reduction algorithm has increased to 62.

The Aspect problem

This model is from Aspect et al. (1982) and deals with so-called quantum non-locality experiments. A nice exposition of ideas involved is given in Gill (2007), and we give below a brief description of what this is about, following Gill’s exposition.

Bell’s theorem states that quantum physics (also ‘quantum mechanics’ or QM) is incompatible with classical physics, in particular with local realism (LR). Under LR, a certain correlation inequality (Bell’s inequality) has to be satisfied, but under QM this inequality can be violated. The experiment described in Aspect et al. (1982) is believed to show that Bell’s inequality can be violated ‘in nature’ and hence to settle the incompatibility in favour of QM. However, this experiment exhibits certain shortcomings and one is therefore still looking for a ‘definitive successful experiment’, settling the matter in favour of QM.

To this end, the sets of all possible joint probability distributions of the outcomes of so-called Bell-type experiments are studied. In this context, Bell’s theorem can be interpreted by saying that the set of LR probability laws is a strict subset of the QM probability laws. An α × β × γ Bell-type experiment has α players, β settings and γ outcome categories. The β settings are alternatively denoted by measurements or tools. The players are conventionally called Alice, Bob, etc., where Alice chooses setting a, Bob setting b, etc. at random from some (discrete) probability density on the β settings. A run of the whole experiment has outcome (a, b, …; x, y, …) = (a, b, …; x_a, y_b, …), where a, b, … belong to the set of β settings and x, y, … to the set of γ outcomes. The probability of the outcome (a, b, …; x, y, …) is given by p(a, b, …; x, y, …). Supposing that we observe N independent copies of (A, B, …; X, Y, …), our log likelihood, divided by N, is of the form:

$$\sum _{a,b,\dots ;x,y,\dots }(N_{a,b,\dots ;x,y,\dots }/N)logp(a,b,\dots ;x,y,\dots ),$$ (5)

where N_{a, b, …; x, y, …}/N are relative frequencies (often replaced by the corresponding expectations in the analysis of these experiments) of the outcomes (a, b, …; x, y, …). Furthermore, under LR, the vector p of probabilities p(a, b, …; x, y, …) has a representation of the form

$$p=Aq,$$ (6)

where A is an (incidence) matrix, filled with zeroes and ones, and the vector q represents a vector of probabilities in [0, 1]^m, where m = γ^αβ. In fact, relation (6) corresponds to the relation:

$$p(a,b,\dots ;x,y,\dots )=\sum _{x_1,\dots ,x_{\beta },y_1,\dots ,y_{\beta },\dots :x_a=x,y_b=y,\dots }{q}_{x_1,\dots ,x_{\beta },y_1,\dots ,y_{\beta },\dots },$$

where q_{x1,…, xβ, y1,…, yβ,…} is the probability that Alice has outcome x₁ with setting 1, outcome x₂ with setting 2, …, outcome x_β with setting β, Bob has outcome y₁ with setting 1, outcome y₂ with setting 2, …, outcome y_β with setting β, etc.

Note that the vector p of probabilities p(a, b, …; x, y, …) has length n = (βγ)^α, and that A is an n × m matrix (of zeroes and ones). One now wants to find the MLE q̂ of the vector q, using the log likelihood (5) and the representation of p in terms of q, given in (6). The ultimate goal is to design a Bell-type experiment in such a way that the Kullback–Leibler distance between the vector of relative frequencies N_{a, b,…; x, y,…}/N and Aq̂ is as large as possible, which would demonstrate a large discrepancy between LR and QM.

Interpreting the model as an incomplete data model, the EM algorithm of Dempster et al. (1977) is a natural algorithm to apply in this setting. Using (6), we have, denoting the ijth element of A by a_ij and the ith row of A by $a_i^{\prime }$,

$$p_i\stackrel{\text{def}}{=}\sum _{j=1}^m{a}_{ij}{q}_j=a_i^{\prime }q,i=1,\dots ,n,q=(q_1,\dots ,q_m{)}^{\prime },m={\gamma }^{\alpha \beta },n={(\beta \gamma )}^{\alpha }.$$

Letting Θ= {1, …, m}, and ℳ₊ be the convex cone of bounded positive measures on Θ, which can be represented by a vector q = (q₁, …, q_m)′ of non-negative numbers, we get that our ML problem is equivalent to the problem of minimizing

$$\psi (q)=-\sum _{i=1}^n{w}_{i}log{a}_i^{\prime }q+\sum _{i=1}^n{a}_i^{\prime }q,$$ (7)

where the weights w_i correspond to the relative frequency N_{a, b, …; x, y, …}/N in (5), and where the term ${\sum }_{i=1}^n{a}_i^{\prime }q$ is a Lagrange term for the side restriction that the q_i s should sum to 1 with a Lagrange parameter λ = 1.

For the present model, the EM algorithm has a particularly simple form. The so-called ‘self-consistency equation’ for the EM algorithm gives rise to the EM iterations:

$$q_j^{(k+1)}=q_j^{(k)}\sum _{i=1}^n\frac{a_{ij}{w}_i}{p_i^{(k)}},j=1,\dots ,m.$$

In Böhning (1995), a ‘vertex exchange method’ (VEM) for obtaining an ML estimator of q is discussed. There, the performance of the VEM is compared with the vertex direction method (VDM) for computing the MLE in mixture models, and some examples are given, showing a better performance of VEM with respect to VDM and the EM algorithm. In simple examples, VEM still can be used, but in the examples below the computing times of VEM were prohibitive. So we omit this in our comparisons.

The support reduction algorithm starts with a probability vector ${\overline{q}}^{(0)}={\left({\overline{q}}_1^{(0)},\dots ,{\overline{q}}_m^{(0)}\right)}^{\prime }$, where all ${\overline{q}}_i^{(0)}$s are strictly positive. For example, we can take: ${\overline{q}}_i^{(0)}=1/m$, i = 1,…, m (the discrete uniform distribution). This gives the vector ${\overline{p}}^{(0)}={\left({\overline{p}}_1^{(0)},\dots ,{\overline{p}}_n^{(0)}\right)}^{\prime }$ via

$${\overline{p}}_i^{(0)}=a_i^{\prime }{\overline{q}}^{(0)},i=1,\dots ,n.$$

After that, one could proceed with the steps of the algorithm and perform unrestricted minimizations. However, these minimizations are essentially different from those in the convex regression problem where the solutions can be found by solving a system of linear equations. Here the minimization has to be done iteratively. We will use the support reduction algorithm to solve the sequential quadratic minimization problems in a Newton scheme. In fact, our experience is that this latter approach is much more stable than the first.

We now describe the first inner loop of the procedure that minimizes the local quadratic approximation of ψ at q̄⁽⁰⁾ over ${\mathbb{R}}_{+}^m$. Suppose that at the kth inner iteration $q^{(k)}={\sum }_{j=1}^{\ell }{q}_{i_j}^{(k)}{e}_{i_j}$ (where e_i denotes the ith unit vector in ℝ^m) minimizes the quadratic form:

$${\psi }_0(q)\stackrel{\text{def}}{=}\frac{1}{2}{q}^{\prime }{A}^{\prime }{C}_w{\left(C\left({\overline{p}}^{(0)}\right)\right)}^{2}Aq-2{\mathbf{1}}_n^{\prime }{C}_{w}C\left({\overline{p}}^{(0)}\right)Aq+{\mathbf{1}}_m^{\prime }q,$$ (8)

over the restricted set of vectors, spanned by the generators e_i1, …, e_iℓ. Here C_w and C (p̄⁽⁰⁾) are the diagonal matrices given by:

$$C_w=\text{diag}(w_1,\dots ,w_n),C\left({\overline{p}}^{(0)}\right)=\text{diag}\left(1/{\overline{p}}_1^{(0)},\dots ,1/{\overline{p}}_n^{(0)}\right),$$

and 1_n and 1_m are vectors of length n and m, respectively, with all components equal to 1.

We then determine the minimum partial derivative among the partial derivatives (Step 2): $\frac{\partial }{{\partial q}_i}{\psi }_0(q){\mid }_{q=q^{(k)}}$. If all partial derivatives are larger than 0 (or, say −10⁻¹⁰), we are through with our inner minimization problem. Otherwise, we add the generator with the index, corresponding to the largest negative partial derivative (Step 3). Note that this must be an index i_{ℓ + 1} outside the ‘working set’ of indices, as the fact that q^(k) minimizes (8) over the working set of indices implies that the partial derivatives of ψ₀ w.r.t. the variables q_ij, j = 1, …, ℓ, are zero at q^(k). Then we enter Step 4, solving the equation

$$A_{i_1,\dots ,i_{\ell +1}}^{\prime }{C}_w{(C({\overline{p}}^{(0)}))}^2{A}_{i_1,\dots ,i_{\ell +1}}\left(\begin{array}{c}{q}_{i_1}\\ \mathrm{..}\\ q_{i_{\ell +1}}\end{array}\right)-2A_{i_1,\dots ,i_{\ell +1}}^{\prime }{C}_{w}C\left({\overline{p}}^{(0)}\right){\mathbf{1}}_n+\left(\begin{array}{c}1\\ \mathrm{..}\\ 1\end{array}\right)=0,$$ (9)

where A_{i1, …, iℓ + 1} is the submatrix of A, consisting of the columns with indices i₁, …, i_{ℓ + 1}.

If all components q_ij of this solution are non-negative, we take this solution vector as our new candidate solution. Otherwise we determine the index for which

$$\frac{q_{i_j}^{(k)}}{q_{i_j}^{(k)}-q_{i_j}}$$ (10)

is minimal among the q_ij < 0. The generator with index i_j is discarded from our set of generators, and we solve again the equation

$$A_{j_1,\dots ,j_{\ell }}^{\prime }{C}_w{(C({\overline{p}}^{(0)}))}^2{A}_{i_j,\dots ,j_{\ell }}\left(\begin{array}{c}{q}_{j_1}\\ \mathrm{..}\\ q_{j_{\ell }}\end{array}\right)-2A_{j_1,\dots ,j_{\ell }}^{\prime }{C}_{w}C\left({\overline{p}}^{(0)}\right){\mathbf{1}}_n+\left(\begin{array}{c}1\\ \mathrm{..}\\ 1\end{array}\right)=0,$$

where {j₁,…, j_ℓ} is the new set of indices, with the index for which (10) is minimal removed. If the solution of this system of linear equations in ℓ variables produces again a solution with a negative component, we determine again the index for which (10) is minimal among the q_ij < 0 and discard the generator with this index from the set of generators, etc., until we obtain a subset for which the solution of the system of equations of the form (9) has non-negative components.

Suppose q̄, minimizing the quadratic function ψ₀(q) over ${\mathbb{R}}_{+}^m$, is obtained in this way. We now find α ∈ (0, 0.9] such that

$$\psi ({\overline{q}}^{(0)}+\alpha (\overline{q}-{\overline{q}}^{(0)}))$$ (11)

is minimal (or we solve this one-dimensional minimization problem only approximately), where ψ is defined by (7). Suppose α₀ minimizes (11). Then we take

$${\overline{q}}^{(1)}={\overline{q}}^{(0)}+{\alpha }_0(\overline{q}-{\overline{q}}^{(0)})$$

as our next iterate in the first outer iteration step, and take as the new vector p for the quadratic minimization problem: p̄⁽¹⁾ = Aq̄⁽¹⁾. We continue this procedure (using support reduction for solving the quadratic minimizations in all outer steps) until condition (3) of lemma 1 is satisfied (within a chosen tolerance) for the original object function ψ given by (7). As in the preceding example, it is easily verified that the conditions A1 to A3 are satisfied for these quadratic minimization problems.

We now turn to an example. This example is a ‘CHSH44 dataset’ of a 2 × 4 × 4 Bell-type experiment, in the terminology of Gill (2007). The sequence of letters CHSH refers to the authors of Clauser et al. (1969). The model is again of the same type as above, but now m = 65, 536 = 4⁸ and n = 16². The weight vector w and the transition matrix A is given at http://dutiosc.twi.tudelft.nl/~geurt/homepage/code/code.htm

For this example we compare the performance of the EM algorithm with that of the support reduction algorithm. As noted above, the problem is too large for VEM (the number of parameters is 65,536 and the computing time for VEM is prohibitive). For this reason, we omit VEM in the comparison. The starting distribution is chosen in the same way as in the example above. We get the following results (Table 2).

Table 2.

Performance of the SR- and EM algorithm for the CHSH44 dataset

	Number of iterations	Time (seconds)
SR	56	329.65
EM	7102	17,830.20

The algorithms were again run until the conditions of lemma 1 were satisfied within a tolerance of 10⁻¹⁰. In this case the EM algorithm takes almost 5 hours to reach the criterion, which is about 53 times longer than the time it takes the support reduction algorithm to reach the criterion. Since EM has to converge from the interior of the q-space to the solution, it has to update all 65,536 parameters at each iteration step in the last example; it cannot profit from the reduction of the number of parameters during the iterations, as the support reduction algorithm does.

In the preceding example of the application of the support reduction algorithm to the Aspect problem, the iterations were started with a vector of zeroes. This works well if the number of points in the support of the solution is not too large. However, if the number of points in the support of the solution is larger than 100, the algorithm, started with the zero vector, slows down considerably, since in that case large systems of linear equations have to be solved in the later iterations.

An example of this type is provided by the ‘CHSH10 data set’ of a 2 × 2 × 10 experiment, which is provided separately with this paper, together with the structure of the transition matrix A. The model is of the same type as the model above, but now m (the number of q_i s) is 104 and n (the number of p_i s) is 202 = 400. The weight vector w and the transition matrix A are again given at http://dutiosc.twi.tudelft.nl/~geurt/homepage/code/code.htm [for more information on the 2 × 2 × γ Bell-type experiments, see Zohren & Gill (2006)].

For this example, the algorithm, as applied above, starting with the zero vector, finds a solution with 356 points with positive mass (we note in passing that the solution is unique in p, but not in q). It took almost 4 hours to arrive at this solution. On the other hand, the EM algorithm only took about 4 minutes to reach the criterion. In a situation of this type, where the number of points of support is so large, it is advantageous to use the ‘top-down’ approach, as in Step 1′ of the support reduction algorithm. We again solved the problem by a sequence of quadratic minimization problems, but now started with the uniform discrete distribution on Θ, starting with a number of steepest descent steps in the unrestricted problem, dropping the points θ with negative weights. After this, we approximately solved the quadratic minimization problems by doing at each inner iteration a number of steepest descent steps in the unrestricted quadratic minimization problem. In the inner iterations, we remove the negative q_i in a similar way as above: we walk along the steepest descent direction until we hit the boundary, next we drop the corresponding point of support and recompute the steepest descent direction for the unrestricted problem, after which we walk again along this new direction till we hit the boundary, etc., until we obtain a soluton in ℳ₊.

Calling the support reduction method, starting at zero, SR1, and the latter support reduction method SR2, we get Table 3.

Table 3.

Performance of SR1, SR2 and EM on the CHSH10 dataset

	Number of iterations	Time (seconds)
SR1	783	12,386.04
SR2	16	69.71
EM	713	243.31

The problem is again much too large for VEM, so we leave this out of the comparison. It was run for 5 hours, but did not reach the criterion. As noticed above, the main drawback of this algorithm is that it only changes generators one by one. In contrast, SR2 jumps down from 10,000 points of support to 4120 points of support at the first iteration step. At the fourth iteration step it is down to 1641 points of support, and the final solution, satisfying the 10⁻¹⁰ criterion, has 1641 points of support. So most of the (16) iterations are spent in ‘fine tuning’ around this solution.

4. Discussion

Efficient algorithms are needed in computationally intensive statistical models. In this paper, an algorithm is described, studied and applied that can be used to compute M-estimators in mixture models by sequentially solving (usually low dimensional) unconstrained optimization problems in terms of a mixing measure. During each iteration, the algorithm adds one ‘support point’ to the existing iterate. After that, as many as possible support points of the measure are deleted, resulting in a sparse next iterate. This again leads to a low-dimensional unconstrained optimization problem during the next iteration. As such, the algorithm can be expected to perform well in problems where the solution is a sparse mixture, due to the speed at which the low-dimensional optimizations can be performed.

Appendix

Proof of lemma 1

First assume that μ̂ minimizes ψ over ℳ₊. Then, since μ̂ + εδ_θ ∈ ℳ₊ for all ε≥0 and θ ∈ Θ, it follows that ψ(μ̂ + εδ_θ) ≥ ψ(μ̂) for all ε ≥ 0 and θ ∈ Θ. Hence,

$$[D_{\theta }(\psi )](\widehat{\mu })=\underset{\epsilon \downarrow 0}{lim}{\epsilon }^{-1}(\psi (\widehat{\mu }+\epsilon {\delta }_{\theta })-\psi (\widehat{\mu }))\ge 0,$$

where existence of the limit follows from the convexity of the mapping u ↦ ψ(μ̂ + uδ_θ), u ≥ 0. By assumption A2, we get for θ ∈ supp(μ̂)

$$-[D_{\theta }(\psi )](\widehat{\mu })=\underset{\epsilon \downarrow 0}{lim}{\epsilon }^{-1}(\psi (\widehat{\mu }-\epsilon {\delta }_{\theta })-\psi (\widehat{\mu }))\ge 0.$$

This, together with the previous inequality, gives the equality part of (3) for θ ∈ supp(μ̂).

Conversely, if μ̂ satisfies the (in)equalities given in (3), we have for any μ ∈ ℳ₊, by convexity of ψ and A1, that

$$\psi (\mu )-\psi (\widehat{\mu })\ge \underset{\epsilon \downarrow 0}{lim}{\epsilon }^{-1}(\psi (\widehat{\mu }+\epsilon (\mu -\widehat{\mu }))-\psi (\widehat{\mu }))=[D_{\mu }(\psi )](\widehat{\mu })-[D_{\widehat{\mu }}(\psi )](\widehat{\mu }),$$

where [D_μ(ψ)] (μ̂) and [D_μ(ψ)](μ̂) can be represented as in (2). Since, by (3), [D_θ(ψ)](μ̂) = 0 for θ in the support of μ̂, we get from this representation: [D_μ̂(ψ)](μ̂) = 0. Hence, by (3),

$$\psi (\mu )-\psi (\widehat{\mu })\ge [D_{\mu }(\psi )](\widehat{\mu })-[D_{\widehat{\mu }}(\psi )](\widehat{\mu })=[D_{\mu }(\psi )](\widehat{\mu })=\int [D_{\theta }(\psi )](\widehat{\mu })\text{d}\mu (\theta )\ge 0.$$

Lemma 2

Suppose ${\mu }^{(k)}={\sum }_{i=1}^{\ell -1}{a}_i{\delta }_{{\theta }_i}$, with a_i > 0 for all i, minimizes ψ over the convex cone of positive measures, spanned by the Dirac measures {δ_θi: 1 ≤ i ≤ ℓ − 1}. Suppose that θ_ℓ:= θ^* is chosen as in the description of the algorithm, so with [D_θ^* (ψ)] (μ^(k)) < 0. Then the minimizer $\stackrel{\sim }{\mu }={\sum }_{i=1}^{\ell }{\stackrel{\sim }{a}}_i{\delta }_{{\theta }_i}$ of ψ over the linear space generated by the measure {δ_θi:1≤ i ≤ ℓ} differs from μ^(k) and ã_ℓ>0. Hence, there exists an ε> 0 such that μ^(k) + ε(μ̃ − μ^(k)) ∈ ℳ₊ and such that

$$\psi ({\mu }^{(k)}+\epsilon (\stackrel{\sim }{\mu }-{\mu }^{(k)}))<\psi ({\mu }^{(k)}).$$

Proof

First note that from the optimality conditions for μ^(k), together with A1 and A2, we get

$$0=\underset{\epsilon \to 0}{lim}{\epsilon }^{-1}(\psi ((1+\epsilon ){\mu }^{(k)})-\psi ({\mu }^{(k)}))=\int [D_{\theta }(\psi )]({\mu }^{(k)})\text{d}{\mu }^{(k)}(\theta ).$$ (12)

Also note that μ̃ ≠ μ^(k) because for ε > 0 sufficiently small ψ(μ^(k) + εδ_θ^*) <ψ(μ^(k)). Then we get, using convexity of ψ,

$$\begin{array}{l}\underset{\epsilon \downarrow 0}{lim}{\epsilon }^{-1}(\psi ((1-\epsilon ){\mu }^{(k)}+\epsilon \stackrel{\sim }{\mu })-\psi ({\mu }^{(k)}))\le \underset{\epsilon \downarrow 0}{lim}{\epsilon }^{-1}((1-\epsilon )\psi ({\mu }^{(k)})+\epsilon \psi (\stackrel{\sim }{\mu })-\psi ({\mu }^{(k)}))\\ =\psi (\stackrel{\sim }{\mu })-\psi ({\mu }^{(k)})<0.\end{array}$$

Hence, using again assumptions A1 and A2, we have,

$$\begin{array}{l}0>\underset{\epsilon \downarrow 0}{lim}{\epsilon }^{-1}(\psi ((1-\epsilon ){\mu }^{(k)}+\epsilon \stackrel{\sim }{\mu })-\psi ({\mu }^{(k)}))=[D_{\stackrel{\sim }{\mu }}(\psi )]({\mu }^{(k)})-[D_{{\mu }^{(k)}}(\psi )]({\mu }^{(k)})\\ =[D_{\stackrel{\sim }{\mu }}(\psi )]({\mu }^{(k)})=\int [D_{\theta }(\mu )]({\mu }^{(k)})\text{d}\stackrel{\sim }{\mu }(\theta )={\stackrel{\sim }{a}}_{\ell }[D_{{\theta }_{\ell }}(\psi )]({\mu }^{(k)}).\end{array}$$

Since [D_θℓ(ψ)(μ^(k)) = [D_θ^*(ψ)(μ^(k)) < 0, this implies a_ℓ > 0.

Proof of theorem 1

Without loss of generality, we assume μ̂ ≠ 0 (this can be checked using the characterization of the solution before starting the algorithm). Hence, we have 0 < μ̂ (Θ) < ∞. By (12) we have for each k,

$$\underset{\epsilon \downarrow 0}{lim}{\epsilon }^{-1}(\psi ({\mu }^{(k)}+\epsilon ({\delta }_{\theta }-{\mu }^{(k)}))-\psi ({\mu }^{(k)}))=[D_{\theta }(\psi )]({\mu }^{(k)}).$$ (13)

As ${(\psi ({\mu }^{(k)}))}_{k=1}^{\infty }$ is a bounded and decreasing sequence of real numbers, it decreases to a limit. Assume for the moment that ψ(μ^(k)) ↓ ψ^* = ψ(μ̂) + δ > ψ(μ̂) for some δ> 0. We show that this leads to a contradiction.

Denote by θ_k, the new support point θ^* selected based on μ^(k). Then

$$\begin{array}{l}[D_{{\theta }_k}(\psi )]({\mu }^{(k)})\le \frac{1}{2}\underset{\theta \in \mathrm{\Theta }}{inf}[D_{\theta }(\psi )]({\mu }^{(k)})\le \frac{\int [D_{\theta }(\psi )]({\mu }^{(k)})\text{d}\widehat{\mu }(\theta )}{2\widehat{\mu }(\mathrm{\Theta })}\\ \le \frac{\psi (\widehat{\mu })-\psi ({\mu }^{(k)})}{2\widehat{\mu }(\mathrm{\Theta })}\le \frac{\psi (\widehat{\mu })-{\psi }^{\ast }}{2\widehat{\mu }(\mathrm{\Theta })}=-\delta /(2\widehat{\mu }(\mathrm{\Theta })).\end{array}$$ (14)

Because ψ(μ^(k)) ≤ ψ(μ⁽⁰⁾) for all k, (13), (14) and assumption A3 imply

$$\psi ({\mu }^{(k+1)})\le \psi ({\mu }^{(k)}+\overline{\epsilon }({\mu }_{{\theta }_k}-{\mu }^{(k)}))\le \psi ({\mu }^{(k)})-\overline{\epsilon }\delta /(4\widehat{\mu }(\mathrm{\Theta }))\text{for}\text{all}k.$$

This contradicts the fact that ψ(μ^(k)) converges.