Abstract
To understand the physical and evolutionary determinants of protein folding, we map out the complete organization of thermodynamic and kinetic properties for protein sequences that share the same fold. The exhaustive nature of our study necessitates using simplified models of protein folding. We obtain a stability map and a folding rate map in sequence space. Comparison of the two maps reveals a common organizational principle: optimality decreases more or less uniformly with distance from the optimal sequence in the sequence space. This gives a funnel-shaped optimality surface. Evolutionary dynamics of a sequence population on these two maps reveal how the simple organization of sequence space affects the distributions of stability and folding rate preferred by evolution.
Keywords: protein folding, protein sequence structure relationships, lattice model, hydrophobic polar, protein evolution
INTRODUCTION
Unlike random heteropolymers, a protein folds from an extended conformation to a stable native structure in a short amount of time, in the order of microseconds to seconds. Two central challenges in molecular biophysics are to understand how this remarkable property is encoded in the protein sequence and native structure, and how it is achieved as a result of evolution. Understanding the physics and evolution of the protein-folding process is not only challenging in its own right but it is also crucial to develop effective methods to predict protein structure from sequence information, design new proteins with desired properties, and organize protein sequences and structures in a rational manner.
Simple analytical and lattice models, such as spin glass models,1 two-dimensional (2D) lattice models,2 and three-dimensional lattice models3 have contributed to our understanding of thermodynamic and kinetic behavior of protein folding. In particular, much insight is gained into the Levinthal paradox, an observation that proteins fold up too fast to be able to exhaustively sample the conformational space.4 Theory and simulation of protein folding suggest that naturally occurring protein sequences are a special subset of all possible sequences due to evolutionary optimization.1,5,6 Starting from diverse random conformations, naturally occurring protein molecules overcome a free energy barrier, finding the native state quickly via different routes without getting lost in the vast conformational space. The energy landscape for protein folding is funnel-like,7–10 decreasing gradually toward the most optimal state. Clearly, evolution must play a crucial role in selecting sequences with these special properties.
Protein evolution can be viewed as an adaptive walk of protein populations over a fitness landscape11 in the sequence space.12 Protein evolutionary dynamics can be simulated indirectly as sequence optimization with Metropolis Monte Carlo techniques,13,14 or more directly as population dynamics of a set of sequences evolving through replication with mutation/recombination and selection.15–21 Two approximations are often used in these studies: 1) sequences that share similar functions share similar structures, and 2) the fitness of a protein sequence is correlated with the thermodynamic and kinetic properties of protein folding. Comprehensive reviews on these studies can be found elsewhere.20,22 Parallel studies on RNA evolution have also been conducted.23,24
Despite the central role of fitness landscapes in protein evolution, we still lack a comprehensive view of the large-scale distribution in sequence space of the various protein properties that contribute to evolutionary fitness. The principal difficulty is that detailed quantification of protein folding thermodynamics and kinetics requires a significant amount of computing resources, and can only be done for a representative sample of protein sequences too small compared to the size of sequence space. Bornberg–Bauer and Chan16 took a first step to bridge this gap. Using a hydrophobic-polar (HP) model with exhaustive conformational enumeration of an 18-mer in two dimensions, they calculated the native stabilities for the entire sequence space and called the resulting funnel-like arrangements of stability superfunnels. Such arrangements in sequence space can also be intuitively understood on the basis of the argument proposed by Li et al.25 Briefly, all sequences and structures can be mapped to points in the same high-dimensional space based on a simple salvation model of protein folding. The number of sequences for which a structure is a unique ground state, also called the designability of the structure,26 is directly related to the volume of the Voronoi polytope around the structure in this high-dimensional space. Intuitively, a sequence located in the center of the Voronoi polytope is most stable for the structure, and a sequence located on the boundary is least stable. Our work builds on these previous studies.
In this article, we provide a comprehensive analysis on large-scale distribution of protein-folding thermodynamics and kinetics in sequence space based on a variation of the HP model with exhaustive conformational enumeration of a 24-mer on a square lattice. Instead of studying protein-folding mechanisms one sequence at a time, we map out protein stability and folding speed for all sequences that share the same structure. These maps provide insights into how protein sequence space is organized globally and how such large-scale organization in sequence space affects population dynamics of protein evolution.
Our study improves on previous studies in three ways. First, our analysis is comprehensive in that both protein-folding thermodynamics and kinetics are considered, resulting in both a stability map and a folding rate map. Comparison and evolutionary simulation of the two maps provide insights into the evolutionary behavior of protein-folding thermodynamics and kinetics. Second, our maps are much larger with the number of sequences sharing the same structure ranging from hundreds to several thousands, which allows for better statistical characterization. Third, we provide a direct visualization of these maps in low dimensions using nonlinear dimensionality reduction techniques.
MATERIALS AND METHODS
Protein Model
Protein conformations are represented by self-avoiding walks that are 24 residues long on a 2D square lattice. We explore all possible self-avoiding chain conformations on the lattice; our search is not limited to just the compact conformations as is often done. Each lattice vertex represents a protein residue and is labeled by H (hydrophobic) or P (polar).27 We use a pairwise contact energy function with eHH = −1 + α, eHP = ePP= α. The parameter α, which measures the extent to which compact structures are favored, is set to be −0.1 (Scheme A, weakly compact favoring) or −1.0 (Scheme B, strongly compact favoring). By comparing the two schemes, we hope to discern robust features of the protein space that are independent of the particular choice of α.
We exhaustively enumerate all possible protein sequence and compute their corresponding native structures. There are a total of 16,777,216 (224) HP sequences and a total of 2,158,326,727 24-mer conformations that are not related by symmetry. Exact determination of all sequences with unique ground states is made possible by using a clever optimization of the enumeration procedure.28 Next, we choose one of the ground states as the target structure and find all sequences that have the particular target structure as their unique global minimum of energy. There are many possible choices of this target structure; we choose a target structure where there are a large number of sequences for which the target structure is the ground state, and the energy gap between the ground state and the next lowest energy state is at least 0.5. The target structures for the two schemes, A and B, are shown in Figure 1.
Fig. 1.
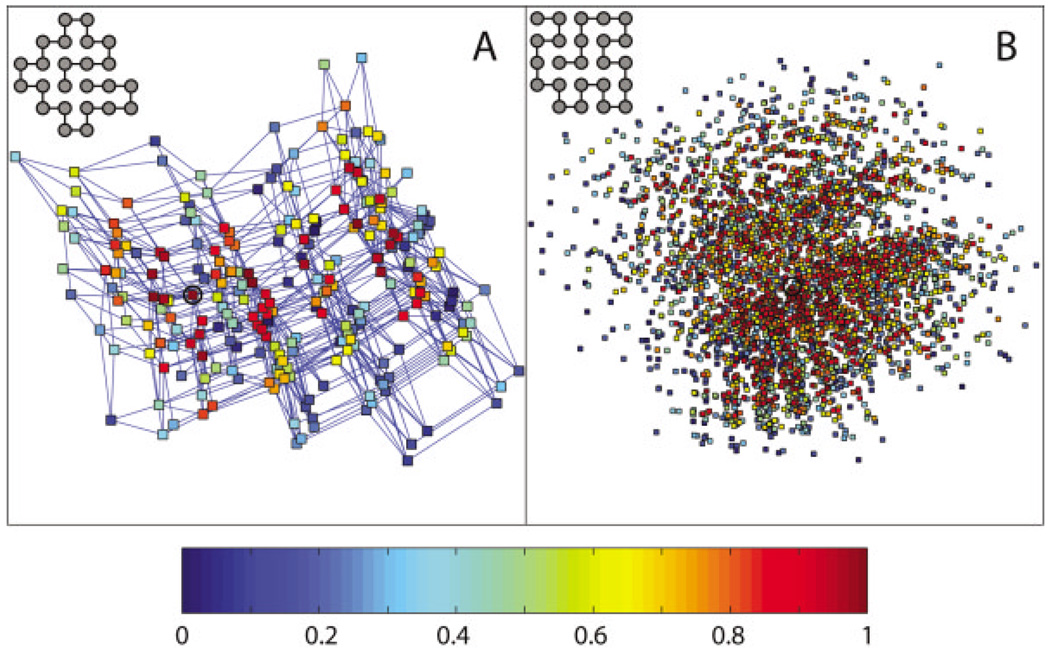
Stability maps in sequence space for (A) Scheme A (α = − 0.1, weakly compact favoring) and (B) Scheme B (α = −1, strongly compact favoring). For each scheme, we show a 2D projection of a subset of sequence space that has the target structure (shown at the upper left corner) as the unique global energy minimum. The sequences shown form a neutral net12 in that sequences differing by a single-point mutation are connected into a network; this network includes all 261 sequences for Scheme A, and 3482 sequences out of a total of 3486 for Scheme B. Each point represents a sequence, and the projection on this page is generated in an optimal way to preserve the shortest path connecting any two points by successive single-point mutations, using the program Isomap.30 Briefly, the geodesic distance is computed for every sequence pair, defined as the length of the shortest path connecting the two sequences in the network. The sequence space is then mapped to two dimensions by performing multidimensional scaling on the geodesic distance matrix. Each sequence is colored according to the fraction of sequences that have lower stability, measured by the folding temperature Tf. A sequence with the highest folding temperature, hence the highest stability, is colored red; a sequence with the lowest folding temperature, hence the lowest stability, is colored blue. In addition, single-point mutations are shown as lines connecting sequences in (A). The most stable sequence is circled in each map.
Measuring Stability
For every sequence with the target structure as the unique global energy minimum, we measure its thermodynamic stability by the folding temperature Tf, defined as the temperature at which the equilibrium concentration of the native structure is one half of the total concentration. The higher the folding temperature Tf, the more stable the sequence is for the native structure. More specifically, Tf solves the equation exp(−Enative/Tf)/Σi exp(−Ei/Tf) = 0.5.
Measuring Folding Rate
For every sequence with the target structure as the unique global energy minimum, we estimate the rate of folding by performing multiple independent Monte Carlo simulations starting from an extended conformation at a certain temperature TMC. At each time step t, all structures that differ from the current structure by one local move that involves one or two residues are identified as s1, s2, …, sN. The move set consists of crankshaft moves, three-bead flips, and end flips.29 The current structure is changed to a new structure si with probability pi = min{exp(−ΔEi/TMC),1}/Nmax and remains unchanged with probability p = 1 − Σipi, where ΔEi is the energy difference between the new structure si and the current structure, and Nmax is the maximal number of structures that differ from any given structure by one local move. The process is iterated until the native structure is first encountered [the number of timesteps this takes is called the first passage time or (FPT)] or the maximal number of timesteps tmax is reached. For reasonable sampling, a total of 100 independent simulations are conducted for each sequence. The folding rate of the sequence is measured by the probability of folding per time step, pf, estimated from a one-parameter maximum likelihood analysis: pf = Σigi/Σiti, where the summation is over all 100 simulations. For the i-th simulation, gi= 1 and ti = FPTi if the native structure is encountered before the maximal number of timesteps is reached, and gi = 0 and ti = tmax if otherwise. For Scheme A, we use TMC = 0.23, tmax = 1011. For Scheme B, we use TMC = 0.4, tmax = 1010.
Mapping Protein Sequence Space with Nonlinear Dimensionality Reduction
For all sequences with the target structure as the unique global energy minimum, we generate a 2D representation of the sequence space using a nonlinear dimensionality reduction program Isomap. Isomap preserves the intrinsic geometry of a high-dimensional space in an optimal way. 30 Briefly, we first convert the sequence space into a graph, where each node in the graph represents a sequence with the selected target structure as the unique global energy minimum, and nodes corresponding to sequence pairs that differ by a single mutation are connected by an edge. Second, we compute the geodesic distance for every sequence pair, defined as the length of the shortest path in the graph connecting the two sequences. Third, we map the sequence space to two dimensions by performing multidimensional scaling on the geodesic distance matrix. Finally, we color the vertices according to the stability/ folding rate of the sequences.
Evolutionary Dynamics in Protein Sequence Space
To simulate protein evolution, we must first quantify the fitness value for each protein that measures its relative reproductive success. We assume that to be biologically active, a protein must be reasonably stable and fold reasonably quickly under physiological conditions. Beyond this, all biologically active proteins will share the same fitness value regardless of stability, folding rate, and folding mechanisms. This is consistent with the observation that most accepted molecular mutations have little effect on the fitness of an organism.31 Following this assumption, we define a sequence to be viable if and only if it has the target structure as the unique global energy minimum and meets a certain stability and/or folding rate cutoff. All viable sequences share the same non-zero fitness value, and all other sequences share zero fitness value. The viable sequence space consists of all viable sequences, and its boundary condition is determined by the viability criteria. In the current study, we simulate evolutionary dynamics with mutation events only. We start with a population of N viable sequences. At each evolutionary timestep, a random sequence is selected from the population, and a random position is mutated. The original sequence is replaced by the mutated sequence if the latter folds into the target structure. Otherwise, it is replaced by a copy of a sequence randomly selected from the rest of the population. This process is repeated until convergence. Evolutionary preference for a sequence can be measured by how frequently the sequence is visited at evolutionary steady state. Evolutionary dynamics with recombination events can be studied in a similar way.21
RESULTS
Maps of Stability and Folding Rate in Protein Sequence Space
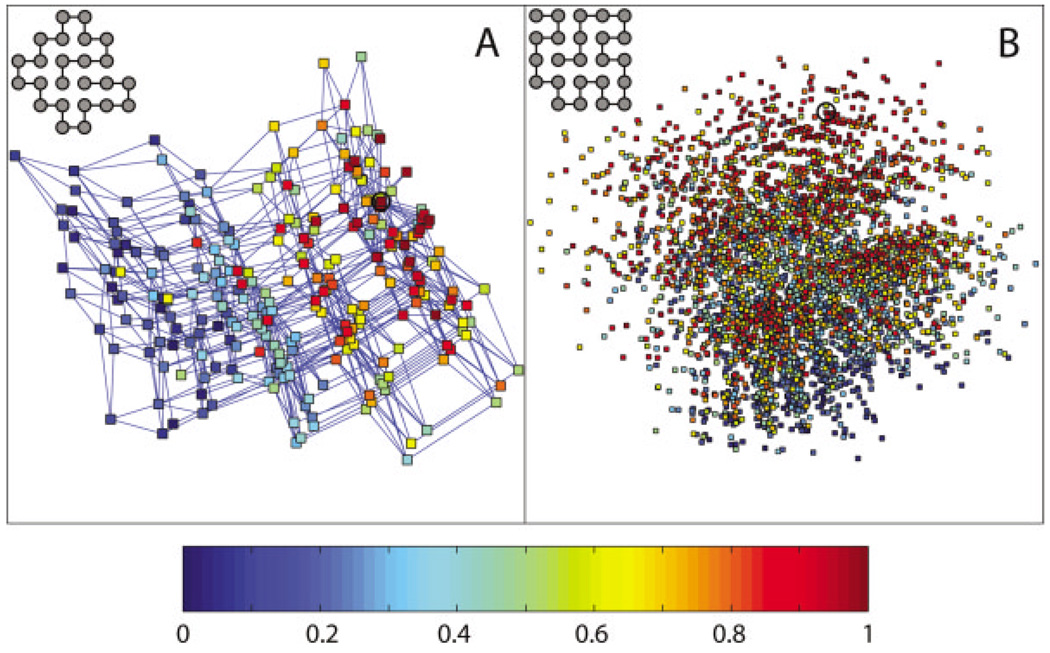
The two Schemes A and B differ by an energy parameter α that measures how much compact structures are favored. For each model, we pick a target structure and identify all sequences with the target structure as the unique global energy minimum, and map these sequences to two dimensions. We then create stability maps and folding rate maps by labeling each sequence in the map by how stable it is for the target structure or how fast it folds to the target structure. The stability maps for Schemes A and B are shown in Figure 1, and the corresponding folding rate maps are shown in Figure 2. These maps allow us to study the global distributions of protein-folding thermodynamics and kinetics in sequence space. We identify common features of the maps that are shared by the two schemes and thus independent of the energetic details. Furthermore, we focus on those organizational principles of the stability and folding rate maps that distinguish them from random maps; we also point out important differences between these two maps.
Fig. 2.
Folding rate maps in sequence space for (A) Scheme A and (B) Scheme B. The figure is generated in the same way as Figure 1, except here each sequence is colored according to the fraction of sequences that have lower folding rate, as measured by the folding probability pf. A sequence with the highest folding probability, hence fastest folding rate, is colored red; a sequence with the lowest folding probability, hence slowest folding rate, is colored blue. The fastest folding sequence is circled in each map.
Similarities Between Stability and Folding Rate Maps
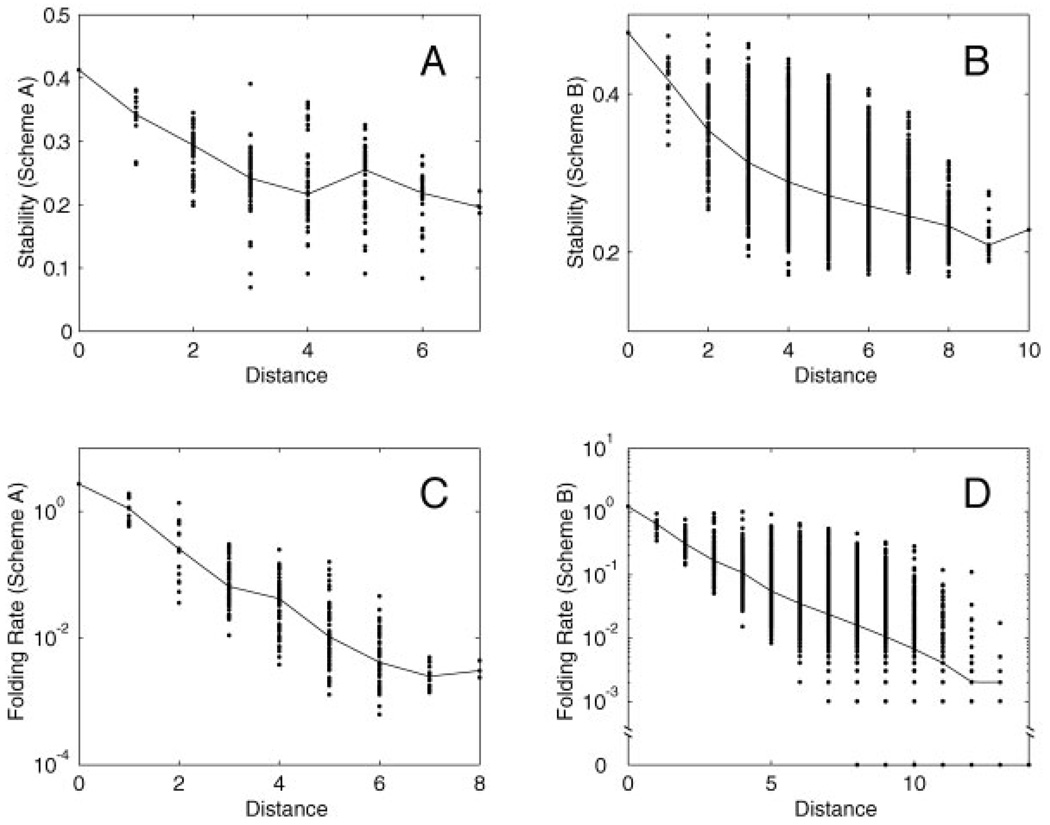
For each protein property (stability or folding rate), there exists an optimal sequence around which the sequence space can be organized. We find that both stability and folding rate maps are organized in a funnel-like fashion. The farther away a sequence is from the optimal sequence in the space, the less optimal the sequence is on average (Fig. 3). A notable exception is that in the stability map for Scheme A, an average sequence five mutations away from the optimal sequence is more stable than an average sequence four mutations away from the optimal sequence. Both stability and folding rate funnels cover a significant portion of the sequence space, and the decay of the average stability/folding rate can be observed many mutations away from the optimal sequence. These funnels are narrow along some directions and wide along other directions. In particular, these funnels are wide along the two dimensions in which the stability and folding rate maps are constructed (see Fig. 1 and Fig 2).
Fig. 3.
Funnel-like organizations of stability and folding rate maps. For each protein property (stability or folding rate), we identify the sequence with the optimal property, and for every sequence in the map, we plot its property against its Hamming distance from the optimal sequence. Dots mark stability/folding rate for each of the sequences in the map. The solid line connects median stability/folding rate for a given distance from the optimal sequence. A,B: Stability versus distance from the optimal sequence for Schemes A and B. C,D: Folding rate versus distance from the optimal sequence for Schemes A and B. Folding rate is plotted on a logarithmic scale.
How rugged are the stability and folding rate maps? To address this question, we perform an edge-based and a node-based analysis (Table I). A node represents a protein sequence with the target structure as the unique global energy minimum, and an edge represents a single mutation that connects two nodes.
TABLE I.
Measuring Ruggedness of Stability and Folding Rate Maps
| Stability map (Scheme A) |
Stability map (Scheme B) |
Folding rate map (Scheme A) |
Folding rate map (Scheme B) |
|||||
|---|---|---|---|---|---|---|---|---|
| da | Ne (re%)b | Nn (rn%)c | Ne (re%)b | Nn (rn%)c | Ne (re%)b | Nn (rn%)c | Ne (re%)b | Nn (rn%)c |
| 1 | 94 (99%) | 13 (–) | 214 (93%) | 17 (–) | 26 (88%) | 10 (–) | 58 (91%) | 10 (–) |
| 2 | 180 (97%) | 48 (96%) | 996 (88%) | 111 (95%) | 106 (84%) | 16 (87%) | 193 (87%) | 34 (88%) |
| 3 | 165 (87%) | 67 (85%) | 2400 (85%) | 373 (97%) | 176 (80%) | 53 (96%) | 547 (83%) | 90 (81%) |
| 4 | 143 (82%) | 53 (77%) | 3428 (81%) | 731 (98%) | 174 (84%) | 64 (95%) | 1171 (85%) | 214 (82%) |
| 5 | 88 (89%) | 51 (98%) | 3050 (77%) | 908 (99%) | 143 (81%) | 56 (98%) | 1852 (76%) | 393 (82%) |
| 6 | 15 (80%) | 25 (100%) | 1735 (76%) | 751 (99%) | 51 (71%) | 43 (100%) | 2325 (75%) | 538 (82%) |
| 7 | 3 (100%) | 568 (76%) | 422 (99%) | 12 (50%) | 15 (100%) | 2349 (73%) | 631 (86%) | |
| 8 | 74 (81%) | 148 (99%) | 3 (100%) | 1943 (71%) | 616 (85%) | |||
| 9 | 1 (0%) | 23 (96%) | 1231 (72%) | 485 (86%) | ||||
| 10 | 1 (0%) | 563 (63%) | 289 (91%) | |||||
| 11 | 197 (63%) | 124 (85%) | ||||||
| 12 | 41 (63%) | 50 (94%) | ||||||
| 13 | 3 (100%) | 10 (90%) | ||||||
| 14 | 1 (100%) | |||||||
d, the distance from the optimal sequence can be defined for a node, which is a sequence with the target structure as the unique global energy minimum, or for an edge, which is a single mutation that connects two nodes. For a node, d is defined as the Hamming distance between the node and the optimal sequence. For an edge, d is defined to be the smaller d of the two nodes it connects. Note that the optimal sequences are different in all four maps studied (see circled sequences in Fig. 1 and Fig. 2).
Edge-based analysis. All edges are classified as either pointing toward the optimal sequence or otherwise. An edge points toward the optimal sequence if and only if between the two nodes that the edge connects, the node closer to the optimal sequence also has a higher stability or folding rate. Ne is the total number of edges for a given distance d from the optimal sequence. re is the percentage of these edges that point toward the optimal sequence.
Node-based analysis. All nodes are classified as either pointing toward the optimal sequence or otherwise. A node points toward the optimal sequence if among the neighboring nodes (including itself), the node with the highest stability or folding rate is also closer to the optimal sequence than the current node. Nn is the total number of nodes for a given distance d from the optimal sequence. rn is the percentage of these nodes that point toward the optimal sequence.
In the edge-based analysis, an edge is said to point toward the optimal sequence if and only if between the two nodes that the edge connects, the node closer to the optimal sequence also has a higher stability or folding rate. For a given distance from the optimal sequence (re), the percentage of edges pointing toward the optimal sequence is a measure of the smoothness of the stability and folding rate funnels; it represents the probability that a greedy hill-climbing algorithm performed on an edge successfully finds the sequence closer to the optimal one. This percentage is 100% if the funnel is perfectly smooth, 50% if the funnel is dominated by noise, and 0% if the funnel is reversed. As the distance from the optimal sequence increases, the average smoothness of the funnel (as measured by the percentage of edges pointing toward the optimal sequence) in general decreases, but the funnel is never dominated by noise over the entire range of the map. This is true for both stability and folding rate maps (Table I). For example, most nodes still point to the optimal sequence, even when the distance between these nodes and the optimal sequence is as far as 6 and 8 mutations in the stability maps for Schemes A and B, and 7 and 13 mutations in the folding rate maps for Schemes A and B. Taking into account that the model protein is only 24 residues long, the sizes of these funnels are strikingly large. Overall, re, the percentage of all edges that point to the optimal sequence is 91% and 81% for stability maps of Schemes A and B and 81% and 75% for folding rate maps of Schemes A and B.
A second way to quantify the ruggedness is a similar node-based analysis. A node is said to point toward the optimal sequence if among all the neighboring nodes (including itself), the node with the highest stability or folding rate is also closer to the optimal sequence than the current node. For a given distance from the optimal sequence, rn, the percentage of nodes pointing toward the optimal sequence, is another measure of the smoothness of the stability and folding rate funnels; it represents the probability that a steepest-descent algorithm performed on a node successfully finds a new node closer to the optimal one. The result of the node-based analysis is shown in Table I. Again, the stability and folding rate maps are relatively smooth over the entire range of the map. Overall, rn, the probability that a steepest-descent algorithm performed on any node successfully finds a new node closer to the optimal one is 90% and 98% for stability maps of Schemes A and B, and 97% and 85% for folding rate maps of Scheme A and B.
Of particular interest is the ruggedness of folding rate maps. The effects of mutation on folding dynamics of 2D lattice proteins are subtle and depend not only on native structure but also on non-native conformations and the choice of move sets.29 Nevertheless, the large-scale distribution of folding rate in sequence space display patterns that are significantly different from random. Generally, folding rate maps are more rugged than stability maps, but surprisingly in at least one case the folding rate map is less rugged than stability map (Scheme A, node-based analysis). Hence, folding rate maps are somewhat more rugged than stability maps but not by a large margin. It should be noted that a 2D HP model may overestimate the ruggedness of conformational energy landscape of folding.29 It is unclear how ruggedness in conformational space relates to ruggedness in sequence space. However, it seems plausible that the ruggedness of folding rate maps in sequence space may be overestimated compared to stability maps. In this case, our conclusion still holds true that folding rate maps are not markedly more rugged than stability maps for real proteins.
Differences Between Stability and Folding Rate Maps
The major difference between the stability and folding rate maps is the location of the center of the funnel that represents the optimal sequence. This reflects the difference between factors that contribute to stability and those that contribute to folding rate. Stability depends on the relative energies of alternative conformational states as compared to the native state, whereas folding rate depends on the depth, width, shape, and location of local energy minima, as well as the height of energy barriers. This means that a small percentage of single mutations have opposing effects on stability and folding rate. This has been demonstrated experimentally by the existence of negative values for the Φ-value analysis32 and the different degrees of optimization of stability and folding rate in small proteins.33
Population Dynamics of Sequence Evolution
The topology of stability and folding rate maps is a major determinant of the dynamical behavior of protein sequence evolution. Population dynamics of sequence evolution can be simulated when the viable region of the sequence space is specified by a combination of stability and folding rate criteria. For example, if we define a sequence to be viable and share the same fitness value if and only if the target structure is the unique global minimum of energy among all structures, we can determine the evolutionary steady-state distribution in sequence space with mutation events only, as shown in Figure 4. Note that this means that all the sequences in each of the neutral nets for Schemes A and B have the same fitness value. Assumptions and protocols for simulating protein evolution are described in Materials and Methods. From these simulation studies, several evolutionary principles are determined and summarized below.
Fig. 4.
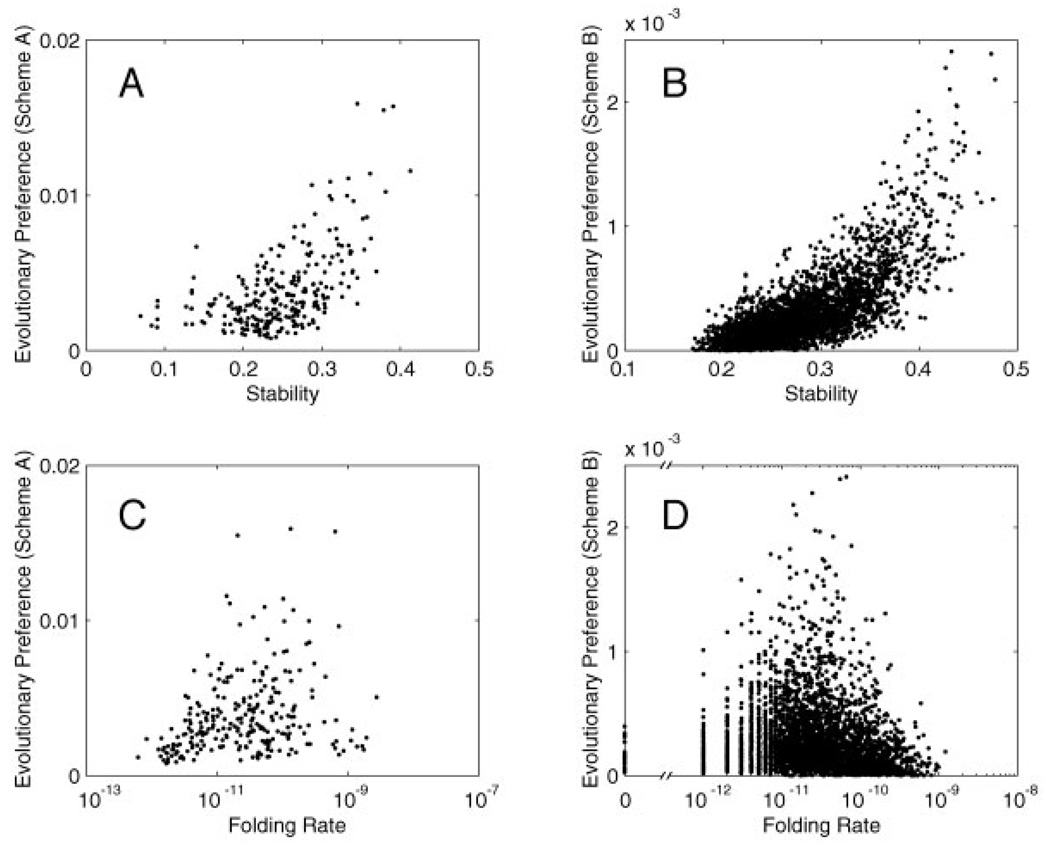
Correlation between evolutionary preference and stability/folding rate. In this example, evolutionary simulation is performed with mutation events only. Sequences share the same non-zero fitness value if and only if they have the target structure as the unique global minimum of energy. Evolutionary preference of a sequence is measured by how often this sequence is sampled at evolutionary steady state. A,B: Evolutionary preference vs. stability for Schemes A and B. C,D: Evolutionary preference versus folding rate for Schemes A and B. Folding rate is plotted on a logarithmic scale. Because in this case the boundary condition for the viable sequence space is determined by thermodynamic criteria, evolutionary preference is correlated more with stability than with folding rate.
First, some sequences are evolutionarily preferred over others even when the fitness landscape is flat. Evolutionary preference for each sequence is determined by the global topology of the viable sequence space, and it correlates largely with the degree centrality of the sequence also called the mutational stability, defined by the number of viable neighbors that differ from the sequence by one mutation.
Second, proteins are more stable and faster folding than necessary as a result of evolutionary dynamics. The degree of optimization is directly affected by the shape of the sequence map, in particular, the ruggedness of stability and folding rate funnels, and the boundary condition for the viable sequence space. When stability and folding rate are highly correlated, sequences that are most stable and fastest folding are preferred by evolution, even when the fitness landscape is flat. On the other hand, if the factors that contribute to stability are different from those that contribute to folding rate, the boundary condition for the viable sequence space plays a crucial role in determining the degree to which evolution favors more stable or faster folding sequences. For example, when the boundary condition is determined largely by thermodynamic criteria, evolutionary preference is more correlated with stability than folding rate (Fig. 4). This can help us understand the experimental observation that for some small proteins,33 sequences are extensively optimized for stability but not folding rate. This is probably not because folding rate is much harder to optimize by evolution than stability. Indeed, the folding rate map is not markedly more rugged than the stability map, as we have shown earlier. Rather, this is probably because evolutionary pressure for these proteins is largely thermodynamic, so the boundary condition for the viable sequence space is determined largely by stability criteria. For larger proteins that fold much slower, the boundary condition of the viable sequence space is likely to be dominated by kinetic criteria, and evolutionary preference is likely to be more correlated with folding rate.
Third, sequence space entropy also plays an important role in determining the average protein property as a result of evolution. When evolution is dominated by mutation events, evolutionary preference for the sequence in the center of the neutral net is not strong enough to overcome the huge size of sequence space. As a result, most of the sequence populations are located near the boundary of the fitness region.15–17,19,21,34 On the other hand, recombination pulls the sequence population more toward the center of the neutral net.21
DISCUSSION
Starting with a simplified model for proteins, we have constructed stability and folding rate maps in sequence space. These maps allow us to study the organizational and evolutionary principles of protein sequence-structure relationships and to address the following questions: how are thermodynamic and kinetic properties distributed in the sequence space? How do mutations affect stability and folding rate? And how does the special sequence space topology affect evolutionary dynamics of protein sequence population?
Our 2D HP model for protein folding is a drastically simplified one. This model is simple enough that the mapping between sequence space and structure space can be conducted in an exhaustive and exact manner. At the same time, the model is able to capture several key features of native proteins such as hydrophobic-hydrophilic partition, chain connectivity, and volume exclusion among residues. Furthermore, both thermodynamic and kinetic behaviors can be explicitly simulated. Because of the simplicity of this model, it is crucial to separate conclusions that are independent of the model details from artifacts that are caused by oversimplifications. For example, a 2D model is known to underestimate the cooperativity of protein folding.35,36 Our focus here is not on detailed mechanistic aspects of protein folding, but rather on the qualitative picture of how stability and folding rate are distributed in sequence space. Thus, our conclusions about the large-scale organization of protein sequence space and its effect on evolution are likely to remain true for other types of protein models.
Much has been learned about protein folding by studying folding mechanisms of single sequences. In this article, we show that additional insights can be revealed by studying protein folding collectively in sequence space by using a well-controlled model system. Even though the process of protein folding is complicated, the large-scale distributions in sequence space of protein folding thermodynamics and kinetics differ significantly from random distributions. Indeed, basins of attraction exist in sequence space, and all sequences are organized around them. Size, shape, and ruggedness of these funnels can be characterized quantitatively. Furthermore, this funnel-like organization in sequence space affects protein evolution and is a major determinant of sequence population favored by evolution. Our next step is to map detailed protein-folding mechanisms in sequence space by using more realistic protein models, with comparison to experiments. We expect this will further extend the organizational and evolutionary principles of protein sequence-structure relationships outlined in this article.
ACKNOWLEDGMENTS
This work is supported by National Institutes of Health to ML. We thank Ken Dill, Marcus Feldman, Hue Sun Chan, Erik Sandelin, and Patrice Koehl for helpful discussions.
Grant sponsor: National Institutes of Health; Grant number: GM63817.
REFERENCES
- 1.Bryngelson JD, Wolynes PG. Spin glasses and the statistical mechanics of protein folding. Proc Natl Acad Sci USA. 1987;84:7524–7528. doi: 10.1073/pnas.84.21.7524. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Lau KF, Dill KA. A lattice statistical-mechanics model of the conformational and sequence-spaces of proteins. Macromolecules. 1989;22:3986–3997. [Google Scholar]
- 3.Sali A, Shakhnovich E, Karplus M. How does a protein fold? Nature. 1994;369:248–251. doi: 10.1038/369248a0. [DOI] [PubMed] [Google Scholar]
- 4.Levinthal C. Are there pathways for protein folding? J Chim Phys. 1968;65:44–45. [Google Scholar]
- 5.Shakhnovich EI, Gutin AM. Implications of thermodynamics of protein folding for evolution of primary sequences. Nature. 1990;346:773–775. doi: 10.1038/346773a0. [DOI] [PubMed] [Google Scholar]
- 6.Shakhnovich EI, Gutin AM. A new approach to the design of stable proteins. Protein Eng. 1993;6:793–800. doi: 10.1093/protein/6.8.793. [DOI] [PubMed] [Google Scholar]
- 7.Wolynes PG, Onuchic JN, Thirumalai D. Navigating the folding routes. Science. 1995;267:1619–1620. doi: 10.1126/science.7886447. [DOI] [PubMed] [Google Scholar]
- 8.Dill KA, Chan HS. From Levinthal to pathways to funnels. Nat Struct Biol. 1997;4:10–19. doi: 10.1038/nsb0197-10. [DOI] [PubMed] [Google Scholar]
- 9.Pande VS, Grosberg AY, Tanaka T, Rokhsar DS. Pathways for protein folding: is a new view needed? Curr Opin Struct Biol. 1998;8:68–79. doi: 10.1016/s0959-440x(98)80012-2. [DOI] [PubMed] [Google Scholar]
- 10.Dobson CM, Karplus M. The fundamentals of protein folding: bringing together theory and experiment. Curr Opin Struct Biol. 1999;9:92–101. doi: 10.1016/s0959-440x(99)80012-8. [DOI] [PubMed] [Google Scholar]
- 11.Wright S. The roles of mutation, inbreeding, crossbreeding and selection in evolution. Proceedings of the Sixth International Congress on Genetics; 1932. pp. 356–366. [Google Scholar]
- 12.Maynard Smith J. Natural selection and the concept of a protein space. Nature. 1970;225:563–564. doi: 10.1038/225563a0. [DOI] [PubMed] [Google Scholar]
- 13.Mirny LA, Abkevich VI, Shakhnovich EI. How evolution makes proteins fold quickly. Proc Natl Acad Sci USA. 1998;95:4976–4981. doi: 10.1073/pnas.95.9.4976. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Tiana G, Broglia RA, Shakhnovich EI. Hiking in the energy landscape in sequence space: a bumpy road to good folders. Proteins. 2000;39:244–251. [PubMed] [Google Scholar]
- 15.Govindarajan S, Goldstein RA. Evolution of model proteins on a foldability landscape. Proteins. 1997;29:461–466. doi: 10.1002/(sici)1097-0134(199712)29:4<461::aid-prot6>3.0.co;2-b. [DOI] [PubMed] [Google Scholar]
- 16.Bornberg-Bauer E, Chan HS. Modeling evolutionary landscapes: mutational stability, topology, and superfunnels in sequence space. Proc Natl Acad Sci USA. 1999;96:10689–10694. doi: 10.1073/pnas.96.19.10689. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Taverna DM, Goldstein RA. The distribution of structures in evolving protein populations. Biopolymers. 2000;53:1–8. doi: 10.1002/(SICI)1097-0282(200001)53:1<1::AID-BIP1>3.0.CO;2-X. [DOI] [PubMed] [Google Scholar]
- 18.Taverna DM, Goldstein RA. Why are proteins so robust to site mutations? J Mol Biol. 2002;315:479–484. doi: 10.1006/jmbi.2001.5226. [DOI] [PubMed] [Google Scholar]
- 19.Taverna DM, Goldstein RA. Why are proteins marginally stable? Proteins. 2002;46:105–109. doi: 10.1002/prot.10016. [DOI] [PubMed] [Google Scholar]
- 20.Cui Y, Wong WH, Bornberg-Bauer E, Chan HS. Recombinatoric exploration of novel folded structures: a heteropolymer-based model of protein evolutionary landscapes. Proc Natl Acad Sci USA. 2002;99:809–814. doi: 10.1073/pnas.022240299. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Xia Y, Levitt M. Roles of mutation and recombination in the evolution of protein thermodynamics. Proc Natl Acad Sci USA. 2002;99:10382–10387. doi: 10.1073/pnas.162097799. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Voigt CA, Mayo SL, Arnold FH, Wang ZG. Computational method to reduce the search space for directed protein evolution. Proc Natl Acad Sci USA. 2001;98:3778–3783. doi: 10.1073/pnas.051614498. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Eigen M. Self-organization of matter and the evolution of biological macromolecules. Naturwissenschaften. 1971;58:465–523. doi: 10.1007/BF00623322. [DOI] [PubMed] [Google Scholar]
- 24.Fontana W, Schuster P. Shaping space: the possible and the attainable in RNA genotype-phenotype mapping. Science. 1998;280:1451–1455. doi: 10.1006/jtbi.1998.0771. [DOI] [PubMed] [Google Scholar]
- 25.Li H, Tang C, Wingreen NS. Are protein folds atypical? Proc Natl Acad Sci USA. 1998;95:4987–4990. doi: 10.1073/pnas.95.9.4987. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Li H, Helling R, Tang C, Wingreen N. Emergence of preferred structures in a simple model of protein folding. Science. 1996;273:666–669. doi: 10.1126/science.273.5275.666. [DOI] [PubMed] [Google Scholar]
- 27.Dill KA, Bromberg S, Yue KZ, Fiebig KM, Yee DP, Thomas PD, Chan HS. Principles of protein-folding: a perspective from simple exact models. Protein Sci. 1995;4:561–602. doi: 10.1002/pro.5560040401. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Irbäck A, Troein C. Enumerating designing sequences in the HP model. J Biol Phys. 2002;28:1–15. doi: 10.1023/A:1016225010659. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Chan HS, Dill KA. Transition-states and folding dynamics of proteins and heteropolymers. J Chem Phys. 1994;100:9238–9257. [Google Scholar]
- 30.Tenenbaum JB, de Silva V, Langford JC. A global geometric framework for nonlinear dimensionality reduction. Science. 2000;290:2319–2323. doi: 10.1126/science.290.5500.2319. [DOI] [PubMed] [Google Scholar]
- 31.Kimura M. The neutral theory of molecular evolution: a review of recent evidence. Jpn J Genet. 1991;66:367–386. doi: 10.1266/jjg.66.367. [DOI] [PubMed] [Google Scholar]
- 32.Goldenberg DP. Finding the right fold. Nat Struct Biol. 1999;6:987–990. doi: 10.1038/14866. [DOI] [PubMed] [Google Scholar]
- 33.Kim DE, Gu H, Baker D. The sequences of small proteins are not extensively optimized for rapid folding by natural selection. Proc Natl Acad Sci USA. 1998;95:4982–4986. doi: 10.1073/pnas.95.9.4982. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Williams PD, Pollock DD, Goldstein RA. Evolution of functionality in lattice proteins. J Mol Graph Mod. 2001;19:150–156. doi: 10.1016/s1093-3263(00)00125-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Abkevich VI, Gutin AM, Shakhnovich EI. Impact of local and nonlocal interactions on thermodynamics and kinetics of protein folding. J Mol Biol. 1995;252:460–471. doi: 10.1006/jmbi.1995.0511. [DOI] [PubMed] [Google Scholar]
- 36.Chan HS. Modeling protein density of states: additive hydrophobic effects are insufficient for calorimetric two-state cooperativity. Proteins. 2000;40:543–571. doi: 10.1002/1097-0134(20000901)40:4<543::aid-prot20>3.0.co;2-o. [DOI] [PubMed] [Google Scholar]