Ricco’s Areas for S- and L-Cone Mechanisms Across the Retina

Abstract

The purposes of this study were to measure areas of complete spatial summation (i.e., Ricco’s area) for S- and L-cone mechanisms and to evaluate whether the sizes of Ricco’s area could be explained in terms of either the densities of photoreceptors or ganglion cells. Increment thresholds were measured at the fovea and at 1.5°, 4°, 8°, and 20° in the superior retina using a temporal two-alternative forced-choice procedure. Test stimuli ranging from −0.36 to 4.61 log area (min²) were presented on concentric 12.3° adapting and auxiliary fields, which isolated either an S- or L-cone mechanism on the plateau of the respective threshold vs. intensity function. The data indicate that from 0–20° retinal eccentricity, the size of Ricco’s area is larger for the S-cone mechanism than the L-cone mechanism, increases monotonically for the L-cone mechanism, and, for both cone mechanisms, increases between 8–20° retinal eccentricity. This latter finding suggests that ganglion cell density rather than cone density defines the size of Ricco’s area in the parafoveal and peripheral retina.

INTRODUCTION

The area of complete spatial summation refers to the psychophysical finding that detection thresholds for relatively small test lights depend upon the total number of quanta that are incident over a discrete area of the retina. The maximal size of this area, known as Ricco’s area,¹ varies with stimulus conditions and retinal eccentricity, and has been explained in terms of stimulating equal numbers of ganglion cells,² or dedicating a constant amount of cortical space based on ganglion cell input to a discrete area within the visual field.³ Recently, Schefrin et al.⁴ have reported results that are consistent with these interpretations. They showed that age-related losses in ganglion cell density are correlated with age-related increases in the size of Ricco’s area under scotopic conditions. That particular study, however, tested only one retinal eccentricity and did not investigate changes in the size of Ricco’s area with changes in cone and ganglion cell densities across the retina. In this study, we measured Ricco’s area for S- and L-cone mechanisms from 0–20° in the superior retina and compared our findings to cone and ganglion cell densities reported in the literature.

METHOD

Measurements were obtained from three observers at five retinal eccentricities along the vertical meridian in the superior retina (0°, 1.5°, 4°, 8°, 20°). All observers had normal color vision, were free of ocular abnormalities, and were refracted for optical infinity. For measurements at 20° retinal eccentricity, the right pupil of each observer was dilated with one drop of Tropicamide (1%).

Three channels of a standard, 5-channel Maxwellian-view optical system were used for this study. Channel 1 created the test stimulus, channel 2 generated the background field, and channel 3 produced the auxiliary field. The temporal, spatial, and spectral characteristics of the stimuli used in this study were based on previous work,⁵ and control studies that measured threshold vs. intensity functions and test sensitivity functions. These conditions ensured that increment thresholds for test flashes involved in determining the size of Ricco’s area were measured near the absolute thresholds for an S- and L-cone mechanism, respectively. The stimulus conditions for isolating an S-cone mechanism were a 50 ms, 440 nm circular test stimulus concentric with a 580 nm, 7.8 log quanta background field, and a 520 nm, 7.2 log quanta auxiliary field. The stimulus conditions for isolating an L-cone mechanism were a 10 ms, 620 nm circular test stimulus concentric with a 480 nm, 7.8 log quanta background field, and a 450 nm, 7.4 log quanta auxiliary field. The sizes of the background and auxiliary fields were 12.3°, while the areas of the test stimuli varied from −0.36 to 4.61 log min². Pinhole-size fixation points aided the observer’s fixation at each retinal eccentricity.

Following 10 min of dark adaptation, observers foveally viewed the appropriate fixation point and chromatically adapted for 3 min to the background and auxiliary field combination. Upon completion of chromatic adaptation, a temporal 2-alternative forced-choice transformed 1-up-3-down staircase⁶ procedure was employed to determine the threshold for the test flash superimposed on the background and auxiliary fields. The geometric mean of the last four intensity values defined the increment threshold for each test size.

RESULTS

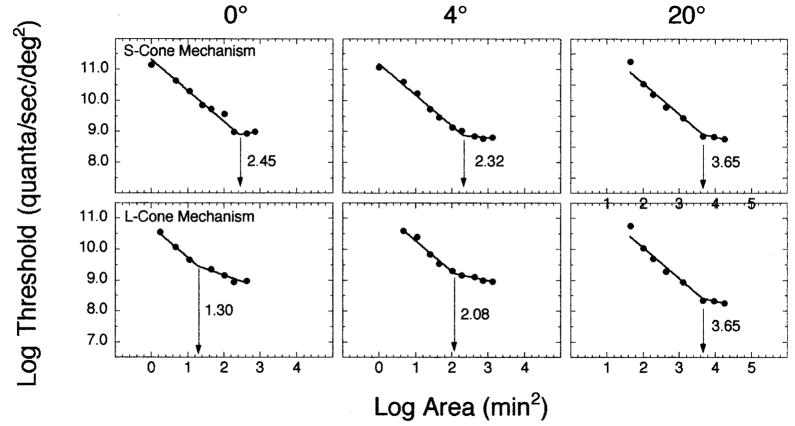
Figure 1 presents the results from one observer for three of the five retinal eccentricities. The upper and lower rows show data from conditions that isolated S-cone and L-cone mechanisms, respectively. A bilinear function was fit to each set of data using a Marquardt least-squares algorithm in Kaleidograph v. 3.08d. In the fitting procedure, the upper limb of the function was constrained to have a slope of − 1.0, in accordance with Ricco’s law, while both the slope and intercept of the lower limb were allowed to vary. The intersection of the two limbs defines Ricco’s area and is indicated by the arrows in each panel. The number in each panel specifies the size of Ricco’s area. As Fig. 1 illustrates, Ricco’s area can be measured for both cone mechanisms across a range of retinal eccentricities.

FIG. 1.

Log threshold (quanta/s/deg²) is plotted as a function of log area (min²) for (upper panels) S-cone and (lower panels) L-cone mechanisms. Each column of panels depicts a different superior retinal eccentricity along the vertical meridian. In each panel, the intersection of the two branches of the best-fitting bilinear function is denoted by an arrow and corresponds to Ricco’s area for that experimental condition.

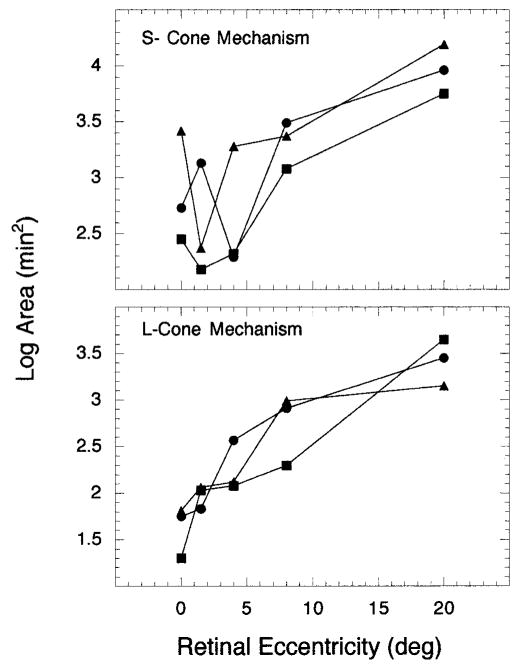
The size of Ricco’s area obtained for all retinal eccentricities tested in this study and for both the S- and L-cone mechanisms is shown in Fig. 2. For all three observers at all retinal eccentricities (except for one observer at 4°, denoted by circles), the size of Ricco’s area is smaller for the L-cone mechanism than the S-cone mechanism. This result is consistent with previous work by Brindley.⁷ Second, the retinal eccentricity associated with the smallest Ricco’s area differs for the two cone mechanisms — 0° for the L-cone mechanism and 1.5° for the S-cone mechanism (squares, triangles). Lastly, for both cone mechanisms, the size of Ricco’s area increases from 8° to 20° retinal eccentricity. This change in size from 8–20° is particularly relevant when comparing the measures of Ricco’s areas from this study to cone and ganglion cell densities.

FIG. 2.

Log area (min²) is plotted as a function of superior retinal eccentricity for (upper panel) S-cone and (lower panel) L-cone mechanisms. Each symbol denotes a different observer.

DISCUSSION

Studies of cone density reveal that changes in S-cone density across the retina differ from changes in M- and L-cone densities. While the peak density for M and L cones occurs at the fovea, the peak density for S cones occurs along the foveal slope between 0.5–1.5° retinal eccentricity.^8–10 A similar pattern for peak density is also found for ganglion cells. The concentrations of both parasol and midget ganglion cells, which receive input from M and L cones, are densest at the fovea. In contrast, the density of blue/yellow bistratified ganglion cells, which receive input from all three cone types, is greatest along the foveal slope.¹¹ All three cone types show a decrease in density from their peak until approximately 8–10° retinal eccentricity; beyond this point, there is little change in cone density with retinal eccentricity. Likewise, ganglion cells show a decrease in density from the area of their peak, but, unlike the cones, ganglion cell density continues to decrease with retinal eccentricity.

Based on the anatomical results discussed above, the size of Ricco’s area is better correlated with ganglion cell density than with cone density. It is generally the case within the central 8° of the retina that all three observers demonstrate a monotonic increase in the size of Ricco’s area as one moves away from the retinal locus corresponding to peak receptor and ganglion cell densities. These results can be explained by either decreases in the density of ganglion cells and/or cones. The crucial finding, however, is that, for all three observers, the size of Ricco’s area associated with each cone mechanism continues to increase from 8–20° retinal eccentricity. Thus, the change in the size of Ricco’s area from 8–20° retinal eccentricity suggests that ganglion cell density and not cone density is the determinant of Ricco’s area.

Because the spatial profiles of the parasol and midget ganglion cell densities are quite similar, although absolute numbers are different, it is difficult to know which ganglion cell type contributes to our findings with the L-cone mechanism. It should be noted, however, that our stimuli for L-cone isolation were small and brief, which strongly favors detection by a nonopponent pathway¹² or the parasol ganglion cells, while stimuli of a longer duration are known to elicit activity in the opponent pathway¹³ or midget ganglion cells.

Optical factors cannot explain our findings. For example, a control study was conducted to examine the effects of chromatic aberration that result from wavelength differences between our test and background fields, which may be particularly important for small test stimuli. Areal summation functions measured with and without an achromatizing lens for both the S- and L-cone mechanisms in the fovea revealed no effects of chromatic aberration on the size of Ricco’s area for either cone mechanism. Experimental values of Ricco’s area were also corrected using optical point spread functions.^14–17 The change in size of Ricco’s area for the S-cone mechanism was minimal, while the change in size of Ricco’s area for the L-cone mechanism was slightly more noticeable; however, the results of this study were not altered by these corrections. Thus, the size differences in Ricco’s area between the S- and L-cone mechanisms, and as a function of retinal eccentricity, cannot be explained by optical factors.

In conclusion, the three primary results of this study are: (1) the size of Ricco’s area increases monotonically for the L-cone mechanism with retinal eccentricity; (2) the size of Ricco’s area is larger for the S-cone mechanism than the L-cone mechanism from 0–20° retinal eccentricity; and (3) the size of Ricco’s area is more likely defined by changes in ganglion cell density than receptor density across the retina.