A New Total Body Potassium Method to Estimate Total Body Skeletal Muscle Mass in Children^,

Abstract

A whole body skeletal muscle [(SM); kg] mass estimation model, based on total body potassium [(TBK); mmol] measured by whole body ⁴⁰K counting (WBC) was developed (SM = 0.0082·TBK) and validated in adults in a previous study. It is unknown whether the adult TBK SM prediction model is applicable for pediatric use. The aim of this study was to derive and validate a pediatric TBK SM prediction equation. SM measured by MRI was used as the criterion and TBK was measured by WBC. The protocol was completed in 116 healthy children, 66 males and 50 females, 11.7 ± 3.5 y (mean ± SD, range = 5–17 y). A strong linear correlation was observed between TBK and SM (r = 0.984; P < 0.001). The SM:TBK ratio was 0.0071 ± 0.0008 kg/mmol in the children studied, much lower than the corresponding value of 0.0082 kg/mmol in adults. An empirical SM prediction equation was developed using TBK alone: SM = 0.0085·TBK − 2.83, r² = 0.97, SEE = 1.39 kg. Bland-Altman analysis did not disclose a significant bias in the prediction of SM. When biological factors entered along with TBK in the general linear model, another prediction equation was developed: SM = 5.52 + 0.001·TBK (mmol) + 0.081·weight (kg) − 0.049·height (cm) + 0.00004·TBK · height + race (−0.60 for Caucasian, 0.49 for African-American, and 0 for Hispanic). Because the adult TBK SM prediction model is not applicable for pediatric use, this study provides new empirical TBK SM prediction equations that should prove useful for studies on nutrition, growth, and development in children.

Introduction

Skeletal muscle (SM)⁸ is the largest component of the tissue-organ level in both children and adults. SM is ~0.75 kg (22–25% of body weight) in newborns and increases to ~28 kg (~40% of body weight) in adult men (1,2). SM plays an important role in physiological processes and energy metabolism. Although of increasing research and clinical importance, the accurate in vivo measurement of SM remains difficult or impractical in children and adolescents. Available methods for pediatric applications are expensive (such as MRI), pose unnecessary radiation risk for children [such as computed tomography (CT)], or are inaccurate (such as antropometry and bioimpedance methods) (3,4).

The whole body ⁴⁰K counting (WBC)-total body potassium (TBK) approach has a long history in body composition research. It was originally applied for predicting total body fat in the 1960s. Although the TBK-fat method is no longer in use, recent studies support the continued use of TBK for total body protein and body cell mass (5).

The limitations of existing SM estimation methods led us to seek a TBK-based method for measuring SM in pediatric studies. In a previous investigation, a TBK SM model was developed and validated in healthy adults: SM (kg) = 0.0082·TBK (mmol). This adult model was derived using a combination of theoretical models and empirical coefficients (6). However, the applicability of the adult prediction model for use in children is questionable. The adult model assumes a stable relationship between SM and TBK independent of age. In adults, ~60% of body potassium is within SM (2). In children, however, the low proportion of lean tissues as SM suggests the existence of a different TBK SM relationship. Therefore, the adult TBK SM prediction model may not be applicable in children.

The aims of this investigation were to explore the association between TBK and SM in healthy children and to derive and validate a TBK SM prediction equation for pediatric studies. Total body SM measured by multi-slice MRI was used as the criterion.

Methods

Subjects

Healthy children aged 5 to 17 y were screened by telephone to exclude those with underlying medical conditions. Each child who passed the screening then completed a medical history, physical examination, maturation assessment (Tanner stage), and routine blood studies to exclude the presence of underlying disease. The Institutional Review Board of St. Luke’s-Roosevelt Hospital Center approved the study protocol and all children and their parents gave written consent prior to participation.

Body composition measurements

Body weight was measured to the nearest 0.1 kg using a digital scale in fasting subjects wearing minimal clothing. Height was measured to the nearest 0.1 cm using a stadiometer (Holtain).

MRI

Total body SM was measured using multi-slice MRI as reported earlier by Ross et al. (7). The children were placed on the MRI scanner (General Electric, 1.5 T 6× Horizon) platform with their arms extended above their heads. One-centimeter-thick images were acquired from the L4–L5 inter-lumbar gap to the distal tips of the toes and fingers with a between-scan gap of 4.0 cm. The protocol involved the acquisition of ~30 axial images, the exact number varying with subject height. All scans were analyzed by a trained observer who completed periodic quality control evaluation. The images were segmented using VECT image analysis software (Tomovision) on a PC. Total body SM mass was calculated based on the measured SM volume and the assumed SM density (1.04 g/cm³) (7). The technical error for between-day measurements of the same scans by the same observer of MRI-derived SM volume was 0.34 ± 1.1% (8).

Whole body counting

The St. Luke’s 4π whole body counter was used to detect the natural 1.46 million electron volts γ-ray of ⁴⁰K. The ⁴⁰K counts were measured over 9 min and TBK, in mmol, was calculated as ⁴⁰K/0.000118 (1). The current precision of the St. Luke’s 4π whole body counter is 2.3% in subjects weighing between 20 and 100 kg (9).

Dual-energy X-ray absorptiometry

Body fat as a percentage of body weight was estimated with dual-energy X-ray absorptiometry [(DXA) Prodigy, GE Lunar; software versions 6.6 and 6.7] as previously reported (10).

Statistical analysis

Data are expressed as the mean ± SD. Statistical comparisons of physical characteristics and body composition between males and females were made by Student’s t test with two-tailed significance (P < 0.05). Simple linear regression analysis and general linear models were used to investigate the associations between TBK and MRI-measured SM. An SM prediction equation was developed based on TBK and biological variables such as age, height, weight, sex, and race. Because the number of subjects in the Asian (n = 3) and other (n = 13) race groups was small, equations 2 and 3 were derived from only 116 subjects, including Caucasian (n = 22), African-American (n = 56), and Hispanic groups (n = 38). However, the significance of variables included in the model was not substantially changed when all race groups were included. The SM prediction equation developed was cross-validated using the leave-one-out method (11). Bland-Altman analysis was used to test for bias in the developed equation against the criterion SM measure (12). Analyses were carried out using SPSS 13.0 for Windows.

Results

Baseline characteristics

A total of 116 healthy children (66 males and 50 females) met the study entry criteria. The subjects ranged in age from 5 to 17 y with a mean age of 11.7 ± 3.5 y. The basic characteristics of the subjects are presented in Table 1. Age, body weight, height, and BMI did not differ between the males and females, although the males had a lower percent body fat (P < 0.001).

TABLE 1.

Subject basic characteristics and body composition¹

Group	Male	Female	Total	Range
n	66	50	116
Age, y	11.9 ± 3.6	11.5 ± 3.3	11.7 ± 3.5	5–17
Body weight, kg	52.4 ± 21.4	49.3 ± 21.1	51.1 ± 21.3	21.4–118.9
Height, cm	154.4 ± 19.7	149.5 ± 13.4	152.3 ± 17.4	116–185
BMI, kg/m2	21.0 ± 4.4	21.3 ± 6.7	21.1 ± 5.5	14.4–49.6
Fat by DXA, %	21.3 ± 11.4	28.4 ± 10.8*	24.4 ± 11.1	4.9–50.7
TBK, mmol	2480 ± 1043	1975 ± 566*	2262 ± 902	937–4907
SM, kg	18.1 ± 9.0	14.2 ± 5.2*	16.4 ± 7.8	5.5–41.2

¹Values are means ± SD.

^*Different from males, P < 0.01.

SM and TBK

SM measured by MRI and TBK measured by WBC were 18.1 ± 9.0 kg and 2480 ± 1043 mmol for the males and 14.2 ± 5.2 kg and 1975 ± 566 mmol for the females. Although males had a larger SM and TBK (P < 0.01), the SM:TBK ratio did not differ between males (0.0071 ± 0.0008 kg/mmol) and females (0.0070 ± 0.0008 kg/mmol). However, the SM:TBK ratio (0.0071 ± 0.0008 kg/mmol) in all children combined was much lower than the mean SM:TBK value of 0.0082 kg/mmol observed in healthy adults (6).

TBK SM prediction model

TBK was the strongest SM predictor identified (r = 0.984; P < 0.001), explaining 96.9% of the observed between-individual variation (Fig. 1). A simple prediction equation was thus derived from the 116 children:

$$\text{SM}(\text{kg})=0.0085·\text{TBK}(\text{mmol})-2.83$$ (Eq. 1)

FIGURE 1.

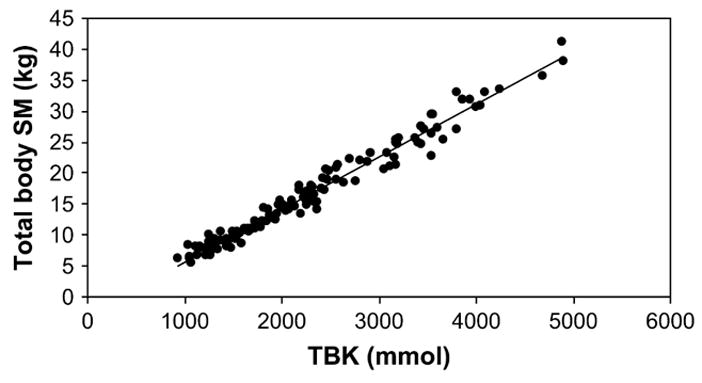
Total body SM of children measured by MRI vs. TBK measured by WBC. SM (kg) = 0.0085·TBK (mmol) − 2.83 (r = 0.984, P < 0.001; SEE = 1.39 kg; n = 116).

The SEE of MRI-measured SM estimation by TBK alone was 1.39 kg.

However, the SM:TBK ratio increased during growth; in this sample, the SM:TBK was positively correlated with age (r = 0.62), weight (r = 0.63), and height (r = 0.86; all P < 0.001), so we would expect the relations between TBK and SM to be altered with growth rather than be stable as in adults. When biological factors (including age, sex, Tanner stage, race, height, and weight, and the interactions of these variables with TBK) were entered along with TBK in general linear models, the following equation was developed (all variables significant at P ≤ 0.002, except TBK, P = 0.50):

$$\begin{array}{l}\text{SM}(\text{kg})=5.52+0.001·\text{TBK}(\text{mmol})+0.081·\text{weight}(\text{kg})\\ -0.049·\text{height}(\text{cm})+0.00004·\text{TBK}·\text{height}\\ +\text{race}(-0.60\text{for}\text{Caucasian},0.49\text{for}\\ \text{African}-\text{American},\text{and}0\text{for}\text{Hispanic})\end{array}$$ (Eq. 2)

The residuals from this model were found to be nonconstant, so a revised model was developed with a square root transformation (Sqrt) applied to the dependent variable (r² = 0.98; SEE = 0.12 kg; all P < 0.001 except age, P = 0.022).

$$\begin{array}{l}\text{Sqrt}(\text{SM},\text{kg})=1.20+0.001·\text{TBK}(\text{mmol})+0.017\\ ·\text{weight}(\text{kg})+0.015·\text{age}(\text{y})+0.0000027\\ ·\text{TBK}·\text{weight}+\text{race}(-0.075\\ \text{for}\text{Caucasian},0.077\text{for}\text{African}-\text{American},\\ \text{and}0\text{for}\text{Hispanic})\end{array}$$ (Eq. 3)

Residuals from this model met assumptions of homoscedasticity. Cross validation by the leave-one-out method showed that the SEE increased from 0.12 to 0.13 kg, indicating that the equation was only slightly influenced by specific data points in this sample and that the equation should work well in other samples drawn from a similar population. Bland-Altman analysis failed to disclose a significant bias in prediction (r = 0.06, P = 0.50) (Fig. 2).

FIGURE 2.

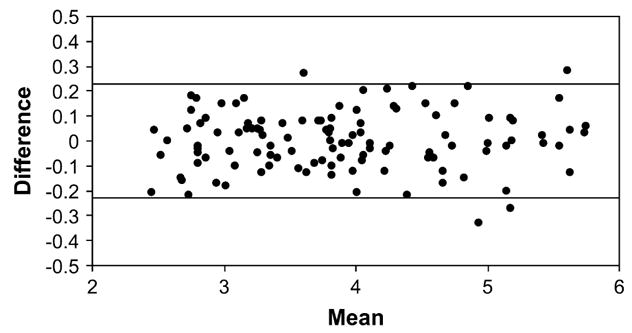
Bland-Altman analysis. The difference (Δ) between MRI-measured Sqrt (SM) and model predicted Sqrt (SM) by Eq. 3 vs. MRI-measured Sqrt (SM) and model predicted Sqrt (SM) mean (SM_MEAN). Δ = 0.01 × SM_MEAN − 0.03; r = 0.06, P = 0.5; n = 116. The 95%[CI] (0.23 kg and −0.23 kg) are shown as the upper and lower lines.

Discussion

In vivo measurements of total body SM are of growing interest in the context of pediatric body composition and nutrition research. The most accurate methods are multi-slice CT and MRI (8). However, the prohibitive radiation exposure of CT limits its applicability in healthy children. Although MRI can be used as the criterion in pediatric study (13,14), its application is limited because of expense and lack of instrument access. Another available SM estimation method is based on DXA. Kim et al. (15,16) reported a DXA SM prediction formula in adults and children. Although the DXA method is practical for application in children, a small radiation exposure should be considered for repeated studies. Other SM estimation methods (e.g. anthropometry, bioimpedance, and urinary creatinine) were developed; however, these methods are less accurate (3,4,13,17).

Potassium is a measurable element in vivo and the use of TBK as an index of body composition has a long history in body composition and nutritional research (1). As an example, the St. Luke’s 4π WBC has good intraclass correlation (r = 0.998) and mean CV (2.3%). Early investigators used the WBC-TBK approach as a measure of lean mass and, by subtraction, body fat. Although this approach was replaced by new methods, the TBK remains valuable for noninvasive estimation of total body protein and body cell mass (18–20).

In this study, we examined the WBC-TBK approach for predicting total body SM in healthy children. A relatively stable SM:TBK ratio (0.0082 kg/mmol) was suggested by our previous study (6). Total body SM mass can be predicted as 0.0082·TBK in adults. Potassium exists in all organs and tissues of the body, not only SM. Therefore, the above TBK SM approach is based on an assumption that the proportion of fat-free mass as SM is relatively stable across adult subjects. If the proportion of fat-free mass as SM changes with growth, then factors other than TBK alone must be considered in an equation to estimate SM.

This study examined the relationship of SM to TBK in children and we found that the mean SM:TBK ratio in children (0.0071 ± 0.0008 kg/mmol) was much lower than the SM:TBK value observed in adults (6). Therefore, the adult TBK SM prediction model cannot be applied to children.

TBK can be safely and noninvasively measured by WBC. Therefore, the WBC approach provides a safe means of estimating total body SM for pediatric studies. It may provide additional precision that the SEE of SM with TBK in adult studies (1.5 kg) has been shown to be smaller than for anthropometric (2.2 kg) and bioelectrical methods (2.7 kg) (21). Moreover, the WBC approach allows us to predict other important body components at same time, including total body protein and body cell mass in both healthy adults and children (19,20).

Our convenience sample did not have an adequate size and racial diversity to accommodate all of the issues surrounding the development of a prediction model. Nor are we able to identify the exact age at which the transition from the pediatric to the adult TBK:SM ratio occurs, because the ages in our sample ranged from 5 to 17 y and our adult sample began at age 20 y. Our analyses were based on a cross-sectional sample and the extent to which subjects’ changes during growth and development over time conform to the model predictions is unknown. We anticipate that our TBK SM prediction model may have application to the study of body composition changes during growth and development, but such application should be treated with caution pending validation of the revised models using longitudinal data.

Our research was initially prompted by the need for safe and accurate total body SM estimation methods. In this study, the potential of WBC in predicting SM in healthy children was examined. Future studies are needed to evaluate the quantitative association between TBK and SM in newborns and populations other than healthy children and adults.