The sources of two components of variance: An example of multifinger cyclic force production tasks at different frequencies

Abstract

In a multifinger cyclic force production task, the finger force variance measured across trials can be decomposed into two components, one that affects the combined force output (“bad variance”), and one that does not (“good variance”). Previous studies have found similar time patterns of “bad variance” and force rate leading to an approximately linear relationship between them. Based on this finding and a recently developed model of multifinger force production, we expected the “bad variance” during cyclic force production to increase monotonically with the rate of force change, both within-a-cycle, and across trials at different frequencies. Alternatively, “bad variance” could show a dependence on task frequency, not on actual force derivative values. Healthy subjects were required to produce cyclic force patterns to prescribed targets by pressing on unidimensional force sensors, at a frequency set by a metronome. The task was performed with only the index finger, and with all four fingers. In the task with all four fingers, the “good variance” increased approximately linearly with an increase in the force magnitude. The “bad variance” showed within-a-cycle modulation similar to that of the force rate. However, an increase in the frequency did not lead to an increase in the “bad variance” that could be expected based on the natural relationships between action frequency and the rate of force change modulation. The results have been interpreted in the framework of an earlier model of multifinger force production where “bad variance” is a result of variance of the timing parameter. The unexpected lack of modulation of the “bad variance” with frequency suggests a drop in variance of the timing parameter with increased frequency. This mechanism may serve to maintain a constant acceptable level of variance under different conditions.

Introduction

When a person performs a task of accurate force production, force variability, estimated as the standard deviation either across trials or over samples of a force time series, typically shows a close to linear increase with the force level (Newell and Carlton 1988). When the force is produced by a set of effectors acting in parallel, for example several fingers pressing on force sensors, each effector's force variability increases with its force level while there is little change in the total force variability with a change in the total force magnitude (Shim et al. 2004; Shapkova et al. 2008). This discrepancy is produced by particular patterns of finger force co-variation that channel the individual finger variability into a sub-space within the space of finger forces that does not affect the total force. This sub-space has been referred to as the uncontrolled manifold (UCM, Scholz and Schöner 1999; Latash et al. 2001), while the hypothetical neural mechanisms that bring about the mentioned patterns of force co-variation have been termed force stabilizing synergies (reviewed in Latash et al. 2002b, 2007).

Studies of force stabilizing synergies commonly used the framework of the UCM hypothesis (Scholz and Schöner 1999; Latash et al. 2002b). According to this hypothesis, the neural controller works in a space of elemental variables and creates in that space a sub-space corresponding to a desired value of a particular performance variable (the UCM). Further, the controller limits variability orthogonal to the UCM (“bad variability”, V_ORT) while allowing relatively high variability within the UCM (“good variability”, V_UCM). In studies of multi-finger force production, the performance variable was the total force, while the role of elemental variables was played by finger modes – hypothetical neural variables corresponding to desired involvement of individual fingers. Note that finger forces show patterns of force interdependence referred to as enslaving or lack of finger individuation (Li et al. 1998; Zatsiorsky et al. 2000). Hence, finger modes can be changed by the neural controller one at a time, at least hypothetically, while finger forces cannot.

Earlier studies have shown that the finger mode variance within the UCM, V_UCM, increases with the force level, while the variance orthogonal to the UCM, V_ORT, shows little change with the force level but is strongly modulated with the first force derivative with respect to time (Latash et al. 2002a; Scholz et al. 2002). Note that variability of the total force depends only on V_ORT, not on V_UCM. Further, these findings formed the basis for a model of multi-finger force variability (Goodman et al. 2005). This model assumed that each finger's force was a time function scaled with two parameters, related to the planned magnitude and timing of that finger's force. Analysis of the experimental data within the model suggested that there was strong co-variation among the magnitude-related parameters for individual fingers, while there was no comparable co-variation among the timing-related parameters. In other words, the central controller seems to be able to co-vary the magnitudes of individual finger involvement such that the total force remains relatively unchanged, while it is unable to co-vary the timing parameters.

Some of the mentioned studies used cyclic force production tasks (Latash et al. 2001; Scholz et al. 2002) while others used discrete tasks (Latash et al. 2002a; Shim et al. 2004). There has been an ongoing debate on whether discrete and cyclic tasks represent two classes with distinct neural control mechanisms or they are different peripheral consequences of basically the same control process (Schaal et al. 2004; Hogan and Sternad 2007). Note that one of the main characteristics of a cyclic process is its frequency while the rate of change of the variable is modulated within the cycle and depends on both frequency and amplitude. Using cyclic tasks allows distinguishing between effects of the rate of force change and of frequency, because it is possible to require an increase in the force rate with an unchanged frequency by changing only the amplitude. This distinction is potentially important because while frequency can be viewed as set at a high control level, the rate of force emerges at the output of the system as a result of the execution. All the mentioned data and the model by Goodman et al. (2005) suggest that V_ORT is defined by the time derivative of force. However, a more recent model (Goodman and Latash 2006) suggests that the two components of variability, V_UCM and V_ORT, emerge at a relatively high control level. According to this model, one could expect a dependence of V_ORT on frequency of the process rather than on the actual rate of force change. In this experiment, both the frequency, and the rate of force were altered in order to disambiguate between these two possible explanations.

We predicted that for a constant amplitude force production task, increasing the frequency will not result in a change in V_UCM, as this is proportional to the force, but we expect V_ORT to be modulated within the cycle with force rate and to increase with an increase in frequency (which causes an increase in the force rate).

Methods

Subjects

Eight right-hand dominant subjects, 4 males and 4 females (mean ± standard deviation: age 26 ± 4 years, weight 69.5 ± 8.0 kg, height 1.68 ± 0.010 m) volunteered to participate in this experiment. All subjects were healthy, with no known neurological or peripheral disorders. All of the subjects gave informed consent according to the policies of the Office for Research Protections at The Pennsylvania State University.

Apparatus

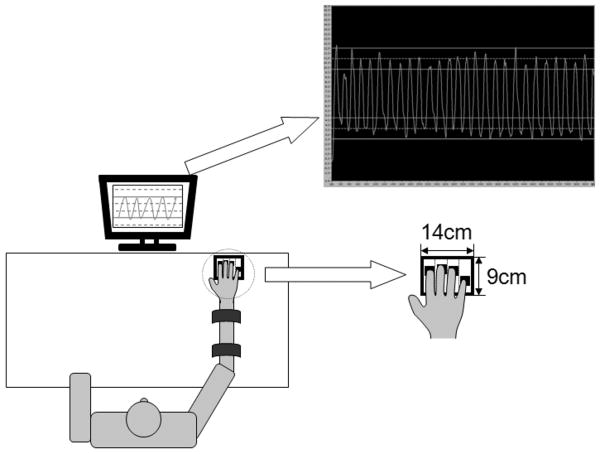
Figure 1 shows the experimental setup. It consisted of four unidirectional piezoelectric force sensors (model 208C02; PCB Piezotronic Inc.), each with a diameter of 1.5 cm, to measure the vertical forces applied by the four finger tips of the right hand. The sensors were spaced at 3.0 cm intervals in the medio-lateral plane, and the forward-backward location of the sensors was adjusted to match the anatomy of the individual subjects. The signals from the force sensors were amplified by signal conditioners (M482M66, PCB Piezotronics, Inc., NY), and then sampled at 200 Hz with 12 bit resolution by a LabVIEW program running on a PC.

Figure 1.

The experimental setup. The subjects pressed on four unidimensional force sensors with the index, middle, little and ring fingers of the right hand, with feedback on either the index finger (I) or all four fingers (IMRL) shown on the screen. The main task of the experiment was to produce sine-wave like trajectories between the targets shown on the screen, with the peaks and troughs coinciding with computer generated beeps at a specific frequency.

During the measurements, the subject sat comfortably in a chair facing the testing table, with his or her right upper arm at approximately 45° abduction in the frontal plane, 45° flexion in the sagittal plane, and with the elbow at approximately 45° flexion. The forearm rested on a horizontal board on a table, and two pairs of Velcro straps were used to prevent the forearm from moving. The fingers rested on a small wooden wedge to ensure that their posture did not change throughout the measurements. Feedback about the required force production was provided on a 17″ LCD screen placed 65 cm in front of the subjects.

Experimental procedure

There were three types of tests, maximal voluntary contraction (MVC) tests, single-finger ramp tests, and cyclic force production tests. In all these tests, the subjects were given feedback on the force produced by the instructed finger(s), by a constantly updating plot of the force magnitude (y-axis) against time (x-axis).

In the MVC task, the maximal force produced by the four fingers (I - index, M - middle, R - ring and L - little) and their combination (IMRL) was measured. The subjects were instructed to initially rest their fingers on the sensors. Then, in a self-paced manner after the cursor passed a vertical line (at 10 s after the start of the trial), they were instructed to press “as hard as possible” with the instructed finger(s). After reaching their maximum force (at a self selected time within 10 s), they were told that they could relax. Each trial lasted for 30 s. Two trials were recorded for each finger or combination of fingers, and the largest force produced between the two trials was used in later analysis. In single-finger MVC tests, the subjects were required not to pay attention to possible force production by the other fingers, but were required to ensure that all fingers remained on the sensors throughout the trial.

In the single-finger ramp tests, the subjects were shown a template on the screen, consisting of a horizontal segment at zero force for the first 5 s, then a slanted line from 0% to 40% of MVC over the next 20 s, then another horizontal segment corresponding to 40% MVC for the last 5 s. In each trial, one of the fingers was instructed to produce a force matching this template, and feedback was provided of the force level of that finger. The scale of the feedback was set such that for every trial, the top of the screen corresponded to 50% MVC of the instructed finger. The other three fingers remained on the force sensors, but no feedback on their force was provided. The subjects were instructed not to pay attention to the forces produced by the other fingers. The trials were performed twice for each of the four fingers, with the order balanced across subjects. A rest period of 30 s was provided between trials. The data from these trials were used to compute the enslaving matrix (see further details in the Data Processing section, and in Zatsiorsky et al., 1998).

During the cyclic force production trials, the subjects were required to produce smooth sine-wave like force patterns with either the index finger (I), or with all four fingers (IMRL) pressing together. During the I-finger trials, no feedback was provided on the forces produced by the other fingers; the subjects were instructed not to pay attention to possible force production by the other fingers of the hand. They were instructed to make the peaks and troughs lie within a given target range, indicated by dashed lines on the monitor, and to make the changes in force magnitude between these target ranges smooth. Additionally, a computer-generated metronome indicated when the peak or trough should take place. An example of a typical performance in the cyclic force production task is shown in Figure 1.

Four different frequencies were used, 0.67 Hz, 0.9 Hz, 1.1 Hz and 1.33 Hz. These frequencies were selected based on a pilot experiment, and spanned the range of frequencies over which subjects could successfully complete the task given the error margins. These frequencies are lower than the preferred frequencies of 1.5 – 2 Hz reported in similar tasks (Latash et al. 2001; Scholz et al. 2002); this is probably due to the stricter explicit accuracy constraints in this experiment. In the previous experiments, only a target line was given, whereas here a target range was given. Additionally, subjects in this experiment were required to match the metronome beat both at the peaks and troughs of the force production, whereas in the previous experiments, the subjects were required to match the metronome only at the force peaks.

The two targets were set at 10% of MVC, and 30% of MVC. For the 0.9 Hz frequency, an additional set of targets was used (10% MVC and 40% MVC). Each target consisted of a solid line, with dashed lines at ± 3% MVC. The scale of the feedback was altered such that feedback was always provided in terms of MVC rather than in N.

For each finger combination and frequency, a 30-s practice trial was performed, followed by three recordings of 30 s each. The order of finger combination/frequency was randomized, while the practice trial and three main trials of a particular combination were consecutive.

Data processing

The data were processed using Matlab (The MathWorks, Natick, MA). The calculations of the variance of the force data was performed on unfiltered data. As the data were smooth to begin with, and the variance is calculated across repetitions of the task, the use of unfiltered force data is not expected to produce different results to using filtered force data as in some of the earlier studies (Latash et al. 2001, 2002a; Scholz et al. 2002). Calculation of the force rate (dF/dt) was performed using a 5-point derivative on filtered data (using a two-way 2^nd order low-pass Butterworth filter at 6 Hz).

The data from the cyclic force production task were analyzed within the framework of the uncontrolled manifold (UCM) hypothesis. The UCM hypothesis offers a method to compute the “good” and “bad” components of variance in the space of commands to individual fingers (reviewed in Latash et al. 2002b, 2007). Briefly, the space of elemental variables (commands to individual fingers, finger modes) is divided into two sub-spaces, one corresponding to a fixed value of the total force (the UCM) and the other leading to changes in the total force (orthogonal to the UCM). Further, variance across trials is compared within the two sub-spaces (per dimension); if significantly more variance lies within the UCM, a conclusion is drawn that a multi-element synergy stabilizes the total force.

Due to the mentioned phenomenon of enslaving (Zatsiorsky et al. 1998, 2000), individual finger forces co-vary positively across tasks and force values. To analyze task-specific patterns of co-variation, forces have to be converted into finger modes (Latash et al. 2001), which can hypothetically be changed by the controller one at a time. This was done using the corresponding enslaving matrix, E.

Single-finger ramp trials were used to generate E for each subject. For each single-finger trial, a linear regression of the forces produced by individual fingers against the total force produced by all four fingers over a 20-s time interval in the middle of the ramp was computed. The ratios between the changes in individual finger forces and the change in the total force were used to construct an enslaving matrix for each subject as follows:

$$\text{E}=\left[\begin{array}{cccc}\frac{\Delta f_{I,I}}{\Delta F_I}& \frac{\Delta f_{I,M}}{\Delta F_M}& \frac{\Delta f_{I,R}}{\Delta F_R}& \frac{\Delta f_{I,L}}{\Delta F_L}\\ \frac{\Delta f_{M,I}}{\Delta F_I}& \frac{\Delta f_{M,M}}{\Delta F_M}& \frac{\Delta f_{M,R}}{\Delta F_R}& \frac{\Delta f_{M,L}}{\Delta F_L}\\ \frac{\Delta f_{R,I}}{\Delta F_I}& \frac{\Delta f_{R,M}}{\Delta F_M}& \frac{\Delta f_{R,R}}{\Delta F_R}& \frac{\Delta f_{R,L}}{\Delta F_L}\\ \frac{\Delta f_{L,I}}{\Delta F_I}& \frac{\Delta f_{L,M}}{\Delta F_M}& \frac{\Delta f_{L,R}}{\Delta F_R}& \frac{\Delta f_{L,L}}{\Delta F_L}\end{array}\right]$$ (1)

where Δf_j,k are the changes of individual finger forces j (j = I, M, R, and L) and ΔF_k are the changes of the respective total forces, produced during the ramp when finger k (k = I, M, R, and L) is the instructed finger. This matrix is a linear approximation of a matrix containing partial derivatives ∂f_j,k / ∂F_k where ∂f_j,k and ∂F_k are the infinitesimal changes of individual and total finger forces.

The force data from the cyclic force production trials f were converted into mode magnitudes m by using the E matrix: m = [E]⁻¹·f.

The force data in the cyclic task were segmented into the periods of force increase, and force decrease. The segmentation for periods of force increase was performed by selecting the data between a local minimum and a local maximum of the force rate (dF/dt), or vice-versa for the force decrease. Only segments where the force crossed the force mid-line (half way between the targets) were considered. Additionally, segments where the start or the end of movement were more than 15% MVC away from the target, or temporally more than 20% of a cycle away from the metronome tick were discarded. For computation of the variance, the segmented force data were first resampled to 100 data points using cubic spline interpolation.

For later statistical analysis, the mean force (I or IMRL) was calculated across trials for each condition. Nine time samples were selected such that the mean force at these times was 12%, 14%, …, 28% of MVC. The variance was then calculated at these times. In this way, the variances are calculated at evenly spaced force levels. Note that the variance was calculated at these times, rather than averaged across the inter-sample time intervals.

In comparing conditions with different amplitudes, rather than selecting samples with equidistant force levels, the variance was instead calculated at ten different time points, which were at phase 10%, 20%, …, 90%,100% (from 100 samples, using the resampled force data). Using this sampling technique, the variance is calculated at evenly spaced time intervals.

In the IMRL task, changes in the value of the total force F_TOT can be written as a function of the changes in the modes dm=[dm_idm_mdm_rdm_l]^T, where T signifies a matrix transpose.

$${\text{dF}}_{\text{TOT}}=\left[\begin{array}{llll}\text{1}\hfill & 1\hfill & 1\hfill & 1\hfill \end{array}\right]\text{df}=\left[\begin{array}{llll}\text{1}\hfill & \text{1}\hfill & \text{1}\hfill & \text{1}\hfill \end{array}\right]\text{E }\text{dm}$$ (2)

where df = [df_idf_mdf_rdf_l]^T. The UCM is defined by an orthogonal set of eigenvectors in mode space e_i that do not alter the total force, i.e.

$$\text{0}=\left[\begin{array}{llll}1\hfill & 1\hfill & 1\hfill & 1\hfill \end{array}\right]\text{E}{\text{e}}_i$$ (3)

These directions can be found by taking the null space of the Jacobian of this transformation ([1 1 1 1] E). The mean-free modes were projected onto these directions and summed, to give

$$f_{\Vert }=\sum _{i=1}^{n-p}\left({\text{e}}_{\text{i}}^T\cdot \text{dm}\right){\text{e}}_{\text{i}}$$ (4)

where n = 4 is the number of degrees of freedom of the m vector, and p=1 the number of degrees of freedom of the performance variable (F_TOT). The component orthogonal to the null space is given by:

$$f_{\perp }=\text{dm}-f_{\Vert }$$ (5)

The amount of variance per DOF parallel to (or within) the UCM is then given by:

$$V_{\text{UCM}}=\frac{\sum {|f_{\Vert }|}^2}{\left(n-p\right)N_{\text{trials}}}$$ (6)

This is the variance that is compensated, that is, it does not alter the total force. Similarly, the amount of variance per DOF orthogonal to the UCM is given by:

$$V_{\text{ORT}}=\frac{\text{∑}_{i=1}^{N_{\text{trials}}}{|f_{\perp }|}^2}{{\text{pN}}_{\text{trials}}}$$ (7)

Statistics

Standard descriptive statistics were used. The accuracy in performing the different conditions was compared using ANOVA on the timing errors (expressed in percent of a half-cycle) and force errors (computed as the distance from the target at force maxima/minima, and expressed in percent of MVC) at the start and end of the force half-cycles, with factors Combination (I or IMRL), Frequency (0.67 Hz, 0.9 Hz, 1.1 Hz, 1.33 Hz), and Direction (force increase, force decrease). These ANOVAs were performed on the data for the amplitude of 20% MVC. To compare the effect of amplitude, additional ANOVAs were performed over the conditions where the frequency was 0.9 Hz with factors Combination, Amplitude (20% or 30% MVC), and Direction.

To compare the variance between the trials with finger combinations I and IMRL, a two-way repeated measures ANOVA was performed, with factors Combination (I or IMRL) and Representative point (beginning of force increase/decrease, at time of peak (or trough) of force rate, end of force increase/decrease).

Repeated measures ANOVAs were performed on the two components of the variance described above, V_UCM and V_ORT with factor Variance Type (V_UCM or V_ORT) and repeated factor of Time (Phase 10%, 20%,…,100%). The variance was calculated at these time samples.

For V_UCM, the variances were calculated at 9 samples corresponding to equidistant force levels as described in the Data Processing section above. To test the hypothesis that V_UCM is dependent on force and not on force rate (which is expected to change with frequency), the factors used were Force (12%, 14%, …, 28% of MVC), Frequency (0.67 Hz, 0.9 Hz, 1.1 Hz, 1.33 Hz) and Direction (force increase, force decrease). Direction was included to test whether the variance changes are symmetrical for force increase and decrease.

For V_ORT, the variances were calculated at 10 equally spaced times (Phase 10%, 20%, …, 100%). To test the hypothesis that V_ORT is dependent on force rate, a repeated measures ANOVA was performed with factors Frequency, Time (Phase 10%, 20%,…,100%) and Direction. Frequency is expected to be linearly related to mean force rate magnitude (across trials). As the force rate changes with time within a trial, Time is expected to also have a significant effect on V_ORT. Direction is again included to capture the differences in force increase and decrease. To prevent the changes in amplitude from affecting the results, only the conditions with 20% amplitude were used for this ANOVA.

To test whether the V_ORT increases with increased force amplitude, a second repeated-measures ANOVA was performed with factors Amplitude (20% and 30% of MVC), Time and Direction. This ANOVA was performed only with the conditions where the frequency was 0.9 Hz (where the amplitude was 20% MVC and 30% MVC).

The data were checked for violations of sphericity, and the Huynh-Feldt (H-F) criterion was used to reduce the number of degrees of freedom where necessary. Post-hoc tests (Tukey's honestly significant difference) were used to further analyze significant effects. The p value for significance was set at 0.05.

Linear Model

In Latash et al. (2002a), a linear model was proposed to describe the relationship between the two components of variance (V_UCM and V_ORT) and the task characteristics such as total force magnitude (F_TOT) and its rate of change (dF_TOT/dt). This model suggested that, for each condition, there was a linear relationship between V_UCM and F_TOT, and a linear relationship between V_UCM and dF_TOT/dt (and to a lesser extent, F_TOT):

$$\begin{array}{l}{V}_{\text{UCM}}=a_1\ast F_{\text{TOT}}+c_1\\ V_{\text{ORT}}=a_2\ast F_{\text{TOT}}+b_2\ast \left|d{F}_{\text{TOT}}/\text{dt}\right|+c_2\end{array}$$ (8)

This model is slightly modified from the version found in Latash et al. (2002a), in that we consider absolute force rate | dF_TOT/dt | rather than force rate dF_TOT/dt. During the force half-cycles when the force is decreasing, dF_TOT/dt will be negative, while V_ORT is always positive, and so using | dF_TOT/dt | ensures that this term is always positive, allowing comparison between the force half-cycles where the force is increasing and decreasing. We used this model and fit its parameters, a₁, c₁, a₂, b₂ and c₂ using linear regression, to the observed variances, force, and force rate magnitudes. The linear regression was performed separately for each subject and for each combination of frequency (0.67 Hz, 0.9 Hz, 1.1 Hz, 1.33 Hz), amplitude (20% and 30% of MVC), direction (force increase and force decrease) and finger combination (I and IMRL), for a total of 20 combinations. The effect of frequency and direction on the parameters was tested by performing ANOVA on all five parameters for all trials with 20% MVC amplitude, with factors Frequency and Direction.

Results

Task performance and accuracy

After one practice trial, the subjects were all able to perform the cyclic task at the acceptable level of accuracy. An example of a typical trial can be found in Figure 1; this Figure shows the cyclic task performed at 0.9 Hz by the index finger. Across subjects, the mean (±standard deviation) percentage of rejected trials for the force increase was 29.0±7.9%, and for the force decrease was 24.9±9.1%.

For the accepted trials, the error in amplitude (the distance from the target line) was approximately 1-2% of MVC. The timing errors were approximately 20% of the duration of the half-cycle. These errors, averaged across subjects, are shown in Table 1. The errors at the end of the force increase half-cycle are not exactly equal to the errors at the start of the force decrease half-cycle because not all half-cycles were accepted. To determine whether these errors varied across the conditions, an ANOVA was performed on the four quantities shown in Table 1, namely the amplitude error and the timing error, at the start and end of the half-cycle, for all conditions with 20% MVC amplitude. The factors were Combination (I or IMRL), Frequency (0.67 Hz, 0.9 Hz, 1.1 Hz, 1.33 Hz), and Direction (force increase, force decrease), and their interactions. A significant main effect was found only for Frequency, for the timing error at the start (F_(3,3) = 4.40, p < 0.01) and end (F_(3,3) = 3.57, p < 0.05) of the half-cycle. A Tukey HSD test showed that at the start of the half-cycle, the error was significantly lower at 0.9 Hz and 1.1 Hz than at 0.67 Hz, while at the end of the half-cycle, the error was significantly lower at 0.9 Hz and 1.1 Hz than at 1.33 Hz. An additional ANOVA was performed to test the effect of amplitude. Only the results with 0.9 Hz were used (at the 20% and 30% MVC amplitudes). The factors were Combination, Amplitude (20% or 30% MVC), and Direction. While no significant main effects were found for Amplitude, for the timing error at the start of the half-cycle, a main effect was found for Direction (F_(1,1) = 4.21, p < 0.05). A t-test showed that the timing error at the start of the half-cycle was significantly smaller for the force decrease half-cycles compared to the force increase half-cycles. In the remainder of the analysis, the force half-cycles were uniformly resampled to 100 points, and so these timing errors will not affect the variance.

Table 1. Indices of performance errors.

Indices of errors (means ± standard errors, across subjects) for the accepted force half-cycles. The errors are shown at the start and end of the half-cycle for the two amplitudes (in % of MVC), defined as the distance from the target line (Amplitude error), and as percent of time of the half cycle, defined as the duration from the closest metronome tick to the start or end of the half-cycle (Timing error). The indices of errors are shown separately for force increase and decrease, as well as for the two finger combinations (I and IMRL). The mean errors were calculated for each subject, then averaged across subjects.

Direction	Combination	Freq (Hz)	Amp. (% of MVC)	Start of half-cycle		End of half-cycle
				Amplitude (% of MVC)	Timing (phase %)	Amplitude (% of MVC)	Timing (phase %)
Force increase	I	0.67	20	1.03 (±0.22)	20.48 (±1.68)	1.49 (±0.28)	17.39 (±1.82)
		0.9	20	1.88 (±0.48)	17.81 (±1.63)	1.42 (±0.27)	15.88 (±2.13)
		0.9	30	1.31 (±0.25)	18.74 (±1.55)	2.14 (±0.33)	15.20 (±1.63)
		1.1	20	1.78 (±0.50)	19.06 (±1.50)	1.58 (±0.27)	13.75 (±1.25)
		1.33	20	2.22 (±0.37)	20.53 (±1.54)	2.13 (±0.30)	17.21 (±1.71)
	IMRL	0.67	20	1.11 (±0.21)	18.82 (±0.93)	1.51 (±0.58)	15.50 (±1.28)
		0.9	20	1.15 (±0.17)	16.88 (±0.84)	1.93 (±0.65)	13.01 (±1.24)
		0.9	30	1.61 (±0.29)	18.12 (±1.57)	2.78 (±0.82)	16.49 (±1.55)
		1.1	20	1.47 (±0.33)	17.34 (±1.02)	1.93 (±0.51)	13.16 (±1.26)
		1.33	20	1.40 (±0.23)	18.48 (±0.90)	2.03 (±0.61)	16.96 (±1.40)
Force decrease	I	0.67	20	1.43 (±0.30)	18.51 (±1.39)	1.20 (±0.17)	17.08 (±0.71)
		0.9	20	1.46 (±0.28)	15.50 (±1.97)	1.86 (±0.45)	16.00 (±1.46)
		0.9	30	2.15 (±0.32)	14.63 (±1.69)	1.44 (±0.24)	16.22 (±0.74)
		1.1	20	1.59 (±0.25)	13.71 (±1.15)	1.79 (±0.51)	16.03 (±1.11)
		1.33	20	2.08 (±0.32)	17.42 (±1.16)	2.14 (±0.34)	18.32 (±1.09)
	IMRL	0.67	20	1.48 (±0.58)	15.63 (±0.94)	1.10 (±0.20)	16.46 (±0.66)
		0.9	20	1.93 (±0.63)	13.16 (±1.13)	1.14 (±0.16)	15.83 (±0.67)
		0.9	30	2.71 (±0.80)	14.76 (±1.01)	1.64 (±0.27)	16.63 (±1.50)
		1.1	20	1.98 (±0.49)	13.39 (±1.24)	1.46 (±0.33)	17.27 (±1.08)
		1.33	20	2.04 (±0.61)	16.16 (±1.50)	1.42 (±0.25)	18.06 (±1.02)

Patterns of total force variance

The variance of the total force was calculated over the accepted repetitions, for each sample of the force time series after the time series were resampled to 100 points, for the force increase and decrease, and for each subject separately. The variance showed a bell-shaped profile for all conditions, with the variance at the end of the force increase slightly higher than at the beginning of force increase, with the variance for the condition with a larger amplitude (30% MVC) higher than for all the other conditions. Figure 2 shows these time profiles averaged across all subjects for both I and IMRL tasks. The variances plotted are all normalized by the square of the relevant MVC.

Figure 2.

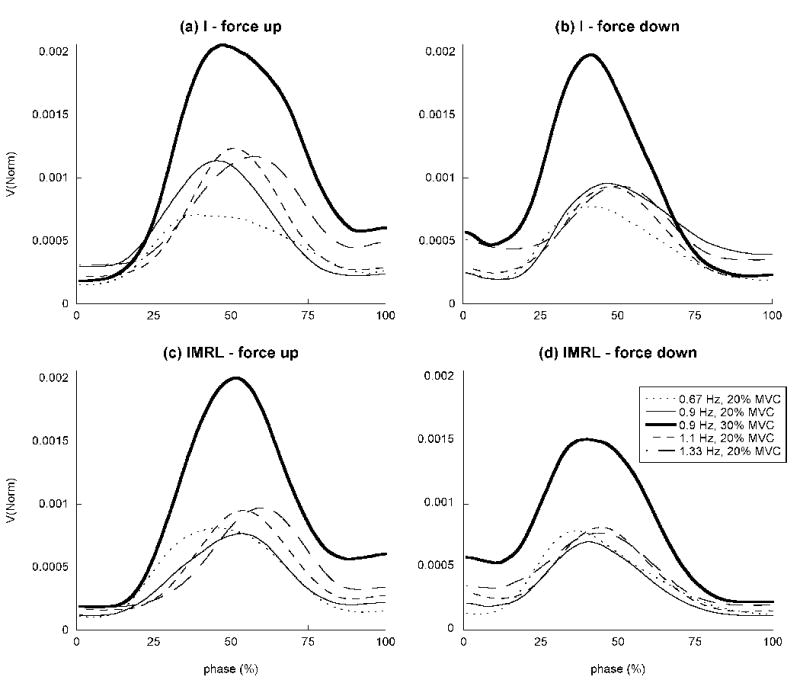
Variance of the total force for the force increase (left) and force decrease (right) half-cycles, for the index finger (I) (top row) and for all four fingers (IMRL) (second row), averaged across subjects. The variance was normalized by the square of the MVC. The normalized variance was generally higher for the I-tasks compared to the IMRL-tasks.

From Figure 2, it can be observed that the normalized total force variance for the four finger combination (IMRL) was generally lower than the normalized variance when using only the index finger. This was found over most subjects and conditions. The mean and standard deviation (across subjects) of the normalized variance for the index finger and the IMRL combination are compared at three representative points: at the beginning of the force increase/decrease, at the end of the force increase/decrease, and at the time of peak force rate (or the trough of force rate for the force decrease segments). These results are displayed in Table 2.

Table 2. Total force variance across all tasks.

Mean and standard deviation (across subjects) of the variance of total force in the I and IMRL tasks, at the start of the force increase (decrease), at the time of peak force rate, and at the end of force increase (decrease). The values are the variance normalized by the squared MVC, and should all be multiplied by 10^-4. The normalized variance is significantly lower for the IMRL combination.

Direction	Freq (Hz)	Amp. (% of MVC)	Start		Peak dF/dt		End
			I (× 10-4)	IMRL (× 10-4)	I (× 10-4)	IMRL (× 10-4)	I (× 10-4)	IMRL (× 10-4)
Force increase	0.67	20	1.51(±1.68)	1.09(±0.92)	9.01(±3.68)	7.71(±4.08)	2.61(±2.15)	1.51(±0.81)
	0.90	20	2.99(±3.70)	1.20(±0.87)	12.70(±5.99)	11.64(±5.85)	2.38(±1.57)	2.21(±0.79)
	0.90	30	1.83(±1.01)	1.87(±0.79)	27.33(±12.53)	24.67(±12.25)	6.03(±4.02)	6.06(±2.37)
	1.10	20	2.19(±1.47)	1.62(±1.19)	12.61(±4.72)	11.77(±4.90)	2.86(±1.79)	2.74(±1.82)
	1.33	20	3.10(±1.32)	1.81(±1.27)	12.49(±3.29)	10.94(±3.73)	4.91(±1.95)	3.41(±1.79)
Force decrease	0.67	20	2.49(±2.36)	1.33(±0.72)	7.14(±3.60)	6.80(±2.87)	1.91(±1.00)	1.29(±1.10)
	0.90	20	2.45(±1.79)	2.13(±0.79)	10.14(±5.76)	6.37(±3.50)	3.96(±4.35)	1.16(±0.77)
	0.90	30	5.69(±3.68)	5.80(±2.61)	15.10(±9.95)	16.12(±12.28)	2.33(±1.24)	2.23(±1.28)
	1.10	20	2.85(±1.60)	3.02(±2.39)	9.02(±4.03)	8.05(±3.63)	2.21(±1.47)	1.54(±0.99)
	1.33	20	5.09(±2.70)	3.51(±2.07)	9.17(±3.45)	8.21(±4.56)	3.51(±1.89)	1.99(±1.49)

This finding was confirmed using a two-way repeated measures ANOVA, with the factors Combination (I or IMRL) and Representative point (beginning of force increase/decrease, at time of peak (or trough) of force rate, end of force increase/decrease). A significant main effect was found for Combination (F_(1,237) =1.04, p < 0.05) and Representative point (F_(2,237) = 90.83, p < 0.0001) but not for the interaction Combination × Representative point. On average, the variance in trials with the combination IMRL was 8.7% less than in trials with just the index finger. The Representative point effect was due to the higher variance at the time of peak force rate. Pair-wise Tukey tests showed that for both combinations, the variance at peak force rate was significantly higher than the variance at the start or end of the force increase/decrease (p < 0.05). An exception to the reduction in variance was for observed for the force half-cycles with 30% MVC amplitude, for this condition, a paired t-test showed no significant difference in variance between the I and IMRL combinations.

Variance within and orthogonal to the UCM

The variances within the UCM (V_UCM), and orthogonal to the UCM (V_ORT) were calculated using equations (6) and (7) at 100 time points, for each subject and condition for the IMRL combination. Common patterns were observed in these two components of the variance across the different conditions. V_UCM increased with time during the force increase and decreased with time during the force decrease. The condition with larger amplitude (30% MVC) showed much higher values for V_UCM, while little difference was seen in the magnitude of V_UCM across the trials with the same amplitude (20% MVC) but different frequencies. In contrast, V_ORT showed a bell-shaped profile for both the force increase and decrease, with its maximum value approximately 50% of the way through the half-cycle, which coincided approximately with the peak value of dF/dt. Examples of these components of the variance are plotted for a typical subject in Figure 3.

Figure 3.

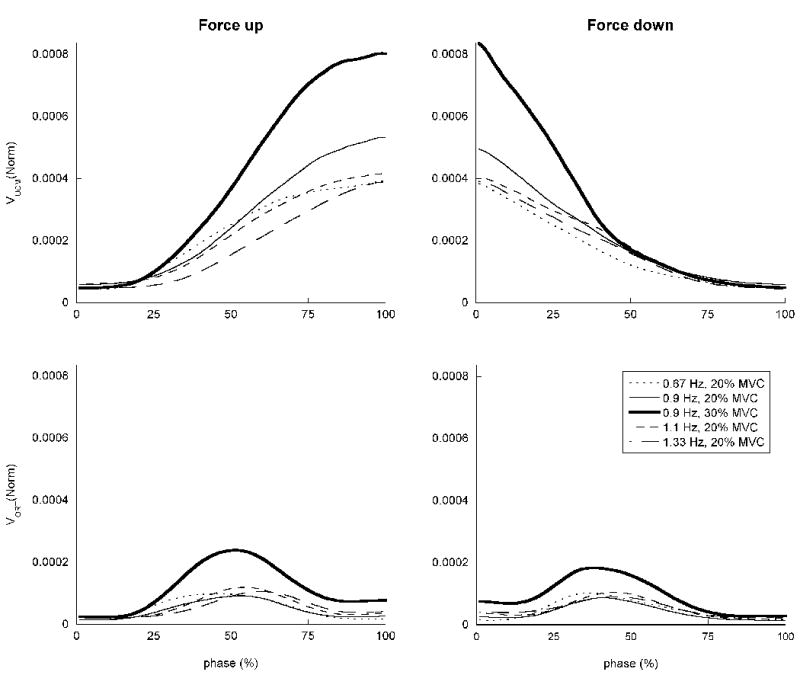
Components of variance within the UCM (V_UCM - upper row) and orthogonal to the UCM (V_ORT - lower row), for force increase (left column) and force decrease (right column) half-cycles, averaged across subjects. The variances are normalized by the square of the MVC and the number of dimensions. While V_UCM increases during force increase, and decreases during force decrease, V_ORT shows a bell-like shape, qualitatively similar to the shape of the force rate.

V_UCM, which does not affect the variance of the total force, was overall much higher than V_ORT, which does affect variance of the total force. A repeated measures ANOVA was performed separately for force increase and force decrease on the variance indices computed over the trials with an amplitude of 20% MVC with factors Variance Type (V_UCM or V_ORT) and Time (phase 10%,20%,…,100%). For both force increase and force decrease, there was a significant main effect for Variance Type (force increase: F_(1,62) = 32.2, p < 0.0001, force decrease: F_(1,62) = 36.8, p < 0.0001), as expected from the observation that V_UCM was much higher than V_ORT, and for Time (force increase: F_(1.3,80.2) = 39.0, p < 0.0001, force decrease: F_(1.3,80.6) = 54.9, p < 0.0001). A significant interaction was found for Variance Type × Time (force increase: F_(1.3,80.2) = 39.0, p < 0.0001, force decrease: F_(1.3,80.6) = 43.0), indicating that the difference in variance changed throughout the cycle. In order to quantify the difference between V_UCM and V_ORT with time, the average and standard deviation of the values of V_UCM and V_ORT at three times – phase 1%, 50% and 100%, were calculated during the force increase and decrease, and are summarized in Table 3. The values are averaged, separately for force increase and force decrease, across all subjects and frequencies for trials with amplitude of 20% MVC. It can be observed that at the end of the force increase half-cycle (phase 100%), and at the start of the force decrease half-cycle (phase 1%), where the force magnitude is high and the force rate is low, V_UCM is approximately an order of magnitude larger than V_ORT, while at the middle and when the force magnitude is low, V_UCM is still on average larger, although the difference is smaller.

Table 3. Variance within and orthogonal to the UCM.

The variance within the UCM (V_UCM) and orthogonal to the UCM (V_ORT) at the start (phase 1%), middle (phase 50%) and end (phase 100%) of the force production tasks. The variances are normalized by the squared MVC, and the number of degrees of freedom. At all three times, the mean V_UCM is larger than the mean V_ORT. The difference is greatest at phase 100% for force increase, and at phase 1% for force decrease, where the force level is high but the force rate is low.

Phase	Force increase		Force decrease
	VUCM (× 10-5)	VORT (× 10-5)	VUCM (× 10-5)	VORT (× 10-5)
1%	5.40(±3.37)	1.82(±1.38)	37.5(±27.4)	2.80(±1.82)
50%	21.6(±16.0)	9.84(±5.66)	15.7(±10.7)	8.54(±4.84)
100%	43.3(±33.6)	3.00(±2.03)	5.16(±3.10)	1.90(±1.55)

Formally, the changes in the components of variance can be considered as functions of the force and force rate. There is an approximately linear relation between the mean force and V_UCM. V_ORT shows a similar profile to the force rate, dF/dt. The two components of the variance are plotted against force in Figure 4. The values plotted are the mean components of the variances across subjects. In the plot of V_UCM, it can be seen that the slopes are similar for the different frequencies. For the plot of V_ORT, while the shapes of the profiles are similar to that of the force rate, the magnitudes of V_ORT for the conditions with 20% amplitude do not scale with different frequencies, rather, their magnitudes show large variation along the cycle but little variation across frequencies.

Figure 4.

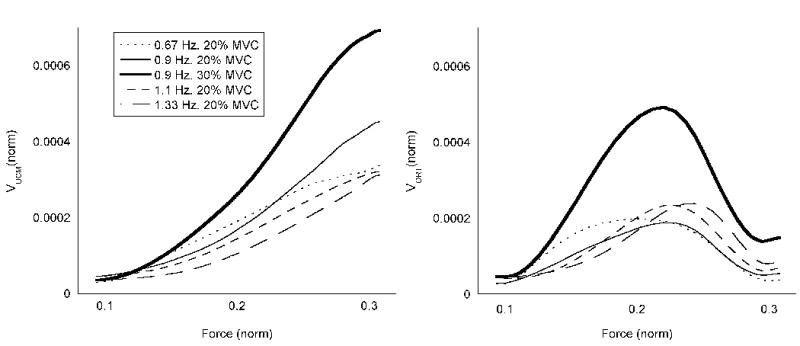
Variance within the UCM (left) and orthogonal to the UCM (right) as a function of mean force (across repetitions and subjects) for the force increase half-cycles. The normalized variance values are the mean across subjects. V_UCM is similar across conditions with the same amplitude. For V_ORT, the variances are similar across conditions with the same amplitude but different frequencies.

The observations about the variation of V_UCM and V_ORT were tested using repeated measures ANOVAs. For V_UCM, the ANOVA was performed on all the trials with 20% MVC amplitude. Three factors were considered – Force (12%, 14%, …, 28% MVC), Frequency (0.67 Hz, 0.9 Hz, 1.1 Hz, 1.33 Hz), and Direction (force increase, force decrease). There was a statistically significant main effect for Force (F_(1.2,49.6)=6.12, p < 0.05). The dependence of V_UCM on force is considered using the linear model in the later analysis. There were no other main effects or significant interactions.

For V_ORT, two repeated measures ANOVAs were performed using the Time factor. For the first ANOVA, only the conditions where the amplitude was 20% MVC were used. The other factors for this ANOVA were Frequency and Direction. A statistically significant main effect was found for Time (F_(2.4,142.9) = 6.38, p < 0.005). The bell-shaped V_ORT profiles observed explain this effect. Also statistically significant were the interactions Time × Direction (F_(2.4,142.9) = 9.31, p < 0.0001) and Time× Frequency (F_(2.4,142.9) = 4.51, p < 0.01). These interaction effects reflect the differences in timing of V_ORT peak. The mean and standard deviation of the times of the V_ORT peak are shown in Table 4. As the frequency increases, the time of the peak V_ORT shifts towards the end of the half-cycle. Also, the time of peak V_ORT is consistently earlier for the force decrease compared to the force increase half-cycle. The other effects were not statistically significant. In particular, there was not a main effect for Frequency, meaning that V_ORT did not increase with increased frequency.

Table 4. The phase of peak V_ORT.

Mean and standard deviation (across subjects) of the phase at peak V_ORT for trials at 20% MVC, for different frequencies, and direction (force increase and force decrease). The timing of the peak is generally later as the frequency increases, and is earlier for force decrease compared to force increase.

	Frequency
	0.67Hz	0.9Hz	1.1Hz	1.33Hz
Force increase	39.50(±10.17)	46.38(±10.29)	52.38(±5.88)	57.62(±8.05)
Force decrease	37.12(±9.79)	40.38(±6.61)	44.25(±7.91)	44.00(±6.70)

The second repeated measures ANOVA tested whether amplitude had a significant effect on V_ORT, and so it was performed only on the data from the conditions with frequency of 0.9 Hz, at 20% and 30% MVC amplitudes. The ANOVA was performed with factors Amplitude, Time and Direction. As expected, a significant main effect was found for Amplitude (F_(1,28) = 22.75, p < 0.0001), with larger V_ORT for the 30% amplitude compared to the 20% amplitude. Interaction effects were significant for Time × Direction (F_(2.3,66.2) = 6.02, p < 0.005) and for Time × Amplitude (F_(2.3,66.2) = 5.35, p < 0.01). The other main effects and interactions were not statistically significant.

Fit to the linear model

The variance within (V_UCM) and orthogonal (V_ORT) to the UCM were fit to a linear model (Equation 8). This model quantifies the dependence of V_UCM on the total force, and V_ORT on the force rate and total force. We expected such linear dependences based on previous studies cited in the Introduction. Due the large differences in the parameters across subjects, the results of this fit for a typical subject are presented in Table 5, rather than averages. All the results were highly significant.

Table 5. Results of regression analysis.

Results of the regression of V_UCM and V_ORT for a typical subject using the linear model in Equation (8) over the different frequencies and amplitudes. All the fits were highly significant. Variation in the parameters was observed across conditions.

VUCM, force increase:
Freq. (Hz)	0.67	0.9	0.9	1.1	1.33
Amplitude (%MVC)	20	20	30	20	20
R2	0.99	0.99	0.87	0.99	0.99
P value	<0.0001	<0.0001	<0.0001	<0.0001	<0.0001
a1 (× 10-4)	35.14	15.22	4.51	13.83	17.07
c1 (× 10-4)	-3.01	-0.63	0.36	-0.90	-1.09
VUCM, force decrease:
Freq. (Hz)	0.67	0.9	0.9	1.1	1.33
Amplitude (%MVC)	20	20	30	20	20
R2	0.97	0.99	0.92	0.99	0.98
P value	<0.0001	<0.0001	<0.0001	<0.0001	<0.0001
a1 (× 10-4)	28.39	14.350	4.73	12.15	15.03
c1 (× 10-4)	-2.61	-0.54	0.09	-0.85	-0.92
VORT, force increase:
Freq. (Hz)	0.67	0.9	0.9	1.1	1.33
Amplitude (%MVC)	20	20	30	20	20
R2	0.66	0.81	0.69	0.70	0.71
P value	<0.0001	<0.0001	<0.0001	<0.0001	<0.0001
a2 (× 10-4)	0.68	0.42	1.57	0.02	-0.55
b2 (× 10-4)	2.09	2.66	1.98	1.66	0.97
c2 (× 10-5)	-2.16	-4.79	-2.49	2.40	6.44
VORT, force decrease:
Freq. (Hz)	0.67	0.9	0.9	1.1	1.33
Amplitude (%MVC)	20	20	30	20	20
R2	0.79	0.61	0.63	0.80	0.72
P value	<0.0001	<0.0001	<0.0001	<0.0001	<0.0001
a2 (× 10-4)	-6.16	-4.82	-2.38	-0.47	-0.84
b2 (× 10-4)	4.07	3.48	2.74	2.96	0.70
c2 (× 10-5)	6.27	5.12	4.76	0.45	7.11

The a₁ parameter quantified the dependence of V_UCM on the force, and ranged across subjects and conditions from 1.32 × 10^-4 to 35.14 × 10^-4, but did not show a clear trend with changes in frequency. An ANOVA performed on the parameter a₁, with factors Direction and Frequency did not show any significant effects. The intercept c₁ had a value close to zero. An ANOVA performed on all trials with amplitude 20% MVC, with factors Frequency and Direction, showed no significant effects.

The b₂ parameter quantified the dependence of V_ORT on force rate absolute magnitude. It showed a decrease with the increase in frequency. This observation was confirmed using an ANOVA on parameter b₂ for all trials with amplitude 20% MVC, with factors Frequency and Direction. A significant main effect was observed for Frequency (F_(1,1) = 2.73, p < 0.05), but not for Direction, or the interaction Frequency × Direction. The mean of b₂ decreased with the increase in frequency, from 3.4 × 10^-4 for 0.67 Hz, to 2.2 × 10^-4 for 1.33 Hz. This reduction in b₂ was due to the approximately constant V_ORT that was observed with increasing frequency (and force rate).

The a₂ parameter quantifies the dependence of V_ORT on force magnitude. Its value was different between the force increase and force decrease half-cycles. ANOVA showed a significant main effect for Direction (F_(1,1) =22.00, p < 0.0001) reflecting higher a₂ for force increase than force decrease, and for Frequency (F_(1,1)=4.29, p < 0.05), although post-hoc Tukey tests did not find significant differences between a₂ across the frequency levels. There was also a significant interaction Frequency × Direction (F_(1,1) = 12.96, p < 0.001) reflecting a decrease in a₂ with increasing frequency during force increase (from a mean of 3.6 × 10⁻⁵ at 0.67Hz to -4.6 × 10⁻⁵ at 1.33 Hz), and an increase in a₂ with increasing frequency, during force decrease (from a mean of -4.4 × 10⁻⁴ at 0.67Hz to -1.1 × 10⁻⁴ at 1.33 Hz).

The intercept c₂ describes the component of V_ORT that is not linearly related to either force or force rate. Its value increased with increasing frequency. An ANOVA performed on c₂ with factors Direction, Frequency and the interaction Frequency × Direction showed significant main effects for Direction (F_(1,1) = 20.74, p < 0.0001) and Frequency (F_(1,1) = 10.85, p < 0.01), as well as for the interaction Frequency × Direction (F_(1,1) = 15.21, p < 0.001). The effect of Direction corresponded to higher c₂ for force decrease, compared to force increase. For Frequency, a post-hoc Tukey HSD means comparison showed that trials with a frequency of 1.33 Hz had significantly higher c₂ than trials with 0.9 Hz and 0.67 Hz, and that trials with a frequency of 0.67 Hz had significantly lower c₂ than trials with frequency of 1.1 Hz and 1.33 Hz. The interaction reflected an increase in c₂ with increasing frequency for force increase (from a mean of −5.4 × 10⁻⁵ at 0.67 Hz to 2.4× 10⁻⁵ at 1.33 Hz), and nearly constant values for force decrease. However, this effect was small (the magnitude of the mean of c₂ was always less than 6 ×10^-5).

Discussion

Our experiments resulted in both expected and unexpected findings. On the one hand, when considered for a single frequency and amplitude, the two components of force mode variance, V_UCM and V_ORT scaled with force and force derivative respectively, as expected based on earlier studies (Latash et al. 2002a; Goodman et al. 2005). On the other hand, while V_ORT showed a strong correlation with force rate within a cycle at each frequency, the peak magnitude of V_ORT did not change with frequency. A change in task frequency without a change in the force amplitude is naturally associated with a change in the values of the force time derivative along the cycle. Why does V_ORT show a linear scaling on dF/dt within a cycle, but the magnitude of V_ORT does not change when the frequency of force production changes? Further in the Discussion, we address implications of these findings for the hypotheses on the origins of the two variance components.

Does adding fingers improve performance accuracy?

We found only minor advantages of the multi-finger combination (IMRL) as compared to performance with the single finger (I) with respect to accuracy of performance. Indeed, force and timing error indices showed no differences between I and IMRL, while normalized force variance was only about 9% lower for the IMRL combination. Note that if individual fingers preserved their variance indices when acting in a group and did not co-vary their force outputs across trials, the IMRL condition would be expected to display a significant drop in the normalized force variance due to the force sharing among the fingers and the well-documented nearly linear scaling of force standard deviation with force magnitude (reviewed in Newell and Carlton 1988). An example presented in Shapkova et al. (2008) demonstrates that a four-finger group is expected to show a nearly 75% drop in the normalized total force variance as compared to individual finger's performance. Our study and a few earlier studies (Latash et al. 2001; Gorniak et al. 2008; Shapkova et al. 2008) have all shown a much lower gain in total force variance, a gain that was sometimes even under the level of statistical significance.

A more detailed analysis in an earlier study (Shapkova et al. 2008) has shown that, when fingers acted in a group, individual finger force variance increased rather dramatically (for comparable finger force values), and this increase was compensated nearly perfectly by co-variation of finger forces – so-called, force stabilizing multifinger synergies. Our study supports this hypothesis indirectly, that is by showing strong multifinger force stabilizing synergies (V_UCM≫V_ORT; see the next subsection) in the absence of a substantial gain in the total force variance or error indices. The nearly perfect match between the increased individual finger force variance and co-variance may be most naturally explained within the feed-forward model of multifinger synergies (Goodman and Latash 2005), where total force variance is defined at a level prior to sharing the total force among the individual fingers.

Two components of variance

As in earlier studies, we performed analysis of variance across cycles at the same task in the space of finger modes, hypothetical variables that are used to generate finger forces (Danion et al. 2003). Using these variables allows avoiding spurious results that might be related to the phenomenon of enslaving, that is, unintended force production by fingers of a hand when one finger produces force intentionally (Li et al. 1998; Zatsiorsky et al. 1998, 2000). The total variance in the finger mode space was quantified separately within two subspaces that kept the total force magnitude constant and that changed the total force, respectively. As in earlier studies (Latash et al. 2001, 2002a; Scholz et al. 2002), the relative amount of variance that did not change total force (V_UCM) was much larger than the amount of variance that did (V_ORT) when the force was relatively high while its rate of change was relatively low. Such observations have been interpreted as multi-finger synergies stabilizing total force (reviewed in Latash et al. 2007). In contrast, at high rates of force change, the difference between V_ORT and V_UCM was less.

The qualitatively different time profiles of V_UCM and V_ORT (see Figures 2 and 3) suggested running a linear regression analysis of these indices against force and force time derivative. As in Latash et al. (2002a), different coefficients were found across conditions. We would like to emphasize the fact that, although the linear regressions showed very good fits, at least one of their coefficients (b₂ in Eq. 4) changed across the tasks in an unexpected way. Namely, an increase in frequency of force production led to a drop in b₂ such that, despite the associated change in the force rate, the amount of V_ORT remained unchanged across the different frequencies. So, the natural increase in dF/dt as the frequency increased was nearly perfectly matched by a reduction in the scaling of V_ORT on dF/dt. This could be seen as a coincidence had it not persisted over all five frequencies explored in the experiment. Note that when a similar scaling of dF/dt was achieved by a change in force amplitude while keeping the frequency constant, V_ORT increased significantly, as it could be expected if the regression coefficient b₂ stayed unchanged. These relations are summarized in Figure 5. So, here is a question: Why does V_ORT scaling with dF/dt remain unchanged as long as the frequency of action stays constant and it adjusts rather precisely as soon as the frequency changes?

Figure 5.

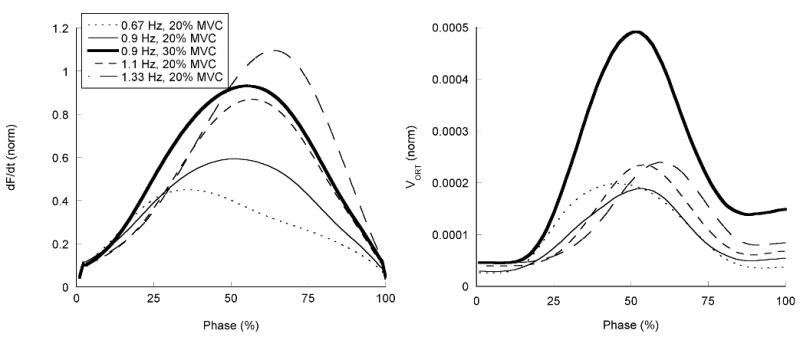
The left graph shows the mean force rate across subjects. As expected, the magnitude of the force rate peak increases proportionally with an increase in frequency. The right graph shows mean V_ORT across subjects. Note similar V_ORT time profiles across the different frequencies. When the amplitude increases (the thick trace), V_ORT shows a large increase.

Timing accuracy and force variance

To look for an answer to the question formulated at the end of the previous subsection, we accept a model of multi-finger variability suggested by Goodman et al. (2005). Force variability within this model originates from two sources. The first one is the parameters that are set at a control level, while the second one is the peripheral consequences of the control process such as actual force values. Within the model, two parameters are set before each trial, namely an amplitude parameter β and a timing parameter, τ. Instead of being set perfectly, these values are selected from distributions with some means and standard deviations. A consequence of this model is that the variance of the total force is linearly related to the force rate multiplied by a term containing the variance of τ, Var(τ). Since variance of the total force is defined by V_ORT, the model suggests a particular importance of Var(τ) for V_ORT; V_UCM is largely defined by Var(β) while being relatively immune to Var(τ).

If Var(τ) does not change across tasks, one could expect an increase in V_ORT with an increase in force rate independently of whether this increase is caused by an increase in the force amplitude or frequency. However, our results suggest that this is not true. Instead, Var(τ) was a function of action frequency. To quantify changes in Var(τ) with frequency, the value of CV(τ) was calculated using the Goodman et al. (2005) model. To perform comparison across tasks, we use coefficient of variation of τ, CV(τ). Figure 6 shows that, as the frequency increases, CV(τ) decreases.

Figure 6.

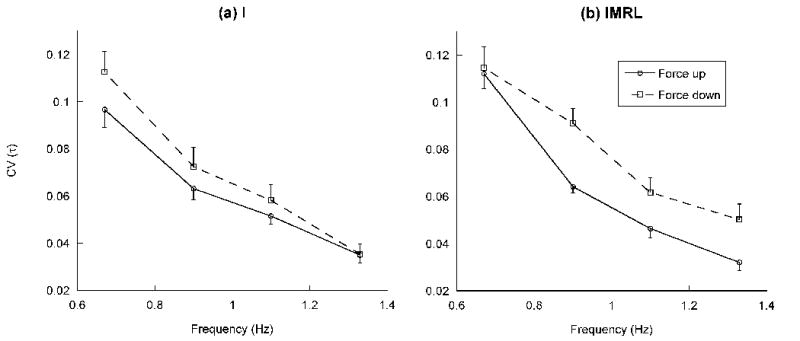
Estimated value of the coefficient of variation of τ for (a) the index finger I and (b) the four finger combination IMRL, for the force increase and decrease half-cycles, averaged across subjects with standard error bars. For both conditions and force directions, the coefficient of variation of τ decreases as the frequency increases, corresponding to an increase in the timing accuracy at higher frequencies.

If CV(τ) remained constant, then V_ORT would increase as the frequency increased. However, the reduction in CV(τ) led to a drop in V_ORT as compared to what could be expected if CV(τ) remained unchanged, resulting in V_ORT being unchanged across difference frequencies with the same amplitude. Hence, within the Goodman et al. model, the results suggest an increase in the relative timing accuracy (lower CV(τ)) with an increase in action frequency. We cannot generalize this trend beyond the range of frequencies explored in this study. It seems natural to assume that this trend would have a ceiling effect or may even reverse after the frequency surpasses the preferred frequency for the action. This conclusion fits some of the published data that have shown an increase in the timing accuracy of actions with an increase in the action frequency, at least up to certain frequency values close to a preferred frequency for that particular action (Yu et al. 2003). Note that in finger force production tasks, preferred frequencies have been reported as about 1.5-2 Hz (Latash et al. 2001; Scholz et al. 2002).

There is a natural relationship between action frequency and accuracy of its timing (reviewed in Ivry and Hazeltine 1995; Ivry and Richardson 2002), which is compatible with our conclusion on the drop in Var(τ) with an increase in the action frequency. It may be organized in this way to ensure comparable (predictable) accuracy in force production independently of the frequency of cyclic actions. However, it seems that the same rule does not apply to discrete tasks. In an earlier study of accurate force pulse production (Goodman et al. 2005), V_ORT scaled within a force pulse magnitude and the scaling increased with a drop in pulse time. This discrepancy may be viewed as an example of a discrete-cyclic control dichotomy in support of the recent hypotheses by Sternad and colleagues (Sternad and Dean 2003; Schaal et al. 2004; Hogan and Sternad 2007). Those authors presented arguments for differentiating between discrete and cyclic tasks based on their kinematic characteristics, such as the mean-squared-jerk (Hogan and Sternad 2007) and based on a fMRI study that has suggested the involvement of different brain circuitries in discrete and cyclic actions (Schaal et al. 2004).