Analysis of association constant for ground state dye-electron acceptor complex of photoinitiator systems and the association constant effect on the kinetics of visible-light-induced polymerizations

Abstract

We investigated the formation of ground state donor/acceptor complexes between xanthene dyes (rose Bengal (RB) and fluorescein (FL)) and a diphenyl iodonium salt (DPI) which is dissolved in 2-hydroxyethyl methacrylate (HEMA) monomer. To characterize the association constant of the complex, we have suggested a new analysis model based upon the Benesi-Hildebrand model. Because the assumption of the original Benesi-Hildebrand model is that the absorption bands are due only to the presence of the complex and that the absorption by the free component is negligible; the model cannot be applied to our systems, which is a dye-based initiator system. For each dye, the molar absorptivity of the ground state complex was evaluated as a function of wavelength and this analysis confirmed the validity of the modified Benesi-Hildebrand model. In addition, we observed the RB/DPI photoinitiator system failed to produce a perceptible polymerization rate but the FL/DPI photoinitiator system provided very high rates of polymerization. Based upon the association constant for these complexes, we concluded that the observed kinetic differences arise from the different association constant values of the ground state dye-acceptor complex, resulting in back electron transfer reaction.

Introduction

Recently, the photoinduced electron transfer (PET) process has been an attractive research area because of its increasing significance with a wide variety of important applications^1–3. A number of current industrial polymer applications involve PET and their potential application fields continue to increase because PET is an important route to produce free radical active centers for photopolymerization^4–8. This approach can be used to produce visible-light photoinitiator systems in which a dye is used as the light absorbing moiety or photosensitizer^4–8. Xanthene dyes (e.g. rose bengal, eosine Y, erythrosine B, fluorescein, etc.) acridinium dyes (e.g. acriflavine), phenazine dyes (e.g. methylene blue), thiazene dyes (e.g. thionine) thioxanthene, xanthone, thioxanthone, ketocoumarin, and merocyanine dyes can be used in the photo-initiator systems for photopolymerizations^4,5. Since the photon energy in the visible spectrum region is less than the bond dissociation energy of most organic molecules, visible-light-induced initiators have been primarily bimolecular systems in which the active centers are produced via electron transfer followed by proton transfer from the electron donor to the electron acceptor^8,9.

In this type of reaction scheme, the photo-excited dye may act as either the electron acceptor (for example, if an amine is used as the second component), or the electron donor (for example, when an iodonium salt is used as the second component). While both reaction pathways are known, electron transfer followed by proton transfer from the electron donor to the photoexcited dye is more common⁴. The combination of a photo-reducible dye and amine system is a typical example of a visible-light-induced two-component initiator system. As an electron donor, amines, sulfinate, enolate, and carboxylates can be used as activators. In this photoinitiator system, back electron transfer generally limits the efficient generation of free radical active centers because back electron transfer is invariably thermodynamically feasible as shown in Scheme 1^10,11. In addition, the radical recombination after separation of the radical pair (with rate constant k_rec) also retards the active initiation step^10,11. Finally, the dye-based radical, PS-H• as shown in Scheme 1, has been recognized as a terminating agent of growing polymer chains^7,8,12,13. These kinetic features limit the efficiency of a dye and amine photoinitiator system.

Scheme 1.

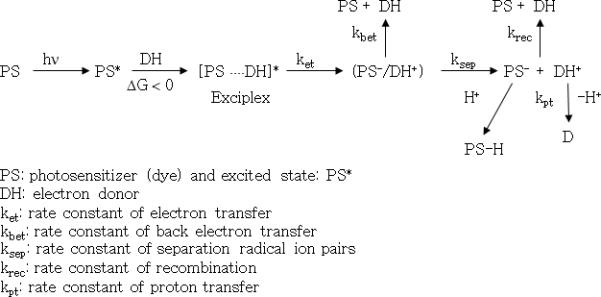
Main kinetic steps of a two-component photoinitiator system containing photosensitizer (PS) and electron donor (DH) for visible-light-induced electron transfer initiation process.

As an alternative, the combination of a photo-oxidizable dye with electron acceptors such as iodonium salts, sulfonium salts and ferrocenium salts have been suggested^14–16. The combination of a photo-oxidizable dye and a diphenyliodonium salt (DPI) is a good example of these initiator systems. Because the reduction potential (E_red) of the diphenyliodonium cation is only −0.2 V (relative to a standard saturated calomel electrode, SCE), a wide variety of dyes undergo thermodynamically feasible electron transfer with iodonium salts⁸. Once the radical ion pair of photo-oxidizable dye and iodonium salt (DPI) escapes the cage complex, a rapid unimolecular fragmentation reaction proceeds without a radical recombination reaction step^6,8 as shown in Scheme 2. Due to the irreversible unimolecular fragmentation reaction of DPI, this photoinitiator system may produce more efficient polymerization reaction kinetics than photo-reducible dye and amine initiating systems. However, it has also been reported that the dye, such as xanthene dyes and porphyrin dyes, forms an electron donor-acceptor ground state complex with the electron acceptor^17–21. For example, rose bengal (RB) forms a ground state donor-acceptor complex with a variety of salts and exhibits changed spectral properties.^14,15,18,19 The structure of complexes have been studied using ¹H-NMR and X-ray crystal structure analyses. ^{15, 18}

Scheme 2.

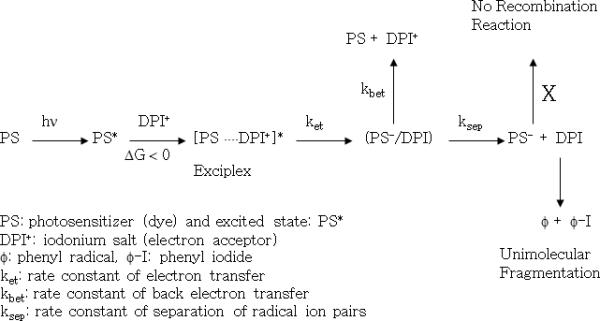
Main kinetic steps of a two-component photoinitiator system containing photosensitizer (PS) and electron acceptor (DPI) for visible-light-induced electron transfer initiation process.

Ground state molecular complexes generally arise from either intermolecular π-π interactions²² or electron donor-acceptor interactions²³ (electrostatic, polarization, charge-transfer, and dispersion interactions all fall into the category of donor-acceptor interactions). For the stabilization of molecular complexes, electron donor-acceptor interactions are controlled by the oxidation and reduction potentials of the components. In contrast, intermolecular π-π interactions are influenced by attractive intermolecular interactions. Stacking of aromatic molecules within a crystal structure²⁴ and aggregation of organic dyes²⁵ in solution are examples of molecular assemblies that arise from intermolecular π-π interactions.

However, formation of ground state dye-electron acceptor complexes also exhibit potential kinetic limitations due to back electron transfer. While formation of such donor-acceptor complex leads to efficient static electron transfer of the photoexcited dye, back electron transfer in the radical ion complex cage structure also easily takes place and does not allow separation of radical ion, thereby preventing generation of the active radical center.¹⁹ In general, quantum yields of separated radical ions are less than 0.1, in which the rate constant of back electron transfer is very much higher than the rate constant of separation of the radical ion pairs.²⁶ The factors to reduce the energy-wasting back electron transfer include separation distance, molecular dimension, solvent polarity, external pressure, molecular charge, and the effect of driving force have been suggested²⁶. In fact, a sterically hindered structure of the electron donor can decrease the magnitude of electronic coupling and provide the separation distance between electron donor and acceptor in the electron transfer reaction²⁶. As a result, steric effects in photoinduced electron transfer reactions can decrease back electron transfer and increase the separation yield of radical ion pairs. In contrast, pre-associated electron donor-acceptor complex in the ground state does not allow separation distance and leads to extremely fast back electron transfer.

As an example, Neckers and coworkers have probed the formation of ground state complexes of xanthene dye/onium salts regarding the synthesis, electron transfer rate constants, and dye life-times^27–32. Recently, we also observed the ground state complex formation for both the RB/DPI and the FL/DPI initiator systems when dissolved in 2-hydroxyethyl methacrylate (HEMA) monomer. In addition, we evaluated the extinction coefficients and the association constants for these complexes, using a modified Benesi-Hildebrand model³³. A number of researchers have reported models to obtain the association constant for complex formation such as Benesi-Hildebrand^{17,19,21,33–36}, Nash plot^37,38, Baba-Suziki relationship^39,40 and fluorescence quenching measurements^41–42.

However, since the assumption of the original Benesi-Hildebrand model is that the absorption bands are due only to the presence of the complex and that the absorption by the free component is negligible; the model cannot be applied to our systems, which involve a dye-based initiator. In addition, all models that have been reported do not simultaneously consider the uv-visible absorption of the complex and the free component. Therefore, we have suggested a new analysis model based upon the Benesi-Hildebrand model which considers absorption contribution by both the ground state complex and free dye. We also determined the molar absorptivity as a function of wavelength for these ground state complexes. Finally, we have characterized the effect of ground state complex of photoinitiator systems on the kinetics of visible-light-induced polymerizations based upon the association constant for these complexes.

Experimental

Materials

The organic dyes rose bengal (RB) and fluorescein (FL) were purchased from Aldrich Chemical Company and were used as received. The chemical structures of RB and FL are shown in Figure 1. The monomer 2-hydroxyethyl methacrylate (HEMA) was obtained from Aldrich and hydroquinone inhibitor was removed by treatment with De-Hibit (from Polysciences) for 3 hours and filtered using an inhibitor removal column (from Polysciences) prior to use. Diphenyliodonium chloride (DPI) and N-methydiethanolamine (MDEA) were purchased from Aldrich and were used as received.

Figure 1.

Chemical structures of rose bengal (RB; left) and fluorescein (FL; right).

UV-Vis

The dyes (RB or FL) dissolved completely upon addition to the monomer (HEMA). The concentration of DPI was varied from 5 × 10⁻⁴ M to 1.0 × 10⁻² M. The UV-Vis absorption spectra of the resulting solutions were obtained using a Hewlett Packard 8452A diode array spectrophotometer. For each dye, spectra were collected for three different dye concentrations and five different concentrations of the iodonium salt. All UV-VIS absorption experiments were performed at room temperature using neat HEMA lacking hydroquinone inhibitor.

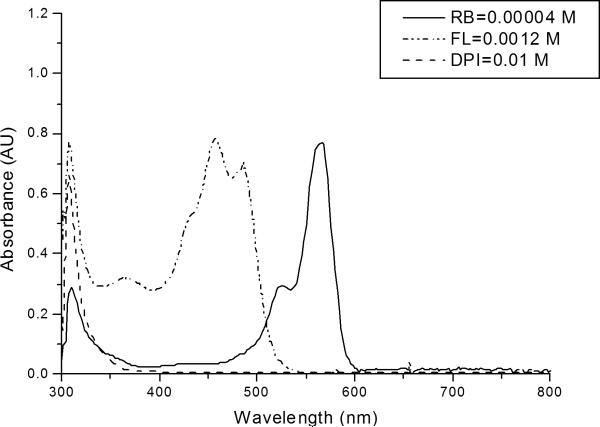
The absorption spectra of the two dyes and DPI as shown in Figure 2 illustrate an iodonium salt absorption band centered at λ_max of 308 nm with diminishing absorbance up to a wavelength of approximately 380 nm. In contrast, FL exhibits a broad, intense absorption structure between approximately 400 and 500 nm, and an additional broad absorption band in the UV region between 300 and 400 nm. RB presents a prominent absorption peak between 550 and 600 nm. Note that, for preparation of this figure, the concentration of FL was 30 times greater than that of RB; therefore, the molar extinction coefficient of RB is higher than that of FL.

Figure 2.

UV-Vis absorption spectrum of the two dyes, rose bengal (RB), fluorescein (FL) and diphenyliodonium chloride (DPI). All components were dissolved in HEMA.

Photo-differential Scanning Calorimetry (Photo-DSC)

The rate of polymerization was measured by a Perkin-Elmer photo-differential scanning calorimeter (Perkin-Elmer Photo-DSC 7) outfitted with a 200 W Oriel mercury-xenon (Hg:Xe) lamp as a photoinitiating light source. The output from the lamp was passed through a 400 nm cut-off filter and therefore, the photosensitizer (dye) is the only component that absorbs in the visible light region. The incident irradiance of filtered light was ~55 mW/cm², as measured by graphite disc absorption. The average sample mass was approximately 12 mg and the reaction temperature was 50 °C. For all samples, [Dye] = 5 × 10⁻⁴ M, [MDEA] = 0.25 M and [DPI] = 0.015 M, in neat HEMA. To control the atmosphere and to eliminate oxygen inhibition, DSC sample chamber was purged with nitrogen gas for 15 min after the light source turned on. The flow rate of nitrogen gas was 20 – 30 cc/min and 20 –30 psi was used to attain this flow. Then, the samples were purged with nitrogen gas for two minutes prior to illumination, and throughout the reaction to eliminate oxygen inhibition of the polymerization. The samples were purged with nitrogen for two minutes prior to illumination, and throughout the reaction to eliminate oxygen inhibition of the polymerization. For each experimental condition, and least three independent measurements were made, and the average values are reported.

Real-time FT-near-infrared (NIR) spectroscopy

The HEMA polymerization conversion profile was monitored in real-time by FT-near-infrared (NIR) spectroscopy (Nicolet Nexus 670, Nicolet Instrument Corp., Madison, WI) equipped with an extended KBr beam-splitter and an MCT/A detector. All photopolymerizations were conducted at room temperature. The absorbance peak area method was used to calculate conversion. The =CH₂ first overtone absorption band at ~ 6167 cm⁻¹ in the NIR region was used to characterize the dynamic concentration of the HEMA double bond. To initiate photopolymerizations, a 100 W Quartz Halogen lamp (Oriel Model 77501 Fiber Optics Source, Newport,) with an adjustable iris, a manual shutter and a silica fiber optic cable was used. The output from the light source was passed through IR blocking filter to remove IR light (wavelengths greater than 800 nm) and thus, effective wavelength is between 385 – 800 nm. Therefore, the photosensitizer, RB or FL is the only component that absorbs the transmitted visible light. The filtered light intensity was ~ 0.15 mW/cm², as measured by a factory-calibrated diode array spectrometer. Samples with the varied photoinitiator component combinations were prepared in a rectangular mold made by glass slides with a thickness of 0.5 mm.

Results and Discussion

Association constant for ground state dye-electron acceptor complex formation

A number of researchers^{14,15,17–19} have illustrated that xanthene dyes form ground state donor-acceptor complexes. For example, Willner, et al. reported¹⁹ that rose bengal, RB²⁻ forms a ground state complex with N,N'-dimethyl-4,4'-bispyridinium, MV²⁺, with an association constant of K_a = 11000 ± 1100 M⁻¹ in an aqueous solution. They illustrated that the intensity of the absorption spectrum was changed and an isosbestic point was formed upon addition of MV²⁺ to the dye solution. This implies the formation of a 1:1 dye-acceptor complex. They also observed the formation of a 1:1 dye-acceptor complex between eosin dye and N,N'-dibenzyl-3,3'-dimethyl-4,4'-bipyridinium with an association constant of K_a = 17000 ± 3400 M⁻¹ using the Benesi-Hildebrand equation. This work demonstrated that electrostatic interactions, charge transfer interactions and π-π intermolecular interactions play important roles in formation of the complexes, which were confirmed by X-ray crystal structure analysis^17,18.

In addition, xanthene dyes can lead to 1:1 and 1:2 complexes for the dianion RB²⁻ with the mono-cation salt as shown in equation (1)^14,15. In this study, we have tried to determine the association constants between xanthene dye and DPI in monomer (HEMA) solution for both 1:1 and 1:2 complexes. Based upon the result, we characterized the effect of ground state dye-electron acceptor complex of photoinitiator systems on the kinetics of visible-light-induced polymerizations.

$${\mathrm{RB}}^{2-}+{\mathrm{Salt}}^{+}\stackrel{{\mathrm{K}}_{\mathrm{a}1}}{\iff }{[\mathrm{RB}\cdot \cdot \cdot \cdot \mathrm{Salt}]}^{-}+{\mathrm{Salt}}^{+}\stackrel{{\mathrm{K}}_{\mathrm{a}2}}{\iff }[\mathrm{RB}\cdot \cdot \cdot \cdot {\mathrm{Salt}}_2]$$ (1)

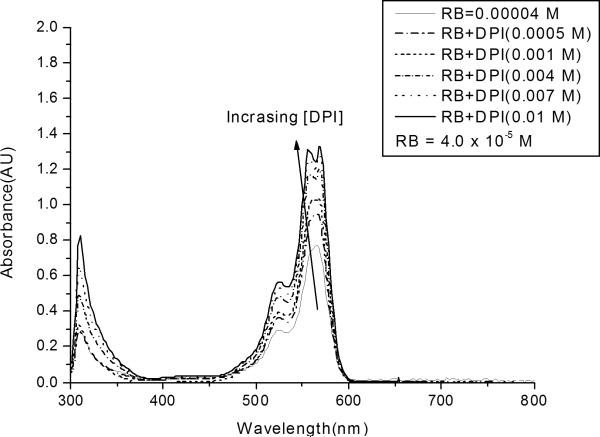
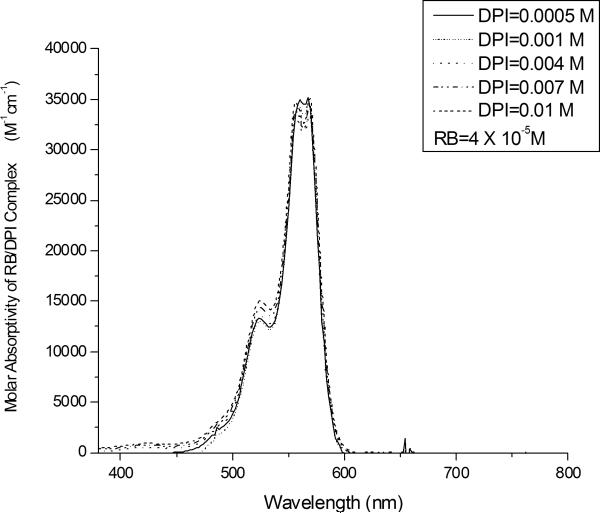
The effect of the DPI concentration on the absorbance spectrum of RB is shown in Figure 3. The intensity of the absorption bands between 500 and 600 nm increases systematically as the iodonium salt concentration is increased from 0 to 0.01 M. This trend can be attributed to the formation of a ground state complex between RB and DPI. These results indicate that the dye-electron acceptor complex at ground state has a higher absorption cross section than RB alone. To analyze the results shown in Figure 3 more quantitatively, we will use a modified Bensei-Hildebrand model³³ outlined below.

Figure 3.

UV-Vis absorption spectrum of RB/DPI system. All systems contain rose bengal at the same concentration (4.0 × 10⁻⁵ M), with differing concentrations of the iodonium salt.

In the first case, we assume that the formation of the equilibrium ground state complex between RB and DPI has a 1:1 stoichiometry, and that RB, DPI, and the complex obey Beer's law at the concentrations investigated. Based upon these assumptions, for wavelengths between 500 and 600 nm, both RB and the complex will absorb light, and the following equation holds:

$$\log [I_0∕I]={\left[RB\right]}_F{\epsilon }_{RB}\ell +\left[c\right]{\epsilon }_c\ell =({\left[RB\right]}_0-\left[c\right]){\epsilon }_{RB}\ell +\left[c\right]{\epsilon }_c\ell$$ (2)

where ε_RB, ε_c : molar extinction coefficients of RB and complex, respectively

ℓ : optical path length

[RB]_F: concentration of free RB

[c]: concentration of complex (= [RB ⋯ DPI])

[RB]₀, [DPI]₀ : initial concentration of RB and DPI, respectively

Note that in this case, the original Benesi-Hildebrand model³³ cannot be applied to the system because the model is based upon the assumption that the absorption bands are due only to the presence of the complex and that the absorption by free component is negligible. On the other hand, the modified Benesi-Hildebrand model takes into account absorption contribution by both the ground state complex as well as free RB as shown in equation (2).

Assuming that the concentration of the complex is very small relative to that of the initial concentration of DPI, i.e. [DPI]₀ >>[c], the association constant of ground state complex, K_a1, between RB and DPI can be given by the following equation (3):

$$K_{a1}=\frac{\left[c\right]}{({\left[RB\right]}_0-\left[c\right])({\left[DPI\right]}_0-\left[c\right])}\approx \frac{\left[c\right]}{{({\left[RB\right]}_0-\left[c\right])\left[DPI\right]}_0}$$ (3)

where K_a1 is the association constant Rearranging equation (3) to solve the concentration of the complex, [c], yields the following:

$$\left[c\right]=\frac{K_{a1}{\left[DPI\right]}_0{\left[RB\right]}_0}{K_{a1}{\left[DPI\right]}_0+1}$$ (4)

Finally, substituting equation (4) into equation (2), and rearranging yields equation (5):

$$\frac{\log [I_0∕I]}{{\left[RB\right]}_0\ell }={\epsilon }_c+\frac{{\epsilon }_{RB}-{\epsilon }_c}{K_{a1}{\left[DPI\right]}_0+1}$$ (5)

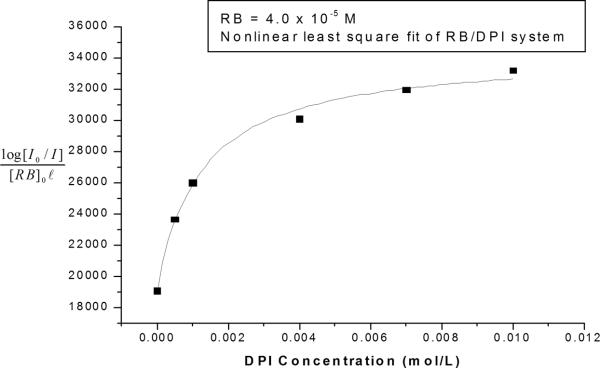
This is the equation that we will use to determine the association constant for the formation of the ground state complex between each dye and the iodonium salt. For example, the UV-visible absorption results at a given wavelength (from Figure 3) were fit to this equation using non-linear regression, to yield values for the equilibrium constant, K_a1, and the extinction coefficient of the complex, ε_c. The results of this analysis are shown in Figure 4, which contains the nonlinear least squares fit superimposed on the original data at a wavelength of 556 nm. The figure illustrates that both the experimental data and the best-fit curve exhibit a characteristic shape in which the absorption increases sharply with increasing iodonium concentration at low DPI concentrations, but increase more gradually at higher concentrations (above about 0.003 M DPI). This diminishing effect of the DPI concentration arises from the depletion of the RB in the system (for example, for a DPI concentration of 0.01 M the free RB is ~3.08 × 10⁻⁶ M, which is only 7.7 % of the initial concentration of RB). This modified Benesi-Hildebrand analysis was performed for three different RB concentrations (2 × 10⁻⁵, 3 × 10⁻⁵, and 4 × 10⁻⁵ M). Based upon these analyses, the association constant for the formation of the ground state complex was found to be 1200 ± 150 M⁻¹, with R²=0.99. The molar absorptivity of the complex, ε_c was also obtained to be 35500 ± 800 (M⁻¹ cm⁻¹) at 556 nm. The good fit of the regression indicates that our assumption is reasonable and the modified Benesi-Hildebrand model is valid for the 1:1 complex.

Figure 4.

Nonlinear least squares fit of association constant and molar extinction coefficient of RB/DPI system. Absorption data were taken at 556 nm.

We also considered the formation of a ground state complex between RB and DPI with 1:2 equilibrium stoichiometry. Here, too, we assumed the complex concentration to be very small relative to that of DPI, i.e. [DPI]₀ >>[c]. The resultant association constant of the ground state complex, K_a2, can be given by equation (6). Following the same aforementioned procedure, the final equation (7) was obtained.

$$K_{a2}=\frac{\left[c\right]}{{({\left[RB\right]}_0-\left[c\right])({\left[DPI\right]}_0-\left[c\right])}^2}\approx \frac{\left[c\right]}{{{({\left[RB\right]}_0-\left[c\right])\left[DPI\right]}_0}^2}$$ (6)

$$\frac{\log [I_0∕I]}{{\left[RB\right]}_0\ell }={\epsilon }_c+\frac{{\epsilon }_{RB}-{\epsilon }_c}{K_{a2}\left[DPI\right]{{}_0}^2+1}$$ (7)

Using equation (7), non-linear regressions were also performed to least squares fit superimposed on the original data at a wavelength of 556 nm for RB; however, we observed that the best-fit curve does not represent the experimental data well. For three different RB concentrations (2 × 10⁻⁵, 3 × 10⁻⁵, and 4 × 10⁻⁵ M), this modified Benesi-Hildebrand analysis did not show good fits with the experimental data (R²= 0.85 ~ 0.72) and lead to wide variation in the association constant. This result indicates that the RB/DPI photoinitiator system in HEMA monomer solution more favorably forms a 1:1 complex rather than a 1:2 complex due to the electrostatic interactions, charge transfer interactions and π-π intermolecular interactions.

The modified Benesi-Hildebrand model assuming a 1:1 complex was also applied to FL absorption data as a function of DPI concentration, as shown in Equation 8.

$$\frac{\log [I_0∕I]}{{\left[FL\right]}_0\ell }={\epsilon }_c+\frac{{\epsilon }_{FL}-{\epsilon }_c}{K_{a1}{\left[DPI\right]}_0+1}$$ (8)

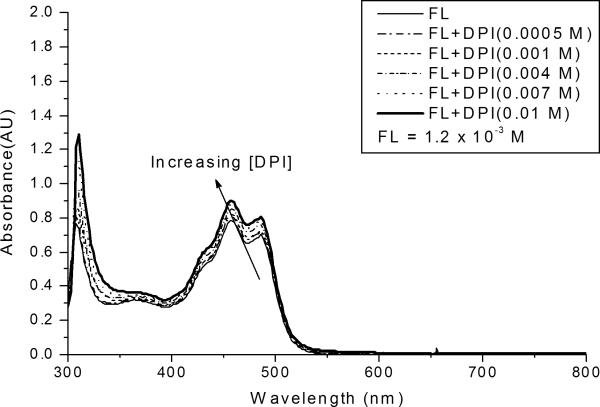
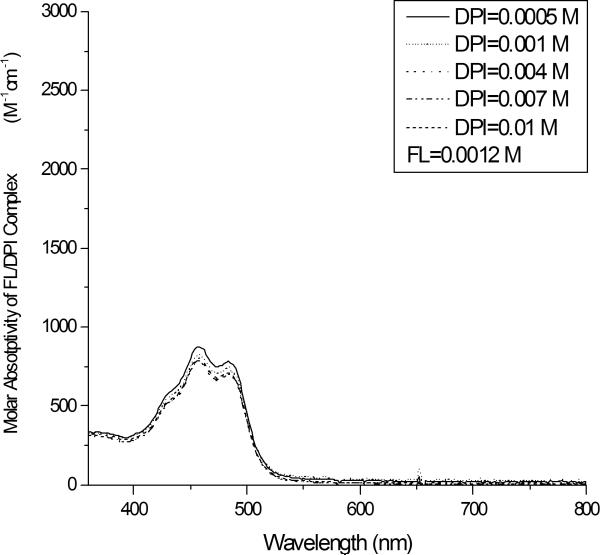
Figure 5 illustrates the effect of the DPI concentration on the FL absorption spectrum. The figure shows that the intensity of the FL absorption bands increase systematically as the iodonium salt concentration is increased; however, the effect is much less pronounced than in the case of RB. The absorption data at a wavelength of 458 nm were fit to equation (8) using nonlinear regression, to yield the best-fit curve. Again, this analysis was completed for three different concentrations (1.2 × 10⁻³, 1.4 × 10⁻³, and 1.6 × 10⁻³ M), and three different absorption wavelengths. The value of the association constant for ground state complex formation was found to be 160 ± 30 M⁻¹, with R²=0.99. The molar absorptivity of the complex, ε_c was found to be 860 ± 20 (M⁻¹ cm⁻¹) at 458 nm. Based upon the association constant, we can determine the free FL concentration, which is ~4.62 × 10⁻⁴ M, for a DPI concentration of 0.01 M. The free FL concentration is 38.5 % of the initial concentration of FL. This free concentration of FL is 5 times higher than the analogous free RB concentration. This result illustrates that approximately 93 % of the RB/DPI system is involved in the formation of the ground state dye-electron acceptor complex while ~ 61 % of the FL/DPI system involves the formation of ground state complex. We have also tried to determine the association constant of a 1:2 complex between the FL and DPI but the modified Benesi-Hildebrand analysis did not fit the experimental data well (R²= 0.89 ~ 0.73) for three different FL concentrations (1.2 × 10⁻³, 1.4 × 10⁻²³, and 1.6 × 10⁻³ M), leading to a broad range of association constant values.

Figure 5.

Absorption spectrum of FL/DPI system. All systems contain fluorescein at the same concentration (1.2 × 10⁻³ M), with differing concentrations of the iodonium salt.

Complex Molar Absorptivity as a Function of Wavelength

To conclusively support the validity of the modified Benesi-Hildebrand model, we determined the molar absorptivity of the ground state complex as a function of wavelength for each of the systems investigated here. We resolved the absorbance spectrum, shown in Figures 3 and 5, into two contributions: the first arising from the free dye (RB in Figure 3 and FL in Figure 5); and the second arising from the ground state complex. The analysis was based on the values of the association constants, K_a1, obtained in the previous section of this paper in combination with equation (3) to determine the concentration of the ground state complex (and therefore the free dye concentration) for each concentration of DPI. Once the concentration of the free dye was determined in this manner, the free dye's contribution to the absorbance spectrum could be determined readily. The plot of the ground state complex molar absorptivity as a function of wavelength was obtained for each DPI concentration using the following procedure: first the calculated contribution from the free dye was subtracted from the experimentally obtained absorption spectrum (from Figure 3 or Figure 5); dividing the resulting curve by the calculated concentration of the complex yields the profile of the complex molar absorptivity as a function of wavelength. The results of the analysis shown in Figures 6 and 7 illustrate the molar absorptivities of the 1:1 RB/DPI and FL/DPI complexes, respectively, as a function of DPI concentration. The molar absorptivities of the complexes are essentially independent of the DPI concentration for both dyes. This suggests that the assumptions made in the analysis are valid and that the modified Benesi-Hildebrand model can be confidently applied to the characterization of association constant and molar absorptivity values of the dye-acceptor ground state complex. The figures also illustrate clearly the molar absorptivity of the RB/DPI complex is much higher than that of the FL/DPI complex.

Figure 6.

Molar absorptivity of the ground state complex as a function of the DPI concentration in the RB/DPI 1:1 complex system.

Figure 7.

Molar absorptivity of the ground state complex as a function of the DPI concentration in the FL/DPI 1:1 complex system.

Effect of ground complex of photoinitiator system on the kinetics of visible-light-induced polymerizations

To investigate the effect of ground state complex on the kinetics and to test our hypothesis outlined in the introduction, the rate of HEMA polymerizations for both RB/DPI and FL/DPI photoinitiator systems (which are dye-electron acceptor systems) were examined using Photo-DSC. We also measured the rate of polymerization for dye-electron donor systems, (which are RB/MDEA and FL/MDEA), and compared the kinetics between dye-electron acceptor system and dye-electron donor system. For each of the photoinitiator systems, thermodynamic feasibility for the photo-induced electron transfer reaction was verified with the Rhem-Weller equation^43,44 as shown in Table 1.

Table 1.

Free energy changes of photo-induced electron transfer reaction.

Dye	Eox (V/SCE)	Ered (V/SCE)	Dye oxidation by DPI		Dye reduction by MDEA
			SΔG (kJ/mol)	tΔG (kJ/mol)	SΔG (kJ/mol)	tΔG (kJ/mol)
RB	0.6513	−1.0013	−130.2	−91.6	−46.3	−7.7
FL	0.9145	−1.1345	−126.3	−80.1	−55.0	−8.7

For these calculations, the singlet and triplet excited state energy of 2.20¹³ and 1.80¹³ eV, respectively, are used for RB. For FL, 2.42⁴⁵ eV is used for the singlet excited state energy and 1.94⁴⁵ eV is used for triplet excited state energy. E_red (DPI)=−0.2⁴⁶ V/SCE and E_ox (MDEA)=+0.72¹³ V/SCE are used for calculation of free energy changes by Rhem-Weller equation, ΔG = (E_ox-E_red)-E*.

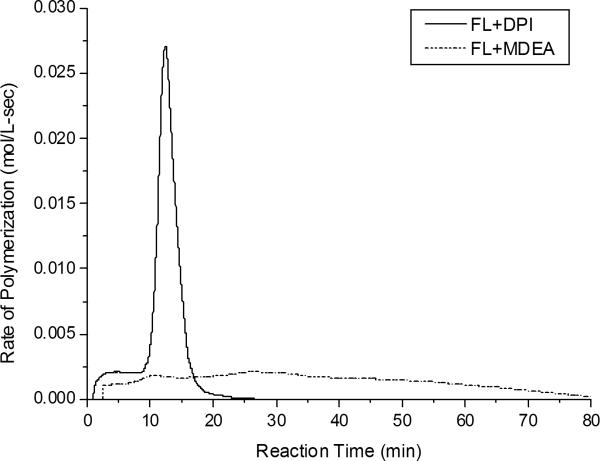
It is notable that the RB/DPI photoinitiator system did not lead to any perceptible generation of free radical active centers while the FL/DPI photoinitiator system generated very high rates of polymerization as shown in Figure 8. Note that both initiator systems are thermodynamically feasible in the photoinduced electron transfer reaction. These kinetic results indicate that the association constant of electron donor-acceptor ground state complex strongly influences the photoinduced electron transfer reactions. The observed differences in kinetics arise from the different values of the association constant of the ground state dye-acceptor complex. Because the ground state complex leads to internal static quenching of the excited singlet state of the photosensitizer as well as not allowing separation distance, the back electron transfer reaction predominates for RB/DPI.

Figure 8.

Rate of HEMA polymerizations with FL/DPI and FL/MDEA photoinitiator systems as measured by Photo-DSC at 50 °C with an incident light intensity of 55 mW/cm². For all samples, [FL] = 5 × 10⁻⁴ M, [DPI] = 0.015 M and [MDEA] = 0.25 M, in neat HEMA.

The formation of dye-electron acceptor complex results in internal static quenching of the excited singlet state of the RB and prevents the formation of the long-lived triplet species^20,21. In general, back electron transfer occurs more favorably in singlet state systems than in triplet state systems because back electron transfer is limited by the rate of spin flip in the triplet state systems^47,48. As a result, laser flash photolysis experiments revealed that triplet state, ³RB²⁻ was quenched only by free electron acceptor^18,19 because the internal static quenching of the excited singlet state of the RB rapidly undergoes back electron transfer reaction. For that reason, laser flash photolysis studies of the photoinitiator system demonstrated that polymerization involves the interaction of the excited triplet state of dye with electron donor or electron acceptor while quenching of the excited singlet state of the dye limits the polymerization^49,50.

In addition, because the pre-associated ground state electron donor-acceptor complex does not allow separation distance and leads to extremely fast back electron transfer, back electron transfer in the radical ion complex cage structure takes place readily, thereby retarding generation of active radical centers²⁶. Therefore, the RB/DPI photoinitiator system could not generate free radical active centers because ~93 % of the initial concentration of RB leads to the formation of dye-electron acceptor complex, which leaves only ~7 % free RB. As previously described, because general quantum yields of separated radical ions, (which are active for initiation), are less than 10 % in bimolecular electron transfer reaction, only ~7 % free RB is not effective for initiation²⁶.

In contrast, the FL/DPI photoinitiator system leads to a very high rate of polymerization because while ~ 61 % of the FL/DPI system is involved in the formation of complex, ~39 % of the initial concentration of FL remains as free dye. Indeed, no polymerization is observed with DPI in the absence of dye. It is also a notable kinetic result that the FL/DPI system exhibited a tremendously faster rate of polymerization than the FL/MDEA system as shown in Figure 8. This kinetic result arises from the fact that DPI undergoes a rapid unimolecular fragmentation reaction without a radical recombination reaction step when the radical ion pair of photo-oxidizable FL and iodonium salt (DPI) is separated as shown in Scheme 2. This irreversible unimolecular fragmentation reaction of DPI produced more efficient kinetics than the photo-reducible dye and amine system, (FL/MDEA), because the latter undergoes back electron transfer and recombination reaction steps. Both FL/MDEA and RB/MDEA systems produced very low polymerization rates in the same way. In addition, because the dye-based radical, PS-H• as shown in Scheme 1, is not active for initiation but is active for termination, the FL/DPI system provided much higher polymerization rates than the FL/MDEA system^7,8,12,13.

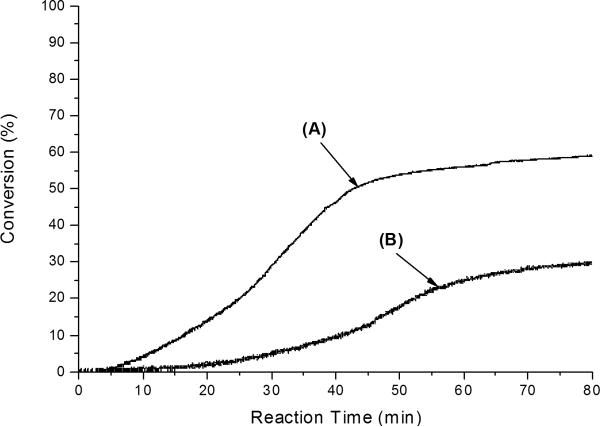
The results are also supported by HEMA photopolymerization kinetic data with FL/DPI and FL/MDEA photoinitiator systems as measured by NIR as shown in Figure 9. Similarly, the RB/DPI photoinitiator system did not lead to any perceptible conversion while the FL/DPI photoinitiator system generated ~ 58 % final conversion as shown in Figure 9. It is also a notable kinetic result that the FL/DPI system exhibited a higher conversion than the FL/MDEA system (final conversion ~ 29 %), as shown in Figure 9. The data clearly indicate that FL/DPI is a more effective system than FL/MDEA for the overall production of radical active centers. Therefore, these results provide very useful information for the rational design of two-component visible light initiator systems because visible light activated polymerizations is dynamically growing for new dental materials and photo-activated biomaterials applications^51–58.

Figure 9.

Conversions of HEMA polymerizations with FL/DPI and FL/MDEA photoinitiator systems as measured by NIR at room temperature with an incident light intensity of 0.15 mW/cm²: (A) FL+DPI and (B) FL+MDEA. For all samples, [FL] = 5 × 10⁻³ M, [DPI] = 0.02 M and [MDEA] = 0.02 M in neat HEMA.

Conclusion

In this contribution, we have shown that both RB/DPI and FL/DPI photoinitiator systems form 1:1 ground state complexes in HEMA monomer. To characterize the molar absorptivities and association constants, we have suggested a new analysis model based on the Benesi-Hildebrand model. By considering the absorption contributions from both ground state complex and free dye, the modified Benesi-Hildebrand model was used because the assumption of the original Benesi-Hildebrand is that the absorption bands are due only to the presence of the complex and that the absorption by free component is negligible. The calculated values of the association constants were found to be 1200 ± 150 M⁻¹ for the RB/DPI system and 160 ± 30 M⁻¹ for the FL/DPI system. For each dye, the molar absorptivity of the ground state complex was evaluated as a function of wavelength. The molar absorptivity of the complex, ε_c was 35500 ± 800 M⁻¹ cm⁻¹ at 556 nm for the RB/DPI system and 860 ± 20 M⁻¹ cm⁻¹at 458 nm for the FL/DPI system. To confirm the validity of the modified Benesi-Hildebrand model, the molar absorptivity of the ground state complex was evaluated as a function of wavelength for each dye. The fact that the molar absorptivities of the complexes were essentially independent of the DPI concentration for both dyes suggests that the assumptions made in the analysis are valid.

In addition, we investigated the effect of ground state complex formation on the kinetics of visible-light-induced polymerizations. We observed the RB/DPI photoinitiator system could not generate free radical active centers but FL/DPI photoinitiator system produced a very high rate of HEMA polymerization. We concluded that the association constant of electron donor-acceptor ground state complex strongly influences the photoinduced electron transfer reactions. The observed differences in the polymerization kinetics arise from the different values of the association constant of the ground state dye-acceptor complex, which correlates with the back electron transfer reaction. These results may allow better characterization of existing photoinitiators while providing useful information for the design of new, more efficient initiator systems. In the future work, we will explore some other factors responsible for the initiation efficiency such as basicity (pK_b) and chemical structures of the initiator systems.