Tuning of the H-Transfer Coordinate in Primitive versus Well-Evolved Enzymes

The nature of an H-transfer reaction catalyzed by a primitive enzyme is examined and compared to the same reaction catalyzed by a mature (highly evolved) enzyme. The findings are evaluated using two different theoretical models. The tunneling correction model[1–3] suggests that the reaction catalyzed by the mature enzyme involves extensive tunneling, while that of the primitive enzyme involves no tunneling contribution. Marcus-like models,[2–5] on the other hand, suggest that the reaction catalyzed by the primitive enzyme has a poorly reorganized reaction coordinate, while the mature enzyme has tuned the reaction coordinate to near perfect reorganization. The latter interpretation does not indicate the degree of tunneling, but it does address the level of system preparation that brings the reaction coordinate to the tunneling conformation. Importantly, the findings indicate that, in contrast to the primitive enzyme, the mature one has evolved to catalyze a reaction with asignificant tunneling contribution or with a perfectly reorganized reaction coordinate for H-tunneling (using tunneling-correction or the Marcus-like models, respectively).

The current study compares the temperature dependence of intrinsic kinetic isotope effect (KIEs). This method has been established in recent years as a critical probe for the nature of the chemical step(H-transfer in this case) in enzymatic reactions.[2,3,6–13] One of the unique features of this tool is that it circumvents the need for complete kinetic examination of the system under study as it directly reports on the nature of the chemical step in question. Temperature-independent KIEs have been reported for many highly evolved enzymes catalyzing H-transfer, and it has been suggested that this phenomenon indicates that these enzymes have evolved to bring the donor and acceptor to a perfect donor–acceptor distance (DAD) for H-tunneling.[2,3,6–8,14–17] Typically, under non-physiological conditions (e.g. low temperature[8] or following a mutation[5,14]), the same enzymes present temperature-dependent KIEs. Thus, testing the temperature dependence of the intrinsic KIE of a system, provides a means to differentiate between systems that involve different degrees of tunneling and/or different levels of reorganization (according to these two theoretical approaches). While the term evolved implies that primitive enzymes would not have as perfect a DAD as their well-evolved counterparts, this has not been tested prior to the current study.

Herein, we examine the reaction catalyzed by dihydrofolate reductase (DHFR), namely the reduction of 7,8-dihydrofolate (H₂folate) to 5,6,7,8-tetrahydrofolate (H₄folate) with the stereo-specific transfer of a hydride from the pro-R C4 position of a nicotinamide ring to the si-face of C6 of the pteridine ring. Highly evolved DHFRs are ubiquitous and can be found in most modern organisms. In response to antibacterial drug pressure, bacteria adopt a plasmid that encodes for a primitive enzyme that has some DHFR activity.[18,19] The two enzymes compared herein are the well-studied, highly evolved, chromosomal enzyme (cDHFR) from E. coli, and the genetically unrelated R-plasmid-encoded DHFR (R67-DHFR). The latter is found in bacterial strains (including E. coli) that have developed resistance to the antibiotic drug trimethoprim (TMP, a picomolar inhibitor of cDHFR). Although both enzymes catalyze the same reaction, they share no sequence or structural similarities (Figure 1).[18]

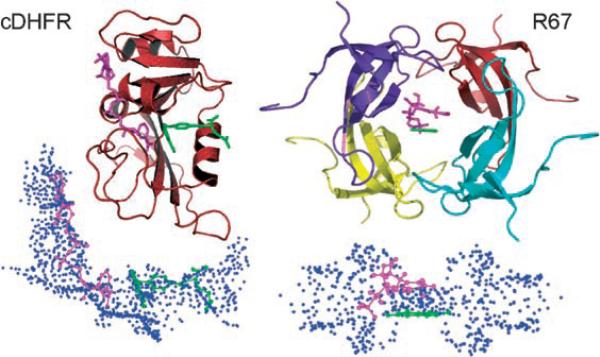
Figure 1.

Top: Structures of cDHFR (PDB ID R1X2; left) and R67-DHFR (PDB ID 1VIF; right). For R67-DHFR, the pteridine ring position (green) of the folate was defined in the crystal structure and the nicotinamide (magenta) was docked in place using DOCK. Bottom: Under each structure we present the reverse images for each active site.[18] In the reverse images, each sphere point describes a potential atom position for use by the docking algorithm. The sphere cluster for cDHFR is shown in approximately the same orientation as its structure. In contrast, the sphere cluster for R67-DHFR is shown sideways, after a 90° rotation along the y axis.

The active site structure of R67-DHFR is quite different from that of cDHFR, resulting in an approximately 10⁶-fold difference in K_i values for TMP.[20,21] As R67-DHFR has been genetically selected due to its ability to confer TMP resistance, it might not necessarily be a very efficient catalyst. For example, R67-DHFR is one of the smallest enzymes known to self-assemble into an active quaternary structure. This is advantageous as it expends less energy and DNA in encoding the genetic information. On the other hand, a major limit to the catalytic efficiency of R67-DHFR arises from the 222 symmetry imposed on the single active site pore in the homotetramer.[18] This situation results in the presentation of a promiscuous binding surface, which allows binding of the non-productive DHF–DHF and NADPH–NADPH complexes as well as the catalytic DHF–NADPH complex. This “catch-222” situation leads to a low catalytic efficiency (by two orders of magnitude relative to cDHFR) and a large entropic contribution to the activation parameters (TΔS^≠₂₅ = −11.3 compared to ΔH^≠ = 6.3 kcal mol⁻¹).[22] A wide variety of structural and kinetic data also support this model,[23–27] including directed evolution experiments where the four active-site residues of R67-DHFR can be substituted by a variety of other residues.[28] Since R67-DHFR is a homotetramer with a single active site pore, this scenario results in sixteen changes per active site; yet, the mutants are as active as the wild-type R67-DHFR. Such tolerance is typical of poorly evolved enzymes.[18,28] To improve R67-DHFR function further, gene duplication or quadruplication, followed by divergence of individual gene copies needs to occur. Such studies with modified enzymes where the 222 symmetry is broken[29] are underway.

A comparison of the nature of the H-transfer step catalyzed by these two enzymes is also of great interest due to their different flexibilities. An examination of the chemical step catalyzed by a rigid vs a flexible enzyme—where both catalyze the same reaction—is of general interest in biophysical and physical chemistry. Mature DHFR is flexible and its motions on many different timescales (ns–ms) appear to be critical to its function.[30,31] The R67-DHFR enzyme, on the other hand, appears to be rigid on all the timescales examined.[32]

The DHFR chemical reaction serves as an excellent model system for testing the role of the protein in catalysis because many of the experimental and theoretical studies discussed herein use the same system.[6,7,12,14,15,33] Furthermore, for cDHFR, it has been demonstrated that mutations that decrease the rate of the H-transfer increase the temperature dependency of KIEs,[14] indicating poorer reorganization and a longer DAD.

The nature of H-transfer in the R67-DHFR-catalyzed reaction is examined by extracting its intrinsic KIEs from their observed values across a temperature range of 5−45 °C. The findings are compared to the same studies conducted with cDHFR.[15] The only modification is the quenching of the R67-DHFR reaction by addition of 5 mm Congo Red, (see Supporting Information) whereas the cDHFR reaction is quenched by addition of methotrexate, which is a nM inhibitor of cDHFR, but not of R67-DHFR).

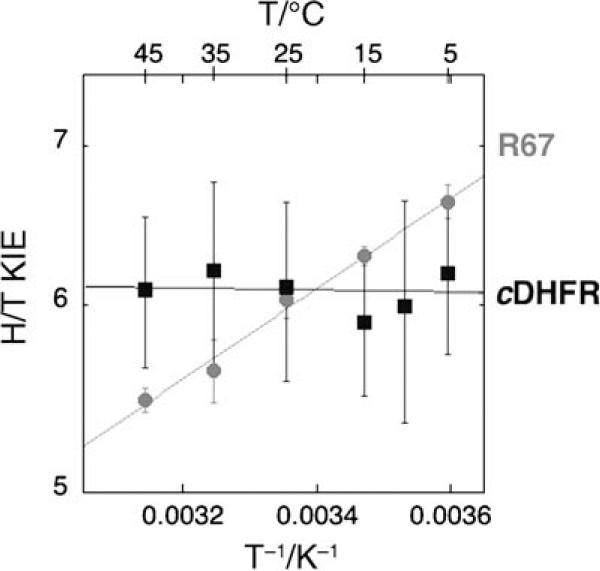
Both H/T and D/T KIEs on the second order parameter (k_cat/K_M) are measured across a temperature range of 5−45 °C (see Supporting Information). In contrast to cDHFR, for which the chemical stepis not rate-limiting (and for which the intrinsic KIEs has to be extracted by using the Northrop method[34]), the H-transfer stepis rate-limiting in the R67-DHFR catalyzed reaction for both first- and second-order enzymatic rate constants (k_cat and k_cat/K_M, respectively).[35] In Figure 2, the temperature dependence of the intrinsic KIEs for R67-DHFR is compared to that of the KIEs measured for cDHFR.[15]

Figure 2.

A comparative Arrhenius plot of the H/T KIEs (log scale) vs the reciprocal of the absolute temperature. The R67-DHFR data are presented as () and the cDHFR data[15] as (■). The lines present the exponential fit of the data to the Arrhenius equation. The standard errors for R67-DHFR are much smaller than those for cDHFR because its observed KIEs are also intrinsic, while for cDHFR extensive error-propagation during calculations of intrinsic KIEs inflate the reported errors.[14]

Exponential fitting of the experimental data to the Arrhenius equation for KIEs (prior to averaging the values at each temperature, see Supporting Information) yields the isotope effects on the activation parameters for both enzymes. The cDHFR KIEs are practically temperature-independent (ΔE_a = −0.1 ± 0.3 kcal mol⁻¹) and their intercept value (the isotope effect on the pre-exponential factor) is similar to the observed KIEs at the experimental temperature (A_H/A_T = 7.4 ± 4.0).[15] The data for R67-DHFR, on the other hand, result in a temperature-dependent KIE (ΔE_a = 0.87 ± 0.03 kcal mol⁻¹) and an isotope effect on the Arrhenius pre-exponential factor (intercept in Figure 3) that is much smaller (A_H/A_T = 1.36 ± 0.07).

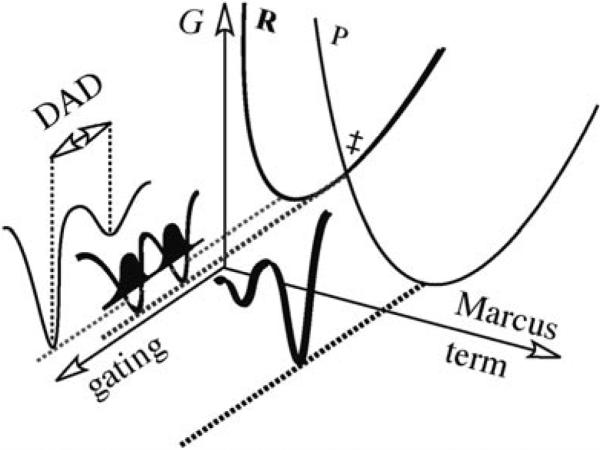
Figure 3.

Illustration of Marcus-like models as expressed in Equation (1). The orthogonal coordinates presented are the Marcus-term (isotopically insensitive), and the fluctuation of the DAD (gating, isotopically sensitive). R is the reactant state and P is the product state. The Franck–Condon term is presented by the probability of finding the hydrogen at the reactant or the product states and is illustrated for the tunneling-conformation as a dark probability function along the gating coordinate.

Theoretical models using a tunneling correction to transition state theory would interpret these findings as indicative of extensive tunneling in the mature cDHFR and no tunneling in the primitive R67-DHFR.[1–3] In recent years, Marcus-like models have been developed that take a different approach to rationalizing temperature-independent and temperature-dependent KIEs.[2–5] According to these models, the temperature-independent KIEs indicate a perfectly reorganized reaction coordinate, and the average DAD of the reactive conformation is ideal for tunneling of both light and heavy isotopes (Figure 3). In this model, temperature-dependent KIEs indicate poor reorganization of the reaction coordinate, for which the average DAD is too long for efficient tunneling. In these cases, fast fluctuations of that distance (a phenomenon denoted as gating) sample more conformations that enable tunneling at higher temperatures. Since the light isotope tunnels from a longer distance than the heavy one, the KIEs increase with decreasing temperature [Eq. (1)]

$$k=C{e}^{-{(\Delta {\mathrm{G}}^{\circ }+\lambda )}^2∕\left(4\lambda \mathrm{RT}\right)}{\int }_{r_0}^{r_1}{e}^{\mathrm{F}\left(\mathrm{m}\right)}{e}^{-{\mathrm{E}}_{\mathrm{F}\left(\mathrm{m}\right)}∕{\mathrm{k}}_{\mathrm{b}}\mathrm{T}}d\mathrm{DAD}$$ (1)

Equation (1) presents a general Marcus-like model[2–5] where the first exponential term is the traditional Marcus-term and is not isotopically sensitive (see Figure 3). The second exponential term is the Franck–Condon term describing H-tunneling (isotopically sensitive, but temperature-independent, illustrated by the probability function in Figure 3). The last exponential term describes the DAD fluctuations (the gating coordinate) and is both isotopically and temperature-sensitive.

In summary, the nature of the chemical steps catalyzed by the highly evolved and flexible cDHFR and the primitive, rigid R67-DHFR enzymes were compared. The cDHFR appears to have a perfectly reorganized reaction coordinate or, put differently, efficient H-tunneling. In contrast, the R67-DHFR enzyme requires significant gating of its DAD prior to tunneling, or, alternatively, there is no tunneling contribution to its catalyzed reaction. These findings provide evidence for the notion that enzymes have evolved to optimize their reaction coordinate for efficient tunneling.

Experimental Section

The material and methods are available in the Supporting Information.