Prediction of periventricular leukomalacia. Part I. Selection of hemodynamic features using logistic regression and decision tree algorithms

Summary

Objective:

Periventricular leukomalacia (PVL) is part of a spectrum of cerebral white matter injury which is associated with adverse neurodevelopmental outcome in preterm infants. While PVL is common in neonates with cardiac disease, both before and after surgery, it is less common in older infants with cardiac disease. Pre-, intra-, and postoperative risk factors for the occurrence of PVL are poorly understood. The main objective of the present work is to identify potential hemodynamic risk factors for PVL occurrence in neonates with complex heart disease using logistic regression analysis and decision tree algorithms.

Methods:

The postoperative hemodynamic and arterial blood gas data (monitoring variables) collected in the cardiac intensive care unit of Children's Hospital of Philadelphia were used for predicting the occurrence of PVL. Three categories of datasets for 103 infants and neonates were used-—(1) original data without any preprocessing, (2) partial data keeping the admission, the maximum and the minimum values of the monitoring variables, and (3) extracted dataset of statistical features. The datasets were used as inputs for forward stepwise logistic regression to select the most significant variables as predictors. The selected features were then used as inputs to the decision tree induction algorithm for generating easily interpretable rules for prediction of PVL.

Results:

Three sets of data were analyzed in SPSS for identifying statistically significant predictors (p < 0.05) of PVL through stepwise logistic regression and their correlations. The classification success of the Case 3 dataset of extracted statistical features was best with sensitivity (SN), specificity (SP) and accuracy (AC) of 87, 88 and 87%, respectively. The identified features, when used with decision tree algorithms, gave SN, SP and AC of 90, 97 and 94% in training and 73, 58 and 65% in test. The identified variables in Case 3 dataset mainly included blood pressure, both systolic and diastolic, partial pressures pO₂ and pCO₂, and their statistical features like average, variance, skewness (a measure of asymmetry) and kurtosis (a measure of abrupt changes). Rules for prediction of PVL were generated automatically through the decision tree algorithms.

Conclusions:

The proposed approach combines the advantages of statistical approach (regression analysis) and data mining techniques (decision tree) for generation of easily interpretable rules for PVL prediction. The present work extends an earlier research [Galli KK, Zimmerman RA, Jarvik GP, Wernovsky G, Kuijpers M, Clancy RR, et al. Periventricular leukomalacia is common after cardiac surgery. J Thorac Cardiovasc Surg 2004;127:692–704] in the form of expanding the feature set, identifying additional prognostic factors (namely pCO₂) emphasizing the temporal variations in addition to upper or lower values, and generating decision rules. The Case 3 dataset was further investigated in Part II for feature selection through computational intelligence.

1. Introduction

Congenital heart disease (CHD) is the most common birth defect requiring intervention in the human, affecting approximately 8:1000 live births. Prior to the early 1970s, most forms of complex CHD were fatal, or resulted in severe limitations in quality of life and a reduced lifespan. However, in the current era, most centers treating even the most complex forms of CHD can offer their patients and families a very high likelihood of survival. As mortality has declined, there has been a growing recognition of a disturbingly high incidence of developmental delays and behavior issues in the survivors. Recent research has shown a high incidence of periventricular leukomalacia (PVL) both before and after surgery in these patients [1-13]. PVL is part of a spectrum of cerebral white matter injury, and is thought to be caused by a combination of abnormal cardiovascular hemodynamics and oxygen delivery to the brain. In preterm newborns, PVL remains the most common cause of brain injury and the leading cause of chronic neurologic morbidity, including cerebral palsy, mental retardation, learning disabilities, attention deficit hyperactivity, problems with visual motor integration, and other features [14-18]. PVL has been recognized by investigators at the Children's Hospital of Philadelphia (CHOP) and others to be a common preoperative and postoperative finding in infants undergoing surgery for complex CHD [4].

While there are many risk factors for brain injury in children with CHD that are unmodifiable (e.g., prematurity, genetic syndromes, socioeconomic status and others), clinical research has focused on potentially modifiable risk factors, particularly those in the operating room such as the conduct and duration of cardiopulmonary bypass. Identifiable risk factors explain less than 30% of variability in outcomes [19]. While much research has been performed in the operating room (where the potential for brain injury can be measured in hours), little is known about the potential for additional injury that may occur in the intensive care unit following surgery (measured in days to weeks). In particular, the immediate postoperative period is a time when the newborn and infant brain is particularly susceptible to low-blood pressure and oxygen levels.

Logistic regression (LR) analysis is one of the popular multivariable statistical tools used in biomedical informatics [20-24]. LR is widely used in medical literature for relating the dichotomous outcomes (diseased/healthy) with the predictor variables that include different physiological data. In LR models, the predicted odds ratio (OR) of positive outcome (e.g., diseased = 1) is expressed as sum of products, each product formed by multiplying the value of independent variable (covariate) and its coefficient. The probability of positive outcome is obtained from the OR through a simple transformation [20,21]. The independent variables (covariates) and their coefficients are computed from the data used for model development. LR has found widespread applications in health sciences due to its ability to predict the outcome in terms of the selected ‘predictor’ variables that are statistically significant. The nomographic representation of LR models [25] that can be used manually without computers is also being developed as an alternative. Applications of LR analysis in the medical domain are numerous [26-30]. There are also attempts to use LR along with data mining techniques such as decision tree [31-34].LR analysis, being based on a statistical approach, has the advantage of greater acceptability but lacks easy interpretation to be useful in practice. In contrast to this, a decision tree (DT), if properly trained, has the advantage of generating rules which are easy to interpret. In addition, DT algorithms, being based on the principle of maximizing information-gain, are expected to result in more robust prediction models than LR in case of ‘noisy’ or missing data [31,32]. In the present work, we combine the advantages of LR and DT algorithms towards the development of a decision support system with easily interpretable rules for prediction of PVL.

In an earlier study, a limited analysis identified postoperative hypoxemia and postoperative diastolic hypotension to be more important factors than intraoperative total cardiopulmonary support time in terms of association with PVL [4]. That study involved a retrospective review of hand-written nursing ‘flowsheets’ for hemodynamic variables at 4 h intervals for the first 48 h after arrival in the intensive care unit. To facilitate the modeling analysis for identification of potential risk factors, only three of those 13 different time points for each variable were taken into account, the admission value, the minimum value in the 48 h epoch, and the maximum value.

Recognizing the limitations of that approach, including missing data points throughout the time-frame of potential brain injury, we sought to better understand the postoperative hemodynamic variables that may be associated with PVL by applying LR and DT algorithms to the dataset. The dataset was further analyzed to extract statistical features of temporal distribution for each of the monitoring variables like mean, standard deviation, skewness and kurtosis. The last two features characterize the temporal distribution of each monitoring variable in terms of asymmetry and abrupt changes (or existence of spikes) compared to a normal distribution. Skewness represents a measure of asymmetry of data distribution with respect to the mean: a zero value represents a normal distribution, a negative value signifies a distribution skewed left and a positive value denotes a distribution skewed right. Kurtosis represents a measure of ‘peaked’ or lack of flatness of data distribution compared to a normal distribution. For a normal distribution, kurtosis is around 0, a negative value indicates a flat distribution whereas a positive value represents a ‘peaked’ distribution. Three categories of data were used in the present work-–(1) original data without any preprocessing, (2) partial data keeping the admission, the maximum and the minimum values of the monitoring variables, similar to [4], and (3) extracted dataset of additional statistical features.

In the first of this two-part paper, the statistical tool of LR analysis and data mining technique of DT algorithms were used to identify the suitable dataset. In the second part, the identified dataset was further analyzed for selection of prognostic features using computational intelligence (CI) techniques. In Part I, the datasets were given as inputs for forward stepwise logistic regression to select the significant variables as ‘predictors’ of PVL occurrence. The selected features from LR models were then used as inputs to the DT induction algorithm for generating easily interpretable rules of PVL prediction. Prediction performances of DT algorithm with and without LR selected features were compared. The present work extends the research reported in [4] in following three areas: (1) consideration of an expanded feature space extracted from the recorded hemodynamic data, (2) identification of additional prognostic factors, and (3) generation of easily interpretable decision rules for prediction of PVL. The present work is a first attempt to combine advantages of LR and DT algorithms for identification of potential postoperative risk factors for prediction of PVL with reasonably simple decision rules.

The paper is organized as follows. Section 2 describes the dataset used and Section 3 deals with the feature extraction process. Logistic regression (LR) analysis and decision tree (DT) algorithm are briefly discussed in Sections 4 and 5, respectively. Section 6 presents the prediction results using the proposed methods (LR and DT) along with their comparisons. In Section 7, limitations of the present work are briefly mentioned and the concluding remarks are summarized in Section 8.

2. Data used

The dataset consisted of handwritten paper flow-sheets and manual extraction of hemodynamic and blood gas analysis data at admission and subsequent 4 h intervals for the first 48 h (13 time points total) after arrival in the cardiac intensive care unit. The seven recorded monitoring variables include heart rate (HR), systolic blood pressure (SBP), diastolic blood pressure (DBP), central venous filling pressure or right atrial pressure (RAP), as well as arterial blood gas data including pH, partial pressure of carbon dioxide (pCO₂), and partial pressure of oxygen (pO₂). From a total of 105 neonates and infants, data were used for 103; 2 patients were excluded from the analysis due to missing data. For each patient, the size of the dataset was 7 × 13 (number of monitoring variables × number of values for each variable over the 48 h period at 4 h intervals). Patient specific demographic and operative variables were excluded from the analysis. All studies were read for the presence of PVL by a single neuroradiologist (RAZ), blinded to clinical status. Interpretation was made from early postoperative MRIs (within 3–14 days after surgery) of the brain for each of the patients. The mean and the standard deviation of the average of each monitoring variable are presented with and without PVL in Table 1 for comparison.

Table 1.

Mean and standard deviation for average monitoring variables with and without PVL.

Variable	Without PVL		With PVL
	μ	σ	μ	σ
HR (bpm)	154	14.4	161	13.6
SBP (mm Hg)	77.7	12.7	70.2	10.7
DBP (mm Hg)	44.3	8.3	37.8	6.4
RAP (mm Hg)	7.68	2.51	7.32	1.44
pH	7.48	0.03	7.49	0.04
pCO2 (mm Hg)	39.5	3.87	39.08	4.33
pO2 (mm Hg)	66.7	29.5	53.5	30.9

3. Feature extraction

Three categories of data were used for each patient. Case 1 consisted of original dataset of 13 values for each of 7 monitoring variables (X: HR, SBP, DBP, RAP, pH, pCO₂, pO₂) without any preprocessing (total of 7 × 13). In some cases, an estimated average was utilized by the primary data extractor. Two-thirds were complete with all the entries; the rest of the patients were transitioned to a less intense care and monitoring regimen within 48 h of admission. Case 2 used partial data keeping the admission (X_adm), the maximum (X_max), and the minimum (X_min) values of the monitoring variables (total of 7 × 3). In Case 3, four additional statistical features, namely, average (X_avg or μ), standard deviation (X_std or σ), normalized third order moment or skewness (X_skw or γ₃) and fourth order normalized moment or kurtosis (X_krt or γ₄) in addition to admission (X_adm), maximum (X_max), minimum (X_min) values were extracted (total of 7 × 7). The extracted features are defined in Eqs. (1a) and (1b) for each monitoring variable of the patient:

$${\gamma }_3=\frac{E\left\{{[x_i-\mu ]}^3\right\}}{{\sigma }^3}$$ (1a)

$${\gamma }_4=\frac{E\left\{{[x_i-\mu ]}^4\right\}}{{\sigma }^4}-3,\mu =E\left(x_i\right),i=1,13$$ (1b)

where x_i represents the ith value of the monitoring variable X (i = 1, 13), and E represents the expected value of the function. This reduces the size of the dataset for each patient from 7 × 13 to 7 × 7.

The Case 1 (original) dataset was used to study if the raw recoded data without any preprocessing would be good enough to predict the occurrence of PVL. The Case 2 (partial) dataset represented the limited pattern of the monitoring variables in terms of three values (admission, the maximum and the minimum), similar to a previously published report [4]. In Case 3 (extracted) dataset, the temporal pattern in terms of average, standard deviation, skewness and kurtosis was used as additional features. The Case 3 dataset was considered in this paper to test if the temporal pattern would serve better than the original dataset (Case 1) and the partial features (Case 2) of [4] for prediction of PVL.

3.1. Training and test datasets

For Case 1, the original dataset of 70 patients with complete entries was used for LR analysis. For Cases 2 and 3, each dataset was divided randomly into two subsets for training and test purposes, each containing about a similar proportion of positive (PVL = 1) and negative (PVL = 0) outcomes. The training dataset included two-thirds of the samples (with 30: PVL = 1; 39: PVL = 0), and the rest one-third was used as test dataset (with 15: PVL = 1; 19: PVL = 0).

3.2. Normalization

The extracted features from each variable (X) were normalized (X_N) in the range of 0–1 for better performance in the classification stage as follows:

$$X_{\mathit{ijN}}=\frac{X_{\mathit{ij}}-X_{j\min }}{X_{j\max }-X_{j\min }}$$ (2)

where the subscripts i and j represent the patient number (i = 1, 103), and the feature number (j =1, 7), respectively, of variable (X). X_jmin and X_jmax represent the minimum and the maximum values of the jth monitoring variable. The subscript N indicates the normalized value. It is worth mentioning that normalization (0 ≤ X_ijN ≤ 1) was necessary to treat all the variables equally in the modeling process, especially in view of the wide ranges of their values.

4. Logistic regression analysis

Logistic regression is a nonlinear regression technique for prediction of dichotomous (binary) dependent variables in terms of the independent variables (covariates) [20,21]. The dependent variable can represent the status of the patient (e.g., diseased, Y = 1 or healthy, Y = 0). The expected probability of a positive outcome P(Y = 1) for the dependent variable is modeled as follows:

$$P(Y=1)\frac{1}{1+{\mathrm{e}}^{-(B_0+\underset{i=1}{\overset{n}{\Sigma }}{B}_i{x}_i)}}$$ (3)

where x_i, i = 1, n are the independent variables (covariates), B_i are the corresponding regression coefficients and B₀ is a constant, all of which contribute to the probability. Eq. (3) reduces to a linear regression model for the logarithm of odds ratio (OR) of positive outcome, i.e.

$$\ln \left(\frac{P(Y=1)}{1-P(Y=1)}\right)=B_0+\underset{i=1}{\overset{n}{\Sigma }}{B}_i{x}_i$$ (4)

In producing the LR model, the maximum-likelihood ratio is used to determine the statistical significance of the independent variables. Using this model, stepwise selections of the variables and the computation of the corresponding coefficients are made through available statistical software packages. In the present work, SPSS package was used for LR analysis.

5. Decision tree algorithms

Decision tree (DT) algorithms are used in data mining for classification and regression. The popularity of DT is due to the availability of decision rules that are easy to interpret. Among the various algorithms used for decision tree induction, C4.5 [31], and classification and regression tree (CART) [32] are quite widely used. One of the main differences between CART and C4.5 is that CART uses strictly binary tree structure (with only two branches at each internal node) whereas C4.5 may have more than two branches at any internal node. The basic steps involved in DT algorithms are briefly discussed here. Readers are referred to texts [31,32] for details.

The input dataset consists of objects each belonging to a class. Each object is characterized by a set of attributes (variables or predictors) that may have numerical and categorical (non-numerical) values. The goal of DT is to use a training dataset with known attribute-class combinations for generating a tree structure with a set of rules for correct classification and prediction of a similar test dataset. The DT consists of a root, internal (non-terminal) decision nodes and a set of terminal nodes or leaves, each representing a class. There are two phases in DT induction: tree building and tree pruning.

5.1. Tree building

The process of tree building starts at the root (first internal node) with the entire dataset being split into two subsets. The recursive partitioning of the dataset (S) into subsets is continued at each internal node (q) based on a measure of information or entropy:

$$E\left(q\right)=\underset{i=1}{\overset{c}{\Sigma }}-p_i\left(q\right){\log }_2{p}_i\left(q\right)$$ (5)

where p_i(q) denotes the proportion of S belonging to class i at node q and c is the total number of classes in the dataset. For a dichotomous dependent variable, c = 2. The selection of the optimal splitting value s* among all splitting variables S at an internal node (q) is decided on the basis of the maximum information-gain:

$$\Delta E(s^{\ast },q)=\max (E\left(q\right)-p_{\mathrm{L}}E\left(q_{\mathrm{L}}\right)-p_{\mathrm{R}}E\left(q_{\mathrm{R}}\right))$$ (6)

where q_L and q_R are the left and right branch nodes, E(q_L) and E(q_R) are the corresponding entropies, p_L and p_R are the proportions of classes at the internal node q. The process is continued recursively till all the objects (data points) in the training dataset are assigned to the terminal (leaf) nodes.

5.2. Tree pruning

The tree generated in the process may become unnecessarily complex to perfectly classify the training dataset. It may lead to an over-fit model with a perfect classification in training but may have less acceptable classification performance in the unknown test dataset. This may be the case especially if the training dataset is ‘noisy’ or if it is not large enough to represent the test dataset. To avoid the over-training, the generated tree is pruned by removing the nonessential terminal branches based on cost-complexity without affecting the classification accuracy [32]. DT leads to a set of easily interpretable rules starting from the root to each terminal node (leaf) for predicting a class.

6. Results and discussion

Datasets were analyzed first using logistic regression for identifying the predictors of PVL occurrence. Next, the independence of ‘predictors’ was investigated through statistical correlation analysis. The classification results were obtained using the LR identified ‘predictor’ variables. Then, the datasets were analyzed using the decision tree induction algorithm for identifying the ‘predictors’ of PVL. Finally, the results of PVL prediction were compared using variables selected by DT and LR.

6.1. Stepwise forward regression

Three sets of data (Cases 1–3) were analyzed through stepwise logistic regression in SPSS for identifying the predictors for PVL. Table 2 shows the coefficient (B), standard error (S.E.) and significance level (p-value) for each of the selected predictors (with p < 0.05). For each case, two sets of ‘predictors’ were selected. In the intermediate stage, four statistically significant predictors were used in each case for comparison. Numbers of features retained finally were 5, 3 and 7 in Cases 1–3, respectively. In Case 1, the predictors represent the values of the monitoring variables at the recorded hours. For example, SBP32 represents systolic blood pressure (SBP) recorded at the 32nd hour. For Case 1 dataset, the retained variables include low values for SBP32, DBP at 4th, 40th and 44th hours, and pO₂ at 40th hour (each with p < 0.05) with regression coefficients (B) of −0.120, −0.138, 0.208, −0.254 and −0.068, respectively. The negative regression coefficients of the retained variables agreed well with the fact that the probability of PVL occurrence increases with any decrease in the values of these variables. However, the interpretation of the probability in terms of 4-hourly variables was not straightforward. It especially was difficult to justify the positive coefficient for DBP40 when all other coefficients were negative.

Table 2.

Logistic regression of each predictor on PVL separately.

Dataset	Number of predictors	Predictor	B	S.E.	p
Case 1	4	SBP32	−0.093	0.032	0.004
		DBP40	0.160	0.065	0.014
		DBP44	−0.258	0.086	0.003
		pO240	−0.064	0.019	0.001
	5	SBP32	−0.120	0.038	0.002
		DBP4	−0.138	0.058	0.017
		DBP40	0.208	0.071	0.003
		DBP44	−0.254	0.089	0.004
		pO240	−0.068	0.021	0.001
Case 2	4	SBPmin	−0.095	0.031	0.002
		DBPadm	−0.063	0.029	0.029
		DBPmin	−0.085	0.056	0.128
		pO2min	−0.036	0.018	0.047
	3	SBPmin	−0.108	0.030	0.000
		DBPadm	−0.079	0.028	0.004
		pO2min	−0.041	0.018	0.024
Case 3	4	HRskw	−0.885	0.339	0.009
		SBPmin	−0.090	0.032	0.005
		DBPadm	−0.090	0.030	0.003
		DBPmin	−0.089	0.054	0.102
	7	HRskw	−1.019	0.382	0.008
		SBPmin	−0.170	0.045	0.000
		SBPskw	1.282	0.477	0.007
		DBPadm	−0.126	0.034	0.000
		DBPskw	−1.741	0.538	0.001
		pCO2krt	0.410	0.172	0.017
		pO2krt	−0.329	0.130	0.011

For Case 2 dataset, the selected features were SBP_min, DBP_adm and pO_2min, each with negative regression coefficient (B) as expected. The retained variables (SBP, DBP and pO₂) agreed qualitatively with [4], with some differences in details. For example, in [4], the retained features were SBP_adm, DBP_min and pO_2min. The difference may be attributed to the consideration of other variables like support time, age at surgery. In [4], the diastolic hypotension (DBP_min) was identified as one of the major predictors along with the chronologic age, but not gestational age, at surgery. In the present study DBP_min (with p > 0.05) was eliminated from the final list of independent variables in LR and was replaced with DBP_adm for Cases 2 and 3.

For Case 3 dataset, the finally selected features were HR_skw, SBP_min, SBP_skw, DBP_adm, DBP_skw, pCO_2krt and pO_2krt, each with negative regression coefficient except for SBP_skw and pCO_2krt. The positive regression coefficient for SBP_skw (pCO_2krt) may be explained in terms of skewed (peaked) pattern of SBP (pCO₂) rather than its average value. The inclusion of pCO₂ in the set of selected variables was interesting and needed further examination as the phenomenon of hypocarbia (low pCO₂) was associated with PVL in prior reports [35,36], and is consistent with the known physiologic effect of hypocarbia on cerebral blood flow. This issue is discussed further in a later section. It should also be noted that some of the variables (SBP, DBP and pO₂) were selected in all three cases though the characteristic details differed. This further confirmed the importance of these variables as ‘predictors’ of PVL.

6.2. Correlation analysis

To study the independence of the retained features, statistical correlation was analyzed in SPSS for each of the datasets. Table 3(a)–(c) show correlations among the variables along with the significance level. For Case 1 dataset, Table 3(a), many of the variables were found to have statistically significant correlation (with p < 0.05). For example, DBP4 was statistically correlated to all other variables, similarly SBP and DBP were also correlated. For Case 2 dataset, Table 3(b), DBP_min was found to be correlated with SBP_min, DBP_adm and pO_2min. This could explain the elimination of DBP_min from the final list of ‘predictors’ in Table 2. In addition, pO_2min was found to be correlated with DBP_adm and DBP_min. The correlations are consistent with results reported in [4]. For Case 3 dataset, Table 3(c), only two variables SBP_skw and DBP_skw showed statistically significant correlation. This implies that the features in Case 3, not being correlated to each other, were better suited for predicting the occurrence of PVL than the datasets of Cases 1 and 2.

Table 3.

Correlations of predictors for different datasets (a) Case 1, (b) Case 2, (c) Case 3.

		SBP32	DBP40		DBP44	pO240		DBP4
(a)
SBP32	Pearson correlation	1	.263(**)		.295(**)	−0.208		.197(*)
	Sig. (two-tailed)		.008		.003	.051		.046
DBP40	Pearson correlation		1		.592(**)	.188		.404(**)
	Sig. (two-tailed)				.000	.079		.000
DBP44	Pearson correlation		Symmetric		1	.310(**)		.527(**)
	Sig. (two-tailed)					.003		.000
pO240	Pearson correlation					1		.366(**)
	Sig. (two-tailed)							.000
DBP4	Pearson correlation							1
	Sig. (two-tailed)
			SBPmin	DBPadm		DBPmin		pO2min
(b)
SBPmin	Pearson correlation		1	.135		.421(**)		−0.147
	Sig. (two-tailed)			.176		.000		.139
DBPadm	Pearson correlation			1		.511(**)		.368(**)
	Sig. (two-tailed)					.000		.000
DBPmin	Pearson correlation			Symmetric		1		.273(**)
	Sig. (two-tailed)							.005
pO2min	Pearson correlation							1
	Sig. (two-tailed)
		HRskw	SBPmin	SBPskw	DBPadm	DBPskw	pCO2krt	pO2krt
(c)
HRskw	Pearson correlation	1	.063	−0.036	.130	.036	.040	.037
	Sig. (two-tailed)		.528	.718	.191	.719	.688	.713
SBPmin	Pearson correlation		1	.185	.135	−0.119	−0.134	−0.066
	Sig. (two-tailed)			.062	.176	.235	.179	.507
SBPskw	Pearson correlation			1	.021	.342(**)	−0.130	.018
	Sig. (two-tailed)				0.834	0.000	0.193	0.859
DBPadm	Pearson correlation				1	.114	.123	.068
	Sig. (two-tailed)					.252	.216	.497
DBPskw	Pearson correlation		Symmetric			1	.018	−0.040
	Sig. (two-tailed)						.859	.687
pCO2krt	Pearson correlation						1	−0.011
	Sig. (two-tailed)							.911
pO2krt	Pearson correlation							1
	Sig. (two-tailed)

^*Significance at 0.05 level (p < 0.05).

^**Significance at 0.01 level (p < 0.01).

6.3. Receiver operating characteristic (ROC) curve

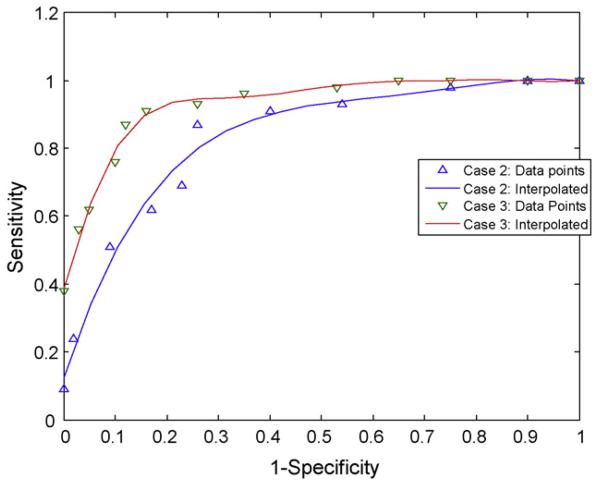
The selected features were used for classification of PVL incidence (yes or no) in SPSS. The cut-off point was varied from 0.1 to 0.9 in classifying the datasets. The classification success was represented in terms of three commonly used performance indices (PI), namely, sensitivity (SN), specificity (SP) and accuracy (AC) [37]. Sensitivity (SN) defines the proportion of patients with positive outcome that are correctly identified by the used dataset. Specificity (SP) is the proportion of patients with negative outcome that are correctly identified. Accuracy (AC) defines the overall proportion of correctly identified cases including both positive and negative outcomes. In literature, SN and SP are also termed as true positive rate (TPR) and true negative rate (TNR), respectively. Another term, 1-SP, is also known as false positive rate (FPR). To compare the diagnostic capabilities of datasets and test algorithms, the sensitivity (SN) versus (1-specificity or 1-SP) curve, or TPR versus FPR, also commonly known as receiver operating characteristic (ROC) curve [37], are plotted for different values of the cut-off point. The area under the ROC curve (AUROC) is used as a measure of diagnostic capability of the dataset. For a perfect diagnostic dataset, AUROC will be 1 with a horizontal line at SN = 1 for all values of (1-SP) whereas using a random guess about the outcome would have an AUROC of 0.5 corresponding to a straight line between (0, 0) and (1, 1) on the ROC. Receiver operating curves were plotted for Cases 2 and 3, as shown in Fig. 1, giving AUROC of 0.796 and 0.886, respectively. The higher AUROC value of Case 3 signifies better diagnostic capability of the Case 3 dataset than Case 2.

Figure 1.

ROC curve for logistic regression analysis.

6.4. Classification success

Table 4 shows the classification results for three cases of datasets without decision tree (DT). In all three cases, higher number of features gave better classification results (in terms of SN, SP and AC). For example, the Case 1 dataset using five features (corresponding to second group in Table 1) gave SN, SP and AC of 83, 79 and 81%, respectively. Dataset with seven selected features (Case 3) gave the best performance of 87, 88 and 87% for SN, SP and AC, respectively which are within the acceptable range of 80–90%. The better performance of Case 3 dataset can be attributed to the fact that the features were without any significant correlation, Table 3(c). The better classification success for Case 3 dataset can also be demonstrated in the higher value of area under ROC (AUROC), Fig. 1.

Table 4.

Classification results with LR identified predictors.

Dataset	Number of predictors	Classification success (%)
		SN	SP	AC
1	4	78	77	77
	5	83	79	81
2	4	76	81	78
	3	69	77	74
3	4	80	83	81
	7	87	88	87

6.5. Results of decision tree

The entire datasets in Cases 2 and 3 were used for training DTs to compare the classification success of DT and LR. Next, the training datasets of Cases 2 and 3 were used for training DTs with and without LR selected features. Prediction results of the trained DTs were compared using the corresponding test datasets.

6.5.1. Classification results with decision tree

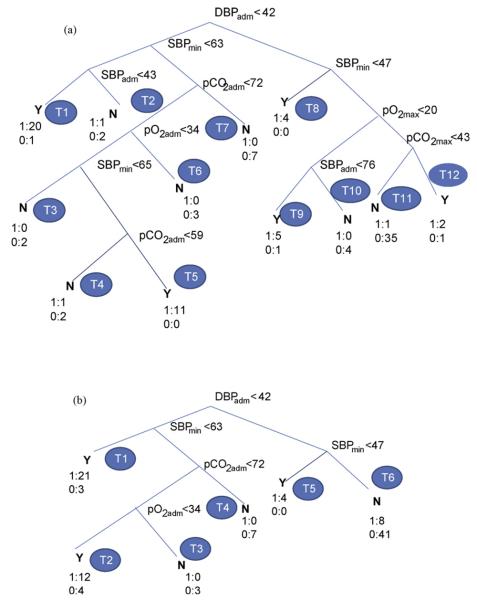
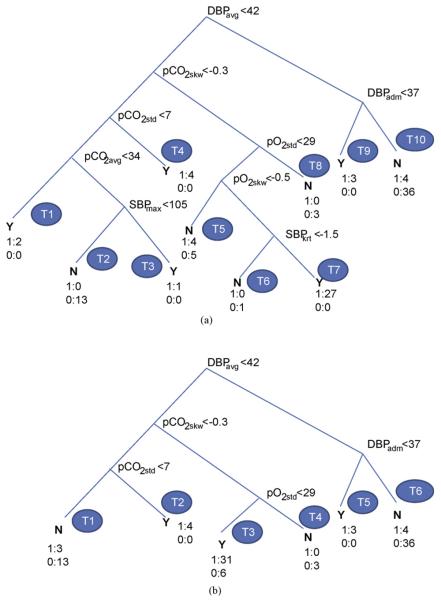
Fig. 2(a) shows the decision tree obtained from the full dataset of Case 2 with DBP_adm, SBP_min, SBP_adm, pCO_2adm, pCO_2max, pO_2adm and pO_2max as the retained features. These included the features selected using LR (Case 2, Table 2) with additional contributions from pCO₂. Fig. 3(a) shows the corresponding decision tree for Case 3 dataset with selected features as DBP_adm, DBP_avg, SBP_max, SBP_krt, pCO_2avg, pCO_2skw, pCO_2std, pO_2std and pO_2skw. It should be mentioned that each tree structure, in terms of the nodal variables and their threshold values, was obtained automatically as an output of the DT algorithm using the principle of maximum information-gain explained in Section 5.1.

Figure 2.

Decision tree with Case 2 dataset: (a) full, (b) pruned (level 2).

Figure 3.

Decision tree with Case 3 dataset: (a) full, (b) pruned (level 2).

The inclusion of pCO₂ in the selected set of variables for both datasets (Cases 2 and 3) confirmed its importance in the prediction of PVL. To some extent, pCO₂ can be measured and controlled in the postoperative care setting, and inclusion here as a variable may indicate its potential role as a modifiable factor in neurodevelopmental outcome. The selection of pCO₂ as one of the potentially modifiable postoperative risk factors for prediction of PVL occurrence is a very interesting finding of the present study. The identification of an extended set of postoperative prognostic factors (including pCO₂) in decision trees is attributed to the better capability of the information-theory-based DT algorithm than the LR technique. The relative importance of the identified postoperative risk factors for PVL prediction needs to be investigated next.

In the DT of Fig. 2(a), the root, DBP_adm represents the most important variable followed by SBP_min. The nodal variables far away from the root have less significance in classifying the data. Rules can be extracted simply following the nodal relations along the tree branches from the root to the terminal nodes (leaves), T1—T12. Each leaf represents a class (Y, PVL = 1 or N, PVL = 0) depending on the majority of its class membership. In Fig. 2(a), 12 rules can be generated corresponding to 12 terminal nodes (T1— T12). For example, rules (R1, R2) can be obtained corresponding to the left most two leaves (T1, T2) as follows:

$$R1:\mathit{If}{\mathit{DBP}}_{\mathit{adm}}<42\mathit{and}{\mathit{SBP}}_{\mathit{min}}<63\mathit{and}{\mathit{SBP}}_{\mathit{adm}}<43\mathit{then}\to \mathit{Class}Y(\mathit{PVL}=1)(20∕21\mathit{or}95\%).$$

$$R2:\mathit{If}{\mathit{DBP}}_{\mathit{adm}}<42\mathit{and}{\mathit{SBP}}_{\mathit{min}}<63\mathit{and}{\mathit{SBP}}_{\mathit{adm}}<43\mathit{then}\to \mathit{Class}N(\mathit{PVL}=0)(2∕3\mathit{or}67\%).$$

Similarly, the rules (R11, R12) corresponding to the leaves T11 and T12 can be written as follows:

$$R11:\mathit{If}{\mathit{DBP}}_{\mathit{adm}}>42\mathit{and}{\mathit{SBP}}_{\mathit{min}}>47\mathit{and}{\mathit{pO}}_{2\max }>20\mathit{and}{\mathit{pCO}}_{2\mathit{max}}<43\mathit{then}\to \mathit{Class}N(\mathit{PVL}=0,35∕36\mathit{or}97\%)$$

$$R12:\mathit{If}{\mathit{DBP}}_{\mathit{adm}}>42\mathit{and}{\mathit{SBP}}_{\mathit{min}}>47\mathit{and}{\mathit{pO}}_{2\max }>20\mathit{and}{\mathit{pCO}}_{2\mathit{max}}<43\mathit{then}\to \mathit{Class}Y(\mathit{PVL}=1,2∕3\mathit{or}67\%)$$

It is interesting to note a curious association in the two rules above, where pCO_2max rising above 43 mm Hg would seem to make the patients more likely, rather than less likely, to have PVL. Although the design of this study prevents definitive ascertainment, the postoperative management style in use during the study period tended to value lower pCO₂ to decrease pulmonary vasoreactivity. Patients in the dataset with higher pCO₂ may have had issues with their ventilatory support leading to altered neurological susceptibility.

Similarly other eight nodes can be followed to extract the remaining rules which are easy to interpret. The complete set of rules is presented in Table 5(a). It is worth mentioning that the full DT, in an attempt to perfectly classify a training dataset, may include nonessential terminal branches leading to possible `over-fitting' as explained earlier (in Section 5.2). The rules R11 and R12 are results from such `nonessential' terminal branches. To simplify the tree structure without reducing significantly the classification success, the full DT was pruned automatically to level 2 as in Fig. 2(b). In the pruning process, the original terminal nodes T1 and T2 of Fig. 2(a) were combined as T1; T3—T6, as T2; and T9—T12, as T6 in Fig. 2(b). Other terminal nodes of Fig. 2(a), T6— T8 were renumbered as T3—T5, respectively. The DT of Fig. 2(b) resulted in six decision rules corresponding to six terminal nodes (T1—T6) as given in Table 5(b). One of these rules, R2 can be written as follows:

$$R2:\mathit{If}{\mathit{DBP}}_{\mathit{adm}}<42\mathit{and}{\mathit{SBP}}_{\mathit{min}}>63\mathit{and}{\mathit{pCO}}_{2\mathrm{adm}}<72\mathit{and}{\mathit{pO}}_{2\mathit{max}}<34\mathit{then}\to \mathit{Class}Y(\mathit{PVL}=1)(12∕16\mathit{or}75\%).$$

Table 5.

Decision rule sets for DT with Case 2 dataset (a) full, (b) pruned (level 2).

Rule #	If DBPadm (mm Hg)	and SBPmin (mm Hg)	and SBPadm (mm Hg)	and pCO2adm (mm Hg)	and pCO2max (mm Hg)	and pO2adm (mm Hg)	and then pO2max (mm Hg)	Class Y(1)/ N(0)	Class/ total	Membership %
(a)
1	<42	<63	<43					Y	20/21	95
2	<42	<63	>43					N	2/3	67
3	<42	>63		<72		<34		N	2/2	100
		<65
4	<42	>65		<59		<34		N	2/3	67
5	<42	>65		<72		<34		Y	11/11	100
				>59
6	<42	>63		<72		>34		N	3/3	100
7	<42	>63		>72				N	7/7	100
8	>42	<47						Y	4/4	100
9	>42	>47	<76				<20	Y	5/6	83
10	>42	>47	>76				<20	N	4/4	100
11	>42	>47			<43		>20	N	35/36	97
12	>42	>47			>43		>20	Y	2/3	67
Rule #	If DBPadm (mm Hg)		and SBPmin (mm Hg)	and pCO2adm (mm Hg)		and then pO2adm (mm Hg)	Class Y(1)/ N(0)	Class/ total		Membership %
(b)
1	<42		<63				Y	21/24		88
2	<42		>63	<72		<34	Y	12/16		75
3	<42		>63	<72		>34	N	3/3		100
4	<42		>63	>72			N	7/7		100
5	>42		<47				Y	4/4		100
6	>42		>47				N	41/49		84

In this rule, the PVL occurrence is predicted when the admission values of DBP, pCO₂ and pO₂ fall below the corresponding threshold values, even if SBP_min is above 63 mm Hg. In rule R3, no occurrence of PVL is predicted if pO_2adm is higher than 34 mm Hg even if the admission values of DBP and pCO₂ are below the corresponding threshold values. This points to the fact that the prediction of PVL occurrence depends on the combination of variables and their values rather than the individual variables. This agrees well with literature on variable and feature selection [38].

The decision tree of Fig. 3(a) corresponds to the Case 3 dataset of extracted features with 10 rules corresponding to 10 leaf nodes (T1—T10). Table 6(a) shows the complete set of decision rules obtained from DTof Fig. 3(a). The first rule (R1) corresponding to the node T1 on the left can be written as follows:

$$\mathit{If}{\mathit{DBP}}_{\mathit{avg}}<42\mathit{and}{\mathit{pCO}}_{2\mathrm{skw}}<-.3\mathit{and}{\mathit{pCO}}_{2\mathrm{sd}}<7\mathit{and}{\mathit{pCO}}_{2\mathrm{avg}}<34\mathit{then}\to \mathit{Class}Y(\mathit{PVL}=1,2∕2\mathit{or}100\%)$$

Table 6.

Decision rule sets for DT with Case 3 dataset (a) full, (b) pruned (level 2).

Rule #	If DBPavg (mm Hg)	and pCO2skw	and pCO2std (mm Hg)	and pCO2avg (mm Hg)	and SBPmax (mm Hg)	and pO2std (mm Hg)	and pO2skw	and SBPkrt	and then DBPadm (mm Hg)	Class Y(1)/ N(0)	Class/ total	Membership %
(a)
1	<42	<−0.3	<7	<34						Y	2/2	100
2	<42	<−0.3	<7	>34	<105					N	13/13	100
3	<42	<−0.3	<7	>34	>105					Y	1/1	100
4	<42	<−0.3	>7							Y	4/4	100
5	<42	>−0.3				<29	<−0.5			N	5/9	56
6	<42	>−0.3				<29	>−0.5	<−1.5		N	1/1	100
7	<42	>−0.3				<29	>−0.5	>−1.5		Y	27/27	100
8	<42	>−0.3				>29				N	3/3	100
9	>42								<37	Y	3/3	100
12	>42								>37	N	36/40	90
Rule #	If DBPavg (mm Hg)		and pCO2skw	and pCO2std (mm Hg)		and pO2std (mm Hg)	and then DBPadm (mm Hg)		Class Y(1)/ N(0)	Class/ total		Membership %
(b)
1	<42		<−0.3	<7					N	13/16		81
2	<42		<−0.3	>7					Y	4/4		100
3	<42		>−0.3			<29			Y	31/37		84
4	<42		>−0.3			>29			N	3/3		100
5	>42						<37		Y	3/3		100
6	>42						>37		N	36/40		90

In other words, the rule (R1) corresponds to the condition of diastolic hypotension and hypocarbia. Remaining nine rules can be obtained from the other nine leaf nodes (T2—T10). The DT of Fig. 3(a) was pruned at level 2 to have a simpler DT of Fig. 3(b) with six terminal nodes (T1—T6) and five retained variables (DBP_adm, DBP_avg, pCO_2skw, pCO_2std and pO_2std). The complete rule set corresponding to six terminal nodes are given in Table 6(b). The importance of pCO₂ levels and temporal variation, among other variables like DBP, pO₂ on PVL prediction is evident from the DTs of Fig. 3(a) and (b) and the corresponding rule sets, Table 6(a) and (b).

The classification results are presented in Table 7 for full and pruned DTs in each case. The full DTwith six features in Case 2, and eight features in Case 3 gave the same overall accuracy, although they had some variations in sensitivity and specificity. With pruning, classification results were better with the Case 3 dataset than Case 2. The classification results of full DTwere better than LR analysis for datasets of both Cases 2 and 3. The better performance of the DT may be attributed to the higher number of features retained in DT than in LR. In Table 7, classification results are presented for a typical run of decision tree training. Next, `leave-oneout' strategy of training and testing the decision trees was used for the entire set giving an average accuracy of 93% in training and 58% in test. These values were similar to the representative results presented in Table 7.

Table 7.

Classification results with DT identified predictors.

Dataset	Decision tree	Number of predictors	Classification success (%)
			SN	SP	AC
2	Full	6	89	95	92
	Pruned (level 2)	4	82	88	85
3	Full	8	82	100	92
	Pruned (level 2)	5	84	90	87

6.5.2. Prediction results with decision tree

Next, decision trees were trained using the training datasets of Cases 2 and 3 and tested using the corresponding test datasets. Table 8 shows training and test results for full and pruned (at level 2) decision trees. Training results were good with a sensitivity of 73—93%, specificity of 97—100% and accuracy of 87—96%. However, test results deteriorated with sensitivity of 27—53%, specificity of 74— 90% and accuracy of 62—65%. One of the probable factors for lower test performance may be the limited size of the training dataset to represent the test cases. The lower test results may also be due to the inherent characteristics of the conventional DTs with fixed boundaries [39,40]. The issue of improvement in DT test performance needs further consideration.

Table 8.

Classification results of decision tree with no LR.

Dataset	Number of features	Training success (%)			Test success (%)
		SN	SP	AC	SN	SP	AC
Case 2	6	93	97	96	53	74	65
	4	73	97	87	27	90	65
Case 3	8	90	100	96	40	79	62
	5	83	97	91	33	90	65

6.5.3. Decision tree results with LR selected features

The selected features from the logistic regression analysis for Cases 2 and 3 were used as inputs to the decision tree algorithm for classification. In each case, the training dataset was used to train the decision tree and next, the trained decision tree was tested using the test dataset. The classification success results are shown in Table 9. Training results were reasonably good with a sensitivity of 83—90%, specificity of 82—97%, accuracy of 83—94%. Test results were worse with a sensitivity of 33—80%, specificity of 58—90%, and accuracy of 65%. Test results for Case 3 with seven features gave very low sensitivity and reasonably good specificity.

Table 9.

Classification results of decision tree with LR identified predictors.

Dataset	Number of features	Training success (%)			Test success (%)
		SN	SP	AC	SN	SP	AC
Case 2	4	87	97	93	80	58	65
	3	83	82	83	53	74	65
Case 3	7	83	92	88	33	90	65
	5	90	97	94	73	58	65

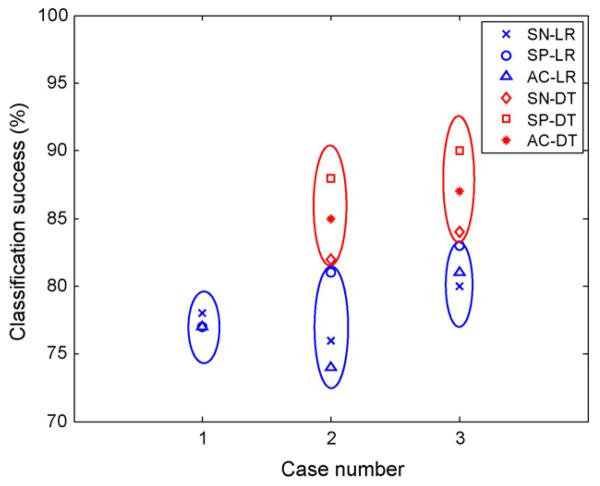
6.6. Comparison of LR and DT

For ease of comparison, the classification results of LR and DT with four selected features for each (except Case 3 DT with five predictors) are shown in Fig. 4. Case 3 dataset gave better classification success than Case 2 for both LR and DT. In either case, DT gave better results than LR. The number of selected features was greater in full DT than LR for Case 2 and 3 datasets, though the selected variables were similar. DT gave better classification success than LR when the entire datasets were used (Tables 4 and 7). For example, best overall classification accuracy was 87% and 92% for LR and DT, respectively with Case 3 dataset. Comparison of Tables 8 and 9 shows slightly better training results with DT selected features than with LR. Test results were similar for both cases with DTand LR. However, the statistical significance of the difference in prediction success needs to be investigated further with larger datasets. In comparison to [4], the automatic selection of pCO₂ in both LR and DT as one of the significant variables in prediction of PVL was encouraging and confirmed the association of hypocarbia with PVL. The role of pCO₂ along with other prognostic variables in the prediction of PVL is further investigated in Part II.

Figure 4.

Comparison of classification success of LR and DT for different datasets.

7. Limitations

The archive of postoperative monitoring data used for this analysis has significant limitations. Waveform data in the ICU is typically sampled at 500 Hz and parametric data is typically sampled at 2—0.001 Hz. ICU nurses typically sample the parametric and waveform data once an hour (0.0003 Hz) with a handwritten line entry on a paper flowsheet. This dataset involved a further reduction with values recorded every 4 h.

However, reducing the sampling rate is not without clinical value at the bedside. Use of a low-frequency sampling rate is less resource intense than higher frequency capture systems which can involve additional computational and analytic expense. Also, our low-frequency system necessarily incorporates artifact and noise filters incorporated in the judgment and experience of CHOP's professional nursing staff. Low-frequency sampling is also easier for the brain to `process' for more rapid decision analysis for patient care. However, high-frequency data would be useful for computer-aided analysis.

8. Conclusions

This analysis presents results of investigations on the applicability of logistic regression and decision tree algorithms for prediction of PVL using the postoperative hemodynamic and arterial blood gas data. The process involved statistical feature extraction, feature selection using logistic regression and generation of classification rules using the decision tree. The use of a reduced number of features through LR and DT based selection process made the rules quite tractable. Although satisfactory, the test success of the decision tree would be even better if the datasets were less limited; the hard boundaries used in conventional decision tree algorithm could also limit the success of the algorithm. The issues of more extensive dataset and improvement of test success in DT will be considered in future work.

This analysis serves to confirm earlier work done in [4] where Galli et al. found an association between incidence of PVL and postoperative hypoxemia and diastolic hypotension. Additionally, the association of PVL incidence with variation in pCO₂ provides interesting information that is the subject of ongoing work in the authors' centers. From a clinician's point of view, use of decision tree analysis may provide an interesting surrogate for the clinical thought process, and it may suggest novel areas of future study to better understand ways that postoperative care can be manipulated to improve outcome.

In this analysis, commonly measured parameters at the bedside of critically ill neonates and infants were evaluated correlating these measurements with a surrogate predictor of neurological outcome. While important, these measurements represent only a small fraction of critical data available using current monitoring technology. Potential use of these analytic techniques include improved neurological outcomes as mentioned above, but may also be applied to reducing the frequency of hospital-acquired infections, predicting cardiac arrest, reducing hospital length of stay and cost, and many others. We are currently exploring techniques for higher resolution ICU data capture and analysis. In addition, the refinement of the prognostic factors will be considered using a direct information theoretic approach.