Abstract
Segregation of the R1 plasmid in bacteria relies on ParM, an actin homolog that segregates plasmids by switching between cycles of polymerization and depolymerization. We find similar polymerization kinetics and stability in the presence of either ATP or GTP and a 10-fold affinity preference for ATP over GTP. We used electron cryo-microscopy to evaluate the heterogeneity within ParM filaments. In addition to variable twist ParM has variable axial rise, and both parameters are coupled. Subunits in the same ParM filaments can exist in two different structural states, with the nucleotide-binding cleft closed or open, and the bound nucleotide biases the distribution of states. The interface between protomers is different between these states, and in neither state is it similar to F-actin. Our results suggest that the closed state of the cleft is required but not sufficient for ParM polymerization, and provide a structural basis for the dynamic instability of ParM filaments.
Keywords: electron microscopy, helical polymers, cytoskeletal filaments
INTRODUCTION
Bacterial survival in an environment containing fungi and heavy metal ions depends on plasmids - extra-chromosomal DNA molecules capable of replicating independently of the host genome. High-copy number plasmids are separated randomly in bacteria, while low-copy number plasmids require an active mechanism of segregation to preserve the maintenance of plasmids in daughter cells following division. Most of our knowledge about plasmid DNA partitioning comes from studies on the large low-copy number plasmid R1 (Nordstrom et al., 1980). The stability operon par encodes three components sufficient for plasmid segregation: parR, and parM genes along with the cis-acting locus, parC (Gerdes et al., 1986). The current model for type II partitioning assumes that ParR binds cooperatively to several repeats of the parC locus while ParM bound to ParR pushes the two newly formed plasmids to the opposite poles of the bacterial cell via ATP-dependent polymerization (Moller-Jensen et al., 2003;Salje et al., 2008;Campbell et al., 2007;Choi et al., 2008). Sequence analysis of ParM (Jensen et al., 1997). has revealed a set of common conserved residues found in the actin superfamily of proteins (Bork et al., 1992), while the crystal structure of ParM unambiguously showed ParM to be a bacterial actin homolog (van den Ent et al., 2002). Nevertheless, alignment of the crystal structures of actin and ParM reveals that regions of actin involved in subunit-subunit interactions within the filament (Oda et al., 2009) are very different from ParM (van den Ent et al., 2002). This coincides with the finding that in contrast to the F-actin right-handed two-start helix, ParM forms a left-handed two start helix (Orlova et al., 2007;Popp et al., 2008) caused by the different subunit-subunit interfaces. It is likely that the structural differences in filament organization between F-actin and ParM result in the substantial differences observed between the polymerization properties of these proteins. ParM nucleates 300 times faster than actin and grows from both ends with the same rate (Garner et al., 2007). Importantly, ParM filaments are dynamically unstable and, upon ATP hydrolysis, can switch from elongation to rapid shortening (Garner et al., 2004). Such instability is crucial for plasmid partitioning, as ParM mutants with reduced ATPase activity in vitro are non-functional in vivo (Jensen et al., 1997). The filaments capped with the ParR/ParC complex are stable and can grow to be long in the cell (Campbell et al., 2007). The ParR/ParC complex may bind to the side of ParM and remain attached to the ATP cap of the growing filament, preventing the dissociation of the cap (Choi et al., 2008). Alternatively, the ParR/ParC complex may form a protective cap on the end of the filament to maintain its integrity via a processive polymerization mechanism (Salje et al., 2008).
However, the structure of the ParM filament is still controversial, and it has been suggested that the intersubunit contacts in ParM are similar to those in F-actin (Popp et al., 2008;Lowe et al., 2009). We show that the ParM filament has both variable twist and variable axial rise, and subunits can coexist within the same filament in two structural states – with the nucleotide cleft closed or open. These states are not simply related to the bound nucleotide, as both states may be found with the same nucleotide bound. However, the nucleotide biases the distribution of states, with ATP shifting the distribution towards the closed state while ADP-Pi shifts the equilibrium towards the open form.
RESULTS
Comparison of negatively stained and frozen hydrated ParM filaments formed in the presence of AMP-PNP and GMP-PNP
A recent paper (Popp et al., 2008) has used x-ray fiber diffraction and negative stain EM to study ParM filaments, and arrived at very different results from the cryo-EM structure that we published (Orlova et al., 2007). Since Popp et al. used GMP-PNP (a non-hydrolyzable analog of GTP) while we used AMP-PNP (a non-hydrolyzable analog of ATP) for our studies, we performed an extensive analysis of the cryo-EM as well as negatively stained ParM filaments formed in the presence of AMP-PNP or GMP-PNP (Figure 1). The overall reconstruction of the ParM-AMP-PNP filaments from cryo-EM (Figure 1B) was very similar to that derived from the negatively stained filaments (Figure 1D). Unexpectedly, we found that the new reconstruction of cryo-EM ParM-AMP-PNP filaments (Figure 1B) was significantly different from the original reconstruction (Orlova et al., 2007). The nucleotide-binding cleft was closed (Figure 1B) similar to that observed in the negatively stained reconstructions (Figure 1D,F). An examination of the original data revealed a mistake in the way the Contrast Transfer Function (CTF) was corrected in those images. This led to an error in the phases of the images, resulting in an artefactual reconstruction.
Figure 1.
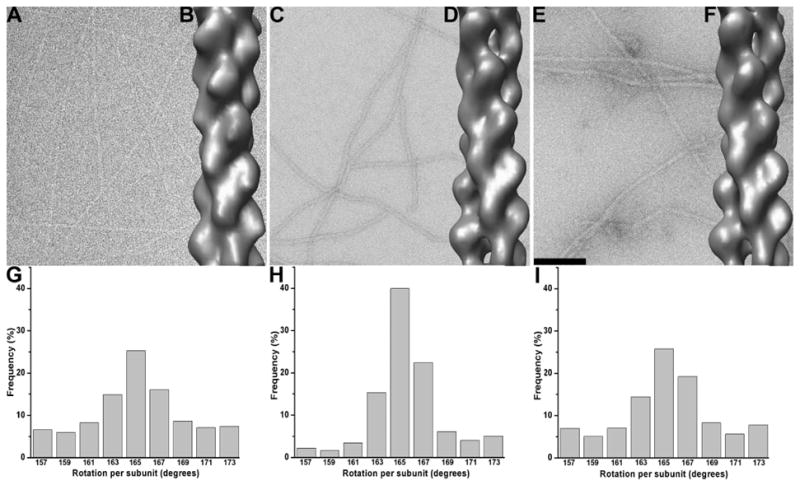
EM images of ParM filaments in the presence of AMP-PNP and GMP-PNP with corresponding global reconstructions and twist distributions. (A) Frozen hydrated and (C) negatively stained ParM filaments polymerized in the presence of AMP-PNP. (E) Same as (C), but with GMP-PNP rather than AMP-PNP. The global 3D reconstructions derived from the segments in A, C and E are shown as solid surfaces in B,D, and F, respectively. Twist distributions of frozen hydrated (G) and negatively stained (H) AMP-PNP ParM filaments. (I) Twist distribution of the GMP-PNP negatively stained ParM. The scale bar in (E) is 1,000Å.
Negatively stained ParM filaments formed in the presence of AMP-PNP (Figure 1C) look similar to the filaments polymerized in the presence of GMP-PNP (Figure 1E), which is consistent with the similarity of the two respective overall reconstructions (Figure 1D,F). Both reconstructions are similar to the reconstruction of ParM-GMP-PNP filaments from Popp et al. (2008). The only difference that we observe between the negatively stained filaments is a slight increase in the twist heterogeneity in the presence of GMP-PNP (Figure 1I) compared to that found in the presence of AMP-PNP (Figure 1H). In the presence of AMP-PNP we observed a slight increase in the variance of twist in the cryo set (Figure 1G) compared to that found with negative stain (Figure 1H), but this may reflect a lower signal to noise ratio in the frozen hydrated sample.
Solution Studies with ATP versus GTP
In agreement with Popp et al. (2008) we find that addition of GTP induces polymerization of ParM filaments. To rule out any effects of labeling with fluorescent dyes we used unlabeled ParM and monitored polymerization by light scattering. At steady state, the apparent critical concentrations of GTP and ATP ParM are approximately equal (not shown). To determine the affinities of ParM for ATP and GTP we performed competition binding experiments using a fluorescent derivative of ATP (etheno-ATP). To prevent polymerization during the experiment we used a ParM concentration of 0.4 μM, well below the ATP critical concentration. Competition with unlabeled ATP yielded a dissociation equilibrium constant of 0.9 μM, which is somewhat weaker than the affinity we measured for etheno-ATP (Garner et al., 2004). Competition with GTP yielded a value of 11.6 μM, indicating that, as in all other actin family proteins studied to date, the nucleotide binding pocket of ParM accommodates ATP more readily than GTP (Figure 2A).
Figure 2.
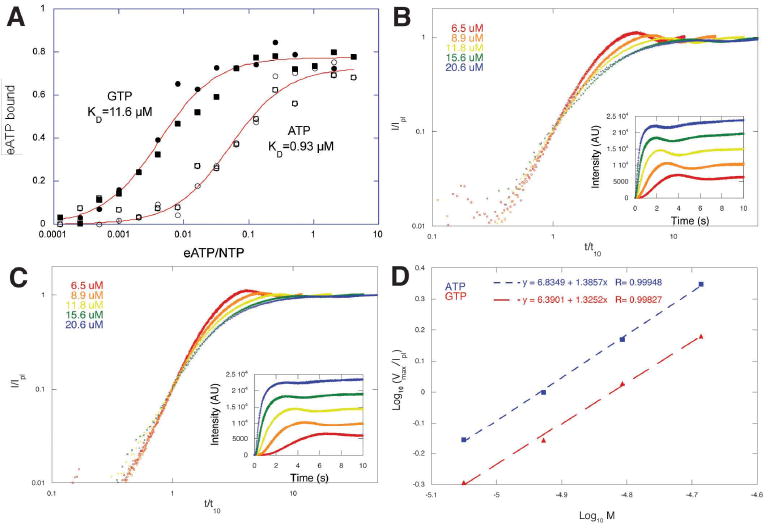
ParM accomodates ATP and GTP. (A) Competition of etheno-ATP away from ParM by ATP and GTP. The affinity of ParM for ATP (Kd=0.9 μM) is more than 10-fold higher than for GTP (Kd=11.6 μM). The experiment was performed three times with identical results. Conditions: Buffer: 100 mM KCl, 1 mM MgCl2, 10 mM Hepes, pH 7.0. Temperature: 24°C. (B) Assembly of five different concentrations of R1 ParM initiated by addition of 5 mM ATP. (C) Assembly of the same concentrations of ParM initiated by addition of 5 mM GTP. Polymerization was monitored by right angle light scattering and the amplitude of the light scattering signal normalized to the value at plateau. Time scale were normalized to the time required to reach 10% of the plateau value. Insets: raw data before normalization. The similarity of the slopes of the curves at early time points indicates that, in each case, the nucleation mechanism is the same at all concentrations tested. (D) Log-log plot of the normalized maximum velocity of polymerization versus ParM concentration. The identical slopes argue that the mechanism of nucleation is the same in both cases. The offset between the lines suggests that spontaneous nucleation is sligthly faster in the presence of ATP.
In rapid mixing experiments at high nucleotide concentrations (5 mM), GTP-ParM filaments assemble rapidly and spontaneously (Figure 2B and 2C) but slightly slower than ATP-ParM filaments. The rate of polymer assembly at early time points and the concentration dependence of the maximum rate of assembly (Figure 2D) both indicate that GTP ParM assembles via the same mechanism as ATP ParM and with the same apparent nucleus size of 3 monomers (Flyvbjerg et al., 1996;Nishida et al., 1983). The slower rate of assembly of GTP filaments is consistent with a slower rate of spontaneous nucleation or a slower rate of nucleotide association.
In low concentrations of nucleotide (below 0.5 mM) GTP ParM filaments assemble and spontaneously disassemble in a manner similar to ATP filaments (Figure 3), suggesting that they exhibit a similar nucleotide hydrolysis-dependent dynamic instability. To investigate the polymer dynamics of GTP ParM filaments more carefully we used total internal reflection fluorescence (TIRF) microscopy of Alexa-488-labeled ParM filaments. Under conditions in which we can observe individual filaments, GTP ParM behaves identically to ATP ParM (Figure 3E and 3F). First we re-measured the dynamics of ATP ParM filaments and obtained rate constants for elongation and catastrophic shortening of 2.9±0.8 μM-1sec-1 (n=7) and 149±63 sec-1 (n=5), respectively. These values are within a factor of two of those we measured previously (Garner et al., 2004g). Like ATP filaments, GTP filaments elongate symmetrically with the same rate constant (2.7±0.8 μM-1sec-1; n=16) at each end. After a period of steady elongation, GTP filaments also switch to a phase of rapid shortening with the same rate of disassembly as that of ATP ParM (135±63 sec-1; n=5) (Figure 3F). Upon switching from elongation to shortening, both ATP and GTP filaments disassemble completely. We never observe rescue of shortening ParM filaments either in the presence of ATP (Garner et al., 2004) or GTP (present study). These results differ substantially from those of Popp et al. (2008) and we discuss the discrepancies below.
Figure 3.
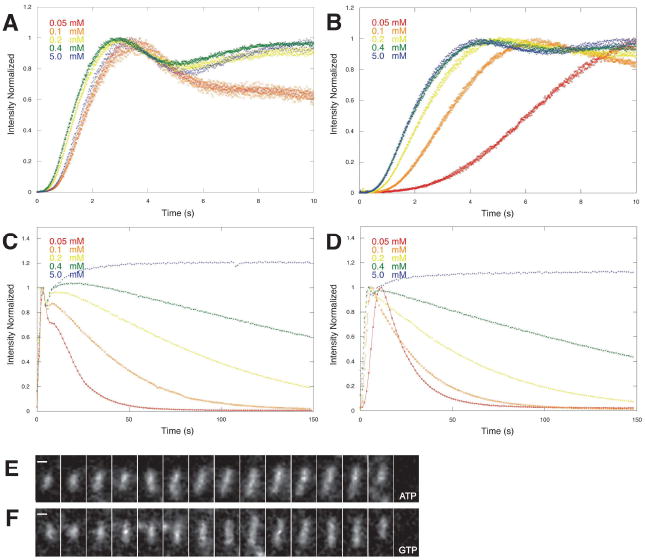
Effects of varying nucleotide concentration on assembly and stability of R1 ParM filaments. Polymerization of 10 μM R1 ParM was initiated by addition of varying amounts of ATP (A, C) or GTP (B, D). For all concentrations between 0.05 mM and 5 mM polymer content reached its maximum value within 10 seconds (A, B). The initial phase of assembly was less sensitive to variations in the concentration of ATP (A) compared to GTP (B), suggesting that the association of GTP is slower than that of ATP. Once assembled, ParM polymer has similar stability at the same concentrations of ATP and GTP (C, D). In 5 mM ATP (C) or GTP (D) the polymer content remains constant for many minutes. At concentrations below 0.5 mM the polymer content decreases significantly within 150 seconds and, at concentrations below 0.1 mM, polymer completely disappears within 120 seconds. TIRF microscopy of ParM filaments assembled in ATP (E) or GTP (F). The rates of elongation and disassembly of individual filaments are identical under the two conditions.
Symmetry of the Filaments
One of the main arguments that Popp et al. made for our original ParM filament model being wrong is that we assigned a symmetry to our filament model that does not match the observed x-ray fiber diffraction patterns. Popp et al. describe the symmetry of their ParM filaments as having 37 subunits in 17 turns of the one-start helix. The repeat, the distance needed to translate a subunit along the axis so that it is in register with another subunit would be 37*(24.5 Å) = 900, where 24.5 Å is the axial rise per subunit. We have argued (Egelman, 2007) that the description of helical symmetry in terms of a repeat is a poor one, as there is no reason that the symmetry of a helical polymer can be best represented by the ratio of relatively small integers. For a helix having a 37/17 symmetry, the rotation between adjacent subunits would be 360°*17/37, or 165.4°. Consider an almost infinitesimal change in the twist of this structure by 0.04° per subunit. The symmetry is now best approximated as having 3,701 subunits in 1,700 turns, with a repeat of 90,675 Å. It is therefore much more useful to simply describe the angle of rotation between subunits, which is a continuously variable parameter.
Popp et al. state that we assigned a symmetry of 31 subunits in 14 turns (162.6°) to our ParM filament model. This is untrue. The header of the PDB file (2QU4) for our ParM model that we deposited and that they used for their simulations states that the rotation needed to generate a filament is 165.4° (the same rotation that they describe). We stated in the text of our paper that in the ParM filament the rotation between every other subunit “is on average approximately -29°”, which would be a rotation of 165.5° between subunits. The consequence of this error in the description of our filament symmetry was that the R-factor between our model and their observed x-ray fiber diffraction pattern was great (0.68), but much of this R-factor simply arises from comparing diffraction patterns having two different sets of spacings. Attempting to match our new three-dimensional reconstruction and filament model with their observed x-ray fiber diffraction pattern (Popp et al., 2008d) has revealed that ParM filaments cannot be described by a single structural state. In fact, we can now show that globally averaged diffraction patterns from ParM filaments, whether from x-ray scattering or cryo-EM, represent a sum of two states.
Subunits in the ParM filament can exist in two different structural states
The global reconstructions of ParM shown in Figure 1B,D,F, as well as from the Maeda group (Popp et al., 2008), are best fit by a subunit having a closed nucleotide-binding cleft. Since ParM has been crystallized in both closed and open forms (van den Ent et al., 2002), we designed two reference volumes composed of protomers having their clefts either closed or open, and arranged into filaments having the same helical symmetry as the global reconstruction (Figure 1B). Surprisingly, almost 20% of segments had the higher correlation with the model having its cleft open (Figure 4A). The reconstructions derived from these two classes (Figure 4A) validated the sorting – no perturbations from the crystal structures of the closed and open states of ParM were needed to fit the crystals into the closed and the open reconstructions (filtered to ~ 20 Å resolution), respectively. The sorting did not introduce any bias into the reconstructions, as both sets of images after sorting were reconstructed using the Iterative Helical Real Space Reconstruction (IHRSR) method (Egelman, 2000) starting from a featureless solid cylinder as an initial model. The IHRSR method has been shown to offer many advantages in the three-dimensional reconstruction of helical polymers that are disordered or heterogeneous (Egelman, 2007). We checked whether segments classified as being in different states came from different filaments, or could be found within the same filaments, by examining the ten longest filaments in our images (data not shown). The conclusion was that all variation (within statistical sampling) was within filaments, and not between filaments.
Figure 4.
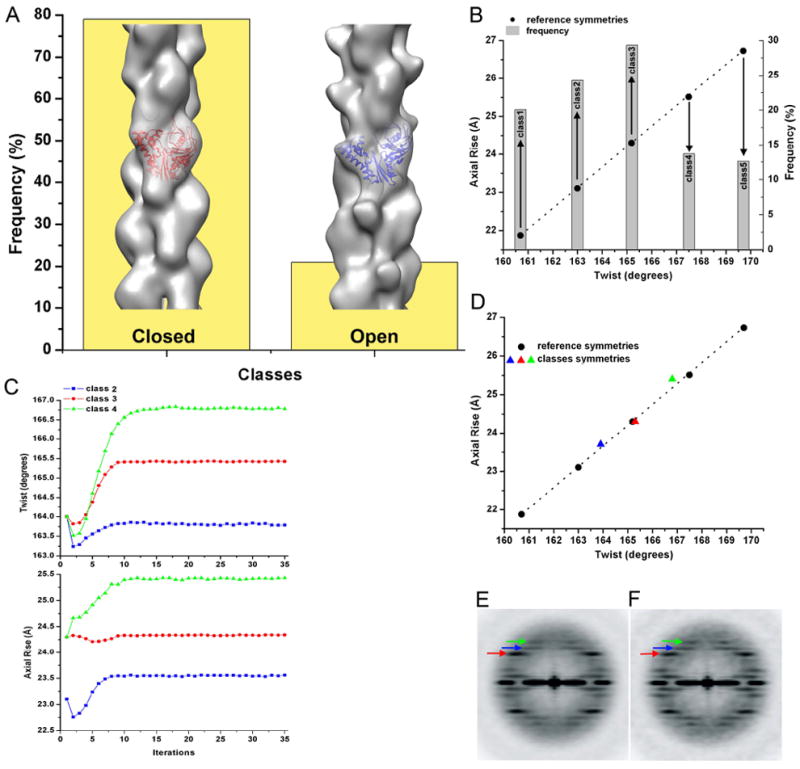
Sorting of frozen hydrated ParM filaments by both the structural state and the helical symmetry. (A) Closed crystal structure (red ribbons, pdb 1MWM) and the open crystal structure (blue ribbons, pdb 1MWK) to generate two reference models (solid surfaces). These models were used to sort out short segments of ParM into classes based on the opening of the nucleotide-binding cleft (yellow bins). (B) Five reference models were designed (see Materials and Methods) to classify closed-cleft segments based on their twist and axial rise. Frequency counts of observed filament segments are shown as grey bins, while black circles represent the corresponding class symmetry. (C) Convergence of classes of images from (B) in the IHRSR procedure validates the sorting shown in (B). (D) The stable solutions after convergence (C) show a strong coupling between the twist and the axial rise. Power spectrum of all closed-cleft segments (E) is compared with the power spectrum from class3 (F), the largest class in (B). Three layer lines are marked with arrows – n=3 is red, n=1 is blue and n=-1 is green. The layer lines from the 1-start helices are stronger in (F) than they are in the global average (E), due to reduced heterogeneity after the symmetry sorting.
Previously, we showed that like F-actin (Egelman et al., 1982), ParM filaments have a variable twist (Orlova et al., 2007). Surprisingly, sorting by the twist did not improve the resolution of the closed ParM reconstruction (data not shown), suggesting that in addition to the variable twist ParM may have other sources of heterogeneity, such as a variable axial rise. The power spectrum of the closed ParM set had a very strong n=3 layer line (Figure 4E, red arrow), while the reflections from the right and left handed 1-start helices were significantly weaker (Figure 4E, blue and green arrows respectively). The power spectrum from the projection of the reconstruction, however, showed significantly stronger 1-start layer lines (Figure 5E, blue and green arrows), revealing a discrepancy with the power spectrum from the images used to generate the reconsruction (Figure 4E). A reasonable explanation is that the pitch of the 3-start helix is less variable than the pitch of the 1-start helices, and such variability would blur the reflections in the averaged power spectrum. The fall in the intensities of layer lines due to the helical disorder has been quantitatively described for F-actin and other helical filaments (Egelman et al., 1982). Reconstructing with the IHRSR method, on the other hand, would tend to align the 1-start helices in spite of their variability, accounting for the discrepancy. To check this possibility we designed five models with a fixed 3-start helical pitch, but with both variable twist and axial rise (see Materials and Methods). The frequency distribution from such a sorting is shown in Figure 4B. The classes 2, 3 and 4 were used in the IHRSR procedure, and converged to the expected symmetry parameters (Figure 4C,D). To validate the sorting independently from the IHRSR method, we calculated the power spectra for these three classes (Supplementary Movie 1). As expected, the position of the 3-start helix layer line in each power spectrum was fixed, while n=1 and n=-1 layer lines positions moved as predicted. A power spectrum from the largest single class (Fig. 4F) shows an enhancement of these 1-start layer lines when compared to the average of the five classes (Fig. 4E), as expected. Thus, there is a very strong correlation between the twist and the axial rise (Fig. 4D), and both show significant variation in ParM filaments.
Figure 5.
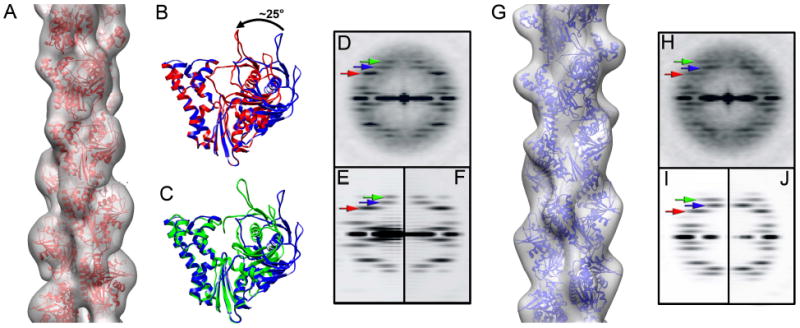
The two pseudo-atomic models of the ParM filament. (A) Reconstruction of the ParM filament in the closed state is filtered to 17 Å resolution, and the corresponding atomic model is shown as red ribbons. (B) The two domains of the APO crystal structure of ParM (blue ribbons) have to be moved towards each other by ~ 25° (red ribbons) to achieve a better fit to the closed state filament (see text for details). (C) The same closing of the nucleotide binding cleft is observed between the APO (blue ribbons) and ADP-bound (green ribbons) crystal structures. Power spectra generated from the raw images (D), and projections of either the three-dimensional reconstruction (E) or the corresponding atomic model of the closed filament (F). Three layer lines are marked with arrows: n=3 is red, n=1 is blue and n=-1 is green. (G) Three-dimensional reconstruction of the ParM filament in the open state is filtered to 19 Å resolution, and the corresponding atomic model is shown as blue ribbons. Power spectra generated from the raw images (H), and projections of either the three-dimensional reconstruction (I) or the corresponding atomic model of the open filament (J). Three layer lines are marked with arrows as in (E)
An obvious question is whether the variability in axial rise could actually be coming from variations in magnification, or from filaments that are tilted out of the plane of the image. If changes in magnification were responsible, then we would see filament reconstructions with different diameters, and we would see shifts in the radial positions of layer line peaks in the power spectra (Supplementary Movie 1). Such changes are not seen. Further, the determination of twist is independent of magnification, so we would see no correlation between twist and axial rise. But we see a strong correlation, eliminating the possibility that our results can be explained by variable magnification. If the differences in axial rise were due to out-of-plane tilt, then a tilt of ~ 23° would be needed to explain a change in axial rise from 25.5 Å to 23.5 Å. Since the filaments are imaged after adsorption to a carbon support film, and do not lie over holes, this possibility seems extremely unlikely. Our results unambiguously show that in addition to the variable twist, ParM has a variable axial rise, and that the twist and the axial rise are coupled. We therefore used this new sorting to generate an improved three-dimensional reconstruction of the closed state of the ParM filament, using the largest class (class3, n=3,116 segments). We did not attempt to sort out the helical heterogeneity in the open ParM state because of the more limited number of total segments (n=3,374).
The two reconstructions are shown as transparent surfaces in Figure 5A,G. To determine the resolution of the map in each case we used a procedure described in (Galkin et al., 2008) which returned the most pessimistic estimation of the resolution of ~17.2 Å for the closed state reconstruction (after sorting for the variable twist and rise), and ~19.5 Å for the open state (no sorting for twist and rise). No perturbations of the crystal structure of ParM in the apo-state (PDB 1MWK) were required to dock it into the reconstruction of the open state at the available resolution (Figure 5G). To get a better fit of the ParM crystal structure into the map of the closed state (Figure 5A) we cleaved the apo-crystal structure of ParM across the hinge region into the two major domains (domains I and II), breaking the bonds at the regions where the large change between the ADP-and apo-states occur. (see Materials and Methods). The best fit was achieved when the two domains were moved towards each other around the hinge by ~25° (Figure 5B). Exactly the same closing of the cleft was observed between the apo- and ADP (PDB 1MWM) states (Figure 5C) (van den Ent et al., 2002). We found that the docking of separate domains from the apo-crystal produced a slightly better fit than when the unperturbed ADP-state crystal structure was used.
Comparisons of the power spectra of the raw images with those obtained from the reconstructions (Figure 5D,E, H,I) show good matches, and it can be seen that the power spectrum from the segments classified as closed is different from that obtained from the segments classified as open. For the closed ParM segments the n=3 layer line (Figure 5D, red arrow) is more prominent than the n=±1 layer lines (Figure 5D, blue and green arrows), while for the open ParM segments all three layer lines have nearly equal intensity (Figure 5H, red blue and green arrows). This can be measured quantitatively, and the ratio of intensities between the n=3 and n=1 layer lines is 2.1 in the closed state (Figure 5D) and 1.0 in the open state (Figure 5H). A similar approach was used to validate our atomic models – the power spectra generated from both atomic models matched well the power spectra of the raw images as well as the power spectra derived from the reconstructions used for the modeling (Figure 5D,E,F, and H,I,J). To evaluate how well the atomic models reflect the features of the reconstructions we calculated the Fourier Shell Correlation (FSC) between the maps and the atomic models (Supplementary Figure 2). The FSC curves reached a value of 0.5 (an arbitrary but conservative measure of the resolution limit) at almost exactly the same values that we previously determined for the resolution of these maps, giving further credibility to these resolution estimates.
In our previous work we showed that there is no nucleotide exchange after ParM polymerization (Orlova et al., 2007), and under the conditions used AMP-PNP should always be bound in the cleft. Despite the fact that in the presence of GMP-PNP ParM was shown to have its cleft closed (Popp et al., 2008), we observe ~20% of segments having the cleft open. We suggest that there is an equilibrium between the closed and the open state within the ParM filament. When either AMP-PNP or GMP-PNP is bound, the equilibrium is shifted towards the closed state, but a fraction of segments can still be found in the open state.
A detailed comparison of the atomic models of the closed and open states of the ParM filament (Figure 6) shows how protomer interfaces change between these two states. In the closed state each ParM promoter makes three longitudinal contacts and one lateral contact with its neighbors (Figure 6A,B). In the open state (Figure 6C,D) the residues 161-164 and 271-274 of the upper protomer, and the residues 212-217 of the lower protomer move away from each other (Figure 6A,C, red arrows). Also, the contact between the residues 298-300 of the upper protomer, and residues 239-341 of the lower protomer is broken in the open state (Figure 6A,C, green arrows). Our atomic models predict that upon opening of the nucleotide binding cleft, the ParM filament would be less stable than when it is in the closed state.
Figure 6.
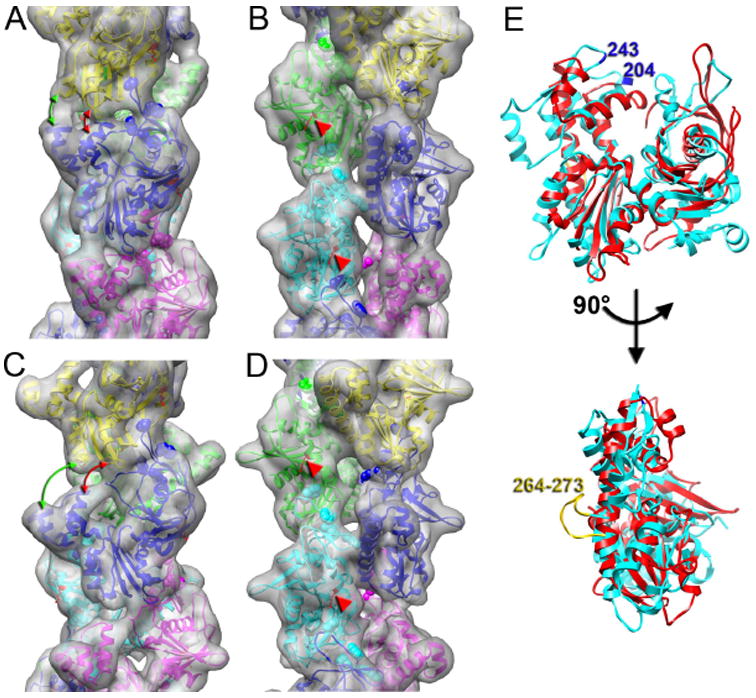
Detailed views of the two structural states of the ParM filament. (A,B) Pseudo-atomic model of the closed state is shown as ribbons and the corresponding view of the model filtered to 10 Å resolution is shown as a transparent surface. The two views are related by 90° rotation around the helical axis. (C,D) Pseudo-atomic model of the open state of the ParM filament. Red arrows mark the distances between residues 161-164 and 271-274 of the upper protomer, and the residues 212-217 of the lower protomer in both closed and open states. Green arrows mark the distances between residues 298-300 of the upper protomer, and residues 239-341 of the lower protomer in both structural states. Residues 33, 34, 36, and 40, which are crucial for filament maintenance, are shown as spheres in (A-D). Residue 123, involved in the interaction with ParR/ParC complex, is indicated in (A-D) with red arrowheads. (E) A comparison between actin (cyan) and ParM (red) shows that while the cores of the two subunits are fairly well conserved, the peripheral regions in actin at the four “corners” of the subunit (responsible for protomer-protomer contacts in F-actin) have no correspondence with the secondary structural elements of ParM in these regions. Two residues (204 and 243) that have been implicated in actin polymerization (Rould et al., 2006) can be seen to be in a region that has no structural similarity in ParM.
Both atomic models are in agreement with the recent mutagenesis data. It has been shown that point mutations of residues 33, 34, 36, and 40 completely abolish ParM polymerization (Salje et al., 2008). In both ParM states these residues lie at the interface between protomers (Figure 6, residues are marked as spheres). Mutation of residue K123, which is located in helix 4 of domain I of ParM (van den Ent et al., 2002) does not affect ParM polymerization, but abolishes the interaction of ParM with the ParR/ParC complex. In our atomic models this residue is located at the side of the filament (Figure 6A-D, red arrow heads), which would explain why this mutation does not alter ParM polymerization, and why binding of ParR/ParC complex does not interfere with ParM polymerization. Both atomic models also show that the interfaces between protomers are completely different from that found in F-actin. This is consistent with the fact that there is no correspondence of secondary structural elements between ParM and actin (Fig. 6E) in the regions of the actin subunit that are known to be involved in the filament interface. For example, mutation of actin residues 204 and 243 has been shown to abolish polymerization (Rould et al., 2006), but there is no structural similarity between ParM and actin in this region of the actin subunit (Figure 6E). Similarly, the “hydrophobic plug” in actin (residues 262-274) has been shown to be essential for filament formation (Reisler et al., 2007), but this element is completely missing from ParM (Fig. 6E).
The opening of the cleft is coupled with ATP hydrolysis
To elucidate the role of the two structural states of ParM filaments found, we imaged ParM filaments under several other conditions (Figure 7). We first determined that negative stain can be used to visualize the two different states. Although we found a smaller fraction of the open state of ParM in the negatively stained AMP-PNP-ParM (Fig. 7A) sample (~10%) compared to the frozen hydrated filaments (~ 20%), the negatively stained reconstructions of the open (Figure 7H) and closed (Figure 7G) states of ParM were very similar at the available resolution to the cryo-EM reconstructions (Figure 5A,G, respectively).
Figure 7.
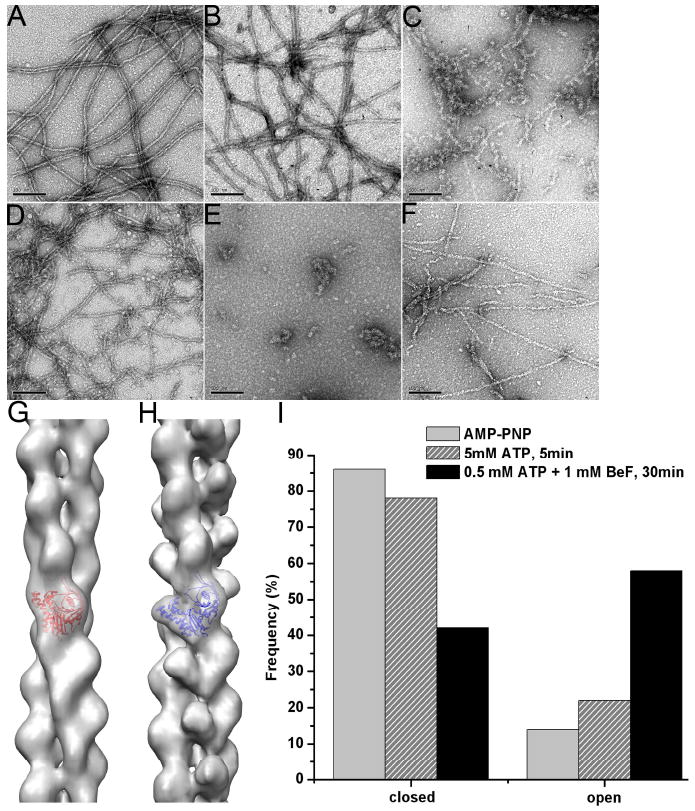
Structural polymorphism of the ParM filaments depends upon the polymerization conditions. EM micrographs of negatively stained ParM filaments formed at different conditions (A-F). Long filaments are formed in presence of AMP-PNP, and these filaments are stable even after several hours (A). In presence of 5 mM ATP shorter filaments are observed after 5 minutes of polymerization (B), and very few filaments along with aggregates are present after 30 minutes (C). After 5 min of polymerization in the presence of 0.5 mM ATP, ParM forms short filaments that tend to form bundles (D), while after 30 min, when all ATP is depleted, only amorphous aggregates are seen (E). Addition of 1 mM BeF to 0.5 mM ATP preserves some filaments even after 30 min incubation (F). Two structural states are found in negatively stained filaments – closed (G), and open (H). These states are shown as grey transparent surfaces with docked crystal structure of ParM in the closed (G, red ribbons) or open (H, blue ribbons) states. The frequency of these states within the filaments shown in (A), (B) and (F) is shown in (I).
When ParM was polymerized in the presence of a large molar excess (5.0 mM) of ATP (Figure 7B), we observed long and quite ordered filaments. These filaments disappeared over time as the ATP was consumed (Figure 7C). Image analysis revealed that over 20% of these ordered segments were in the open conformation (Figure 7I), suggesting that the opening of the nucleotide binding cleft in ParM was associated with ATP hydrolysis (since ~ 10% of these segments had an open cleft with the non-hydrolyzable AMP-PNP). Using a lower concentration of ATP (0.5 mM) resulted in shorter filaments after 5 minutes of polymerization (Figure 7D), and almost no filaments were observed after 30 minutes (Figure 7E). The addition of BeF3-, used to mimic the ADP-Pi state in F-actin (Combeau et al., 1988), rescues ParM filaments from depolymerization (Garner et al., 2004). When BeF3- was added shortly after polymerization at low ATP concentration (see Materials and Methods), even after 30 minutes we observed long ParM filaments (Figure 7F). Interestingly, in comparison to AMP-PNP-filaments (Figure 5A), or ATP-filaments after short times (Figure 7B), BeF3--filaments (Figure 7F) had a quite different appearance, similar to the “ragged” morphology of F-actin after short times of polymerization (Steinmetz et al., 1997;Orlova et al., 2004). Cross-correlation sorting revealed that the majority of these segments were in the open state (Figure 7I), and showed that BeF3- stabilized the open conformation of the ParM subunits in the filament.
DISCUSSION
Nucleotide preference of ParM
ParM is a member of the actin superfamily, which includes eukaryotic actins, actin related proteins (ARPs), prokaryotic actin-like proteins (ALPs), chaperones (Hsc70 and DnaK), and sugar kinases (e.g. hexokinase). The family is defined by a shared nucleotide binding motif called the “actin fold” (Bork et al., 1992) which, in all known cases, prefers ATP over GTP. For some family members this preference is not strong. DnaK and some forms of hexokinase, for example, are only two-to four-fold more selective for ATP over GTP (Liberek et al., 1991). Most conventional eukaryotic actins bind 500-1000 times more tightly to ATP than GTP, although some actins are less discriminating. The best studied example of a weakly discriminating actin is that of budding yeast, which has only nine-fold greater affinity for ATP. In the presence of GTP, yeast actin assembles into filaments indistinguishable from ATP filaments, with a critical concentration only five-fold higher than in the presence of ATP (Wen et al., 2002). The difference in nucleotide selectivity between yeast and animal actins is due in large part to a single amino acid difference in the nucleotide binding pocket (Phe versus Tyr at position 305), a substitution that is widely conserved among fungi and plants and suggests a selective advantage for the ability to utilize GTP. van den Ent (2001) also showed that the bacterial actin like protein MreB will polymerize in both ATP and GTP but did not determine nucleotide binding preference.
Popp et al. (2008) recently showed that ParM can also polymerize in the presence of GTP. Although these authors did not measure the relative affinities of ParM for different nucleotides they suggested that, unlike other members of the actin superfamily, ParM prefers GTP over ATP and is “a predominantly GTP-driven molecular switch”. To determine whether this is the case we measured the affinities of ParM for ATP and GTP by competition binding and found that, similar to yeast actin, ParM has a 10-fold higher affinity for ATP. Thus, at cellular ratios of ATP to GTP (generally >1.0), ParM will be predominantly ATP bound.
Popp et al. (2008) also report that, while ATP ParM filaments undergo dynamic instability, rapid shortening of filaments is often terminated by ‘rescue’ and the filaments rarely or never completely disassemble. In contrast, they report that, upon switching from elongation to shortening, GTP ParM filaments disassemble completely. We also compared the assembly dynamics of ATP and GTP ParM using bulk light scattering assays and TIRF microscopy. In agreement with Popp et al. (2008) we find that the apparent critical concentrations of ATP and GTP ParM are identical, suggesting that the filaments have a similar stability and by TIRF microscopy we find no difference in the behavior of individual GTP and ATP ParM filaments. Both elongate bi-directionally and, upon switching to disassembly, both depolymerize completely. Some discrepancies between our results and those of Popp et al. (2008) are likely due to the fact that Popp et al. performed TIRF experiments on large filament bundles generated by a crowding agent, polyvinyl alcohol. The difference in the state of the protein under the two different imaging conditions is dramatic. Under our conditions almost all observed filaments are short (<3 μM), uniform in intensity, unbranched, and highly dynamic. Electron microscopy of filaments prepared under these conditions confirms that fewer than 2% are associated with other filaments (Garner et al., 2004;Choi et al., 2008). In Popp et al. almost all observed filaments are >5 μm in length, of variable fluorescence intensity, and often display branching or fraying at the ends, typical of filament bundles. Lateral interactions within a large bundle could act to stabilize filaments and it is possible that GTP filaments have a lower propensity to form tight bundles than ATP filaments. This, however, cannot explain all the discrepancies between our results. In a previous study we used methylcellulose to form long, stable bundles of ATP ParM filaments between particles coated with ParR/parC complexes. When we cut the bundles in the middle to expose ADP filament ends both halves of the bundle completely disassembled, despite the presence of the crowding agent. Another potential source of difference could be our fluorescent labeling protocols. Popp et al. use ParM labeled randomly with multiple rhodamine molecules on surface-exposed lysines. In our hands rhodamine labeled ParM has a dramatically enhanced tendancy to bundle, even in the absence of crowding agents (data not shown). In our TIRF experiments we used ParM labeled with a single Alexa-488 on an engineered C-terminal cysteine. Our data disagree with the view that ParM is “a predominantly GTP-driven molecular switch” and support the idea that, like other members of the actin superfamily, ParM is a preferential ATPase with the capacity to bind GTP, albeit with a lower affinity.
Equilibrium between open and closed states of the ATP-binding cleft is common to proteins of the actin super-family
A number of papers have proposed an atomic model of the ParM filament (van den Ent et al., 2002;Orlova et al., 2007;Popp et al., 2008). We think that the structural heterogeneity within the ParM filament precludes the formulation of a single atomic model for the ParM filament. The majority of segments in the presence of AMP-PNP have subunits with a closed cleft, and the atomic model derived from this state is consistent with the recently published ParM model (Popp et al., 2008). The second structural state, where protomers have their cleft open to the same extent as seen in the apo crystal structure of ParM (van den Ent et al., 2002), is also present in filaments, even though the same nucleotide (AMP-PNP) is believed bound to both states. The evidence for a bound nucleotide in both states comes from the observation (Orlova et al., 2007) that there is no appreciable exchange of nucleotide in these filaments. The notion that a bound ligand may bias a distribution of states of a protein, rather than simply determining the conformation, has been described in many other systems. For example, it has been shown that there is an equilibrium between the discrete positions of tropomyosin on F-actin that is shifted by Ca2+, as opposed to being directly linked to the divalent cation (Pirani et al., 2005).
The two structural states of ParM that we observe are very similar to the two states previously visualized by crystallography (van den Ent et al., 2002), and support the notion that all members of the actin super-family can undergo large domain-domain motions (Bork et al., 1992). Recent observations of another bacterial actin homolog, AlfA, suggest that the subunits within the AlfA filament are mainly in an open conformation (Polka et al., 2009). It has been suggested that the opening of the nucleotide binding cleft in F-actin is coupled with ATP hydrolysis (Belmont et al., 1999). Within crystals of G-actin the binding of ATP or ADP does not change the opening of the cleft (Rould et al., 2006c), but it is possible that crystal-packing interactions may trap actin in the closed state. We have found both states of an actin subunit coexisting in actin filaments – the canonical state has the ATP-binding cleft closed (Galkin et al., 2008), while in the tilted state of F-actin the cleft is open (Galkin et al., 2002;Orlova et al., 2007). This suggests that in the mature actin filament, containing ADP-bound protomers, there is an equilibrium between the two states. While this equilibrium is shifted towards the closed state, ADP-protomers having their cleft open can still be found in actin filaments.
The closed state of the cleft is required but not sufficient for ParM polymerization
Actin can form filaments in presence of ATP, ATP analogs, ADP, and even without any nucleotide bound, so modifications to impair its ability to polymerize, or co-complexes with other proteins, are required for the crystallization of actin. This is consistent with the very small differences between the non-polymerizable ATP-bound and ADP-bound crystals of actin that mainly involve subtle movement of the sensor loop (Rould et al., 2006). Is the opening of the ATP binding cleft in ParM coupled with ATP hydrolysis? In contrast to actin, ParM can polymerize only in the presence of NTP, or NTP analogs like AMP-PNP or GMP-PNP. This suggests that ParM monomers that have ATP bound are structurally different from ADP-ParM monomers. A crystal structure of non-polymerizable ATP-ParM is required to understand what precludes ADP-ParM from forming filaments.
It was shown that BeF3- stabilizes actin filaments by mimicking the ADP-Pi state of the filament (Combeau et al., 1988). Interestingly, BeF3- can rescue ParM filaments from the fast depolymerization that occures upon ATP hydrolysis, but does not promote filament elongation (Garner et al., 2004). Our EM observations show the stabilization of the preformed ParM filaments by BeF3- after the depletion of ATP (Figure 7D-F). Together, these results imply the existence of at least two structural states of the ParM monomers – one structural state allows them to polymerize, while the other state can occur only in the preformed filament, and monomers in this state can not spontaneously polymerize. We found that in the presence of BeF3- after the depletion of ATP the majority of segments had the cleft widely open (Figure 7I). This strongly suggests that the open state of the ParM filament is the dominant form in the ADP-Pi state, but monomers with the open cleft can not support elongation, or form new filaments. The closed state of the cleft is required but not sufficient for ParM polymerization.
In the model proposed by Popp et al. (2008), both the GTP-and GDP-bound ParM monomers in a filament adopt a similar ‘closed’ conformation. When GDP ParM monomers are exposed at the end of a filament the loss of nucleotide causes a change in conformation from the ‘closed’ to the ‘open’ state and promotes monomer dissociation. That is, catastrophic shortening requires that the terminal ParM monomer in the filament be in the nucleotide-free or apo form. The requirement that the rapidly dissociating monomers are nucleotide-free appears to be based entirely on the fact that in the crystal structures solved by the Lowe group, ADP ParM appears in a closed conformation while apo ParM is open. We find that ParM filaments contain monomers in both the open and closed form and that the relative amounts in each form depend on the nucleotide bound. Thus, there is no need to invoke the existence of apo ParM monomers to explain a conformational change-driven increase in the rate of monomer dissociation from filament ends. Furthermore, we previously (Garner et al., 2004) found that addition of exogenous ADP to preformed ParM filaments increased their rate of disassembly. The best explanation for this observation is that, as in conventional actin (Teubner et al., 1998), the terminal monomers of a ParM filament can exchange bound nucleotide with nucleotides in solution. If ADP ParM monomers were more stable than apo monomers, the addition of excess ADP should slow down dissociation rather than accelerate it.
The opening of the ATP-binding cleft may be required for phosphate release
After short times of polymerization, when F-actin hydrolyzes ATP and releases the inorganic phosphate, filaments have a ragged morphology which evolves over time into more ordered filaments (Steinmetz et al., 1997;Orlova et al., 2004). This ragged morphology coincides with the increased number of actin protomers in the tilted state (Galkin et al., 2002;Orlova et al., 2004). In the tilted state, F-actin has its cleft open and lacks one of its longitudinal contacts (Galkin et al., 2002;Orlova et al., 2004). These observations explain why young actin filaments are less stable than aged ones (Kueh et al., 2008). In the mature frozen hydrated actin filaments the majority of segments are in the closed state (Orlova et al., 2007), which is consistent with the closed cleft observed in the crystal structure of ADP-G-actin (Rould et al., 2006). This suggests that in F-actin the opening of the cleft is coupled with ATP hydrolysis, and once this process is completed the cleft closes.
Stabilization of ParM filaments with BeF3- provides insight into what happens to protomers upon ATP hydrolysis. We show here that ParM protomers in the ADP-Pi state (mimicked by BeF3-) are mainly in the open form. Importantly, ParM filaments that are stabilized with BeF3- after ATP depletion a have ragged morphology (Figure 7F) similar to that observed in young actin filaments. Since actin and ParM have a substantial structural homology in the ATP-binding cleft region, we suggest that the opening of the ATP-binding cleft in the tilted state of F-actin, similarly to what is seen with ParM, reflects the ADP-Pi state.
Why is ParM, in contrast to F-actin, dynamically unstable? We may speculate that once the inorganic phosphate is released, the cleft in F-actin closes and it returns to the stable conformation. ParM is structurally homologous to actin only in the core region, while it is very different from F-actin in the regions of subunit-subunit contacts within the filament. This explains why ParM forms left handed two-start helices with contacts between the protomers that are absolutely unrelated to the contacts observed in F-actin (Figure 6). It is possible that because of this difference, the cleft in ParM can not be closed upon phosphate release, and protomers can not switch back to the closed state. The open conformation of ParM that we describe as the ADP-Pi state is an intermediate state between the stable ATP-and highly unstable ADP-filament. ParM filaments shrink from the ends (Garner et al., 2004). The structural alterations in the ParM filament that arise from the opening of the cleft in the ADP-Pi state preclude the addition of ATP-bound protomers to the ends of the filament, and thus prevent the formation of the protective ATP caps (Figure 8). The structural changes in ParM that accompany Pi release are inconsistent with filament existence.
Figure 8.
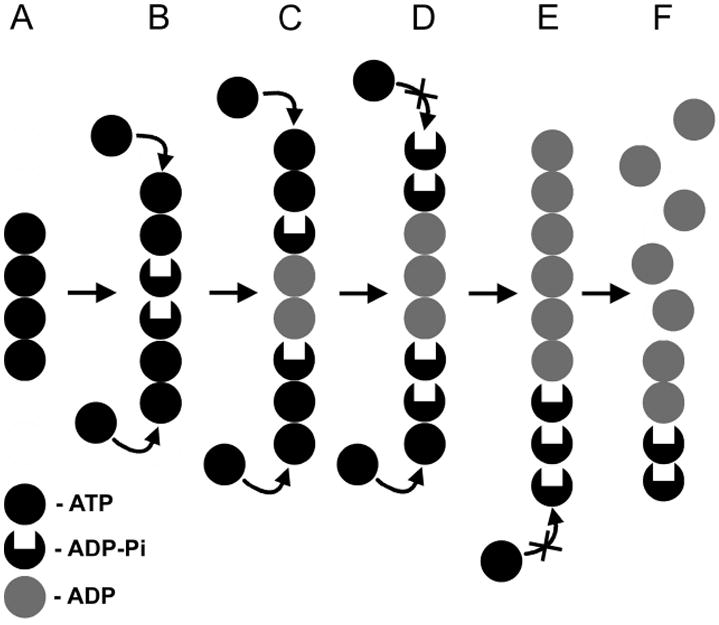
Model for the dynamic instability of ParM filaments. ParM filament is shown as a stack of circles, where each circle represents a ParM protomer. Black circles represent ParM-ATP; grey circles represent ParM-ADP, and black circles with deleted center stand for the intermediate ParM-ADP-Pi state. Shortly after polymerization ParM filament is comprised of ATP subunits (A), which over time turn into ADP-Pi state (B) followed by the ADP state (C). The integrity of the filament in (A-C) is preserved by the ATP-cap. Inorganic phosphate release inhibits the formation of the protective ATP-cap (D). Finally, the ADP subunits are exposed (E), and the filament depolymerizes (F).
Implications for ParR/ParC binding
Atomic models derived from both open and closed states are consistent with the mutagenesis data (Salje et al., 2008), and place the ParR/ParC binding site on the side of the ParM filament. We suggest that alteration of the side of the filament upon ATP hydrolysis allows the ParR/ParC complex to sense the nucleotide state of the filament and remain attached to subunits within the ATP cap. Since filaments capped with the ParR/ParC complex are stable and can grow to be long in the cell (Campbell et al., 2007), it is likely that interaction of the ParR/ParC complex with the side of the filament may stabilize the ATP cap.
MATERIALS AND METHODS
Sample preparation and electron microscopy
ParM protein was overexpressed and purified as described (Orlova et al., 2007). ParM in 30 mM Tris-HCL, pH 7.5, 0.1M KCL, 2mM MgCl2, 1mM DTT was diluted to 3-4 μM, and polymerized by the addition of AMP-PNP (5 mM) or GMP-PNP (5 mM), and after 5–10 min incubation 5 μl was applied to glow-discharged carbon-covered 300-mesh copper grids. Alternatively, polymerization was started by the addition of 100μM – 5mM ATP. For ADP-Pi state 1mM BeSO4 and 5mM NaF were added after 2-4 min of polymerization. The mixture was incubated up to 15-30 min at room temperature.
The grids were either negatively stained with 1% (w/v) uranyl acetate or blotted and plunged into liquid ethane. Images were collected on film using a Tecnai 12 (80 kV and X30,000 magnification) for negatively stained samples or a Tecnai 20 FEG (200 kV and X50,000 magnification) for frozen-hydrated samples. The 31 different images used for the cryo-EM reconstruction had defocus values ranging from 2.0 to 4.0 μm. Films were scanned on a Nikon Coolscan 8000 with a sampling of 4.16 Å per pixel for negative-stain images and 2.38 Å per pixel for cryo-EM.
Image analysis
The SPIDER package (Frank et al., 1996) was used for most image processing, but the BSOFT package (Heymann et al., 2007) was used to determine the defocus values in the micrographs while EMAN (Ludtke et al., 1999) package was used to extract filament images from micrographs.
Image analysis of frozen hydrated AMP-PNP-ParM-filaments
All cryo-EM images were multiplied by the theoretical contrast transfer function (CTF) to correct for phase reversals and to optimize the signal-to-noise ratio. Final reconstructions were then divided by the weighted sum of the squared CTF functions and corrected for the envelope function of the EM with the use of negative B-factors. The segments were classified as shown in Figure 4A. First, a global reconstruction was generated using all segments (n=18,870). The crystal structure of the closed state of ParM (pdb entry 1MWK) was docked into the global map using the UCSF Chimera software (Pettersen et al., 2004), and subsequently used to generate a model filament in the closed state. The ParM crystal structure in the open state (pdb entry 1MWK) was used to generate a model filament having the cleft open. The position of the first domain of ParM in the closed and the open states models were identical, so the only difference was the opening of the cleft and the breakage of the contact between the protofilaments (Figure 6, red and green arrows). These models were used as references for an initial sorting (Figure 4A). These two reference volumes were scaled to 4.76 Å per pixel and projected into 100 × 100-pixel images with an azimuthal rotational increment of 4°, generating 180 reference projections (2 × 90). The ParM segments were down-sampled to 4.76 Å per pixel and cross-correlated with the 180 reference projections. Reconstructions were independently generated from the two classes of segments – closed (n=12,523), and open (n=3,374). The validity of the sorting was confirmed by two independent means. First, power spectra of segments from both classes were indistinguishable from the power spectra of the 3D-reconstructions (Figure 5). Second, we used the IHRSR approach (Egelman, 2000) to show the convergence of the two classes to their unique solutions independently form the starting point (Supplementary figure 1). The 3D-reconstruction of the open set yielded symmetry of 165°/24.2Å and was used to build up an atomic model of the ParM filament in the open state (Figure 6C and D). The closed set was sorted by the twist and the axial rise. Five model volumes were created by imposing five corresponding symmetries on the crystal structure of ParM in the closed state (pdb entry 1MWM). The symmetries were chosen to keep the pitch of the 3-start helix fixed at 1/194 Å-1 as follows: 160.7°/ 21.87Å, 163°/ 23.11Å, 165.2°/ 24.3Å, 167.5°/ 25.51Å, and 169.7°/ 26.73Å. These five volumes were scaled to 4.76 Å per pixel and projected into 100 × 100-pixel images with an azimuthal rotational increment of 4°, generating 450 reference projections (5 × 90). The ParM segments were down-sampled to 4.76 Å per pixel and cross-correlated with the 450 reference projections. The power spectra of segments from three largest bins were calculated (Figure 4E), and behave exactly as predicted by the twist and axial rise values shown in the histogram (Figure 4B). Second, we used the IHRSR approach to separately reconstruct these three bins, and each class converged to the expected symmetry (Figure 4C and D). The reconstruction form the largest class number 3 (n=3,611) iterated at the original scale of 2.38 Å per pixel yielded the symmetry of 165.2°/24.3Å, and was used to build up an atomic model of the ParM filament in the closed state (Figure 6A and B).
To validate our maps we iterated each set from the two very different symmetries to check the convergence of the set to the same solution (Supplementary Figure 1). We observed a nice convergence to the same solution within each set. Our extensive work with IHRSR package proved that heterogeneous sets would never generate the same 3D-reconstruction if iterated from the different starting points. Also, to avoid model biasing, both sets were reconstructed starting from a features solid cylinder (Supplementary Figure 1).
The conservative FSC = 0.5 criterion was used for resolution determination. A widely used approach has been to split an aligned data set into two halves yielding two volumes for FSC comparison, but this method can yield an overly optimistic resolution value due to alignment of noise. To avoid that we divided the images into two sets and then used the IHRSR procedure on these two sets starting each from a different helical symmetry. The two structures converge to a common symmetry, and the resultant volumes did not have noise aligned to a common reference. However, the smaller number of images present in each half data set would underestimate the resolution in the combined reconstruction, under conditions where the resolution was likely to be limited by the number of particles. Thus, the 17.2 Å resolution that was measure by this method in our closed map, and the 19.5 Å resolution determined for the open state, were the most pessimistic resolution estimations.
Image analysis of negatively stained samples
We extracted 10,181 overlapping segments of negatively stained AMP-PNP ParM filaments, and 11,173 segments prepared in presence of GMP-PNP, each 416 Å in length. First, a global reconstruction of each set was generated using all segments. After 60 cycles of IHRSR refinement, the AMP-PNP set yielded a stable solution of 165.2°/24.7 Å (Figure 1B, yellow surface), while the GMP-PNP set converged to 165.3°/24.7 Å (Figure 1C, yellow surface). This global reconstruction of the AMP-PNP set was then deformed into 9 different twist states ranging from 157 to 173° with a step of 2°, and these models were used as references for the twist sorting (Figure 1E and F).
We selected 4,726 segments of ParM formed in the presence of 0.5 mM ATP after 5 min of polymerization. Similarly to the frozen hydrated sample, segments were divided into the two classes based on the opening of the nucleotide binding cleft. The majority of segments (n=3,680) had the better correlation with the closed cleft reference, and yielded an IHRSR reconstruction shown in (Figure 7 G) with the symmetry of 165.2°/24.7 Å. The smaller set that represented the open state subset (n=1,046) converged to 164.8°/24.8 Å symmetry.
Filaments formed in presence of 0.5 mM ATP and subsequently stabilized with the addition of 2 mM BeF3- possessed a ragged morphology (Figure 7F). We selected only segments that were straight within the 416 Å long box, which was the length of the segments used in IHRSR procedure. Thus, only 1,070 segments were selected and sorted into two classes based on the structural state. More than half of the images (n=599) were assigned to the open state class and yielded a reconstruction shown in (Figure 7H), having the symmetry of 165.4°/24.7 Å. The smaller subset that represented the closed state converged to 164.8°/24.9 Å symmetry.
Supplementary Material
Convergence of the closed (top), and open (bottom) sets of ParM segments to their common solutions is robust. The result of the reconstruction procedure does not depend on either the starting model, or the starting symmetry, used in the iterative procedure.
The variation of the twist and the axial rise in the ParM filament is coupled. We designed five models with a fixed 3-start helical pitch, but with both variable twist and axial rise (see Materials and Methods). The frequency distribution from such a sorting is shown in Figure 4B. The three classes from the center of the distribution were used to calculate the power spectra for these three classes. Three layer lines are marked with arrows: n=3 (red), n=1 (blue) and n=-1 (green). The position of the 3-start helix layer line in each power spectrum is fixed, while n=1 and n=-1 layer lines positions move as predicted by the symmetry sorting.
The resolution of the closed state (A) and the open state (B) was determined using a conservative 0.5 criterion in the FSC approach (black curves). The similarity between the 3D-reconstructions and the corresponding atomic models was assessed using FSC 0.5 criterion (red curves). The drop in the correlation between the atomic models and the maps in the spatial frequencies of ~ 1/25 Å-1 arises from the drop in the contrast transfer function at the defocus values used for imaging (C, red asterisk).
Acknowledgments
This work was supported by NIH GM081303 (E.H.E.) and GM61010 (R.D.M.)
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- Belmont LD, Orlova A, Drubin DG, Egelman EH. A change in actin conformation associated with filament instability after Pi release. Proc Nat Acad Sci USA. 1999;96:29–34. doi: 10.1073/pnas.96.1.29. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bork P, Sander C, Valencia A. An ATPase domain common to prokaryotic cell cycle proteins, sugar kinases, actin, and hsp70 heat shock proteins. Proc Nat Acad Sci USA. 1992;89:7290–7294. doi: 10.1073/pnas.89.16.7290. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Campbell CS, Mullins RD. In vivo visualization of type II plasmid segregation: bacterial actin filaments pushing plasmids. J Cell Biol. 2007;179:1059–1066. doi: 10.1083/jcb.200708206. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Choi CL, Claridge SA, Garner EC, Alivisatos AP, Mullins RD. Protein-nanocrystal conjugates support a single filament polymerization model in R1 plasmid segregation. J Biol Chem. 2008;283:28081–28086. doi: 10.1074/jbc.M803833200. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Combeau C, Carlier MF. Probing the mechanism of ATP hydrolysis on F-actin using vanadate and the structural analogs of phosphate BeF-3 and A1F-4. J Biol Chem. 1988;263:17429–17436. [PubMed] [Google Scholar]
- Egelman EH. A robust algorithm for the reconstruction of helical filaments using single-particle methods. Ultramicroscopy. 2000;85:225–234. doi: 10.1016/s0304-3991(00)00062-0. [DOI] [PubMed] [Google Scholar]
- Egelman EH. The iterative helical real space reconstruction method: surmounting the problems posed by real polymers. J Struct Biol. 2007;157:83–94. doi: 10.1016/j.jsb.2006.05.015. [DOI] [PubMed] [Google Scholar]
- Egelman EH, DeRosier DJ. The Fourier transform of actin and other helical systems with cumulative random angular disorder. Acta Cryst. 1982;A38:796–799. [Google Scholar]
- Flyvbjerg H, Jobs E, Leibler S. Kinetics of self-assembling microtubules: an “inverse problem” in biochemistry. Proc Natl Acad Sci U S A. 1996;93:5975–5979. doi: 10.1073/pnas.93.12.5975. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Frank J, Radermacher M, Penczek P, Zhu J, Li Y, Ladjadj M, Leith A. SPIDER and WEB: Processing and visualization of images in 3D electron microscopy and related fields. J Struct Biol. 1996;116:190–199. doi: 10.1006/jsbi.1996.0030. [DOI] [PubMed] [Google Scholar]
- Galkin VE, Orlova A, Cherepanova O, Lebart MC, Egelman EH. High-resolution cryo-EM structure of the F-actin-fimbrin/plastin ABD2 complex. Proc Natl Acad Sci U S A. 2008;105:1494–1498. doi: 10.1073/pnas.0708667105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Galkin VE, VanLoock MS, Orlova A, Egelman EH. A new internal mode in F-actin helps explain the remarkable evolutionary conservation of actin’s sequence and structure. Cur Biol. 2002;12:570–575. doi: 10.1016/s0960-9822(02)00742-x. [DOI] [PubMed] [Google Scholar]
- Garner EC, Campbell CS, Mullins RD. Dynamic instability in a DNA-segregating prokaryotic actin homolog. Science. 2004;306:1021–1025. doi: 10.1126/science.1101313. [DOI] [PubMed] [Google Scholar]
- Garner EC, Campbell CS, Weibel DB, Mullins RD. Reconstitution of DNA segregation driven by assembly of a prokaryotic actin homolog. Science. 2007;315:1270–1274. doi: 10.1126/science.1138527. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gerdes K, Molin S. Partitioning of plasmid R1. Structural and functional analysis of the parA locus. J Mol Biol. 1986;190:269–279. doi: 10.1016/0022-2836(86)90001-x. [DOI] [PubMed] [Google Scholar]
- Heymann JB, Belnap DM. Bsoft: image processing and molecular modeling for electron microscopy. J Struct Biol. 2007;157:3–18. doi: 10.1016/j.jsb.2006.06.006. [DOI] [PubMed] [Google Scholar]
- Jensen RB, Gerdes K. Partitioning of plasmid R1. The ParM protein exhibits ATPase activity and interacts with the centromere-like ParR-parC complex. J Mol Biol. 1997;269:505–513. doi: 10.1006/jmbi.1997.1061. [DOI] [PubMed] [Google Scholar]
- Kueh HY, Brieher WM, Mitchison TJ. Dynamic stabilization of actin filaments. Proc Natl Acad Sci U S A. 2008;105:16531–16536. doi: 10.1073/pnas.0807394105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liberek K, Skowyra D, Zylicz M, Johnson C, Georgopoulos C. The Escherichia coli DnaK chaperone, the 70-kDa heat shock protein eukaryotic equivalent, changes conformation upon ATP hydrolysis, thus triggering its dissociation from a bound target protein. J Biol Chem. 1991;266:14491–14496. [PubMed] [Google Scholar]
- Lowe J, Amos LA. Evolution of cytomotive filaments: The cytoskeleton from prokaryotes to eukaryotes. Int J Biochem Cell Biol. 2009;41:323–329. doi: 10.1016/j.biocel.2008.08.010. [DOI] [PubMed] [Google Scholar]
- Ludtke SJ, Baldwin PR, Chiu W. EMAN: semiautomated software for high-resolution single-particle reconstructions. J Struct Biol. 1999;128:82–97. doi: 10.1006/jsbi.1999.4174. [DOI] [PubMed] [Google Scholar]
- Moller-Jensen J, Borch J, Dam M, Jensen RB, Roepstorff P, Gerdes K. Bacterial mitosis: ParM of plasmid R1 moves plasmid DNA by an actin-like insertional polymerization mechanism. Mol Cell. 2003;12:1477–1487. doi: 10.1016/s1097-2765(03)00451-9. [DOI] [PubMed] [Google Scholar]
- Nishida E, Sakai H. Kinetic Analysis of Actin Polymerization. J Biochem. 1983;93:1011–1020. doi: 10.1093/oxfordjournals.jbchem.a134224. [DOI] [PubMed] [Google Scholar]
- Nordstrom K, Molin S, Agaard-Hansen H. Partitioning of plasmid R1 in Escherichia coli. I. Kinetics of loss of plasmid derivatives deleted of the par region. Plasmid. 1980;4:215–227. doi: 10.1016/0147-619x(80)90011-6. [DOI] [PubMed] [Google Scholar]
- Oda T, Iwasa M, Aihara T, Maeda Y, Narita A. The nature of the globular-to fibrous-actin transition. Nature. 2009;457:441–445. doi: 10.1038/nature07685. [DOI] [PubMed] [Google Scholar]
- Orlova A, Garner EC, Galkin VE, Heuser J, Mullins RD, Egelman EH. The structure of bacterial ParM filaments. Nat Struct Mol Biol. 2007;14:921–926. doi: 10.1038/nsmb1300. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Orlova A, Shvetsov A, Galkin VE, Kudryashov DS, Rubenstein PA, Egelman EH, Reisler E. Actin-destabilizing factors disrupt filaments by means of a time reversal of polymerization. Proc Natl Acad Sci U S A. 2004;101:17664–17668. doi: 10.1073/pnas.0407525102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pettersen EF, Goddard TD, Huang CC, Couch GS, Greenblatt DM, Meng EC, Ferrin TE. UCSF Chimera--a visualization system for exploratory research and analysis. J Comput Chem. 2004;25:1605–1612. doi: 10.1002/jcc.20084. [DOI] [PubMed] [Google Scholar]
- Pirani A, Xu C, Hatch V, Craig R, Tobacman LS, Lehman W. Single particle analysis of relaxed and activated muscle thin filaments. J Mol Biol. 2005;346:761–772. doi: 10.1016/j.jmb.2004.12.013. [DOI] [PubMed] [Google Scholar]
- Polka J, Kollman JM, Agard DA, Mullins RD. The structure and assembly dynamics of a plasmid actin, AlfA, imply a novel method of DNA segregation. J Bact. 2009 doi: 10.1128/JB.00676-09. in press. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Popp D, Narita A, Oda T, Fujisawa T, Matsuo H, Nitanai Y, Iwasa M, Maeda K, Onishi H, Maeda Y. Molecular structure of the ParM polymer and the mechanism leading to its nucleotide-driven dynamic instability. EMBO J. 2008a;27:570–579. doi: 10.1038/sj.emboj.7601978. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Popp D, Narita A, Oda T, Fujisawa T, Matsuo H, Nitanai Y, Iwasa M, Maeda K, Onishi H, Maeda Y. Molecular structure of the ParM polymer and the mechanism leading to its nucleotide-driven dynamic instability. EMBO J. 2008;27:570–579. doi: 10.1038/sj.emboj.7601978. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Reisler E, Egelman EH. Actin structure and function: what we still do not understand. J Biol Chem. 2007;282:36133–36137. doi: 10.1074/jbc.R700030200. [DOI] [PubMed] [Google Scholar]
- Rould MA, Wan Q, Joel PB, Lowey S, Trybus KM. Crystal structures of expressed non-polymerizable monomeric actin in the ADP and ATP states. J Biol Chem. 2006;281:31909–31919. doi: 10.1074/jbc.M601973200. [DOI] [PubMed] [Google Scholar]
- Salje J, Lowe J. Bacterial actin: architecture of the ParMRC plasmid DNA partitioning complex. EMBO J. 2008;27:2230–2238. doi: 10.1038/emboj.2008.152. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Steinmetz MO, Goldie KN, Aebi U. A correlative analysis of actin filament assembly, structure and dynamics. J Cell Biol. 1997;138:559–574. doi: 10.1083/jcb.138.3.559. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Teubner A, Wegner A. Kinetic evidence for a readily exchangeable nucleotide at the terminal subunit of the barbed ends of actin filaments. Biochemistry. 1998;37:7532–7538. doi: 10.1021/bi972176s. [DOI] [PubMed] [Google Scholar]
- van den Ent F, Moller-Jensen J, Amos LA, Gerdes K, Lowe J. F-actin-like filaments formed by plasmid segregation protein ParM. EMBO J. 2002;21:6935–6943. doi: 10.1093/emboj/cdf672. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wen KK, Yao X, Rubenstein PA. GTP-yeast actin. J Biol Chem. 2002;277:41101–41109. doi: 10.1074/jbc.M204025200. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Convergence of the closed (top), and open (bottom) sets of ParM segments to their common solutions is robust. The result of the reconstruction procedure does not depend on either the starting model, or the starting symmetry, used in the iterative procedure.
The variation of the twist and the axial rise in the ParM filament is coupled. We designed five models with a fixed 3-start helical pitch, but with both variable twist and axial rise (see Materials and Methods). The frequency distribution from such a sorting is shown in Figure 4B. The three classes from the center of the distribution were used to calculate the power spectra for these three classes. Three layer lines are marked with arrows: n=3 (red), n=1 (blue) and n=-1 (green). The position of the 3-start helix layer line in each power spectrum is fixed, while n=1 and n=-1 layer lines positions move as predicted by the symmetry sorting.
The resolution of the closed state (A) and the open state (B) was determined using a conservative 0.5 criterion in the FSC approach (black curves). The similarity between the 3D-reconstructions and the corresponding atomic models was assessed using FSC 0.5 criterion (red curves). The drop in the correlation between the atomic models and the maps in the spatial frequencies of ~ 1/25 Å-1 arises from the drop in the contrast transfer function at the defocus values used for imaging (C, red asterisk).


