Describing small-scale structure in random media using pulse-echo ultrasound

Abstract

A method for estimating structural properties of random media is described. The size, number density, and scattering strength of particles are estimated from an analysis of the radio frequency (rf) echo signal power spectrum. Simple correlation functions and the accurate scattering theory of Faran [J. J. Faran, J. Acoust. Soc. Am. 23, 405–418 (1951)], which includes the effects of shear waves, were used separately to model backscatter from spherical particles and thereby describe the structures of the medium. These methods were tested using both glass sphere-in-agar and polystyrene sphere-in-agar scattering media. With the appropriate correlation function, it was possible to measure glass sphere diameters with an accuracy of 20%. It was not possible to accurately estimate the size of polystyrene spheres with the simple spherical and Gaussian correlation models examined because of a significant shear wave contribution. Using the Faran scattering theory for spheres, however, the accuracy for estimating diameters was improved to 10% for both glass and polystyrene scattering media. It was possible to estimate the product of the average scattering particle number density and the average scattering strength per particle, but with lower accuracy than the size estimates. The dependence of the measurement accuracy on the inclusion of shear waves, the wavelength of sound, and medium attenuation are considered, and the implications for describing the structure of biological soft tissues are discussed.

INTRODUCTION

The radio frequency (rf) echo spectrum has been used extensively in medical ultrasound research to interrogate noninvasively the structural properties of biological media.^1–8 One approach is to use the frequency dependence of the rf backscatter spectrum. If the medium can be modeled as a random suspension of many small particles and the characteristics of the instrumentation eliminated, the rf spectrum can effectively be used to describe the structure of that medium. In this case, structure is broadly denned to include the composition, geometrical properties and organization of the elements that interact with the sound waves. For example, it is well known^1,9 that the frequency dependence of the rf spectrum depends on the size, shape, and elastic properties of the scattering materials, while its magnitude depends on the size and number density of scatterers (number per volume) and on their scattering strength (fractional variation in acoustic impedence between the scatterers and the surrounding medium). Accurate estimation of these structural properties for random inhomogeneous media requires that the correlation function for the medium and the elastic properties of its components be known. Although the correlation functions and elastic properties for most biological tissues are poorly understood, several research groups have demonstrated relationships between spectral data from liver using simple correlation function models and liver structure using optical microscopy.^3,6–8

In this paper, a method for estimating the average particle size and the product of the number density and the scattering strength is described. These properties are estimated from the frequency dependence of the rf backscatter spectrum, which has been normalized to eliminate the frequency characteristics of the instrumentation. Using the established framework of single-body scattering theory,^1,9 the connection between the normalized backscatter spectrum and the correlation function for the medium is made in terms of an acoustic form factor. The acoustic form factor, defined in Sec. I B, is proportional to the Fourier transform of the correlation function for the medium, and describes in frequency space the geometrical properties and organization of the scattering targets.

To exploit the simple relationships between properties of the medium and the backscatter spectrum, several assumptions are required. We assume that the coherence among particles is small compared to the incoherent scattering component; the dimensions of the scattering particles are taken to be less than or on the order of the wavelength of sound in the medium; and the attenuation within the gated sample volume must be negligible. In addition, the method currently limits pulse-echo data acquisition to the focal zone of weakly focused transducers. Preliminary results with test samples were used to validate the method, observe the importance of shear waves, and examine the feasibility of measurements in tissues.

The scattering models are described in Sec. I, the data acquisition and analysis is described in Sec. II, and the experimental results are presented and discussed in Secs. III and IV.

I. FORM FACTOR MODELS

A. A review of the scattering of plane waves from random media

If the random scattering medium is a tenuous distribution of particles, then single-scatter theory¹ is adequate to explain many experimental observations. In the single-scatter approximation, the incident wave is essentially unchanged as it propagates through the scattering medium, and the particles are assumed to interact with the incident pressure field only once, i.e., all double and multiple scatterings are assumed to be negligible. Single-scatter theory is well established in the literature and is used in many applications, including estimation of parameters that describe soft tissue microstructure.^2–8 The following section briefly reviews this theory with regard to estimation of scattering particle sizes. The methods described here are based on the theoretical work found in two standard references in acoustic scattering.^1,9

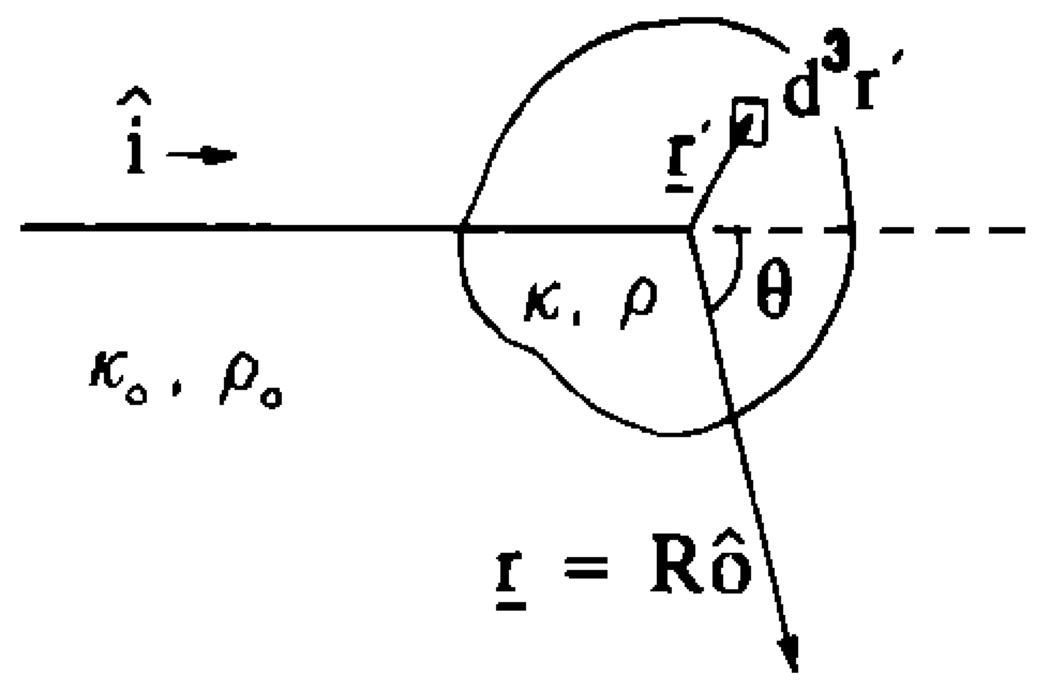
Consider a plane wave of amplitude one incident on a scattering volume V with equilibrium compressibility κ₀ and density ρ₀. Scattering occurs at sites in V where there exist variations in compressibility and density. The term particle will be used to indicate a scattering site even though the variations may not be discrete but continuously varying. At an observation point r, which is far from V (Fig. 1), the scattered field for each particle behaves as a spherical wave, and is given by

$$p_s(\mathbf{r})=(e^{ikR}/R)\mathrm{\Phi }(\mathbf{K}),R>(4a^2/\lambda ),$$ (1)

where a is a dimension of the particle, for example its radius, R = |r|, λ is the wavelength of the plane wave in the medium, and k = 2π/λ is the wavenumber. The factor Φ(K) is called the complex scattering amplitude⁹ and describes the spatial frequency dependence of the scattered pressure; Φ is a function of the scattering vector K = k(î − ô) whose magnitude is given by |K| = 2k sin θ/2, where θ is the angle of scattering between the unit vectors specifying the directions of the incident plane wave î and the observer ô. For backscatter, ô = −î and K = 2kî. An integral expression for Φ at an observation distance far from a single particle has been derived by Morse and Ingard,⁹ using a Green’s function approach. The scattering amplitude for a unit amplitude, simple harmonic source at r′, and with the source term k²γ_κ p − ∇·[γ_ρ∇_p], is given by

$$\begin{array}{cc}\mathrm{\Phi }(\mathbf{K})=\hfill & \frac{k^2}{4\pi }{\displaystyle {\int }_V({\gamma }_{\kappa }(\mathbf{r}\prime )p(\mathbf{r}\prime )-i{\gamma }_{\rho }(\mathbf{r}\prime )\frac{\mathbf{ô}}{k}·\mathbf{\nabla }\prime p(\mathbf{r}\prime ))}\hfill \\ \hfill & \times e^{-ik\mathbf{ô}·\mathbf{r}\prime }{d}^{3}r\prime ,\hfill \end{array}$$ (2)

where p(r′) is the total pressure, the sum of the incident and scattered pressures at the observation point r′, V is a volume containing the scattering particle, and

$$\begin{array}{cc}{\gamma }_{\kappa }(\mathbf{r})\hfill & =[\kappa (\mathbf{r})-{\kappa }_0]/{\kappa }_0\hfill \\ \hfill & =\text{fractional variation in medium compressibility},\hfill \\ {\gamma }_{\rho }(\mathbf{r})\hfill & =[\rho (\mathbf{r})-{\rho }_0]/\rho (\mathbf{r})\hfill \\ \hfill & =\text{fractional variation in medium density}.\hfill \end{array}$$

The quantities κ and ρ are the compressibility and density at position r, and κ₀ and ρ₀ are the average values for the surrounding medium. The source term (parentheses) arises from a scattering source, a region of space within the surrounding medium that redirects rather than generates acoustic energy. The first term describes the interaction between the pressure field and fluctuations in compressibility; the second terms describes the interaction between the pressure field and fluctuations in density. Also, to first order there is a monopole contribution from γ_κ and a dipole contribution from γ_ρ. These contributions are a consequence of the scattering particle with nonzero γ_ρ moving back and forth with respect to the surrounding medium, as opposed to the simple direct scatter with no relative motion for particles with γ_ρ = 0 and γ_κ nonzero. If the particle is weakly scattering (the Born approximation), then we substitute the incident plane wave for the total pressure in Eq. (2) and obtain

$$\mathrm{\Phi }(\mathbf{K})\simeq \frac{k^2}{4\pi }{\displaystyle {\int }_V\gamma (\mathbf{r}\prime )e^{i\mathbf{K}·\mathbf{r}\prime }{d}^{3}r\prime ,}$$ (3)

where

$$\gamma (\mathbf{r}\prime )={\gamma }_{\kappa }(\mathbf{r}\prime )+{\gamma }_{\rho }(\mathbf{r}\prime )\text{cos}\theta .$$

Equation (3) states that in the Born approximation and for incident plane waves, the compressibility and density contributions to the scattered pressure are identical, except for their relative weights γ_κ and γ_ρ cos θ.

FIG. 1.

Scattering geometry illustration showing a point r′ inside the scattering volume.

The scattered field from a randomly positioned ensemble of particles is the sum of the individual pressure fields

$$p_s(\mathbf{r})=\frac{e^{ikR}}{R}{\displaystyle \sum _{j=1}^N{\mathrm{\Phi }}_j(\mathbf{K})e^{i\mathbf{K}·{\mathbf{r}}_j},}$$ (4)

where r_j is the position of the jth particle with respect to the origin and N is the total number of particles in the scattering volume V. The field p_s(r) is a random function of position r, and can be written as the sum of the average field 〈p_s〉 and the fluctuating field $p_s^{\prime }$,

$$p_s(\mathbf{r})=\langle p_s(\mathbf{r})\rangle +p_s^{\prime }(\mathbf{r}),$$

where 〈 〉 represents the ensemble average and $\langle p_s^{\prime }(\mathbf{r})\rangle =0$. The average field is called the coherent field and the fluctuating field is called the incoherent field.¹ The relationship between the average scattering intensity 〈I〉 and the average pressure field is

$${\rho }_0{c}_0\langle \mathit{I}\rangle =\langle |p_s{|}^2\rangle =|\langle p_s\rangle {|}^2+\langle |p_s^{\prime }{|}^2\rangle ,$$ (5)

where | |² represents the squared modulus of the quantity and c₀ is the average longitudinal sound speed in the medium.

From Eq. (5), the average differential cross section per unit volume σ_d may be calculated for the ensemble. The quantity σ_d is defined for large observation distances as the power scattered into a unit solid angle divided by the product of the incident intensity and the scattering volume.^1,4,10 The average scattering intensity is given by 〈I〉 = 〈|Φ|²〉/ρ₀c₀R² and the incident intensity for plane waves of unit amplitude if I₀ = 1/ρ₀c₀ (Ref. ⁹). Therefore,

$${\sigma }_d=\frac{{\mathit{R}}^2}{\mathit{V}}\frac{\langle \mathit{I}\rangle }{{\mathit{I}}_0}=\frac{1}{\mathit{V}}\langle |\mathrm{\Phi }(\mathbf{K}){|}^2\rangle .$$ (6)

Equations (3) and (6) may be combined to express σ_d in terms of the spatial autocorrelation function B_γ of the scattering medium as follows:

$$\begin{array}{cc}{\sigma }_d\hfill & =\frac{k^4}{16{\pi }^2\mathit{V}}\langle {\displaystyle {\int }_V\gamma ({\mathbf{r}}_1)}{e}^{-i\mathbf{K}·{\mathbf{r}}_1}{d}^3{r}_1{\displaystyle {\int }_V\gamma ({\mathbf{r}}_2)e^{i\mathbf{K}·{\mathbf{r}}_2}{d}^3{r}_2}\rangle ,\hfill \\ \hfill & =\frac{k^4}{16{\pi }^2\mathit{V}}{\displaystyle {\int }_V{\displaystyle {\int }_V\langle \gamma ({\mathbf{r}}_1)\gamma ({\mathbf{r}}_2)\rangle e^{-i\mathbf{K}·({\mathbf{r}}_1-{\mathbf{r}}_2)}}}\hfill \\ \hfill & \times d^3{r}_1{d}^3{r}_{2,}\hfill \end{array}$$ (7)

where γ(r) is now a random function describing the distribution of scatters in V. Equation (7) may be reduced by introducing the sum and difference variables u = (r₁ + r₂)/2 and Δr = r₁ − r₂ (Ref. ⁴) to yield

$${\sigma }_d=\frac{k^4}{16{\pi }^2}{\displaystyle {\int }_V{B}_{\gamma }(\mathrm{\Delta }\mathbf{r})e^{-i\mathbf{K}·\mathrm{\Delta }\mathbf{r}}{d}^3\mathrm{\Delta }r,}$$ (8)

where

$$\begin{array}{cc}{\mathit{B}}_{\gamma }(\mathrm{\Delta }\mathbf{r})\hfill & =\frac{1}{\mathit{V}}{\displaystyle {\int }_V\langle \gamma (\mathbf{u}+\frac{\mathrm{\Delta }\mathbf{r}}{2})\gamma (\mathbf{u}-\frac{\mathrm{\Delta }\mathbf{r}}{2})\rangle }{d}^{3}u\hfill \\ \hfill & =\langle \overline{\gamma ({\mathbf{r}}_1)\gamma ({\mathbf{r}}_2)}\rangle .\hfill \end{array}$$

The overbar represents the volume-average value. The volume average is equal to the ensemble average for statistically homogeneous (stationary) scattering media, and therefore the overbar has subsequently been omitted. To assume that the random process {γ(r)} is weakly stationary,¹¹ 〈γ(r₁)〉 and 〈γ(r₁)γ(r₁ + Δr)〉 must not vary with position r₁. Consequently, 〈γ(r₁)γ(r₂)〉 depends only on the difference Δr.

For convenience, we define γ₁ = γ(r₁) and γ₂ = γ(r₂). Then, as in Eq. (5), B_γ(Δr) can be expanded into its average and fluctuating components:

$$\begin{array}{cc}{\mathit{B}}_{\gamma }(\mathrm{\Delta }\mathbf{r})\hfill & =\langle {\gamma }_1\rangle \langle {\gamma }_2\rangle +\langle ({\gamma }_1-\langle {\gamma }_1\rangle )({\gamma }_2-\langle {\gamma }_2\rangle )\rangle \hfill \\ \hfill & =|\langle \gamma \rangle {|}^2+C_{\gamma }(\mathrm{\Delta }\mathbf{r}),\hfill \end{array}$$ (9)

where C_γ(Δr) is the autocovariance function. Here C_γ(Δr) may be further expanded into the product of the variance 〈|γ − 〈γ〉|²〉 and the correlation coefficient b_γ(Δr) (Ref. ¹¹), such that

$${\mathit{B}}_{\gamma }(\mathrm{\Delta }\mathbf{r})=|\langle \gamma \rangle {|}^2+\langle |\gamma -\langle \gamma \rangle {|}^2\rangle b_{\gamma }(\mathrm{\Delta }\mathbf{r}),$$ (10)

where b_γ(0) = 1 and b_γ(∞) = 0. The correlation coefficient depends on the structure of the scattering medium.

Substituting Eq. (10) into Eq. (8) and arranging terms, results in a two-term expression for σ_d: the first term is the coherent component of the scattering cross section and the second is the incoherent component:

$$\begin{array}{cc}{\sigma }_d=\hfill & \frac{k^4}{16{\pi }^2}\left(\right|\langle \gamma \rangle {\displaystyle {\int }_V{e}^{-i\mathbf{K}·\mathbf{r}}{d}^{3}r}{|}^2\hfill \\ \hfill & +\langle |\gamma -\langle \gamma \rangle {|}^2\rangle {\displaystyle {\int }_{-\infty }^{\infty }{b}_{\gamma }(\mathrm{\Delta }\mathbf{r})e^{-i\mathbf{K}·\mathrm{\Delta }\mathbf{r}}{d}^3\mathrm{\Delta }r)}.\hfill \end{array}$$ (11)

Because we assume the medium is random and isotropic, the coherent component is negligible and σ_d is due entirely to incoherent scattering. Moreover, for incoherent scattering, where each scatters in V scatters sound independently of the others, the variance in γ is given by the mean-square variation in acoustic impedence per particle ${\gamma }_0^2$, times the fractional volume of scatterers in V, ω≃n̄V_s, where n̄ is the average number of particles per unit volume and V_s is the average particle volume.¹⁰ The differential cross section per unit volume in Eq. (11), therefore, reduces to

$${\sigma }_d=\frac{k^4{\mathit{V}}_s}{16{\pi }^2}\overline{n}{\gamma }_0^2{\displaystyle {\int }_{-\infty }^{\infty }{b}_{\gamma }(\mathrm{\Delta }\mathbf{r})e^{-i\mathbf{K}·\mathrm{\Delta }\mathbf{r}}{d}^3\mathrm{\Delta }r}$$ (12a)

$$=4{\pi }^4{k}^4\overline{n}{\mathrm{\Gamma }}^2(\mathbf{K}),$$ (12b)

where Γ²(K) is the power spectral density function for the medium fluctuations γ (Ref. ⁹):

$${\mathbf{\Gamma }}^2(\mathbf{K})=\frac{{\gamma }_0^2{\mathit{V}}_s}{{(2\pi )}^6}{\displaystyle {\int }_{-\infty }^{\infty }{b}_{\gamma }(\mathrm{\Delta }\mathbf{r})e^{i\mathbf{K}·\mathrm{\Delta }\mathbf{r}}{d}^3\mathrm{\Delta }r.}$$

The power spectral density function gives the spatial frequency dependence of σ_d. It also describes structural properties of the scattering medium, such as the average particle size, shape, number density, and scattering strength per particle (i.e., ${\gamma }_0^2$). The same structural information is contained in B_γ(Δr) and b_γ(Δr), but in this case in the spatial domain. In the next section, we examine three correlation functions that may be useful for modeling backscatter cross sections in random media and possibly soft biological tissue. From the resulting cross sections, a method is described that enables estimation of the average particle size, number density, and scattering strength.

B. Three correlation models for random media

The differential backscatter cross section per unit volume σ_b, also called the backscatter coefficient,¹⁰ may be computed using Eq. (12a). For particles with spherical symmetry b_γ depends only on the radial coordinate, so that the angular coordinates may be integrated over to give the one-dimensional integral

$${\sigma }_b=\frac{k^3{\mathit{V}}_s\overline{n}{\gamma }_0^2}{8\pi }{\displaystyle {\int }_0^{\infty }{b}_{\gamma }(\mathrm{\Delta }r)\text{sin}(2k\mathrm{\Delta }r)\mathrm{\Delta }rd\mathrm{\Delta }r.}$$ (12c)

Recall that for backscatter K = 2kî.

In the first model, the particles are assumed to be homogeneous fluidlike spheres of radius a. The three-dimensional (3D) correlation coefficient for a fluid sphere is (Ref. ²³, p. 419)

$$b_{\gamma }(\mathrm{\Delta }r)=1-\frac{3|\mathrm{\Delta }r|}{4a}\frac{|\mathrm{\Delta }{r}^3|}{16a^3},0\le \frac{|\mathrm{\Delta }r|}{2a}\le 1.$$

By substituting this function into Eq. (12c) and making the appropriate computations, the backscatter coefficient for the fluid sphere model may be expressed as

$$\begin{array}{cc}{\sigma }_{b1}=\frac{\overline{n}{\mathit{V}}_s^2{\gamma }_0^2{k}^4}{16{\pi }^2}{\left(\frac{3}{2ka}{j}_1(2ka)\right)}^2& (\text{fluid sphere}).\end{array}$$ (13)

The function j₁ is a spherical Bessel function of the first kind, first order. The product $\overline{n}{\mathit{V}}_s^2$ has the units of volume and is proportional to a³. Equation (13) is a well-known result from acoustic and electromagnetic scattering theory (Ref. ¹, Eq. 2.41). Equation (13) may be recognized as being proportional to the 3D Fourier transform of a sphere. This follows immediately from Eq. (3) if incoherent scattering is assumed.

In the second model, the compressibility of the spheres is assumed to be significantly lower than that of the surrounding medium, i.e., γ_κ is approximately – 1.0. These spheres are rigid in the sense that the sound field does not penetrate or deform the particles. The corresponding scattering function is a spherical shell impulse, whose 3D correlation coefficient is given by

$$b_{\gamma }(\mathrm{\Delta }r)=\{\begin{array}{cc}\delta (r-a)***\delta (r-a)=a/6\mathrm{\Delta }r,\hfill & 0\le \mathrm{\Delta }r/2a\le 1,\hfill \\ 0,\hfill & \text{otherwise},\hfill \end{array}$$

where δ is the Dirac delta function and the *** denotes 3D autocorrelation. (This result was generalized from the 2D solution in Ref. 23, p. 403.) Following substitution of this correlation function into Eq. (12c), it is straightforward to express the backscatter coefficient for the spherical shell model as

$$\begin{array}{cc}{\sigma }_{b2}=\frac{\overline{n}{\mathit{V}}_s^2{\gamma }_0^2{k}^4}{16{\pi }^2}{[j_0(2ka)]}^2& (\text{spherical shell}),\end{array}$$ (14)

where j₀ is a spherical Bessel function of the first kind, zero order. The spherical shell model arises from questionable physical properties and, as we show in the next section, is in poor agreement with the classic solution for scattering from rigid, immovable spheres—the case for which it was developed. However, it closely agrees with theoretical predictions and experimental scattering data from test materials containing glass microspheres in agar, as shown in the following section, and is therefore of interest in this study.

In the small-scatterer or long-wavelength limit, i.e., ka→0, the Bessel functions j₁(2ka)→2ka/3 and j₀(2ka)→1, so that Eqs. (13) and (14) converge to the Rayleigh equation for spheres^1,9:

$${\sigma }_0=(\overline{n}/9)k^4{a}^6{\gamma }_0^2.$$ (15)

From Eqs. (13)–(15), we define an acoustic scattering intensity form factor F as the ratio of the backscatter coefficient for a test material having scatterers with finite size to that of a similar material consisting of point scatterers:

$$F(2k)={\sigma }_b/{\sigma }_0.$$ (16)

As with the spectral density function, the form factor describes the geometric nature of the scattering particles, in particular size and shape, from the frequency dependence of the backscattered intensity. Here, F is the ratio of backscattering intensity from particles with finite size to that from point sources.¹² In the range where particles are small compared to the wavelength, such that ka ≪ 1, F is approximately constant and equal to 1.0 for all values of k. For larger particles, where ka ≤ 1, the form factor is a decreasing function of k, where the k dependence of F is determined primarily by particle size. For ka > 1, this simplified interpretation breaks down. The k dependence is then primarily determined by particle shape and the elastic properties of the materials, including the effects of shear wave propagation.

The relation between F and Γ² is found from the ratio of Eqs. (12b) and (15), where

$${\mathbf{\Gamma }}^2(2k)=(a^6{\gamma }_0^2/36{\pi }^4)F(2k)$$ (17)

and F(0) = 1 and F(∞) = 0. It is obvious from Eq. (17) that the magnitude of Γ²(2k) depends on the size and scattering strength of the particles.

From the above examples of scattering from spheres, the corresponding form factors may be found:

$$\begin{array}{cc}{F}_1(2k)={[(3/2ka)j_1(2ka)]}^2& (\text{fluid sphere}),\end{array}$$ (18)

$$\begin{array}{cc}{F}_2(2k)={[j_0(2ka)]}^2& (\text{spherical shell}).\end{array}$$ (19)

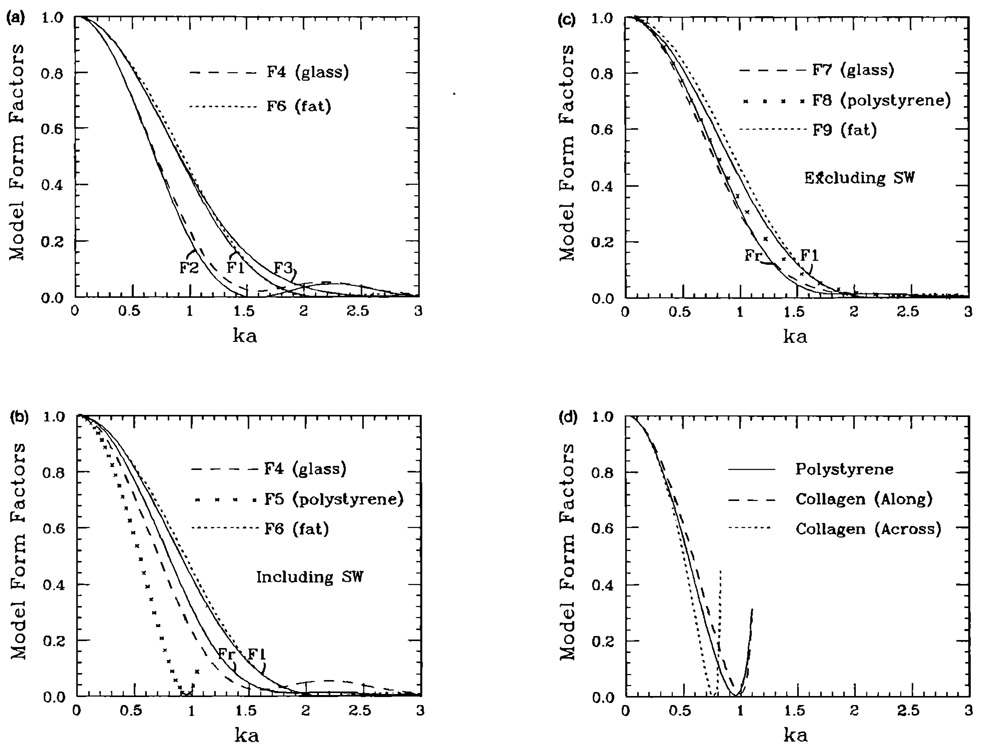
Equations (18) and (19) are plotted in Fig. 2(a).

FIG. 2.

(a) Form factors for the fluid sphere model F₁, the spherical shell model F₂, and the Gaussian model F₃; F₄ and F₆ are form factors calculated from the Faran scattering theory¹³ for microspheres made of glass and fat, respectively. (b) Form factor for the rigid, immovable sphere F_r is plotted along with the fluid sphere model F₁ (solid lines) and that calculated for glass, polystyrene, and fat microspheres from the Faran scattering theory.¹³ These data include the effects of shear waves generated inside the particle. (c) Same as (b), except that the glass, polystyrene, and fat data are calculated from the theory of Morse and Ingard.⁹ These results do not include the effects of shear waves. (d) Form factors for collagen along and across the fibers. The results are computed using the Faran theory and the parameters are taken from the work of Cusak and Miller.¹⁷ These results show that scattering from collagen spheres may be approximated by that of polystyrene.

In the third model, the scattering sources are assumed to be continuously varying fluctuations in the acoustic properties of the medium. The correlation coefficient has a Gaussian form:

$$b_{\gamma }(\mathrm{\Delta }r)=e^{-\mathrm{\Delta }{r}^2/2d^2},$$

where d is a characteristic dimension. The Gaussian model has been used by many investigators to study the structure of random test media⁵ and biological tissues.^3,6–8 The backscatter coefficient for the Gaussian model is easily computed by substitution into Eq. (12c) and is equal to

$$\begin{array}{cc}{\sigma }_{b3}=(\overline{n}{k}^4{\mathit{V}}_s^2{\gamma }_0^2/16{\pi }^2)e^{2k^2{d}^2}& (\text{Gaussian}),\end{array}$$ (20)

where ${\mathit{V}}_s^2={(2\pi d^2)}^3$. In the long-wavelength limit, Eq. (20) reduces to

$${\sigma }_0=\overline{n}{k}^4{\mathit{V}}_s^2{\gamma }_0^2/16{\pi }^2.$$ (21)

Setting Eqs. (15) and (21) equal, the relation between d and an effective particle diameter 2a_eff is 2a_eff ≃ 3.11d. Thus, from Eq. (16), the form factor for the Gaussian model is given by

$$\begin{array}{cc}{F}_3(2k)=e^{-2k^2{d}^2}\simeq e^{-0.827k^2{a}_{\text{eff}}^2}& (\text{Gaussian}).\end{array}$$ (22)

Equation (22) is also plotted in Fig. 2(a).

C. Comparisons with scattering theory

The three correlation models outlined above are simple in form but only approximately valid. They cannot realistically describe backscattering if ka is much greater than one or if the scattering material is nonrigid and supports shear wave motion. Under these conditions, higher-order effects not included in the models, e.g., resonance phenomena, have considerable influence on the scattering energy. As shown below, these simple models agree very well with experimentally proven theoretical predictions when ka < 1.2 and when the scattering material does not support shear waves or is fairly rigid and dense.

The scattering theory of Faran [Ref. ¹³, Eq. (31)] was used to indicate which elementary form factor models were appropriate for analyzing a specified target material. This theory very accurately predicts the differential backscattering cross section for a distant observation point from a single target in a fluidlike medium at all ka, and accounts for the effects of shear wave motion inside the target. Experimental verification of this theory was provided by Faran¹³ and by Burke et al. using a steel sphere in an agar medium.¹⁴ A form factor was calculated from the theoretical cross sections by dividing the results by Eq. (15) and setting n̄ = 1.

Morse and Ingard have derived equations (Ref. ⁹, Eqs. 8.2.15 and 8.2.16), which describe the scattering of plane waves from fluid spheres but ignored the effects of shear waves. (Fluid spheres can support compressional wave but not shear wave motion.) They were compared with the Faran equations to study the effects of shear waves. With the Morse and Ingard equations, form factors for nonrigid spheres were calculated using Eq. (16). For comparison, a form factor corresponding to the rigid, immovable sphere solution was generated from the Faran equations by setting the density and longitudinal sound speed of the scattering spheres to arbitrarily large values: at least five orders of magnitude greater than the surounding medium.

Three target materials were examined in this fashion: glass spheres in agar, polystyrene spheres in agar, and fat spheres in a nonfat tissue medium. The first two materials were made and studied experimentally (see Sec. III); the third is an example of a biological tissue and was analyzed theoretically. Essential parameters for applying Faran’s theory are density (glass 2.38 g/cm³, polystyrene 1.06 g/cm³, fat 0.94 g/cm³), Poisson’s ratio [glass 0.21, polystyrene 0.35, fat 0.4993 (Ref. ¹⁵)], and longitudinal speed of sound (glass 5570 m/s, polystyrene 2350 m/s, fat 1460 m/s). The agar and nonfat tissue materials were taken to be waterlike with a density of 1.0 g/cm³; a longitudinal sound speed of 1540 m/s was used. The resulting form factors for a glass microsphere in agar, polystyrene microsphere in agar, and fat microsphere in nonfat tissue are plotted in Fig. 2(a) and (b) (including the effects of shear waves) and in Fig. 2(c) (excluding the effects of shear waves).

Comparing the curves in Fig. 2(a), we observed that the fat sphere data, labeled F₆, are most similar to the fluid sphere model F₁ as expected, and the fluid sphere F₁ and Gaussian F₃ models are nearly identical for ka < 1. This suggests that either F₁ or F₃ may be used to interpret scattering from some biological media, assuming the fat particles are more or less spherical and are the dominant scatterer. Close agreement between the glass sphere results F₄ and the spherical shell model F₂ was surprising considering how poorly F₂ resembles the rigid-immovable sphere model F_r [Fig. 2(b)]. It seems that the close agreement is coincidental, due more to the elastic properties of glass and agar than to the physics of the model. Nevertheless, its simplified form makes it useful for studying glass sphere in agar test media (Sec. III). As shown in Fig. 2(b), the glass sphere data F₄ varied significantly from the rigid, immovable sphere data F_r, and the polystyrene sphere data F₅ did not resemble any of the models. These differences are mainly due to the presence of shear waves.

Accounting for the effects of shear wave motion inside the scatterer is important to accurately describe structural properties of solid-particle scattering media using backscatter spectra. When shear waves are not generated or excluded from the scattering equations, the measured form factor for a scatterer is expected to fall between the two extremes F_r and F₁ depending on the degree to which the pressure field penetrates the target, as shown in Fig. 2(c). The agreement between F_r and F₇ in Fig. 2(c) suggests that glass (κ~2.7 × 10⁻¹¹ m²/N) may be considered fairly rigid as compared to the surrounding agar (κ~42 × 10⁻¹¹ m²/N). Figure 2(b), however, shows that the presence of shear waves in glass significantly changes the frequency dependence of scattering. The results for glass, polystyrene, and fat in Fig. 2(b) were calculated using Faran’s equations which include the effects of shear waves, and the results in Fig. 2(c) were calculated using Morse and Ingard’s equations which do not include shear waves. The frequency dependence of scattering from polystyrene is dominated by resonances, which, for ka < 1, decreases the slope of the form factor. [Compare F₅ in Fig. 2(b) with F₈ in Fig. 2(c).] Since the form factor for large particles decreased with frequency faster than for small particles, using the simple models F₁, F₂, and F₃ when shear waves are present tends to systematically result in an overestimation of particle sizes.

The polystyrene results raise many questions regarding the possibility of sizing tissue scatterers. Although scattering from fatty structures can occur in soft tissues, the collagenous tissue stroma is considered to be the dominant source of scattering in most tissues.¹⁶ Parameters for collagen reported in the literature are similar to those for polystyrene given above, so that shear waves are likely to be a factor. We investigated the possibilities of scattering from collagen by computing a theoretical form factor for a collagen sphere suspended in the nonfat medium described above. The parameters given by Cusack and Miller¹⁷ for native collagen were used: density (1.12 g/cm³), Poisson’s ratio (0.42), and longitudinal sound speed (2640 m/s along the fibers and 1890 m/s across the fibers). The resulting form factors are very similar to that of polystyrene data F₅, as shown in Fig. 2(d). The effects of shear waves are discussed further in Sec. IV.

II. FORM FACTOR MEASUREMENTS

A. The echo signal spectrum

The ideal conditions for estimating form factors include monochromatic plane waves incident on an isolated volume containing scatterers. In practice, a broadband pulse from a focused transducer is used to probe an extended medium, for example, the body. Consequently, an expression more general than Eq. (1) is needed to describe scattering under practical conditions. An expression for the scattered pressure at frequency ω due to the incident pressure p_ωi is given by⁹

$$\begin{array}{cc}{p}_{\omega s}(\mathbf{r},t)\hfill & ={\displaystyle {\int }_V[k^2{\gamma }_{\kappa }(\mathbf{r}\prime )p_{\omega i}(\mathbf{r}\prime ,t)G_{\omega }(\mathbf{r},\mathbf{r}\prime )}\hfill \\ \hfill & +{\gamma }_{\rho }(\mathbf{r}\prime )\mathbf{\nabla }\prime p_{\omega i}(\mathbf{r}\prime ,t)·\mathbf{\nabla }\prime G_{\omega }(\mathbf{r},\mathbf{r}\prime )]d^{3}r\prime ,\hfill \end{array}$$ (23)

where the Green’s function is G_ω (r,r′) = exp(ik |r − r′|)/(4π|r − r′|) and |r − r′| is the distance from the observation point to points in the scattering medium V. In writing Eq. (23) and substituting p_ωi for p_ω, we have assumed that the scattered pressure is small compared to the incident pressure, i.e., the Born approximation,⁹ and that the incident pressure is of the time harmonic form exp(−iωt). Equation (23) reduces to Eqs. (1) and (3) for incident plane waves and farfield observation.

We wish to apply Eq. (23) to the analysis of backscattering from a single-element focused transducer operated in pulse-echo mode. In this situation, the incident pressure at frequency ω is given by the expression^18,19

$$p_{\omega i}(\mathbf{r},t)=i{\rho }_0{c}_{0}kA(\mathbf{r},k)U(\omega )e^{-i\omega t},$$ (24a)

where the radiating transducer surface is assumed to move uniformly with speed U(ω)exp(−iωt). The product U(ω)exp(−iωt)A(r,k) has been called the velocity potential,¹⁸ where

$$\mathit{A}(\mathbf{r},k)=\frac{1}{2\pi }{\displaystyle {\int }_{A_0}\frac{e^{ik|\mathbf{r}-\mathbf{r}\prime |}}{|\mathbf{r}-\mathbf{r}\prime |}d{\mathit{A}}_0,}$$ (24b)

and A₀ is the radiating surface area of the transducer element.

The force on the transducer element f_ω(t) is found by integrating the scattered pressure over the transducer aperture

$$f_{\omega }(t)={\displaystyle {\int }_{{\mathit{A}}_0}{p}_{\omega s}(\mathbf{r},t)d{\mathit{A}}_0.}$$

Since Eq. (24b) gives

$${\displaystyle {\int }_{A_0}G(\mathbf{r},\mathbf{r}\prime )dS=\frac{1}{2}\mathit{A}(\mathbf{r},k),}$$

then

$$\begin{array}{cc}{f}_{\omega }(t)\hfill & =\frac{1}{2}{\displaystyle {\int }_V[k^2{\gamma }_{\kappa }(\mathbf{r}\prime )p_{\omega i}(\mathbf{r}\prime ,t)\mathit{A}(\mathbf{r}\prime ,k)}\hfill \\ \hfill & +{\gamma }_p(\mathbf{r}\prime )\mathbf{\nabla }\prime p_{\omega i}(\mathbf{r}\prime ,t)·\mathbf{\nabla }\prime \mathit{A}(\mathbf{r}\prime ,k)]d^{3}r\prime \hfill \\ \hfill & =\frac{1}{2}i{\rho }_0{c}_{0}kU(\omega )e^{-i\omega t}{\displaystyle {\int }_V[k^2{\gamma }_{\kappa }(\mathbf{r}\prime ){\mathit{A}}^2(\mathbf{r}\prime ,k)}\hfill \\ \hfill & +{\gamma }_{\rho }(\mathbf{r}\prime )\mathbf{\nabla }\prime \mathit{A}(\mathbf{r}\prime ,k)·\mathbf{\nabla }\prime \mathit{A}(\mathbf{r}\prime ,k)]d^{3}r\prime .\hfill \end{array}$$ (25)

The second form is found by using Eq. (24a) to define p_ωi.

The frequency dependence of the compressibility and density source terms is the same when

$$-k^2{\mathit{A}}^2(\mathbf{r}\prime ,k)=\mathbf{\nabla }\prime \mathit{A}(\mathbf{r}\prime ,k)·\mathbf{\nabla }\prime \mathit{A}(\mathbf{r}\prime ,k).$$

For plane waves, the above relation is always true. However, Ueda and Ichikawa²⁰ have shown that this relation also holds for focused and nonfocused transducers when the transducer-to-target distance is greater than the transducer diameter. Lizzi et al. have arrived at the same conclusion by showing that the cross-range component of ∇′p_ωi(r′,t) is small compared with the range component.²

Consequently, the integrand in Eq. (25) is approximately equal to k²γ(r′)A²(r′,k), and the force on the transducer element reduces to

$$f_{\omega }(t)=\frac{1}{2}i{\rho }_0{c}_0{k}^{3}U(\omega )e^{-i\omega t}{\displaystyle {\int }_V{\mathit{A}}^2(\mathbf{r}\prime ,k)\gamma (\mathbf{r}\prime )d^{3}r\prime ,}$$ (26)

where γ(r′) = γ_κ(r′) − γ_ρ(r′). As with Eqs. (1) and (3), two powers of the wavenumber k result from the compressibility and density source terms; however, an additional power of k has apparently been introduced into Eq. (26) by the use of a transducer beam. The relation between the transducer beam and the frequency dependence of the echo spectrum is discussed in Sec. II D.

The echo signal $s_m^{\prime }(t)$ recorded in an experiment is given by multiplying Eq. (26) by the acoustoelectric transfer function T(ω) and a temporal gating function g(t), and integrating over all frequencies. The result is

$$\begin{array}{cc}{s}_m^{\prime }(t)\hfill & =g(t){\displaystyle {\int }_{-\infty }^{\infty }T(\omega )f_{\omega }(t)d\omega }\hfill \\ \hfill & =\frac{1}{2}i{\rho }_0{c}_0{\displaystyle {\int }_{-\infty }^{\infty }{k}^3}T(\omega )U(\omega )e^{i\omega t}d\omega \hfill \\ \hfill & \times {\displaystyle {\int }_{-\infty }^{\infty }{\mathit{A}}^2(\mathbf{r}\prime ,k)g(\mathbf{r}\prime )\gamma (\mathbf{r}\prime )d^{3}r\prime .}\hfill \end{array}$$ (27)

In the above equation, we have expressed the temporal gate g(t) as a spatial gate g(r) without loss of generality. The factors A²(r,k) and g(r) define the scattering volume, hence, the second integral is over all space.

The measured echo spectrum $S_m^{\prime }(\omega )$ is the Fourier transform of the echo signal:

$$\begin{array}{cc}{S}_m^{\prime }(\omega )\hfill & =\frac{1}{2}i{\rho }_0{c}_0{k}^{3}T(\omega )U(\omega )\hfill \\ \hfill & \times {\displaystyle {\int }_{-\infty }^{\infty }{\mathit{A}}^2(\mathbf{r}\prime ,k)g(\mathbf{r}\prime )\gamma (\mathbf{r}\prime )d^{3}r\prime .}\hfill \end{array}$$

Defining the factor $C(k)=\frac{1}{2}{\rho }_0{c}_{0}T(\omega )U(\omega )$, the spectrum is written as a function of the spatial frequency variable k:

$$S_m(k)=i{k}^{3}C(k){\displaystyle {\int }_{-\infty }^{\infty }{\mathit{A}}^2(\mathbf{r}\prime },k)g(\mathbf{r}\prime )\gamma (\mathbf{r}\prime )d^{3}r\prime .$$ (28)

B. Measurements near the transducer focus

Often constraints are placed on the experimental conditions to further simplify the expressions. For example, we confine our measurements to the focal zone of a weakly focused transducer, where the phase front of the incident beam is nearly planar and normal to the beam axis. In the focal zone, the integral of Eq. (24b) may be simplified to the well-known result of O’Neil¹⁸:

$$\mathit{A}(\mathbf{r},k)=({\mathit{A}}_0/2\pi r)e^{ikr}\mathit{H}(\theta ),$$ (29)

where

$$\mathit{H}(\theta )=[2J_1(k{a}_0\text{sin}\theta )/k{a}_0\text{sin}\theta ]$$

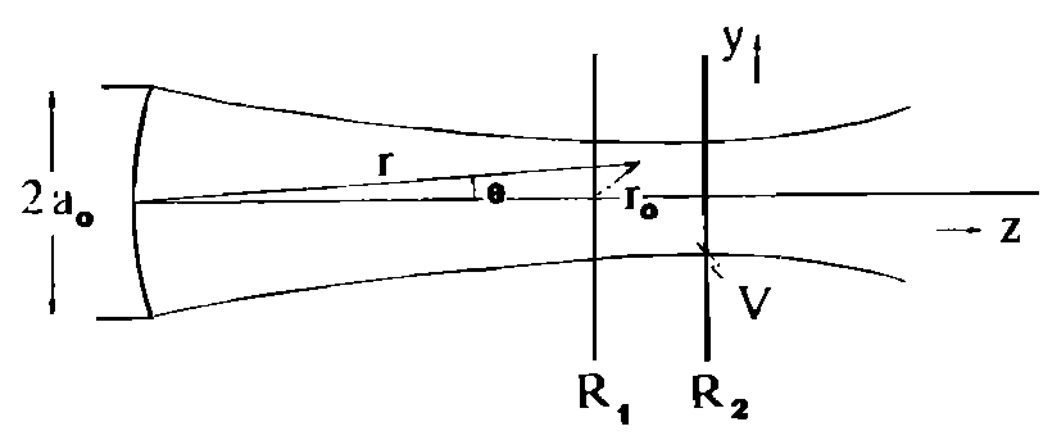
is the directivity function, J₁ is a Bessel function, r and θ are the position coordinates defined with respect to the center of the transducer (Fig. 3), a₀ is the transducer radius, and A₀ is its area.

FIG. 3.

Transducer geometry in the y,z plane.

With the assumption of local plane waves, the directivity function may be specified entirely in the (x,y) plane, i.e., H(θ)~H(x,y), and the gating function may be approximated by a range gate, i.e., g(r)~g(z) (Ref. ²). Also, if the beam width is narrow compared to the transducer-scattering volume distance, then r is approximately R₁ + r₀, where R₁ is the on-axis distance from the transducer to the onset of the gate and r₀ is the distance from the onset of the gate, on axis, to points in V (Fig. 3). In that case, A(r,k) is given by

$$\mathit{A}(\mathbf{r},k)\simeq ({\mathit{A}}_0/2\pi {\mathit{R}}_1)e^{ik{R}_1}{e}^{ik{r}_0}\mathit{H}(x,y).$$ (30)

Combining Eqs. (28) and (30) yields an expression for the spectrum of the echo signal from the focal region of the transducer:

$$\begin{array}{cc}{S}_m(k)\hfill & \simeq \frac{i{\mathit{A}}_0^2{k}^{3}C(k)e^{i2k{R}_1}}{{(2\pi {\mathit{R}}_1)}^2}{\displaystyle {\int }_{-\infty }^{\infty }{\mathit{H}}^2(x_0,y_0)g(z_0)\gamma ({\mathbf{r}}_0)}\hfill \\ \hfill & \times e^{i2k{r}_0}{d}^3{r}_0.\hfill \end{array}$$ (31)

Attenuation along the beam path may be included by defining a complex wavenumber k = ω/c₀ + iα(ω) where α(ω) is the frequency-dependent attenuation coefficient.

C. Spectral normalization

The spectrum in Eq. (31) reflects the frequency dependence of both the instrumentation and the tissue. Spectral normalization is a standard procedure in acoustic measurements for removing instrument effects and obtaining spectral estimates that are representative of the scattering medium. The spectral normalization method used in the present work follows that of Lizzi et al.²

The first step in the normalization process is to measure the spectrum for a reference target; for example, a planar surface may be placed at the focus, perpendicular to the beam axis. The source function for a plane reflector is given by the product

$$\gamma ({\mathbf{r}}_0)=\gamma \prime h(z_0-z_c),$$ (32)

where γ′ is the reflection coefficient for the surface and h(z₀ − z_c) is a step function located at the center of the gate z_c = (R₂ − R₁)/2 (see Fig. 3). Substituting Eq. (32) into Eq. (31) and performing an integration by parts gives the reference signal spectrum S₀

$$\begin{array}{cc}{S}_0(k)\hfill & ={({\mathit{A}}_{0}k/2\pi {\mathit{R}}_1)}^2[\gamma \prime C(k)e^{i2k(R_1+{\mathrm{z}}_c)}/2]\hfill \\ \hfill & \times {\displaystyle \int {\displaystyle {\int }_{-\infty }^{\infty }{\mathit{H}}^2(x_0,y_0)d{x}_{0}d{y}_0,}}\hfill \end{array}$$

where we have defined g(z_c) = 1. It may be shown using Parseval’s theorem²¹ that the integral of the squared directivity function is equal to

$${\displaystyle \int {\displaystyle {\int }_{-\infty }^{\infty }{\mathit{H}}^2(x_0,y_0)d{x}_{0}d{y}_0=\frac{{\lambda }^2{({\mathit{R}}_1+z_c)}^2}{{\mathit{A}}_0}}\simeq \frac{{\lambda }^2{\mathit{R}}_1^2}{{\mathit{A}}_0}},$$

so that the reference spectrum reduces to

$$S_0(k)=\frac{1}{2}{\mathit{A}}_0\gamma \prime C(k)e^{i2k(R_1+z_c)}.$$ (33)

The normalized echo spectrum S is then defined from Eqs. (31) and (33) as

$$\begin{array}{cc}S(k)\hfill & =(\gamma \prime /2)e^{i2k{z}_c}(S_m/S_0)\hfill \\ \hfill & =\frac{i{\mathit{A}}_0{k}^3}{{(2\pi {\mathit{R}}_1)}^2}{\displaystyle {\int }_{-\infty }^{\infty }{\mathit{H}}^2(x_0,y_0)g(z_0)\gamma ({\mathbf{r}}_0)e^{i2k{r}_0}{d}^3{r}_0.}\hfill \end{array}$$ (34)

In practice, Eq. (34) is multiplied by exp[−2α], where α is the difference in attenuation coefficients between the media for the measured echo signals and reference echo signals, and k is taken to be real. Improperly accounting for attenuation in the beam path can result in errors in determining the frequency dependence of backscatter.

The objective of spectral normalization is the elimination of C(k) from the spectral estimate. Here, C(k) expresses the frequency dependence of the pulse spectrum and the acoustoelectric sensitivity of the transducer.

D. The power spectrum

The backscattered power is estimated from the mean-square of the spectrum S averaged over many spatial locations.²³ For statistically homogeneous media, the average normalized power spectrum W for a region of interest (ROI) is given by¹¹

$$\mathit{W}(k)=\frac{1}{{\mathit{N}}_l}{\displaystyle \sum _{l=1}^{N_l}|S_l(k,{\mathit{Z}}_l){|}^2,}$$ (35)

where N_l is the number of gated waveform segments of length Z_l. The average function W approaches the expected power spectrum as N_l approaches infinity, assuming the signals are statistically independent. Equation (35) is analogous to Eq. (6).

The normalized power spectrum in terms of Eq. (34) is given by

$$\begin{array}{cc}\mathit{W}(k)\hfill & =\frac{{\mathit{A}}_0^2{k}^6}{{(2\pi {\mathit{R}}_1)}^4}{\displaystyle \int {\displaystyle {\int }_{-\infty }^{\infty }{\mathit{H}}^2(x_0,y_0){\mathit{H}}^2(x_1,y_1)g(z_0)}}\hfill \\ \hfill & \times g(z_1)\langle \gamma ({\mathbf{r}}_0)\gamma ({\mathbf{r}}_1)\rangle e^{i2k(r_0-r_1)}{d}^3{r}_0{d}^3{r}_1.\hfill \end{array}$$ (36)

The average 〈γ(r₀)γ(r₁)〉 results from averaging over the ensemble of waveform segments, as in Eq. (35). The directivity and gating function are nonstochastic, and therefore have been taken outside the averaging operation.

As in Eq. (8), weak stationarity is assumed, which means that the autocorrelation function for the medium B_γ(r₀,r₁) = 〈γ(r₀)γ(r₁)〉 is a function of only the difference variable Δr = r₀ − r₁. Rewriting W in terms of sum and difference variables u = (r₀ + r₁)/2 and Δr = r₀ − r₁ (Ref. ⁴), the power spectrum may be expressed as the Fourier transform of the product of autocorrelation functions:

$$\begin{array}{cc}\mathit{W}(k)\hfill & =\frac{{\mathit{A}}_0^2{k}^6}{{(2\pi {\mathit{R}}_1)}^4}{\displaystyle {\int }_{-\infty }^{\infty }{\mathit{B}}_H(\mathrm{\Delta }x,\mathrm{\Delta }y){\mathit{B}}_g(\mathrm{\Delta }z){\mathit{B}}_{\gamma }(\mathrm{\Delta }\mathbf{r})}\hfill \\ \hfill & \times e^{i2k\mathrm{\Delta }r}{d}^3\mathrm{\Delta }r,\hfill \end{array}$$ (37)

where

$$\begin{array}{cc}{\mathit{B}}_H(\mathrm{\Delta }x,\mathrm{\Delta }y)\hfill & ={\displaystyle {\int }_{-\infty }^{\infty }{\mathit{H}}^2\left(u_x+\frac{\mathrm{\Delta }x}{2},u_y+\frac{\mathrm{\Delta }y}{2}\right)}\hfill \\ \hfill & \times {\mathit{H}}^2\left(u_x-\frac{\mathrm{\Delta }x}{2},u_y-\frac{\mathrm{\Delta }y}{2}\right)d{u}_{x}d{u}_{y,}\hfill \\ \hfill {\mathit{B}}_g(\mathrm{\Delta }z)& ={\displaystyle {\int }_{-\infty }^{\infty }g(u_z+\frac{\mathrm{\Delta }z}{2})g(u_z-\frac{\mathrm{\Delta }z}{2})d{u}_z.}\hfill \end{array}$$

B_H is the autocorrelation of the pulse-echo transducer-beam directivity, and B_g is the autocorrelation of the range gate. If B_γ becomes negligibly small before either B_H or B_g changes significantly, then we can assume B_H and B_g are constants given by their value at zero lag.^2,4 The power spectrum is then equal to

$$\begin{array}{cc}\mathit{W}(k)\hfill & \simeq \frac{{\mathit{A}}_0^2{k}^6}{{(2\pi {\mathit{R}}_1)}^4}{\mathit{B}}_H(0,0){\mathit{B}}_g(0){\displaystyle {\int }_{-\infty }^{\infty }{\mathit{B}}_{\gamma }(\mathrm{\Delta }\mathbf{r})e^{i2k\mathrm{\Delta }r}{d}^3\mathrm{\Delta }r}\hfill \\ \hfill & \simeq \frac{4{\pi }^2{\mathit{A}}_0^2{k}^6\overline{n}}{{\mathit{R}}_1^4}{\mathit{B}}_H(0,0){\mathit{B}}_g(0){\mathbf{\Gamma }}^2(2k),\hfill \end{array}$$ (38)

where the integral above has already been defined for incoherent scattering in Eqs. (10) and (12) as (2π)⁶n̄Γ²(2k). Since B_H(0,0) and B_g(0) can easily be calculated for the experimental conditions described above, Eq. (38) may be used to estimate Γ²(2k), and hence the form factor F(2k), from a measurement of the normalized power spectrum.

Ueda and Ozawa²² have reduced B_H(0,0) assuming ka₀ ≫ 1, to

$$\begin{array}{cc}{\mathit{B}}_H(0,0)\hfill & ={\displaystyle {\int }_{-\infty }^{\infty }{\mathit{H}}^4(u_x,u_y)d{u}_{x}d{u}_y}\hfill \\ \hfill & =2\pi {\left(\frac{{\mathit{R}}_1}{k{a}_0}\right)}^2{\displaystyle {\int }_0^{\infty }{\left(\frac{2{\mathit{J}}_1(\zeta )}{\zeta }\right)}^4\zeta d\zeta }\hfill \\ \hfill & =\frac{0.46}{{\mathit{A}}_0}{\left(\frac{2\pi {\mathit{R}}_1}{k}\right)}^2.\hfill \end{array}$$ (39)

The integral in Eq. (39) was evaluated numerically to give a value of 0.92. Notice that although the transducer beam seems to contribute the factor k² to the echo signal power spectrum, Eq. (38), the quantity B_H(0,0) is proportional to k⁻². The net result is that the transducer beam does not influence the frequency dependence of the normalized power spectrum.

In our experiments, the echo signal is gated with a Hanning window (Ref. ¹¹, Eq. 11.108) given by the expression

$$g(z)=\{\begin{array}{cc}\frac{1}{2}|1-\text{cos}(2\pi z_0/2z_c)|,\hfill & {\mathit{R}}_1\le z_0\le {\mathit{R}}_{2,}\hfill \\ 0,\hfill & \text{otherwise}.\hfill \end{array}$$

The corresponding autocorrelation function may be evaluated to give

$${\mathit{B}}_g(0)={\displaystyle {\int }_{-\infty }^{\infty }{g}^2(u_z)d{u}_z=0.75z_c.}$$ (40)

Using Eqs. (38)–(40), the normalized power spectrum can be reduced to

$$\begin{array}{cc}\mathit{W}(k)\hfill & \simeq (0.34{\mathit{A}}_0{z}_c/{\mathit{R}}_1^2){(2\pi k)}^4\overline{n}{\mathbf{\Gamma }}^2(2k)\hfill \\ \hfill & \simeq (0.34{\mathit{A}}_0{z}_c/{\mathit{R}}_1^2)4{\sigma }_b.\hfill \end{array}$$ (41)

The experimental parameters A₀, z_c, and R₁, will scale the magnitude of W, but do not modify its frequency dependence. The frequency dependence of the normalized power spectrum depends only on the backscatter coefficient σ_b.

E. Parameter estimation

The estimated form factor F̂(2k), which accounts for attenuation losses, is computed from Eqs. (15), (16), and (41):

$$\widehat{F}(2k)={\sigma }_b/{\sigma }_0\simeq (0.73{\mathit{R}}_1^2/{\mathit{A}}_0{z}_c{\sigma }_0)\mathit{W}(k)e^{4\alpha (R_1+z_c)}.$$

The result may be grouped into three factors:

$$\widehat{F}(2k)\simeq \left(\frac{6.5{\mathit{R}}_1^2}{{\mathit{A}}_0{z}_c}\right){(\overline{n}{a}^6{\gamma }_0^2)}^{-1}(k^{-4}\mathit{W}(k)e^{4\alpha (R_1+z_c)}).$$ (42)

The first two factors scale the third, such that 0≤F̂≤1. The first factor is easily calculated from the geometry of the experiment. The second factor describes unknown properties of the medium that we seek to determine: the number density of particles n̄, size a, and the average scattering strength per particle ${\gamma }_0^2$. The third factor describes the frequency dependence of the power spectrum that is due to the geometry and the internal degrees of freedom of the particle under the physical boundary conditions. The third factor can be determined independently of the first two by computing the normalized power spectrum W(k), accounting for k⁴ and attenuation as in Eq. (42), and rescaling the result to have a value of one at k = 0. With the elimination of the first two factors and the assumption that the appropriate scattering function (i.e., form factor model) is known, particle sizes may be estimated independently of the other unknown properties.

The strategy for estimating particle sizes involves standard least-squares methods. First, a scattering model is chosen, e.g., Eqs. (18), (19), or (22). Next, a set of model form factors is calculated and stored in a look-up table (LUT). The set contains the functions F(2k) at a range of particle sizes for which the chosen model is valid; there is one function F for each particle size a. Finally, the data, i.e., third factor in Eq. (42), are “compared” with each model F(2k) in the set (Fig. 4). The size estimate â is determined from the model with the minimum average squared deviation (MASD):

$$\mathbf{\text{MASD}}=\text{min}{\left(\frac{1}{m}{\displaystyle \sum _{i=1}^m{(X-\overline{X})}^2}\right)}_a,$$ (43)

where X = 10 log[W(k)exp(4α(R₁ + z_c))/k⁴F(2k)] and

$$\overline{X}=\frac{1}{m}{\displaystyle \sum _{i=1}^m{X}_i.}$$

The sums are over all frequencies in the bandwidth of the data. The quantity X is the ratio of the measured form factor to the modeled form factor, expressed in decibels (dB). Subtracting the average X̅ from X accomplishes the rescaling discussed in the previous paragraph.

FIG. 4.

Measured (noisy line) and modeled (smooth line) form factors for a 105-µm-diam glass microsphere sample (Table I) scanned using a 5-MHz broadband transducer (Table II). The spherical shell model F₂ with a 95-µm-diam sphere size gave the best fit (MASD) to the data over the transducer bandwidth.

Once â is determined, its value can be used in Eq. (42) to estimate the average net scattering strength $\overline{n}{\gamma }_0^2$. It is convenient to use X̅ for this purpose. Converting X̅ from dB gives the geometric mean exp(0.2303X̅) which equals the inverse product of the first two factors on the right side of Eq. (42). The average net scattering strength is therefore approximated by

$$\overline{n}{\gamma }_0^2\simeq (6.5{\mathit{R}}_1^2/{\mathit{A}}_0{z}_c{\mathit{â}}^6)\text{exp}(0.2303\overline{X}).$$ (44)

Without additional information n̄ and ${\gamma }_0^2$ cannot be determined independently.

III. TESTS OF THE METHOD

A. The experiment

The methods for estimating the average particle size and the average net scattering strength $\overline{n}{\gamma }_0^2$ were tested using well-defined test materials. Each material contained either glass or polystyrene microspheres. In both cases the microspheres were randomly positioned in agar, and the distribution of diameters found in any one sample was strongly peaked about the mean so that a single particle size could be assumed. Microsphere diameter distributions were measured by the manufacturer using an optical microscope with an eyepiece reticle calibrated with an NBS certified stage micrometer.²⁴ Sample materials were formed into a cylindrical shape 2.5 cm thick and 7.5 cm in diameter. Physical properties of the component materials are given in Sec. I C. Table I is a list of the samples by number, along with values of mean sphere diameter, number density, speed of sound, and bulk attenuation. Attenuation and speed of sound were measured using a broadband, through-transmission technique.²⁵

TABLE I.

A summary of the properties of ten scattering phantoms used to test the method. The first nine contain glass microspheres (g); the tenth contains polystyrene microspheres (p).

Sample	Nominal sphere diameter (µm)	Number density (mm−3)	Speed of sound (m/s)	Attenuation (dB/cm)
1	40 ± 3(g)	14.6	1544	0.17f1.4
2	41 ± 2(g)	24.2	1540	0.17f1.2
3	41 ± 2(g)	24.2	1542	0.19f1.2
4	75 ± 3(g)	3.00	1543	0.26f1.1
5	85 ± 3(g)	12.1	1548	0.17f1.2
6	105 ± 4(g)	1.46	1547	0.18f1.5
7	120 ± 4(g)	4.35	1545	0.17f1.3
8	175 ± 6(g)	0.15	1545	0.17f1.6
9	175 ± 6(g)	0.73	1544	0.20f1.4
10	81 ± 4(p)	4.2	1565	0.17f1.1

Data were obtained using one of four focused transducers whose properties are listed in Table II. Samples were placed in distilled water at 22 °C and oriented such that the axis of the sample cylinder was parallel to the beam axis. Each sample was positioned in the focal zone of the transducer, where 25 pulse-echo waveforms were recorded. The transducer was translated 5 mm lateral to the beam axis between recordings. A rectilinear scanning motion was used to span a sample cross-sectional area of approximately 400 mm². Waveform segments were recorded at 25 Msamples per second, each 512 points long. Waveform segments were multiplied by a Hanning window,¹¹ the spectrum for each segment was computed using an FFT algorithm, and the results were averaged to give the sample spectrum. A reference spectrum was computed from an average of ten waveforms recorded using a Lucite plate also positioned in water at a distance corresponding to the center of the gated region (R₁ + z_c). From the sample and reference spectra, the normalized power spectrum W(k) was determined using Eq. (35).

TABLE II.

Characteristics of transducers used in the phantom measurements.

Transducer	Nominal center frequency diameter	Measured peak frequency (MHz)	12-dB bandwidth (MHz)	Measured focal length (mm)
1	2.25 MHz/19 mm	2.2	1.7	99
2	3.5 MHz/13 mm	4.0	4.0	73
3	5.0 MHz/13 mm	4.6	3.7	90
4	7.5 MHz/9 mm	7.8	4.0	36

Many of the samples were covered by a plastic membrane to retard desiccation. This 50-µm-thick membrane (ρ ~ 1.7 g/cm³,c_L ~ 2500 m/s) introduced a significant frequency-dependent loss at the water–sample interface. This loss was accounted for by dividing W(k) by the square of the intensity transmission coefficient calculated for a thin layer at normal incidence (Ref. ¹⁹, Eq. 6.13).

B. Results

Form factors were estimated from recorded waveforms over a 12-dB bandwidth and fit to model functions. The minimum average squared deviation Eq. (43) was the criterion used to determine the best fit and hence the most likely particle size. For example, see Fig. 4 where the 105-µm-diam glass microsphere sample was scanned at 5.0 MHz (ka ~ 1). The data (noisy line) fit the 95-µm model (smooth line) with the minimum averaged squared deviation (MASD). Model functions between 20 and 500 µm in 1-µm increments were calculated and stored in an LUT for comparisons with the data. These size estimates were then used in Eq. (44) to compute scattering strength estimates. All results are summarized in Table III.

TABLE III.

Estimates of scattering-particle size (2â) and the scattering strength $(\overline{n}{\gamma }_0^2)$ are summarized below. The spherical shell form factor model [Eq. (19)] was used to calculate the results of column A, and that of Faran (Ref. ¹³ and Sec. I C) was used for column B.

				Results A		Results B
Sample	Nominal sphere diameter (microns)	Nominal $\overline{n}{\gamma }_0^2$ (mm−3)	Center frequency (ka)	Estimated sphere diameter 2â (µm)	Estimated $\overline{n}{\gamma }_0^2$ (mm−3)	Estimated sphere diameter 2â (µm)	Estimated $\overline{n}{\gamma }_0^2$ (mm−3)
	glass
1	40 ± 3	40	7.5 MHz(0.61)	40 ± 7	42	38	47
2	41 ± 2	66	7.5 MHz(0.61)	42 ± 8	78	37	120
3	41 ± 2	66	7.5 MHz(0.61)	49 ± 5	21	41	71
4	75 ± 3	8.2	5.0 MHz(0.76)	73 ± 32	…	73	…
5	85 ± 3	33	3.5 MHz(0.61)	102 ± 12	20	84	54
			5.0MHz(0.87)	87 ± 11	26	87	26
6	105 ± 4	4.1	5.0 MHz(1.07)	95 ± 9	5.2	105	2.1
7	120 ± 4	12	3.5 MHz(0.86)	111 ± 9	7.5	115	10
			5.0 MHz(1.22)	95 ± 8	13	113	8.2
8	175 ± 6	0.15	2.25 MHz(0.80)	169 ± 33	…	165	…
9	175 ± 6	0.73	2.25 MHz(0.80)	186 ± 30	…	170	…
10	polystyrene	0.93	2.25 MHz(0.37)	not applicable	not applicable	86	2.5
	81 ± 4		5.0 MHz(0.83)			83	6.6

Values reported in column A of Table III were determined by fitting F₂ functions, the spherical shell form factor model, to the data. Here, F₂ was chosen because it closely agreed with the form factor for glass microspheres computed using the theory of Faran [Fig. 2(a)]. Overall, the estimated and nominal sphere diameters agree to within 20%. The scattering strength estimates were highly variable, but, in general, were correlated with the nominal values.

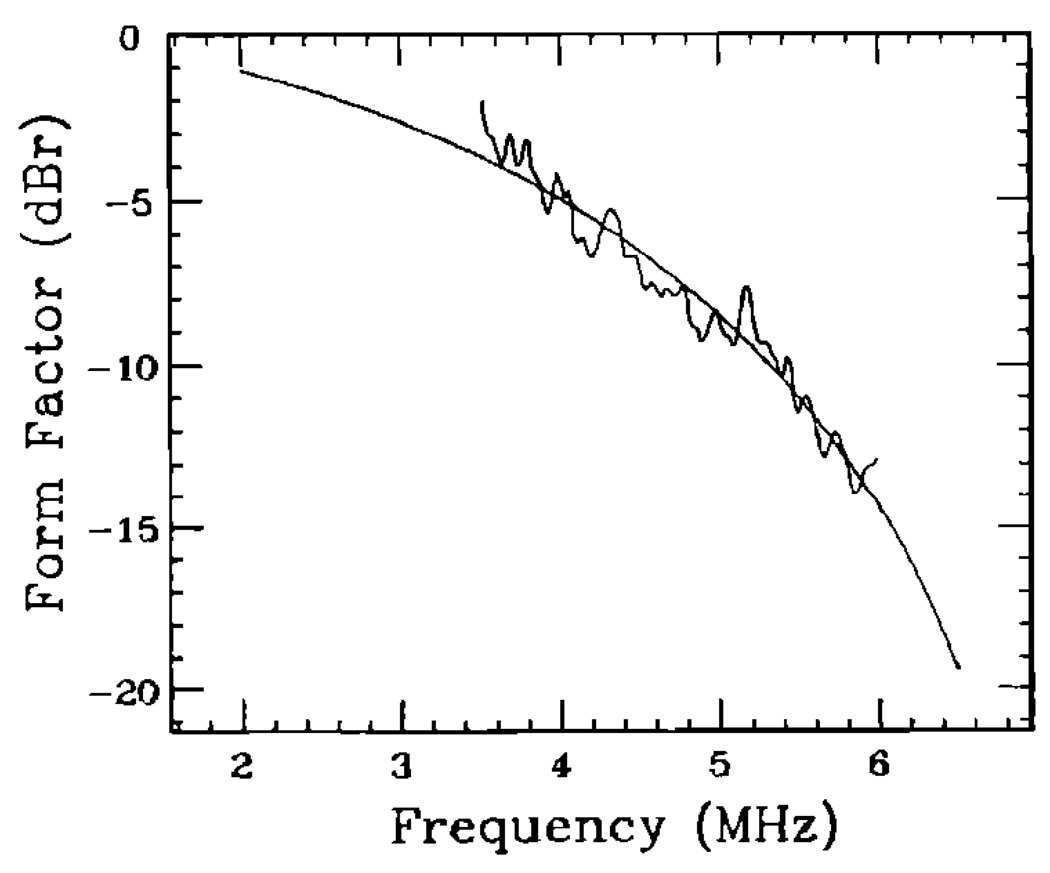
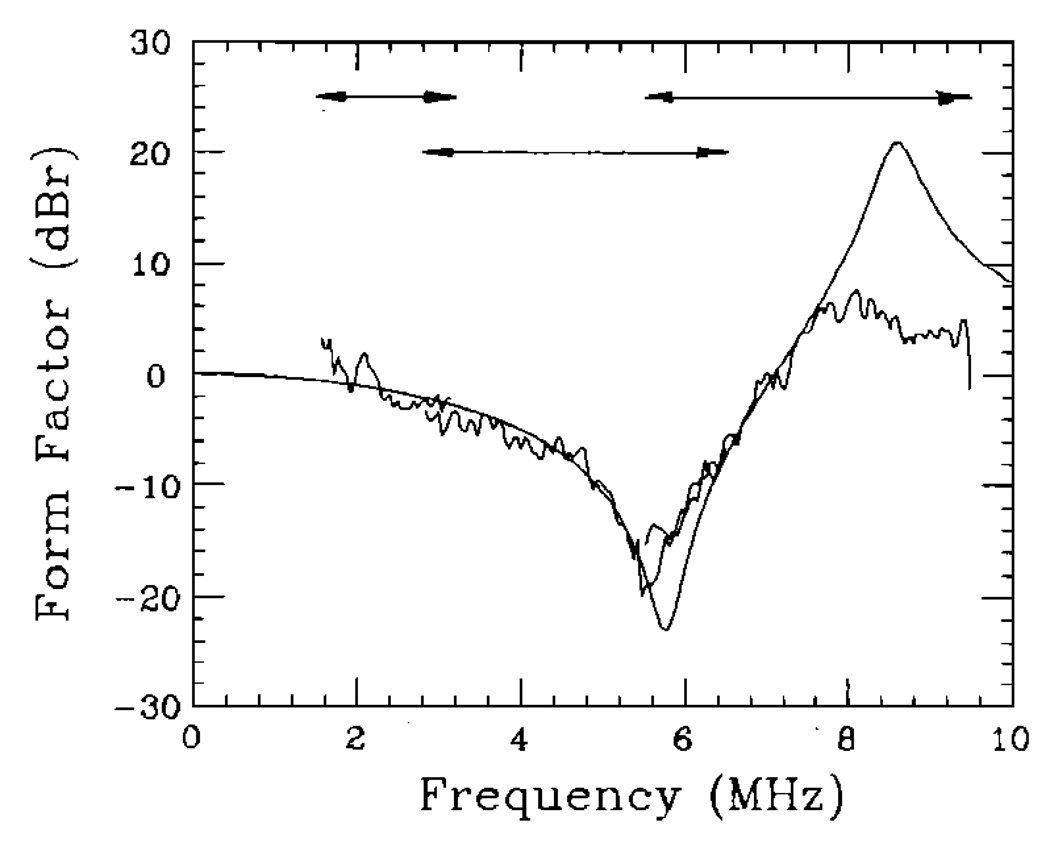
Values reported in column B of Table III were determined by fitting the data to form factors computed using the theory of Faran, as described in Sec. I C. Because this theoretical model is valid at all ka and includes the effects of shear waves, we expected closer agreement between the estimated and nominal values. We found that, for the glass microsphere samples, the accuracy of the size estimates improved to within 10%, but observed no improvement in the accuracy of scattering strength estimates. This scattering model allowed us to estimate the size of the 81-µm polystyrene microspheres in sample 10 to within 10%. The frequency dependence of the estimated form factor data for the polystyrene sample may be compared to that of the Faran model in Fig. 5, from 1.5 MHz (ka = 0.25) to 9.5 MHz (ka = 1.6). Pictured is the best fit between the data and the model, which occurred at 83 µm. Three transducers were used to span this range of frequencies. The magnitude of each data segment was adjusted in order to give the appearance of a continuous data set.

FIG. 5.

Comparison between form factors measured for the 81-µm polystyrene microsphere sample (noisy lines) and modeled using the scattering theory of Faran¹³ and assuming 83-µm-diam spheres (smooth line). Three transducers were used to span the range of 1.5–9.5 MHz as indicated. A 2.25-MHz transducer was used to obtain data from 1.5 to 3.2 MHz, a 5.0-MHz transducer from 2.8 to 6.5 MHz, and a 7.5-MHz transducer from 5.5 to 9.5 MHz. The three data segments were scaled individually to give the appearance of a continuous line. No modifications to the frequency dependence of the data were made.

The uncertainties in particle size estimates listed in column A were approximated by the equation

$$\text{var}(\mathit{X})=\text{var}(2\mathit{â}){\left(\frac{\partial \mathit{X}}{\partial (2a)}\right)}_{2\mathit{â},k_c}^2,$$

where var(X) is the variance in X, defined below Eq. (43), and var(2â) is the variance in the size estimate 2â. The last factor is the square of the derivative of X with respect to the particle size, evaluated at the estimate 2â and at the wavenumber corresponding to the center frequency of the transducer k_c.

The estimated variance in X is given by a rescaled Eq. (43): var(X) = m/(m − 1) MASD, and, for the data in column A,

$$\frac{\partial \mathit{X}}{\partial (2a)}=-10\frac{\partial }{\partial (2a)}\text{log}{\mathit{F}}_2.$$

Therefore, the standard deviation in the particle size estimates in column A was computed using

$$\mathrm{s}.\mathrm{d}.(2\mathit{â})={\left(\frac{m}{1-m}\mathbf{\text{MASD}}\right)}^{1/2}{\left(10\frac{\partial }{\partial (2a)}\text{log}{\mathit{F}}_2\right)}^{-1}.$$

This expression is only approximately true since the derivative is a weak function of k and, in practice, also depends on the uncertainty in attenuation.

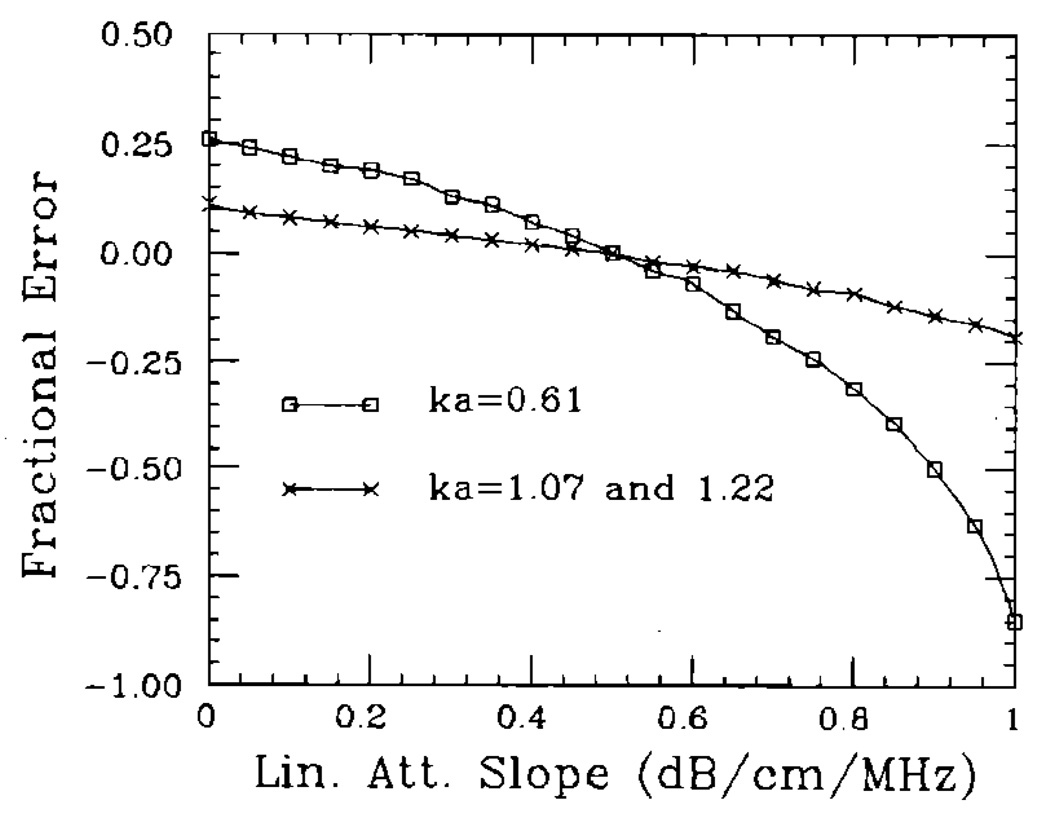
Errors in size estimates that are generated by an uncertainty in the linear attenuation slope are shown in Fig. 6. Assuming the actual attenuation slope was 0.5 dB/cm, values between 0.0 dB/cm and 1.0 dB/cm were used to compute the size estimates. Overestimation of the attenuation slope resulted in a larger error than underestimation, as seen in Fig. 6, and the magnitude of the error depended on the value of ka. The ka dependence observed results from low measurement sensitivity: The frequency dependence of scattering is of greatly affected by particle size for small values of ka. Because of the low attenuation in the test samples, the uncertainty in attenuation estimates was not a significant factor in the results of Table III.

FIG. 6.

Plots of the variation in particle size estimates with an uncertainty in the linear attenuation slope estimate. The results depend on the value of ka, and span the range of attenuation values typical in soft biological tissues. The errors for ka = 1.22 and ka = 1.07 are identical. Lower values of ka give rise to larger errors.

IV. DISCUSSION

Our intent was to use elementary scattering functions to describe the microscopic structure of random inhomogeneous media. Experimental results using glass-in-agar media show it is possible to estimate an average particle size and the scattering strength. The accuracy of the measurements, however, depended on the choice of correlation model (form factor) for the medium and the experimental conditions.

If the scattering medium does not support shear wave propagation and if data are acquired in the range ka < 1, the choice of model is not critical. At long wavelengths, all the models converge. Yet at very long wavelengths, the frequency dependence of scattering, as measured by the form factor, is only slowly varying with particle size, and that means reduced measurement sensitivity in the presence of noise. A compromise between the trade-offs in sensitivity and the need to use a more detailed model is to estimate particle sizes in the transition region where 0.5 < ka < 1.2. In the 1.0- to 10.0-MHz range of frequencies used in medical ultrasound, this corresponds to particle sizes between 20 and 500 µm.

If shear waves are generated in the scattering particles, as was the case for the polystyrene microsphere sample, then a more detailed scattering model is needed to accurately describe the scattering structure. When the Faran theory was used in our analysis (column B, Table III), the accuracy of particle size estimates increased for the glass samples, and it was possible to obtain size estimates for the polystyrene sample, which has a significant shear wave component. The lack of agreement between the model and the data observed in Fig. 5 at high frequencies is likely due to small uncertainties in the elastic properties of polystyrene used to generate the model function, e.g., density, sound speed, and Poisson’s ratio. In general, the elastic properties for a material depend on the size and shape of the material: we used bulk properties, as did Faran.

Faran showed how to predict when shear waves are significant. He demonstrated that the complicated wave structure that constitutes resonance phenomena, i.e., vibrations inside the scatterer, occurs at lower frequencies with shear waves than without shear waves. With relatively incompressible materials such as glass, all resonances occur at fairly large values of ka (> 1.5) (see Fig. 17, Ref. 13). Therefore, in the range 0 < ka < 1.2, the variation between the form factor for glass spheres in agar and the rigid immovable sphere is not very great [see Fig. 2(b)]. As the scatterer material becomes more compressible, such as with polystyrene, the resonances associated with shear waves move to lower values of ka. These resonances significantly change the frequency dependence of scattering. This change is shown in Fig. 2(b) for polystyrene as an increase in the curvature of the form factor for ka < 1. The increased curvature results in an overestimation of particle sizes and a concomitant underestimation in scattering strength.

Estimates of the scattering strength were generally accurate to within a factor of 2, and the accuracy did not obviously depend on the model used. The uncertainty in this measure is greatly influenced by errors in the particle size estimate. Small errors in the estimate â translate into large errors in the scattering strength, since $\overline{n}{\gamma }_0^2\propto {\mathit{â}}^{-6}$. This method for estimating the scattering strength is overextended in the sense that two unknowns are determined from one data set.

Describing the scattering structure of biological tissues will be more difficult than it was for the agar samples. What is known about many tissues is that the scattering is dominated by collagen,¹⁶ and, although the correlation function for tissue is unknown, the Gaussian model has provided a consistent description of tissue structures.^3,6–8 The relevant elastic properties of collagen available in the literature¹⁷ suggest that, like with polystyrene, shear waves play a significant role in scattering. Therefore, if we can model tissue structures with simple shapes such as spheres or cylinders and as the elastic properties become better defined, the scattering theory of Faran would be the most accurate model for describing tissue structures. Acoustic microscopy studies may eventually provide this information. Until that time, simple scattering functions, such as Eqs. (18), (19), and (22), may be useful in probing tissues for relative changes in the collageneous tissue stroma that charaterize many pathological processes. In images formed using these measures, it is the relative, rather than the absolute changes in tissue properties that provides the contrast needed for detectability. Methods that are highly sensitive to small changes in tissue structures can provide an important diagnostic tool for tissue characterization.

LIST OF SYMBOLS

Most of the symbols used here are the same as those used by Ishimaru,¹ Campbell and Waag,⁴ and Morse and Ingard.⁹

a

particle radius

â

particle radius estimate

a₀

transducer radius

A₀

transducer surface area

A

function proportional to the Rayleigh integral

b_γ

correlation coefficient

B

autocorrelation function

c,c₀

longitudinal sound speed inside the scatterer and inside the surrounding medium

C

system frequency response factor

C_γ

autocovariance function

d

characteristic dimension for a Gaussian correlation coefficient

f

acoustic force on the transducer

F,F̂

computed, estimated intensity form factors

g

gating function

G

Green’s function

H

directivity function

î

unit vector for incident plane waves

j_n

spherical bessel function of the first kind

J_n

bessel function of the first kind

k

wavenumber, ω/c

K

scattering vector

MASD

minimum average squared deviation

n̄

average particle number density

ô

unit vector for scattered waves

p_i, p_s, p

incident, scattered, and total acoustic pressure

r

position vector

R₁, R₂

the on-axis distance between the transducer and the proximal, distal surface of the gated region

s_m, S_m

sample echo signal and its frequency spectrum

S₀

reference echo frequency spectrum

S

normalized echo frequency spectrum

T

acoustoelectric transfer function

U

speed of the transducer surface motion

v

Poisson’s ratio

V

scattering volume

w

fractional volume of scatterers in V

W

average normalized echo power spectrum

X

a spectral measure

z_c

(R₂ − R₁)/2

α

attenuation efficient

γ_κ, γ_ρ, γ₀

the fractional variation in compressibility and density and the combined value per particle

Γ²

the power spectral density function for the medium fluctuations γ

ζ

an integration variable

θ

a scattering angle

κ, κ₀

the compressibility of a scatterer and the surrounding medium

λ

wavelength

ρ, ρ₀

the density of a scatterer and the surrounding medium

σ_d, σ_b, σ₀

differential scattering cross sections per unit volume as a function of angle, at 180° (backscatter coefficient), and at 180° in the Rayleigh limit, respectively

Φ

complex scattering amplitude

ω

angular frequency