Automated main-chain model building by template matching and iterative fragment extension

A method for automated macromolecular main-chain model building is described.

Abstract

An algorithm for the automated macromolecular model building of polypeptide backbones is described. The procedure is hierarchical. In the initial stages, many overlapping polypeptide fragments are built. In subsequent stages, the fragments are extended and then connected. Identification of the locations of helical and β-strand regions is carried out by FFT-based template matching. Fragment libraries of helices and β-strands from refined protein structures are then positioned at the potential locations of helices and strands and the longest segments that fit the electron-density map are chosen. The helices and strands are then extended using fragment libraries consisting of sequences three amino acids long derived from refined protein structures. The resulting segments of polypeptide chain are then connected by choosing those which overlap at two or more C^α positions. The fully automated procedure has been implemented in RESOLVE and is capable of model building at resolutions as low as 3.5 Å. The algorithm is useful for building a preliminary main-chain model that can serve as a basis for refinement and side-chain addition.

1. Introduction

Model building is a key and often time-consuming step in macromolecular structure determination. This step is important because model building is the initial interpretation of the experimental electron-density map in terms of the locations of atoms in the structure. If the resolution of the X-ray data is high (<2 Å), then atomic refinement of the model is highly effective and errors in the initial interpretation can often be corrected. If the resolution of the X-ray data is low (∼3 Å), however, atomic refinement is less effective and it may be very difficult to correct any errors in this initial interpretation (Kleywegt & Jones, 1997 ▶). Although manual model building using a very good electron-density map can require less than a day for 100 or more residues, when the electron-density map is less clear the process can be much slower.

It has been recognized for some time that automated procedures for model building would speed up the macromolecular structure determination process considerably and several procedures for doing this have been developed. Most of these procedures are based on the connectivity of the polypeptide chain or on the presence of regular structure (helices and β-strands, common motifs) in the chain. Greer (1985 ▶) devised a rapid procedure (‘bones’) for tracing the path of the polypeptide chain using the connectivity of regions of high electron density in the map. This procedure was extended by Swanson (1994 ▶) to allow threshold-independent tracing of connected regions in a map. Feigenbaum et al. (1977 ▶) used artificial intelligence methods to identify features in electron-density maps. Jones & Thirup (1986 ▶) and Jones et al. (1991 ▶) fitted electron density with fragments from known protein structures. Oldfield (2002 ▶) described a method for automated model building that began by identifying helices and strands and then extending these segments one amino acid at a time to trace a polypeptide chain. Cowtan (1998 ▶, 2001 ▶) and later Terwilliger (2001 ▶) used FFT-based approaches to identify the locations of helices, β-strands and other structure in an electron-density map by template matching. Holton et al. (2000 ▶) used machine-learning techniques to identify side chains in a map. McRee (1999 ▶) has described a semi-automated method for building main-chain and side-chain models in a map, beginning with the identification of C^α positions and fitting fragments from a main-chain library and continuing with using a rotamer library to fit side chains. Pavelcik et al. (2002 ▶) described an alternative and very rapid method for template matching of arbitrary fragments of structure to a map. Levitt (2001 ▶) uses a stepwise approach to model building, beginning with the ‘bones’ of Greer (1985 ▶) to identify helices and strands and extending them one amino acid at a time using ψ, ϕ angles from tables of allowed values. The most widely used automated model-building procedure in current use, ARP/wARP, has been described by Lamzin & Wilson (1993 ▶), Perrakis et al. (1999 ▶) and Morris et al. (2002 ▶). This procedure is very different from all those described above because it is based on an interpretation of the electron-density map in terms of individual atoms, iteratively followed by atomic refinement and an interpretation of the atomic coordinates in terms of a polypeptide chain. The requirement for atomicity limits the application of the method to electron-density maps at a resolution of about 2.3 Å, but for data at this resolution or better the method is exceptionally powerful for automatic model building and atomic refinement.

Here, we describe a procedure for automated model building that is related to those described by Oldfield (2002 ▶), McRee (1999 ▶) and Levitt (2001 ▶), but which uses alternative approaches to carry out each of the constituent steps. The method of Cowtan (1998 ▶) is used as a sensitive method for identifying the locations of helices and β-strands. Correlations of template density and map density rather than density at atomic coordinates are used for refinement of the position and orientation of fragments. A fragment-placement method based on tripeptides from refined protein structure and related to the method of Jones & Thirup (1986 ▶) is used to extend segments of structure. Chain connectivity and the correct chain direction are determined by requiring that independently built segments must overlap at two or more consecutive C^α positions before they are merged into a single segment.

2. Methods

As in previous methods for main-chain model building at moderate resolution (Oldfield, 2002 ▶; Levitt, 2001 ▶), our procedure is carried out in hierarchical steps. Firstly, helices and β-strands are located and fitted, with multiple interpretations of each of these secondary structures typically kept. Each helix or strand is then extended in an iterative fashion with libraries of tripeptides from refined protein structures. The collection of (overlapping) partially extended fragments are then assembled into a polypeptide chain by requiring that two or more consecutive C^α positions overlap for two segments to be merged, by requiring that there be no atomic overlaps and by beginning with the best-fitting segments. Each of these steps and the generation of templates and fragment libraries is described below. In all steps, space-group symmetry is used to identify positions that are equivalent in the unit cell and the distance between two points is considered to be the smallest distance between one of the points and any point symmetry-related to the other.

2.1. Helical and β-strand templates

An averaged helical template similar to that described in Terwilliger (2001 ▶) was used to identify helical segments in a map. This template consists of the average electron density calculated from a collection of α-helical segments six amino acids in length (from phycoerythrin; PDB code 1lia; Chang et al., 1996 ▶; Berman et al., 2000 ▶), all superimposed on a standard α-helical segment (from myoglobin; PDB code 1a6m; Vojtechovsky et al., 1999 ▶; Berman et al., 2000 ▶). The template included all points within 4 Å of a main-chain or C^β atom in the standard segment. The template was calculated at a resolution of 3 Å. An averaged β-strand template was constructed in the same fashion, except that the segments used in the template were four amino acids long.

2.2. Fragment libraries

Four fragment libraries were constructed. One consisted of 17 α-helical segments from six to 24 residues long in the protein phycoerythrin. Each segment of more than six residues was superimposed on the standard helical segment in three positions: one with the N-terminal six residues of the segment superimposed on the standard segment, one with the C-terminal six residues superimposed and one with the middle six residues superimposed. In this way, a short helical segment that is identified can potentially be extended in either direction. A second library consisted of 17 β-strand segments from four to nine amino acids long from chain A of carboxypeptidase A (PDB code 1bav; Massova et al., 1996 ▶; Berman et al., 2000 ▶), superimposed on the standard β-strand fragment in the same way as for the helical segments.

The third and fourth libraries consisted of segments of protein structure three amino acids in length chosen to represent all three-amino-acid segments in a set of refined protein structures [chosen arbitrarily from non-redundant PDB files (Hobohm et al., 1993 ▶) with R factors of 20% or lower and resolution 1.8 Å or better]. The two libraries differed in that one contained all main-chain and C^β atoms of a tripeptide and the other contained the C^α, C and O of one residue plus the following two full residues. The first library was designed for extending a polypeptide chain in the N-­terminal direction by superimposing the last C^α, C and O atoms of the template with the corresponding atoms of the N-­terminal residue in a chain. The second library was designed for extending in the C-terminal direction, superimposing the same three atoms. The two libraries were subsets of the set of all tripeptides (or tripeptides minus the N) in a set of refined protein structures. In each case, the library was constructed by picking members that differed from each other by at least 0.5 Å r.m.s. and such that all tripeptides matched a member of the library with an r.m.s. deviation of less than 0.5 Å. The N-­terminal library was based on 298 proteins and contained 9232 members, and the C-terminal library was based on 567 protein structures and contained 4869 members.

2.3. Convolution-based identification of the locations of helical and β-strand segments

The approximate locations and orientations of helices and β-­strands were identified using the helical and β-strand templates mentioned above and an FFT-based convolution method for identifying locations of molecular fragments in a map (Cowtan, 1998 ▶, 2001 ▶) as implemented in Terwilliger (2001 ▶). The rotation-angle step size (θ) was typically 30°. In order to minimize the number of orientations that needed to be tested, the helical and β-strand templates described above were oriented so that the axis of the helix and the strand direction were both along the x axis. In this way, the step size of the sampling of possible rotations around the x axis could be maximized and the number of rotations minimized. The rotation step size about x is 30° for helical templates and 40° for strands. The number of rotations was reduced for the helical template by only considering 100° of rotation about the helical axis, as any further rotation yields a near-duplicate that differs by translation. The number of rotations was further decreased by skipping all rotations that through space-group symmetry resulted in a convolution that duplicated any other rotation. With these reductions, a typical convolution search in space group C2 at a resolution of 2.6 Å requires about 100 rotations for the helical template and 950 rotations for the β-­strand template.

2.4. Correlation-based refinement of orientation and location of helices and strands

The convolution search for helical and β-strand segments results in a list of locations and orientations sorted by the overlap integral of the template with the map at those locations and with those orientations. The locations and orientations were refined by maximizing the correlation of the template with the map. After refinement, the lists of helices and strands were shortened by removing all those with low correlation coefficients, typically cutting off at a correlation of ½〈m〉, where 〈m〉 is the mean figure of merit of the data used to calculate the map.

2.5. Helix- and strand-fragment placement

The refined position and orientation of each β-strand and helical fragment is then used as a potential location of a strand or helix. Each member of the β-strand or helical fragment libraries is then placed in one such position and orientation and tested for a match to the electron density nearby. For each position/orientation of the standard helical fragment, for example, all 43 members of the helical fragment library were superimposed on the standard fragment, each in three different positions as described above. Then, for each placement of a helical fragment, a segment from the fragment is chosen that fits the electron density in the region. The segment included is the longest contiguous segment of the helix in which the mean density for all atoms is above a threshold (r _overallρ_c, typically r _overall = ¾, where ρ_c is the mean density at atoms near the center of the fragment) and the atoms on the ends were in density above a second threshold (r _endρ_c, typically r _end = ½). An identical procedure is used for β-strand segments. Each placement of a segment of helix or strand is then scored with a score Q based on the mean electron density at coordinates of atoms in the segment and the number of atoms in the segment: Q = 〈ρ〉N ^1/2. For each position/orientation, the top-scoring segment is saved. Once all helix and strand placements have been analyzed in this fashion, the mean and standard deviation of scores for helices and for strands are calculated, and a Z score is obtained for each placement, Z = (Q − 〈Q〉)/σ(Q). At this point, all placements where the top-scoring segment has a Z score below a threshold (typically 0.5) are discarded.

2.6. Segment extension

Construction of a segment of a polypeptide chain is accomplished by iterative fragment extension. The goal in extending a segment by one or a few residues is to find a configuration of the main chain that is physically reasonable, that matches the electron-density map and that can be further extended into additional density. A look-ahead procedure was used to extend segments in either the N-terminal or C-terminal directions. The essence of the procedure is to extend with a tripeptide that matches the density and which can itself be extended with a second tripeptide that also matches the density. To accomplish this, each tripeptide from the C-terminal library is tested as a possible extension by superimposing the first residue of the tripeptide on the last residue in the current segment and evaluating the mean density in the map at the coordinates of atoms in the next two residues of the fragment. The top-scoring ‘first-level’ fragment or fragments are then tested for steric overlaps (distance of any atom in the fragment of <3.5 Å from any C^α atoms at least two residues away in the segment already built) and any physically implausible fragments are rejected. Then the look-ahead step is carried out. Each of these first-level top-scoring fragments is then used as a starting point for a second extension and the second-level top-scoring addition to each is noted. The overall score for each of the first-level fragments is the mean electron density at the coordinates of atoms in the fragment plus its extension (i.e. at the positions of atoms in four amino acids). The top-scoring first-level fragment (two amino acids) is then used to extend the segment.

In this extension process, all main-chain atoms in the fragment are required to be above a threshold (r _minρ_r.m.s., typically r _min = 1, where ρ_r.m.s. is the r.m.s. of the map in the region of the macromolecule) or they are rejected. Additionally, each fragment to be considered as an extension is tested to verify that the density is relatively uniform in the fragment. The procedure described above for truncation of helical segments to the region of helical density is followed (identifying the longest contiguous segment of the helix in which the mean density for all atoms is above a threshold and where the atoms at the ends were in density above a second threshold) and any fragments for which either end is removed by this procedure are rejected.

The procedure for extension described above will stop if no fragment can be found to extend the segment. Several backup procedures are used in this case. Firstly, the procedure is repeated testing a larger number of first-level fragments (one was tested on the first try, ten were tested on the second try and 40 on the third). If this also fails, then the procedure is repeated starting one amino acid back in the segment (fragments are added two amino acids at a time, so backing up one is a new starting point). If this fails, no further additions are made to this end of the segment.

When a segment can no longer be extended in either direction, it is scored, with the score equal to the mean density at coordinates of atoms in the segment times the square root of the number of atoms in the segment.

2.7. Chain assembly

The procedures described above generate a set of segments that may correspond to portions of polypeptide chain. As they begin from helices or strands that may have been overlapping, some pairs of segments may be almost identical. Also, as they may have had extensions on either end, the segments may overlap through their extensions. The goal of the chain-assembly step is to identify sets of segments that are likely to correspond to a continuous polypeptide chain. The step is carried out iteratively. In each cycle, the top-scoring segment identified above that is not already used and that does not overlap with a previously built chain is taken as a starting point for building a continuous chain. All segments are then considered, in order of their scores, as a possible extension to this new chain. If a segment matches the current new chain at two C^α atoms or more including one or both ends (matching typically defined as within r _match < 1.6 Å), extends it in either direction and the extension does not result in any implausibly close atoms (distance < 3.5 Å), then the chain is extended using the residues in the segment. This becomes the new current chain and the process is repeated until no further additions can be made to the chain. A new chain is then begun as above and the overall chain-assembly process is repeated until no new chains can be created. This results in a set of continuous polypeptide chains, none of which overlap with any other.

3. Results and discussion

3.1. Optimizing values of parameters

The automated model-building procedure described here has been incorporated into the RESOLVE software (Terwilliger, 2000 ▶). The model-building procedure described here depends on a number of parameters mentioned above. To test the sensitivity of the model-building procedure to the values of key parameters, the density-modified electron-density map for NDP kinase (Pédelacq et al., 2002 ▶) was used as a starting point, parameters were systematically varied and their effects on the number of residues built and the r.m.s. difference from the refined structure were examined. The NDP kinase map was chosen because it was at moderate resolution (2.6 Å), a moderate fraction of residues could be successfully built (78%) and the map was of moderate quality after density modification (〈m〉 = 0.56).

The parameters in the model-building procedure that seem most likely to affect the overall results of the procedure include θ, the rotation-angle step for the convolution-based search for helices and strands, r _min, the minimum normalized electron density allowed at atomic positions, and r _match, the maximum distance two C^α atoms can be from each other to be considered a match for fragment assembly. Each of these was tested for its effects on the NDP kinase model building. In these tests, the values of all the parameters except the one to be varied were fixed at the values of θ = 30°, r _min = 1 and r _match = 1 Å. (The value of r _match used in this test is not the optimal value of 1.6 Å; however, as noted below, the results are relatively insensitive to this parameter and this test was carried out before the optimum was known.) The quality of each of the models was assessed by comparing it to the refined model of NDP kinase. As the sequence is not assigned in the main-chain models, we assessed this quality as the r.m.s. coordinate difference between each main-chain atom in the models and the nearest atom with the same name in the refined structures, excluding any atoms more than 10 Å from any atoms in the refined structures.

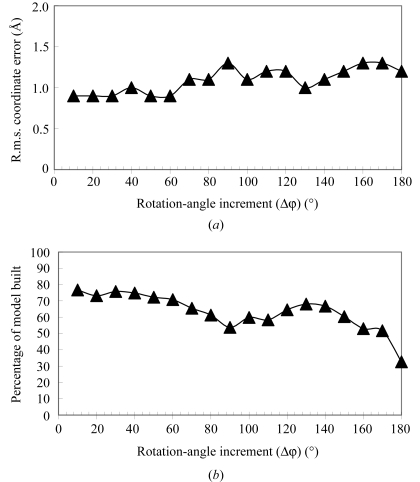
Figs. 1 ▶, 2 ▶ and 3 ▶ shows the results of these tests. For each value of each parameter, the number of residues built and the r.m.s. deviation of the model coordinates from the refined coordinates of NDP kinase were determined. Fig. 1 ▶ illustrates the effect of varying the sampling interval in the FFT-based fragment search. As expected, the coordinate error is lowest (0.9 Å) and the completeness of the model is highest (77%) when the fragment search is carried out on a fine grid (10–30° intervals, with a total of 5000 rotations considered for the 10° interval and 138 rotations considered for the 30° interval). Somewhat surprisingly, however, even at the most coarse grid considered (nominally 180°, but actually six rotations considered for the β-strand template) fragments could still be identified and much of the model could still be built. The r.m.s. difference between the coordinates of atoms in the model built automatically and those of the refined model increased slightly (from 0.9 to 1.3 Å) as the grid was made more coarse. Based on this experiment, it appears that a grid search with a nominal interval of about 30° is optimal for this model-building procedure.

Figure 1.

Effect of sampling interval on the FFT-based fragment search. Models were built for NDP kinase (Pédelacq et al., 2002 ▶) as described in the text, varying only the values of the angular increment between FFT-based fragement searches. The percentage of the model built and the r.m.s. coordinate difference between the resulting (main chain and C^β) model and the refined model of NDP kinase are shown.

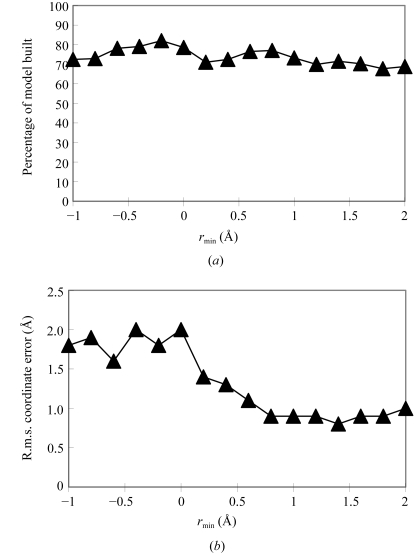
Figure 2.

Effect of minimum-density cutoff at atomic positions on model building. Models were built and tested as in Fig. 1 ▶, varying only r _min, the minimum allowed density, normalized to ρ_r.m.s., the r.m.s. of the map in the region occupied by the macromolecule.

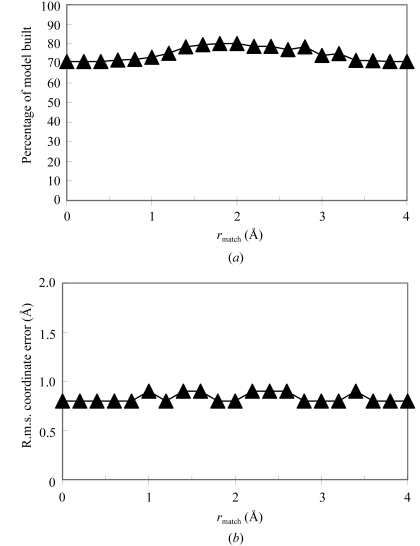
Figure 3.

Effect of maximum-distance cutoff for matching atoms in chain assembly. Models were built and tested as in Fig. 1 ▶, varying only r _match, the maximum distance between matching C^α atoms to be considered a match for fragment assembly.

Fig. 2 ▶ shows the effect of varying the minimum density allowed at the coordinates of main-chain atoms added during fragment extension. For values of r _min (the minimum allowed density, normalized to ρ_r.m.s., the r.m.s. of the map in the region occupied by the macromolecule) of about 0.5 or less, the coordinate error is quite high (1.5–2 Å), while for values of about 1 or greater, the coordinate error is about 0.9 Å. The fraction of the model built decreases somewhat as this parameter is increased. It does not drop to zero because much of the model is built of fragments obtained in the FFT-based search and that part of model-building is not affected by this parameter.

Fig. 3 ▶ illustrates the effect of changing the value of r _match, the maximum distance between matching C^α atoms to be considered a match for fragment assembly. There is only a slight dependence of the model building on this parameter, but for intermediate values (1.5–2.5 Å) somewhat more residues could be built than for lower or higher values. The r.m.s. error in the coordinates also increases slightly for these intermediate values, however. When the value of this parameter is very low, no chain assembly is performed. The number of residues built does not go to zero, however, because the chain can still be built up by extension of the templates from their ends.

3.2. Tests with structures solved by MAD and SAD

The procedure for automated main-chain model-building described here was further tested by applying it to a set of eight experimental maps with varying resolution, quality (figure of merit) and number of residues in the asymmetric unit. Two of these maps (NDP kinase and gene 5 protein) were used in the development of the algorithm, so that parameters could potentially be specifically optimized for them. The other six were not used to optimize parameters and therefore can give a somewhat more independent evaluation of the procedure. In each case, experimental MAD or SAD phases were first improved with statistical density modification (Terwilliger, 2000 ▶) including non-crystallographic symmetry information in the analysis. The resulting maps were used for model building. The values of the parameters tested in Figs. 1 ▶, 2 ▶ and 3 ▶ were fixed at values of θ = 30°, r _min = 1 and r _match = 1.6 Å. In the cases tested in Table 1 ▶, from 51 to 93% of the main chain could be built. Even the relatively poor map at 3.5 Å of granulocyte-stimulating factor could be partially interpreted, although the chain direction was incorrect in several instances for this model.

Table 1. Test structures for which models have been built with RESOLVE .

Structure	Resolution (Å)	Figure of merit (after ML density modification) 〈m〉	No. of residues in refined model	No. of residues built	Percentage of residues built (%)	Main-chain r.m.s.coordinate difference from refined structure (Å)
Gene 5 protein (Skinner et al., 1994 ▶)	2.6	0.62	87	57	66	0.9
Granulocyte-stimulating factor (Rozwarski et al., 1996 ▶)	3.5	0.70	242	121	50	1.6
Initiation factor 5A (Peat et al., 1998 ▶)	2.1	0.85	136	121	89	0.6
β-Catenin (Huber et al., 1997 ▶)	2.7	0.72	455	407	89	1.1
NDP kinase (Pédelacq et al., 2002)	2.6	0.56	556 (3 × 186)	397	71	0.9
Hypothetical (P. aerophilum ORF, NCBI accession No. AAL64711; Fitz-Gibbon et al., 2002 ▶)	2.6	0.58	494 (2 × 247)	451	91	0.6
Red fluorescent protein (Yarbrough et al., 2001 ▶)	2.5	0.91	936 (4 × 234)	854	91	0.5
2-Aminoethylphosphonate (AEP) transaminase (Chen et al., 2000 ▶)	2.6	0.84	2232 (6 × 372)	2037	91	0.7

This r.m.s. coordinate difference between the models built with the present method and refined models ranged from 0.6 Å (for maps at resolutions of 2.1 and 2.6 Å) to 1.6 Å (for the map at a resolution of 3.5 Å). Considering that the models have been built from fragment libraries designed to match fragments from known proteins within about 0.5 Å and no refinement has been carried out, this agreement is quite close. It seems possible that even closer agreement might be achieved by using larger fragment libraries, but this would come at the expense of more time spent examining the fits of fragments to the map. Alternatively, the agreement could be improved by refinement of the models that are obtained.