Abstract
We present new quantitative diffusion-tensor imaging (DTI) tractography-based metrics for assessing cerebral white matter integrity. These metrics extend prior work in this area. Tractography models of cerebral white matter were produced from each subject's DTI data. The models are a set of curves (e.g., “streamtubes”) derived from DTI data that represent the underlying topography of the cerebral white matter. Nine metrics were calculated in whole brain tractography models and in three “tracts-of-interest” (TOI): transcallosal fibers, and the left and right cingulum bundles. The metrics included the number of streamtubes and several metrics based on the summed length of streamtubes in including some that were weighted by scalar anisotropy metrics and normalized for estimated intracranial volume. We then tested whether patients with subcortical ischemic vascular disease (i.e., vascular cognitive impairment or VCI) vs. healthy controls (HC) differed on the metrics. The metrics were significantly lower in the VCI group in whole brain and in transcallosal TOI but not in the left or right cingulum bundles. The metrics correlated significantly with cognitive functions known to be impacted by white matter abnormalities (e.g., processing speed) but not with those more impacted by cortical disease (e.g., naming). These new metrics help bridge the gap between DTI tractography and scalar analytical methods and provide a potential means for examining group differences in white matter integrity in specific tracts-of-interest.
Introduction
Diffusion tensor imaging (DTI) is a magnetic resonance imaging (MRI) technique that measures the directionally dependent rate of water self-diffusion in each image voxel. These measures are in the form of a second-order diffusion tensor (Basser, Mattiello, & LeBihan, 1994), which can be decomposed into three non-negative eigenvalues and three eigenvectors that describe the magnitude and orientation of water diffusion in each image voxel. Water diffusion in cerebral white matter tends to be anisotropic due to the highly linear organization of white matter fibers. That is, water will preferentially diffuse more rapidly along white matter tracts because physical barriers such as axonal walls restrict water movement in other directions (Beaulieu, 2002; Sun et al., 2005). Medical conditions such as subcortical ischemic injury, inflammation, neurodegenerative diseases, and traumatic brain injury cause reductions in the linear organization of white matter pathways with corresponding reductions in linear anisotropy (Beaulieu, 2002; Sun et al., 2005). DTI is sensitive to these changes in linear anisotropy making it a powerful in vivo imaging tool for studying the microstructural integrity of cerebral white matter.
The majority of studies using DTI to assess white matter microstructure in clinical samples have been based on two-dimensional greyscale maps of scalar values such as mean diffusivity (MD), a measure of the rate of diffusion in each image voxel, and fractional anisotropy (FA), a measure of the extent to which that diffusion is directionally restricted. Generally, these basic scalar measures are derived from the eigenvalues of the multi-valued tensor data and do not incorporate eigenvector information. The scalar values in each image voxel are then mapped to two-dimensional grayscale images. An exception is the colorized FA maps in which color indicates fiber orientation based on the principal eigenvector (e.g.,Pajevic & Pierpaoli, 1999; Wakana, Jiang, Nagae-Poetscher, van Zijl, & Mori, 2004). With respect to anisotropy, the work presented in this paper is based mainly on Westin et al.'s (1997) linear anisotropy measure which is based on the principal eigenvalues and describes the direction of fastest diffusion.
Tractography methods complement scalar methods by providing detailed information about the orientation and curvature of white matter pathways as they course through the brain. These methods utilize both the tensor eigenvalues and the eigenvectors to calculate trajectories in the direction of fastest diffusion. The trajectories are then portrayed graphically using curved lines (Xue, van Zijl, Crain, Solaiyappan, & Mori, 1999) or glyphs such as hyperstreamlines, which were initially proposed by Delmarcelle and Hesselink (1993) as a means of visualizing other types of second-order tensor fields and then subsequently applied to DT-MRI data by Zhang et al. (2003). Tractography has gained widest acceptance in neuroscience studies exploring white matter connectivity, effects of pathologies on connectivity, and improvement of data acquisition and visualization methods (e.g., Huang et al., 2005; Wakana et al., 2004; Wakana et al., 2005).
Only a few preliminary methodological studies have explored the utility of combining tractography with quantitative scalar measures (i.e., “quantitative tractography”) for clinical research where group comparisons are important. For example, Ciccarelli et al. (2003), studied the reproducibility of tract-“normalized” volume (NV) and FA in three white matter pathways traced by the fast marching tractography (FMT) algorithm (Parker, 2000; Parker, Stephan et al., 2002; Parker, Wheeler-Kingshott, & Barker, 2002). The results (Ciccarelli, Parker et al., 2003) showed variability in measures of tract volume and fractional anisotropy across different fiber bundles suggesting that fiber organization has an impact on the reproducibility of tractography algorithms. Ciccarelli et al. (2003) also examined the extent of intersubject variability in the anterior corpus callosum, optic radiations, and pyramidal tracts. They found that the tractography maps corresponded well to known anatomy and that there was greater intersubject variability at the terminal ends of tracts adjacent to cerebral cortex, but lower variability in the core of tracts and no right-left differences in variability. Ding et al. (2003) also demonstrated good reproducibility of tractography-based metrics such as curvature, torsion, parallel diffusivity, and perpendicular diffusivity along bundle length. Huang et al. (2005) have also used quantitative methods for parcellating projections from the corpus callosum to cortical regions. Smith et al. (2006) developed tract-based spatial statistics which combines tractography with voxel-based morphometry metrics to derive a white matter fiber “skeleton” of FA values that can then can be compared on a voxel-by-voxel basis across groups. Jiang et al.(2006) have developed the freely available software DTIStudio (www.mristudio.org) which calculates tractography models from raw diffusion data and then provides an interface that allows users to identify white matter tracts-of-interest. The program provides tractography-based statistics such as length and number of streamtubes but no weighting for scalar values is provided. MedINRIA, another freely available DTI software package (Fillard, Souplet, & Toussaint, 2007), wwwsop.inria.fr/asclepios/software/MedINRIA/ provides metrics similar to that provided by DTIStudio. Philips Medical Systems (Best, Netherlands) offers a similar software package called PRIDE (Philips Research Integrated Development Environment). Others (e.g., (Ashtari et al., 2007) have used elaborate registration algorithms that permit overlaying of tracts-of-interest derived from tractography models produced by programs such as DTIStudio, MedINRIA, or PRIDE onto scalar FA maps to determine the structural integrity of the selected tracts. Each of these methods demonstrated the potential utility of using quantitative tractography.
The present study proposes several new quantitative tractography metrics for quantifying cerebral white matter integrity in whole brain white matter and in specific white matter tracts-of-interest (TOIs). The impetus for developing these metrics was to quantify observed qualitative differences in the tractography models of patients with known vascular white matter disease compared to age matched controls. The rationale for the metrics and their potential clinical utility is as follows: Acquired reductions in white matter structural integrity result in local decreases in linear diffusion anisotropy. When these decreases reach or exceed a certain pre-specified threshold, they cause the streamtube algorithm (or other similar tractography generating algorithms) to terminate prematurely. This should result in shorter streamtubes and possibly either fewer or greater numbers of streamtubes depending on the nature of the white matter injury; for example, fiber drop out should result in fewer streamtubes whereas injuries that cause diffusion changes without incomplete drop out should result in a greater number of short streamtubes. Thus, the motivation for the metrics is not purely descriptive; rather we assume that the output of streamtube generation algorithms is, in fact, reflective of underlying acquired white matter pathology. Also, compared with traditional scalar metrics such as linear anisotropy or fractional anisotropy, the metrics proposed in this paper operate on a part of or the entire tractography model, therefore they might be more effective in detecting tract-specific changes. Moreover, we assume that the quantitative tractography metrics such as those used in DTIStudio (Jiang et al., 2006), MedINRIA (Fillard et al., 2007), PRIDE and the ones presented in this paper are capable of detecting important subtle differences in the structural integrity of specific white matter pathways between groups of individuals with and without white matter injury.
In this report, we define the metrics and demonstrate their stability across multiple streamtube models derived from a single dataset for one healthy control. Then, as an initial and preliminary validity test, we compare the metrics between a small cohort of patients with known vascular white matter injury (i.e., vascular cognitive impairment, VCI) and a demographically-matched cohort of healthy controls. VCI provides a good model for assessing the clinical and research utility of quantitative DTI since ischemic white matter injury is associated with a characteristic pattern of increased diffusivity and decreased anisotropy (Jones et al., 1999). These diffusion changes are thought to reflect axonal loss (Beaulieu, 2002) with possible contributions from demyelination (Le Bihan et al., 2001), gliosis (Larsson, Englund, Sjobeck, Latt, & Brockstedt, 2004), or other pathological processes.
Materials and Methods
DTI acquisition
MRI data was collected on a 1.5T Siemens Symphony scanner. First, an anatomic 3D T1 MPRAGE (one acquisition, sagittal) was acquired as follows: 0.85 mm slices, no gap, 176 slices, 256 × 256 matrix, 21.7 × 21.7 cm FOV, TR = 1900, TE = 4.31, TI = 1100, NEX = 1, and flip angle = 15; acquisition time was just over 8 minutes. For the DTI data, Siemens MDDW protocol was used to collect three co-registered sagittal double spin-echo, echo-planar diffusion-weighted volumes of the entire brain. After the initial scan, subsequent acquisitions were spatially offset in the slice direction by 1.7mm and 3.4mm. Parameters for each acquisition were as follows: 5mm thick slices, 0.1mm inter-slice spacing, 30 slices per acquisition, matrix = 128×128, FOV = 21.7cm × 21.7cm, TR = 7200 ms, TE = 156 ms, no partial echoes, and NEX = 3. Bipolar diffusion encoding gradients (b=0, 1000mm/s2) were applied in 12 non-collinear directions (the maximum number available under our licensing agreement at the time of data collection) calculated automatically by Siemens software (the precise gradient directions and strengths are available on request). The reverse polarity during the second echo of the double-spin-echo acquisition unwinds eddy currents that accumulate during the first echo (Reese, Heid, Weisskoff, & Wedeen, 2003). Total time for the three acquisitions was slightly less than 15 minutes. The three acquisitions were interleaved to achieve 1.7mm3 resolution images and then up-sampled (equivalent to zero-filling) to 0.85mm3 isotropic voxels for analysis. The interleaving overlaps the slice profiles of the acquisition making through-plane interpolation possible and produces isotropic voxels which reduces tractography bias related to fiber orientation (Laidlaw et al., 2004). While this is an unusual protocol, it avoids aliasing artifacts and produces images that are only slightly less sharp in the through-plane direction than within plane while retaining sub-millimeter voxel dimensions. Typically, DTI acquisitions for use with tractography require more diffusion encoding directions than were used here.
Motion was controlled with the use of a vacu-pillow head restraint system provided by the scanner manufacturer. We also used repeated reminders during the scan session of the importance of remaining motionless and other measures (e.g., relaxation videos) to promote subject comfort in the scanner. We found that these methods worked well for most cases. All datasets included in the current paper were screened for excessive motion artifact. Since the effect of motion correction methods on tractography models is not fully understood, we did not institute post-acquisition motion correction to the data due to concerns of introducing misalignment of adjacent voxels on a streamtube from the rearrangement of the spatial locations of the tensors. There is no reason to suspect a group x motion interaction that would bias our results. Therefore, motion would be considered a source of random variability affecting both groups equally.
Streamtube generation
Custom in-house software was used to calculate tensors and then derive the three principle eigenvalues and eigenvectors for each image voxel after interleaving of the three sets of diffusion-weighted images (Ahrens et al., 1998). Streamtube models of cerebral white matter were created for each subject based on the major eigenvector field of the diffusion tensor field as described in detail in Zhang et al. (2003). Briefly, the streamtubes were generated by seeding in the data volume with a density of one seed per 0.85 mm3. Seed points were chosen to ensure that streamtubes pass through all regions of high linear anisotropy and are not restricted to the sample points of the volume image. Tricubic B-spline functions were used to interpolate the tensor field so that there is no limit to the number of seed points, locations of the seed points, or the trajectory of the streamtube. The location of each seed point was randomly jittered across the underlying grid to avoid aliasing artifacts. In our method, streamtubes begin from a seed point and propagates along the major eigenvector field bidirectionally with a step size of 1 mm. The trajectory of the streamtube passing through the seed point is found using second-order Runge-Kutta integration. Streamtube trajectories are restricted to regions of high linear anisotropy and are clipped to the data volume and to regions seeding scheme of one seed per 0.85 mm3 of sufficiently high signal-to-noise ratio. The produces an overly dense set of streamtubes that are culled using an algorithm based on three metrics: the length of a trajectory (minimum = 10.0 mm), the linear anisotropy along a trajectory (minimum = 0.10), and the distance between them (minimum = 1.7 voxels) that ensures culling of fibers that are highly similar in their trajectory and spatial proximity as these may be considered redundant. For the definition of the distance between two streamtubes and the details of the streamtube generation, please see Zhang et al. (2003). We have found that these parameters limit the number of anatomically implausible fibers in regions of low anisotropy while retaining linear structures in most of the white matter. The resultant models bear a close resemblance to known white matter structures such as cortical u-fibers, corpus callosum, superior longitudinal fasciculus, uncinate fasciculus, and cingulum bundles; other white matter structures are also easily identified. Moreover, other groups (Jiang et al., 2006; Wakana et al., 2004) have demonstrated good correlations between physical white matter anatomy and DTI models of white matter fibers. All streamtube models used in group comparisons were generated with an input seeding that initiated a streamtube in every voxel (0.85mm3) of the volume. This seeding dimension was selected in an attempt to capture features as small as one-half of the intrinsic 1.7 mm resolution of the data. Other seeding dimensions were tested in the reproducibility study (see below).
Tract-of-Interest selection
We implemented a method for interactive tract-of-interest (TOI) selection similar to the volume-of-interest (VOI) approach of Akers et al. (2004) and bears a similarity to the more recent methods published by Mori and colleagues (Jiang et al., 2006) and others (Fillard et al., 2007). Briefly, our interactive user interface permits the operator to view the streamtube model alongside the T2-weighted images. The user can rotate and translate the streamtube model in all three axes using a computer mouse. This allows the user maximum flexibility in viewing the model from different perspectives and to zoom in our out on specific structures of interest. In addition, the user has the ability to threshold models by linear anisotropy in order to see deeper white matter pathways that may be obscured by ones nearer the surface. The user can then define three-dimensional box-shaped “voxels-of-interest.” The size and shape of the boxes are controlled by the user and can be dragged and placed anywhere in the streamtube model using the computer mouse or by inputting specific values for the box dimensions and location. There is no limit to the number of boxes that can be placed in a model. Once placed, a series of Boolean operations allows the user to select only fibers that pass through a box or that connect two or more boxes and in this way, identify the TOIs. TOIs selected in this manner are manually edited to remove streamtubes that have an anatomically questionably trajectory (i.e., streamtubes with sharp directional changes). Upon selecting a TOI, the user can then calculate quantitative measures such as the number or summed lengths of streamtubes included in the TOI.s
Since the tractography volumes are three-dimensional and TOI selection is based on each participant's own anatomy, co-registration is not necessary. For each subject, we quantified the streamtube data for the whole brain and three TOIs: transcallosal fibers, and the left and right cingulum bundles. TOI selection was performed by an experienced rater (TV) trained and supervised by two faculty with good knowledge of white matter anatomy (SC and DT). The rater ensured that streamtube models were displayed at a consistent magnification and orientation prior to each TOI selection. Transcallosal fibers were defined as all streamtubes passing through the corpus callosum using a long narrow box placed down the midline of the corpus callosum and encompassing its inferior-superior extent. The left and right cingulum bundles were identified visually in the models and were segmented by the roughly placing three equal sized voxels-of-interest along the length of the bundle in the second, fourth, and most posterior sixth of the bundle. Given the potential errors that can occur in DTI fiber tracking (Jiang et al., 2006; Mori & van Zijl, 2002), we adopted a conservative approach to identifying and removing anatomically questionable fibers on the basis of their trajectory with reference to anatomical guides (e.g., (Carpenter, 1991; Haines, 2004; Wakana et al., 2004). The final TOI results were inspected by SC and DT for appropriateness.
Proposed metrics
For each TOI we derived the following quantitative tractography metrics: 1) total length (TL), 2) total weighted length (weighted for linear anisotropy) (TWLCL), 3) total weighted length (weighted for FA) (TWLFA), 4) number of streamtubes (NS), 5) normalized total length (NTL), 6) normalized total weighted length – linear anisotropy (NTWLCL), 7) normalized total weighted length – FA (NTWLFA), 8) normalized number of streamtubes (NNS), and 9) average length (AL). Three metrics, TL, NS, and AL are comparable to metrics output by DTIStudio (Jiang et al., 2006), MedINRIA (Fillard et al., 2007), and PRIDE. As described below, the other metrics extend these including scalar metrics and therefore should provide more subtle but potentially important information about the white matter integrity. Abbreviations and descriptions of these metrics are summarized in Table 1. The metrics are defined conceptually and mathematically as follows: Total length of a TOI was defined as:
| (1) |
where Ls is the length in millimeters of a single streamtube s contained within the set of streamtubes S in the given TOI. This metric should provide a coarse marker of the overall microstructural integrity of a TOI.
Table 1.
Metric abbreviations and definitions
| Abbreviation | Definition |
|---|---|
| TL | Total Length: The total summed length of all streamtubes in the tract of interest |
| TWLCL | Total Weighted Length: The total summed length of all streamtubes in the tract of interest after weighting each streamtube by its average linear anisotropy (CL) |
| TWLFA | Total Weighted Length: The total summed length of all streamtubes in the tract of interest after weighting each streamtube by FA |
| NS | Number of Streamtubes: The total number of streamtubes in the tract of interest |
| NTL | Normalized Total Length: TL normalized for estimated intracranial volume. |
| NTWLCL | Normalized Total Weighted Length: TWLCL normalized by intracranial volume. |
| NTWLFA | Normalized Total Weighted Length: TWLFA normalized by intracranial volume. |
| NNS | Normalized Number of Streamtubes: The total number of streamtubes corrected for estimated intracranial volume. |
| ATL | Average Total Length: The total summed length of all streamtubes divided buy the number of streamtubes in a tract-of-interest. |
We calculated two total weighted length (TWL) metrics. One weights TL by the average linear anisotropy, i.e., Westin's (1997) cl (TWLCL) of the streamtubes comprising the TOI; the other weights TL by fractional anisotropy (TWLFA). These weighted metrics potentially provide additional information about the integrity of the tract. For example, they might be sensitive to differences in tract integrity across groups (i.e., differences in the average linear anisotropy or fractional anisotropy of the tract) that are insufficient to impact TL, but nonetheless reflect a disease state. TWLCL and TWLFA differ in that the former only considers the linear component of the diffusion tensor whereas the latter considers all three of the principal diffusion tensor eigenvalues and as such may be a more robust marker of white matter integrity. The TWL metrics are defined as follows:
| (2) |
| (3) |
where Cs is the average linear anisotropy and FAz is average fractional anisotropy along a streamtube (i.e., summed across all vertices used to generate a streamtube and divided by the number of vertices). We would expect the TWL metrics to be inversely correlated with TOI injury.
NS quantifies the number of streamtubes in a TOI:
| (4) |
NS may provide useful information about white matter integrity not captured by the length metrics and may be sensitive to white matter changes, particularly in shorter, denser tracts. NS might provide a compliment to the length metrics. For example, lower TL could occur because of broken fibers due to local minima in linear anisotropy or to loss of fibers. In the former situation, lower TL might be accompanied by higher NS, whereas in the latter situation, both TL and NS might be decreased.
The value of NS, TL, and the two TWL metrics, however, are likely influenced by brain size, and thus may require further correction. Therefore, we normalized these metrics by approximate intracranial volume. We chose to normalize by intracranial volume instead of brain volume because it likely provides a better index of brain size prior to the impact of age and pathology (Bigler, 2004).
The volume of the intracranial vault was approximated from MPRAGE volumes using SPM5 (http://www.fil.ion.ucl.ac.uk/spm/). Images were segmented into grey matter, white matter, and cerebrospinal fluid tissue compartments (including surface CSF) using default parameter settings and retained in native space and then further threshold was applied to assure 95% probability of a voxel being included in the final maps. The estimated intracranial volumes (ICV) were obtained by summing the three probability maps.
We normalized NS, TL, and the two TWL metrics by dividing our length metrics by the ratio of each participant's approximate intracranial volume to the average intracranial volume of all participants. That is, we computed normalized number of streamtubes (NNS), normalized total length (NTL), and two normalized total weighted length metrics (NTWLCL and NTWLFA) as follows:
| (5) |
| (6) |
| (7) |
| (8) |
where V is approximate intracranial volume, and V̄ is the mean approximate intracranial volume for the healthy controls and VCI subjects combined. The ratio in the denominator is designed to avoid confusing and difficult to interpret units such as mm/ml in the final metrics. Normalizing the tractography metrics by total intracranial volume permits direct comparison across participants by controlling for differences that might be present in our models due to head size (larger head size may influence the number and length of tracts generated).
Our final metric AL is a non-normalized measure of the average length of streamtubes in a TOI.
| (9) |
AL may provide slightly different information from TL, possibly helping to discriminate between individuals with similar TL values but different white matter integrity. For example, an individual with good white matter integrity reflected in long streamtubes vs. one with poor white matter integrity reflected by many shorter streamtubes. We additionally calculated normalized AL and average values for our other length metrics by dividing each by NS but chose to omit them from these analyses due to the high degree of colinearity between the measures (r > .72). For thoroughness, we also determined the average FA across all streamtubes in the whole brain model and in each specific TOI.
The nine metrics are clearly interdependent and in most cases will behave similarly in most disorders impacting white matter. That is, the pathology will drive all metric values in the same direction (e.g., fewer and shorter streamtubes). However, the different metrics likely have different implications for the nature of white matter integrity loss in various diseases. For example, inflammatory processes such as multiple sclerosis might reasonably lower diffusion anisotropy but if this loss does not fall below the anisotropy threshold in the streamtube generation algorithm, then fibers will still be generated despite having reduced integrity. In this scenario, the length metrics that are weighted for linear or fractional anisotropy (e.g., NTWLFA, NTWLCL) might be more sensitive to the pathology than TL and NS precisely because the latter metrics do not capture subtle differences in anisotropy that fall above the pre-specified threshold for streamtube generation. Alternatively, diseases associated with multiple subcortical lacunar infarcts that cause complete tissue necrosis might actually result in a greater number of short tubes (i.e., long tubes that have become discontinuous as a result of an infarct) than might result from disorders that cause fiber dropout (e.g., Wallerian degeneration in Alzheimer's disease). In brief, conventional MRI has such limited specificity for characterizing the precise pathophysiological underpinnings of white matter changes that consideration of all nine metrics seems reasonable in this initial study of this approach to quantifying the integrity of entire white matter TOIs.
Reproducibility study
Two important factors potentially affect the reliability of our metrics: 1) the degree to which our streamtube generation algorithm yields consistent results; and 2) the degree to which our DTI acquisition parameters yield consistent results. Two studies were conducted to address these issues: one in which we evaluated the stability or our metrics across multiple models of the same dataset, and one in which we measured their consistency across multiple acquisitions of the same subject. In each of these, we evaluated only our three core metrics of NS and TL, and TWLCL. We focused only on these three metrics because they are directly affected by our algorithm and by the DTI acquisition. The other metrics are mathematical derivatives of these core metrics based on averaging or on factors such as intracranial volume or the manner in which anisotropy is calculated. Such derivatives are independent of our streamtube generation algorithm or the raw data and therefore will not impact the coefficient of variance metric we used to determine reliability.
Consistency of streamtube generation
Our jittered seeding method for streamtube generation reduces the likelihood of the output model being overly influenced by the grid, that is, it helps to ensure that no places in the image volume are systematically under sampled. The cost for this small random jitter is that each run of the algorithm on a single dataset produces slightly different streamtube models, even if the input data and parameters are held constant. Differences in the location of seed points likely affect the specific voxels that the streamtubes pass through which in turn will affect their number, length, and anisotropic weighting. Such inconsistencies introduce error variance in our metrics which, if too great, could mask true group differences (i.e., increased risk of Type 2 error). To address this concern, we assessed the consistency of our metrics in seven streamtube models derived from one dataset of a single healthy control subject. The seven models were produced for each of three different seeding parameters that varied by coarseness (i.e., 1.7mm3, 0.85mm3, and 0.64mm3) for a total of 21 models. Other streamtube parameters were held constant as described previously. We then assessed the coefficient of variance in our metrics across the seven whole brain models produced at each seeding parameter. This method allowed us to determine the impact of both random jitter and different seeding parameters on the consistency of our metrics
Consistency of data acquisition
To examine the consistency of our DTI acquisition protocol, we examined the consistency of our metrics across data collected from a single healthy 45-year-old, right-handed control subject scanned on three different occasions.
Validity Study
Participants
To have utility for clinical research, our metrics must acquire different values in patients with known white matter injury compared to those presumed to have normal white matter. We addressed this by comparing the values of our metrics in a group of patients with known vascular white matter injury (i.e., vascular cognitive impairment or VCI) vs. a group of demographically similar healthy control subjects. VCI is a form of late-life cognitive impairment related to white matter injury from subcortical ischemic microvascular disease (Erkinjuntti, 2002; P. Sachdev, 1999). Patients with VCI typically have impairments that are greater than expected for age in the cognitive domains of processing speed, attention, and executive functioning, and somewhat milder deficits in memory (de Jager, 2004; Desmond, 2004; O'Brien et al., 2003; P. S. Sachdev et al., 2004). The level of cognitive impairment and its impact on daily functioning is insufficient to warrant a diagnosis of dementia (Rockwood, 2002). The neuroimaging features of VCI include subcortical white matter hyperintensities on T2-weighted MRI and a subcortical lacunar infarction on T1-weighted MRI (Erkinjuntti, 2002).
Participants included 14 patients with VCI (mean age = 59.23 ± 12.17, range = 40.18 – 79.22) and 18 healthy individuals (mean age = 64.36 ±14.16, range = 43.77 – 83.62) who served as control group. VCI was diagnosed by consensus at multidisciplinary case conferences considering data from clinical history, neurological exam, neuropsychological testing, and clinical brain MRI scans and using previous criteria specified by (Erkinjuntti, 2002). All VCI participants had impairments (i.e., performance falling more than 1.0 standard deviations below demographically-corrected means) on tests of executive cognitive functioning and/or memory and had MRI evidence of subcortical ischemic vascular disease (i.e., subcortical white matter hyperintensities on T2-weighted images and/or lacunar infarction on T1-weighted images) that was greater than expected for age. None had neuroimaging or clinical evidence of large vessel stroke. None met diagnostic criteria for dementia. In eight patients, VCI was due to CADASIL (cerebral autosomal dominant arteriopathy with subcortical infarction and leukoencephalopathy), a genetic form of subcortical ischemic microvascular disease with earlier onset compared to the more common non-genetic form (Salloway & Desbiens, 2004). Healthy control participants were screened by self-report to ensure the absence of current clinically relevant neurological or psychiatric symptoms and all had normal global cognition as evidenced by scores of 25 or greater on the 30-item Mini-Mental State Exam (Folstein, Folstein, & McHugh, 1975). All data were collected as part of ongoing studies of DTI and cognitive and behavioral functioning in patients with disorders known to adversely impact white matter integrity (e.g., Brennan-Krohn et al., 2004; Correia, Brennan-Krohn, Schlicting et al., 2005; Correia, Brennan-Krohn, Zhang et al., 2005). Each of these research studies was conducted with approval from our Institutional Review Boards, and all subjects provided written informed consent prior to participation.
Cognitive tests
If our metrics are valid, clinically-relevant markers of white matter integrity, then they should correlate more strongly with cognitive variables thought to be sensitive to white matter injury than with those thought to be more strongly associated with cortical pathology. We explored these associations in the entire sample (i.e., VCI and controls combined) using whole brain models only while controlling for age. We controlled for age to help control for the known effects of age on cognitive function especially processing speed (Kirasic, Allen, Dobson, & Binder, 1996) and on white matter integrity measured by DTI (Sullivan, Adalsteinsson, & Pfefferbaum, 2005). The Trail Making Test parts A & B (TMT-A&B) (Reitan, 1958), were used as measures of psychomotor processing speed and executive function (cognitive set switching), respectively. Poorer performance on these cognitive domains has been shown to be associated with increases in white matter hyperintensities thought to reflect subcortical small vessel ischemic injury on T2-weighted images (Gunning-Dixon & Raz, 2000). The Boston Naming Test (BNT) (Kaplan, Goodglass, & Weintraub, 1983) is a test of confrontational naming thought to be sensitive to cortical dysfunction (Lukatela, Malloy, Jenkins, & Cohen, 1998; Votaw et al., 1999).
Statistical analyses
All statistical analyses were performed using SPSS 14.0 for Windows (Chicago, IL).
Reliability
The stability of our metrics across repeated acquisitions of the same subject was examined using percent differences between the same metrics acquired at different times. To evaluate the stability of our metrics, coefficients of variance (COV, mean-centered) were calculated for NS, TL, and TWLCL from the seven streamtube models produced at each of the three seeding parameters in a randomly selected healthy control dataset. COV for these metrics were calculated in whole brain streamtube models only. Intrarater and interrater reliability for the corpus callosum and cingulum bundles were assessed using intraclass correlation coefficients (two-way random model, absolute agreement).
Correlation analyses
We used bivariate Pearson correlation coefficients to explore the association between our metrics and age in the whole brain models in healthy controls and in VCI participants. We used partial correlations, controlling for age, to assess the association between our whole-brain metrics including average FA and cognition. Cognitive variables were subjects' performance on TMT-A, TMT-B, and BNT.
Group comparisons
As a preliminary step, we examined the distributions of our variables for normality and homogeneity of variance. We used MANCOVA to test for significant differences in our nine metrics plus average FA between the VCI and healthy control groups in whole brain models while controlling for age. We expected that patients with VCI would have lower values than healthy controls on all our metrics. For thoroughness, we retained all nine metrics in our analyses of whole brain models since each potentially captures slightly different information about the integrity of a specific TOI. Moreover, we had no a priori assumptions about which metric would perform best at differentiating the groups. However, retaining such a large number of highly collinear variables (see results for the whole brain analysis below) for all analyses increases the risk of Type I error. Therefore, for the transcallosal and cingulum TOI analyses we retained only the five metrics that both differed significantly between groups and that had the largest effect sizes in the whole brain analysis. This approach also limits the risk of Type II error that could arise from the inclusion of weaker metrics in TOI analysis which may have lower statistical power due to the smaller number of streamtubes. As further protection against Type I error, alpha was set at .05 for each omnibus MANCOVA and to .01 for subsequent pair-wise comparisons. Given the results of our tests for normality (see Results), we repeated the analyses using non-parametric Mann-Whitney U tests to evaluate the extent to which violations of normality may have influenced our results. We applied an alpha level of .01 for the non-parametric analyses.
Results and Discussion
For clarity, we present the results of each analysis followed immediately by a brief discussion. We start with the reproducibility study and then follow with the results and discussion for whole brain and the three TOIs: transcallosal fibers and the left and right cingulum bundles. These sections are followed by an overall discussion.
Results: Reproducibility study
Consistency of streamtube generation
We assessed the stability of our metrics vis-à-vis our streamtube generation algorithm in multiple models from a single dataset of a healthy control. Seven streamtube models produced for each of three different seeding parameters (1.7 mm3, 0.85 mm3 seeding, and 0.64 mm3) (21 total models). The metrics were measured in whole brain models. Coefficients of variance (COV) were calculated for TL, NS, and TWLCL across the seven models for each seeding point. In the whole brain models, COV did not exceed 1.0% for NS, TL, or TWLCL at any of the three seeding densities of (see Table 2). The results showed comparable COV when using coarser seeding parameters (see Table 2). Note that all other metrics reported in this paper were measured in models generated with a seeding spacing of (0.85mm3) to match the voxel dimensions in our datasets.
Table 2.
Consistency of the metrics across multiple iterations of the streamtube algorithm and three acquisitions of a single healthy control (mean ± SD and coefficient of variance (COV).
| Seed | NS | TL (mm) | TWLCL (mm) |
|---|---|---|---|
| 1.70 mm3 | 7895 ± 11 | 108978 ± 844 | 26874 ± 256 |
| COV = 0.1% | COV = 0.8% | COV = 1.0% | |
| 0.85 mm3 | 11856 ± 28 | 138752 ± 823 | 33639 ± 245 |
| COV = 0.2% | COV = 0.8% | COV = 0.9% | |
| 0.64 mm3 | 13406 ± 40 | 151180 ± 703 | 36381 ± 157 |
| COV = 0.3% | COV = 0.8% | COV = 0.4% |
cell values are calculated from seven models at each seeding parameter
cell values are calculated based on three models – one for each acquisition
NOTE: all values are rounded.
Consistency of data acquisition
The consistency of our metrics with respect to different data acquisition was assessed in three datasets acquired from a single healthy control participant collected at three different time points. This test was also limited to NS, TL, and TWLCL evaluated in a single whole-brain streamtube model for each acquisition. For this test we used a seeding parameter of 0.85 mm3. COVs on the percent-difference metric are presented in Table 3 and did not exceed 1.3%.
Table 3.
Consistency of the metrics across three separate acquisitions of a single healthy control at a seeding dimension of 0.85 mm3 (mean ± SD and coefficient of variance (COV).
| Seed | NS | TL (mm) | TWLCL (mm) |
|---|---|---|---|
| 0.85 mm3 | 17210 ± 47 | 549166 ± 5072 | 148967 ± 1998 |
| COV = 0.3% | COV = 0.9% | COV = 1.3% |
cell values are calculated from seven models at each seeding parameter
cell values are calculated based on three models – one for each acquisition
NOTE: all values are rounded.
TOI selection has a subjective element to it. Intrarater and interrater reliability for transcallosal and the left and right cingulum bundles was assessed for NS and TL in ten datasets selected at random. We report only on these two metrics because they are the only two metrics that are directly affected by raters' decisions (anisotropy weighting is not directly affected by raters' decisions) and all remaining metrics are derived from these. Reliability for the remaining metrics can be assumed to be comparable. Intraclass correlation coefficients were 0.95 or greater for both metrics across the three TOIs. Interrater reliability was .87 or greater for both metrics across all three TOIs.
Discussion: Reproducibility study
These results demonstrate that our core metrics are stable across subjects with respect to subtle differences in the tractography models that could arise from jittering the seed points in the streamtube generation algorithm. The results also show that our metrics are stable across multiple datasets acquired at different times. These results indicate that our metrics are robust to issues that can arise with serial data collection such as differences in head placement in the scanner or subtle changes in the scanner itself. Our intrarater and interrater reliability analysis indicates that trained raters can be consistent over time and with each other in TOI selection, at least for the relatively large and easily identified fiber bundles analyzed in this project.
Results: Validity Study (whole brain metrics)
The groups did not differ significantly by age (t = 1.08; p = .29). The intracranial volume estimates for healthy controls (1571 mL ± 160 mL) and VCI groups (1679 mL ± 171 mL) did not differ significantly (t = −1.84, p = .08).
Levene's test revealed adequate homogeneity of variance between groups for most metrics across TOIs. Exceptions included NNS in the whole brain (p = .05) and NS in the corpus callosum (p = .04). Shapiro-Wilks tests revealed that the assumption of normality was met for most but not all metrics, but there was no consistent pattern of any one metric not meeting this assumption across groups in each TOI. No single case in either group was a clear and/or consistent outlier across the metrics and TOIs. Given the results of the normality and outlier assessment, we decided to retain all cases and to examine the consistency of results using both parametric and non-parametric techniques to test for group differences in the metrics in the whole brain and various TOIs. Assumptions of homogeneity of variance and normality were met for whole brain average FA.
Figure 1 shows sagittal views of whole brain streamtube models for one healthy control and one patient with VCI. In the healthy control group, age was significantly correlated with NS, NNS, TL, TWLCL, and TWLFA (all r > −.50, p < .01) but not with average TL, NTL, NTWLCL, or NTWLFA. Thus, averaging streamtube length by the number of streamtubes or normalizing by intracranial volume appears to control for any association between the metric and age in healthy controls. In the VCI group, age was not significantly correlated with any of the metrics. Age was significantly correlated with average FA for the whole fiber model (r = −.48, p = .05) in the healthy controls but not in the VCI group.
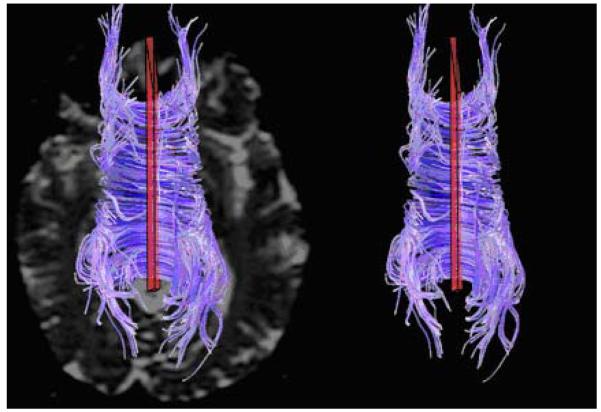
Figure 1.
Whole brain streamtube models (sagittal view) for a 72-year-old healthy volunteer (left) and a 60-year-old patient with VCI (right). Note that the density of streamtubes is clearly decreased in the VCI subject despite the younger age. This observed difference provided the motivation for our metrics.
A Pearson bivariate correlation matrix revealed strong and statistically significant inter-correlations among all nine metrics and average FA with r values ranging from 0.51 for AL vs. NS to 0.99 for TWLCL vs. TWLFA and NTWLCL vs. NTWLFA (all p ≤ .003).
A MANCOVA was conducted to evaluate group differences for the nine metrics and average FA with age as a covariate. The overall model showed a non-significant effect of age (F = 1.72 p = .14) and a significant effect of group (F = 2.62; p = .03). Seven of the nine metrics and average FA had significantly lower values in the VCI group compared to the healthy controls (i.e., p ≤ .01, see Table 4) with NS and TL showing trends toward significance (p = .06, .02, respectively). Effect sizes across the nine metrics were generally small (partial η2 = .12 to .29) and observed power ranged from .48 to .91. Non-parametric Mann-Whitney U test showed similar results with the VCI group showing significantly lower values compared to the NC group on ATL, NTL, NTWLCL, NTWLFA, and average FA (all p ≤ .01) and trend-level results for NNS, TL, TWLCL, and TWLFA (p = .03 to .05); NS was not significantly different between groups (p = .19). The results of the non-parametric analysis suggest that the impact of violations of normality and homogeneity of variance on isolated variables were insufficient to invalidate the parametric MANCOVA procedure. Moreover, the only metric that was not significant in the parametric test, NS, did not violate assumptions of normality or homogeneity of variance.
Table 4.
Age-corrected group comparison of metrics in whole brain, transcallosal fibers, and cingulate bundles.
| Metric | Healthy Controls (n=18) | VCI (n=14) | F(1,29) | p |
|---|---|---|---|---|
| Whole brain | ||||
| NS | 12713± 2112 | 11628 ± 2804 | 3.86 | .059 |
| NNS | 13055 ± 1583 | 11226 ± 2580 | 8.96 | .006 |
| TL (mm) | 397170 ± 84975 | 331754± 102162 | 6.49 | .016 |
| ATL (mm) | 31 ± 3 | 28 ± 3 | 8.70 | .006 |
| NTL (mm) | 408273 ± 78982 | 320580 ± 97119 | 9.97 | .004 |
| TWLCL (mm) | 104108 ± 24599 | 81525 ± 28112 | 8.61 | .006 |
| NTWLCL (mm) | 107068 ± 23948 | 78854 ± 26689 | 11.78 | .002 |
| TWLFA (mm) | 189134 ± 45313 | 149674 ± 51852 | 8.15 | .008 |
| NTWLFA (mm) | 194255 ± 42582 | 144716 ± 48999 | 11.61 | .002 |
| Average FA | .4367 ± .0170 | .4144 ± .0255 | 11.61 | .002 |
| Transcallosal fibers | ||||
| NNS | 723 ± 98 | 558 ± 160 | 12.45 | .001 |
| NTL (mm) | 44462± 9888 | 29864 ± 11810 | 13.86 | .001 |
| NTWLCL (mm) | 46369 ± 12634 | 29145 ± 11388 | 14.25 | .001 |
| NTWLFA (mm) | 24078 ± 5698 | 15461 ± 6855 | 14.69 | .001 |
| Average FA | .4780 ± .0406 | .4539± .0371 | 5.26 | .029 |
| Left cingulum bundle | ||||
| NNS | 51 ± 20 | 42 ± 20 | 2.54 | .112 |
| NTL (mm) | 3197± 1590 | 2864 ± 1874 | .49 | .491 |
| NTWLCL (mm) | 879 ± 456 | 799 ± 614 | .29 | .593 |
| NTWLFA (mm) | 1573 ± 802 | 1387 ± 1012 | .53 | .474 |
| Average FA | .4752 ± .0352 | .4640 ± .0340 | .92 | .345 |
| Right cingulum bundle | ||||
| NNS | 44 ± 15 | 40 ± 19 | .93 | .342 |
| NTL (mm) | 2828 ± 1131 | 2550 ± 1457 | .70 | .408 |
| NTWLCL (mm) | 859 ± 366 | 728 ± 449 | 1.35 | .255 |
| NTWLFA (mm) | 1449 ± 592 | 1249 ± 765 | 1.16 | .290 |
| Average FA | .4751 ± .0352 | .4658 ± .0356 | .681 | .416 |
We used partial correlation controlled for age to examine the association between all nine metrics including average FA and performance on our pre-selected cognitive measures (TMT-A, TMT-B, and BNT). We controlled for age because of the significant correlation between age and TMT-B (r = .40, p = .025). The other cognitive variables were not significantly correlated with age (p ≥ .28). Also, some metrics were significantly correlated with age (see above). Results showed that all metrics except ATL correlated significantly with TMT-A and/or TMT-B (all p ≤ .05) and the correlations were strongest for TWLCL, NTWLCL and NTWLFA and TMT-B (see Table 4). There were no significant correlations between any metric and BNT.
Discussion: Whole-brain
In whole brain streamtube models, our metrics were significantly correlated with age in the healthy controls. This is not unexpected given prior research demonstrating significant associations between age and white matter volume (Guttmann et al., 1998; Jernigan et al., 2001) and age and microstructural integrity measured by DTI (Pfefferbaum & Sullivan, 2003; Pfefferbaum et al., 2000). The absence of significant correlations between age and our metrics in the VCI group may reflect an alteration of the normal relationship between age and white matter integrity in the presence of subcortical vascular disease.
There is a high degree of collinearity among the nine metrics. This is not unexpected since all of the length-based metrics are derived from TL and because TL is clearly positively associated with NS. That is, in almost all cases higher NS will correspond to higher TL and lower NS will correspond to lower TL except possibly in cases where there are lots of short broken fibers. The significant correlation between average FA and the other metrics is also not surprising since average FA was calculated across the streamtubes only. This result suggests that we could have reduced the number of variables in our analyses by choosing one of the metrics. However, as noted previously, there are conceptual differences between what aspects of white matter integrity each metric is capturing. Therefore, we decided to retain all metrics in this initial test of their efficacy in the whole brain fiber models, recognizing that, given the collinearity effects, it would be unlikely for any one metric to outperform the others. As noted previously, we balanced this approach in the subsequent TOI analysis by limiting the number of variables to those that performed the best. One could argue that these metrics provide little additional information than average FA since it correlates strongly with the other metrics and because it the largest effect size for separating groups. However, consideration of FA in isolation potentially omits certain important features of the white matter such as the number and length of fibers in a TOI – information that might have clinical value to assessing the overall health of a fiber bundle in certain disorders.
Compared to healthy controls, the VCI group had significantly lower values for average FA and for seven of the nine metrics after controlling for age in these whole brain models. The remaining two metrics were nearly significant. This result is not at all unexpected given that the VCI group was selected for the presence of subcortical ischemic white matter changes on T2-weighted MRI. The importance of the results for the current validation study is that they provide evidence that our metrics are sensitive to white matter changes in a group of individuals with known vascular white matter injury.
The results of our correlation analysis indicate that as NTWLFA decreased time to complete the TMT-A & B tasks increased. In contrast, our metrics correlated very weakly with BNT and did not approach significance. These preliminary results need to be verified in a larger sample. Nonetheless, they provide additional support for the validity of our metrics; specifically, that they appear to capture clinically relevant information about white matter integrity and its association with cognitive status.
Whole brain TOI metrics could be viewed as providing a “brute force” method for comparing groups on overall white matter integrity. The potential advantage of this approach is that the whole brain TOI provides a measurement of white matter integrity that takes into account white matter that appears both normal and abnormal on conventional MRI. Thus, our whole brain TOI metrics may provide more robust markers of white matter structural integrity than either volumetric measures of T2-lesions obtained from conventional images or scalar DTI measures taken from region-of-interest analyses in normal-appearing white matter. The whole brain approach, however, is not useful for testing hypotheses about the integrity of particular white matter pathways or their relation to cognitive and behavioral function. To explore the potential utility of our metrics for answering such questions, we examined whether the VCI and healthy control groups differed on our metrics for three discrete TOIs: 1) transcallosal fibers (TCF) and the 2) left and right cingulum bundles. We chose to focus on these TOIs because they are prominent and easily identified aspects of the anatomy and because they represent two distinct categories of white matter fibers: commissural (i.e., inter-hemispheric) and association (i.e., intra-hemispheric) fibers; thus they seemed to be appropriate targets to test our new method.
Results: Validity Study (discrete tracts-of-interest)
The five metrics with the largest effect sizes in the whole brain analysis were NTWLCL, NTWLFA, NTL, average FA, and NNS (partial η2 = .289, .286, .256, .247, and .236, respectively). These five metrics were compared between groups in transcallosal and cingulum TOIs. Means and standard deviations for these five metrics in each TOI are reported in Table 4.
Transcallosal fibers
Figure 2 shows the TCF selection in a healthy control.
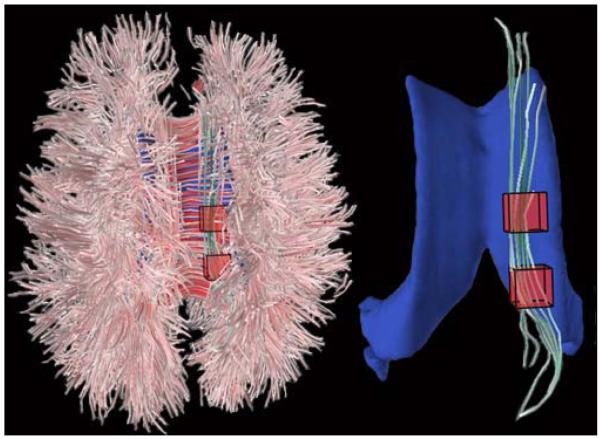
Figure 2.
Transcallosal fibers for a 48-year-old healthy volunteer showing placement of voxels-of-interest (in red) in axial view (top of image is anterior); for context, the left panel shows the fibers superimposed on a b=0 grey scale image.
The overall MANCOVA model revealed a non-significant effect of age (F = 1.51; p = .22); and a significant effect of group (F = 3.64; p = .02). The VCI group had significantly lower values on all five metrics compared to the healthy controls (Table 3). Effect sizes across the seven metrics were small to moderate with partial η2 ranging from .15 for average FA and from .30 to .34 for the remaining metrics. Observed power ranged from .60 for average FA and from .93 to .96 for the remaining metrics. NTWLFA had the largest effect size and highest observed power. The group differences for the metrics were also significant when tested using the non-parametric Mann-Whitney U test with p ≤ .01 for all metrics except average FA (p = .04). The results of the non-parametric analysis suggest that the impact of violations of normality and homogeneity of variance on isolated variables were insufficient to invalidate the parametric MANCOVA procedure.
Cingulum Bundles
Figure 3 shows an example of cingulum bundle selection in a patient with VCI.
Figure 3.
Cingulum bundles segmented from a 76-year-old patient with VCI. Left image shows placement of voxels-of-interest in axial view (top of image is anterior). Right image shows segmented cingulum bundle. Lateral ventricles are depicted in blue for reference purposes.
For the left cingulum bundle, the overall model showed an effect of age at the trend level of statistical significance (F = 1.54; p = .20). There was a significant overall effect of group (F = 6.92; p ≤ .01). In contrast, the pair-wised tests showed no significant group differences for any of the metrics (see Table 3), although all values were lower in the VCI group. Effect sizes and observed power were small with partial η2 ≤ .08 and observed power ≤ .34. No significant group differences across the metrics were found using Mann-Whitney U tests (all p ≥ .11).
For the right cingulum bundle, the overall model was not significant for age (F = .40; p = .85) or group (F = 1.54; p = .21). Effect sizes for the individual metrics were small effect sizes with partial η2 ≤ .04 and observed power ≤ .20. The values for the individual metrics were in the expected direction being lower in the VCI group. No significant group differences across the metrics were found using Mann-Whitney U tests (all p ≥ .31). These results parallel those for the left cingulum bundle.
Discussion: Discrete Tracts-of-Interest
These results demonstrate that for transcallosal fibers, the VCI group has significantly lower standing on each of the metrics than the healthy control group suggesting poorer white matter integrity with both fewer and shorter streamtubes. Interestingly, effect sizes were smallest for average FA suggesting that the new metrics may provide a more robust marker of the integrity of transcallosal fibers. The results for the transcallosal fibers are not surprising as callosal and pericallosal T2-weighted hyperintensities are frequently observed for patients with VCI. In contrast no significant group differences were found for any metric in the cingulum bundles although the values of all metrics were in the expected direction.
The absence of significant differences in either parametric or non-parametric tests in the smaller cingulum bundles was unexpected. There are several potential reasons for these generally negative results: The cingulum TOIs are smaller with fewer streamtubes than the transcallosal TOI suggesting that insufficient statistical power may have been the key reason for the result. In fact, observed power was quite low for each metric in the cingulum bundles. An alternative potential explanation is that VCI might have a less potent impact on the cingulum bundles compared to transcallosal fibers possibly reflecting subtle differences in the vascular supply of the cingulum compared to deep white regions. For example, the cingulate cortex has a relatively robust ipsilateral and collateral supply and is not perfused by small penetrating or deep lenticulostriate arteries that are prone to hypertensive arteriosclerotic changes (Cosgrove, personal communication August 10, 2006 2006). Examination of the standard deviations of the metrics for the cingulum raises the possibility that our metrics may be more variable in smaller TOIs such as the cingulum bundles (see Table 3) and that this contributed to the lack of significant results. Intrarater and interrater reliability was quite good for the cingulum bundles and so rater error seems unlikely as a main reason for disappointing findings.
Overall Discussion
In this section we first provide an overview of the results. Next, we describe the potential utility of our metrics and present our thoughts on which of our several metrics we are now focusing on for other analyses. We then discuss the relationship of our quantitative tractography metrics to scalar metrics and other tractography algorithms. Methodological concerns, the impact of image resolution and partial volume effects on our metrics, and issues related to sample size and conventional T2 metrics are addressed in subsequent sections.
Our results replicate and extend other work on quantitative tractography (e.g., Ashtari et al., 2007; Ciccarelli, Parker et al., 2003; Ciccarelli, Toosy et al., 2003; Ding et al., 2003; Fillard et al., 2007; Huang et al., 2005; Jiang et al., 2006; Parker, 2000; Parker, Stephan et al., 2002; Parker, Wheeler-Kingshott et al., 2002; Smith et al., 2006). The results show that quantitative tractography metrics, including the ones presented here and those previously developed by others e.g., DTIStudio (Jiang et al., 2006), MedINRIA (Fillard et al., 2007), and PRIDE), have utility for assessing the integrity of specific white matter pathways. Our metrics span the gamut from quantitative tractography metrics that describe fiber length and number and scalar anisotropy metrics that provide information about intra-voxel structural integrity. The results support the validity and reliability of quantitative tractography metrics and indicate that white matter integrity is reduced in patients with VCI compared to healthy individuals in whole brain tractography models and in fibers passing through the corpus callosum. Moreover, the pattern of correlations with measures of cognitive functioning suggests that the information captured by the metrics is clinically relevant. The lack of significant group differences in the cingulate bundles was unexpected and possibly reflects either low statistical power due to the relatively smaller number of streamtubes in the cingulate TOIs or differences in their vulnerability to vascular injury.
The results demonstrate some impact of age on our metrics in the healthy control group in the whole brain models suggesting that VCI disrupts the normal association between age and white matter integrity. Not surprisingly, there is considerable and significant shared variance among the metrics. This suggests that the metrics are somewhat interchangeable from a statistical perspective. However, conceptually each metric provides somewhat unique information about the underlying white matter integrity. Therefore, retaining them in the whole brain analysis in this initial validation study seemed justified.
Potential Utility of our Metrics
Our metrics that weight length by linear or fractional anisotropy and then normalize to intracranial volume may be especially useful in the context of acquired white matter injury where aspects of length or number of streamtubes are unchanged despite lowered anisotropy resulting from pathological processes such as inflammation or incomplete infarction. These length-based metrics might also be useful for gauging the magnitude of age-related reductions in white matter integrity and its impact on cognitive functioning. For example, the total length of myelinated axons is reduced by as much as 47% in old age, with the greatest loss evident in small-diameter fibers, which myelinate later in life in frontal regions of the brain (Pakkenberg, 1989). Such changes may well be related to the decline in circumscribed executive cognitive functions seen in aging (Brennan, Welsh, & Fisher, 1997; Wecker, Kramer, Wisniewski, Delis, & Kaplan, 2000).
The effect sizes obtained for the transcallosal fibers suggest that our metrics, particularly NTWLFA, are more robust than average FA as markers of the structural integrity of white matter tracts. This finding is in line with our presumption that metrics such as NTWLFA capture more complete information about the integrity of a tract than average FA. The effect sizes for NTLWFA and NTWLCL were similar in both whole brain and transcallosal fibers reflecting the similarity between FA and CL. However, we have focused our ongoing work on NTWLFA since FA incorporates both linear and planar anisotropy in a single metric possibly making it a conceptually more attractive and possibly more sensitive metric than NTWLCL which quantifies only the linear anisotropy. Moreover, because it captures both linear and planar anisotropy, NTWLFA might perform better in regions where fibers cross because of the tendency of these regions to show reductions in linear anisotropy that are accompanied by increases in planar anisotropy. It is important to note, however, that our work focuses mainly on adults with pathological loss of white matter integrity and that it is possible that other metrics have greater applicability to other clinical conditions.
Relationship to Scalar Metrics and Other Tractography Algorithms
Our metrics and conventional scalar metrics provide complementary information about white matter integrity. The relative utility of the two approaches depends in large part on the research question. For example, voxel-based morphometric or tract-based spatial statistics may be more useful than quantitative tractography for initial exploration of white matter regions that differ between diagnostic groups. These approaches might be followed with quantitative tractography analyses for further characterization of the structural integrity of specific tracts and their relationship to behavior and cognition.
Our metrics could also be used in combination with scalar metrics to provide different levels of information about white matter integrity. In one sense, a tract-of-interest simply identifies a set of voxels that comprise a functionally meaningful anatomical structure. Scalar metrics such as mean diffusivity, intravoxel coherence, and parallel or radial diffusivity derived from the diffusion tensor of the voxels included in a tract-of-interest could help further characterize its structural integrity and provide clues to the nature of group differences in tract integrity. For example, consider a situation where one group has significantly lower NTWLFA than another group in a particular tract-of-interest. Follow-up analysis of using scalar metrics such as radial and parallel diffusivity might provide insight as to whether the differences in NTWLFA reflect demyelination compared to some other process (Budde et al., 2007; Song et al., 2002; Song et al., 2005). Variability in structural integrity along the trajectory of a tract-of-interest could help isolate specific regions that are vulnerable to injury. These regions could be identified by examining the distribution of scalar values along the voxels that comprise the tract (Clayden, Zhang, Correia, & Laidlaw, 2007). Scalar metrics may also be useful in disambiguating quantitative tractography results in areas of crossing fibers (see “Image Resolution and Partial Volume Effects” below). One important caveat is that there may be limitations to the combined analysis of our metrics and scalar metrics in the same statistical model due to colinearity.
Another area of concern regards the validity of our metrics when applied to alternative fiber tracking methods or to data acquired differently or at higher field strengths. Since most tractography algorithms solve an integration problem in the first eigenvector field of the diffusion tensor field, the basic principle underlying our metrics should hold with other fiber tracking methods. This expectation assumes that there is relative uniformity across methods in terms of the topography and density of fiber pathways generated. Of course, the metrics are quite likely to acquire different values across methods or with different parameter settings on the same method making direct comparison of results based on alternative fiber tracking algorithms difficult.
Methodological Issues
Our emphasis on length measures derives from an observation of shorter fibers in the tractography models of individuals with white matter injury. It also reflects the likelihood that many acquired disorders affecting white matter produce local reductions in diffusion anisotropy that, in turn, impact the number and length of streamtubes output by the streamtube generation algorithm. The extent of this effect, however, depends on the predetermined minimum linear anisotropy and length thresholds set in the algorithm for streamtube generation. The anisotropy and minimum length criteria (≥ 10 mm) in our algorithm were chosen to limit the number of spurious, anatomically implausible fibers while retaining a maximal number of anatomically plausible fibers. Moreover, our experience is that lower levels of anisotropy cause streamtubes to intrude on regions that are obviously grey matter. Adjusting these parameters could impact the magnitude of the obtained metrics but are unlikely to change the pattern of results. This expectation is supported by the results of a repeat of the current study using a higher anisotropy setting (results not shown) in which the value of our metrics changed, but the pattern of group differences remained unchanged.
The TOI used in this study were relatively easy to identify and segment from surrounding precisely because they stand out from fibers around them and are quite homogeneous in their topography. We anticipate that our metrics would be sensitive to changes in white matter integrity even in less discrete fiber bundles or in regions that are topographically ambiguous because of high numbers of crossing or kissing fibers (e.g., inferior anterior internal capsule). However, this assumption has not been tested.
The anatomical correctness of our streamtube models (or any other tractography method) key for assuring accurate tract-of-interest. This issue has been addressed by others using color coding and identification of specific white matter tracts by experts who are knowledgeable about white matter anatomy (e.g., (Wakana et al., 2004)). Preliminary work in our lab (data not shown) has shown that the TOIs used in this analysis and others (e.g., uncinate fasciculus, superior longitudinal fasciculus, inferior longitudinal fasciculus, forceps major and minor), are easily and reliably identified by expert raters (S Zhang, Correia, Tate, & Laidlaw, 2006).
An argument could be made that normalization of our metrics would be most appropriate if done according to some yet-to-be-defined length metric rather than by intracranial volume which divides length (or number of streamtubes) by volume. In the absence of some such measure, the term in the denominator of our normalization formula was designed to avoid unwieldy and difficult-to-interpret units such as mm/mL. Examination of the values of the F statistic reported in Table 3 suggests that normalizing our metrics reduced some degree of error variance.
Subject motion during scanning can impact the derivation of streamtube models, which, in turn, may affect calculation of our metrics. Qualitatively, our datasets had minimal motion artifact. Although patients with dementia may be less apt to remain still during a scan than healthy controls, the level of cognitive impairment in our patients was quite mild and none met diagnostic criteria for dementia. Accordingly, it is reasonable to believe that motion artifact was sufficiently similar in both groups to conduct this initial test of the metrics. Applying motion correction before calculating tensors may improve the reliability and robustness of the results, but at this time there is no true consensus on optimal method for implementing motion correction in DTI data.
Image Resolution and Partial Volume Effects
Our tractography algorithm was based on diffusion data acquired in 12 directions and our image resolution (prior to interleaving) is relatively low. Other studies have stressed the importance of acquiring data in more directions to improve the anatomical accuracy of tractography models (Hirsch, Schwenk, Rossmanith, Hennerici, & Gass, 2003; Ozarslan & Mareci, 2003). However, the extent of this benefit is debated (Wedeen, Hagmann, Tseng, Reese, & Weisskoff, 2005). Our use of 12 gradient directions in this study is based on two main factors. First, our data acquisition began prior to the wider acceptance and implementation of high-angular resolution scanning. Second, because of non-technical institutional constraints, 12 directions was the maximum that we could obtain on our scanner when we started data acquisition. A higher number of gradient directions and higher overall image resolution might have improved the representativeness of the tractography models and the absolute values obtained in our analysis. Our core assumptions that streamtube length and number capture important features of the underlying anatomy seem likely to hold with additional diffusion encoding directions and higher spatial resolution, although this has not been tested. A related issue is the potential impact of having more diffusion encoding directions and higher spatial resolution on rater reliability. Such improvements ought to permit raters to make more fine-grained decisions about what fibers should be included or excluded from a tract-of-interest but whether this would improve or reduce intra-rater or inter-rater reliability has not been determined.
One area of concern that we have not directly assessed is the reliability of our method in regions with high partial volume effects or of crossing or kissing fibers causing incoherent diffusion. Tractography methods that rely on the principle direction of diffusion may have difficulty moving past such regions. This is a well-known problem in tractography and our method, which depends on tractographic results as a building block, will be impacted by it. It is likely that the different metrics will be impacted in different ways. For example, the total length of a tract-of-interest will likely be shorter because fibers will not pass through regions of incoherent diffusion if linear anisotropy drops below the pre-specified threshold for fiber propagation. The number of fibers may go up, if what would have otherwise been a single path is divided where a second tract crosses the tract of interest. The specific effects on the metrics will also be somewhat dependent on the decisions made to segment the tract such as where segmentation boxes are placed relative to the location of diffusion ambiguity.
In healthy normal brains, regions of crossing or kissing fibers should not produce a significant subject-by-region bias. Rather, they should simply be a source of noise that is relatively stable across individuals (although intra- and inter-rater reliability may suffer due to the ambiguity in the tractography results in these regions). However, it is possible that in patient groups, the metrics could acquire misleading values in areas of fiber crossing if one group of fibers is selectively impacted by the disease (e.g., Wallerian degeneration following a distal focal lesion). This potential problem might be partly minimized by coupling tractographic methods with higher angular resolution acquisitions to produce paths that continue accurately through regions of crossing fibers. These paths could then be used to calculate our un-weighted metrics thereby reducing some of the ambiguity we currently have. Ideally, the metrics could be weighted by some yet-to-be-determined scalar metric (other than FA or CL) that captures the relative linearity of each fiber compartment in a region of crossing or kissing fibers. This would further attenuate the problems caused by partial volume effects and produce metrics that are more directly coupled to the underlying anatomy and pathology. Alternatively, conventional scalar DTI metrics such as mean diffusivity, planar anisotropy, and isotropy (Westin et al., 2002) might help resolve ambiguity about the nature of diffusion characteristics in such regions. For example, differences arising from disruption of all fibers in a crossing region should cause local increase in isotropy whereas preferential disruption of one crossing fiber bundle might result in decreased planar anisotropy and increased linear anisotropy or changes in their orientation.
Sample Size and Relation to T2 Metrics
Further validation of our metrics in larger samples and with other disorders impacting white matter will help confirm the validity and clinical utility of our metrics. In particular, it will be important to evaluate the extent to which our metrics add incremental predictive accuracy over and above other measurements of white matter integrity such as region-of-interest approaches using scalar DTI metrics and T2 white matter lesion volume for discriminating patients from controls. Of course, incremental predictive validity depends on the patient population and specific tracts-of-interest being studied. Preliminary data from our lab (not shown) suggests that NTWLFA and NTWLCL are more strongly correlated with cognitive function than T2-weighted lesion volume in patients with CADASIL (Patel et al., 2007) and in patients with mild cognitive impairment (Patel, Correia, Laidlaw, & Salloway, 2008).
Summary and Conclusion
We explored the potential clinical utility of nine metrics derived from cerebral DTI tractography data. The validity of the metrics was evaluated in whole brain white matter and in three distinct TOIs in patients with VCI vs. healthy controls. After controlling for age, the VCI group had significantly lower metric values than the healthy controls in whole brain models and in transcallosal fibers. The metrics were not significantly different between groups in the left and right cingulum bundles, although the VCI group had lower standing on all metrics in the analysis. This study extends prior work showing that quantitative metrics can be derived from DTI tractography data that provide clinically-relevant information about the microstructural integrity of cerebral white matter. In particular, the metrics presented here provide a means for combining basic metrics that describe white matter morphology (e.g., length and number of fibers) with intra-voxel scalar anisotropy metrics while considering tracts in their entirety. The metrics can be used in whole brain models of white matter connectivity or in specific white matter pathways. A potential strength of our approach is that since the models are defined in a 3D environment, TOI selection can occur on a dataset-by-dataset basis so that the unique individual variability in white matter bundle shape considered in its entirety can be persevered - information that may be lost with sophisticated image registration to a common template. Quantitative tractography metrics are potentially a powerful alternative to the non-tractography scalar-based approaches to DTI analysis commonly used clinical studies and provide researchers with robust and conceptually valid tools for assessing the structural integrity of specific white matter pathways.
Table 5.
Partial correlations (controlled for age) between nine metrics and cognitive tests in whole brain TOI (whole sample, n = 32)
| Cognitive Test |
|||
|---|---|---|---|
| Metric | TMT-A | TMT-B | BNT |
| NS | −.41* | −.38* | .02 |
| NNS | −.42* | −.41* | .03 |
| TL | −.39* | −.42* | .17 |
| ATL | −.28 | −.38 | .35 |
| NTL | −.37* | −.43* | .19 |
| TWLCL | −.41* | −.45** | .19 |
| NTWLCL | −.39* | −.45** | .21 |
| TWLFA | −.41* | −.44* | .17 |
| NTWLFA | −.39* | −.45** | .19 |
| Average FA | −.40* | −.33 | −.08 |
.05 ≤ p .02
p = .01
NOTE: TMT-A = Trail Making Test part A (a test of psychomotor processing speed); TMT-B = Trail Making Test part B (a test of executive function, cognitive set switching); BNT = Boston Naming Test (a measure of confrontational naming).
REFERENCES
- Ahrens ET, Laidlaw DH, Readhead C, Brosnan CF, Fraser SE, Jacobs RE. MR microscopy of transgenic mice that spontaneously acquire experimental allergic encephalomyelitis. Magn Reson Med. 1998;40(1):119–132. doi: 10.1002/mrm.1910400117. [DOI] [PubMed] [Google Scholar]
- Akers D, Sherbondy A, Mackenzie R, Dougherty R, Wandell B. Exploration of the brain's white matter pathways with dynamic queries; Paper presented at the IEEE Visualization '04; San Antonio. 2004. [DOI] [PubMed] [Google Scholar]
- Ashtari M, Cottone J, Ardekani BA, Cervellione K, Szeszko PR, Wu J, et al. Disruption of white matter integrity in the inferior longitudinal fasciculus in adolescents with schizophrenia as revealed by fiber tractography. Arch Gen Psychiatry. 2007;64(11):1270–1280. doi: 10.1001/archpsyc.64.11.1270. [DOI] [PubMed] [Google Scholar]
- Basser PJ, Mattiello J, LeBihan D. MR diffusion tensor spectroscopy and imaging. Biophys J. 1994;66(1):259–267. doi: 10.1016/S0006-3495(94)80775-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Beaulieu C. The basis of anisotropic water diffusion in the nervous system - a technical review. NMR Biomed. 2002;15(78):435–455. doi: 10.1002/nbm.782. [DOI] [PubMed] [Google Scholar]
- Bigler ED. Neuropsychological results and neuropathological findings at autopsy in a case of mild traumatic brain injury. J Int Neuropsychol Soc. 2004;10(5):794–806. doi: 10.1017/S1355617704105146. [DOI] [PubMed] [Google Scholar]
- Brennan-Krohn T, Correia S, Zhang S, Laidlaw D, Malloy P, Salloway S. Diffusion-Tensor Imaging and Executive Function in Vascular Cognitive Impairment; Paper presented at the International Society of Magnetic Resonance in Medicine: Workshop on Aging Connections: Advanced MRI of Age-Related White Matter Changes in the Brain (poster); Boston. 2004, October 21-23; 2004. [Google Scholar]
- Brennan M, Welsh MC, Fisher CB. Aging and executive function skills: an examination of a community-dwelling older adult population. Percept Mot Skills. 1997;84(3 Pt 2):1187–1197. doi: 10.2466/pms.1997.84.3c.1187. [DOI] [PubMed] [Google Scholar]
- Budde MD, Kim JH, Liang HF, Schmidt RE, Russell JH, Cross AH, et al. Toward accurate diagnosis of white matter pathology using diffusion tensor imaging. Magn Reson Med. 2007;57(4):688–695. doi: 10.1002/mrm.21200. [DOI] [PubMed] [Google Scholar]
- Carpenter MB. Core Text of Neuroanatomy. 4th ed. Williams & Wilkins; Baltimore: 1991. [Google Scholar]
- Ciccarelli O, Parker GJ, Toosy AT, Wheeler-Kingshott CA, Barker GJ, Boulby PA, et al. From diffusion tractography to quantitative white matter tract measures: a reproducibility study. Neuroimage. 2003;18(2):348–359. doi: 10.1016/s1053-8119(02)00042-3. [DOI] [PubMed] [Google Scholar]
- Ciccarelli O, Toosy AT, Parker GJ, Wheeler-Kingshott CA, Barker GJ, Miller DH, et al. Diffusion tractography based group mapping of major white-matter pathways in the human brain. Neuroimage. 2003;19(4):1545–1555. doi: 10.1016/s1053-8119(03)00190-3. [DOI] [PubMed] [Google Scholar]
- Clayden J, Zhang S, Correia S, Laidlaw D. Fine-grained comparison of anisotrophy differences between groups of white matter tracts; Paper presented at the Proceedings of the International Society of Magnetic Resonance in Medicine; Berlin, Germany. 2007. [Google Scholar]
- Correia S, Brennan-Krohn T, Schlicting E, Zhang S, Laidlaw D, Malloy P, et al. Diffusion-tensor imaging in vascular cognitive impairment and mild cognitive impairment: relationship with executive functioning. (Poster abstract); Paper presented at the 2nd Congress of the International Society for Vascular, Cognitive and Behavioural Disorders (VAS-COG); Florence, Italy. 2005, June 8-12. [Google Scholar]
- Correia S, Brennan-Krohn T, Zhang S, Laidlaw D, Malloy P, Salloway S. Diffusion-tensor imaging and executive function in subcortical ischemic vascular disease and mild cognitive impairment; Paper presented at the 33rd Annual Meeting of the International Neuropsychological Society; St. Louis, MO. 2005, February 2-5; 2005. [Google Scholar]
- Cosgrove RG. personal communication. Aug 10, 2006.
- de Jager CA. Changes over time in memory, processing speed and clock drawing tests help to discriminate between vascular cognitive impairment, mild cognitive impairment and Alzheimer's disease. Neurol Res. 2004;26(5):481–487. doi: 10.1179/016164104225016209. [DOI] [PubMed] [Google Scholar]
- Delmarcelle T, Hesselink L. Visualizing second-order tensor fields with hyperstream lines. IEEE Computer Graphics and Applications. 1993;13(4):25–33. [Google Scholar]
- Desmond DW. The neuropsychology of vascular cognitive impairment: is there a specific cognitive deficit? J Neurol Sci. 2004;226(12):3–7. doi: 10.1016/j.jns.2004.09.002. [DOI] [PubMed] [Google Scholar]
- Ding Z, Gore JC, Anderson AW. Classification and quantification of neuronal fiber pathways using diffusion tensor MRI. Magn Reson Med. 2003;49(4):716–721. doi: 10.1002/mrm.10415. [DOI] [PubMed] [Google Scholar]
- Erkinjuntti T. Diagnosis and management of vascular cognitive impairment and dementia. J Neural Transm Suppl. 2002;(63):91–109. doi: 10.1007/978-3-7091-6137-1_6. [DOI] [PubMed] [Google Scholar]
- Fillard P, Souplet J, Toussaint N. Medical Image Navigation and Research Tool by INRIA (MedINRIA) France: 2007. [Google Scholar]
- Folstein M, Folstein E, McHugh P. Mini-Mental State Exam: A practical method for grading the cognitive status of patients. Journal of Psychiatric Research. 1975;12:189–198. doi: 10.1016/0022-3956(75)90026-6. [DOI] [PubMed] [Google Scholar]
- Gunning-Dixon FM, Raz N. The cognitive correlates of white matter abnormalities in normal aging: a quantitative review. Neuropsychology. 2000;14(2):224–232. doi: 10.1037//0894-4105.14.2.224. [DOI] [PubMed] [Google Scholar]
- Guttmann CR, Jolesz FA, Kikinis R, Killiany RJ, Moss MB, Sandor T, et al. White matter changes with normal aging. Neurology. 1998;50(4):972–978. doi: 10.1212/wnl.50.4.972. [DOI] [PubMed] [Google Scholar]
- Haines D. Neuroanatomy: An atlas of structures, sections, and systems. 6th ed. Lippincott Williams & Wilkins; Baltimore: 2004. [Google Scholar]
- Hirsch JG, Schwenk SM, Rossmanith C, Hennerici MG, Gass A. Deviations from the diffusion tensor model as revealed by contour plot visualization using high angular resolution diffusion-weighted imaging (HARDI) Magma. 2003;16(2):93–102. doi: 10.1007/s10334-003-0011-y. [DOI] [PubMed] [Google Scholar]
- Huang H, Zhang J, Jiang H, Wakana S, Poetscher L, Miller MI, et al. DTI tractography based parcellation of white matter: application to the mid-sagittal morphology of corpus callosum. Neuroimage. 2005;26(1):195–205. doi: 10.1016/j.neuroimage.2005.01.019. [DOI] [PubMed] [Google Scholar]
- Jernigan TL, Archibald SL, Fennema-Notestine C, Gamst AC, Stout JC, Bonner J, et al. Effects of age on tissues and regions of the cerebrum and cerebellum. Neurobiol Aging. 2001;22(4):581–594. doi: 10.1016/s0197-4580(01)00217-2. [DOI] [PubMed] [Google Scholar]
- Jiang H, van Zijl PC, Kim J, Pearlson GD, Mori S. DtiStudio: resource program for diffusion tensor computation and fiber bundle tracking. Comput Methods Programs Biomed. 2006;81(2):106–116. doi: 10.1016/j.cmpb.2005.08.004. [DOI] [PubMed] [Google Scholar]
- Jones DK, Lythgoe D, Horsfield MA, Simmons A, Williams SC, Markus HS. Characterization of white matter damage in ischemic leukoaraiosis with diffusion tensor MRI. Stroke. 1999;30(2):393–397. doi: 10.1161/01.str.30.2.393. [DOI] [PubMed] [Google Scholar]
- Kaplan E, Goodglass H, Weintraub S. The Boston Naming Test. 2nd ed. Lea and Febiger; Philadelphia: 1983. [Google Scholar]
- Kirasic KC, Allen GL, Dobson SH, Binder KS. Aging, cognitive resources, and declarative learning. Psychol Aging. 1996;11(4):658–670. doi: 10.1037//0882-7974.11.4.658. [DOI] [PubMed] [Google Scholar]
- Laidlaw D, Zhang S, Bastin ME, Correia S, Salloway S, Malloy P. Ramifications of isotropic sampling and acquisition orientation on DTI analyses. (poster); Paper presented at the Twelfth Scientific Meeting and Exhibition, International Society for Magnetic Resonance in Medicine; Kyoto, Japan. 2004. [Google Scholar]
- Larsson EM, Englund E, Sjobeck M, Latt J, Brockstedt S. MRI with diffusion tensor imaging postmortem at 3.0 T in a patient with frontotemporal dementia. Dement Geriatr Cogn Disord. 2004;17(4):316–319. doi: 10.1159/000077162. [DOI] [PubMed] [Google Scholar]
- Le Bihan D, Mangin JF, Poupon C, Clark CA, Pappata S, Molko N, et al. Diffusion tensor imaging: concepts and applications. J Magn Reson Imaging. 2001;13(4):534–546. doi: 10.1002/jmri.1076. [DOI] [PubMed] [Google Scholar]
- Lukatela K, Malloy P, Jenkins M, Cohen R. The naming deficit in early Alzheimer's and vascular dementia. Neuropsychology. 1998;12(4):565–572. doi: 10.1037//0894-4105.12.4.565. [DOI] [PubMed] [Google Scholar]
- Mori S, van Zijl PC. Fiber tracking: principles and strategies - a technical review. NMR Biomed. 2002;15(78):468–480. doi: 10.1002/nbm.781. [DOI] [PubMed] [Google Scholar]
- O'Brien JT, Erkinjuntti T, Reisberg B, Roman G, Sawada T, Pantoni L, et al. Vascular cognitive impairment. Lancet Neurol. 2003;2(2):89–98. doi: 10.1016/s1474-4422(03)00305-3. [DOI] [PubMed] [Google Scholar]
- Ozarslan E, Mareci TH. Generalized diffusion tensor imaging and analytical relationships between diffusion tensor imaging and high angular resolution diffusion imaging. Magn Reson Med. 2003;50(5):955–965. doi: 10.1002/mrm.10596. [DOI] [PubMed] [Google Scholar]
- Pajevic S, Pierpaoli C. Color schemes to represent the orientation of anisotropic tissues from diffusion tensor data: application to white matter fiber tract mapping in the human brain. Magn Reson Med. 1999;42(3):526–540. [PubMed] [Google Scholar]
- Pakkenberg B. What happens in the leucotomised brain? A postmortem morphological study of brains from schizophrenic patients. J Neurol Neurosurg Psychiatry. 1989;52(2):156–161. doi: 10.1136/jnnp.52.2.156. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Parker GJ. Tracing fibre tracts using fast marching. Proceedings of the International Society of Magnetic Resonance in Medicine. 2000;85 [Google Scholar]
- Parker GJ, Stephan KE, Barker GJ, Rowe JB, MacManus DG, Wheeler-Kingshott CA, et al. Initial demonstration of in vivo tracing of axonal projections in the macaque brain and comparison with the human brain using diffusion tensor imaging and fast marching tractography. Neuroimage. 2002;15(4):797–809. doi: 10.1006/nimg.2001.0994. [DOI] [PubMed] [Google Scholar]
- Parker GJ, Wheeler-Kingshott CA, Barker GJ. Estimating distributed anatomical connectivity using fast marching methods and diffusion tensor imaging. IEEE Trans Med Imaging. 2002;21(5):505–512. doi: 10.1109/TMI.2002.1009386. [DOI] [PubMed] [Google Scholar]
- Patel K, Correia S, Foley J, Schlicting E, Zhang S, Laidlaw D, et al. Cognitive Impairment, Hippocampal Volume, and White Matter Integrity in CADASIL; Paper presented at the 35th Annual Meeting of the International Neuropsychological Society; Portland, OR. 2007. [Google Scholar]
- Patel K, Correia S, Laidlaw D, Salloway S. Functional implications of white matter vs. grey matter changes in mild cognitive impairment; Paper presented at the 36th Annual Meeting of the International Neuropsychological Society; Waikoloa, HI. 2008, Feb. 6-9. [Google Scholar]
- Pfefferbaum A, Sullivan EV. Increased brain white matter diffusivity in normal adult aging: Relationship to anisotropy and partial voluming. Magn Reson Med. 2003;49(5):953–961. doi: 10.1002/mrm.10452. [DOI] [PubMed] [Google Scholar]
- Pfefferbaum A, Sullivan EV, Hedehus M, Lim KO, Adalsteinsson E, Moseley M. Age-related decline in brain white matter anisotropy measured with spatially corrected echo-planar diffusion tensor imaging. Magn Reson Med. 2000;44(2):259–268. doi: 10.1002/1522-2594(200008)44:2<259::aid-mrm13>3.0.co;2-6. [DOI] [PubMed] [Google Scholar]
- Reese TG, Heid O, Weisskoff RM, Wedeen VJ. Reduction of eddy-current-induced distortion in diffusion MRI using a twice-refocused spin echo. Magn Reson Med. 2003;49(1):177–182. doi: 10.1002/mrm.10308. [DOI] [PubMed] [Google Scholar]
- Reitan R. Validity of the Trail Making Test as an indicator of organic brain damage. Perceptual and Motor Skills. 1958;8:271–276. [Google Scholar]
- Rockwood K. Vascular cognitive impairment and vascular dementia. J Neurol Sci. 2002;203-204:23–27. doi: 10.1016/s0022-510x(02)00255-1. [DOI] [PubMed] [Google Scholar]
- Sachdev P. Vascular cognitive disorder. Int J Geriatr Psychiatry. 1999;14(5):402–403. [PubMed] [Google Scholar]
- Sachdev PS, Brodaty H, Valenzuela MJ, Lorentz L, Looi JC, Wen W, et al. The neuropsychological profile of vascular cognitive impairment in stroke and TIA patients. Neurology. 2004;62(6):912–919. doi: 10.1212/01.wnl.0000115108.65264.4b. [DOI] [PubMed] [Google Scholar]
- Salloway S, Desbiens S. CADASIL and Other Genetic Causes of Stroke and Vascular Dementia. In: Paul R, Cohen R, Ott B, Salloway S, editors. Vascular Dementia: Cerebrovascular Mechanisms and Clinical Management. Humana Press; Totowa, NJ: 2004. pp. 87–98. [Google Scholar]
- Smith SM, Jenkinson M, Johansen-Berg H, Rueckert D, Nichols TE, Mackay CE, et al. Tract-based spatial statistics: voxelwise analysis of multi-subject diffusion data. Neuroimage. 2006;31(4):1487–1505. doi: 10.1016/j.neuroimage.2006.02.024. [DOI] [PubMed] [Google Scholar]
- Song SK, Sun SW, Ramsbottom MJ, Chang C, Russell J, Cross AH. Dysmyelination revealed through MRI as increased radial (but unchanged axial) diffusion of water. Neuroimage. 2002;17(3):1429–1436. doi: 10.1006/nimg.2002.1267. [DOI] [PubMed] [Google Scholar]
- Song SK, Yoshino J, Le TQ, Lin SJ, Sun SW, Cross AH, et al. Demyelination increases radial diffusivity in corpus callosum of mouse brain. Neuroimage. 2005;26(1):132–140. doi: 10.1016/j.neuroimage.2005.01.028. [DOI] [PubMed] [Google Scholar]
- Sullivan EV, Adalsteinsson E, Pfefferbaum A. Selective Age-related Degradation of Anterior Callosal Fiber Bundles Quantified In Vivo with Fiber Tracking. Cereb Cortex. 2005 doi: 10.1093/cercor/bhj045. [DOI] [PubMed] [Google Scholar]
- Sun SW, Song SK, Harms MP, Lin SJ, Holtzman DM, Merchant KM, et al. Detection of age-dependent brain injury in a mouse model of brain amyloidosis associated with Alzheimer's disease using magnetic resonance diffusion tensor imaging. Exp Neurol. 2005;191(1):77–85. doi: 10.1016/j.expneurol.2004.09.006. [DOI] [PubMed] [Google Scholar]
- Votaw JR, Faber TL, Popp CA, Henry TR, Trudeau JD, Woodard JL, et al. A confrontational naming task produces congruent increases and decreases in PET and fMRI. Neuroimage. 1999;10(4):347–356. doi: 10.1006/nimg.1999.0471. [DOI] [PubMed] [Google Scholar]
- Wakana S, Jiang H, Nagae-Poetscher LM, van Zijl PC, Mori S. Fiber tract-based atlas of human white matter anatomy. Radiology. 2004;230(1):77–87. doi: 10.1148/radiol.2301021640. [DOI] [PubMed] [Google Scholar]
- Wakana S, Nagae-Poetscher LM, Jiang H, van Zijl P, Golay X, Mori S. Macroscopic orientation component analysis of brain white matter and thalamus based on diffusion tensor imaging. Magn Reson Med. 2005;53(3):649–657. doi: 10.1002/mrm.20386. [DOI] [PubMed] [Google Scholar]
- Wecker NS, Kramer JH, Wisniewski A, Delis DC, Kaplan E. Age effects on executive ability. Neuropsychology. 2000;14(3):409–414. doi: 10.1037//0894-4105.14.3.409. [DOI] [PubMed] [Google Scholar]
- Wedeen VJ, Hagmann P, Tseng WY, Reese TG, Weisskoff RM. Mapping complex tissue architecture with diffusion spectrum magnetic resonance imaging. Magn Reson Med. 2005;54(6):1377–1386. doi: 10.1002/mrm.20642. [DOI] [PubMed] [Google Scholar]
- Westin CF, Maier SE, Mamata H, Nabavi A, Jolesz FA, Kikinis R. Processing and visualization for diffusion tensor MRI. Med Image Anal. 2002;6(2):93–108. doi: 10.1016/s1361-8415(02)00053-1. [DOI] [PubMed] [Google Scholar]
- Westin CF, Peled S, Gubjartsson H, Kikinis R, Jolesz F. Geometrical diffusion measures for MRI from tensor basis analysis; Paper presented at the Internation Society for Magnetic Resonance in Medicine; Vancouver, Canada. 1997. [Google Scholar]
- Xue R, van Zijl PC, Crain BJ, Solaiyappan M, Mori S. In vivo three-dimensional reconstruction of rat brain axonal projections by diffusion tensor imaging. Magn Reson Med. 1999;42(6):1123–1127. doi: 10.1002/(sici)1522-2594(199912)42:6<1123::aid-mrm17>3.0.co;2-h. [DOI] [PubMed] [Google Scholar]
- Zhang S, Correia S, Tate D, Laidlaw D. Correlating DTI fiber clusters with white matter anatomy; Paper presented at the 14th ISMRM Scientific Meeting & Exhibition; Seattle, WA. 2006. [Google Scholar]
- Zhang S, Demiralp C, Laidlaw D. Visualizing diffusion tensor MR images using streamtubes and streamsurfaces. IEEE Transactions on Visualization and Computer Graphics. 2003;9(4):454–462. [Google Scholar]