Solid State NMR Studies of Molecular Recognition at Protein-Mineral Interfaces

1. Introduction to Biomineralization

Nature has evolved sophisticated strategies for engineering hard tissues through the interaction of proteins, and ultimately cells, with inorganic mineral phases. The remarkable material properties of bone and teeth thus result from the activities of proteins that function at the organic-inorganic interface. The underlying molecular mechanisms that control biomineralization are of significant interest to both medicine and dentistry, as disruption of biomineralization processes can lead to bone and tooth demineralization, atherosclerotic plaque formation, artificial heart valve calcification, kidney and gall stone build-up, dental calculus formation, and arthritis [1–3]. A better understanding of the biomolecular mechanisms used to promote or retard crystal growth could provide important design principles for the development of calcification inhibitors and promoters in orthopedics, cardiology, urology, and dentistry. Similarly, a better understanding of how these proteins recognize and assemble in bioactive form on inorganic mineral phases could also aid in the development of surface coatings to improve the biocompatibility of implantable biomaterials and for hard tissue engineering and regeneration technologies.

At the level of fundamental science, it is important to note the lack of molecular structure information available for biomineralization proteins in general, and in particular for mammalian proteins that directly control calcification processes in hard tissue. Even the most fundamental questions about how the proteins interact at the biomineral surface, such as their general structure and orientation on the calcium phosphate surfaces, or whether the acidic residues are truly interacting directly with the crystal surface, remain largely uncharacterized at the experimental level. In order to develop a better structure-function level understanding of protein-crystal molecular recognition, we have begun to utilize solid-state NMR techniques to determine the molecular structure of proteins and peptides on calcium phosphate surfaces. In addition, these same techniques have provided interesting molecular dynamics information for the proteins on the biomineral surface. In this review, we will highlight recent work that is providing insight into the structure and crystal recognition mechanisms of an exemplary salivary protein model system, but which also provides a general approach to studying protein-crystal interactions in molecular detail.

Understanding the function of a biomineralization protein requires that the secondary and tertiary structure of the molecule be defined within its biological context, i.e. the protein in contact with the crystal surface. In addition, the precise nature of the interactions between the protein and the crystal which underlie the recognition process must be understood. This requires knowledge of the contacts formed between the amino acid side chains of the protein and the ions in the crystal faces. The involvement of water molecules in these interactions must be understood as well.

Current investigations of protein-mineral interactions are frequently conducted with techniques that characterize the macroscopic behavior of proteins in the presence of mineral crystals. Equilibrium properties such as protein-crystal binding constants are derived via adsorption isotherm measurements, where data are usually analyzed by assuming a simple Langmuir model of protein adsorption onto the crystal faces. But the most commonly-used approach for determining protein-crystal interactions in vitro are kinetic experiments in which a small amount of protein is dissolved in a saturated solution of a particular inorganic salt and the time required for crystals to form is compared to a control solution in which no protein is present. Assays also exist for determining selective binding of a particular crystal face by a protein as well as oriented nucleation of crystals in the presence of acidic proteins [4]. Recently, isothermal titration calorimetry has been used to determine binding enthalpies and binding affinities for proteins to mineral surfaces [5].

However, to extend beyond macroscopic aspects of protein-crystal interactions, high resolution spectroscopic methods must be used to provide information about the atomic level structure of the protein on the crystal face, under physical conditions that are biologically relevant (physiological levels of hydration and pH). Information about the secondary structural motifs and tertiary folding that characterize the adsorbed protein, together with information on the exposure of protein side chains to the crystal face, may lead to an understanding of how particular proteins promote or inhibit nucleation.

The lack of high resolution structural data for proteins on surfaces is the result of a lack of high resolution structural methods that can be brought to bear on relevant problems. The conventional methods of high resolution structural biology, i.e. X-ray crystallography and solution nuclear magnetic resonance (NMR) spectroscopy, have provided information on a few biomineralization proteins in the pure crystalline and solution states [6–9], but both techniques are severely limited in their abilities to elucidate the structures of proteins on biomineral surfaces. Although traditional surface science methods like photo-electron spectroscopy and NEXAFS have provided important information on protein adsorbed onto planar surfaces, and in particular may be used to characterize the degree of long range ordering in systems of adsorbed proteins on polymer surfaces as well as average structural properties, these techniques have yet to provide detailed atomic-level structural information for surface-adsorbed proteins. In addition, surface diffraction methods and many optical techniques are not applicable to proteins adsorbed onto surfaces of porous materials (e.g. porous plastics) or to other surfaces lacking long-range ordering.

To fully appreciate the utility of solid state NMR in the study of protein structure at biomaterial interfaces, it is important to recognize the complex nature of the protein–surface problem. There is first the familiar structural aspect, alluded to briefly above, which includes defining the secondary and tertiary structures of the adsorbed protein and by implication any structural changes which occur upon binding to the surface. Secondly, the structure and chemical composition of the crystal surface in contact with the protein side chains must also be understood. The dynamics of the adsorbed protein are a less familiar but no less important aspect. It is desirable that the protein be observed on the surface under biologically relevant conditions, i.e. fully hydrated. Dehydration of the sample may alter not only the structure of the protein from its biologically relevant form but may quench the dynamics of the protein on the surface. Here we refer to both whole-molecule dynamics describing the protein’s rigid body kinematics on the surface and to internal dynamics wherein the protein’s conformation may be labile on the NMR time scale.

2. NMR Methods for the Study of Protein Structure at Biomaterial Interfaces

Solid state NMR has long been used to identify and characterize the structures of small organic molecules adsorbed onto catalytic surfaces [10–12], argon matrices [13], silica and alumina surfaces [14–16]. There similarly exist a number of solid state NMR pulse techniques capable in principle of reporting the structures of surface-adsorbed proteins. The most straightforward approach is to evaluate the secondary structure of surface-adsorbed proteins from the chemical shifts of ¹³C spins located in the protein backbone or on side chain positions immediately adjacent to the backbone. This approach basically exploits the fact that the isotropic chemical shifts of the backbone carbonyl, alpha, and beta ¹³C spins of each amino acid residue are to varying extents sensitive to the local secondary structure of the protein. Although recent work by Oldfield and coworkers has placed structural interpretation of isotropic ¹³C chemical shifts of proteins on a quantitative basis [17–19], in the past, analyses of structures using chemical shift data have been done empirically by comparing experimentally observed ¹³C chemical shifts for backbone ¹³C spins to a large body of data, derived via ¹³C Cross Polarization/Magic Angle Spinning (CPMAS) experiments from polypeptides of known secondary structure in the condensed state. An excellent example of this type of analysis is the seminal work by Fernandez et al. [20] who studied the structures of polyglutamic acid and polylysine adsorbed to hydroxyapatite and silica using ¹³C CPMAS. In addition to studies of the conformations of polypeptides on apatite and silica surfaces, ¹³C MAS has been used to study the incorporation of carbonate ions in bone and synthetic apatites [21], and ³¹P MAS has been used to characterize the structures of various calcium phosphates found in biological systems [22–24].

Isotropic chemical shift information can be supplemented by quantitative structural data obtained via orientational constraints and/or distance and torsion angle constraints. Angular constraints, usually obtained from magnetic interaction tensors located in the backbone of proteins oriented in mono-domain lipid bilayers, have been used to determine the orientation of protein helices in lipid bilayers [25]. Distance and torsion angle constraints have been acquired for proteins in microcrystalline form [26] as well as for amyloid peptides in fibrillar form [27].

Here we will briefly review the solid state NMR methods used to date to obtain structural models of proteins adsorbed onto biomaterial surfaces. No attempt will be made here to comprehensively cover all the alternative NMR structural methods, their relative advantages and disadvantages. The reader is referred to general review articles on the subject of dipolar recoupling for more extensive treatments of dipolar recoupling [28, 29]. The following discussion is provided simply to clarify some general properties of dipolar recoupling sequences referred to in description of the studies carried out on surface-adsorbed proteins.

Solid state NMR spectra of spin ½ nuclei are dominated by two magnetic interactions, the chemical shift anisotropy (CSA) and the direct nuclear dipolar interaction (see Fig. 1). As discussed above, the former interaction is valuable as a qualitative probe of protein structure. The dipolar interaction has a straightforward structural interpretation because the dipolar coupling constant is proportional to the inverse cube of the internuclear distance. However, in many systems composed of coupled spin ½ nuclei, the magnitude of the CSA may exceed the magnitude of the dipolar interaction. For example, for two sp³ hybridized, directly bonded ¹³C spins the CSAs may approach 200 ppm, corresponding to over 20,000 Hz in a 9.4 Tesla magnetic field. On the other hand, the dipolar interaction for this directly bonded spin pair will not exceed 2300 Hz, and may be even smaller for non-bonded ¹³C spins. Therefore the dipolar coupling constant may not easily be discerned in spectral data when the CSA exceeds the dipolar interactions by orders of magnitude, so it is necessary to use NMR methods which suppress one of these interactions and thereby enable straightforward detection of the other.

Fig. 1.

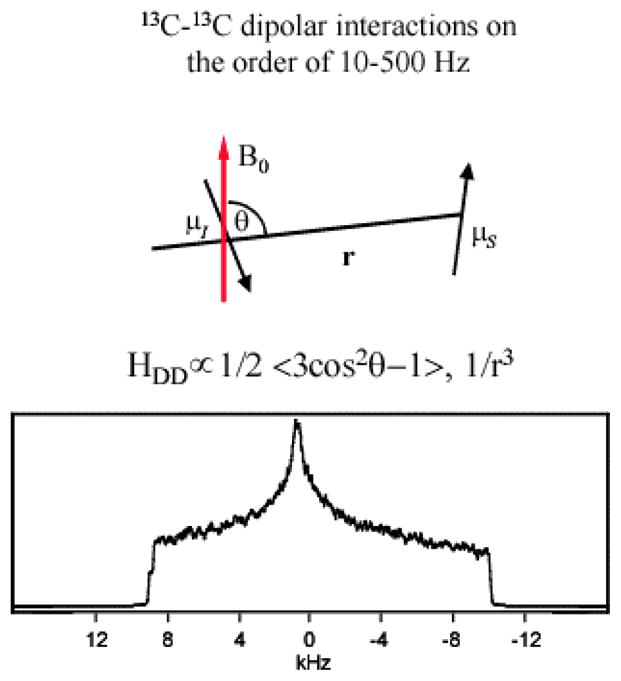
The dipolar coupling tensor is a uniaxial second rank tensor. Its principal axis frame has the z axis along the internuclear vector. The dipolar coupling strength is proportional to the second order Legendre polynomial 〈 $\frac{3}{2}{cos}^2\theta -\frac{1}{2}$ 〉, where θ is the angle between the internuclear vector and the magnetic field and inversely proportional to the cube of the internuclear distance 〈 1/r³ 〉. In a polycrystalline sample, the solid state NMR spectrum of a pair of dipolar-coupled spin ½ nuclei with negligible CSA values gives rise to a Pake powder pattern, from which the dipolar coupling constant may be extracted. However, if the coupled spin ½ nuclei have CSAs much larger than the dipolar coupling it becomes difficult to extract the dipolar coupling constant from the NMR powder spectrum. The figure shows the powder spectrum of two dipolar coupled ¹³C spins, each with a CSA on the order of 20 kHz and with a dipolar coupling of 500 Hz corresponding to a ¹³C pair separated by 2.48 Å. The spectrum is clearly dominated by the CSA and it is very difficult to discern the presence of a dipolar coupling in the spectral data.

Physical rotation of the sample (i.e. Magic Angle Spinning [30], MAS) coherently averages spatial parts in the spin interaction Hamiltonian that transform as second rank tensors. Since both the dipolar and the chemical shift Hamiltonians transform as second rank tensors in Cartesian space, MAS removes the effect of both interactions from solid-state NMR spectra. The objective of dipolar recoupling is to use MAS and radio frequency (r.f.) irradiation in synchrony, with the ultimate objective of suppressing the chemical shift while preserving the dipolar coupling. Because information on internuclear distances can be recovered using dipolar recoupling techniques, these pulse sequences are widely used in structural studies of molecular solids.

The three dipolar recoupling pulse sequences that will be discussed in the context of structural studies of proteins adsorbed at biomaterial interfaces are the heteronuclear recoupling experiment REDOR (Rotational Echo Double Resonance) [31], and the homonuclear recoupling experiments DRAWS (Dipolar Recoupling with a Windowless Sequence) [32] and SEDRA (Simple Excitation for Dephasing of Rotational-echo Amplitudes) [33,34]. REDOR, developed by Schaefer and coworkers is commonly used to measure the distance between heteroatoms [35]. In studies of surface-adsorbed biopolymers, REDOR has had a number of uses including: (1) Direct characterization of the surface, as was done by Pan [36] who used ³¹P–¹⁹F REDOR to study the distribution of ¹⁹F on fluoroapatite surfaces; (2) ¹³C–¹⁵N REDOR to confirm helical secondary structures in surface-adsorbed proteins by measuring the distance between the ¹³C carbonyl spin of the (i) residue to the ¹⁵N amide spin of the (i+4) residue; (3) ¹³C–¹⁹F REDOR to measure long range distances that constrain the tertiary fold of the adsorbed protein; (4) probing dipolar interactions from ¹³C and ¹⁵N spins in protein side chains to NMR-active spins in the surface, such as ³¹P spins in hydroxyapatite and ¹⁹F spins in fluoropolymers to detect proximity and orientation of the adsorbed biomolecules to the surface. REDOR, typically used to detect heteronuclear dipolar couplings, can be used to indirectly obtain also homonuclear dipolar information. We also demonstrated an application of the basic REDOR experiment to I₂S spin triads (where I and S are heteronuclear spins) which enables the extension of the structural parameters deduced from the measurement relying on homonuclear as well as heteronuclear dipolar recoupling during spin evolution. The reference experiment (S₀) in the REDOR experiment with alternating pulses can recouple the dipolar interaction between homonuclear spins when coupled I spins are in the observe channel and the S spin is in the dephase channel. Applying a set of 180° pulses in synchrony with the rotor period will recover the homonuclear dipolar interaction between the I spins. When the I₂ represent ¹³C labels are on two adjacent backbone carbonyl carbons at positions (i−1, i) the S₀ experiment shows a SEDRA effect where the pulses modify the 0^th order rotational resonance recovery of the dipolar coupling by the chemical shift difference tensor and consequently the relative orientation of the carbonyl carbons CSA tensors and the distance between them can be extracted. An S spin label of choice e.g. an amide nitrogen ¹⁵N label at backbone position (i+4) or a fluorine atom ¹⁹F label replacing a hydrogen on a side chain position can provide secondary or tertiary structural data respectively. In the dephase experiment (S/S₀) the two heteronuclear dipolar interactions with their orientation relative to the CSA tensors principle axes systems is deduced. Analysis of the magnetization decay both in the reference experiment (S₀) to obtain homonuclear dipolar couplings and in the normalized dephasing experiment (S/S₀) to derive heteronuclear dipolar couplings yields complete characterization of the spin triad and enables us to extend accurate structural information deduced from selective labeled sample.

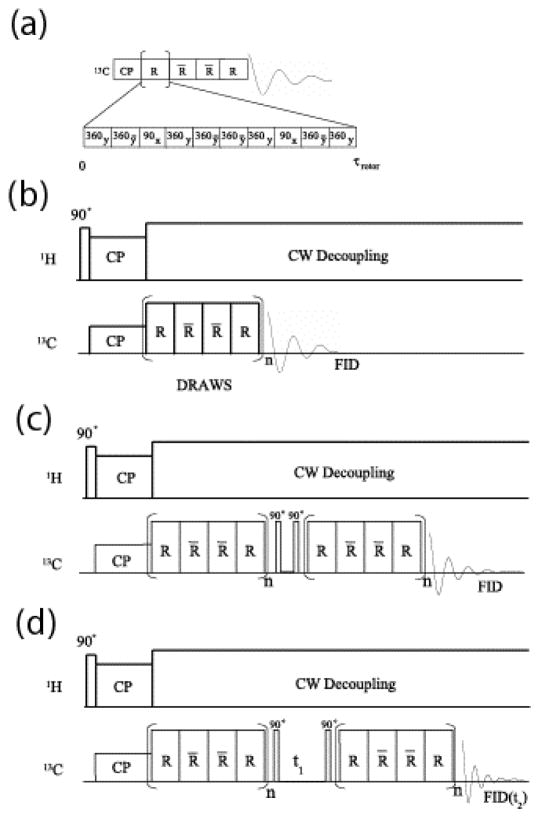
Dipolar recoupling with a windowless sequence (DRAWS) is well suited to measuring distances between backbone carbonyl carbons in peptides and proteins [37–40]. Dipolar couplings of less than 40 Hz between carbonyl ¹³C spins have been detected in biopolymers at high magnetic fields [41–44], attesting to the ability of DRAWS to suppress large CSAs and at the same time detect small dipolar couplings between non-bonded ¹³C spins. Fig. 2 shows three forms of the DRAWS dipolar recoupling pulse sequence. In the DRAWS experiment, the unit pulse cycle (Fig. 2(a)) is applied synchronously with the sample spinning and thus the duration of the unit cycle is exactly equal to one rotor period, τ_rotor. The DRAWS experiment, which utilizes a four step supercycle (Fig. 2(a)), is commonly employed in the context of a CPMAS experiment (Fig. 2(b)). The basic strategy is to detect the amplitude of transverse magnetization that remains after an integral number of DRAWS supercycles are applied. Repeating this measurement as a function of the number of DRAWS supercycles results in a “dephasing” curve. Simulation of this dephasing curve results in a value for the internuclear distance.

Fig. 2.

In most dipolar recoupling pulse sequences, pulsed irradiations are applied synchronously with the sample rotation. In DRAWS (Dipolar Recoupling with a Windowless Sequence), the eight 360° degree pulses (alternating X and X̄ phases) and two 90° degree pulses (Y phases) that constitute the unit pulse cycle (R) are applied within a single period of the rotor (τ_rotor). (a) The unit pulse cycle for DRAWS is supercycled as RR̄R̄R, where R̄ indicates a unit cycle phase-shifted by 180° degrees. (b) DRAWS applied in the context of a CPMAS experiment. (c) Pulse Sequence for Double-Quantum-filtered DRAWS. (d) Pulse sequence for two dimensional double quantum DRAWS (DQDRAWS).

The DRAWS dephasing curve is a useful measurement for determining protein secondary structure because the carbonyl-carbonyl distance is directly related to the Ramachandran torsion angle ϕ. Therefore, using DRAWS distance measurements, the torsion angle ϕ may be determined at several positions in a peptide in a model-independent fashion. Additionally, DRAWS can also measure conformational heterogeneity since the dipolar recoupling efficiency is independent of any correlation between chemical shift and peptide secondary structure. This allows the determination of the distribution of peptide conformers in a given sample.

DRAWS dephasing curve data may be difficult to quantify in terms of an internuclear distance if a large background signal occurs from ¹³C spins at natural abundance. The ¹³C background arises from portions of the protein that are not enriched with ¹³C or may come from the surface itself if the mineral contains carbon (e.g. calcite) or if the mineral contains organic impurities (e.g. carbonate incorporated into apatite crystals). In such cases NMR signals arising from dipolar coupled spin pairs are separated from the natural abundance signal, which arises mainly from isolated spins, by filtering the DRAWS signal through a double quantum state. The preparation of double quantum coherence using DRAWS dipolar recoupling is called DQDRAWS. The DQDRAWS filtering experiment is shown in Fig. 2(c). Applying a DRAWS pulse sequence for a preparation time τ (typically 3–6 ms for adjacent carbonyl ¹³C spins in the backbone of a surface-adsorbed protein) generates dipolar-correlated spin coherence (also called anti-phase magnetization). Applying a 90° pulse then generates double quantum coherence. In the double quantum buildup experiment, this coherence is immediately transferred back to anti-phase magnetization by a second 90° pulse and then to observable magnetization by reapplying the DRAWS mixing sequence for the same amount of time. The coherence that did not go through a double quantum state is filtered by proper phase cycling. The buildup of double quantum coherence is then monitored as a function of the DRAWS mixing time to determine dipolar couplings and hence internuclear distances. As in the simple DRAWS experiment, the DQDRAWS filtering experiment can quantify the carbonyl-carbonyl distance and hence the Ramachandran angle ϕ.

Detection of the evolution in the double quantum coherent state results in a simultaneous measurement of the (ϕ, ψ) Ramachandran angles [38,45]. As in other multiple quantum experiments, a double quantum state is detected via a two dimensional experiment, the pulse sequence is shown in Fig. 2(d). In the 2-dimensional DQDRAWS experiment, the DRAWS pulse sequence is again applied for a preparation time τ to generate the antiphase state. After the magnetization is transferred to the double quantum state by a 90° pulse it is allowed to evolve under the chemical shift interactions for a time t₁. The magnetization is then transferred back to observable single quantum coherence by a second 90° pulse and reapplying the DRAWS mixing sequence for the same amount of time. Monitoring the free induction decay (FID) during the detection time t₂ as a function of double quantum evolution time t₁ yields a two dimensional interferogram. Two dimensional Fourier transformation of the time domain data followed by projection onto the ω₁ axis (i.e. the double quantum frequency axis) yields the double quantum spectrum. The double quantum spectrum consists of a “fundamental” frequency, which occurs at the sum of the isotropic chemical shift frequencies of the coupled ¹³C spins, together with side bands at integral multiples of the spinning frequency. The double quantum spinning side band intensities are dependent on the principal values of the sum chemical shift tensor. Because the individual chemical shift tensors add as second rank tensors, the sum tensor is sensitive to the mutual orientation of the principal axis systems of the CSA tensors of the coupled ¹³C spins. Since carbonyl carbons in peptides possess highly anisotropic CSAs, they are particularly sensitive to the DQDRAWS approach. The third torsion angle, ω, of the carbonyl carbon CSAs to the peptide amide bonds are known to be fixed to ±180(±5)° except around a proline residue, and thus the torsion angles (ϕ, ψ) can be extracted by simulating the DQ spectrum. The determination of (ϕ,ψ) with this level of accuracy at consecutive points along the backbone yields secondary structure at this region in the protein.

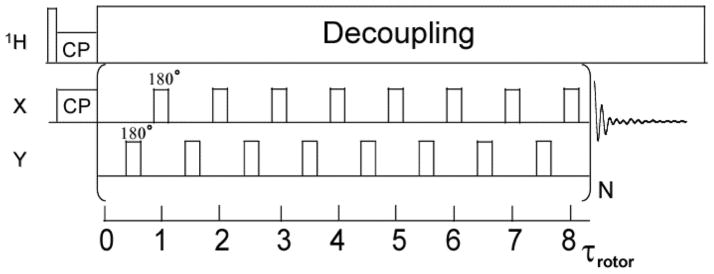
Simple excitation for dephasing of rotational-echo amplitudes (SEDRA) [33,34] is discussed here because it implicitly comes out from running REDOR with alternating pulses on I₂S spin triads. The reference experiment in REDOR (S₀) applied to the I spins, in that particular case, is similar to the SEDRA experiment between two homonuclear coupled spins. The SEDRA pulse experiment utilizes a train of 180° pulses to reintroduce the dipolar interaction coherently averaged under magic angle spinning. This pulse experiment employs modulation of the chemical shift interactions by the r.f. pulses to recouple the dipolar interaction owing to the non-commutation property of the two interactions in the toggling frame. In the SEDRA experiment (Fig. 3), transverse magnetization excited by either a 90° pulse or by cross polarization from protons is increasingly attenuated as the applied π-pulse trains (SEDRA mixing) is incremented. Individual magnetization components of different crystallites lose their phase coherence in this experiment in proportionality to the dipolar interaction recoupled through the difference chemical shift tensor. As in the case of the sum chemical shift anisotropy, the difference chemical shift tensor is sensitive to the relative orientation of the CSAs of the two spins. In proteins one can utilize the dependence of SEDRA on the CSA difference tensor in order to extract the backbone dihedral angles between consecutive amino acid residues. In particular, the principle components of the carbonyl carbon CSA tensor have known directions in the peptide bond molecular frame. Therefore, the orientation of two CSA tensors will be dependent only on the two dihedral angles (ϕ, ψ) separating the two atoms. Since the distance between the carbonyl carbon atoms is dependent on the ϕ angle, the SEDRA dephasing curve, in this case, can be used to obtain the backbone conformation information. The chemical shift and the dipolar parameters deduced from the SEDRA-type of REDOR reference experiment are utilized to obtain the heteronuclear dipolar parameters in the dephase experiment and ergo to enable a complete structural characterization of these spin triads. As noted above, this allows homonuclear and heteronuclear dipolar information to be combined in order to obtain in a standard REDOR experiment an extensive set of structural parameters.

Fig. 3.

The SEDRA pulse experiment is comprised of a train of 180° pulses applied in synchrony with the rotor cycle, one pulse per rotor cycle. Following cross polarization the SEDRA mixing pulses are applied and the free induction decay of single quantum magnetization is collected. The Fourier transformed signal intensity is recorded as a function of the length of the SEDRA mixing time and analyzed to obtain the dipolar coupling between like spins. The version of SEDRA shown here has a basic mixing period of 8 rotor periods (8τ_rotor) and employs an XY-8 phase cycling of the pulses to correct for field inhomogeneity. Proton decoupling is applied through the SEDRA mixing and detection periods.

3. Statherin: A protein that regulates crystallization of hydroxyapatite (HAP)

We focus in this review on a salivary protein that has evolved to control the nucleation and growth dynamics of hydroxyapatite (HAP) in saliva. Tooth enamel structural integrity is maintained through the supersaturation of saliva with respect to calcium and phosphate salts and through the lubricative action of proteins in the pellicle coating the oral surfaces [46–50]. Statherin and the proline-rich proteins (PRPs) prevent formation of accretions on the tooth surface by inhibiting both spontaneous calcium phosphate precipitation and hydroxyapatite (HAP) secondary crystal growth [51,52]. Statherin, a small 43 amino acid protein, readily binds calcium ions in solution and adsorbs to HAP surfaces with a significant binding affinity and coverage [53–55]. The proximity of statherin side chains to the surface and the mechanism of adsorption to HAP were recently investigated [55–57]. The viscoelastic properties of statherin, PRPs and mucins in the salivary pellicles reduce by 20-fold the mastication load [50,58]. Statherin also plays a role in the onset of periodontal diseases, which are marked by the adherence and colonization of various bacteria to supra- and sub-gingival surfaces [59–61]. Statherin and the PRPs mediate the adhesion of bacterial species to the tooth surface [62–67]. These organisms preferentially adhere to immobilized statherin on hydroxyapatite surfaces rather than to the free protein in solution [64,67], leading to the hypothesis that surface adsorption exposes receptor sites in statherin to bacterial fimbrillin binding. Recent studies identified the C-terminal residues 29 to 43 and residues 33 to 39 in statherin as binding domains for Porphyromonas gingivalis and Fusobacterium nucleatum fimbriae respectively [65,67].

Statherin efficiently hinders the crystallization of hydroxyapatite in the supersaturated environment of saliva [68–73]. The statherins have historically served as one of the best characterized models for understanding the functional activities of proteins in the physical-chemical control of hydroxyapatite growth. The N-terminus of statherin contains a pSpSEE (where pS is phosphorylated serine) acidic motif that is also found in larger proteins such as osteopontin and β-casein that contain calcium binding domains, as well as in non-mammalian biomineralization proteins that regulate calcium carbonate crystallization [74].

The effects of native statherin on hydroxyapatite growth kinetics have been extensively characterized [73,75]. Nancollas has demonstrated that N-terminal peptides from statherin also display functional activities in controlling HAP growth [76,77]. Secondary structure predictions suggest that the N-terminus has a propensity for α-helix formation. Circular dichroism and NMR studies [78,79] found that in water statherin is structurally disordered while in 50% trifluoroethanol (TFE)/water mixtures, statherin exhibits an α-helical structure at the N-terminal region (residues 1-16), a polyproline type II (P_II) helix in the intermediate region (residues 19-35) and a 3₁₀ helix in the C-terminal region (residues 36-43) [78]. The prevalence of polyproline helices in disordered or partially folded proteins is now viewed as a pre-organization of secondary motifs designed to accelerate the folding process [80].

4. NMR Structural Study of HAP-bound Statherin

In this review we describe recent solid state NMR studies which encompass structure determination of the full length 43 amino acid statherin protein adsorbed onto the mineral surface. Previous solid state NMR measurements on fragments of statherin adsorbed to hydroxyapatite are reviewed elsewhere [81–83]. Investigation of full length surface-bound statherin was aimed initially at secondary structure elucidation of the protein’s N-terminus [40]. Here we also review work aimed at secondary structure measurements in the C-terminal bacterial binding domain and long distances measurements to obtain the tertiary fold of surface-bound statherin [84]. Statherin samples are prepared by adsorbing quantities of protein that are lower than the saturation coverage to minimize interference from intermolecular interactions in the structural measurements. The accumulated measurements are successful in providing a solid basis for construction of the three-dimensional model of statherin’s structure in its adsorbed state.

4.1 Secondary Structure of the HAP Binding Domain

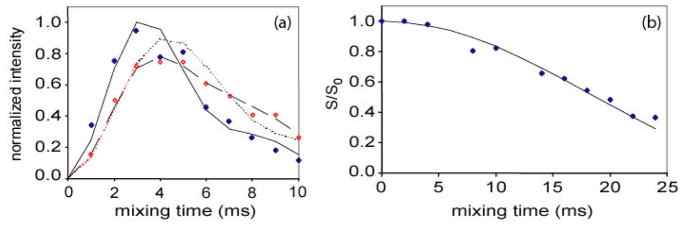
To probe the molecular backbone structure of statherin on HAP under buffered, hydrated conditions, isotopic labels were selectively incorporated at the pS2, pS3, F7, L8, I11 and G12 backbone carbonyl carbons or nitrogens in five different samples of statherin. By way of example, the backbone ϕ angle was determined with the DQDRAWS techniques at the pS2pS3 positions. In Fig. 4(a), the build-up of DQ coherence is plotted for statherin adsorbed onto HAP crystals and fully hydrated (solid diamonds) and for lyophilized samples (open diamonds). The line drawn through the solid diamonds is the DQDRAWS data simulated for an α-helical secondary structure. REDOR was used to measure the (i) to (i+4) distance with pS3F7 and L8G12 labeling schemes (for sample data see Fig. 4(b)). The composite results clearly define this N-terminal, 12 amino acid long HAP binding domain as α-helical on HAP surface. The strongly acidic N-6 region displays a nearly ideal α-helical distance of 4.2 Å across the pS3F7 hydrogen bond, while the helix across the L8G12 hydrogen bonding position has a longer pitch at 4.8 Å [40].

Fig. 4.

(a) DQDRAWS buildup curves for hydrated, surface adsorbed pS₂pS₃ statherin (◆), lyophilized, bound pS₂pS₃ Statherin (◇), and simulations for φ torsion angles of −60° (——), −85° () and a combination of 35% α-helix (−57°) and 65% β-sheet (−120°) (– – –). The increase in torsion angle on lyophilization correlates well with the loss of α-helical secondary structure. (b) REDOR dephasing curves for hydrated, surface adsorbed pS₃F₇ Statherin(◆) and simulations for a carbon-nitrogen distance of 4.2 Å (——). The pS₃F₇ distance across the hydrogen bond fits best to a distance of 4.2 Å, indicating that the region is well described by an ideal α-helix.

The α-helix has been previously suggested as a general structural mechanism for aligning acidic side chain residues with HAP, either through lattice matching or through more general electrostatic complementarity [8]. Our data are consistent with this hypothesis and further point to the possible importance of bridging water in protein-HAP recognition.

The dynamic properties of the immobilized protein are a critical aspect of molecular recognition at the protein biomineral interface, and related to the function of proteins once adsorbed. Measurements of the dynamic properties of statherin in the presence and absence of water provide striking evidence that a binding footprint is centered on the acidic residues in the N-terminal pentapeptide region. The ¹³C rotating frame relaxation, T_1ρ, values remain largely unchanged for the phosphoserines, indicating little or no motion is present in either the lyophilized or hydrated states. However, the T_1ρ relaxation constants are considerably shorter in the hydrated samples at the F7, L8, I11, and G12 positions, indicating motion on the kilohertz time scale when water is present. Fig. 4(b) shows the pS2-pS3 doubly carbon-labeled statherin sample under hydrated conditions, normalized to the natural abundance methyl region to account for any differences in the amounts of bound protein.

4.2 Secondary Structure of the Bacterial Binding Domain

Placement of isotopic labels for REDOR and DQDRAWS NMR studies of the fifteen N-terminal amino acids was guided by solution NMR studies and circular dichroism data that indicated the HAP-recognition region is very likely structured as a α helix. In the case of the C-terminal domain, little prior knowledge of local secondary structure existed to guide placement of isotopic labels. We therefore implemented structural modeling as a guide for determining placement of isotopic labels at locations with high probabilities for significant measurements of a secondary structural elements and tertiary folding.

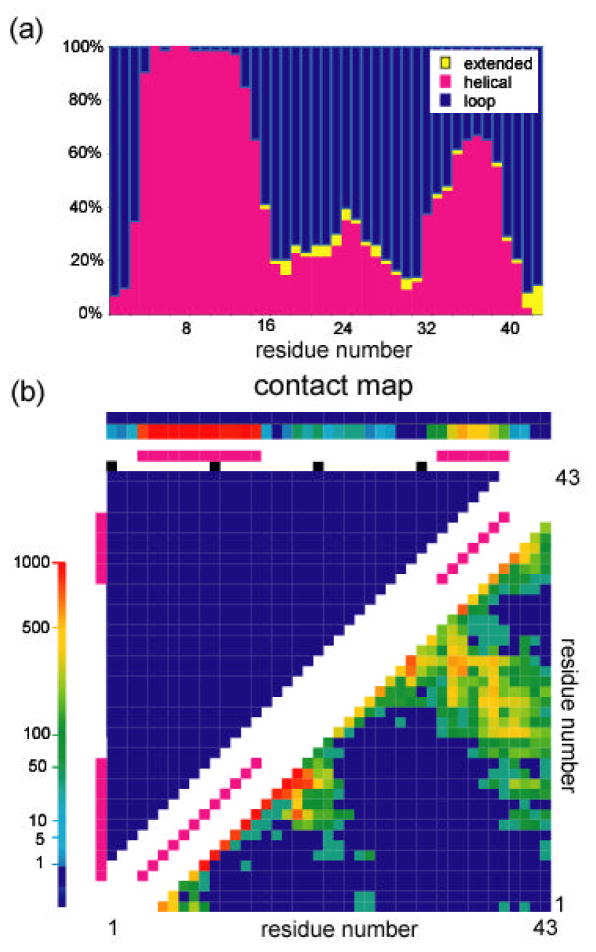
Since no structural homologues were available for the sequence of human statherin, the ab initio protocol of the structure modeling program ROSETTA [85] was used to generate structural models of the protein. Nearly all 1,000 models in the starting set predicted that the protein’s N-terminus (residues 3-15) is α-helical, as previously demonstrated experimentally. The models were then divided into subsets based on their structural similarity with the largest cluster consisting of 31 models. The histogram showing the percentage for this subset of either an extended, helix or loop backbone secondary structure, together with the contact map correlating residues by their spatial proximity are depicted in Fig. 5. In both structural representations, an α-helical segment at the C-terminus of the protein (residues 32-40) is predicted. The intermediate segment has a higher structural dispersion with two turn regions at G19 and P31 that are common to some of the models as seen in the contact map. Selection of an isotope labeling scheme for the protein sample was derived from analysis of the torsion angles and distances between pairs of atoms across the models and using only positions that are conserved between different species. Histograms of these structural parameters for the selected label positions are given in Fig. 6. Two consecutive carbonyl atoms on residues 33 and 34 were ¹³C labeled and an amide on tyrosine 38 was ¹⁵N labeled to extract the secondary structure in this region. Replacement of hydrogen with a fluorine atom on the 4′ position of proline 23 was employed for long range carbon-fluorine distance measurements between carbonyl carbon labels in the C-terminus and the sidechain of a proline near the protein center. The following labels, DpSpSEEKFLRRIGRFGYGY[2-¹³C]G19PYQ[4′-¹⁹F]P23VPEQPLYPQ[1-¹³C]P33[1-¹³ C]Y34QPQ[¹⁵N]Y38QQYTF were therefore incorporated in the synthesis of statherin.

Fig. 5.

Modeling statherin structure using the ROSETTA ab initio algorithm. (a) A histogram showing percentage of the 3 basic secondary motifs along the backbone in the predicted 31-model cluster. (b) Contact map for the 31-model cluster. Pink squares, shown along the diagonal, indicate short contacts between adjacent residues characteristic of an α helix structure. Contacts that are shown as colored squares perpendicular to the main diagonal in the lower left triangle indicate long range contacts between residues far apart in the sequence. Common features between the models were used to select sites on the protein for incorporation of NMR labels.

Fig. 6.

Histograms showing distribution of torsion angles and distances between labels across the 31-model cluster. (a) Φ angle and (b) Ψ angle values for the backbone torsion angles between the two carbonyl labels [1-¹³C]P33 and [1-¹³C]Y34. Nitrogen-carbon distances between the (c) [¹⁵N]Y38 label and the [1-¹³C]P33 label and between the (d) [¹⁵N]Y38 label and the [1-¹³C]P34 label. Fluorine-carbon distances between the (e) [4′-¹⁹F]P23 label and the [1-¹³C]P33 label and between the (f) [4′-¹⁹F]P23 label and the [1-¹³C]P34 label.

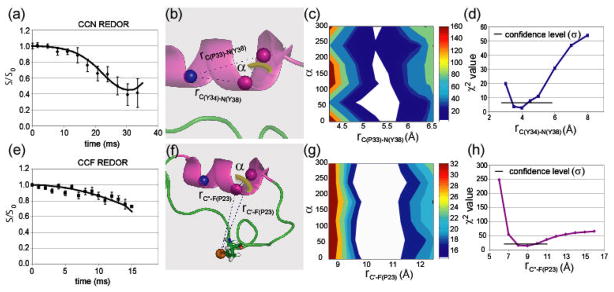
Using this labeling scheme, CN-REDOR measurements provided us with both the (ϕ, ψ) angles, CC distance, and the CN distances. Additional information relating the CN dipolar vector to the CSA principal axis system gave the complete geometry of the CCN triangle. The reference experiment (So) usually carried out as part of the REDOR measurement is analogous to a SEDRA experiment (Fig. 3) and therefore induced recoupling of the carbonyl carbon dipolar couplings due to a non-zero difference CSA tensor. Analysis of the dephasing curve obtained in the So experiment in terms of the torsion angles between the two labels gave rise to a pair of angles without ambiguity. The resulting angles are consistent with a compact α-helical conformation of the backbone at this position (Fig. 7). The CN-REDOR curve gave rise to a [1-¹³C]Y34-[¹⁵N]Y38 distance of 4.0 Å (Fig. 8(a),8(d)) that is indicative of a hydrogen bond stabilizing the α-helical structure. The angle between the [1-¹³C]Y34-[¹⁵N]Y38 and the [1-¹³C]P33-[¹³C]Y34 vectors was found to be 95(±5)°, implying that the hydrogen bond is nearly parallel to the helix axis (Fig. 8(c)). In the case of a compact backbone conformation in particular, this typical C(i−1)-C(i)-N(i+4) labeling scheme can be informative and extends the information derived due to a triangulation effect. It is noted that whenever an extended conformation of the backbone exists the spin triad is not expected to be determined. Rather a negative result of not observing a REDOR dephasing would exclude the presence of a compact conformation in favor of an extended one. In special cases where carbonyl CSA orientation in the molecular axis is not known the measurement will be complicated by added unknown parameters.

Fig. 7.

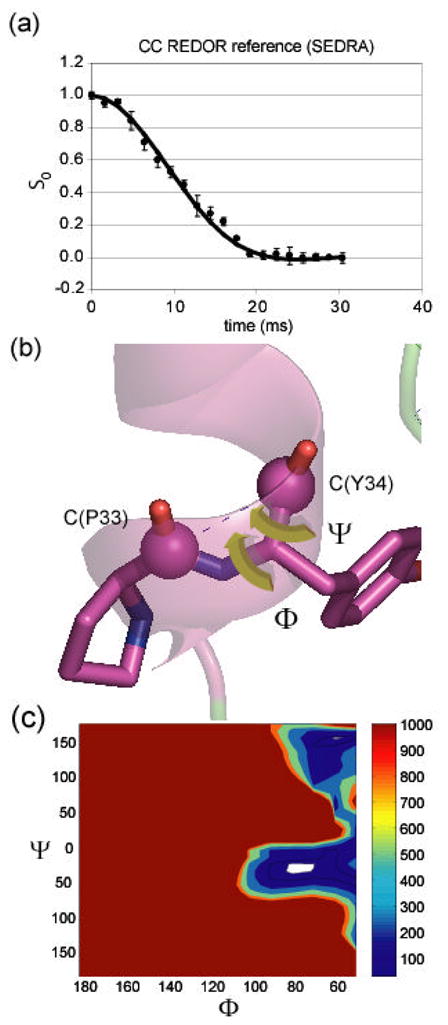
¹³C SEDRA NMR decay curves (obtained at a ¹H frequency of 500 MHz) showing the carbon signal intensity as a function of the length of time the pulses are applied. (a) ¹³C signal decay in the REDOR reference experiment showing dephasing behavior due to recoupling of the ¹³C-¹³C dipolar interaction. The fit to this decay curve is used to extract the structural parameters. (b) structural parameters that influence the decay curve. Graphic visualization of the relation between the mutual orientation of chemical shift anisotropy tensors (green) and the Φ and Ψ angles in the two carbonyl labels. (c) χ² analysis of data based on simulations utilizing the torsion angle dependence. A contour plot of the χ²(Φ,Ψ) function showing angular values in the SEDRA data are best fit. Confidence level of σ is shown as the lowest contour (white).

Fig. 8.

¹³C-¹⁵N and ¹³C-¹⁹F REDOR NMR decay curves (obtained at ¹H frequencies of 300 MHz and 500 MHz, respectively) showing the carbon signal intensity as a function of the length of time the pulses are applied. (a) ¹³C signal decay from recoupling of the ¹³C-¹⁵N dipolar couplings in a REDOR experiment. (b) Dipolar interaction parameters in the C(P33)-C(Y34)-N(Y38) spin triad. (c) The contour plot of the χ²(r_{C(P33)-N(Y38)},α) function (middle) and (d) the graph of the χ²(r_{C(Y34)-N(Y38)}) function (bottom) showing values for which the CN REDOR data is minimized. (e) ¹³C signal decay from recoupling of the ¹³C-¹⁹F dipolar couplings in a REDOR experiment. The fits to these decay curves are used to extract the structural parameters. Graphic visualization of the structural parameters that influence the decays and χ² analysis of simulation and data based on these parameters. The parameter α represents rotation of the heteronuclear dipolar vectors around the CC vector. (f) Dipolar coupling parameters in the C(P33)-C(Y34)-F(P23) spin triad. Here, we denote the two carbons as C′ and C″ since they are indistinguishable in the ¹³C spectrum. (g) The contour plot of the χ²(r_C′_-F(P23),α) function and (h) the graph of the χ²(r_C″_-F(P23)) function demonstrate values for which the CF REDOR data are fit by simulations. Confidence level of σ is shown as the lowest contour (white).

4.3 Tertiary Folding of Statherin on HAP

Addition of a [4′-¹⁹F] label on P23 enables another triangulation using long range CCF REDOR measurements. The complete characterization of the spin interactions in the ¹³C-¹³C spin pair can be utilized to extract from the REDOR dephasing experiment both the two CF distances and their vector orientation relative to the CSAs principal axis system. The CF-REDOR curve (Fig. 8(e)) demonstrates that the C-terminus labels are in proximity to the fluorine label, constraining the distance of these labels from the [4′-¹⁹F]P23 label to 8.8 Å and 10.3 Å (Figs. 8g and 8h). The two labeled carbonyl carbons are unresolved in the ¹³C NMR spectra, and thus the assignment of the closer carbon atom cannot be determined. The two distances demonstrate that the α-helical motif measured at 33–38 is folded back onto the intermediate part of the protein which contains P23.

4.4 Protein Sidechain–Surface Interactions

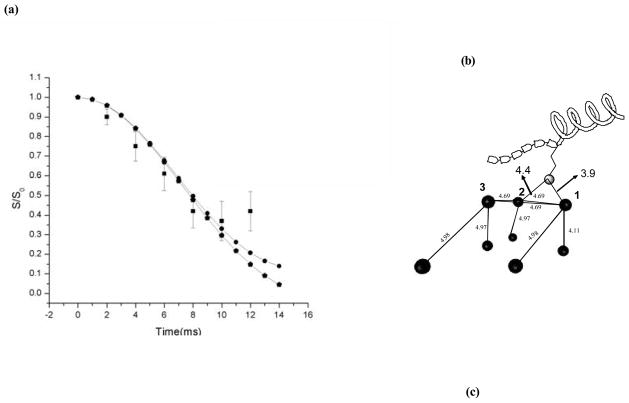
The strength of interaction between statherin and the HAP surfaces relies on bonds created between side chains on the protein and exposed groups on the surfaces to which that protein adsorbs. Distance measurements between side chains on the SN-15 derivative and NMR active ³¹P atoms on the HAP surface were used to learn about the proximity of particular residues to the surface. NP-REDOR measurements were carried out on a ¹⁵Nε(K6) labeled SN15 sample [57,86]. Analysis of REDOR measurements in the case where an atom on the protein might be coupled to several phosphate groups on the surface was detailed in two publications [57,87]. Analysis of the REDOR data yields at least two possible geometries of the ¹⁵N spin to multiple³¹P spins in the HAP surface. The relatively short distances to the phosphorous atom imply possible hydrogen bonds created upon adsorption. A χ² analysis of the data in reference 87 is shown in Fig. 9(a), it assumes a NPP system with a ³¹P-³¹P effective dipolar coupling of 600Hz, and shows a well-defined minimum for ¹⁵N-³¹P distances of 3.8 Å and 4.8 Å from the ³¹P spins (Fig. 9(a), filled circles). In addition to the simplified three spin model, we have simulated a ¹⁵N spin from the lysine side chain approaching two spins on the (004) crystal plane of HAP as shown in Fig. 9(b). These spins are connected to six other spins at distances shown in Table 1 [57]. We obtained a fit similar to the one obtained from the simple model, described above, but with slightly different ¹⁵N-³¹P distances of 3.9 Å and 4.4 Å (Fig. 9(a), filled pentagons).

Fig. 9.

(a) Statistical χ² analysis of ¹⁵N-³¹P REDOR study of binding of ¹⁵N K6 of SN-15 to HAP indicates a well-defined minimum distances of 3.8 A and 4.8 A suggesting a possible hydrogen bond between the K6 side-chain and the HAP atoms. The filled squares are the experimental data while the filled circles denote the simulation that gives rise to the χ² minimum and the pentagons indicate the multiple spin simulation of a ¹⁵N K6 approaching the (004) crystal plane of hydroxyapatite (parameters used for the simulation are defined thoroughly in (b)). (b) Model of a ¹⁵N K6 sidechain of SN-15 approaching the (004) crystal plane of hydroxyapatite. The figure depicts all the spins that were used the above mentioned simulation. The dark circles denote the spins while the lighter shaded circle depicts the ¹⁵N spin on the lysine side-chain. The blocks on the peptide depict the six N-terminal residues of SN-15 that are known to be in an extended conformation.

Table 1.

³¹P-³¹P nearest neighbor distances lying within a sphere of radius 6 Å for the 004 crystal plane in in monoclinic HAP. The two spins P1 and P2 were assumed to be connected to the approaching ¹⁵N-lysine side-chain.

P1	P2
4.69 Å (P2)	4.69 Å (P1)
4.69 Å (P3)	4.69 Å (P3)
4.98 Å	4.98 Å
4.11 Å	4.97 Å
P3 is connected to another phosphorus spin at a distance of 4.97Å

Although acidic and basic amino acids are thought to constitute the primary means by which proteins interact with apatitic surfaces, the role of aromatic rings has attracted study. Constant composition techniques have shown that phenylalanine has the highest HAP affinity constant of the non-polar amino acids [88], and because the N-terminus of statherin has two phenylalanines, the role these residues play in surface recognition is of interest.

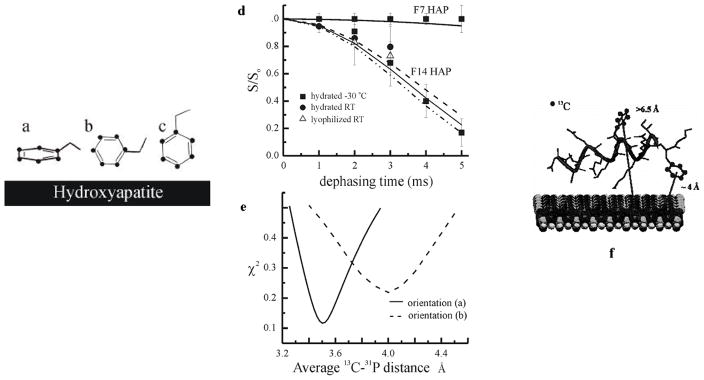
Two samples containing ¹³C labels on the phenyl ring of phenylalanine 7 (F7) and phenylalanine 14 (F14) were bound to HAP [89]. Isotropic chemical shifts, chemical shift anisotropies (CSAs), NMR line width information, ¹³C rotating frame relaxation measurements, as well as direct detection of correlations between ¹³C spins on protein side chains and ³¹P spins in the crystal surface with ¹³C–³¹P REDOR NMR show that in the peptide fragment derived from the N-terminal 15 amino acids of salivary statherin (i.e. SN-15), the side chain of the phenylalanine nearest the C-terminus of the peptide (F14) is dynamically constrained and oriented near the surface, whereas the side chain of the phenylalanine located in the middle of the peptide (F7) is more mobile and is oriented away from the hydroxyapatite surface, as shown in Fig. 10. The relative dynamics and proximities of F7 and F14 to the surface together with prior data obtained for the side chain of SN-15’s unique lysine (K6) were used to construct a new picture for the structure of the surface-bound peptide and its orientation to the crystal surface.

Fig. 10.

Three different orientations of the phenyl ring with respect to the HAP surface were considered: (i) the ring plane is parallel to the HAP surface, (ii) a line perpendicular to the C₂-C₃ and C₅-C₆ bonds is also perpendicular to the HAP surface, and (iii) a line from C₁ to C₄ is perpendicular to the HAP surface. (b) REDOR analysis of the both samples bound to HAP is shown. The experimental data and best simulated fits are shown for both samples. (c) A χ² map is shown for the F14 sample based on the orientations (i) and (ii) depicted in Fig. 10(a). (d) A modified SN-15 model with peptide bound to HAP is presented, in which the C-terminus loses its α-helicity, and both the K6 and F14 side chains are within close proximity to the HAP surface.

5. Towards a Model for Surface-Bound Protein Structure

The dipolar recoupling measurements described in Sections 4a, b, c were used in conjunction with ROSETTA to construct the folding of the mineral-bound protein. Refinement of the statherin structure was done by constraining the original 1,000 model set with the long CF distance measurements and the geometric measurements in the C-terminus. The resultant eight structures, aligned along the backbone atoms in the two helices, are given in Fig. 11. They exhibit an average pair RMSD of 2.5 Å with higher structural dispersion in the intermediate region where constraints have not yet been measured. The small folded core is created by the folding of the C-terminus helical region (33–38) back onto the intermediate region through a loop region defined by proline residues. The C-terminus helix can be tilted at different angles with respect to the N-terminus helix due to the limited number of constraints between the two regions. The resultant torsion angle and distance values are not 1:1 correlated with maxima in the calculated values in the histograms (e.g. φ angle). Only a single model out of the eight is common to the 31-model cluster used for labelling selection underscoring the predisposition that the predicted structure serves as a guideline for selection of label sites. The ROSETTA program thus successfully narrowed the search for structural elements in the folded protein and then enabled a construction of the protein fold based on the experimental distance constraints.

Fig. 11.

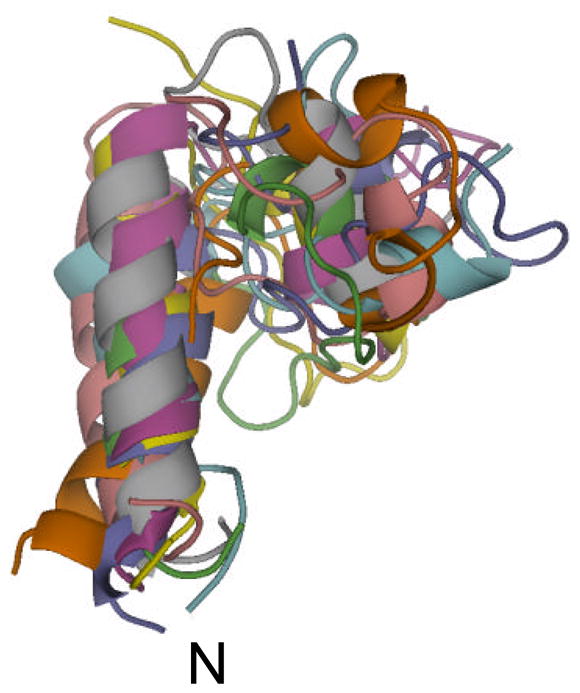
Superposition of the 8 models that agree with the constraints derived from the solid state NMR measurements. These models are derived from the full set of 1,000 models. Alignment of the models in the figure was based on root-mean-square deviation calculation of segments (1–15) and (33–38) between the 8 models.

The view of the structure of surface-bound statherin that emerges from NMR measurements and structural modelling by ROSETTA is that of a protein with α-helical secondary structure encompassing the first twelve amino acids in the N-terminus. This region is known to be necessary for HAP binding and accordingly, ¹⁵N–³¹P and ¹³C–³¹P REDOR measurements detected close approaches between surface phosphate groups and side chains of basic and aromatic amino acids. In addition, the C-terminus (which is known to contain a binding site for bacterial antenna proteins) is also helically structured. Long distance ¹³C–¹⁹F measurements show that, unlike the condition in solution where statherin appears unfolded and displays a 3₁₀ helical structure near the C-terminus, on the mineral surface the C-terminal α helix is folded over the intermediate region of the protein.

The next stage towards obtaining a detailed structure of the protein and its preferred orientation on the surface of hydroxyapatite is to complement additional constraints on the structure and additional information regarding the proximity and hence interaction strength of the protein outer shell with a simulative effort that accounts for the potential energy that the protein encounters at the different faces of the mineral as it adsorbs. The degree to which the structure of statherin can be influenced by the surface potential is not known yet although for other proteins it was reported that changes as severe as total unfolding, especially on hydrophobic surfaces, are often observed. Current protein structure prediction programs cannot predict the folded state of a protein in the presence of another macromolecule or surface starting from an unfolded or random coil conformation. The ultimate goal of computational technique development would be to assert the experimental observation of a transition from an unfolded state to an active folded state upon exposure to the potential energy of the surface.

6. Conclusions

At the present time solid state NMR dipolar coupling measurements are used to obtain high resolution structures for proteins in microcrystalline form, for proteins oriented in lipid bilayers and lipid vesicles and for proteins in fibrillar form. The present review demonstrates that the same solid state dipolar recoupling techniques can be used to obtain the structure of proteins at biomineral surfaces. Therefore, solid state NMR structural techniques can be extended to a broad class of biomaterial structural problems intractable to traditional structural biology techniques.

These results of the NMR studies of HAP-bound statherin have numerous biological implications. Statherin mediates the binding of several bacterial fimbriae via its C-terminal region only when it is adsorbed onto hydroxyapatite. Previous work has suggested that this recognition site is being exposed during the adsorption of statherin to the mineral surface. The α–helical conformation in the bacterial recognition site, shown here to form upon adsorption, provides a clear avenue for the differential recognition of immobilized vs. free statherin by bacteria. NMR measurements of statherin in 50% TFE solution report a 3₁₀ helix in a C-terminus region that slightly overlaps with the region where the solid state NMR measurements were taken. The C-terminus is helical on the surface, but the CN-REDOR measurements rule out the presence of a 3₁₀ helix between residue 34 and residue 38.

The C-terminus of statherin has been previously shown to be key to the lubricative action of statherin on tooth enamel, and the connection between helical secondary structure and viscoelastic function has been made with human serum albumin [90]. The folding of statherin’s C-terminus into an α-helical conformation thus serves as a structural context to understand both fimbrillin binding and consequently bacterial adhesion, as well as the important lubricative properties of bound statherin. The lubricative action of statherin in concert with other proteins in the pellicle should be greatly influenced by the structure the protein assumes when adsorbed. Particularly, if a cooperative mechanism of friction reduction exists, recognition between different proteins requires that statherin adopts a well-determined structure in the pellicle.

In general, statherin is a paradigmatic system whose structural transition upon adsorption to mineral surfaces may explain the structural basis of the biological function of the protein complement of the extracellular matrix (ECM). Many ECM proteins like osteopontin when studied in solution have been found to be unstructured [91]. In the case of statherin, the folding of the protein on the mineral surface may remove hydrophilic residues from solution, thus preventing further nucleation. In other words, the tertiary folding of statherin is the basis for its inhibition of HAP secondary crystallization, and this folding is naturally induced by contact between the HAP surface and the protein. Thus a protein that is unstructured in solution may nevertheless be functional on a surface where a folding transition occurs. This remarkable feature of statherin reverses the common paradigm observed in many proteins which unfold when surfaces, especially hydrophobic surfaces, are contacted.