Calculation of adsorption free energy for solute-surface interactions using biased replica-exchange molecular dynamics

Abstract

The adsorption behavior of a biomolecule, such as a peptide or protein, to a functionalized surface is of fundamental importance for a broad range of applications in biotechnology. The adsorption free energy for these types of interactions can be determined from a molecular dynamics simulation using the partitioning between adsorbed and nonadsorbed states, provided that sufficient sampling of both states is obtained. However, if interactions between the solute and the surface are strong, the solute will tend to be trapped near the surface during the simulation, thus preventing the adsorption free energy from being calculated by this method. This situation occurs even when using an advanced sampling algorithm such as replica-exchange molecular dynamics (REMD). In this paper, the authors demonstrate the fundamental basis of this problem using a model system consisting of one sodium ion (Na⁺) as the solute positioned over a surface functionalized with one negatively charged group (COO⁻) in explicit water. With this simple system, the authors show that sufficient sampling in the coordinate normal to the surface cannot be obtained by conventional REMD alone. The authors then present a method to overcome this problem through the use of an adaptive windowed-umbrella sampling technique to develop a biased-energy function that is combined with REMD. This approach provides an effective method for the calculation of adsorption free energy for solute-surface interactions.

I. Introduction

The adsorption behavior of a biomolecule, such as a peptide or protein, to a functionalized surface is of fundamental importance for a broad range of applications including biomaterials for implant^1–4 and drug-delivery applications,^5,6 biosensors,^7,8 and bioseparations.⁹ Molecular simulation provides a very powerful tool to study these types of interactions theoretically at the atomic level for the calculation of structural, thermodynamic, and kinetic parameters at the solute-surface interphase.^4,10,11 We are particularly interested in the calculation of the free energy of solute adsorption in an aqueous solution. The accurate calculation of adsorption free energy requires sufficient sampling of both the conformational space of the solute and its position with respect to the surface as a function of the surface separation distance (SSD).

The determination of thermodynamic properties by molecular simulation can be accomplished using either molecular dynamics (MD) or Monte Carlo (MC) methods to sample the phase space of the molecular system of interest.¹² MC methods are often more efficient for the determination of gas- or condensed-phase thermodynamic properties of relatively simple molecular systems.¹³ Also, because of the ability to make nonphysical moves, they are particularly useful for the conformational sampling of macromolecules either in isolation,^14–17 with continuum solvent approximations,^16,18 or which are restricted to conformational moves within a defined lattice.^14,19,20

MC sampling, however, can be problematic for macromolecules within explicitly represented solvent because the surrounding solvent molecules tend to severely restrict the ability to make conformational moves of the macromolecule without overlapping atoms of the solvent, thus leading to unacceptably high energy levels and poor sampling efficiency.^12,21 MD simulation methods are therefore more often used to simulate these types of systems, with sampling moves then controlled by the laws of Newtonian dynamics. Because we are interested in the behavior of peptides and proteins in explicitly represented physiological saline solution, we have primarily focused our efforts on the development and application of methods for the determination of adsorption free energy using MD simulations.

In a previous study, we attempted to perform conventional MD simulations with the probability-ratio method²² to calculate the adsorption free energy of a model peptide on functionalized self-assembled monolayer (SAM) surfaces.¹¹ Use of the probability-ratio method for the calculation of adsorption free energy requires that adequate sampling be achieved over the entire SSD space, with the SSD parameter extending far enough from the surface such that the solute no longer feels the effects of the surface (defined here as SSD_∞), thus representing bulk solution conditions. The probability of the peptide being at a particular SSD position, SSD_i, relative to the probability of it being in the bulk solution (SSD_∞) can then be used to calculate the relative free energy of the peptide as a function of SSD. The relative free energy values can be integrated over the SSD coordinate with proper weighting by their probability density to calculate the overall adsorption free energy.¹¹ The results from this previous study clearly demonstrated that the application of a conventional MD simulation approach to this type of molecular system resulted in two types of sampling problems, both of which inhibit the accurate calculation of adsorption free energy: (1) trapping of the peptide near the surface if strong peptide-surface interactions occur, which prevents the calculation of a relative probability at SSD_∞, and (2) limited sampling of the peptide's own conformation space due to the presence of the relatively high energy barriers separating local low-energy minima of the dihedral angles of the peptide. These deficiencies clearly indicate that more advanced types of sampling are needed for the calculation of adsorption free energy for this type of molecular system.

Efficient conformational sampling of a solute molecule in solution or at a surface can be provided through the use of advanced sampling methods that enable relatively high potential-energy barriers separating local low-energy states to be readily crossed, such as those separating dihedral rotations of a peptide chain. Conventional temperature-based replica-exchange molecular dynamics (REMD) methods have been shown to be fairly efficient in overcoming this type of sampling problem.^23,24 However, for the situation where a sampling problem exists due to the need to sample states with relatively large differences in free energy, such as when strong interactions occur between a solute and a surface,^11,25 a solute will still tend to become trapped within a tight range of SSD values close to the surface even in a REMD simulation. This occurs because the resulting Boltzmann distribution of sampled states will still overwhelmingly favor the low free-energy states. The high-lying states may be sampled by the high-temperature replicas, but will not be represented in the Boltzmann ensemble at the temperature of interest generated by the lowest-temperature replica (see Fig. 1). Other types of advanced sampling algorithms, such as biased-energy methods,^26,27 are better suited to address this particular type of sampling problem. However, although readily applicable to problems dealing with a single coordinate of interest, such as SSD, biased-energy methods generally become too complex for practical implementation when attempts are made to address multiple coordinate dimensions, such as controlling both SSD and peptide conformational sampling at the same time. In this paper, we present a biased-energy REMD method that we developed and applied to overcome both of these sampling problems in a single simulation for the calculation of the adsorption free energy of solute-surface interactions.

Fig. 1.

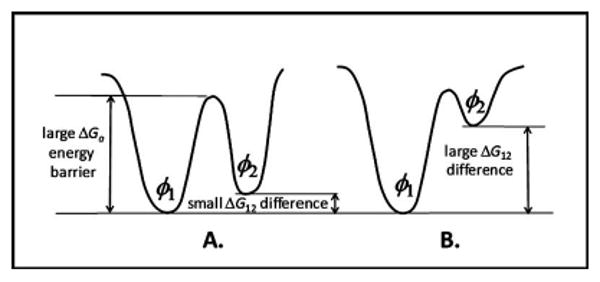
Illustration of two different situations that lead to sampling problems. (a) Two states (φ₁ and φ₂) with relatively small differences in free energy, ΔG₁₂, separated by a relatively large free-energy barrier, ΔG_a. A typical MD simulation will not be able to cross the energy barrier within a reasonable simulation time if ΔG_a≫k_BT, and thus will sample only one or the other, but not both states. A conventional REMD simulation can effectively sample this type of system by using elevated temperatures to enable this barrier to be readily crossed. The two states will still be sampled according to a Boltzmann distribution, with the probability of sampling state φ₁ relative to that of sampling state φ₂ given by P₁₂=P(φ₁)/P(φ₂)=exp(−ΔG₁₂/k_BT). For example, for a free energy difference of 2 kcal/mol, the relative sampling probabilities at 310 K are P₁₂=27:1, with both states thus being well sampled in the simulation. (b) Two states (φ₁ and φ₂) with relatively large differences in free energy separated by a relatively large free energy barrier. In the case where ΔG₁₂≫k_BT, a conventional REMD simulation is ineffective in sampling the system because the resulting Boltzmann distribution will mean that state φ₂ is sampled at a much lower probability than state φ₁ in the low-temperature replica. For example, with a free energy difference of 9 kcal/mol, the relative sampling probabilities at 310 K are P₁₂=exp(−ΔG₁₂/k_BT)=2.6×10⁶:1, with the higher free energy state thus being insufficiently sampled for any simulation with less than many millions of time steps.

To demonstrate this type of problem at a fundamental level, we investigated the behavior of a relatively simple solute-surface system consisting of one sodium ion (Na⁺) over a functionalized alkanethiol self-assembled monolayer (SAM) surface presenting one negatively charged carboxylate (COO⁻) group in explicit water. This system serves to illustrate the shortcomings of the conventional REMD method for this type of sampling problem, while retaining the most important characteristics of the system; i.e., a strong solute-surface interaction that results in a relatively deep energy well that tends to trap the solute close to the surface. It is taken for granted in our study that REMD is able to provide sufficient conformational sampling of a solute, as this has been shown in numerous previous studies related to peptide folding.^23,24 The single-ion adsorption system was purposely selected to eliminate the need for conformational sampling of the solute to allow focus to be placed on adapting the REMD method to overcome the SSD-sampling problem. We demonstrate that sufficient sampling along the SSD as a degree of freedom cannot be obtained by conventional REMD alone for this system. We then show that an effective biased-energy function can be developed using an adapted windowed-umbrella sampling method that we have developed for this application. When combined with REMD, this method can overcome this problem and enable sufficient sampling to be achieved over the full range of SSD space for the accurate calculation of adsorption free energy for solute-surface interactions.

II. Methods

A. Overview of advanced sampling methods

The probability-ratio method²² is a standard statistical mechanics technique that can be used for constructing a potential of mean force (PMF) profile (equivalent to a free energy profile) to characterize an adsorption process. This method relates the PMF to the natural logarithm of the probability density of sampled states, P(φ), as a function of a predefined reaction coordinate as follows:

$$W\left(\phi \right)=-k_{B}Tln\left\{P\left(\phi \right)\right\},$$ (1)

where φ denotes the reaction coordinate, W is the PMF value at φ, k_B is Boltzmann's constant, and T is the absolute temperature.

The precision of this method depends heavily on the sufficient and adequate estimation of P(φ). The estimation of this function, however, is known to be problematic for conventional MD and Monte Carlo simulations.^11,28,29 This is due to the fact that energetic barriers or entropic bottlenecks may not be sampled sufficiently in a simulation of finite duration, because of their high free energy, which may then prevent the sampling of the low free-energy states that are separated by these conditions. In addition, molecular configurations with relatively high free energy may also need to be sampled, as in the case of solute adsorption, so that the relative differences in free energy between the high and low free-energy states can be calculated.

Since the 1970s, this problem has attracted a large amount of attention and many excellent simulation protocols have been proposed to overcome this limitation.^30–32 The basic concept behind these algorithms is that of biasing the statistical mechanical factors that control the Boltzmann probability distribution of the system, thus causing the rare events to occur much more frequently in a simulation so they can be sufficiently sampled in the simulation trajectory. This is accomplished by multiplying the probability density function, P(φ), with a reweighting factor that effectively adjusts the probability density of a rare event as follows:

$$P^{\ast }(\phi )=\gamma \left(\phi \right)\times P\left(\phi \right),$$ (2)

where γ(φ) is the reweighting factor, P*(φ) is the adjusted probability measure, which is non-Boltzmann, and P(φ) is the original Boltzmann-weighted probability density function. The simulation is then performed on the adjusted, or reweighted, probability basis, and the original, unbiased probability measure can subsequently be calculated from the resulting biased probability distribution as

$$P\left(\phi \right)=\gamma {\left(\phi \right)}^{-1}\times P^{\ast }\left(\phi \right).$$ (3)

Collectively, all of the protocols that use a reweighting factor to improve the sampling efficiency are non-Boltzmann algorithms and procedures based on this class of algorithms are called non-Boltzmann sampling methods.

1. Construction of reweighting factors

Broadly, there are two different ways to apply the non-Boltzmann reweighting. The Boltzmann distribution³³ is a function both of the energy of the state φ, E(φ), as well as the temperature T at which the sampling is performed,

$$P\left(\phi \right)=\alpha e^{-\beta E\left(\phi \right)},$$ (4)

where α is a normalization constant [which also accounts for the degeneracy of the state(s) represented by φ and β = (k_BT)⁻¹]. Thus, in modifying the Boltzmann probabilities, one common approach is to modify the temperature, with the simulation performed at a biased (usually higher) temperature; the other is to modify the system Hamiltonian (usually through an add-on “umbrella” potential) so that the simulation is performed with a biased potential energy. It less convenient to bias the distribution via the degeneracy of a particular state, because, unlike temperature and potential energy, the degeneracy does not explicitly enter into the molecular dynamics simulation algorithm (and is typically not known a priori). We describe both types of non-Boltzmann reweighting factors in detail in the following subsections.

2. Umbrella-potential-based reweighting factors

If we denote a biasing potential as E_b(φ), then from the fundamental Eq. (4), the probability of being in configurational state φ for the nonbiased case can be expressed as

$$P\left(\phi \right)=\alpha e^{-\beta E\left(\phi \right)}$$ (5)

and, for a biased case, the probability can be expressed as

$$P_b(\phi )=\alpha e^{-\beta E_b\left(\phi \right)}.$$ (6)

The reweighting factor can then be written as

$$\gamma \left(\phi \right)=P_b\left(\phi \right)/P\left(\phi \right),$$ (7)

which, after substitution of Eqs. (5) and (6) into Eq. (7), yields

$$\gamma \left(\phi \right)=e^{-\beta \{E_b\left(\phi \right)-E\left(\phi \right)\}}=e^{-\beta \Delta E}.$$ (8)

This type of reweighting factor is utilized in umbrella sampling^26,34,35 and adaptive umbrella sampling^27,36–38 methods.

3. Temperature-based reweighting factors

The construction of temperature-based reweighting factors follows a very similar mathematical procedure as the umbrella potential-based methods. From the fundamental Boltzmann statistics in Eq. (4), given two different inverse temperatures β₁ and β₀, the probabilities of being in a configurational state φ with energy E(φ) can be expressed respectively as

$$P_{{\beta }_1}\left(\phi \right)=\alpha e^{-{\beta }_{1}E\left(\phi \right)}$$ (9)

and

$$P_{{\beta }_0}(\phi )=\alpha e^{-{\beta }_{0}E\left(\phi \right)}.$$ (10)

A reweighting factor can then be expressed as

$$\gamma \left(\phi \right)=P_{{\beta }_1}\left(\phi \right)/P_{{\beta }_0}\left(\phi \right).$$ (11)

Substituting the expressions of Eqs. (9) and (10) into Eq. (11) gives

$$\gamma \left(\phi \right)=e^{-({\beta }_1-{\beta }_0)E\left(\phi \right)}=e^{-\Delta \beta E\left(\phi \right)}.$$ (12)

This class of reweighting factor forms the basis of several advanced sampling and analysis methods, including single histogram analysis,²² multiple-histogram analysis,^39,40 the multicanonical algorithm,^41,42 replica-exchange methods,^42–44 and temperature-weighted histogram-analysis methods.⁴⁵

As indicated by their mathematical similarity, both the energy- and temperature-based methods effectively perturb the probability distribution that is obtained during an MD simulation, one by artificially reducing the energy levels separating the configurational states and the other by providing increased thermal energy to the system; both of which effectively result in a situation where transitions between states occur at a higher frequency, thus substantially improving sampling.

B. Model molecular system

The molecular system selected for this study is shown in Fig. 2. It consists of only one sodium counter-ion (Na⁺) in TIP3P water⁴⁶ over a COOH-functionalized alkanethiol self-assembled monolayer (SAM) surface⁴⁷ consisting of 90 chains with a single deprotonated chain (i.e., -COO⁻) positioned in the center of the surface to create a negatively charged surface group to strongly attract the sodium ion through electrostatic attraction. All atoms of the SAM surface were constrained to prevent them from moving, except for the top layer of the carboxylic acid functional groups (and central carboxylate group) in order to keep the SAM intact during the subsequent REMD simulations at elevated temperatures. The 3-D periodic unit cell was orthogonal with dimensions 44.73×43.04×60.00 ų. The top 15.0 Å layer of the water box was constructed from a preequilibrated layer of bulk water, which was then placed at the top of the simulation cell and constrained to remain fixed. This was done to prevent the imaged hydrophobic bottom surface of the SAM layer from perturbing the water structure in this part of the model, which may in turn influence the behavior of the sodium ion as it approached the top of the simulation cell. By design, this provides a model system where the solute is so strongly attracted to the surface that the SSD between the Na⁺ and the SAM surface during a conventional MD simulation remains within a narrow range within about 3.0 Å of the surface, thus exhibiting a substantial sampling problem. Furthermore, by selecting a single ion species as the solute, complications related to the question of conformational sampling of the solute itself in solution are avoided, with the simulations thus focusing solely on the problem of addressing the sampling limitation due to energy differences as a function of the SSD reaction coordinate.

Fig. 2.

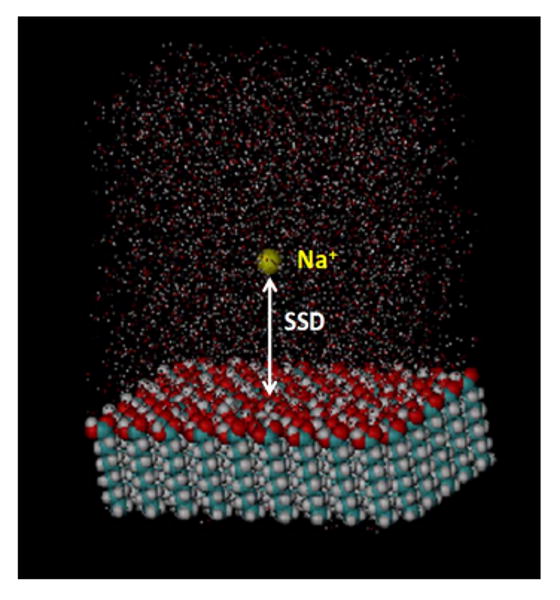
Model system designed for testing the biased-REMD sampling method in comparison to the conventional REMD method. It consists of a single sodium ion in TIP3P water over a carboxylic acid-functionalized SAM surface with one ionized COO⁻ functional group in the middle of the surface to strongly attract the sodium ion. The surface separation distance (SSD) represents the distance between the sodium ion in solution and the carboxylate group on the surface.

This model system was used in a series of simulations to demonstrate that a substantial sampling problem exists with such electrostatically charged aqueous adsorption systems such that the 310 K adsorption free energy cannot be properly determined from the trajectory data for simulations of reasonable length, even when performing a conventional REMD simulation. We then demonstrate that this problem can be overcome by combining a biased-energy function with the REMD algorithm to perform a biased-energy REMD simulation, with the resulting trajectory data then providing sufficient sampling for the calculation of adsorption free energy.

C. Conventional REMD simulation

REMD is one of the most widely applied temperature-based reweighting methods that has been used for peptide folding simulations because of its extreme versatility and relative simplicity in application. Sugita and Okamoto²³ presented the first paper that describes the molecular dynamics version of this replica exchange method in 1999. They pointed out that the major advantage of REMD over other generalized-ensemble methods, such as the multicanonical algorithm and simulated tempering, lies in the fact that the reweighting factor is automatically generated during the simulation, while in the latter algorithms the determination of the reweighting factor requires relatively laborious iterative methods. REMD also provides a great advantage over umbrella potential-based reweighting algorithms in that it operates on all degrees of freedom of the system simultaneously without requiring that a specific reaction coordinate be defined. A brief overview of the most important features of this method is provided here and readers are referred to the original paper by Sugita and Okamoto²³ for its rigorous formulation.

A REMD simulation results in the construction of a Boltzmann-weighted ensemble of states by generating independent trajectories at different temperatures, T_m(m = 1, …, N_r), with N_r being the number of temperature levels, or replicas, represented in the overall simulation. During the simulation, each replica at its designated temperature level is run in an independent manner for a short period of time (typically between 100 and 1000 fs), following which comparisons are made between the potential energy of the replica at temperature T_i and the replica at the next higher temperature T_j. An exchange attempt is then made using a Metropolis-based criterion, which is described by

$$\begin{array}{lll}\text{If}:& E_j-E_i\le 0,& \text{then exchange replicas};\\ \text{if}:& E_j-E_i>0,& \text{then exchange replicas if}\\ \multicolumn{3}{c}{\text{RAND}\left(0–1\right)\le e^{-({\beta }_i-{\beta }_j)(E_j-E_i)},}\end{array}$$ (13)

where RAND(0–1) indicates a random number between 0 and 1, inclusively. If this exchange condition is satisfied, the atomic position and momentum coordinates between replicas at T_i and T_j are exchanged and the momentum coordinates [p(T_i) and p(T_j)] are updated by

$$p\left(T_i\right)=\sqrt{\frac{T_i}{T_j}}p(T_j),p\left(T_j\right)=\sqrt{\frac{T_j}{T_i}}p(T_i)$$ (14)

to rapidly adjust each replica to its new temperature level. The temperatures of each replica are typically spaced in an exponential manner over the designated temperature range, with the width of the temperature intervals set to achieve an exchange acceptance level of between 0.15 and 0.20.²³

Enhanced sampling is provided by a REMD simulation because of both the large number of independent replicas that are sampling different configurational states of the system and the additional thermal energy provided at the higher temperature levels, which greatly increases the probability of crossing the energy barriers that separate the different states of the system. The Metropolis criterion then effectively applies the temperature reweighting factor to control the sampling process. Once properly equilibrated, the REMD procedure provides a Boltzmann-weighted sampling of states at each temperature. When such a simulation is continued for a sufficiently long time (typically for at least several nanoseconds) over a sufficiently large range of temperature, it permits sampling across barriers that could not be overcome at the low temperature alone within a reasonable time frame. As shown below, however, the REMD method does not solve all of the sampling problems that are encountered for a solute-adsorption process. Because it generates a Boltzmann-weighted ensemble of states at a given temperature level, it still exhibits sampling problems for events that normally occur with low probability. To demonstrate this limitation, we conducted a conventional REMD simulation on the model Na⁺/water/SAM system described in Sec. II A.

In our REMD simulation, we used 21 replicas spanning a temperature range from 310 K to 400 K, with the temperature levels distributed exponentially as recommended to obtain near-uniform rates of exchange between adjacent temperature levels.²³ Simulations were run using the CHARMM molecular simulation program^48,49 and the CHARMM27 force field,^48,49 with the REMD algorithm applied using a Python module designed by our group as a peripheral to CHARMM. The system was controlled with a constant number of atoms (N), under constant volume (V), and constant temperature (T) conditions using a Berendsen thermostat [i.e., in the canonical (NVT) ensemble] with periodic boundary conditions. Both van der Waals and electrostatic interactions were handled using a 12–14 Å switching function-based cut-off.^49,50 Cut-offs were used for electrostatic interactions as opposed to particle-mesh Ewald to prevent unphysical interactions between the sodium ion and periodic images of the charged SAM surface. Simulations were carried out for 5.0 ns at each of the designated temperature levels using the Verlet integrator with a 2 fs time step and bond length constraints applied to all bonds using SHAKE.^48,49 Exchanges between neighboring temperatures were attempted every 1.0 ps using the criterion shown above in Eq. (13). The trajectory results generated from the REMD simulation were then analyzed to describe the resulting probability distribution of the sampled SSD space, which was then converted to a PMF profile using the probability-ratio method.²²

D. Adaptive windowed-umbrella sampling

If the shape of the free energy surface is known a priori for a reaction coordinate of interest, then the negative of this surface, when applied as a biasing function, will result in a flattened trajectory with every state exhibiting the same probability of occurrence.^23,51 Unfortunately a priori knowledge of the free energy surface is rarely available for a system of practical interest. Windowed-umbrella sampling bypasses this shortcoming by dissecting the reaction coordinate into a series of overlapping regions, or “windows,” and assigning each window a defined harmonic restraining potential that forces sampling to occur around a specified region; usually with the following form:

$$H_b=\frac{k}{2}{\left(\theta -{\theta }_i\right)}^2,i=1,2,\dots N_W,$$ (15)

where H_b denotes the harmonic biasing potential that is added to the force field equation, k is the harmonic spring constant, θ is value of the reaction coordinate (SSD in our case), θ_i denotes the middle point of the ith window, and N_W is the total number of windows sampled. An independent canonical simulation is then performed for each separate window and the results are combined and then analyzed using the weighted-histogram analysis method (WHAM),^39,40,45 which enables a PMF profile to be calculated as a function of the underlying reaction coordinate over its full range of values. The resulting profile is then fit by an appropriate curve-fitting function that is continuous and differentiable, in order to form the biasing-energy function.

The traditional approach for the development of the curve-fitting function for the PMF profile is to use a combination of both polynomial and triangular functions to interpolate the discrete results from the WHAM analysis. However, taking into account the specific characteristics of our system, i.e., surface adsorption, we developed a more efficient approach for this based on the Derjaguin, Landau, Verwey, Overbeek (DLVO) theory.^52,53 DLVO theory represents the adsorption free energy profile with a combination of electrostatic and van der Waals interactions that underlie an adsorption process. These interactions typically follow the relationship as shown in Fig. 3, which can be approximated with a functional form of

Fig. 3.

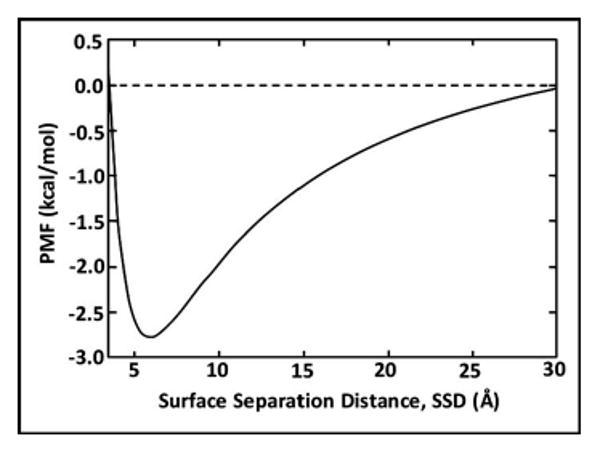
Typical curve shape represented by the potential of mean force (PMF) profile as a function of the surface separation distance (SSD) using the DLVO-type relationship shown in Eq. (16).

$${\text{PMF}}_{\text{DLVO}}(r)=a{(r-r_o)}^{-1}+b{(r-r_o)}^{-6}+c{(r-r_o)}^{-12}+d,$$ (16)

where the first term accounts for electrostatic interactions, the second and third terms account for the attractive and repulsive van der Waals interactions, respectively, r (or SSD for our case) represents the distance of the ion from the surface, and a, b, c, d, and r_o are all coefficients obtained from least-squares fitting of the PMF versus SSD profile results from a WHAM analysis of the simulation trajectories.

For our specific studies, windowed-umbrella sampling (WUS) simulations were performed by dividing the overall SSD space for the system into a series of 30 windows with a window spacing of 1.0 Å and with k=1.0 kcal/mol/Å [see Eq. (15)]. MD simulations were conducted under conditions similar to those described for the conventional REMD simulation. In the present study, we have developed a computationally efficient approach to WUS, which we call adaptive windowed-umbrella sampling (AWUS). In this method, we conduct a series of short 200 ps WUS simulations with the results of each simulation being used in an iterative manner to generate the converged PMF profile.

Accordingly, a 200 ps WUS simulation was first conducted with our molecular system and WHAM analysis was applied to approximate the shape of the PMF potential over the full range of SSD-coordinate space. Equation (16) was then fitted to the resulting PMF profile to develop an equation expressing the PMF as a function of SSD. The negative of the calculated PMF versus SSD profile was then used as a biasing-energy function for each window (in addition to the harmonic umbrella potential) and a new series of 200 ps WUS simulations was run. A WHAM analysis was again performed on the resulting SSD-trajectory data and used to generate a residual PMF profile from the biased-energy simulation data. The residual PMF profile was then evaluated for its flatness, which provided an indicator of how closely the applied biased-energy profile negates the true underlying PMF profile of the system (i.e., if perfectly matched and adequately sampled, the PMF profile for a biased-energy WUS simulation would be zero for all SSD values). If not sufficiently flat (i.e., absolute value ≤2 kcal/mol for all SSD positions), a new estimate of the unbiased PMF potential was generated and a new DLVO versus SSD function was fit to the PMF profile and applied as the biased-energy function in another series of WUS simulations. This process was continued until the resulting residual PMF profile was considered to be sufficiently flat, thus indicating that the applied biased-energy potential was an adequate representation of (the negative of) the underlying PMF profile of the system. This biasing potential was then used for the subsequent biased REMD simulation.

The AWUS method has two advantages over simpler applications of WUS. First, it helps to ensure that a converged PMF is obtained with the minimum amount of sampling time. Second, it is more amenable to parallelization on a heterogeneous computer cluster, as the granularity of the simulations is smaller.

E. Biased-REMD simulation

Biased-REMD is a hybrid non-Boltzmann sampling method, which implements a biased potential energy function within an otherwise conventional REMD simulation to simultaneously overcome the two types of sampling problems illustrated in Fig. 1: (1) the need to readily cross relatively high energy barriers separating states with similar energy levels, which is provided by REMD, and (2) the need to sample states spanning a relatively large range of energy levels, which is provided by the biasing potential. In this protocol, the negative of the final PMF versus SSD profile generated from the AWUS method is used in a subsequent REMD simulation as a biasing potential for every replica.

Accordingly, for our simulations, we first generated the PMF profile from the AWUS simulation as described in Sec. II D. We subsequently conducted a REMD simulation following the same procedures as described in Sec. II C for the conventional REMD simulation, except that the negative of the PMF profile from the AWUS method was added to the potential energy function, thus performing a biased-REMD simulation. The resulting biased trajectory was then analyzed using the WHAM method and corrected for the biased energy function to obtain the final unbiased PMF profile, which represents the free energy of the system over the entire range of SSD space. These results were then compared to those obtained from the conventional REMD simulation to demonstrate the effectiveness of this hybrid non-Boltzmann sampling method.

III. Results and Discussion

A. Conventional REMD simulation

A conventional (i.e., unbiased) REMD simulation was conducted as described in Sec. II C for comparison with biased-REMD results. Table I shows the neighboring replica temperature pairs and the corresponding acceptance ratios (middle column) obtained for this simulation. Statistically, the acceptance ratios were distributed around a mean of μ=0.18 with standard deviation of σ=0.03, thus showing that an adequate level of exchange was achieved between all neighboring temperature levels.

Table I.

Temperature-level pairs and the associated acceptance ratios for both the conventional and the biased-REMD simulations.

Temperature pairs Ti−Tj (K)	Conventional REMD acceptance ratio	Biased-REMD acceptance ratio
310–313	0.204	0.259
313–318	0.107	0.075
318–322	0.176	0.156
322–326	0.173	0.149
326–330	0.187	0.179
330–334	0.174	0.162
334–338	0.179	0.180
338–343	0.153	0.120
343–347	0.191	0.193
347–352	0.160	0.129
352–356	0.186	0.189
356–361	0.156	0.136
361–365	0.221	0.208
365–370	0.196	0.149
370–375	0.173	0.152
375–380	0.187	0.148
380–384	0.233	0.229
384–389	0.206	0.187
389–394	0.181	0.156
394–400	0.119	0.088
Mean ± std. dev.	0.18 ± 0.03	0.16 ± 0.04

Figure 4(a) presents a plot showing which replica occupied the lowest temperature level (310 K) over the 5 ns conventional REMD simulation. This plot demonstrates that a random walk across the designated temperature space was satisfactorily obtained, with nearly every replica visiting the 310 K temperature level during the course of the 5 ns REMD simulation. Figure 4(b) presents the resulting histogram of the SSD space sampled during this simulation and Fig. 4(c) presents the resulting box-plot statistical analysis^54,55 of the histogram. The box-plot method of representation is used here to provide a simple graphical representation of the overall degree of statistical sampling that was achieved during the simulation. As indicated in Fig. 4(c), a box-plot shows the median of the population (thick line inside the box), the first (Q1) and third quartiles (Q3) of the sampled states about the mean (box around the median), range bars (lines or “whiskers”) above and below the quartile boxes, and population outliers [dotted points outside of the range bars; see the caption for Fig. 4(c)]. These results show that the position of the sodium ion was primarily restricted to be within about 7.0 Å from the SAM surface, thus clearly demonstrating that a substantial sampling problem occurred in this simulation.

Fig. 4.

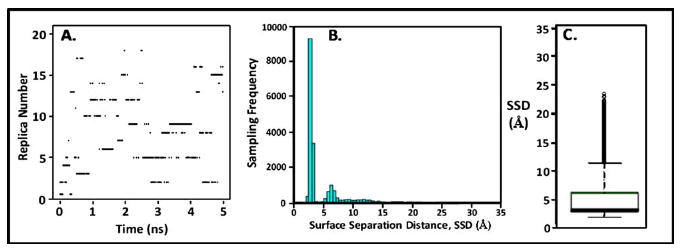
(a) Time series replica diffusion for the 5 ns conventional (unbiased) REMD simulation. Dark dashes indicate which of the 21 replicas occupied the 310 K temperature level at a given point in time. (b) Histogram showing the degree of sampling for each increment of SSD space. (c) Box-plot statistical analysis of the histogram presented in (b) showing the median (thick line in box), first (Q1) and third quartiles (Q3) (box around the median), range bars (lines (whiskers) above and below the box, lower range ≡ Q1−1.5 [Q3–Q1], upper range ≡ Q3+1.5 [Q3–Q1]), and population outliers (dotted points outside of the range bars).

B. AWUS smulation

The dashed line in Fig. 5(a) represents the first iteration of the AWUS method. In this iteration, no DLVO-type biasing potential was applied in the simulation; only harmonic umbrella potentials [i.e., Eq. (15)] were applied to each window in the simulation to keep sampling centered about the central SSD position of each of the windows. The resulting PMF profile was constructed with WHAM and fitted with the DLVO-type functional form [Eq. (16)]. This initial estimate of the PMF had a minimum near 2.7 Å with a well depth of about −4.3 kcal/mol. From our experience with this approach, the first iteration using this AWUS method generally results in the depth of the PMF profile being substantially underestimated, due to insufficient sampling of the high free energy states in the absence of a biasing potential. While repeated iterations can be used to converge the PMF profile, we have found that this process can be shortened by three or four iterations by simply amplifying the results of the first 200 ps iteration prior to conducting the second iteration attempt. Thus, to accelerate this iterative process, the DLVO-type fitting function obtained from Fig. 5(a) (solid line) was subjectively multiplied by a factor of about 4, and the negative of this function was then used as a biasing potential for the second iteration. The residual PMF profile obtained from this iteration indicated that the biasing potential used in the simulation was overly strong and that another iteration of the process was necessary. A new estimate of the real PMF profile was then generated using the WHAM analysis of the sampling provided from the second iteration; the results of this analysis are shown by the lower dashed line in Fig. 5(b). This profile was then again fitted with Eq. (16) [lower solid line, Fig. 5(b)] to provide the biasing potential for the third 200 ps iteration of AWUS. The dashed-dotted line of Fig. 5(b) presents the residual PMF profile obtained following the third 200 ps iteration, which represents a total of only 600 ps of MD simulation, with the residual PMF profile then considered to be sufficiently flat (absolute magnitude of PMF values ≤2 kcal/mol) within the SSD range from 2 to 16 Å. These results thus indicated that the process had sufficiently converged and that the applied DLVO-based biasing function represented a reasonable estimate of the true PMF profile of the system. The negative of this DLVO function [upper dashed line, Fig. 5(b)] was then used as the biasing potential for the subsequent biased-REMD simulation. The values of the parameters for this final functional form of the DLVO function are provided in Table II.

Fig. 5.

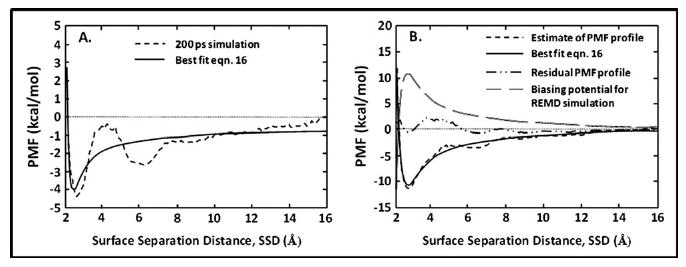
Development of the biased energy function by the AWUS iterative method. (a) The PMF vs SSD profile provided by the initial 200 ps simulation with no biasing energy applied (dashed line) and the best fit of the DLVO function [Eq. (16)] to the data plot (solid line). (b) Revised estimate of PMF vs SSD profile based on the sampling from two 200 ps simulation iterations (lower dashed line) and the best fit of the DLVO function to this PMF profile (solid line). The middle dashed-dotted line presents the residual PMF vs SSD profile obtained from the third 200 ps iteration when the best-fit DLVO function (solid line) was used to define the biased-energy function; the residual PMF profile is now considered to be acceptably flat (absolute value ≤2 kcal/mol over the entire SSD range). The upper dashed curve is the negative of the best-fit DLVO function (solid line); this represents the biased-energy function that was then applied in the subsequent biased-REMD simulation.

Table II.

Final set of DLVO parameters [Eq. (16)] for the PMF profile generated from the adaptive windowed-umbrella sampling (AWUS) simulations.

	Parameters for final PMF profile
Parameter	a	b	c	d	ro
Value	−27.598	−22 410	2.7575×107	1.3453	−0.77671
Units	(kcal Å)/mol	(kcal Å6)/mol	(kcal Å12)/mol	kcal/mol	Å

C. Biased-REMD simulation

Table I (column 3) shows the acceptance ratios for each pair of temperatures in the biased-REMD simulation. Statistically, the acceptance ratios were distributed around a mean of μ=0.16 with standard deviation σ=0.04, thus showing that an adequate level of exchange was achieved between all neighboring temperature levels. Figure 6(a) presents a plot showing which replica occupied the lowest 310 K temperature level over the 5 ns biased-REMD simulation. This plot demonstrates that a random walk across temperature space was satisfactorily obtained for the simulation, with nearly every replica visiting the 310 K temperature level during the course of the 5 ns REMD simulation. Figure 6(b) presents the resulting histogram of the SSD space sampled during this simulation and Fig. 6(c) presents the resulting box-plot statistical analysis^54,55 of the histogram. These results clearly show that the use of the biasing potential enabled the sodium ion to readily escape from the surface and effectively sample the entire range of SSD space during the 5 ns simulation, as desired.

Fig. 6.

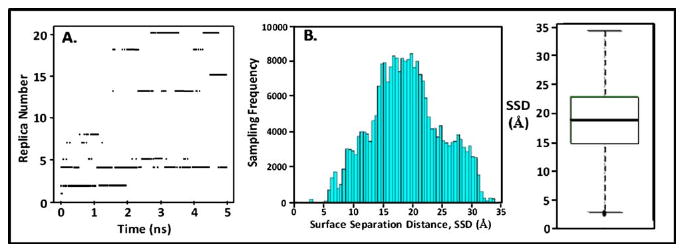
(a) Time series of replica diffusion for the 5 ns biased-REMD simulation. Dark dashes indicate which of the 21 replicas occupied the 310 K temperature level at a given point in time. (b) Histogram showing the density of sampling for each increment of SSD space. (c) Box-plot statistical analysis of the histogram presented in (b) showing the median (thick line in box), first and third quartiles (box around the median), range bars (lines (whiskers) above and below the box, lower range ≡ Q1−1.5 [Q3–Q1], upper range ≡ Q3+1.5 [Q3–Q1]), and population outliers (dotted points outside of the range bars).

To address the question of whether or not the SSD histogram for the biased-REMD simulation represented a converged sampling distribution, the histogram from the 5 ns biased-REMD simulation was compared with a histogram generated following only 2 ns of simulation. Figures 7(a) and 7(b) show the histograms of the 2 and 5 ns simulations, respectively, and Fig. 7(c) presents a box-plot statistical comparison^54,55 of these results. As shown, the results from the 5 ns simulation agree closely with the 2 ns results, with each distribution exhibiting a mean around μ=18.6 Å with a standard deviation of σ=6.1 Å, thus indicating that sampling had converged even after 2 ns and that adequate sampling of the system was indeed provided by the 5 ns biased-REMD simulation.

Fig. 7.

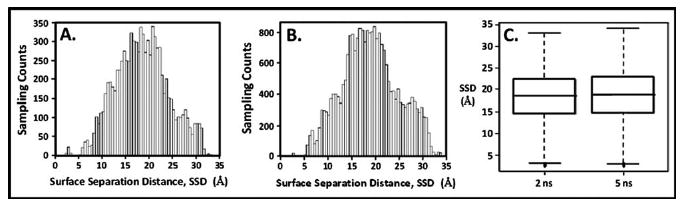
Sampling distribution analysis for the biased-REMD simulation. (a) Sampling histogram after 2 ns. (b) Sampling histogram after 5 ns. (c) Box-plot statistical analyses of sampling distributions from the 2 and 5 ns histograms showing the median (thick line in box), first and third quartiles (box around the median), range bars lines (whiskers) above and below the box, lower range ≡ Q1−1.5 [Q3–Q1], upper range ≡ Q3+1.5 [Q3–Q1]), and population outliers (dotted points outside of the range bars).

D. PMF profile comparisons

Figure 8 compares the PMF profiles constructed from a probability-ratio method analysis for the 5.0 ns conventional REMD simulation (dashed line), the 5.0 ns biased-REMD simulation (solid line), and the simple expression of Coulomb's law (dashed-dotted red line) for an ion pair separated by r=SSD [PMF_Coul=(q₁q₂)/(4πε_oεr), where q₁ and q₂ are +1 and −1 units of electronic charge on the sodium ion and carboxylate group, respectively, ε_o is the permittivity of free space, and ε is the relative dielectric constant of TIP3P bulk water, which was taken to be 80].⁵⁶

Fig. 8.

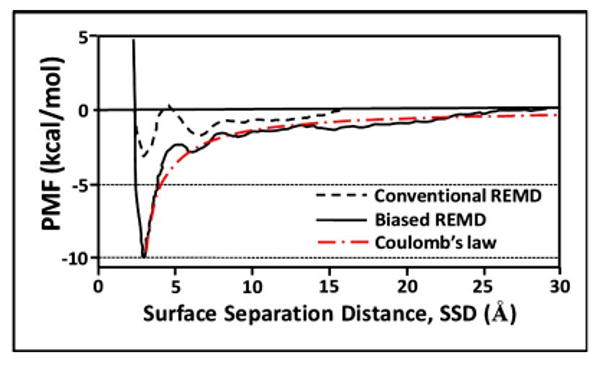
Final PMF vs SSD profiles from the 5.0 ns conventional REMD simulation (dashed line), the 5.0 ns biased-REMD simulation (solid line), and the theoretical profile predicted from Coulomb's law for an ion pair with SSD separation (dashed-dotted red line).

Due to the insufficient sampling provided by the conventional REMD algorithm [as evident from the histogram shown in Fig. 4(b)], its PMF profile is substantially underestimated and does not contain any observations of SSD values greater than about 15 Å. In comparison, the PMF profile from the biased-REMD simulation was constructed with adequate sampling over the full range of SSD space [as evident from the sampling histogram shown in Fig. 6(b) with sampling convergence indicated in Fig. 7]. As indicated in Fig. 8, the resulting profile shows a relatively deep free energy well, with the overall profile being generally in excellent agreement with the theoretical prediction provided by Coulomb's law.

As expected, the PMF profile generated from the biased-REMD simulation is in excellent agreement with the PMF profile from the last iteration of the AWUS simulation shown in Fig. 5(b), which serves to further validate the biased-REMD method. This occurs for this special case, however, because the molecular system was purposely selected to highlight the problem of SSD sampling when using the conventional REMD method while avoiding unnecessary complications related to solute conformational sampling. Now that we have validated this method, it can confidently be applied to calculate the adsorption free energy for more complex solutes, such as a peptide over a functionalized surface. For a peptide adsorption system, the REMD algorithm will primarily provide thermal energy for enhanced conformational sampling of the peptide, while the biased-energy algorithm incorporated within the REMD simulation will enable adequate sampling to be achieved over the SSD coordinate.

IV. Conclusions

Adequate system sampling is essential if adsorption free energy for solute-surface interactions is to be calculated from the trajectory of a molecular dynamics simulation. As described in this paper, this type of system inherently involves two types of sampling problems: the need to adequately sample the internal conformational space of the solute and the need to sample its position over the surface, ranging from tight adsorption to the desorbed state under bulk-solution conditions. While a conventional REMD simulation is able to overcome free energy barriers in order to provide adequate conformational sampling of a solute in solution, and umbrella sampling can be applied to ensure adequate sampling over SSD space, neither of these methods alone is able to overcome both types of sampling problems. However, when a biasing potential provided by AWUS is combined with REMD to form a biased-REMD simulation, both of these sampling problems can be readily overcome and the free energy profile can be confidently calculated from the resulting simulation trajectory.

Based on the successful development of these methods, we are currently applying this approach to calculate the free energy of adsorption of model peptides over SAM surfaces presenting a wide range of surface chemistries. These values are being compared with experimental results obtained from surface plasmon resonance spectroscopy to assess the accuracy of the CHARMM force field, and to provide a basis for force field optimization for the development of an interphase force field that is specifically parameterized for the accurate simulation of protein adsorption behavior on biomaterials surfaces.