Gains in power for exhaustive analyses of haplotypes using variable-sized sliding window strategy: a comparison of association-mapping strategies

Abstract

Linkage disequilibrium (LD)-based association mapping is often performed by analyzing either individual SNPs or block-based multi-SNP haplotypes. Sliding windows of several fixed sizes (in terms of SNP numbers) were also applied to a few simulated or real data sets. In comparison, exhaustively testing based on variable-sized sliding windows (VSW) of all possible sizes of SNPs over a genomic region has the best chance to capture the optimum markers (single SNPs or haplotypes) that are most significantly associated with the traits under study. However, the cost is the increased number of multiple tests and computation. Here, a strategy of VSW of all possible sizes is proposed and its power is examined, in comparison with those using only haplotype blocks (BLK) or single SNP loci (SGL) tests. Critical values for statistical significance testing that account for multiple testing are simulated. We demonstrated that, over a wide range of parameters simulated, VSW increased power for the detection of disease variants by ∼1–15% over the BLK and SGL approaches. The improved performance was more significant in regions with high recombination rates. In an empirical data set, VSW obtained the most significant signal and identified the LRP5 gene as strongly associated with osteoporosis. With the use of computational techniques such as parallel algorithms and clustering computing, it is feasible to apply VSW to large genomic regions or those regions preliminarily identified by traditional SGL/BLK methods.

Introduction

Case–control association studies provide a powerful tool for dissecting the genetic basis of complex human diseases, especially for those with a late-age of onset.¹ Recent advances in high-throughput genotyping technologies have allowed us to test allele frequency differences between case and control populations on a genome-wide scale.²

The linkage disequilibrium (LD)-based association analysis can be performed by analyzing either individual single-nucleotide polymorphism (SNP) loci or multi-SNP haplotypes. For indirect LD association mapping, the haplotype-based association method may be more powerful than the single locus test, as multi-SNP haplotypes may capture the available LD information in a particular region.³ However, single locus test may outperform the haplotype-based analysis under some scenarios, for example, when a causal locus is genotyped directly.⁴ In practice, both single locus and haplotype-based analyses are widely used in genetic association studies.

A challenge for association mapping is how to make full use of the information embedded in a set of SNPs genotyped in an analysis. So far, the haplotype-based association has mainly been applied to haplotype blocks, which are defined as discrete chromosome regions containing SNPs in high LD and haplotypes with low diversity.⁵ Although a number of algorithms have been developed for haplotype block partitioning, the block structures and boundaries are somewhat discrepant across different methods.^{6, 7}

An alternative strategy is based on the sliding-window methodology. A few studies applied this strategy with several fixed window sizes. Durrant et al⁸ applied sliding widows of sizes 4, 6, 8, and 10 markers through cladistic analysis of SNP haplotypes. Cheng et al⁹ explored all possible widths of haplotypes under the preset maximum window size of five markers on the simulated data set from the Genetic Analysis Workshop (GAW) 12, using both population-based and family-based designs.¹⁰ More recently, a graphical assessment of P-values from sliding window haplotype tests of association were developed with window sizes of 2–6.¹¹ In addition, some investigators performed sliding window analyses in fine mapping of complex diseases (such as Alzheimer's disease, hypertensions, asthma and so on), candidate genes or regions.^{12, 13, 14}

For a set of genotyped SNPs, the maximum detection power for association with the study traits can be achieved only when the authentic block or window or single SNPs that contain or best capture LD with a disease susceptibility locus is selected to conduct the association test.¹⁵ Single SNPs may not best capture LD with a disease susceptible locus. In block-based association mapping, it is possible to miss the potential perfect window of SNPs, thus losing power. This situation may also arise for the sliding window approach when a limited number of window widths are applied.

In contrast, exhaustive testing based on variable-sized sliding windows (VSW) of all possible sizes over a genomic region has the best chance to capture the optimum markers (single SNPs of haplotypes) that are most significantly associated with study traits. The strategy essentially combines both the strength of single-marker analyses and that of haplotype analyses and overcomes the potential problems with defining haplotype blocks. However, the potential cost is the increased number of multiple tests and increased amount of computation.

In this study, we present a strategy that exhaustively tests haplotypes based on VSW to analyze disease association studies. Extensive simulations and an empirical data study were conducted to probe the extent of power gain for this strategy in contrast with traditional haplotype blocks (BLK) and single SNP loci SGL tests. We also evaluated how statistical power of VSW, in comparison with BLK and SLG methods, varies with changes in magnitude of LD, sample size and disease effects. Strategies are proposed for the application of our VSW method when the capability of computation becomes a problem in practice.

Methods

Test statistic

For demonstration, here we use a simple test statistic for the haplotype association test in case–control study with unrelated individuals. Suppose that N affected individuals (cases) and N unaffected individuals (controls) are genotyped. For each window or block, the haplotype frequency data can be arranged in a 2^*k contingency table, where k is the number of distinct haplotypes. The null hypothesis H₀ to be tested is that haplotype frequencies in affected and unaffected individuals will be equal. A conventional χ² statistic for testing H₀ can be written as follows:

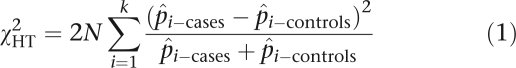where p̂_i−cases and p̂_i−controls are the observed frequencies of the ith haplotype in cases and controls respectively. Under the null hypothesis of no association, the above statistic has an asymptotical χ² distribution with k−1 d.f.⁴ The test statistic using individual marker allele data is the same as χ_HT² except that haplotype frequencies are replaced by the observed marker allele frequencies in the cases and controls, respectively.

For the VSW strategy, a set of all possible windows w_b≤e(b, e) consisting of consecutive markers were constructed in a simulated genomic region beginning at position B and ending at position E, where b≥B and e≤E. Haplotype association analyses described above were performed to search for associations of any single SNPs and/or possible haplotype window with the disease. Haplotypes with very low frequency (<0.001) were pooled together to avoid bias on association test. The association evidence at a marker position x in the region is defined as the smallest P-value among all analyses of this marker and/or all possible haplotype windows containing this marker,

We then conducted power comparison between strategies that use VSW, BLK, and single SNP loci (SGL) to analyze disease association studies respectively. For easy demonstration, we formulated our comparisons based on standard χ² statistics which are conceptually straightforward and have been widely applied in many association studies.^{1, 16} We utilized Java to implement this approach, which includes the module of functions for performing permutations.

For the BLK approach, block partitioning was accomplished through a commonly used algorithm proposed by Gabriel et al,¹⁷ the default block partition algorithm used in Haploview¹⁸ for HapMap data. Specifically, intervals for D′ (D′=D/D_max, proportion of observed LD of maximum possible LD) values for all pairs of SNPs are first estimated by bootstrap method. Then, SNP pairs are defined to be in ‘strong' LD if the one-sided upper 95% confidence bound is larger than 0.98 and the lower bound is larger than 0.70. A haplotype block is identified when at least 95% of SNP pairs within a chromosomal region meet the criteria for strong LD.

Simulation scheme for power comparison

We simulated SNP haplotypes through the coalescent process with a recombination rate implemented in program MS.¹⁹ To simulate regions with different extents of LD, the recombination rate per site per generation is set to 10⁻⁹, 10⁻⁸, and 10⁻⁷, corresponding to high, moderate LD region, and low LD region, respectively. In each simulation, with an effective population size of 10 000, genealogies of 2000 haplotypes were generated for a 30 kb human chromosome region, containing 30 SNPs with minor allele frequencies over 0.05. One SNP with minor allele frequency in the range of 0.10–0.12 was randomly selected as the disease-causing variant in the region. Then each subject of the simulated sample was created by randomly pairing the haplotypes according to different sample sizes. The disease status was determined by the commonly used multiplicative disease model. Based on this model,⁴ suppose that D and d are the high- and low-risk alleles at the disease locus, the probability of being affected for genotypes DD, Dd, and dd are f, fγ, and fγ², separately, where f is the phenocopy rate and γ is the relative risk. Given disease prevalence P, γ and disease allele frequency q, f can be calculated using the following equation:

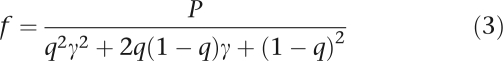For the simulation, we set the disease prevalence to be 0.05 and four levels for the genotype relative risk (1.5, 1.75, 2.0, and 2.25). Different sample sizes (600, 800, 1000, and 1200) including equal number of cases and controls were considered in the simulations. Before statistical analysis, genotypic information of the selected causal SNP was removed from the simulated haplotypes for all cases and controls. We took haplotype phase and frequency of the simulated data set as unknown, and used EM algorithm for estimation.

Construction of null distribution under H₀

For the VSW strategy, overlapping sliding windows and correlated neighboring SNPs may confound the issue of multiple testing. Bonferroni correction¹ is overly conservative to correct for multiple testing in the presence of correlation and information overlapping. Simulations under H₀ are usually employed to construct the null distribution of a new test statistic. Many genetic mapping studies have used such simulations to establish significance levels while accounting for multiple testing and related testing.^{20, 21} In this study, 10 000 replications were first generated to construct the null distribution for each set of parameters to determine the critical value of P for a given false-positive error rate (α=0.05) over the simulated region, that is, the smallest P-value of each replication over the simulated region were collected to form the null distribution. We used the same genealogies of haplotypes generated for power study and then we randomly assigned the affection status independent of the individual genotype. Subsequently, according to the established critical values, we assessed the power (the rate of declaring association is based on the smallest P-values over the simulated region at the significant level of corresponding critical values) to detect the disease association under varying conditions, such as the extent of LD, sample size, and risk effect.

Results

Simulation studies

Critical values under the null hypothesis

Table 1 displays the critical values for all the three strategies based on the given significant level of α=0.05 over the simulated haplotype region. As expected, the critical values of VSW strategy were most conservative, ranging from 0.0011 to 0.0023. Less conservative critical values were obtained for SGL. BLK achieved the least stringent critical values. The extent of LD may have an influence on the determination of the critical values over the simulated regions. We noted that critical values were slightly more conservative in lower LD regions. However, critical values for different sample sizes were found to be similar for each method.

Table 1. Empirical critical values (α=0.05).

	Sample size
	600	800	1000	1200
High LD region ra=10−9
VSWb	0.0023	0.0021	0.0020	0.0021
BLKc	0.0092	0.0091	0.0090	0.0089
SGLd	0.0043	0.0039	0.0039	0.0037
Medium LD region r=10−8
VSW	0.0018	0.0018	0.0016	0.0018
BLK	0.0085	0.0081	0.0082	0.0078
SGL	0.0036	0.0035	0.0034	0.0034
Low LD region r=10−7
VSW	0.0014	0.0013	0.0012	0.0011
BLK	0.0043	0.0041	0.0042	0.0042
SGL	0.0019	0.0020	0.0020	0.0019

^ar represents the recombination rate per site per generation.

^b,c,dVSW, BLK, and SGL denote association-mapping strategy using variable-sized sliding windows, haplotype blocks, and single SNP loci, respectively.

P-value distribution under the alternative hypothesis

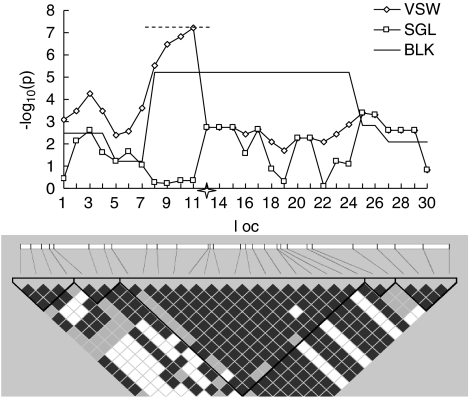
To intuitively compare the P-values between the three proposed strategies, Figure 1 shows the distribution of P-values obtained by each of the proposed strategies in an example randomly selected from the power simulation studies. To be convincing, empirical P-values for each strategy were obtained through 10 000 permutations based on this simulated sample. In this region, SNP 12 was selected and removed as the causal locus (Figure 1). Five blocks with high LD, with sizes ranging from 2 to 16 SNPs, were identified by Gabriel's block-partitioning method.¹⁷ As expected, the most significant P-value (−log₁₀P=5.2143, empirical P=0.0073) for BLK strategy was achieved at the biggest block consisting of SNPs from 8 through 24, covering the causal variant. Impressively, the VSW approach successfully detected the disease locus with the highest peak (−log₁₀P=7.2171, empirical P=0.0005) obtained at the nearest SNP. The best window (consisting of SNP 7 to SNP 13) for VSW strategy was much more narrow than the most significant block of BLK, with five markers (SNP 8, SNP 9, SNP 10, SNP 11, SNP 13) overlapping. The SGL analysis almost missed the association signal, with all values of −log₁₀P were less than three (the smallest empirical P=0.0174).

Figure 1.

The −log₁₀ of raw P-values obtained through the three proposed strategies in an example randomly selected from the power simulation studies and its LD structure. VSW, BLK and SGL denote association-mapping strategy using variable-sized sliding windows, haplotype blocks, and single SNP loci, respectively. Four hundred cases and an equal number of controls were simulated, with medium recombination rate (10⁻⁸ per site per generation). The x axis shows the simulated loci and the 4-point star in the middle of x axis indicates the location of the putative locus with relative risk of two. The dashed line on top, covering SNP 7 to SNP 13, indicates the best window with which the smallest P-value for VSW was achieved. LD block structure is shown in the bottom frame. The color from white to black represents the increasing strength of LD.

Power comparison

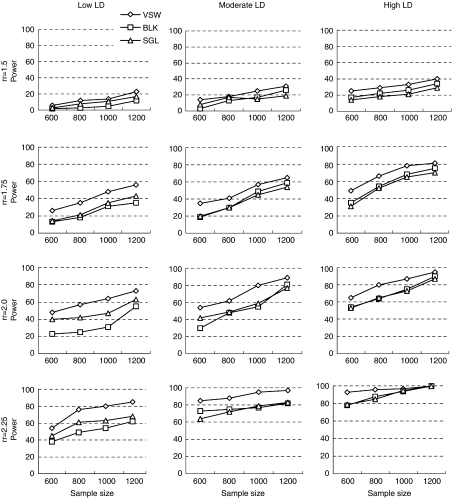
Based on our simulation studies, the power to detect an association between the putative allele and disease status was affected by risk effect, sample size and recombination rate (see Figure 2). With larger risk effect, larger sample size, and lower recombination rate, the detection power for all three proposed methods increased, which is consistent with previous findings.²² Almost full power (over 90%) was achieved when detecting putative locus with a large relative risk (2.25) in the high LD region. In all cases, the detection power for VSW strategy was consistently greater than the other two strategies (∼1–15%), and the improved performance was more significant in the lower LD region with larger risk effect and larger sample size.

Figure 2.

Detection power for the three proposed mapping strategies. Disease relative risk (rr) was set to 1.5, 1.75, 2.0, and 2.25 (four rows). Extent of LD was categorized as low, moderate, and high LD (three columns), with recombination rate (r) per site per generation in the simulation region set to 10⁻⁷, 10⁻⁸ and 10⁻⁹, separately. Disease prevalence was 5%. VSW, BLK and SGL denote association-mapping strategy using variable-sized sliding windows, haplotype blocks, and single SNP loci, respectively.

Empirical data analyses

We evaluated and compared the relative performance of the study strategies by analyzing a published empirical data set from Xiong et al.²³ In their studies, a Chinese cohort including the genotypes of 21 SNPs of 733 unrelated participants (369 men and 364 women) was collected to study the genetic association between the LRP5 gene and osteoporosis. The subjects were selected from an expanded database for osteoporosis research by choosing those having top (366 controls) and bottom (367 cases) bone mineral density (BMD) values at the total hip.²³

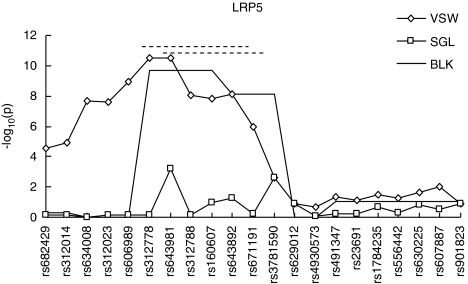
In our analyses, we used the three proposed strategies to perform association analyses between BMD statuses and the LRP5 gene. Haplotype frequencies for this sample were estimated through EM algorithm.²⁴ We also conducted 10 000 permutations to obtain the empirical P-values based on the studied sample. The results are summarized in Figure 3. The most significant association signals were obtained at rs312778 and rs643981 (−log₁₀P=10.48, empirical P<0.0001) by VSW. Block 3 consisting of four SNPs (rs312778, rs643981, rs312788, rs160607) defined by BLK captured less significant association results (−log₁₀P=9.70, empirical P=0.0001). SGL strategy only achieved the smallest P-value of 0.0006 at rs643981 (empirical P=0.0049). These findings are much more significant than those from Xiong et al,²³ in which BMD was treated as a quantitative trait.

Figure 3.

Association results obtained by each of the three proposed strategies between the LRP5 gene and hip BMD. The x axis shows the tested SNPs and the other figure legends are the same as those in Figure 1. The two dashed lines on top indicate the covering region of the best windows for VSW.

Discussion

We implemented and investigated a strategy of exhaustively testing haplotypes based on VSW to detect disease association. We compared the performance of this approach with those using BLK and SGL through both a range of simulated conditions and an empirical data analysis. To the best of our knowledge, this is the first study to demonstrate that under a variety of simulation conditions, the statistical power of VSW is uniformly greater than both BLK and SGL, in the framework of standard χ² statistics. This suggests that the VSW strategy might gain potential valuable association results, which could be missed by using SGL or BLK. Therefore, with available genotypes for dense markers, the VSW mapping is strongly recommended to capture the greatest number of significant signals.

As genome-wide association studies on complex disease become increasingly visible, the VSW strategy for haplotype association mapping can be ideally used for replication, follow-up, and fine mapping of previously identified genomic regions of interest. A common finding in genome-wide association studies is to have only a small number of SNPs or block regions that exceed the specific significance level (ie, 10⁻⁷). However, many of the less significant but suggestive markers or regions are usually ignored because of their lack of statistical significance. This raises the possibility of missing certain causal loci due to a failure to use the best window size for constructing the test. Based on the findings of the current study, the application of the VSW strategy is highly recommended for additional haplotype association analyses around such suggestive regions in a genome-wide association study.

Compared with the BLK/SGL approach, VSW has its own advantages. First, VSW in nature has the advantages of both single-marker analyses and haplotype analyses. Second, VSW does not require a priori knowledge of the most appropriate haplotype window size for detecting a susceptibility site. Rather, it examines haplotypes in each sliding window of varying size. If the susceptibility loci are detectable in the study sample, exhaustively testing based on VSW of all possible sizes over a genomic region is most likely to discover the optimum markers or regions that are significantly associated with the study traits. Third, it also does not require prior knowledge of the LD structure, which is a requirement of BLK for haplotype block partition, thus avoiding the potential problems of haplotype block boundaries. With considerable haplotype variation among global populations²⁵ because of locus-specific factors (recombination, mutation, and gene conversion) as well as population-specific factors (recent migration and admixture, expansions and bottlenecks and random drift),²⁶ VSW is helpful for association mapping of complex diseases in those isolated populations without proper reference LD structure in the International HapMap data.²⁷

The power gain for VSW over lower LD regions is reasonable. According to common application, we used indirect association mapping strategy in our simulation study. The genotype information of the causal locus was removed and thus was unavailable to analysis methods. In lower LD region, SGL has very low detection power because single marker carries very little information about the causal locus. BLK in low LD region will identify limited small haplotype blocks, which may not cover the causal locus at all. For VSW, it tests all the possible windows in the region and will always cover the causal locus. This may help VSW gain more power over low LD regions. However, we realize that all the methods are far from powerful in low LD regions.

Although VSW is a more powerful test, using it to estimate large haplotypes with multiple SNPs (ie, EM algorithm) may be fraught with delays due to a heavy computation load and limitations of computer memory, because the analysis grows exponentially with the number of loci. For whole genome, or a chromosome, exhaustive searching with the window size as big as that of a chromosome is impossible. A question is raised regarding how to decide the maximum window size to balance between the detection power and the computational complexity. One choice is to preset the maximum window size, larger than that chosen by Cheng et al,^{9, 10} possibly up to 500 kb, as most LD blocks are less than 500 kb.²⁸ However, as LD patterns are expected to vary widely across genome regions, this pre-fixed maximum window size may cause problems where there are too many haplotypes in a hot-spot region. At the time of this writing, Li et al²⁹ suggested a method to decide the maximum window size based on the local haplotype diversity and the available sample size. To minimize the computation load and maximize the feasibility of VSW for whole genome association, we suggest the following strategies: first carry out a preliminary SGL/BLK analysis for the whole genome; then, select those loci with suggestive signals (eg, P<10⁻³) and determine the maximum window sizes for each region according to Li et al,²⁹ that is, the number of distinct haplotypes in a window should be no greater than the sample size; and finally limit VSW analysis to these regions. The initial scan of whole genome association may potentially miss some signals. It is a problem faced by many current analysis methods for GWAS. Without a better choice, we would focus on those most likely regions with suggestive evidences, such as P<10⁻³. Our proposed VSW strategy may thus be better suited for replication, follow-up and fine mapping particular genomic regions of interest.

To illustrate that the proposed method is computationally practical, we assessed the CPU time required by the program in simulation and empirical data analyses. All the analyses were carried out on a computer with Intel® Pentium® 4 3.4 GHz dual processors and 2.0 GB RAM. It took ∼3.2days (76 h 40 min) for VSW to complete simulation analyses for all 20 simulated scenarios (including power and critical values analyses) and 1 h 55 min for the empirical data set analyses (including 10 000 permutations to get the empirical P-values). That is, an average of ∼0.69 s (76 h 40 min divided by 20 simulation combinations and 20 000 simulation replicates) is required to analyzing one set of simulated data. This indicates that the computation time required for simulation and empirical data analyses is acceptable, and thus our method is practical for association analyses in the field of candidate gene/region. Furthermore, with improvements in computer technology, computationally efficient methods such as parallel programs that are widely used in many scientific fields (ie, multiple eQTL/QTL interval mapping) can be applied. Distributing the heavy computing load into clustered processors is another alternative approach, which can significantly reduce the computing time, making tasks such as exhaustively searching sliding windows feasible.

To address the multiple-testing problem, which is still a challenge in genome-wide association studies; we performed a large number of simulations under the null distribution to determine the expected significance threshold for our simulated region. The Bonferroni correction for multiple testing is usually too conservative in the presence of correlated markers. Another option is to use the permutation for each replication. For VSW, the computational cost becomes a problem in a huge number of permutations for large numbers of simulation replications. Fortunately, in experimental practice, the considerable amounts of permutations are relatively easy to carry out to obtain empirical P-values for the studying sample (eg, we did permutations for our experimental data), as implemented in several association mapping programs, for example, PlINK.³⁰ To make power comparison, we utilized simulations under the null hypothesis to determine the empirical critical values for each proposed method, keeping the false-positive error rates under the region-wide level (α=0.05).

The VSW strategy can be easily extended to other haplotype association mapping algorithms. In recent years, extensive efforts have been devoted to exploring a number of statistical methods for association analysis.¹ The VSW strategy implemented in this study is in terms of the most natural χ² statistic, which is commonly used in genetic association literature. A more efficient association method could be incorporated straightforward into an association mapping strategy based on sliding windows. For example, haplotype clustering methods were proposed for dealing with low frequency concern and reducing the haplotype dimensionality.³¹ Moreover, an approach has been suggested to quantitatively incorporate existing information of SNPs (conservation, functional category, linkage, and so on) into the analysis to enrich the association signal.³²

In summary, the haplotype association mapping strategy based on VSW outperforms the other two approaches in both our simulated studies and an experiment data set, with an expense of higher computation cost. With rapid advances in computation technology, the application of VSW is feasible for large genomic regions or those regions preliminarily identified by the traditional SGL/BLK methods. With the promise of genome-wide association studies for revealing genetic mysteries that underlie complex diseases, such improvements are therefore necessary and welcome.