Density and architecture have greater effects on the toughness of trabecular bone than damage

Abstract

Bone damage has been cited as an important aspect of bone quality. As such, understanding the effects of damage on the toughness of trabecular bone should provide insight into trabecular bone behavior during energy-limiting cases, such as falls. The effects of damage on the toughness of 35 bovine trabecular bone specimens was studied. Damage was induced by compressing the on-axis specimens to either 1.5% or 2.5% strain, followed by compression to 7.5% strain. The overloads resulted in significant decreases in both modulus and elastic toughness, with significantly greater decreases for the high-damage group than the low-damage group. Following damage, the elastic toughness of the high-damage group was also lower than the undamaged elastic toughness of the control group. In contrast, there was no detectable effect of damage level on toughness measured to 7.5% strain. Toughness increased linearly with BMD (R² = 0.50) and by a power law relationship with volume fraction (BV/TV) (R²=0.65). Microarchitectural parameters also predicted the toughness in the absence of BV/TV or BMD. Toughness decreased with increasing slenderness ratio (Tb.Sp/Tb.Th) and structure model index (SMI) (R²=0.68, multiple regression), again independent of damage level, suggesting that failure is influenced by trabecular buckling. Taken together, the results show that normal variations in toughness due to density and architecture dominate the changes due to damage at the levels induced in this study. Moreover, measuring toughness is sensitive to the final strain, as differences found in the elastic and initial plastic regions were undetectable at higher strains. The self-limiting nature of microcracks in trabecular bone, or the trabecular architecture itself, may inhibit microcracks from propagating to macroscopic trabecular fractures, thereby limiting the effect of damage on toughness and making it difficult to detect in comparison to normal population variability.

Introduction

Osteoporosis is a skeletal disease characterized by low bone mass and architectural deterioration that leads to decreased bone strength and increased fracture risk [1]. Bone mineral density (BMD) is the standard clinical measure to quantify fracture risk. However, BMD, as measured by DEXA, identifies only half of incident osteoporotic fractures [2]. As such, several other factors, often referred to as bone quality [3], must affect fracture risk. Material properties, collagen and mineral chemistry, and microarchitecture have all been suggested [4]. Another commonly cited aspect of bone quality is the microdamage burden. Microdamage occurs in vivo in the trabecular bone of vertebral bodies [5, 6] and femoral heads [7, 8]. Degradation of the tissue mechanical properties by microdamage incurred during a fall could also play a role in the reported increase in fracture risk following non-fracturing falls [9] or in so-called spontaneous fractures [10].

Microdamage can be induced experimentally by overloading, and is associated with modulus reductions. The mechanical properties of bovine [11–13] and human [14, 15] trabecular bone degrade when overloaded. For example, the elastic modulus of bovine trabecular bone decreased when strains ≥ 1.0% were applied, and the strength decreased for strains exceeding 2.5%, independent of initial modulus [11]. In human trabecular bone, the relative strength reduction was greater for specimens with lower apparent densities [14]. On-axis compressive overloads caused transverse modulus reductions of 35% in vertebral trabecular bone [15], and shear modulus reductions of 2.47% in bovine tibial trabecular bone [16], indicating a dependence on loading orientation and mode. Modulus degradation is a direct measure of mechanical damage [17, 18], which is related to microdamage accumulation in the bone tissue [12, 13, 19]. Microcrack density increases exponentially with increasing modulus reduction, and individual trabeculae begin to fracture at 2% applied strain [13].

While the strength and modulus of trabecular bone and their relation to density and damage have been studied, toughness has received less attention. Toughness represents a material’s ability to absorb energy, and could be a relevant measure of bone’s ability to withstand fracture during falls, which are energy-limited. The damage formation process acts as a toughening mechanism in human and bovine cortical bone [20]. However, pre-existing damage in canine ribs had a negative effect on the toughness in 3-point bending [21]. Indeed, a mechanically damaged material, all other things being equal, must have a lower toughness than the equivalent undamaged material. The goal of this study was to investigate the role of pre-existing microdamage in determining the toughness of trabecular bone along its principal mechanical axis. Specifically, the aims were to: 1) induce damage in trabecular bone samples; 2) compare the toughness of undamaged and damaged trabecular bone samples in uniaxial compression; and 3) quantify the relative effects of damage, density, and architecture on toughness.

1. Materials and methods

1.1. Specimen Preparation

Thirty-five on-axis cylindrical specimens were prepared from the proximal metaphyses of 22 bovine tibiae (approximately 2 years old). The axis of each specimen was aligned with the principal mechanical axis using micro-CT imaging combined with finite element analysis [22]. Briefly, a parallelepiped was cut from the bone and scanned at 30 μm resolution in a micro-CT scanner (μCT-80, Scanco Medical AG, Bassersdorf, Switzerland). The images were converted to micro-finite element models, which were used to find the principal mechanical axes [23]. A custom jig was used to align the sample, and a diamond coring drill (Starlite Industries, Bryn Mawr, PA) was used to cut a cylindrical sample aligned with the calculated principal mechanical axis. On average, the cylindrical axes of the specimen were only 7.32 ± 3.24° (mean ± SD) from the principal fabric orientations with a median of 7.56°. The mean diameter and gage length of the specimens were 8.06 ± 0.17 mm and 22.12 ± 3.21 mm, respectively.

Prior to testing, the trabecular architecture of the specimens was quantified. The specimens were scanned by micro-CT at 20 μm isotropic resolution while saturated in buffered saline. The scanning time was approximately one hour. Architectural parameters were computed using a model free method (μCT Evaluation program V4.3, Scanco Medical AG, Bassersdorf, Switzerland) (Table 1). The tissue bone mineral density (BMD_Tissue), which excludes the marrow space, and the apparent level BMD were measured using the scanner’s calibration [24].

Table 1.

Trabecular density and architecture of the specimens quantified using micro-CT (n=30).

Parameters1	Mean	SD	Range
BMD (g-HA/cc)	0.189	0.068	0.049 – 0.326
BMDTissue (g-HA/CC)	0.872	0.027	0.822 – 0.931
BV/TV	0.244	0.058	0.147 – 0.376
Tb.N (mm−1)	1.501	0.136	1.199 – 1.856
Tb.Th (mm)	0.186	0.037	0.139 – 0.278
Tb.Sp (mm)	0.589	0.059	0.452 – 0.767
Tb.Sp/Tb.Th	3.324	0.628	2.202 – 4.802
SMI	0.922	0.499	0.046 – 1.924
Conn.D, (mm−3)	7.045	2.587	3.052 – 14.497
DA	2.092	0.417	1.314 – 3.088

¹BMD = bone mineral density, BV/TV= volume fraction, Tb.N = trabecular number, Tb.Sp = trabecular separation, Tb.Th/Tb.Sp = slenderness ration, SMI = structure model index, Conn. D. = connectivity density, and DA = degree of anisotropy. BMD and BMD_Tissue were measured on the total volume and bone tissue volume, respectively.

The samples were tested using techniques to minimize end artifacts. They were fixed in brass endcaps using cyanoacrylate glue (Prism 401, Loctite, Newington, CT) [25]. The effective gage length was taken as the exposed length plus one-half of the embedded length of the specimen for all strain measurements [25]. The marrow was removed to facilitate gluing, but this should not affect the mechanical properties at the strain rates studied [26]. The prepared specimens were wrapped in gauze saturated with saline, and stored at −20°C in airtight containers until mechanical testing.

1.2. Mechanical Testing

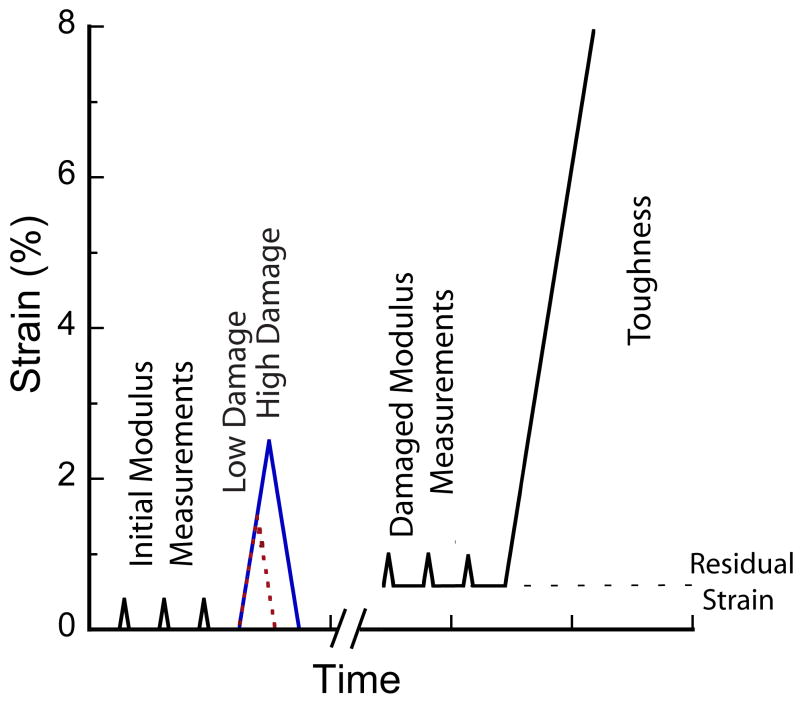
Specimens were assigned to one of three groups for testing based on apparent density (p=0.75, ANOVA). Group I was a control group (n=12), while groups II (n=12) and III (n=11) were low-and high-damage groups, respectively. Three nondestructive compressive loads to 0.4% strain were applied to measure the initial elastic modulus (E_i). Samples in groups II and III were then overloaded to either 1.5% (low) or 2.5% (high) strain, then returned to zero load. These strains produce significantly different levels of mechanical damage in this type of bone, as measured by modulus reduction [13]. Three additional non-destructive load cycles were applied to measure the damaged modulus (E_d) in groups II and III. To avoid unintended damage, group I was not subjected to these modulus measurement loads or a sham overload. Finally, all specimens were destructively loaded to 7.5% strain (Fig. 1).

Figure 1.

Testing protocol for overloading specimens in uniaxial compression. Following the overload, the samples were unloaded to zero force resulting in a residual strain, which was the baseline strain for subsequent modulus and toughness measurements, indicated by the horizontal dashed line. To avoid unintentional damage, the control group was subjected to only the three modulus measurements and the final load to failure.

All tests were performed at room temperature using an Instron model 8821s biaxial servo-hydraulic load frame (Instron Corp., Canton, MA) under strain control at a strain rate of 0.5% s⁻¹. Data were collected at 100 Hz. Specimens were kept hydrated at all times by wrapping in gauze saturated in buffered saline around the exposed length of the specimen.

The data were processed to determine the relevant mechanical properties, after noise reduction with a low pass filter (GCVSPL) [27]. The moduli were calculated from the derivative of quadratic curve fits from 0.0% to 0.2% strain at zero load on the stress-strain curves [28] and averaged for three loading curves. This method has been shown to be more precise than a linear fit to a portion of the stress strain curve [28]. The relative reduction between the undamaged and damaged modulus was used as a macroscopic measure of damage [29]. The undamaged and damaged strengths were determined by the local maximum value of stress reached during overloading and failure, respectively. The yield point was determined by the 0.2% offset method.

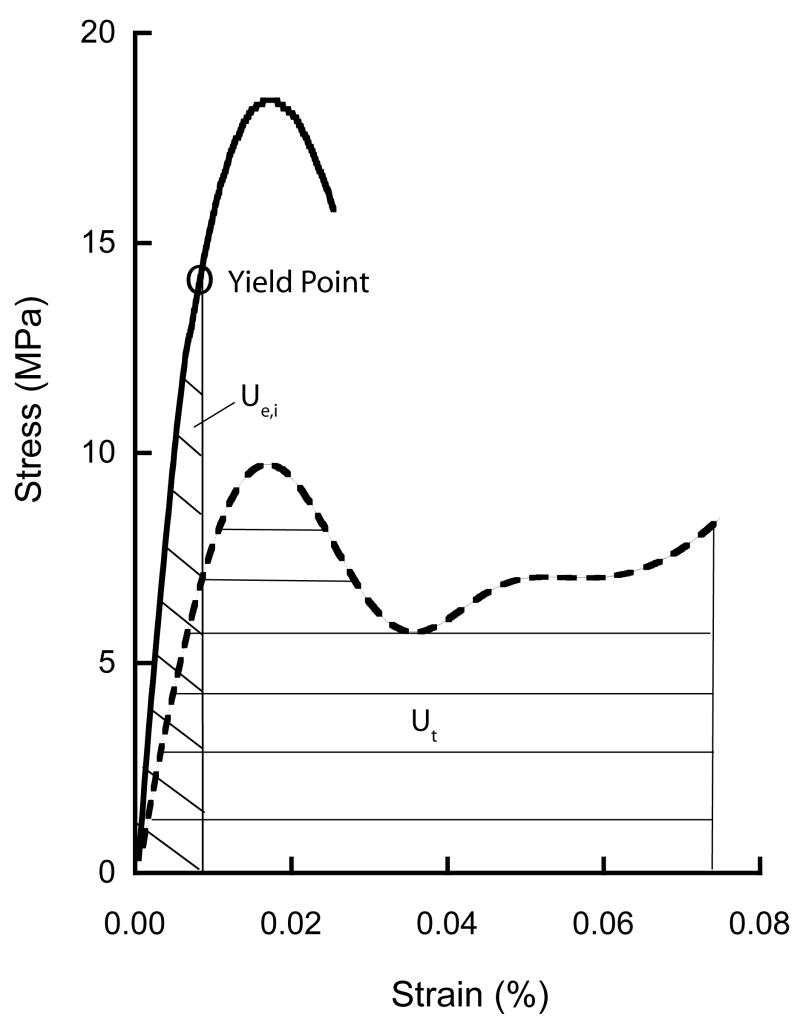
The initial and damaged elastic toughness (U_e,i and U_e,d, respectively) were calculated as the area under the stress-strain curve to the yield point. Toughness was also calculated to 7.5% strain (U_t) (Fig. 2). Toughness was calculated using the trapezoid rule, summing at constant intervals of 0.01% strain. Linear and power law regressions were used to determine the dependence of toughness on density and architectural parameters.

Figure 2.

Representative curve of stress-strain behavior for typical on-axis specimen subject to initial overload of 2.5% strain (solid line) and then to failure of 7.5% strain (dashed line). The initial elastic toughness (U_e,i) and toughness to 7.5% strain (U_t) are indicated by shading on the graph. U_e,i was measured using the yield strain based on the 0.2% offset method.

Statistical analysis was performed with JMP IN 5.1 (SAS Institute Inc., Cary, NC), with a significance level of 0.05. Comparisons between groups were made using ANOVA with Tukey’s post-hoc test. The mechanical properties were compared by ANCOVA to account for dependence on the architecture, density or modulus.

Five specimens were lost during mechanical testing. One specimen fractured prematurely when the extensometer slipped, and four specimens were not properly embedded.

2. Results

On average, the initial modulus (E_i) for all specimens was 1682 ± 691 MPa (mean ± SD), independent of group (p = 0.22, ANCOVA with BV/TV as covariate) (Table 2). The low overload resulted in relative modulus reductions for 9 of 10 specimens and the high overload for 10 of 10 specimens. One specimen in the low-damage group had a small increase in modulus (< 2%) but was included in the analysis, because no error in the preparation or testing could be identified. On average, the modulus decreased 9.65 ± 7.66% in the low-damage group compared to 19.47 ± 11.17% in the high-damage group (p = 0.03, ANOVA, Fig. 3a), independent of BMD and architecture (p > 0.07, ANCOVA). The secant modulus, defined as the quotient of the stress at maximum strain and the maximum applied strain during the overload [13], decreased by 50.8 ± 11.8% and 70.4 ± 6.4%, on-average, in the low-and high-damage groups, respectively (p = 0.0002, ANOVA).

Table 2.

Initial and damaged strength (S_i, S_d), modulus (E_i, E_d), elastic toughness (U_e,i, U_e,d) and toughness to 7.5% strain (U_t) of bovine trabecular bone subject to three prescribed damage levels (mean ± SD). P-values are based on ANCOVA between groups with initial modulus (E_i) as a covariate (unless otherwise noted). Levels not connected by the same letter are significantly different.

	Control	Low Damage	High Damage	Average	P
Ei (MPa)	1497 ± 6191	1710 ± 822	1537 ± 644	1682 ± 691	0.222
Ed (MPa)	1497 ± 618	1586 ± 836	1453 ± 467	1512 ± 638	0.422
Si (MPa)	11.21 ± 3.461	---	15.36 ± 6.42	13.28 ± 5.45	0.19
Sd (MPa)	11.21 ± 3.46	10.91 ± 4.99	11.61 ± 5.30	11.24 ± 4.50	0.20
Ue,i (mJ-mm−3)	0.031± 0.0081	0.033 ± 0.012	0.050 ± 0.023	0.038 ± 0.018	0.08
Ue,d (mJ-mm−3)	0.031 ± 0.008A	0.024 ± 0.012AB	0.022 ± 0.011B	0.025 ± 0.011	0.02
Ut (mJ-mm−3)	0.593 ± 0.21	0.565 ± 0.26	0.639 ± 0.22	0.599 ± 0.23	0.32

¹The initial strength and modulus for the control group were also used as the damaged values to allow for correlations across groups. However, only one modulus, elastic toughness, and strength measurement were performed on the control group.

²BVTV was used as the covariate for ANCOVA of the modulus measurements.

Figure 3.

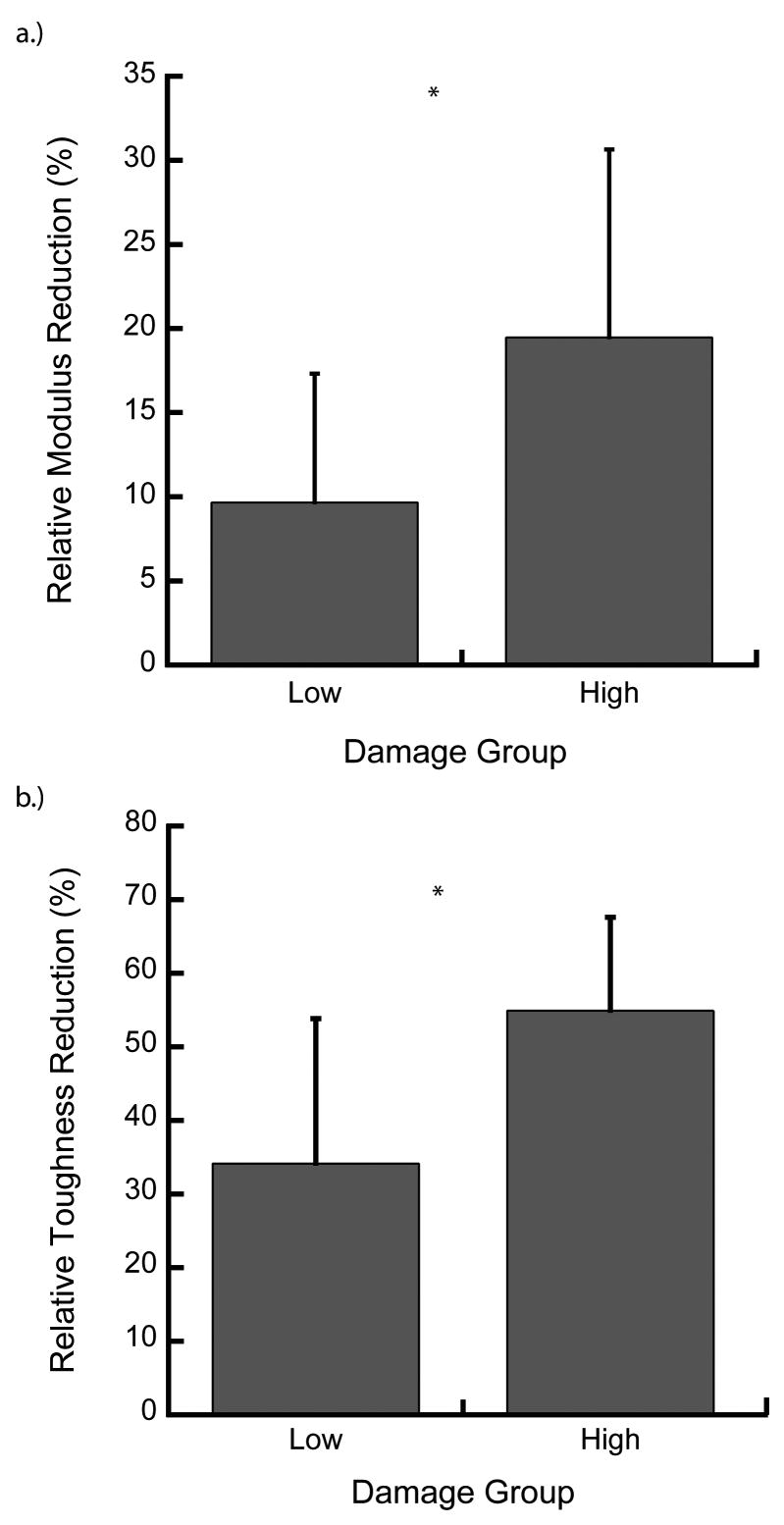
The relative modulus (a) and elastic toughness (b) reductions were greater in the high- vs low-damage group (*p < 0.04). The modulus increased for one specimen in the low-damage group, but the mean modulus and elastic toughness decreased for both the low-and high-damage groups (paired t-test). Error bars are one S.D.

The overloads decreased the strength of the samples. During the initial overload, the ultimate strength was only reached for specimens in the high-damage group (Fig. 2). In this group, the strength decreased by 24.75 ± 13.98% (p = 0.0009, paired t-test), independent of BMD or architecture (p > 0.60, ANOVA). Although the specimens in the low-damage group did not reach their ultimate strength during the overload, seven of ten reached a higher maximum stress during the overload than during the final failure load, indicating that the ultimate strength before damage would have been higher. The average maximum stress was 6.25 ± 15.46% higher than the ultimate stress following damage. Only two of 30 specimens were completely fractured at 7.5% compressive strain.

On average, the damaged elastic toughness (U_e,d) was smaller compared to the initial elastic toughness (U_e,i) in both the low- and high-damage groups. After overloading, the elastic toughness decreased from 0.033 ± 0.012 to 0.024 ± 0.012 mJ/mm³ and from 0.050 ± 0.023 mJ/mm³ to 0.022 ± 0.011 mJ/mm³ in the low- and high-damage group, respectively (p < 0.01, paired t-test, Table 2). The relative reduction in the elastic toughness of the high-damage group was greater than the low-damage group (p = 0.01, ANOVA, Fig. 3b).

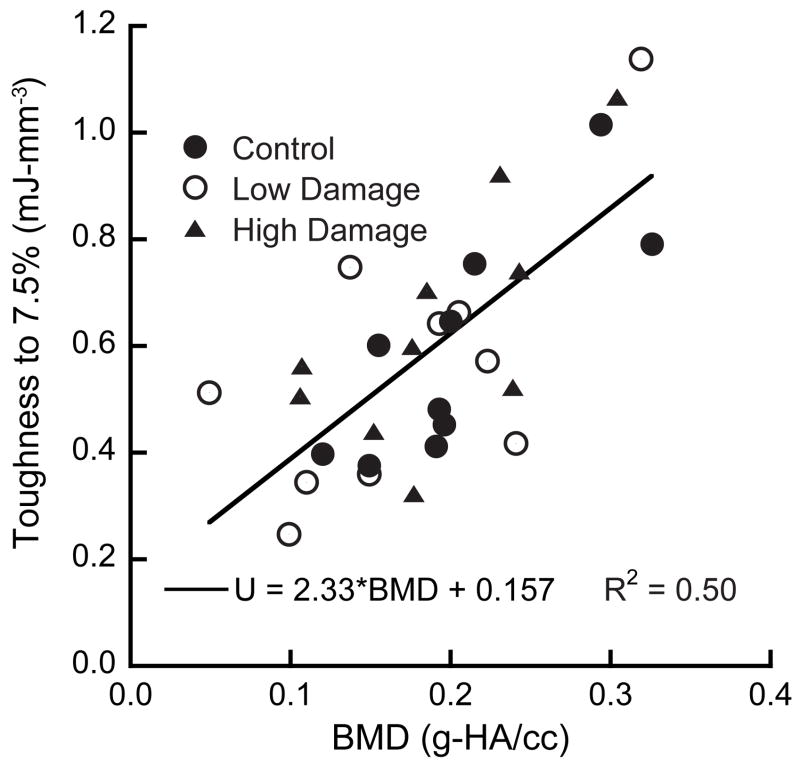
The measured toughness to 7.5% strain (U_t) increased linearly with increasing BMD (R² = 0.50, p < 0.001) and nonlinearly with increasing volume fraction (BV/TV) (R² = 0.65, p < 0.001, power law regression, Fig. 4). U_t did not depend on the damage level (p=0.58, ANCOVA, with BMD as a covariate). Post-hoc power analysis showed that an additional 45 samples per group would be necessary to detect differences between groups.

Figure 4.

Toughness to 7.5% compressive strain (U_t) increased with increasing BMD (p < 0.001) independent of damage level (p = 0.58).

U_t was correlated to a number of architectural measures. Toughness increased with BMD_Tissue (R² = 0.13, p < 0.05), trabecular thickness (Tb.Th) (R² = 0.53, p < 0.001) and degree of anisotropy (DA) (R² = 0.25, p = 0.005). U_t decreased with structure model index (SMI) (R² = 0.61, p < 0.001) and slenderness ratio, which was defined as the ratio of Tb.Sp/Tb.Th (R²=0.59, p < 0.001, Table 3). This ratio is analogous to the slenderness ratio in the Euler buckling formulae, and was used to detect increased susceptibility to buckling.

Table 3.

P-values, coefficients of determination, and slopes from linear regression (unless otherwise noted) relating architectural parameters to toughness.

Parameters	Linear Regression	Multiple linear regression
BMD (g-HA/cc)	p < 0.0001
	R2 = 0.49	---
	Slope = 2.33
BMDTissue (g-HA/cc)	p < 0.05
	R2 = 0.13	---
	Slope = 2.97
BV/TV	p < 0.0001
	R2 = 0.65*	---
	---
Tb.N. (mm−1)	p = 0.88
	---	---
	---
Tb.Th. (mm)	p < 0.001
	R2= 0.53	---
	Slope = 4.61
Tb.Sp. (mm)	p = 0.27
	---	---
	---
Conn.D. (mm−3)	p = 0.25
	---	---
	---
DA	p = 0.005
	R2= 0.25	---
	Slope = 0.27
Tb.Sp/Tb.Th	p < 0.001	p = 0.03
	R2= 0.59
	Slope = −0.28	Slope = −0.14
SMI	p < 0.001	p = 0.01
	R2= 0.61
	Slope = −0.37	Slope = −0.22

Significant values are bold.

^*indicates power law relationship: U_t = 3.46*BV/TV^1.27

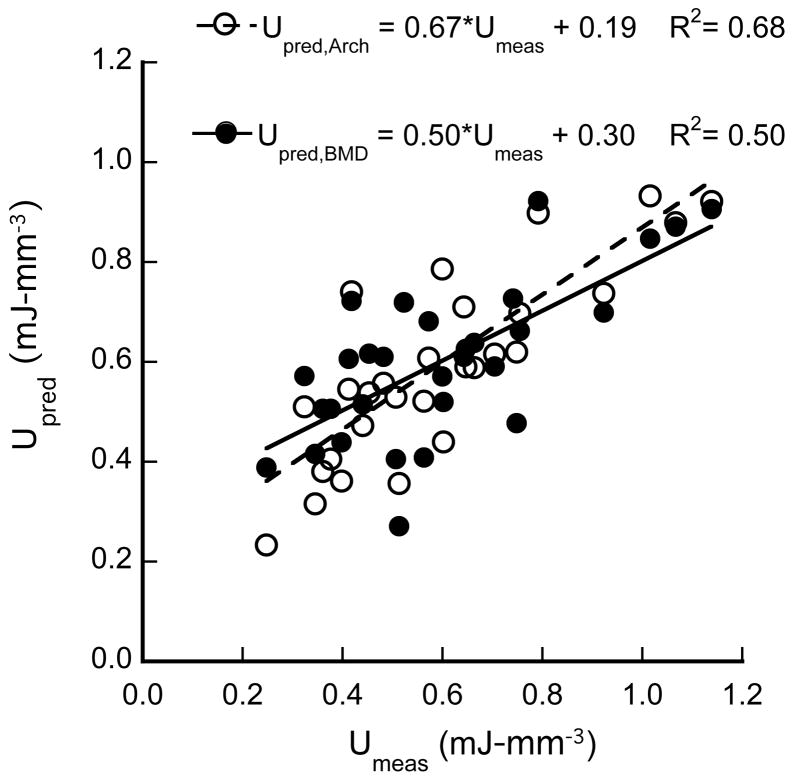
To determine whether combinations of architectural parameters also played a role in toughness, multiple linear regression was used. Two parameters that could mechanistically explain trabecular collapse were considered: slenderness ratio and SMI. Trabecular number (Tb.N) was not considered because it is highly correlated to Tb.Sp (p < 0.001). Similarly, connectivity density (Conn.D.) was correlated to both Tb.Sp (p = 0.0001) and Tb.Th (p = 0.01), while DA was correlated to Tb.Th (p = 0.0002) and SMI (p = 0.004). Therefore, only SMI, Tb.Sp, and Tb.Th were included with the latter two combined as the slenderness ratio. The toughness depended on both the slenderness ratio (p = 0.03) and SMI (p = 0.01) (R²=0.68, Fig. 5). The multiple regression resulted in an R² value greater than that for the univariate regression with BV/TV as well as BMD.

Figure 5.

Multiple regression with microarchitectural parameters resulted in a higher R² value than BMD alone when predicting the toughness of trabecular bone. U_pred,Arch = −0.22*SMI − 0.14*Tb.Sp/Tb.Th + 1.27 and U_pred,BMD = 2.33*BMD + 0.157.

3. Discussion

Understanding the effects of damage on the failure behavior of trabecular bone is important for elucidating its role in osteoporosis and age related fragility. Microdamage accumulation has been associated with a degradation of material properties, but its role in fractures is not fully understood. As such, we sought to establish the relative effects of BMD, architecture, and damage on the toughness of trabecular bone. Because of the destructive nature of the tests, we did not directly measure microdamage, but instead used modulus reduction as a surrogate. The toughness of samples was dependent on the bone mineral density and on architectural parameters. In contrast, damage did not measurably affect the toughness to failure for on-axis loading, regardless of the magnitude of modulus reduction. Although the damaging loads decreased the modulus, strength, and elastic toughness, the overall toughness was primarily determined by the total strain to failure. This indicates that the normal variations in toughness due to density and architecture of trabecular bone are greater than the changes due to damage at the levels induced in this study. The effects of damage on toughness may be limited because formation of new damage dominates the propagation of existing microdamage in trabecular bone [12, 13].

There are several notable strengths of this study. First, it considered the effects of damage on toughness, rather than strength. Because toughness represents a material’s ability to absorb energy, the data provide better insight into the relative roles of the effects of damage and architecture on fractures due to falls, which are energy-limited. Second, the two strain levels were selected to induce damage to two levels to quantify the effects of damage and were based on reported data of trabecular bone yield and ultimate strains [13]. These strain levels have been shown to produce damage levels consistent with in vivo damage in human bone [12], and the presence of damage was verified by the decreases in modulus and elastic toughness. Finally, well-validated testing methods were used to ensure precision of measurements [25, 28].

There are also several limitations to our experimental protocol that should be considered when interpreting the data. First, the specimens were taken from a single anatomic site with limited architectural variability. Additionally, the bone was taken from young animals and may not represent the aging human skeleton. However, the use of this bone eliminated the confounding effects of pre-existing damage and heterogeneity of mineralization, which would be unavoidable in human bone. The toughness was measured at a strain to 7.5% rather than to overt fracture. Indeed, only two of the 30 specimens actually fractured at this strain level. Moreover, identifying the fracture point during testing or by analyzing the data was inconsistent. We also investigated the differences in toughness measured to the ultimate strain (data not shown) and found no difference between overload and failure curves in the high-damage group. The lack of direct histological measurements to quantify the microdamage is also a limitation. However, based on existing literature, the level of microdamage in both damage groups would be expected to be greater than in the control group, as young bovine bone has almost no in vivo microdamage [12, 13, 19] while microdamage increases with increasing modulus reduction [13]. Finally, this study focused on damage in excised trabecular bone specimens. However, it is also important to understand the role of microdamage on the failure behavior of the whole bone at any anatomical site. The surrounding trabecular network and the cortical shell will also play a role in whole bone fracture. This study provides data that could be incorporated into such whole bone studies.

Measuring toughness in trabecular bone is sensitive to the protocol used. Although the elastic toughness significantly decreased following overloading, the toughness measured to the ultimate strain did not. Decreases in the ultimate stress were accompanied by increases in ultimate strain, resulting in no overall change in toughness to the ultimate stress. This suggests that changes in trabecular bone toughness measurements occur primarily in the elastic and initial plastic ranges, prior to the ultimate strain. Given the relatively small effects of microdamage on toughness to the ultimate and higher strains, the role of microdamage in trabecular bone quality may primarily be in the elastic behavior and its affect on stress redistribution in the whole bone.

Architectural parameters can provide insight into the mechanisms of trabecular bone toughness, but the effects can be obscured by those of BV/TV, which is highly correlated to several relevant architectural parameters. We found that SMI and trabecular slenderness were the key architectural features to determine toughness. The sensitivity of the toughness to each parameter was quantified by substituting the mean values into the relationships and varying each parameter by one standard deviation. A one standard deviation increase in BV/TV and BMD resulted in a 31.0% and 27.4% increase in toughness, respectively. Toughness was similarly sensitive to changes in slenderness, with a one standard deviation decrease resulting in a 18.3% increase in toughness, while a decrease in SMI led to a 16.2% increase in toughness. In contrast, the decrease in elastic toughness due to damage averaged 34.2 ± 19.7% and 54.9 ± 12.7% for the low- and high-damage groups, respectively.

Together, SMI and slenderness ratio can be interpreted in the context of cellular solid modeling [30]. Decreasing trabecular slenderness results in plastic yielding of the trabeculae rather than buckling [30], and hence a greater energy absorption. Similarly, lower SMI indicates a transition to a network of plates, which are subject to buckling along a single axis whereas rods are less constrained. In large-deformation finite element analysis of human trabecular bone, such a transition from plates to rods was the primary factor mediating the failure mechanisms of trabecular bone [31].

Mechanical damage, rather than microdamage, was used to differentiate between groups in this study. However, propagation of microcracks into trabecular fractures would be one expected mechanism of toughness degradation. As such, variability in microdamage levels within groups may have affected the outcome. Microdamage increases with increasing SMI, decreasing BV/TV, and decreasing Tb.Th in both mechanically damaged bovine trabecular bone [12] and in human vertebral trabecular bone [32]. These same variables affected the toughness in this study. However, even after correcting for these parameters, the effects of damage level were not detectable between groups. As such, accounting for the mechanical effects of microdamage using population-based studies may prove difficult, and highly controlled experimental designs are needed to reduce these effects.

The modulus reductions found in this study were lower than previous reports. Modulus reductions in bovine tibial trabecular bone compressed to 1.5% and 2.5% strain were 38.5% and 64.7%, respectively [11], compared to 9.6% and 24.3% here and in previous studies from our lab [12, 16]. These differences are in part due to the method used to determine the modulus in this study [28] compared to earlier work [11, 33]. Moduli measured from the initial slope of the stress strain curve are consistently higher than those measured using linear fits, and reflect the nonlinear elastic behavior of trabecular bone [28]. When the secant modulus at the end of overloading was used, as in previous studies [11, 13], the modulus reductions were comparable.

The results complement a recent study where overloads did not significantly affect the strength or toughness of human vertebral trabecular bone in orthogonal loading directions [15]. Similarly, we found that the ultimate strengths following damage were not significantly different between damage groups. Likewise, the damaged toughness measured to the ultimate strength was not significantly different between groups. However, in contrast to our results, these authors reported that on-axis toughness was correlated with Tb.N but not SMI, Tb.Th, or DA [15]. This may be attributed to the larger range of architectural parameters in our specimens. For example, the variation in SMI in these samples was over two times larger than in the samples studied by Badiei [15], which allows for stronger correlations. In addition, differences in tissue level behavior between aged human and young bovine trabecular bone may play a role.

In an in vivo study, treatment with raloxifene for 12 months increased the microdamage burden in dogs, indicated by a significantly higher mean crack length versus the control group. However, the toughness was unchanged or higher compared to controls in canine vertebral and femoral trabecular bone, respectively [34, 35]. These results are consistent with the present findings that density and architecture are the primary contributors to trabecular bone toughness.

Taken together, the data provide insight into the mechanisms of fracture risk reduction by anti-resorptive treatments. Although these agents are known to increase the microdamage burden [36–39], they also increase bone mineral density [37, 40–42] and prevent degradation of architecture [36, 43]. For example, microdamage levels of 2.9 and 3.7 times that of controls were found in dogs treated with clinically relevant doses of risedronate and alendronate, respectively, which are similar to the effects reported in humans [44]. After normalizing for volume fraction, there was no significant difference in toughness between the treatment and vehicle groups, although the alendronate group tended toward significant differences in toughness [35]. In a more recent study, the energy to failure as a function of BMD was lower in alendronate treated dogs than in control or risedronate treated dogs [45]. As such, toughness may begin to decline at higher microdamage burdens. Moreover, the affects may be different in osteoporotic bone due to degradation of architecture and density. As such, additional controlled studies are warranted.