Ising-like dynamics in large-scale functional brain networks

Abstract

Brain “rest” is defined -more or less unsuccessfully- as the state in which there is no explicit brain input or output. This work focuss on the question of whether such state can be comparable to any known dynamical state. For that purpose, correlation networks from human brain Functional Magnetic Resonance Imaging (fMRI) are constrasted with correlation networks extracted from numerical simulations of the Ising model in 2D, at different temperatures. For the critical temperature T_c, striking similarities appear in the most relevant statistical properties, making the two networks indistinguishable from each other. These results are interpreted here as lending support to the conjecture that the dynamics of the functioning brain is near a critical point.

I. Introduction

The human cerebral cortex is organized as a very complex network comprising approximately 10¹⁰ interconnected neurons. Thanks to the impressive progress in brain imaging techniques given by the development of positron emission tomography and functional Magnetic Resonances Imaging (fMRI) an increasing amount of spatiotemporal brain data is now available. The analysis of this large and complex information is of such unprecedented magnitude that conceptual approaches grounded in statistical physics are needed[1].

Recently, and departing from the tradition of using stimulus-response techniques, the study of brain imaging dynamics “at rest”, have received ample attention[2–5]. Brain “rest” is defined -more or less unsuccessfully- as the state in which there is no explicit brain input or output. The analysis of experiments under such quasi-stationary state revealed an active network of brain areas engaged during the resting state. Typically, these areas are active during rest, and they deactivate immediately when the subject engages in any minimal cognitive task; for example when asked to visually track a moving object on a screen. This evidence, now expanded by other studies, indicates the existence of a so-called brain “resting state network” or also “default mode network” in which several cortical regions are activated on a complex dynamical interaction[2]. Results from brain imaging experiments as well as graph theory analysis already agree on some fundamental common features, which can be summarized as follow:

1. There are dense local correlations with only few long range links, resembling a Small World network [6–10].

2. The distribution of the number of links is scale-free[7, 10], when measured with the appropriate resolution.

3. Brain networks are assortative, indicating a tendency for nodes with similar number of links to be directly connected [10–12].

4. Large positively correlated domains coexist with equally large anti-correlated non-local structures [14].

5. Large-scale correlated patterns (or their graphs counterpart) have been observed during subject execution of a task, as well as under “brain rest” conditions (absence of an overt stimulus) [10, 14, 15] and even under general anesthesia [19].

6. A portion of these observations cannot be explained by the brain's underlying “anatomical” connectivity [11].

Although there is at least one colloquial explanation for each of the points listed above, a single mechanistic explanation that satisfies all these observations at once is still lacking. This is already in itself an important theoretical deficit, but it is additionally highlighted by the fact that in certain brain dysfunctions some of these global properties are known to be affected[15, 20, 21].

As a starting point we ask here whether the brain resting state could be comparable to any known dynamical state. We have proposed that the brain stays near the critical point of a second order phase transition, where neuronal groups generate a diversity of flexible collective behaviors, due to the known abundance of metastable states at the transition. It is from this viewpoint, that the dynamics of brain resting might correspond to a critical state. This conjecture is tested here comparing fMRI brain resting state data from healthy subjects with a paradigmatic critical system, the Ising model [22]. This model has been the “fruitfly” for the development of concepts and techniques in statistical thermodynamics. It is chosen based on the qualitative similarities between some of its dynamics and the brain's fMRI spatiotemporal patterns which contain long-range correlations[10, 15–18] and a mixture of ordered and disordered structures. It must be noted from the outset that we are not suggesting that the brain's equation are isomorphic with those of the Ising model. Nevertheless, the results in this paper do suggest that important lessons can be learned from the striking similarities between the brain data and the dynamics emerging from the Ising model at critical temperature. The important point is that the numerical experiments here are not simulations prepared to replicate and further study a given experimental finding. To the contrary, the phenomenology to be discussed, is not written in any way in the model equations, nevertheless all the features listed above for the brain appear spontaneously in the Ising model near the critical temperature.

The paper is organized as follows. The next section is dedicated to describing the data from the brain and from the numerical simulations of the Ising model. Also it contains the steps used to extract the networks from both, brain and model time series. Section III contains the main finding organized as a side-by-side comparison of the statistical properties of the brain and Ising model networks. It is shown that key statistical and topological properties of the brain networks are intriguingly similar to those of the networks extracted from the Ising (only) at the critical temperature. Finally Section IV summarizes and discuss the relevance of these similarities and their biological significance in terms of brain functioning.

II. Experimental and Numerical Methods

In this work, two types of complex networks are analyzed in detail. The first network is derived from time series of brain fMRI images collected from healthy human volunteers. The second network is extracted from numerical simulations of the Ising model[22] in 2D. In both systems networks are defined in the same manner by linking sites with strongest correlations, often called “correlation networks”, as it will be explained in detail below.

A. The brain fMRI data

Functional magnetic resonance data was acquired using a 3T Siemens Trio whole-body scanner with echo-planar imaging (EPI) capability using the standard radio-frequency head coil (scanning parameters were as in [15]). Data used here correspond to five healthy females with ages ranging between 28 and 48 years old. They were all right-handed, and all gave informed consent to procedures approved by Northwestern University IRB committee. Participants were scanned following a typical brain resting state protocol [2], in which the subject is lying in the scanner and asked to keep their mind blank, eyes closed and avoid falling asleep. A total of 300 images are obtained spaced by 2.5 sec. in which the brain oxygen level dependent (BOLD) signal is recorded for each one of the 64×64×49 sites (so-called voxels of dimension 3.4375mm × 3.4375mm × 3mm). Typically, only 10% of those voxels correspond to brain activity, the type of time series used here. Preprocessing of BOLD signal was performed using FMRIB Expert Analysis Tool (FEAT, [23], http://www.fmrib.ox.ac.uk/fsl), involving motion correction using MCFLIRT; slice-timing correction using Fourier-space time-series phase-shifting; non-brain removal using BET; spatial smoothing using a Gaussian kernel of full-width-half-maximum 5mm.

B. The Ising model

The Ising model considers a lattice containing N sites and assumes that each lattice site i has an associated variable s_i, where s_i = +1 stands for an “up” spin and s_i = −1 for a “down” spin. A particular configuration of the lattice is specified by the set of variables s₁, s₂, …, s_N for all lattice sites. The energy in absence of external magnetic field is given by

$$E=-J\sum _{i,j=nn(i)}^N{s}_i{s}_j$$ (1)

where N = L×L, L is the size of the lattice, J is the coupling constant, and the sum over j run over the nearest neighbors of a given site i (nn(i)). As in almost all statistical mechanics models there exists a competition between thermal fluctuations (given by the interaction with the environment) that give the system a tendency to be disordered, and the interaction between particles (sites of the lattice) that tends to organize the system in some particular way that depends on the interaction or coupling between particles.

We implement the Metropolis Monte Carlo algorithm [24, 25] for the evolution of the Ising model in 2D with periodic boundary conditions. This algorithm takes into account that the system is in contact with a heat bath at temperature T. In this work, instead of working with asymptotic configurations and equilibrium averages, we deal with temporal series of single spin dynamics observed at a certain timescale. All simulations are implemented on a lattice of L = 200 and every time step corresponds to Δt = L × L Monte Carlo steps (which corresponds, on average, to running once over the entire lattice, giving each spin the possibility to flip). We take the Boltzman constant equal 1, J = 1, and after thermalization, we take 2000 lattice configurations (each separated by Δt), obtaining the dynamics of each spin ({s₁(t), s₂(t), …, s_N(t)} time series).

As mentioned in the introduction some of the key properties exhibited by the brain resemble the dynamics of the Ising model at the critical temperature T_c, where a transition between the ordered and disordered states takes place. At lower temperatures almost all the spins are aligned, while at temperatures above critical, spins are randomly distributed and the total magnetization is approximately zero. At the critical temperature T_c however, the system displays a fractal structure, with clusters of aligned spins of different sizes as well as long range temporal correlations. For the simulations discussed in the Results section a critical temperature T_c = 2.3 was used, a subcritical one of T = 2.0 and a supercritical temperature of T = 3. A final note concerns the choice of a lattice with nearest neighbors ferromagnetic interactions, considering that the brain is not a lattice and that includes inhibitory (i.e., anti-ferromagnetic) interactions. This is chosen deliberately as the worst case scenario ir order to demonstrate the higher significance of the critical dynamics over the structural connectivity of the model. We restricted ourselves to the discussion of the present Ising configuration, since the main results are connected with the critical state itself, however they are expected to be observed after changes in the connectivity and type of interactions, provided that the system is tuned near the critical state [26, 27].

C. Correlation Networks

In general terms, networks are collections of nodes joined by links. For certain systems, the nodes as well as the links are self evident and easily identifiable. This is not the case at hand, because in the brain both are part of the problem, where both the nodes and their interactions need to be uncovered from the data. Although there are “anatomical” templates that can be used to identify nodes, we choose here to approach the problem from the limit of maximum ignorance and use instead a data-driven strategy. The assumption is that the brain time series contain enough information to define the networks in a self-consistent manner. Since the correlations are computed from the time series collected from fMRI voxels, this approach is often called voxel-based brain functional networks. The current approach is in contrast with most recent related work[8, 9, 13, 28], where the network's nodes are predefined based on a priori knowledge, and only the possible links between these predefined nodes are determined. It will be seen that these differences per se can be responsible for conflicting results.

Here networks are defined by the correlations among the activity at each location (i.e., either a voxel in the case of the brain, or a lattice site in the Ising model). Thus the correlation coefficient, r, is used to measure the degree of linear dependence between all pairs of sites, as was done in [10]. The correlation coefficient between sites i and j is:

$$r(i,j)=\frac{\langle x_i(t)x_j(t)\rangle -\langle x_i(t)\rangle \langle x_j(t)\rangle }{\sigma (x_i(t))\sigma (x_j(t))},$$ (2)

where ${\sigma }^2(x_l(t))=\langle x_l^2(t)\rangle -{\langle x_l(t)\rangle }^2$, and x_l(t) is the BOLD signal of voxel l if we are studying the brain data, or the spin time series (of site l) from the Ising model. 〈.〉 represents averages taken over the length of the time series (300 and 2000 points for the brain and the Ising model, respectively).

Links between sites i and j are defined here whenever the correlation r(i,j) is greater or equal to a given threshold, ρ. The network's nodes are those sites with a non-zero number of links. That completes the definition of a network. Depending on the sign of ρ, two types of networks can be extracted. Those using a positive threshold ρ⁺ will be called positively correlated networks and those using a negative threshold ρ− negatively correlated networks. It is relevant to make this differentiation because anti-correlated dynamics are ubiquitous in the brain, as will be discussed latter.

The next section contains a side-by-side analysis of the positively and negatively correlated networks extracted from the brain and the Ising model.

III. Results

Networks are extracted from the data using the site-to-site temporal correlations. Fig. 1 shows the density distribution for the N(N − 1)/2 correlations (i.e., Eq. 2) computed between all pairs of time series of the brain (in Panel a) and the Ising model (in Panel b). In the case of the brain, the results from the five participants are plotted and for the Ising model, the densities correspond to correlations computed at three different temperatures: subcritical, critical and supercritical.

FIG. 1.

(Color online) Panel (a): Brain's fMRI correlation density distribution for each of the five control subjects recorded under resting conditions. Panel (b) Ising model correlation density distribution for T = 2 (green, dashed line), T = 2.3 (red, continuos line), and T = 3 (black, dot dashed line). Insets in both panels show the log-linear plot of the same density distributions.

A visual inspection shows that besides the differences in variance, which can not be expected to be equal, the densities for both brain and Ising model are distributed approximately equally. Both have a small skewness towards positive values, which it is more clearly seen in the insets using logarithmic scale. An important point to appreciate in Panel B of Fig. 1 is the well known increase in the variance of the correlations at the critical temperature. It is only near T_c that equally oriented spins coalesce in large domains thus generating the two sides of the distribution we observe here. In the brain, at any moment in time, in order to produce a given motor or cognitive behavior, of even during rest, similar dynamics occur: large regions of the brain activate in bulk at the same time that other regions de-activate. A remark here is that it is inconceivable to think about the brain's ongoing dynamics in any other way. Given the brain extensive connectivity, this balance in which a region is shutting down while another is excited is clearly the only possibility to avoid both total quiescence, in which the brain is shutdown, and massive excitation in which the entire cortex is fired up. Thus, while the reason for the distribution shown in Fig. 1a is trivial, it is not trivial how the brain does it, or in other words, which is the mechanism in place to maintain such balanced correlations [29].

A. Networks average statistical properties

Given the differences in correlation variance discussed above, a criterion needs to be established to compare brain and Ising networks. One proven to be useful is to scan a range of ρ thresholds while computing the average degree of the resulting networks. After that, a comparison can be made between networks of similar average degree. This is plotted in Fig. 2 as a function of ρ for positively correlated networks in panel (a) and for negatively correlated networks in panel (c). This is done for the brain data of the five subjects, and for the Ising data at three temperatures. Given the distributions in Fig. 1, it is clear that, as ρ grows, there are fewer connections, and consequently a smaller average degree, 〈k〉. Despite the expected difference in the value of ρ it can be seen that the parametric dependence of ρ and 〈k〉 in both brain and Ising networks allows us to confidently study and compare networks of a given 〈k〉.

FIG. 2.

(Color online) Average degree, 〈k〉, as a function of threshold ρ for positive (a) and negative (c) correlation networks. Variance of degree, ${\sigma }_k^2,$ as a function of 〈K〉 for positively (b) and negatively (d) correlated networks. The dashed black line (in panels b and d), corresponds to the expected behavior of a Poisson distribution. In all graphs the Ising model data at three temperatures T = 2, T = 2.3, and T = 3 is presented, as well as the data from the five subject's fMRI brain networks.

Next we looked at the degree variance, ${\sigma }_k^2=\langle k^2\rangle -{\langle k\rangle }^2$, plot as a function of the average degree in Fig. 2(b) and (d). Note that the brain and the Ising data at the critical temperature share a similar ${\sigma }_k^2-<k>$ functional dependence, a fact that suggest potential similarities between the degree distributions of the brain and Ising model at T_c, an aspect that will be explored in the next section. The dashed line corresponds to a Poisson distribution $({\sigma }_k^2=\langle k\rangle )$, indicating that none of the networks seems to obey a Poisson degree distribution.

Next we computed and compared some of the network's most basic properties. These include the network's clustering coefficient C, estimating the number of mutual connections, the average path length L, defining the average number of steps along the shortest paths for all possible pairs of network nodes. Another property is the diameter D, which is defined as the maximal distance between any two nodes in the network. Also similar properties C_ran, L_ran, D_ran are computed for an equivalent random network rewired as described in [31]. Table I contains the results of these calculations for networks defined with a positive ρ and Table II the results for negatively correlated networks. The Ising data correspond to the already described generated networks at different temperatures, and the brain network corresponds to the subject whose correlation is plotted with dashed line in Fig. 1 (Internal Code Subject01). In all cases, we impose similar 〈k〉, by choosing the appropriate ρ value given by the results in Fig. 2 a and c.

TABLE I.

Average statistical properties of the positively correlated brain and Ising networks.

Ising network
T	ρ+	N	〈k〉	C	L	D	Cran	Lran	Dran
2.0	0.1	40000	133	0.065	2.72	4	0.0054	2.61	4
2.3	0.3	40000	127	0.516	6.83	31	0.048	2.71	5
3.0	0.09	40000	128	0.064	2.73	4	0.0034	2.65	4
Brain network
	0.623	26985	128	0.4536	4.4	13	0.061	2.62	5

TABLE II.

Average statistical properties of the negatively correlated brain and Ising networks.

Ising network
T	ρ−	N	〈k〉	C	L	D	Cran	Lran	Dran
2.0	-0.0575	29370	26	0.0105	3.24	5	0.013	3.38	8
2.3	-0.38	4784	26	0	4.17	13	0.095	2.95	7
3.0	-0.105	40000	23	0.00003	3.72	6	0.0007	3.7	6
Brain network
	-0.71	1684	27	0	3.54	11	0.14	2.69	5

The most remarkable result in Table I is the fact that the Ising model network become small world only at T_c. As expected by the divergence of correlations at criticality, the diameter of the network is seen here to grow from a few nodes to a length towards the lattice maximum (i.e., ∼ $\sqrt{{(L/2)}^2+{(L/2)}^2}$). At the same time, the average minimum path L only doubles. Also, it is only at criticality that the clustering coefficient, which is descriptive of the “local” connectivity, grows several orders of magnitude compared with either sub or supercritical networks. It is interesting to realize that the network became small world at T_c, not by adding short cuts to a previously ordered lattice, as in the Watts & Strogatz [32] scenario. Instead, here it seems as if the disordered small blobs coalesce (or group) at T_c producing an increase of C while increasing the D and maintaining the same L. The other important point to remark on here is the fact that a purely dynamical property (i.e., criticality) is able to dramatically change the network properties. This has deep relevance to brain function, since these emergent properties are directly related to the efficiency of information transport in the network [33, 34]. Turning to the brain data in Table I, it can be seen that it compares well with the Ising data at T_c, and also that it is a small world network, something reported earlier for subjects performing minimal tasks [10]. The data also agree extremely well with a very recent report for resting state networks[7]. Compare, for instance, Fig.3 (c) and (d) in [7] with Fig.3 here.

FIG. 3.

(Color online) Normalized network clustering (Panel a) and path length (Panel b) as a function of average degree. Solid lines denote results for the Ising model at T_c and dashed lines the results for the brain.

The properties of negatively correlated networks necessarily mirror the networks already discussed, with one important exception. Considering the Ising model for description sake, in the negatively correlated network edges connect spins of opposite signs. Thus the clustering coefficient C is by definition zero since two spins mutually opposite are necessarily similar. For the case of the brain, of course, although the details are different the mechanics are the same.

Of course the above mentioned results depend on the values of chosen 〈k〉. Nevertheless, we have verified that at least in the range of 〈k〉 < 130 the correspondence between the Ising model at T_c and the brain data continues. As the mean degree 〈k〉 increases the clustering increases and the average path length diminishes, mainly because we are adding connections to the network. A similar dependence of these average statistical quantities on 〈k〉 was recently reported in [7] for positively correlated brain fMRI networks. To summarize the dependence of these quantities on 〈k〉, Fig. 3, shows the normalized clustering, γ = C/C_ran (panel (a)), and average path length, λ = L/L_ran (panel (b)), as a function of mean degree (〈k〉). For the positively correlated networks, the relative large values of γ together with relatively small λ indicate that both networks display small world properties. For the negatively correlated network, the clustering is zero (γ = 0), and λ is near one and notoriously almost insensitive to 〈k〉.

The results described so far show that the dynamics of the Ising model at T_c as captured by the correlation networks exhibit average statistical properties resembling those observed in the brain networks at resting conditions. In the next section, the extent of these similarities is further expanded to other network topological features.

B. Degree distribution and degree correlations

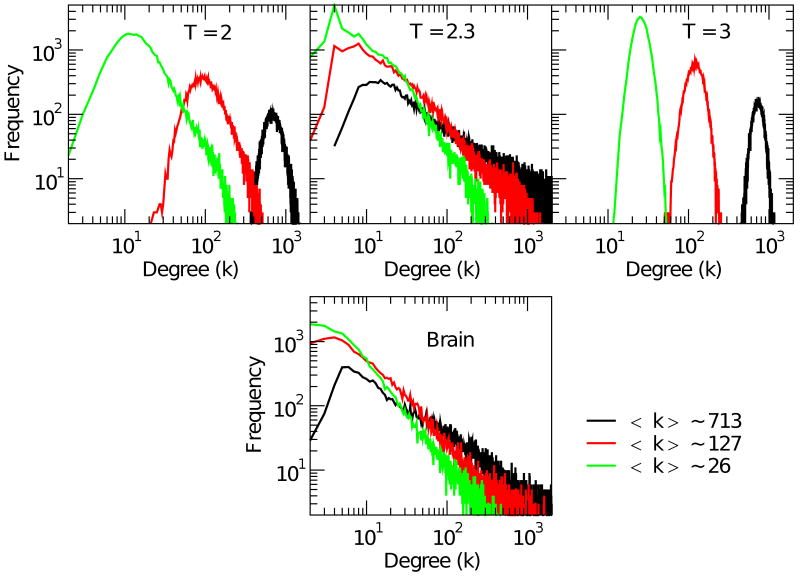
In this section we analyze the distribution of the networks edges and their mutual correlation. First we analyze and compare the degree distribution P(k), shown in Fig. 4. The plots in the top three graphs correspond to the degree distribution for the Ising model at the three temperatures. Each of the three curves in each graph corresponds to networks with average degree 〈k〉 ≈ 26, 127 and 713 imposed by choosing appropriate values of ρ⁺ as done before. The bottom graph in Fig. 4 shows the degree distribution for the brain network. As anticipated, the networks extracted from the Ising model show a dramatic change at T_c. At criticality the degree distribution exhibits a long tail that persists for all 〈k〉 explored. The power law exponent of the degree distribution and the 〈k〉 are connected, which is not surprising. The bottom panel shows the same analysis for the brain network, which exhibits all the relevant features seen for the Ising model at T_c. Besides the agreement on the gross features of the distribution, it is even possible to identify, a noticeable maximum at k = 4 (or k = 6 in the brain), which is trivially related to the number of the nearest neighbors (this is especially notorious at relatively large ρ⁺, see for instance Fig. 2 of Eguiluz et al. [10]). The power law behavior in the tail of the degree distribution for positive correlation networks was already reported in brain fMRI of human subjects performing minimal attention task [10] and recently in an extensive study in subjects during resting state [7].

FIG. 4.

(Color) Degree distribution for positively correlated networks. Top three panels depict the degree distribution for the Ising networks at T = 2, T = 2.3 and T = 3 for three representative values of 〈k〉 ≈ 26, 127, and 713. Bottom panel: Degree distribution for positively correlated brain network for the same three values of 〈k〉.

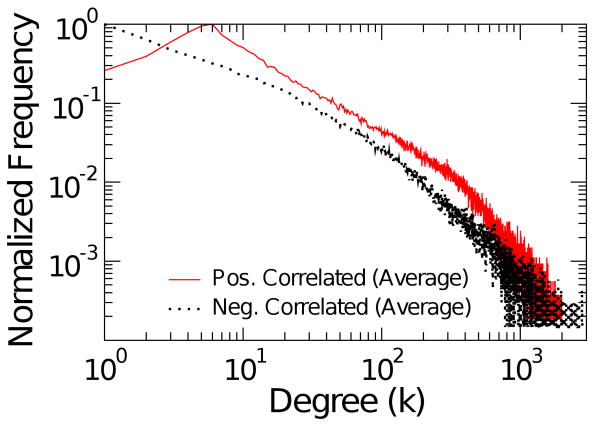
Turning the attention to the negatively correlated networks, in Fig.5 the degree distribution is shown for three temperatures and two values of 〈k〉 ≈ 49, 127 and 277. As seen before with other network features, there is also a qualitative change at T_c in the tail of the degree distribution which follows a power law. The bottom panel of Fig.5 shows the degree distribution for the brain negative correlation network which presents similar features as those seen in the Ising at T_c. The average for five subjects is shown in Fig. 6.

FIG. 5.

(Color) Degree distribution for negatively correlated networks. Top three panels depict the degree distribution for the Ising networks at T = 2, T = 2.3, T = 3 respectively for two representative values of 〈k〉 ≈ 49,127 and 277. Bottom panel: Degree distribution for negatively correlated brain network for the same three values of 〈k〉.

FIG. 6.

(Color online) Brain network's average degree distribution computed from five volunteers for 〈k〉 ≈ 127.

In some complex networks, a node's degree and its neighbors' degree can be related. The correlation between node degree and neighbor degrees, as well as the dependence of other measures on a node's degree are investigated in Fig. 7. The bottom panels of Fig. 7 illustrate the relation between the clustering, C(k), and the degree for positively correlated networks. In can be seen that for the most part C(k) is independent of k in both the brain and the Ising model networks at T_c.

FIG. 7.

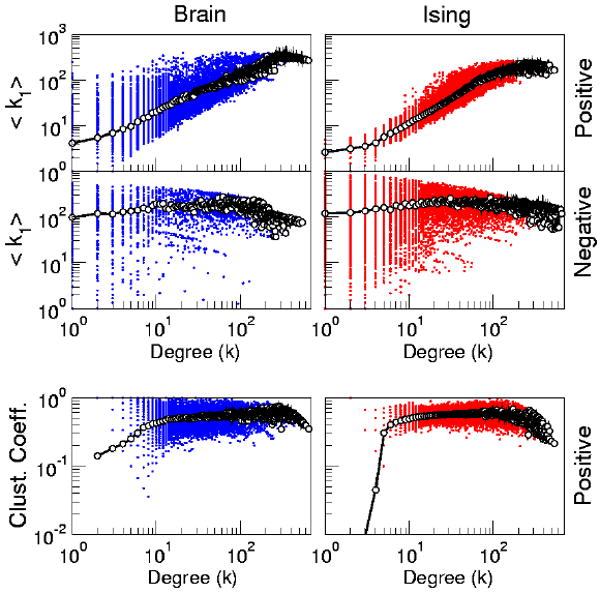
(Color online) Top four panels: Neighbor Degrees Correlation. Plot of the nearest neighbor degree, 〈k₁〉, as a function of own degree k for the two type of networks extracted from the brain (left) and from the Ising model at T_c (right). Bottom panels: Clustering, C, as a function of the degree k for positively correlated networks extracted from the brain (left) and from the Ising model at T_c: In all plots dots represent individual nodes, and empty circles joined by lines represent averages. Positively correlated networks correspond to 〈k〉 ≈ 26 and negatively correlated network correspond to 〈k〉 ≈ 49.

The top four panels of Fig. 7 compare the nearest neighbor degree, 〈k₁〉, as a function of own degree k for the two types of networks extracted from the brain and from the Ising model at T_c. In both positively correlated networks one can see the so called assortative property, by which highly connected nodes tend to be connected with highly connected neighbors. The presence of this feature, first described in Eguiluz et al[10], can now be understood considering that is linked with the dense domains of equally oriented spins (or voxels). Sites located deep into the bulk of the domain then will have a larger degree, and by the same reasoning sites located in the domain's periphery will result in nodes with smaller degree. Then the assortative property is, in this context, trivially related to the geographical location of each node. This is not the case in the negatively correlated networks, since nodes are located distant from each other, (see Fig. 8) resulting in the degree independence shown in Fig. 7.

FIG. 8.

(Color online) Typical brain (top) and Ising (bottom) correlation profiles. Correlations (i.e., Eq. 2.) are computed between the site with the largest degree and the rest of the time series and plotted at its respective normalized distance

The same reasoning can reconcile apparently conflicting results (reviewed in[35]), in which brain network degree distributions were found not to be scale free. In this work the fMRI time series inside relatively large predefined cortical areas were first averaged. Then the correlation between these averages (a few dozen for the entire brain) were used to define the networks. From the discussion above it is clear that the averages remove the main source of the long tails we observe here. The local averaging precludes the possibility of observing these details. A gross comparison would be the effect of recalculating the degree distribution of the United States' airline traffic, which is known to be scale free, by no longer considering airports as its nodes, but rather averaging traffic between entire states. Of course, this averaging obscures the hubs and prevents the observation of such scales.

In passing it should be mentioned that a discussion of the relevance of this spatial aspect over spurious clustering coefficients was reported recently [36] for networks constructed from pressure levels representative of the general circulation (wind flow) of the atmosphere.

C. Back to plain correlations

Previous sections demonstrate striking similarities between the correlation properties of the brain and the Ising model at T_c. This was done comparing the correlation networks, a technique that as commented in the introduction allows for a compact description. However, to be consistent those similarities should be evident by looking at plain correlations as discussed next.

In previous work we reported already that on the average correlations in the brain decay very slowly with distance[10]. We revisit this aspect here both for the brain and the Ising model. This is shown in Fig. 8. The first observation is that significant correlations extend to the length of the system. Near the origin, there is a notorious bias toward positive correlations, followed by a somewhat rough landscape of both positive and negative correlations. In the case of the brain, the peaks of this landscape reveal areas with common anatomical and (probably) functional properties.

It is important to recognize that the valleys of negative correlation may or may not be related to negative interactions. Since there are no negative interactions in Eq. 1, it is clear that in the Ising model the emergence of significant negative correlations is a collective effect arising only at the critical point. In the brain the situation is not that clear. Nevertheless there is a pervasive preference to link anti-correlated dynamics with negative interactions. For instance it is commonly heard that “In the human brain, neural activation patterns are shaped by the underlying structural connections that form a dense network of fiber pathways linking all regions of the cerebral cortex” [11]. This mind set, which equates dynamics with structure, is so entrenched in brain science that it always seems reasonable to search for the connections responsible for any given dynamical pattern. The results discussed here suggest that as a change in the temperature can lead to the emergence of correlations in a substrate that lacks such ability, the brain cortex can be operating in the same way. In fact the puzzle of how the brain can be highly coherent over long lengths have prompted some authors to postulate even non-classical explanations, while the results here seems to suggest that if the brain is at criticality such coherence can be achieved naturally.

The second observation is that the fraction of sites which have positive correlations is about the same as the fraction of sites with negative correlations. Again, this feature can be easily understood for the Ising model at criticality but it is hard to reconcile for the brain, unless a critical scenario is invoked. This finding might have deep implications. For instance, we have recently reported[15] that although such a balance is maintained in healthy individuals, it is disrupted in some pathologies. Specifically, the disruption found is a reduction of the number of anti-correlated sites, compared with normal conditions, somewhat analogous to subcritical temperatures in the Ising model, a situation dominated by equally oriented domains.

D. Brain Functional Connectivity vs Collectivity

Probably is worth to place the present results in the context of current brain imaging approaches. The literature specialized on the analysis of brain neuro-imaging time-series includes a very productive chapter of functional connectivity dedicated to formalize findings on a cohesive picture. Three basic concepts in this area are: brain functional connectivity effective connectivity and structural connectivity [37–39]. The first one “is defined as the correlations between spatially remote neurophysiological events” [37]. Per se, the definition is a statistical one, and “is simply a statement about the observed correlations; it does not comment on how these correlations are mediated”[37]. The second concept, effective connectivity is closer to the notion of a neuronal connection and “is defined as the influence one neuronal system exerts over another”. Finally the concept of structural or anatomical connectivity refers to the identifiable physical or structural (synaptic) connections linking neuronal elements.

These three concepts, intentionally or not, emphasize the connection between brain elements. And it is despite of cautionary comments emphasizing explicitly that “depending on sensory input, global brain state, or learning, the same structural network can support a wide range of dynamic and cognitive states”[39]. In this regard, the present results are specific examples of the emergence of nontrivial collective states over an otherwise trivial regular lattice (i.e. the Ising's structural connectivity). It is clear that if the Ising's collective states have a counterpart in the brain they can not be adequately described in the framework of connectivity, rather it would be more appropriate to define another framework in terms of brain functional collectivity, already discussed in related terms elsewhere[40, 41]. A pedestrian starting point, would be to review instances in which the data from the brain structural connectivity and the functional correlations disagree, as indications of collective phenomena.

IV. Summary and Discussion

In this work statistical properties of brain correlation networks have been compared with those of networks derived from the 2D Ising model. The main finding here is that at the proper temperature Ising networks and brain networks are undistinguishable from each other. Their main topological properties and even more refined features of network structure including degree distribution, neighbor degree and clustering correlations with own degree, all behave in the same manner.

The biologically most relevant lesson is related to the well known central result in critical phenomena. Namely that the dynamics of a system near a critical point include spatiotemporal patterns correlated and anti-correlated over long distances, despite having only nearest neighbor positive interactions. The similarities exposed by the comparison made in this paper suggest that collective dynamics with similar mechanics are present in the brain.

Nevertheless, the main point is not that a simple model completely orphan of neural details is able to replicate the experimental observations. The main point is that the model gets the correct phenomenology without explicitly plugging components for such phenomenology into its equations. Whatever ends up replicating the observations, it is a collective effect that only happens at a certain temperature. Naturally, this runs against common sense in brain science because, as discussed in previous sections, the prevailing mind set implies that if two brain regions act in some coherent way, there must be a direct connection between them. Thus, this commonly held view seems to see the brain as a low temperature Ising system and as such often explains long distance correlations with an underlying physical connection or deactivation by inhibitory connections. This is in analogy with the correlations among spins at low T which are ruled only by the underlying Ising connectivity, meanwhile at the critical temperature, the system displays long distance correlations and anticorrelations (i.e.,“functional connections”) even when the connectivity is only ferromagnetic and to nearest neighbors.

The above discussion suggests that it might be worth to study the consequences of relatively broad and completely unspecific factors over brain dynamics. The suggestion is that some types of global changes (e.g., mood, arousal, attention, etc) might be brought about in the same way that fluctuation in the coherent domains arise at the critical temperature in critical systems. Despite the relative abundance of approaches, including sophisticated ones, as far as we know, no neural model relies solely on this kind of dynamical transition as a mechanism to produce different behaviors. While there are several neural models that exhibits criticality, yet there is no model whose “output” can be related with something even remotely connected with animal mood, actions or behavior. Thus, despite its attractiveness, it need to be recognized that criticality has not yet been shown to increase the animal behavioral repertoire by virtue of its abundance of metastable states.

In summary we have compared networks derived from the fMRI signal of human brains with similar networks extracted from the Ising model. We found that near the critical temperature the two networks are indistinguishable from each other for most relevant statistical properties. These results are interpreted here as lending support to the conjecture that the dynamics of the functioning brain is near a critical point.

V. Appendix

A. Ising Model

In the Ising model we consider a lattice containing N sites and assume that each lattice site i has associated with a number s_i, where s_i = +1 for an “up” spin and s_i = −1 for a “down” spin. A particular configuration of the lattice is specified by the set of variables s₁, s₂, …, s_N for all lattice sites. The energy in absence of external magnetic field is given by

$$E=-J\sum _{i,j=nn(i)}^N{s}_i{s}_j$$ (3)

where N = L×L is the size of the lattice, J is the coupling constant and the sum over j run over the nearest neighbors of a given site i (nn(i)). Here we implemented the Metropolis Monte Carlo algorithm [24, 25] to solve the Ising model, which take into account that the system is in contact with a heat bath at temperature T. The algorithm can be summarized as follow:

1. Establish a initial configuration (i.e. all spins random).

2. Choose a spin at random and flip it.

3. Compute the change in energy ΔE = E_trial − E_old due to the flip.

4. If ΔE ≤ 0 accept the change and keep the new configuration of the lattice.

5. If ΔE > 0 compute the transition probability w = e^−ΔE/kT.

6. Generate a random number r in the unit interval.

7. If r ≤ w accept the change and keep the new configuration of the lattice. Otherwise, keep the previous configuration

8. Go to 1.

With this method we generate asimptotically configurations with the desired Boltzman probability. In the present simulations, a lattice of L = 200 (N = 200×200 nodes) was used and every time step corresponds to a single flip spins. We take k = 1 (Boltzman constant) and J = 1. We termalized the system (letting the system goes to configurations according to the temperature T) over N_equil = 10⁸ time steps. After that, we chose N_time = 2000 configurations every N_sample = L×L = 10⁴ steps (which corresponds, on average, to run over the entire lattice given the possibility to each spin either flip or not). The observables used to analyze the system are the temporal series of each one of the spins of the lattice (s_i = ±1).

B. Networks definitions

As was specified in section II-C, i.e., networks are constructed as previously[10] by computing linear correlations between temporal series of all pairs of voxels (sites) and connecting them with a link if correlations were greater of a given threshold ρ⁺ (positive correlation networks) or lower than a given negative threshold (ρ⁻). Following this procedure, a list of connected pairs is obtained in both cases which define the functional complex networks analyzed further. An undirected graph[34], (as is the case we use in this work) G(N, L) consist of two sets N and L such that N ≠ and L is a set of unordered pairs of elements of N. The elements of N = n₁, n₂, …, n_N are the nodes (or vertices, or points) of the graph G, while the elements of L = (l₁, l₂, …, l_K) are its links (or edges, or lines). It is often useful to consider a matricial representation of a graph. A graph G = (N, L) can be completely described by giving the adjacency (or connectivity) matrix A, a N×N square matrix whose entry a_ij = (i,j = 1, …, N) is equal to 1 when the link l_ij exists, and zero otherwise.

What follows are the usual definitions for the network properties:

1. Degree

The degree k_i of a node i is the numbers of direct connections or links that emerge of a given node, an can be defined in terms of the adjacency matrix as:

$$k_i=\sum _j{a}_{ij}$$ (4)

A basic representation of a graph G can be obtained in terms of the degree distribution P(k), which is defined as the probability of a node chosen uniformly at random has degree k, or as the fraction of nodes of the network having degree k. The n-moment of the distribution is defined as

$$<k^n>=\sum _k{k}^{n}P(k)$$ (5)

The first moment of the distribution is the mean degree of the network. The second moment measures the fluctuations in the network connectivity.

2. Average Path length and Diameter

The ability of a network to propagate information will depend of separation among nodes. If the shortest path between nodes i and j is represented by the quantity d_ij, a measure of the typical separation between two nodes in the graph is given by the average shortest path length, also known as characteristic path length, defined as the mean of geodesic lengths over all couples of nodes [32]:

$$L=\frac{1}{N(N-1)}\sum _{i,j,i\ne j}{d}_{ij}.$$ (6)

The maximum value of d_ij is called the diameter of the network. In this work, we use the breadth-firth method [43] to numerically estimate d_ij.

3. Clustering coefficient

The clustering coefficient is a measure of how well connected are the neighbors of a given node, and is an indication of local connectivity of the network. It can be defined as in [32], denoting the clustering coefficient of node i, c_i, as the number of connections between all neighbors of node i, e_i, divided as the total number of possible links, k_i(k_i − 1)/2,

$$c_i=\frac{2e_i}{k_i(k_i-1)}=\frac{{\sum }_{j,m}{a}_{ij}{a}_{jm}{a}_{mi}}{k_i(k_i-1)}$$ (7)

Then, the clustering coefficient C is the average of c_i,

$$C=<c_i>=\frac{1}{N}\sum _i{c}_i$$ (8)

4. Nearest Neighbor degree

The degree distribution completely determines the statistical properties of uncorrelated networks. However, a large number of real networks are correlated in the sense that the probability that a node of degree k is connected to another node of degree, say k₁ depends on k. In these cases, it is necessary to introduce the conditional probability P(k/k₁), being defined as the probability that a link from node of degree k points to a node of degree k₁. Although the degree correlations are formally characterized by P(k/k₁), the direct evaluation of the conditional probability gives extremely noisy results for most of real networks because of their finite size N [34]. This problem can be overcome by defining the average nearest neighbors degree of a node i as

$$k_{nn,i}=\frac{1}{k_i}\sum _j{k}_j=\frac{1}{k_i}\sum _{j=1}^N{a}_{ij}{k}_j$$ (9)

where the sum runs on the set of first neighbors of i.

Correlated networks are classified as assortative if k_nn(k) is an increasing function of k, whereas they are referred to as disassortative when k_nn(k) is a decreasing function of k [44]. In other words, in assortative networks the nodes with similar degree tend to connect each other, while in disassortative networks nodes with low degree are more likely connected with highly connected ones.

5. Randomization

The randomization consisted in perform a random sort of all links, keeping fix the number of nodes, N, the number of links, l, and the degree of each node, k.